Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method

Liu, Xingxia; Zhang, Lijun; Sun, Jianan

doi:10.3390/sym16040438

Open AccessArticle

Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method

by

Xingxia Liu

^1,*,

Lijun Zhang

¹ and

Jianan Sun

²

¹

School of Electronic Information and Electrical Engineering, Tianshui Normal University, Tianshui 741000, China

²

College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China

^*

Author to whom correspondence should be addressed.

Symmetry 2024, 16(4), 438; https://doi.org/10.3390/sym16040438

Submission received: 5 February 2024 / Revised: 27 March 2024 / Accepted: 1 April 2024 / Published: 5 April 2024

(This article belongs to the Section Physics)

Download

Browse Figures

Versions Notes

Abstract

:

By employing the cubic B-spline functions, a collocation approach was devised in this study to address the Modified Regularized Long Wave (MRLW) equation. Then, we derived the corresponding nonlinear system and easily solved it using Newton’s iterative approach. It was established that the cubic B-spline collocation technique exhibits unconditional stability. The dynamics of solitary waves, including their pairwise and triadic interactions, were meticulously investigated utilizing the proposed numerical method. Additionally, the transformation of the Maxwellian initial condition into solitary wave formations is presented. To validate the current work, three distinct scenarios were compared against the analytical solution and outcomes from alternative methods under both

L_{2}

- and

L_{\infty}

-error norms. Primarily, the key strength of the suggested scheme lies in its capacity to yield enhanced numerical resolutions when employed to solve the MRLW equation, and these conservation laws show that the solitary waves have time and space translational symmetry in the propagation process. Finally, this paper concludes with a summary of our findings.

Keywords:

numerical simulations; MRLW equation; solitary waves; collocation method; cubic B-splines

1. Introduction

Nonlinear partial differential equations are of great importance in elucidating various phenomena in all sorts of fields. However, exact solutions are not available for all such equations. Thus, it is necessary to employ different numerical methods to explore their possible solutions.

The form of a regularized long wave (RLW) equation is as follows:

u_{t} + u_{x} + δ u u_{x} - μ u_{x x t} = 0,

(1)

The equation, characterized by the positive parameters

δ

and

μ

, was initially put forth by Peregrine [1] to illustrate the dynamics of an undular bore, according to the symmetry and conservation law of time translation. He pioneeringly employed the finite difference method to formulate the first numerical approach for solving the RLW equation. This equation specifically encompasses events characterized by slight nonlinearity and dispersion, such as the nonlinear lateral waves occurring in shallow waters, ion-acoustic and magnetohydrodynamic disturbances within plasmas, and phonon propagations in nonlinear crystalline structures. This equation’s existence and singularity were identified by Refs. [2,3] in 1973. Later, Refs. [4,5,6,7,8,9,10] and other scholars contributed to the topic by exploring its numerical resolutions from the perspectives of the finite difference and finite element method.

So far, a multitude of numerical approaches, such as finite element methods and analytical solution strategies, have been proposed for addressing the RLW equations. According to references [11,12,13,14,15], the finite difference approaches and finite element methodologies like collocation methods that utilize quadratic, cubic, and up-to-date septic B-splines have been employed to resolve the RLW equation. Indeed, the RLW equation is a special case of the generalized long wave (GRLW) equation that has the following form:

u_{t} + u_{x} + δ u^{p} u_{x} - μ u_{x x t} = 0,

(2)

This equation is characterized by a positive integer

p

in this paper. The Generalized Regularized Long Wave (GRLW) equation has attracted little attention from researchers, with Zhang [16] exploring it through a finite difference approach to addressing a Cauchy problem and Kaya [17] employing the Adomian Decomposition Method (ADM). This work, however, delves into a distinct variant of the GRLW equation known as the Modified Regularized Long Wave (MRLW) equation. Numerical resolutions for the MRLW equation have been developed using various techniques. The finite difference method was utilized in [18], while [19,20] applied collocation methods with quintic B-splines. In a separate study, Refs. [21,22,23] employed cubic B-splines for the same purpose. The cubic B-spline Galerkin finite element method was then adopted to derive numerical solutions in [24,25,26]. The authors discuss the mixed finite element method for solving a coupled wave equation in [27] and for solving a damped Boussinesq equation in [28].

In this scheme, we continue to use the cubic B-splines for the same purpose, but we focus on temporal discrete values with a half time layer, and it is found that our scheme has better accuracy and stability than that presented in [20] for three solitary waves and for Maxwellian pulse splitting in the numerical simulation, indicating that our scheme satisfies the conservation laws perfectly.

In this study, a cubic-B-spline-based collocation technique was employed to address the MRLW equation. Section 2 details the collocation approach employed for resolving this equation, while Section 3 presents an examination of the method’s linear stability. To validate its precision, analytical solutions and conservation laws are utilized in the assessment process. The dynamics of solitary waves, including their interactions and the transformation of Maxwellian initial conditions into solitary waves, are investigated through numerical simulations in Section 4. Finally, conclusions are drawn in the closing section.

2. Governing Equation and Cubic B-Spline Collocation Method

The MRLW equation is expressed as follows:

u_{t} + u_{x} + 6 u^{2} u_{x} - μ u_{x x t} = 0

(3)

Here, the notations

x

and

t

symbolize differentiation, with the equation subject to boundary conditions characterized by

u \to 0

as

x \to \pm \infty

. For the scope of this research, periodic boundary conditions are adopted within the domain

a \leq x \leq b

under examination.

\begin{array}{l} u (a, t) = u (b, t) = 0, \\ u_{x} (a, t) = u_{x} (b, t) = 0 . \end{array}

(4)

The analytical solution of this equation can be written as

u (x, t) = \sqrt{c} sech (p (x - (c + 1) t - x_{0})),

(5)

where

p = \sqrt{\frac{c}{μ (c + 1)}}

, and

x_{0}

and

c

are arbitrary constants.

Partition the interval [a,b] at points by

x_{j}

, where

a = x_{0} < x_{1} < \dots < x_{N} = b

Here,

h = x_{j + 1} - x_{j} = \frac{b - a}{N}

,

j = 0, \dots, N - 1

. Let

{B_{j}}_{j = - 1}^{N + 1}

the knot points denoted by

x_{j}

; the cubic B-splines collectively constitute a foundation of functions that span across the interval [a, b]. A global approximation solution

u_{N} (x, t)

is expressed in terms of the cubic B-splines and unknown time-dependent parameters as follows:

u_{N} (x, t) = \sum_{j = - 1}^{N + 1} c_{j} B_{j} (x)

(6)

Here,

c_{j}

denotes unforeseen time-varying entities that are to be derived through the collocation approach, considering the constraints of boundary and initial conditions.

The cubic-B spline functions are as follows.

B_{j} (x) = \frac{1}{h^{3}} \{\begin{cases} {(x - x_{j - 2})}^{3}, x \in [x_{j - 2}, x_{j - 1}], \\ h^{3} + 3 h^{2} (x - x_{j - 1}) + 3 h {(x - x_{j - 1})}^{2} - 3 {(x - x_{j - 1})}^{3}, x \in [x_{j - 1}, x_{j}], \\ h^{3} + 3 h^{2} (x_{j + 1} - x) + 3 h {(x_{j + 1} - x)}^{2} - 3 {(x_{j + 1} - x)}^{3}, x \in [x_{j}, x_{j + 1}], \\ {(x_{j + 2} - x)}^{3}, x \in [x_{j + 1}, x_{j + 2}], \\ 0, otherwise . \end{cases}

By employing Equation (6), the estimation of nodal values

c_{j}

, along with the first and second derivatives

c_{j}^{'}

and

c_{j}^{″}

at the nodal points, can be readily derived.

\begin{array}{l} u_{j} = c_{j - 1} + 4 c_{j} + c_{j + 1}, \\ u_{j}^{'} = \frac{3}{h} (c_{j - 1} - c_{j + 1}), \\ u_{j}^{″} = \frac{6}{h^{2}} (c_{j - 1} - 2 c_{j} + c_{j + 1}) . \end{array}

(7)

Let us write the MRLW equation in the following form:

\frac{\partial (u - μ u_{x x})}{\partial t} + u_{x} + 6 u^{2} u_{x} = 0 .

(8)

Following the method used by S.I. Zaki [21] to solve the the KdVB equation, we adapt his technique to derive a recursive formula for numerically resolving Equation (8), with the temporal focus set at

(n + \frac{1}{2}) Δ t

. Here,

Δ t

represents the time interval, and we employ a Crank–Nicholson methodology:

{(u_{t})}^{n + \frac{1}{2}} = \frac{u^{n + 1} - u^{n}}{Δ t},

(9)

{(u)}^{n + \frac{1}{2}} = \frac{u^{n + 1} + u^{n}}{2},

(10)

{(u^{2} u_{x})}^{n + \frac{1}{2}} = \frac{{(u^{2} u_{x})}^{n + 1} + {(u^{2} u_{x})}^{n}}{2},

(11)

Here, the notations n and n + 1 denote the chronological sequence of time steps. These computations correspond to second-order precise estimations of the values occurring at the specific time instance. Then, Equation (8) becomes

(u^{n + 1} - μ u_{x x}^{n + 1}) - (u^{n} - μ u_{x x}^{n}) + \frac{Δ t}{2} (u_{x}^{n + 1} + u_{x}^{n}) + 3 Δ t ({(u^{2} u_{x})}^{n + 1} + {(u^{2} u_{x})}^{n}) = 0,

(12)

Introducing Equation (7) into Equation (12) yields

\begin{array}{l} {a_{j}}^{n + 1} - \frac{6 μ}{h^{2}} {b_{j}}^{n + 1} + \frac{3 Δ t}{2 h} {c_{j}}^{n + 1} + \frac{9 Δ t}{h} ({({a_{j}}^{n + 1})}^{2} {c_{j}}^{n + 1}) \\ = {a_{j}}^{n} - \frac{6 μ}{h^{2}} {b_{j}}^{n} - \frac{3 Δ t}{2 h} {c_{j}}^{n} - \frac{9 Δ t}{h} ({({a_{j}}^{n})}^{2} {c_{j}}^{n}), \\ j = 0, 1, \dots, N . \end{array}

(13)

where

{a_{j}} = c_{j - 1} + 4 c_{j} + c_{j + 1}, {b_{j}} = c_{j - 1} - 2 c_{j} + c_{j + 1},

{c_{j}} = c_{j - 1} - c_{j + 1}, j = 0, 1, \dots, N .

The system that emerges from Equation (13) is of a nonlinear nature. It can be effectively addressed through Newton’s iterative approach, typically achieving convergence after just two iterations.

3. Linear Stability Analysis

In order to examine the equilibrium stability of Equation (13) when linearized, we employ the Von Neumann methodology. The nonlinear term

u^{2} u_{x}

is linearized by using u as a constant

σ

. Let

c_{j}^{n} = q^{n} e^{i k j h}

; by incorporating this into Equation (13), we obtain

\begin{array}{l} q^{n + 1} [(e^{i k h} + 4 + e^{- i k h}) - \frac{6 μ}{h^{2}} (e^{i k h} - 2 + e^{- i k h}) + (\frac{3 Δ t}{2 h} + \frac{9 Δ t σ^{2}}{h}) (e^{i k h} - e^{- i k h})] e^{i k j h} \\ = q^{n} [(e^{i k h} + 4 + e^{- i k h}) - \frac{6 μ}{h^{2}} (e^{i k h} - 2 + e^{- i k h}) - (\frac{3 Δ t}{2 h} + \frac{9 Δ t σ^{2}}{h}) (e^{i k h} - e^{- i k h})] e^{i k j h}, \end{array}

After some manipulations, the following can be obtained:

q^{n + 1} = \frac{[(2 \cos (k h) + 4) - \frac{6 μ}{h^{2}} (2 \cos (k h) - 2) - i (\frac{3 Δ t}{h} + \frac{18 Δ t σ^{2}}{h}) \sin (k h)]}{[(2 \cos (k h) + 4) - \frac{6 μ}{h^{2}} (2 \cos (k h) - 2) + i (\frac{3 Δ t}{h} + \frac{18 Δ t σ^{2}}{h}) \sin (k h)]} q^{n},

The amplification factor is given by

e^{α k} = \frac{a - i b}{a + i b},

(14)

where

a = 2 \cos (k h) + 4 - \frac{6 μ}{h^{2}} (2 \cos (k h) - 2),

b = (\frac{3 Δ t}{h} + \frac{18 Δ t σ^{2}}{h}) \sin (k h) .

From Equation (13), we can deduce that

|e^{α k}| = 1

for all values of k.

So, this scheme is unconditionally stable.

4. Numerical Examples and Results

Evaluating numerical methods for evolutionary equations involves validating specific characteristics; these methods must faithfully reproduce the chronological evolution of solitary wave behavior. Throughout their propagation, the solution must maintain compliance with equivalent conservation principles. The accuracy in the movement of solitary waves can be objectively measured through the calculation of both the

L_{2}

-error norm

L_{2} = {‖u^{e x a c t} - u_{N}‖}_{2} = \sqrt{h \sum_{j = 0}^{N} {|u_{j}^{e x a c t} - {(u_{N})}_{j}|}^{2}},

(15)

and

L_{\infty}

-error norm

L_{\infty} = {‖u^{e x a c t} - u_{N}‖}_{\infty} = \max_{j} |u_{j}^{e x a c t} - {(u_{N})}_{j}| .

(16)

Equation (3) has the following conserved quantities [19]:

\begin{array}{l} I_{1} = \int_{a}^{b} u d x, \\ I_{2} = \int_{a}^{b} (u^{2} + μ u_{x}^{2}) d x, \\ I_{3} = \int_{a}^{b} (u^{4} - μ u_{x}^{2}) d x . \end{array}

(17)

These characteristics facilitate the assessment of numerical methods, particularly in scenarios where analytical solutions are non-existent and during the dynamics of soliton collisions.

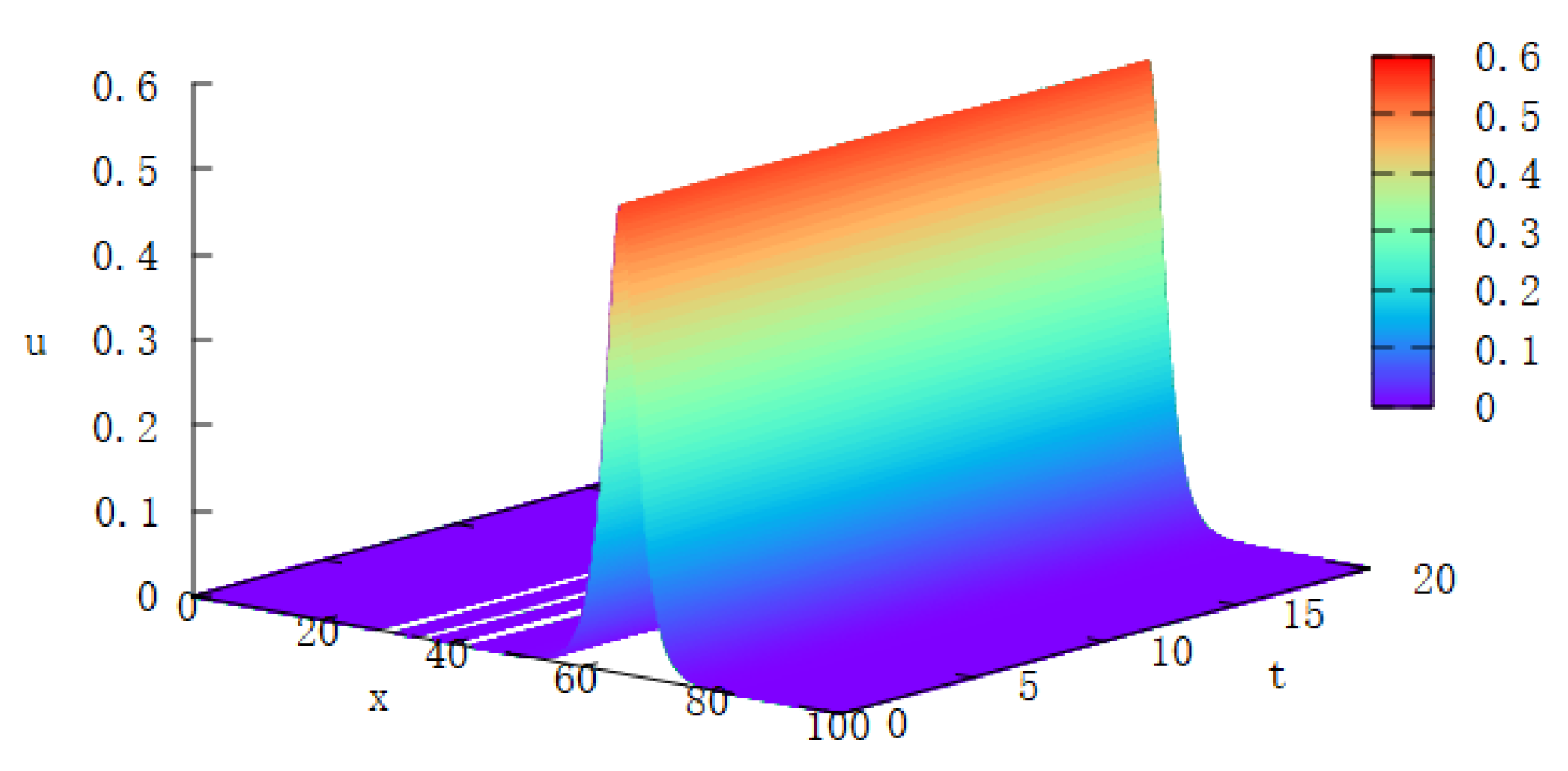
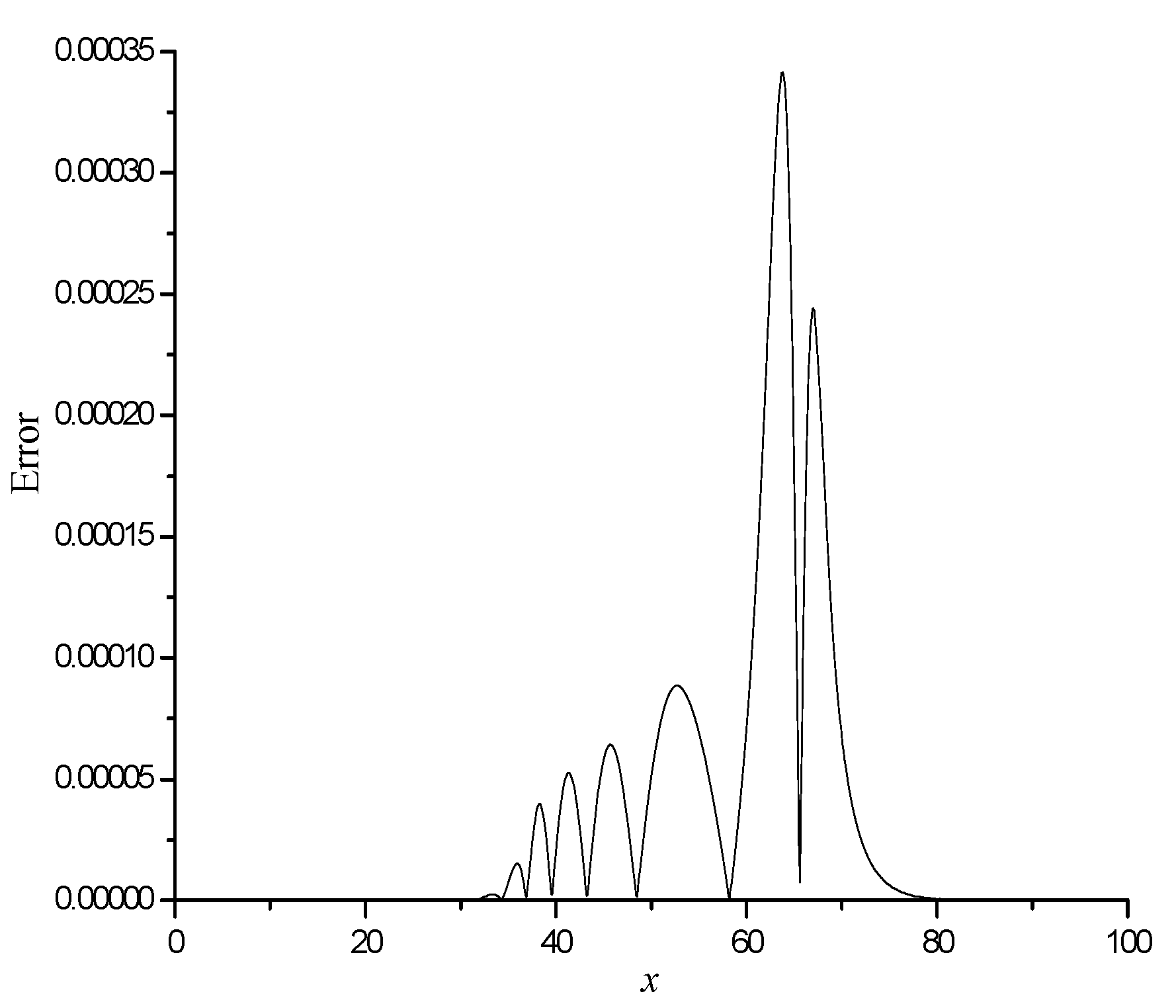
4.1. Single Solitary Waves

In case I, we set c = 0.3,

μ

= 1,

x_{0}

= 40, h = 0.1, and

Δ t

= 0.01 with the following range: [0, 100]; thus, the amplitude is 0.54772. The simulations were conducted up to t = 20. The errors in

L_{2}

-norms and

L_{\infty}

-norms are satisfactorily small, as

L_{2}

-error = 7.10258

\times

10⁻⁴ and

L_{\infty}

-error = 3.41575

\times

10⁻⁴ at t = 20. Table 1 exhibits the findings pertaining to case II. The visual representation of the solitary wave’s progression at various temporal stages is depicted in Figure 1. A graphical comparison of the discrepancies between the analytical and computational solutions at t = 20 can be found in Figure 2, where the highest absolute error value surfaces approximately at the crest of the solitary wave.

Furthermore, when comparing the results obtained using the proposed method with the results from [19,20] in Table 2, we find that when the solitary wave has an amplitude of 0.54772 (c = 0.3), our method provides the same results as the cubic B-spline collation methods [20].

4.2. Interaction of Two Solitary Waves

The second segment of this numerical investigation explores the interaction dynamics of two solitary waves within the context of the MRLW equation. The initial scenario is established by considering a linear superposition of two distinct, amplitude-varied solitary waves that are spatially well-distinguished.

u (x, 0) = \sum_{i = 1}^{2} A_{i} sech (p_{i} (x - x_{i})),

(18)

where

A_{i} = \sqrt{c_{i}}

,

p_{i} = \sqrt{\frac{c_{i}}{μ (c_{i} + 1)}}

,

i = 1, 2

.

This experiment observes the interaction of dual solitary waves, differing in amplitude yet propagating co-directionally. Upon collision, they proceed to reemerge without any alteration in their initial states. The solitary wave interaction problem was solved in the interval [0, 250] for t = 0 to t = 20 with

c_{1}

= 4,

c_{2}

= 1,

μ

= 1,

x_{1}

= 25,

x_{2}

= 55, a space step h = 0.2, and time step

Δ t

= 0.025; then, the amplitudes are in a ratio of 2:1, where

A_{1}

= 2

A_{2}

. Table 3 depicts the invariants across various temporal stages. A graphical representation of the interaction among these solitary waves at distinct time levels is depicted in Figure 3.

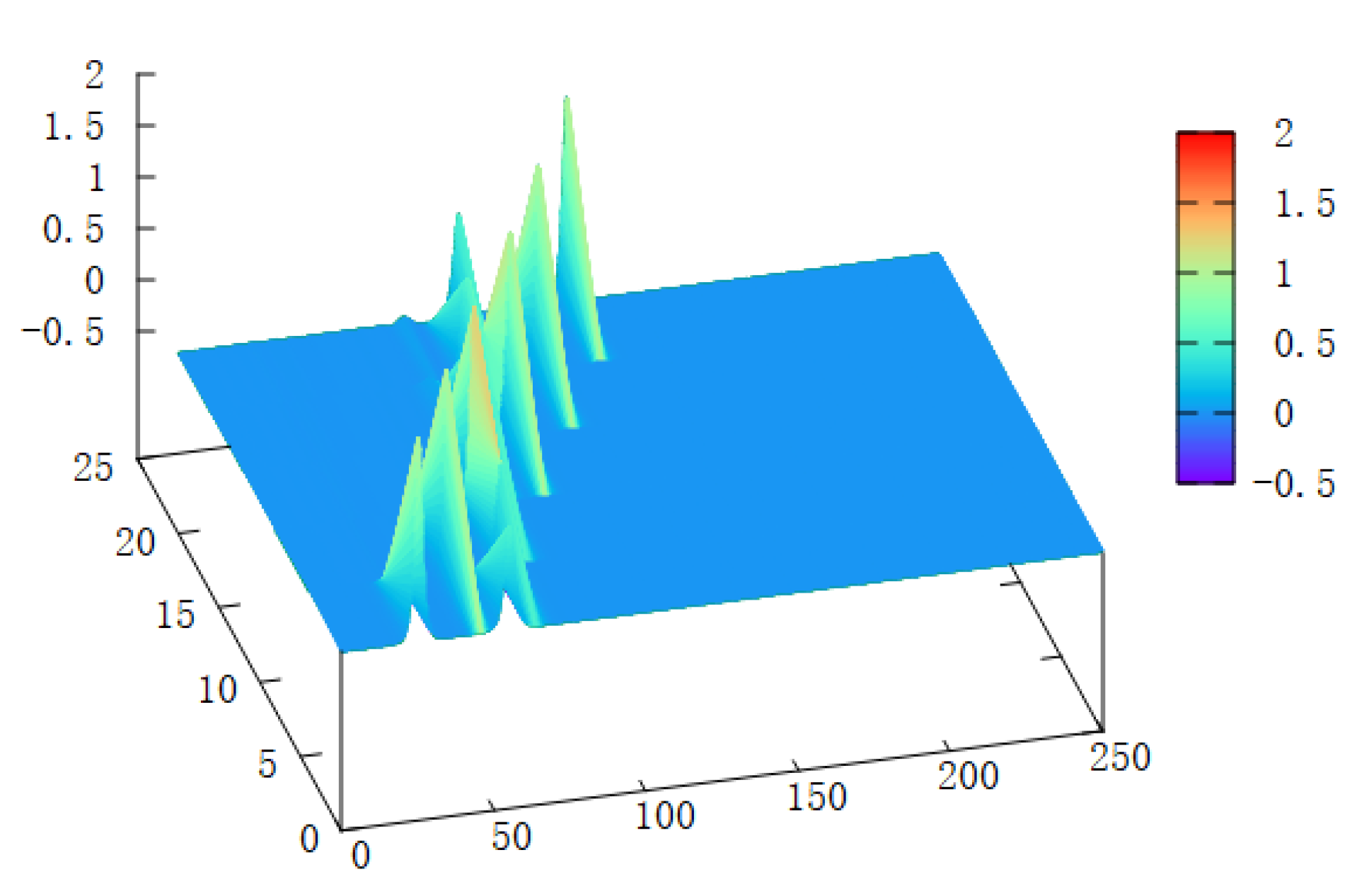
4.3. Interaction of Three Solitary Waves

This section focuses on investigating the dynamic interaction between three distinct-amplitude MRLW solitons moving co-directionally. This examination is carried out using the MRLW equation, which incorporates initial conditions that represent a linear combination of three well-spaced solitary waves, each with a unique amplitude.

u (x, 0) = \sum_{i = 1}^{3} A_{i} sech (p_{i} (x - x_{i})),

(19)

where

A_{i} = \sqrt{c_{i}}

,

p_{i} = \sqrt{\frac{c_{i}}{μ (c_{i} + 1)}}

,

i = 1, 2, 3

.

In our computational study, we opt for the following parameters:

c_{1}

= 4,

c_{2}

= 1,

c_{3}

= 0.25,

μ

= 1,

x_{1}

= 15,

x_{2}

= 45,

x_{3}

= 60, h = 0.2, and

Δ t

= 0.025, with the domain spanning from 0 to 250. The amplitude proportions are set at a ratio of 4:2:1; it is noteworthy that

A_{1}

= 2

A_{2}

= 4

A_{3}

.

Our computational study reveals that the invariants

I_{1}

,

I_{2}

, and

I_{3}

for the solitary wave collisions remain constant, even with significant wave magnitudes. These observations are documented in Table 4. The intricate dynamics of these solitary waves at various temporal stages are depicted in Figure 4, extending up to t = 45.

4.4. The Maxwellian Initial Condition

This section examines the progression of simulations with the adoption of a Maxwellian-based starting state,

u (x, 0) = \exp (- {(x - 40)}^{2}),

(20)

As a train of solitary waves, it is applied to the problem for different cases: (I)

μ

= 0.1, (II)

μ

= 0.04, (III)

μ

= 0.015, and (IV)

μ

= 0.01. The simulations are conducted up to t = 15. The values of the quantities

I_{1}

,

I_{2}

, and

I_{3}

are given in Table 5. However, when

μ

is reduced, more solitary waves formed. For case (I), only a single soliton is generated, as shown in Figure 5a, while for case (II), the Maxwellian pulse develops into a train of at least two solitary waves, as shown in Figure 5b. Similarly, Figure 5c shows that for case (III), three stable solitons are generated, and Figure 5d indicates that for case (IV), the Maxwellian initial condition has decayed into four stable solitary waves. The peaks of the well-developed wave lie on a straight line, so their velocities are linearly dependent on their amplitudes and a small oscillating tail appearing behind the last wave, as shown in Figure 5. The values of the quantities

I_{1}

,

I_{2}

, and

I_{3}

for cases

μ

= 0.1, 0.04, 0.015, and 0.01 are given in Table 5.

Table 6 presents a comparison between the cubic B-spline collocation approach [20] and our scheme according to the maximum changes

Δ I_{1}

,

Δ I_{2}

, and

Δ I_{3}

of invariants

I_{1}

,

I_{2}

, and

I_{3}

in the above computed examples. It shows that, generally, our scheme provides smaller maximum changes of the three invariants than the cubic B-spline collocation method [20], which indicates that our scheme is satisfactorily conservative.

The following is a comparison of the numerical results: In the simulation of Section 4.1 and Section 4.2, the results of the two algorithms are equivalent, but in the simulation of Section 4.3 and Section 4.4, our algorithm’s result is closer to the analytical solution, and the maximum variation of the conserved quantity is smaller, indicating that our algorithm has higher accuracy and better satisfies the conservation law of the equation.

5. Conclusions

A collocation approach employing cubic B-splines was established for generating solitary waves in the context of the MRLW equation. It was found that this approach exhibits marginal stability and surpasses other cubic B-spline collocation methods in terms of precision [19]. It was also shown in the computed examples provided in this paper that the conservation laws are substantially satisfied, where the maximum changes of three invariants in our scheme are all smaller than those in the collocation scheme [20]. We propose that these algorithms can be used to obtain numerical solutions to nonlinear differential equations. Most importantly, the use of the collocation method is especially advisable for deriving the solitary waves of nonlinear differential equations containing high-power nonlinear terms.

Author Contributions

X.L.: Conceptualization, Writing—original draft preparation, and Software, L.Z.: Writing—review and editing, J.S.: Revising and Visualization. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Tianshui Natural Science Foundation (No. 2020-FZJHK-9757, 2023-FZJHK-3157).

Data Availability Statement

Datasets created and scrutinized in this study can be accessed upon reasonable request made to the corresponding author.

Acknowledgments

The authors express their sincere gratitude to the anonymous reviewer for their constructive feedback that significantly enhanced this paper’s clarity.

Conflicts of Interest

The authors declare no conflict of interest.

References

Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
Bona, J.L.; Pyrant, P.J. A mathematical model for long wave generated by wave makers in nonlinear dispersive systems. Proc. Comp. Philos. Soc. 1973, 37, 91. [Google Scholar]
Bona, J.L.; Pritchard, W.G.; Scott, L.R. Numerical scheme for a model of nonlinear dispersive waves. J. Comput. Phys. 1985, 60, 167–176. [Google Scholar] [CrossRef]
Eilbeck, J.C.; McGuire, G.R. Numerical study of regularized long wave equation I: Numerical methods. J. Comput. Phys. 1975, 19, 43–57. [Google Scholar] [CrossRef]
Alexander, M.E.; Morris, J.H. Galerkin method for some model equation for nonlinear dispersive waves. J. Comput. Phys. 1979, 30, 428–451. [Google Scholar] [CrossRef]
Evans, D.J.; Raslan, K.R. The Tanh function method for solving some important nonlinear partial differential equations. Int. J. comput. Math. 2005, 82, 897–905. [Google Scholar] [CrossRef]
Jain, P.C.; Shankar, R.; Single, T.V. Numerical solutions of RLW equation. Commun. Numer. Meth. Eng. 1993, 9, 587–594. [Google Scholar] [CrossRef]
Bhardwaj, D.; Shankar, R. A computational method for regularized long wave equation. Comput. Math. Appl. 2000, 40, 1397–1404. [Google Scholar] [CrossRef]
Zaki, S.I. Solitary waves of the spitted RLW equation. Comput. Phys. Commun. 2001, 138, 80–91. [Google Scholar] [CrossRef]
Gardner, L.R.T.; Gardner, G.A.; Dogan, A. A least squares finite element scheme for the RLW equation. Commun. Numer. Meth. Eng. 1996, 12, 795–804. [Google Scholar] [CrossRef]
Dag, I. Least squares quadratic B-splines finite element method for the regularized long wave equation. Comput. Meth. Appl. Mech. Eng. 2000, 182, 205–215. [Google Scholar] [CrossRef]
Soliman, A.A.; Raslan, K.R. Collocation method using quadratic B-spline for the RLW equation. Int. J. Comput. Math. 2001, 78, 399–412. [Google Scholar] [CrossRef]
Dag, I.; Saka, B.; Irk, D. Application of cubic B-splins for numerical solution of the RLW equation. Appl. Math Comput. 2004, 195, 373–389. [Google Scholar]
Raslan, K.R. A computational method for the regularized long wave (RLW) equation. Appl. Math. Comput. 2005, 176, 1101–1118. [Google Scholar] [CrossRef]
Soliman, A.A.; Hussien, M.H. Collocation solution for RLW equation with septic splines. Appl. Math. Comput. 2005, 161, 623–636. [Google Scholar] [CrossRef]
Zhang, L. A finite difference scheme for generalized long wave equation. Appl. Math. Comput. 2005, 168, 962–972. [Google Scholar] [CrossRef]
Kaya, D. A numerical simulation of solitary wave solutions of the generalized regularized long wave equation. Appl. Math. Comput. 2004, 149, 833–841. [Google Scholar] [CrossRef]
Khalifa, A.K.; Raslan, K.R.; Alzubaidi, H.M. A finite difference scheme for the MRLW and solitary wave interactions. Appl. Math. Comput. 2007, 189, 346–354. [Google Scholar] [CrossRef]
Gardner, L.R.T.; Gardner, G.A.; Ayoub, F.A.; Amin, N.K. Approximations of solitary waves of the MRLW equation by B-spline finite element. Arab. J. Sci. Eng. 1997, 22, 183–193. [Google Scholar]
Tirmizi, I.A. A numerical technique for solution of the MRLW equation using quartic B-splines. Appl. Math. Model. 2010, 34, 4151–4160. [Google Scholar]
Khalifa, A.K.; Raslan, K.R.; Alzubaidi, H.M. A collocation method with B-splines for solving the MRLW equation. J. Comput. Appl. Math. 2008, 212, 406–418. [Google Scholar] [CrossRef]
Iqbal, A.; Abd Hamid, N.N.; Md. Ismail, A.I. Soliton solution of Schrödinger equation using cubic B-spline Galerkin method. Fluids 2019, 4, 108. [Google Scholar] [CrossRef]
Iqbal, A.; Abd Hamid, N.N.; Ismail, A.I.M. Cubic B-spline Galerkin method for numerical solution of the coupled nonlinear Schrödinger equation. Math. Comput. Simulat. 2020, 174, 32–44. [Google Scholar] [CrossRef]
Zaki, S.I. A quintic B-spline finite elements scheme for the KdVB equation. Comput. Methods Appl. Mech. Engrg. 2000, 188, 121–134. [Google Scholar] [CrossRef]
Karakoç, S.B.G.; Uçar, Y.; Yağmurlu, N.M. Numerical solutions of the MRLW equation by cubic B-spline Galerkin finite elements method. Kuwait J. Sci. 2015, 42, 141–159. [Google Scholar]
Lu, C.; Huang, W.; Qiu, J. An Adaptive moving mesh finite element solution of the Regularized Long Wave Equation. J. Sci. Comput. 2018, 74, 122–144. [Google Scholar] [CrossRef]
Parvizi, M.; Khodadadian, A.; Eslahchi, M.R. Analysis of Ciarlet–Raviart mixed finite element methods for solving damped Boussinesq equation. J. Comput. Appl. Math. 2020, 379, 112818. [Google Scholar] [CrossRef]
Parvizi, M.; Khodadadian, A.; Eslahchi, M.R. A mixed finite element method for solving coupled wave equation of Kirchhoff type with nonlinear boundary damping and memory term. Math. Methods Appl. Sci. 2021, 44, 12500–12521. [Google Scholar] [CrossRef]

Figure 1. Single solitary wave with c = 0.3.

Figure 2. Errors (c = 0.3) at time t = 20.

Figure 3. Interaction of two solitary waves.

Figure 4. Interaction of three solitary waves.

Figure 5. The Maxwellian initial condition with (a)

μ

= 0.1, (b)

μ

= 0.04, (c)

μ

= 0.015, and (d)

μ

= 0.01.

Figure 5. The Maxwellian initial condition with (a)

μ

= 0.1, (b)

μ

= 0.04, (c)

μ

= 0.015, and (d)

μ

= 0.01.

Table 1. Invariants and errors for a single solitary wave with c = 0.3.

Time	$I_{1}$	$I_{2}$	$I_{3}$	$L_{2} \times 10^{4}$	$L_{\infty} \times 10^{4}$
0	3.58197	1.34508	0.153723	0	0
2	3.58197	1.34508	0.153723	1.67168	1.13519
4	3.58197	1.34508	0.153723	2.77610	1.63633
6	3.58197	1.34508	0.153723	3.52219	1.90878
8	3.58197	1.34508	0.153723	4.12108	2.13960
10	3.58197	1.34508	0.153723	4.65688	2.35813
12	3.58197	1.34508	0.153723	5.16261	2.57283
14	3.58197	1.34508	0.153723	5.65426	2.78427
16	3.58197	1.34508	0.153723	6.13872	2.99420
18	3.58197	1.34508	0.153723	6.62082	3.20474
20	3.58197	1.34508	0.153723	7.10258	3.41575

Table 2. Errors and invariants of single solitary wave.

Schemes		Analytical	Our Scheme	Cubic B-Splin Coll-CN [20]
c = 0.3 t = 20	$I_{1}$	3.58197	3.58197	3.58197
	$I_{2}$	1.34508	1.34508	1.34508
	$I_{3}$	0.153723	0.153723	0.153723
	$L_{2} \times 10^{4}$	0	7.10258	6.06885
	$L_{\infty} \times 10^{4}$	0	3.41575	2.96650

Table 3. Invariants for interaction of two solitary waves.

Time	$I_{1}$		$I_{2}$		$I_{3}$
Time	Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	CubicB-Splin Coll-CN [20]
0	11.4677	11.4677	14.6291	14.6291	22.8806	22.8806
2	11.4677	11.4677	14.6297	14.6292	22.8805	22.8807
4	11.4677	11.4677	14.6294	14.6292	22.8803	22.8807
6	11.4677	11.4677	14.6296	14.6295	22.8806	22.8806
8	11.4677	11.4677	14.6336	14.6451	22.8850	22.8454
10	11.4677	11.4677	14.6337	14.5963	22.8878	22.8913
12	11.4677	11.4677	14.6293	14.6287	22.8808	22.8814
14	11.4677	11.4677	14.6295	14.6295	22.8805	22.8807
16	11.4677	11.4677	14.6296	14.6294	22.8804	22.8808
18	11.4677	11.4677	14.6296	14.6293	22.8804	22.8809
20	11.4677	11.4677	14.6294	14.6292	22.8803	22.8809
Analytical	11.467698		14.629243		22.880466

Table 4. Invariants for interaction of three solitary waves.

Time	$I_{1}$		$I_{2}$		$I_{3}$
Time	Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	Cubic B-Splin Coll-CN [20]
0	14.9801	13.6891	15.8374	15.4549	23.0083	22.8816
5	14.9801	13.6891	15.8381	15.3109	23.0081	22.6939
10	14.9801	13.6891	15.8516	15.6514	23.0202	22.8388
15	14.9801	13.6891	15.8392	15.6548	23.0077	22.9347
20	14.9802	13.6891	15.8382	15.6557	23.0083	22.9330
25	14.9802	13.6892	15.8379	15.6559	23.0084	22.9336
30	14.9802	13.6894	15.8379	15.6559	23.0084	22.9348
35	14.9802	13.6913	15.8379	15.6564	23.0084	22.9343
40	14.9802	13.7015	15.8379	15.6566	23.0084	22.9335
45	14.9441	13.7043	15.8379	15.6563	23.0055	22.9303
Analytical	14.9801		15.8218		22.9923

Table 5. Invariants of MRLW equation using the Maxwellian initial condition.

$μ$	Time	$I_{1}$	$I_{2}$	$I_{3}$
0.1	3	1.77247	1.37737	0.76204
	6	1.77247	1.37737	0.76204
	9	1.77247	1.37737	0.76204
	12	1.77247	1.37737	0.76204
	15	1.77247	1.37737	0.76204
0.04	3	1.77254	1.29950	0.83975
	6	1.77254	1.29951	0.83974
	9	1.77254	1.29952	0.83973
	12	1.77254	1.29952	0.83973
	15	1.77254	1.29952	0.83973
0.015	3	1.77302	1.26345	0.88107
	6	1.77302	1.26344	0.88109
	9	1.77302	1.26343	0.88100
	12	1.77302	1.26341	0.88090
	15	1.77302	1.26341	0.88087
0.01	3	1.77364	1.25554	0.89927
	6	1.77363	1.25548	0.89905
	9	1.77361	1.25525	0.89763
	12	1.77361	1.25528	0.89778
	15	1.77363	1.25551	0.89920

Table 6. The maximum changes of invariants

I_{1}

,

I_{2}

, and

I_{3}

.

Table 6. The maximum changes of invariants

I_{1}

,

I_{2}

, and

I_{3}

.

Computed Examples			$Δ I_{1}$		$Δ I_{2}$		$Δ I_{3}$
Computed Examples			Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	Cubic B-Splin Coll-CN [20]	Our Scheme	Cubic B-Splin Coll-CN [20]
Single solitary waves	c = 1 (t = 10)		0	0	0.00001	0.00003	0.00001	0.00005
Single solitary waves	c = 0.3 (t = 20)		0	0	0	0	0	0
Two solitary waves (t = 20)			0	0	0.0046	0.032	0.0075	0.0459
Three solitary waves (t = 45)			0.0361	0.0102	0.0142	0.3	0.0147	0.241
The Maxwellian initial condition (t = 15)		$μ$ = 0.1	0	0	0	0.00005	0	0.000063
		$μ$ = 0.04	0	0.00001	0.00002	0.00002	0.00002	0.000028
		$μ$ = 0.015	0	0.00001	0.00004	0.00004	0.00012	0.000248
		$μ$ = 0.01	0.00003	0.00004	0.00026	0.0004	0.00164	0.001722

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Liu, X.; Zhang, L.; Sun, J. Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method. Symmetry 2024, 16, 438. https://doi.org/10.3390/sym16040438

AMA Style

Liu X, Zhang L, Sun J. Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method. Symmetry. 2024; 16(4):438. https://doi.org/10.3390/sym16040438

Chicago/Turabian Style

Liu, Xingxia, Lijun Zhang, and Jianan Sun. 2024. "Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method" Symmetry 16, no. 4: 438. https://doi.org/10.3390/sym16040438

APA Style

Liu, X., Zhang, L., & Sun, J. (2024). Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method. Symmetry, 16(4), 438. https://doi.org/10.3390/sym16040438

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method

Abstract

1. Introduction

2. Governing Equation and Cubic B-Spline Collocation Method

3. Linear Stability Analysis

4. Numerical Examples and Results

4.1. Single Solitary Waves

4.2. Interaction of Two Solitary Waves

4.3. Interaction of Three Solitary Waves

4.4. The Maxwellian Initial Condition

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI