MHD Time-Periodic Plane Poiseuille Flow of Generalized Burgers Fluids through a Porous Medium

Abstract

The time-periodic plane Poiseuille flow of electrically conducting incompressible generalized Burgers fluids through a porous medium is analytically and numerically investigated in the presence of a transverse uniform magnetic field. The main purpose is to provide analytical expressions for the dimensionless steady-state fluid velocity, non-trivial shear stress and Darcy’s resistance, which can be used to bring to light important characteristics concerning fluid behavior. Similar solutions corresponding to the Poiseuille flow of the same fluids induced by a constant pressure gradient are obtained as limiting cases of previous results. The present results reduce to known solutions from the literature when magnetic and porous effects are neglected, and their validation is graphically proved. The needed time to reach a steady state has been graphically determined. It was found that the steady state is later obtained in the absence of a magnetic field and porous medium. The impact of a magnetic field and porous medium on the fluid velocity, shear stress and flow resistance has been systematically examined and elucidated through graphical representations. The findings reveal that the presence of a magnetic field or porous medium results in a reduction in the fluid velocity, accompanied by an increase in the flow resistance.

1. Introduction

The channel flow, as it was named by Coleman et al. [1], is the flow of a fluid between two infinite parallel plates that are both at rest. Such a flow, induced by the sudden application of a constant pressure gradient or due to a time-periodic pressure gradient, was called the Poiseuille flow or time-periodic plane Poiseuille flow by Spurk and Axel [2] and Rajagopal [3], respectively. Analytical solutions for the velocity field corresponding to motions of the incompressible Newtonian fluids produced by constant and time-dependent pressure gradients have been established by Mendiburu et al. [4] and Erdogan [5]. The first exact steady-state or long-time solutions for the time-periodic plane Poiseuille flows of non-Newtonian fluids seem to be those of Rajagopal [3], corresponding to incompressible second-grade fluids. These solutions were later extended by Hayat et al. [6] to incompressible Oldroyd-B fluids and by Fetecau et al. [7] for incompressible generalized Burgers fluids (IGBFs). Exact analytical solutions for such motions between parallel plates have been determined by Danish et al. [8] for third-grade fluids. Interesting results regarding the unsteady Poiseuille flow of second-grade fluids with slip boundary conditions have been recently obtained by Baranovskii [9].

Magnetohydromagnetic (MHD) motions of fluids between parallel plates have significant applications to polymer technology, the petroleum industry, power generators and pumps, geothermal systems, electrostatic precipitation and many others. The interplay between a moving electrically conducive fluid and a magnetic field generates effects with different applications in chemistry, physics and engineering. The MHD effects on the formation of such a motion have been investigated early by Tao [10] and Katagiri [11]. Singh and Ram [12] studied the MHD flow of incompressible Newtonian fluids through a channel induced by a time-periodic pressure gradient using Laplace transform. Steady solutions for MHD Couette flow between infinite parallel plates were relatively recently obtained by Kiema et al. [13] using the Sumudu transform. At the same time, the dynamics of fluid motion through porous media finds varied applications in the fields of geophysics and astrophysical studies, petroleum industry, oil reservoir technology and agricultural engineering. Relatively recently, Safdar Rabia et al. [14] studied the MHD flow of Burgers fluids due to a pressure gradient through a porous medium. Other exact solutions for MHD motions of Burgers fluids through a porous medium have been obtained by Fetecau and Vieru [15]. Unfortunately, such solutions for MHD motions of IGBFs induced by a periodic or constant pressure gradient through a porous plane channel seem to be lacking in the literature.

The purpose of this work is to provide analytical expressions for the steady-state solutions corresponding to MHD motions of IGBFs induced by a periodic or constant pressure gradient in a porous plane channel. These solutions can be easily particularized to give similar solutions for incompressible Burgers, Oldroyd-B, Maxwell and Newtonian fluids performing the same motions. For validation purposes, the steady-state velocity fields are presented in two distinct forms, and their equivalence is established through graphical representations. The convergence of initial solutions (numerical solutions) to their steady-state components is graphically validated, and the requisite time to attain the steady state is determined. Additionally, the impact of a magnetic field and porous medium on fluid velocity, shear stress and flow resistance is underscored and comprehensively discussed. It is worth mentioning the fact that the profiles of these entities against z are symmetric with respect to the median plane.

2. Problem Presentation

Let us consider an electrically conducive, incompressible, generalized Burgers fluid (ECIGBF) at equilibrium, confined between two infinitely expansive horizontal parallel plates within a porous medium. The Cauchy stress tensor T and the extra-stress tensor ${\mathit{T}}_E$ corresponding to these rate-type fluids are mandated to satisfy to the following constitutive equations [7]:

$$\mathit{T}=-p\mathit{I}+{\mathit{T}}_E, \left(1+a_1\frac{D}{Dt}+a_2\frac{D^2}{D{t}^2}\right){\mathit{T}}_E=2\eta \left(1+a_3\frac{D}{Dt}+a_4\frac{D^2}{D{t}^2}\right)\mathit{D} ,$$

(1)

where I is the identity tensor, D is the rate of deformation tensor [1], p is the hydrostatic pressure, $\eta$ is the dynamic viscosity of the fluid, D/Dt denotes the time upper-convected derivative and $a_i (i=1,2,3,4)$ are dimensional material constants. If $a_4=0, a_4=a_2=0$ or $a_4=a_3=a_2=0$ in the second part of Equation (1), the corresponding equations characterize other classes of rate type fluids, namely, Burgers, Oldroyd-B and Maxwell fluids, respectively. Burgers fluids, whose frame-indifferent three-dimensional constitutive equations have been developed by Krishnan and Rajagopal [16], correspond to $a_4=0$. Newtonian fluids are obtained when all constants are zero.

Let us assume that at the moment $t=0^{+}$, a time-periodic pressure gradient

$$\frac{\partial p}{\partial z}=-\rho P\cos (\omega t) \mathrm{or} \frac{\partial p}{\partial z}=-\rho P\sin (\omega t); t>0,$$

(2)

is applied along the y-direction of a suitable Cartesian coordinate system x, y and z whose z-axis is perpendicular to the plates (see Figure 1).

Here, $\rho$ is the fluid density, $\omega$ is the frequency of oscillations and P is constant. At the same time, an external uniform magnetic field of magnitude $B_0$ begins to act vertically to the plates. We suppose that the fluid is finitely conducting, the magnetic Reynolds number is small enough (at least ionized fluids and metallic liquids satisfy this condition [17]) and there is no surplus electric charge distribution. Consequently, the induced magnetic field and Joule heating can be neglected. In addition, the Hall effects are neglected due to moderate values of the Hartman number. Since the plates are unbounded, the velocity vector corresponding to the resulting flow is given by the next relation [18,19,20]:

$$\mathit{u}=\mathit{u}(z,t)=u(z,t){\mathit{e}}_y; 0<z<d, t>0,$$

(3)

where ${\mathit{e}}_y$ is the unit vector along the y-axis and d is the distance between the plates. For such motions, the continuity equation is identically verified.

We also assume that the extra-stress tensor ${\mathit{T}}_E$, as well as the velocity vector u, is a function of z and t only. Introducing the velocity vector $\mathit{u}(z,t)$ from Equation (3) in the second relation (1), and bearing in mind the fact that the fluid has been at rest up to the initial moment $t=0$, it is not difficult to show that the non-trivial shear stress $\tau (z,t)=T_{Eyz}(z,t)$ has to satisfy the partial differential equation

$$\left(1+a_1\frac{\partial }{\partial t}+a_2\frac{{\partial }^2}{\partial t^2}\right)\tau (z,t)=\eta \left(1+a_3\frac{\partial }{\partial t}+a_4\frac{{\partial }^2}{\partial t^2}\right)\frac{\partial u(z,t)}{\partial z}; 0<z<d, t>0.$$

(4)

The balance of linear momentum reduces to the partial differential equation [19]

$$\rho \frac{\partial u(z,t)}{\partial t}=\frac{\partial \tau (z,t)}{\partial z}-\frac{\partial p}{\partial z}-\sigma B_0^{2}u(z,t)+R(z,t)=0; 0<z<d, t>0.$$

(5)

Here, $\sigma$ is the electrical conductivity of the fluid, while $R(z,t)$ is the Darcy’s resistance, which has to satisfy the partial differential equation [19]

$$\left(1+a_1\frac{\partial }{\partial t}+a_2\frac{{\partial }^2}{\partial t^2}\right)R(z,t)=-\eta \frac{\phi }{k}\left(1+a_3\frac{\partial }{\partial t}+a_4\frac{{\partial }^2}{\partial t^2}\right)u(z,t); 0<z<1, t>0,$$

(6)

in which $\phi$ ($0<\phi <1$) is porosity and k ($>0$) represents the permeability of the porous medium. The volume flux $Q(t)$ across a plane normal to the flow direction per unit width of this plane can be determined by means of the relation

$$Q(t)={\displaystyle \underset{0}{\overset{d}{\int }}u(z,t)dz; t>0.}$$

(7)

The adequate initial and boundary conditions are

$$u(z,0)=0, {\frac{\partial u(z,t)}{\partial t}|}_{t=0}=0, {\frac{{\partial }^{2}u(z,t)}{\partial t^2}|}_{t=0}=0; 0<z<d,$$

(8)

respectively, when

$$u(0,t)=u(d,t)=0; t>0.$$

(9)

Utilizing the following non-dimensional variables, functions and parameters

$$\begin{array}{l}{z}^{\ast }=\frac{1}{d}z, t^{\ast }=\frac{Pd}{\nu }t, u^{\ast }=\frac{\nu }{P{d}^2}u, {\tau }^{\ast }=\frac{1}{\rho Pd}\tau , R^{\ast }=\frac{1}{\rho P}R,\\ Q^{\ast }=\frac{\nu }{P{d}^3}Q, p^{\ast }=\frac{1}{\rho Pd}p, {\omega }^{\ast }=\frac{\nu }{Pd}\omega \end{array}$$

(10)

and eliminating the star notation, one finds the non-dimensional forms

$$\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)\tau (z,t)=\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)\frac{\partial u(z,t)}{\partial z}; 0<z<1, t>0,$$

(11)

$$\mathrm{Re}\frac{\partial u(z,t)}{\partial t}=\frac{\partial \tau (z,t)}{\partial z}-\frac{\partial p}{\partial z}-{\mathrm{Ha}}^{2}u(z,t)+R(z,t)=0; 0<z<1, t>0,$$

(12)

$$\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)R(z,t)=-K\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)u(z,t); 0<z<1, t>0,$$

(13)

of the motion equations.

In Equations (10), (12) and (13), $\nu =\eta /\rho$ is the kinematic viscosity of the fluid, while the Reynolds and Hartmann numbers Re and Ha, respectively, and the porous parameter K is given by the next relations:

$$\mathrm{Re}=\frac{Vd}{\nu }, {\mathrm{Ha}}^2=\frac{\sigma B_0^2}{\rho } \frac{d^2}{\nu }=\frac{d^2}{\eta }\sigma B_0^2=M, K=\frac{\phi }{k}{d}^2,$$

(14)

where $V=P{d}^2/\nu$ is the characteristic velocity. In addition, the dimensionless constants $\alpha , \beta , \gamma$ and $\delta$ are given by the relations

$$\alpha =\frac{Pd}{\nu }{a}_1, \beta ={\left(\frac{Pd}{\nu }\right)}^2{a}_2, \gamma =\frac{Pd}{\nu }{a}_3, \delta ={\left(\frac{Pd}{\nu }\right)}^2{a}_4.$$

(15)

The non-dimensional volume flux $Q(t)$ is given by the relation

$$Q(t)={\displaystyle \underset{0}{\overset{1}{\int }}u(z,t)dz; t>0.}$$

(16)

Eliminating $\tau (z,t)$ and $R(z,t)$ between Equations (11)–(13), one finds the following partial differential equation for the dimensionless velocity field $u(z,t)$:

$$\begin{array}{l}\mathrm{Re}\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)\frac{\partial u(z,t)}{\partial t}=\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)\frac{{\partial }^{2}u(z,t)}{\partial z^2}-\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)\frac{\partial p}{\partial z}\\ -{\mathrm{Ha}}^2\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)u(z,t)-K\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)u(z,t); 0<z<1, t>0,\end{array}$$

(17)

The appropriate initial and boundary conditions are

$$u(z,0)=0, {\frac{\partial u(z,t)}{\partial t}|}_{t=0}=0, {\frac{{\partial }^{2}u(z,t)}{\partial t^2}|}_{t=0}=0; 0<z<1,$$

(18)

respectively, for

$$u(0,t)=u(1,t)=0; t>0,$$

(19)

while the relations in (2) take the dimensionless forms

$$\frac{\partial p}{\partial z}=-\cos (\omega t) \mathrm{or} \frac{\partial p}{\partial z}=-\sin (\omega t); t>0.$$

(20)

In the next sections, for their distinction, we denote by $u_c(z,t)$,${\tau }_c(z,t)$,$R_c(z,t)$ and $u_s(z,t)$, ${\tau }_s(z,t)$, $R_s(z,t)$ the dimensionless start-up solutions corresponding to the two motion problems of ECIGBFs. These solutions characterize the fluid behavior some time after its initiation. After this time, the fluid behavior can be described by the dimensionless steady-state (long time) solutions $u_{cp}(z,t)$,${\tau }_{cp}(z,t)$,$R_{cp}(z,t)$ or $u_{sp}(z,t)$, ${\tau }_{sp}(z,t)$, $R_{sp}(z,t)$. This is the time needed to reach the steady state. The two notions “steady-state solution” and “long time solution” have been used in the literature, for instance, by Erdogan [21] and Prusa [22], respectively, for similar solutions describing fluid motion over an infinite plate that oscillates in its plane. They are different from the steady solutions corresponding to the Poiseuille flow due to a constant pressure gradient (which are obtained in Section 3.1). To ascertain the time evolution of a given motion, it is adequate to discern the dimensionless steady-state solutions. Accordingly, the ensuing section will be dedicated to the derivation of analytical expressions encapsulating these solutions. Subsequently, these expressions will be employed to elucidate the impact of both the magnetic field and porous medium on the necessary time for attaining a steady state, as well as on the fluid’s flow resistance.

3. Analytical Expressions for the Dimensionless Steady-State Solutions

The dimensionless steady-state velocity fields $u_{cp}(z,t)$ and $u_{sp}(z,t)$ have to satisfy the governing Equation (17) and the boundary conditions (19). They are independent of the initial conditions (18), so that these conditions are ignored in what follows. In order to determine them and to be sure of their correctness, two different methods will be used. Firstly, let us use the steady-state complex velocity

$$u_p(z,t)=u_{cp}(z,t)+i{u}_{sp}(z,t); 0<z<1, t\in R,$$

(21)

in which i is the imaginary unit. This dimensionless steady-state complex velocity has to fulfill the partial differential equation

$$\begin{array}{l}\mathrm{Re}\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)\frac{\partial u_p(z,t)}{\partial t}=\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)\frac{{\partial }^2{u}_p(z,t)}{\partial z^2}+\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right) {\mathrm{e}}^{i\omega t}\\ -{\mathrm{Ha}}^2\left(1+\alpha \frac{\partial }{\partial t}+\beta \frac{{\partial }^2}{\partial t^2}\right)u_p(z,t)-K\left(1+\gamma \frac{\partial }{\partial t}+\delta \frac{{\partial }^2}{\partial t^2}\right)u_p(z,t); 0<z<1, t\in R,\end{array}$$

(22)

with the boundary conditions

$$u_p(0,t)=u_p(1,t)=0; t>0.$$

(23)

Direct calculations show that $u_p(z,t)$ can be represented in the simple form

$$u_p(z,t)=\left[1-\frac{\cos \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\right]\frac{q{\mathrm{e}}^{i\omega t}}{r^2}; 0<z<1, t\in R,$$

(24)

where the complex constants r and q are defined by the relations

$$r=\sqrt{\frac{({\mathrm{Ha}}^2+i\omega \mathrm{Re})(1-\beta {\omega }^2+i\omega \alpha )+K(1-\delta {\omega }^2+i\omega \gamma )}{1-\delta {\omega }^2+i\omega \gamma }}, q=\frac{1-\beta {\omega }^2+i\omega \alpha }{1-\delta {\omega }^2+i\omega \gamma }.$$

(25)

Consequently, the velocity fields $u_{cp}(z,t)$ and $u_{sp}(z,t)$ are given by the relations

$$u_{cp}(z,t)= \Re e\left\{\left[1-\frac{\cos \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\right]\frac{q{\mathrm{e}}^{i\omega t}}{r^2}\right\}; 0<z<1, t\in R,$$

(26)

$$u_{sp}(z,t)= \mathrm{Im}\left\{\left[1-\frac{\cos \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\right]\frac{q{\mathrm{e}}^{i\omega t}}{r^2}\right\}; 0<z<1, t\in R,$$

(27)

where $\Re e$ and Im denote the real and imaginary part, respectively, of that which follows.

Steady-state shear stresses ${\tau }_{cp}(z,t)$, ${\tau }_{sp}(z,t)$ and Darcy’s resistances $R_{cp}(z,t)$, $R_{sp}(z,t)$ corresponding to these motions, namely

$${\tau }_{cp}(z,t)=-\Re e\left\{\frac{\sin \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\frac{{\mathrm{e}}^{i\omega t}}{r}\right\}; 0<z<1, t\in R,$$

(28)

$${\tau }_{sp}(z,t)=-\mathrm{Im}\left\{\frac{\sin \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\frac{{\mathrm{e}}^{i\omega t}}{r}\right\}; 0<z<1, t\in R,$$

(29)

$$R_{cp}(z,t)=-K\Re e\left\{\left[1-\frac{\cos \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\right]\frac{q{\mathrm{e}}^{i\omega t}}{r^2}\right\}; 0<z<1, t\in R,$$

(30)

$$R_{sp}(z,t)=-K\mathrm{Im}\left\{\left[1-\frac{\cos \mathrm{h}[r(z-1/2\left)\right]}{\cos \mathrm{h}(r/2)}\right]\frac{q{\mathrm{e}}^{i\omega t}}{r^2}\right\}; 0<z<1, t\in R,$$

(31)

have been obtained using Equations (11), (13), (26) and (27). Simple calculations show that $u_{cp}(z,t)$, ${\tau }_{cp}(z,t)$, $R_{cp}(z,t)$ and $u_{sp}(z,t)$, ${\tau }_{sp}(z,t)$, $R_{sp}(z,t)$ given by the above relations satisfy Equations (11)–(13) and the boundary conditions (19).

Equivalent expressions for the dimensionless steady-state velocity fields $u_{cp}(z,t)$, $u_{sp}(z,t)$ can be obtained using the finite Fourier sine transform [23]. Multiplying Equation (17) by $\sin (n\pi )$, integrating the obtained result between zero and one when $\partial p/\partial z=-\cos (\omega t)$ and bearing in mind the identity (15) of Section 13 from the reference [23], one obtains the following ordinary differential equation for the finite Fourier sine transform $u_{Fn}(t)$ of $u(z,t)$:

$$\begin{array}{l}\beta \mathrm{Re}\frac{d^3{u}_{Fn}(t)}{d{t}^3}+b_n\frac{d^2{u}_{Fn}(t)}{d{t}^2}+c_n\frac{d{u}_{Fn}(t)}{dt}+({\lambda }_n^2+K_{eff})u_{Fn}(t)\\ -\frac{1+{(-1)}^{n+1}}{{\lambda }_n}\left[(1-\beta {\omega }^2)\cos (\omega t)-\alpha \omega \sin (\omega t)\right]=0; t>0, n=\mathrm{1.2.3},\dots \end{array}$$

(32)

Here, ${\lambda }_n=n\pi$ with $n=1,2,3,\dots ,$ $K_{eff}=K+{\mathrm{Ha}}^2$ is the effective permeability and

$$b_n=\alpha \mathrm{Re} +\beta {\mathrm{Ha}}^2+\delta ({\lambda }_n^2+K), c_n=\mathrm{Re} +\alpha {\mathrm{Ha}}^2+\gamma ({\lambda }_n^2+K).$$

(33)

The steady-state component $u_{Fmp}(t)$ of the start-up solution $u_{Fm}(t)$ of the ordinary differential Equation (32) is given by the relation

$$\begin{array}{l}{u}_{Fmp}(t)=4\cos (\omega t)\frac{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)(1-\beta {\omega }^2)-\alpha {\omega }^2(\beta {\omega }^2\mathrm{Re}-c_m)}{{\lambda }_m[{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2]}\\ -4\omega \sin (\omega t)\frac{\alpha ({\lambda }_m^2+K_{eff}-b_m{\omega }^2)+(1-\beta {\omega }^2)(\beta {\omega }^2\mathrm{Re}-c_m)}{{\lambda }_m[{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2]},\end{array}$$

(34)

where $m=2n-1$. Carrying out the inverse finite Fourier sine transform in the last equation, one finds the analytic expression of the steady state velocity $u_{cp}(z,t)$, namely

$$\begin{array}{l}{u}_{cp}(z,t)=4\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)(1-\beta {\omega }^2)-\alpha {\omega }^2(\beta {\omega }^2\mathrm{Re}-c_m)}{{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2}}\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m}\\ -4\omega \sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{\alpha ({\lambda }_m^2+K_{eff}-b_m{\omega }^2)+(1-\beta {\omega }^2)(\beta {\omega }^2\mathrm{Re}-c_m)}{{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2}\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m};} 0<z<1, t\in R.\end{array}$$

(35)

Analogous computations allow us to show that $u_{sp}(z,t)$ is given by the relation

$$\begin{array}{l}{u}_{sp}(z,t)=4\omega \cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{\alpha ({\lambda }_m^2+K_{eff}-b_m{\omega }^2)+(1-\beta {\omega }^2)(\beta {\omega }^2\mathrm{Re}-c_m)}{{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2} }\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m}\\ +4\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)(1-\beta {\omega }^2)-\alpha {\omega }^2(\beta {\omega }^2\mathrm{Re}-c_m)}{{({\lambda }_m^2+K_{eff}-b_m{\omega }^2)}^2+{\omega }^2{(\beta {\omega }^2\mathrm{Re}-c_m)}^2} }\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m}; 0<z<1, t\in R.\end{array}$$

(36)

Figure 2 clearly shows that the expressions of $u_{cp}(z,t)$ and $u_{sp}(z,t)$ given by Equations (26) and (35) and by Equations (27) and (36), respectively, are equivalent.

As was specified in Section 2, the steady-state solutions corresponding to incompressible Newtonian, Maxwell, Oldroyd-B and Burgers fluids can be obtained as limiting cases of the solutions to (26)–(31). Taking $\alpha =\beta =\gamma =\delta =0$ in Equations (26)–(31), for instance, the dimensionless steady-state solutions

$$u_{Ncp}(z,t)=\Re e\left\{\left[1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\right]\frac{{\mathrm{e}}^{i\omega t}}{K_{eff}+i\omega \mathrm{Re}}\right\}; 0<z<1, t\in R,$$

(37)

$$u_{Nsp}(z,t)=\mathrm{Im}\left\{\left[1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\right]\frac{{\mathrm{e}}^{i\omega t}}{K_{eff}+i\omega \mathrm{Re}}\right\}; 0<z<1, t\in R,$$

(38)

$${\tau }_{Ncp}(z,t)=-\Re e\left\{\frac{\sin \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\frac{{\mathrm{e}}^{i\omega t}}{\sqrt{K_{eff}+i\omega \mathrm{Re}}}\right\}; 0<z<1, t\in R,$$

(39)

$${\tau }_{Nsp}(z,t)=-\mathrm{Im}\left\{\frac{\sin \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\frac{{\mathrm{e}}^{i\omega t}}{\sqrt{K_{eff}+i\omega \mathrm{Re}}}\right\}; 0<z<1, t\in R,$$

(40)

$$R_{Ncp}(z,t)=-K\Re e\left\{\left[1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\right]\frac{{\mathrm{e}}^{i\omega t}}{K_{eff}+i\omega \mathrm{Re}}\right\}; 0<z<1, t\in R,$$

(41)

$$R_{Nsp}(z,t)=-K\mathrm{Im}\left\{\left[1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}+i\omega \mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}+i\omega \mathrm{Re}}/2)}\right]\frac{{\mathrm{e}}^{i\omega t}}{K_{eff}+i\omega \mathrm{Re}}\right\}; 0<z<1, t\in R,$$

(42)

corresponding to incompressible Newtonian fluids performing the same motions are obtained.

Equivalent forms for the velocity fields $u_{Ncp}(z,t)$ and $u_{Nsp}(z,t)$, namely

$$\begin{array}{l}{u}_{Ncp}(z,t)=4\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{({\lambda }_m^2+K_{eff})\sin ({\lambda }_{m}z)}{{\lambda }_m[{({\lambda }_m^2+K_{eff})}^2+{(\omega \mathrm{Re})}^2]} }\\ +4\omega \mathrm{Re}\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m[{({\lambda }_m^2+K_{eff})}^2+{(\omega \mathrm{Re})}^2]}; 0<z<1, t\in R, }\end{array}$$

(43)

$$\begin{array}{l}{u}_{Nsp}(z,t)=-4\omega \mathrm{Re}\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{\sin ({\lambda }_{m}z)}{{\lambda }_m[{({\lambda }_m^2+K_{eff})}^2+{(\omega \mathrm{Re})}^2]} }\\ +4\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{({\lambda }_m^2+K_{eff})\sin ({\lambda }_{m}z)}{{\lambda }_m[{({\lambda }_m^2+K_{eff})}^2+{(\omega \mathrm{Re})}^2]}; 0<z<1, t\in R, }\end{array}$$

(44)

have been obtained from Equations (35) and (36). To the best of our knowledge, the Newtonian solutions from Equations (35)–(44) are also new. From relations (37)–(40), (43) and (44), it results that the steady-state velocities $u_{Ncp}(z,t)$, $u_{Nsp}(z,t)$ and the shear stresses ${\tau }_{Ncp}(z,t)$, ${\tau }_{Nsp}(z,t)$ corresponding to these motions of incompressible Newtonian fluids do not depend on the Hartmann number Ha and the porosity parameter K independently but on the effective permeability $K_{eff}=K+{\mathrm{Ha}}^2$. Consequently, the investigation of these entities corresponding to MHD steady-state motions of ECIGBFs in the presence or absence of a porous medium is exactly the same task both analytically and computationally, and a two-parameter approach is superfluous.

3.1. Limiting Case $\omega \to 0$ (Poiseuille Flow Due to a Constant Pressure Gradient)

Making $\omega \to 0$ in Equations (37), (39) and (41), one obtains the steady components

$$u_{Cp}(z)=\frac{1}{K_{eff}}\left[1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}}/2)}\right]; 0<z<1, t>0,$$

(45)

$${\tau }_{Cp}(z)=-\frac{\sin \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}}\right]}{\sqrt{K_{eff}}\cos \mathrm{h}(\sqrt{K_{eff}}/2)}; 0<z<1, t>0,$$

(46)

$$R_{Cp}(z)=-\frac{K}{K_{eff}}\left\{1-\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{K_{eff}}\right]}{\cos \mathrm{h}(\sqrt{K_{eff}}/2)}\right\}; 0<z<1, t>0,$$

(47)

of the dimensionless start-up solutions $u_C(z,t), {\tau }_C(z,t)$ and $R_C(z,t)$ corresponding to the MHD Poiseuille flow of ECIGBFs through a porous medium induced by a constant pressure gradient $-\rho P$. As expected, these solutions are identical to those corresponding to electrically conducting incompressible Newtonian fluids performing the same motion. This is possible because the governing equations corresponding to the steady motions of incompressible Newtonian and non-Newtonian fluids are identical.

Substituting the steady dimensionless velocity $u_{Cp}(z)$ from Equation (45) in Equation (16), one obtains the corresponding expression of the non-dimensional volume flux, namely

$$Q_{Cp}=\frac{\sqrt{K_{eff}}\cos \mathrm{h}(\sqrt{K_{eff}}/2)-2\sin \mathrm{h}(\sqrt{K_{eff}}/2)}{K_{eff}\sqrt{K_{eff}}\cos \mathrm{h}(\sqrt{K_{eff}}/2)}.$$

(48)

It results that the volume flux $Q_{Cp}$ across a plane normal to the flow direction as well as the fluid velocity $u_{Cp}(z)$ do not depend on Ha and K independently.

3.2. Reductions to Known Results from the Existing Literature

The steady-state solutions for same motions of ECIGBFs when the magnetic field or porous medium is absent can be obtained by making $\mathrm{Ha}=0$ or $K=0$, respectively, in the general results. In the absence of magnetic and porous effects, the proper solutions are obtained by taking $\mathrm{Ha}=K=0$ in the respective relations. In this case, the velocity fields $u_{cp}(z,t)$ and $u_{sp}(z,t)$ given by the relations (26) and (27) take the simplified forms

$$u_{cp}(z,t)=\frac{1}{\omega \mathrm{Re}}\sin (\omega t)+\frac{1}{\omega \mathrm{Re}}\Re e\left\{\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{i\omega q\mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{i\omega q\mathrm{Re}}/2)}i{\mathrm{e}}^{i\omega t}\right\}; 0<z<1, t\in R,$$

(49)

$$u_{sp}(z,t)=-\frac{1}{\omega \mathrm{Re}}\cos (\omega t)+\frac{1}{\omega \mathrm{Re}}\mathrm{Im}\left\{\frac{\cos \mathrm{h}\left[\right(z-1/2\left)\sqrt{i\omega q\mathrm{Re}}\right]}{\cos \mathrm{h}(\sqrt{i\omega q\mathrm{Re}}/2)}i{\mathrm{e}}^{i\omega t}\right\}; 0<z<1, t\in R.$$

(50)

The dimensional forms $u_{cp}^{dim}(z,t)$ and $u_{sp}^{dim}(z,t)$ of the non-dimensional velocities $u_{cp}(z,t)$ and $u_{sp}(z,t)$ from Equations (49) and (50), namely

$$u_{cp}^{dim}(z,t)=\frac{P}{\omega }\sin (\omega t)+\frac{P}{\omega }\Re e\left\{\frac{\cos \mathrm{h}\left[\mathrm{m}\right(z-d/2\left)\right]}{\cos \mathrm{h}(md/2)}i{\mathrm{e}}^{i\omega t}\right\}; 0<z<1, t\in R,$$

(51)

$$u_{sp}^{dim}(z,t)=-\frac{P}{\omega }\cos (\omega t)+\frac{P}{\omega }\mathrm{Im}\left\{\frac{\cos \mathrm{h}\left[\mathrm{m}\right(z-d/2\left)\right]}{\cos \mathrm{h}(md/2)}i{\mathrm{e}}^{i\omega t}\right\}; 0<z<1, t\in R,$$

(52)

are identical to those obtained by Fetecau et al. [7] in Equations (38) and (39). In the above relations, the imaginary constant m is given by the relation

$$m=\sqrt{\frac{\omega }{2} \frac{\omega [a_3-a_1+(a_1{a}_4-a_2{a}_3){\omega }^2]+i[1-(a_2+a_4){\omega }^2+(a_1{a}_3+a_2{a}_4{\omega }^2){\omega }^2}{{(1-a_4{\omega }^2)}^2+{(a_3\omega )}^2}}.$$

(53)

Furthermore, taking the limit of the relations (45), (46) and (48) when the effective permeability $K_{eff}\to 0$, we find the steady solutions

$$u_{Cp}(z)=-(z^2-z)/2, {\tau }_{Cp}(z)=-z+1/2, Q_{Cp}=1/12; 0<z<1,$$

(54)

corresponding to the steady Poiseuille flow of ECIGBFs or incompressible Newtonian fluids generated by a constant pressure gradient $\partial p/\partial z=-\rho P$ in the absence of magnetic and porous effects. The dimensional forms of these last solutions are given by the next relations:

$$u_{Cp}^{dim}(z)=\frac{1}{2\mu }(z^2-dz)\frac{\partial p}{\partial z}, {\tau }_{Cp}^{dim}(z)=(z^2-d/2)\frac{\partial p}{\partial z}, Q_{Cp}^{dim}=-\frac{d^3}{12\mu } \frac{\partial p}{\partial z}; 0<z<1.$$

(55)

The first of the last three relations, as expected, is identical to that in Equation (11) obtained by Mendiburu et al. [4]. This result, as expected, is also in accordance with the relation (6.19) of Spurk and Aksel [2] when both walls are at rest. Taking $d=2b$ in the last Equation (55), we recover the result obtained by Erdogan [5] (Equation (20)), namely

$$Q_{Cp}^{dim}=-\frac{2b^3}{3\eta }\frac{\partial p}{\partial z}.$$

(56)

The dimensional average velocity $w_{Cpa}^{dim}=Q_{Cp}^{dim}/d$ and the maximum velocity $w_{Cp\max }^{dim}$, as they result from Equations (55)₃ and (55)₁, respectively, are given by the relations

$$w_{Cpa}^{dim}=-\frac{d^2}{12\mu }\frac{\partial p}{\partial z}, w_{Cp\max }^{dim}=-\frac{d^2}{8\mu }\frac{\partial p}{\partial z}=\frac{3}{2}{w}_{Cpa}^{dim}.$$

(57)

These results are also in accordance with those of Spurk and Axel ((Section 6.1) in ref. [2]).

4. Numerical Results and Discussing

In this work, we provide exact analytical expressions for the dimensionless steady-state velocity, non-trivial shear stress and Darcy’s resistance corresponding to the time-periodic plane Poiseuille flow of ECIGBFs through a porous medium in the presence of a uniform transversal magnetic field. These expressions have been used to find similar solutions for the Poiseuille flow of same fluids due to a constant pressure gradient. The results that have been found here can be particularized to give steady-state solutions for incompressible Burgers, Oldroyd-B, Maxwell and Newtonian fluids performing the same motions. Moreover, most of them reduce to known results from the existing literature.

To gain a deeper understanding of the acquired results, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 have been prepared for increasing values of time t, distinct values for K and Ha, fixed values of the frequency $\omega$ and of the material constants $\alpha ,\beta ,\gamma$ and $\delta$: namely, $\omega =\pi /6,\alpha =0.7,$ $\beta =0.6,\gamma =0.5$ and $\delta =0.4$. 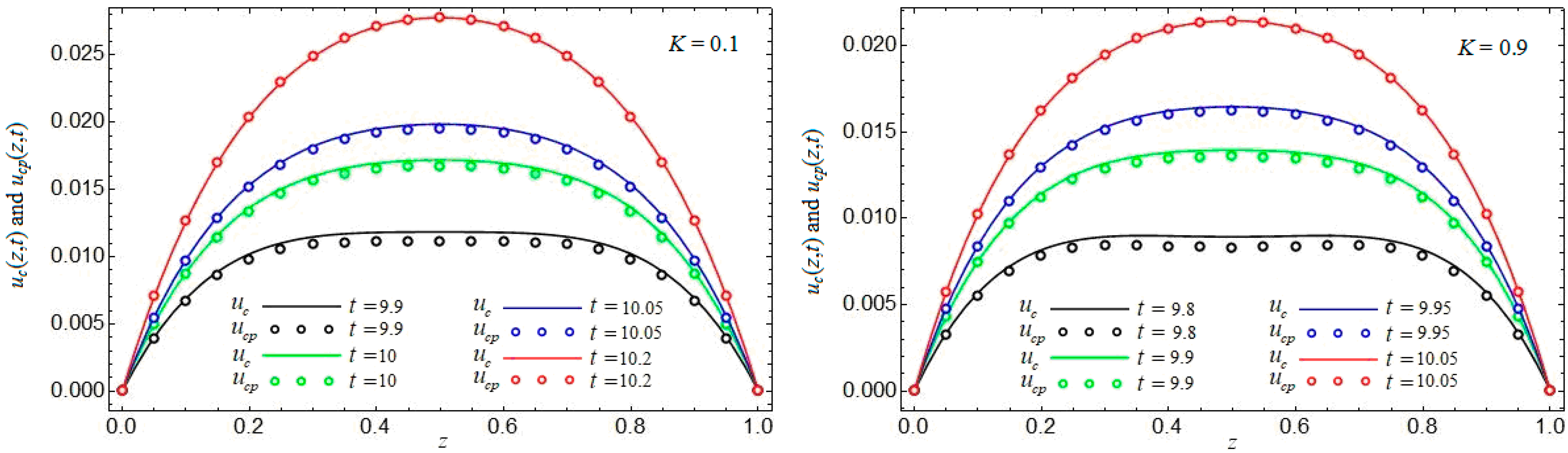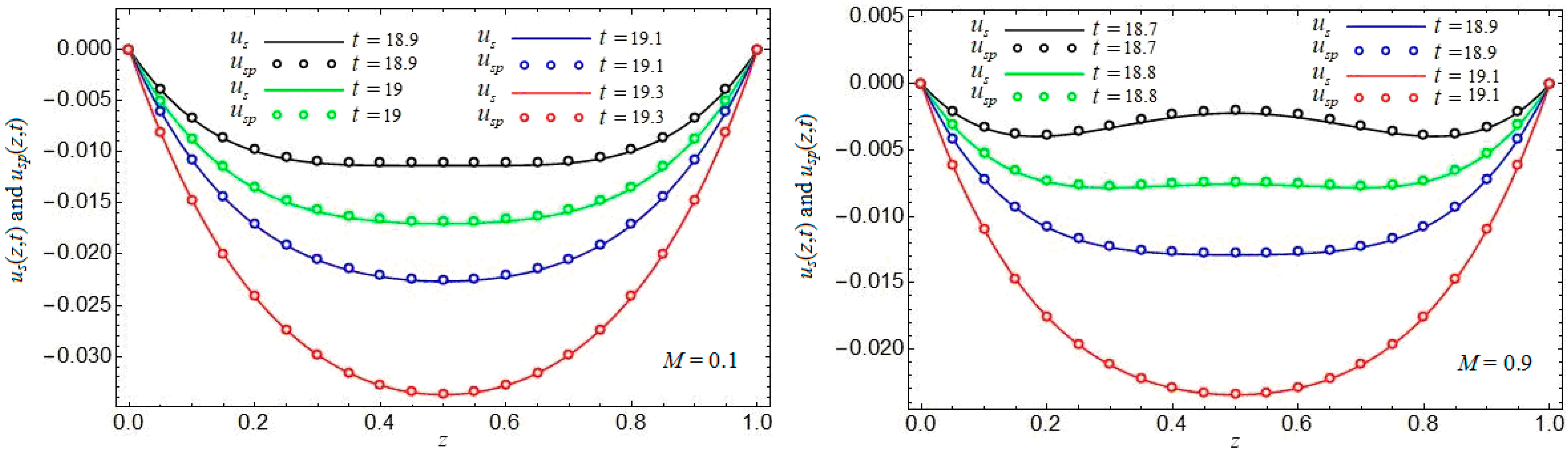Figure 3, Figure 4, Figure 5 and Figure 6, which show the convergence of starting solutions $u_c(z,t)$, $u_s(z,t)$ to their steady-state components $u_{cp}(z,t), u_{sp}(z,t)$, give the time needed to reach a steady state. This is the time after which the diagrams of the starting solutions overlap with those of their steady-state components. From these figures, it also results that the fluid velocity diminishes for increasing values of the parameter M or K. Consequently, the fluid flows slower in the presence of a magnetic field or porous medium. A similar result has been recently obtained by Kulkarni [24] for the MHD flow of a water-based hybrid nanofluid about a permeable rotating disk.

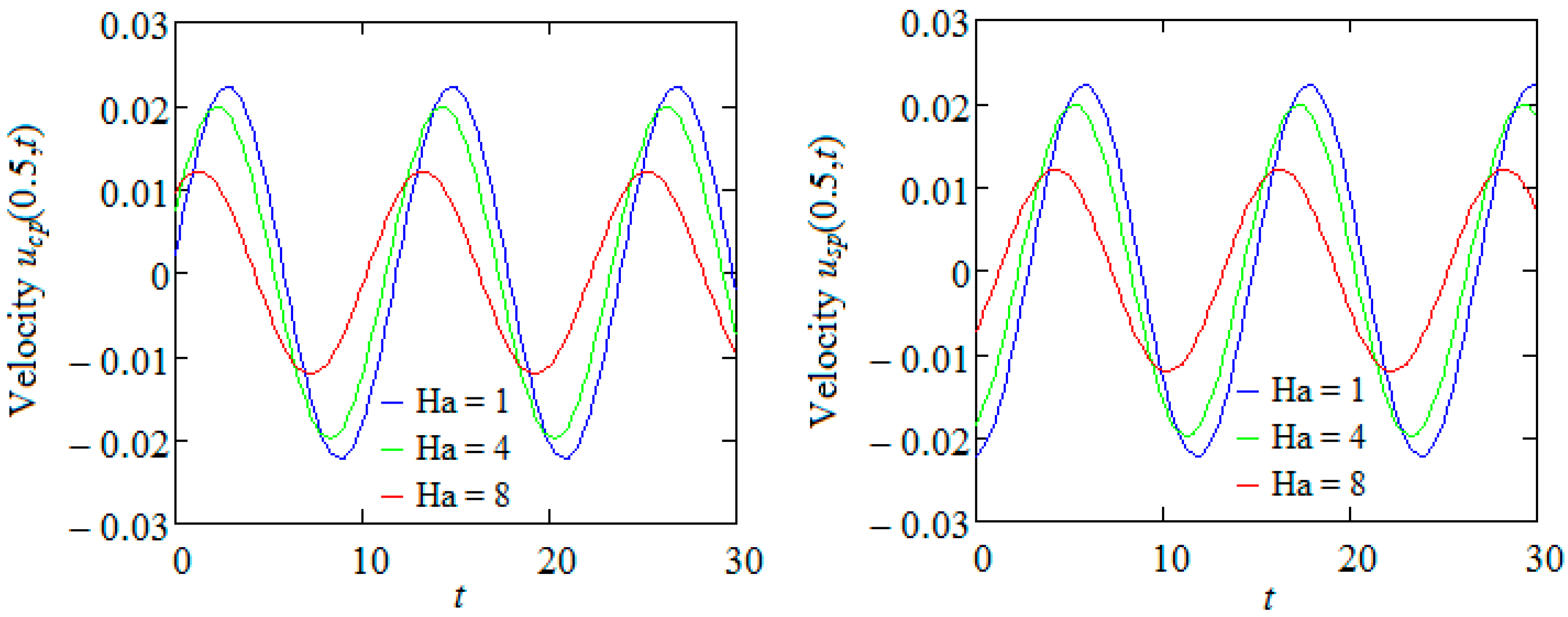
The variations in time of the steady-state velocities $u_{cp}(z,t)$ and $u_{sp}(z,t)$ given by Equations (26) and (27) at the middle of the channel are together depicted in Figure 7 and Figure 8 at distinct values of the Hartmann number Ha and porous parameter K. In each instance, the phase difference and the oscillatory behavior of the two motions are easily visualized. Moreover, as expected, the amplitudes of oscillations are identical for motions due to cosine or sine oscillations of the pressure gradient, and they decline for increasing values of Ha or K. Consequently, the fluid velocity diminishes in the presence of a magnetic field or porous medium. It means that, as we previously mentioned, the fluid moves faster in the absence of a magnetic field or porous medium.

Profiles of the steady-state velocity $u_{Cp}(z)$ and of the shear stress ${\tau }_{Cp}(z)$ are presented in Figure 9 at three values of the effective permeability $K_{eff}$. The fluid velocity, whose maximum values are touched at the middle of the channel in each case, is a decreasing function with regard to this parameter.

It results that the fluid flows slower in the presence of a magnetic field or porous medium. The shear stress is positive in the first half of the channel and negative in the other part. However, in absolute value it is a decreasing function with respect to $K_{eff}$ on the whole flow domain and takes a zero value at middle of the channel.

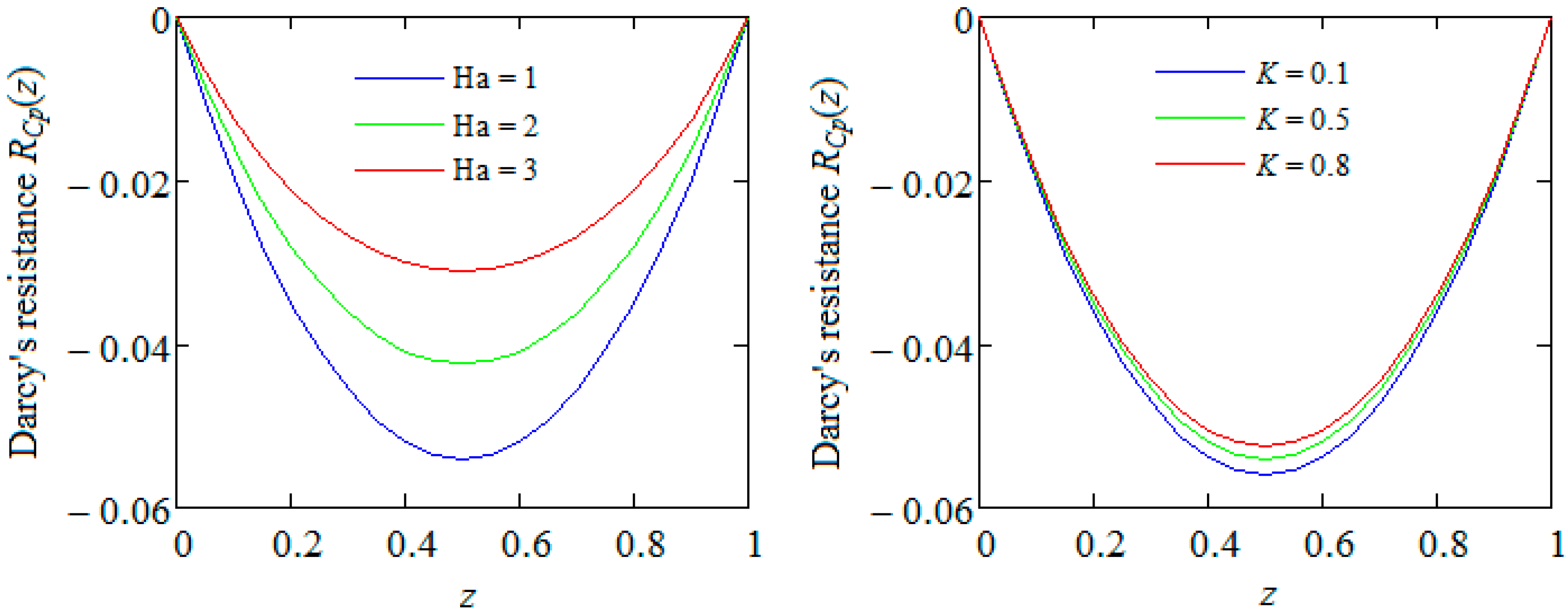
In the last Figure 10 are depicted the profiles of Darcy’s resistance $R_{Cp}(z)$ for increasing values of Ha and K, respectively. Their symmetry with respect to the median plane is clearly visualized. In all situations, as expected, the Darcy’s resistance has the minimum value in $z=0.5$, has maximum values equal to zero on the two plates and is an increasing function with respect to the Hartman number Ha and porous parameter K. It means that the fluid flows faster if the magnetic field or porous medium is absent. Of course, this outcome is in accord with those coming from Figure 7, Figure 8 and Figure 9.

5. Conclusions

Isothermal Poiseuille flows of ECIGBFs through an infinite plane channel have been investigated when magnetic and porous effects are taken into consideration. Closed-form expressions, which are new in the literature, have been established for steady-state solutions corresponding to Poiseuille flows induced by oscillatory and constant pressure gradients. Their correctness was graphically proved by means of Figure 1 or comparison with known results from the literature. More exactly, as it results from Section 3.2., known solutions from the existing literature were obtained as limiting cases of present results. In addition, the obtained results have been graphically used to bring to light the influence of a magnetic field and porous medium on the steady state and flow resistance of fluid. The main outcomes that have been obtained here are as follows:

-

The requisite time to attain the steady state diminishes with increasing values of the Hartmann number Ha or the porosity parameter K. Consequently, the steady state is achieved sooner in presence of a magnetic field or porous medium.

-

Fluid velocity is a decreasing function with respect to the effective permeability. It means that the flow velocity increases in the absence of a magnetic field or porous medium.

-

As expected, spatial variations in the fluid velocity, non-trivial shear stress and Darcy’s resistance are symmetric with respect to the median plane.