Abstract
In this paper, the -dimensional seventh-order Caudrey–Dodd–Gibbon–KP equation is investigated through the Lie group method. The Lie algebra of infinitesimal symmetries, commutative and adjoint tables, and one-dimensional optimal systems is presented. Then, the seventh-order Caudrey–Dodd–Gibbon–KP equation is reduced to nine types of -dimensional equations with the help of symmetry subalgebras. Finally, the unified algebra method is used to obtain the soliton solutions, trigonometric function solutions, and Jacobi elliptic function solutions of the seventh-order Caudrey–Dodd–Gibbon–KP equation.
1. Introduction
Nonlinear partial differential equations (NPDEs) have a wide range of applications in the natural sciences and engineering. In these fields, it is common to search for exact solutions to NPDEs, as these solutions provide precise descriptions of complex phenomena such as heat conduction and wave propagation. There are currently several powerful methods available for constructing exact solutions of NPDEs. These methods include the Bäcklund transformation method [1], Darboux transformation method [2,3], Lie group method [4,5,6], Hirota bilinear method [7], unified algebraic method [8], and so on.
The Lie group method is well known as a powerful tool for reducing high-dimensional equations into low-dimensional ones, or simplifying equations with a high number of variables into simpler ones. Furthermore, this method enables the discovery of similar solutions through symmetry reduction [9,10,11,12,13,14,15,16,17,18,19,20]. Therefore, it has become a commonly used technique in the field of differential equations research due to its widespread applicability.
The Korteweg–de Vries (KdV) equation, a fundamental equation in the field of integrable systems, is commonly used to describe weakly nonlinear shallow water waves [21],
where represents the nth order partial derivative with respect to x.
As a -dimensional extension of the KdV equation, the Kadomtsev–Petviashvili (KP) equation can be used to describe the evolution of nonlinear, long waves of small amplitude with slow dependence on the transverse coordinates [22],
where represents the 2nd order partial derivative with respect to y.
Due to the inability of the KdV Equation (1) to provide the detailed description of many important features observed in laboratory experiments, such as the non-monotonic relationship between solitary wave speed and amplitude, it becomes necessary to consider higher-order forms of the KdV equation such as the fifth-order KdV (fKdV) equation [23],
and the seventh-order KdV (sKdV) equation [24],
where and are arbitrary constants. Due to the arbitrariness of parameters , and , fKdV Equation (3) often manifests in several distinct representations, such as the Sawada–Kotera (SK) equation, the Caudrey–Dodd–Gibbon (CDG) equation, the Lax equation, the Kaup–Kuperschmidt (KP) equation, and the Ito equation. The fKdV Equation (3) is an essential model for many physical phenomena in fluid dynamics and magneto-acoustic waves. Similarly, the sKdV equation also has various forms including the Sawada–Kotera–Ito equation and the CDG equation, and these higher-order KdV equations play an important role in mathematical physics, engineering and applied sciences.
In this paper, our main focus is on the -dimensional seventh-order Caudrey–Dodd–Gibbon–KP (sCDG-KP) equation, which is formed by combining the seventh-order CDG equation and the KP equation,
The one and two soliton solutions of sCDG-KP Equation (5) are obtained using the simplified Hirota bilinear method [25].
Because of the complexity of the sCDG-KP Equation (5), there is currently limited research on it. The Lie group method is extremely effective for studying integrable or non-integrable NPDEs. Particularly for high-dimensional NPDEs, the application of the Lie group method can reduce the dimensionality of the given NPDEs, thereby enabling the possibility of obtaining exact solutions to the given NPDEs further. This paper employs the Lie group method and the unified algebraic method to investigate the optimal system of one-dimensional subalgebras, group-invariant solutions, symmetry reduction, and exact solutions of sCDG-KP Equation (5).
The structure of this paper is as follows. Section 2 presents the infinitesimal generators and vector fields that represent the symmetries of sCDG-KP Equation (5). Section 3 derives commutator relations for the infinitesimal generators and uses adjoint relations to construct a one-dimensional optimal system. Section 4 obtains some -dimensional equations by means of the symmetry reduction. Finally, exact solutions of sCDG-KP Equation (5) are obtained with the help of the unified algebra method.
2. Lie Point Symmetries
The construction of the symmetric algebras of the given NPEDs is a crucial step in the Lie group method. In this section, we first construct the infinitesimals of Equation (5). Based on the Lie group method, the one-parameter Lie group of point transformations in is defined as follows:
where , , , are infinitesimals, and is a group parameter. The vector field associated with the transformation group is
To obtain the Lie point symmetries for sCDG-KP Equation (5), the associated vector fields must satisfy the following invariant condition:
where represents the 8th order prolongation of vector field ,
and , , , , , are defined as follows:
and , , are the total derivatives of x, y, t. represents the k-order total derivative of x. .
Thus, invariant Equation (8) can be explicitly written as follows:
Substituting (10) into (11) and collecting coefficients of u and its various partial derivatives yields a set of determinant equations. The solutions of these determining equations provide the following infinitesimals for Equation (5):
where are arbitrary constants.
Thus, the Lie algebra of infinitesimal symmetries of Equation (5) is spanned by the five vector fields
One of the most significant applications of symmetry theory is the construction of group-invariant solutions. For each subgroup within the symmetry group, there exists a corresponding set of group-invariant solutions. Given that any linear combination of arbitrary infinitesimal quantities remains infinitesimal, this implies that a differential equation possesses infinitely many different symmetry subgroups. Consequently, enumerating all potential group-invariant solutions is virtually an impossible task. This gives rise to the classification problem of group-invariant solutions, also known as the optimal system. Constructing optimal systems of subgroups is equivalent to constructing optimal systems of subalgebras. For one-dimensional subalgebras, we only need to take the most general form of the Lie algebra, and then apply various adjoint transformations on it to simplify the algebraic form as much as possible. Next, we use this method to construct a one-dimensional optimal system of Lie algebra (13).
3. One-Dimensional Optimal System
In this section, we use the Hu–Li–Chen algorithm to construct the optimal system of the sCDG-KP Equation (5) [26,27]. In order to obtain the one-dimensional optimal system of Lie algebra, we first calculate the commutation relations of the Lie algebra (13). Via using these commutation relationships, the infinitesimals shown in (13) can be written as linear combination of :
Moreover, we derive the adjoint relations and obtain the symmetry subalgebras of the sCDG-KP equation.
3.1. Invariants of Lie Algebra
The Lie bracket for the infinitesimal generators is defined as
Hence, the commutation relations among the Lie algebra (13) can be derived, as shown in Table 1, the entry in row i and the column j representing .

Table 1.
Commutator table.
From Equation (16), for any , the following condition holds:
where .
3.2. Adjoint Matrix

Table 2.
Adjoint table.
The adjoint action of on V is given by
and therefore we have
Thus, the general adjoint transformation matrix A is derived as
where
3.3. Classification of Symmetry Algebra
The adjoint transformation equation of sCDG-KP Equation (5) is given by
where A is the adjoint transformation matrix (21). Direct calculation yields
According to the Hu–Li–Chen algorithm, there are two cases: and .
Case 1: For , we select a representative element, ; then, substituting , and into (23), we have
Case 2: For , substituting , into (18), we obtain a new invariant . Here are the three cases: , , and .
Case 2.1: Evidently, or .
Case 2.1.1: For , we let the representative element be . Then, by substituting and , into (23), we obtain
Case 2.1.2: For , we let the representative element be ; by substituting and , into (23), we obtain
Essentially, is equivalent to .
Case 2.2: . In this case, or .
Case 2.2.1: For , we let the representative element be ; by associating with (23), we obtain
Case 2.2.2: For , we select the representative element as .
Substituting to (23), we obtain
Case 2.3: . In this case, there are three cases: ; ; .
Case 2.3.1: .
For and , by substituting and , into (23), we have
For and , by substituting and , into (23), we have
Case 2.3.2: .
Substituting into (18), we obtain a new invariant
which includes the following three cases: , , .
When and , by substituting and , into (23), we obtain
When and , by substituting and , into (23), we obtain
When and , by substituting , , and , , into (23), we obtain
and
When , we obtain , by substituting and , into (23); the solution is
Similar to case 2.1.1, when and , the results are essentially the same; thus, we select the result corresponding to as the essential element.
Case 2.3.3: . We select and as the representative element.
Eventually, the symmetry subalgebras of the one-dimensional optimal system for the sCDG-KP Equation (5) are as follows:
4. Similarity Reductions
In this section, we apply the results of the one-dimensional optimal system discussed earlier to perform various symmetry reductions on sCDG-KP Equation (5). On the basis of (7), its corresponding characteristic equation is
4.1. Subalgebra
Based on vector field , Equation (25) becomes
Equation (26) provides the invariant functions of Equation (5),
and reduction equation
Since the calculation process is exactly the same as that of Case 1, we only list the results hereafter.
4.2. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.3. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.4. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.5. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.6. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.7. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.8. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.9. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
4.10. Subalgebra
The vector field is and the characteristic equation is
Similarity solutions are given by
The reduction equation is given by
One can observe that the -dimensional equation resulting from the reduction using and is identical.
5. Exact Solution
The unified algebraic method, which is one of the effective approaches for solving NPDEs, is employed in this section to derive solutions for sCDG-KP Equation (5).
For sCDG-KP Equation (5), we consider its solution to be of the following form:
where . By substituting (56) into Equation (5), we obtain the single soliton solution and the trigonometric solution
as well as three Jacobi periodic solutions
where
The physical characteristics of the exact solutions of sCDG-KP Equation (5) can be seen more clearly via Figure 1, Figure 2 and Figure 3. As is well known, soliton solutions are a type of localized and stable solution with broad applications in fields such as fiber optics, material physics, and nuclear physics. The Jacobi elliptic function solutions can degenerate into soliton solutions as .
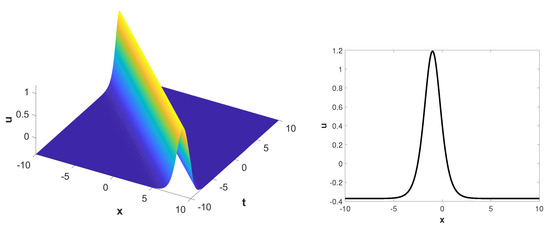
Figure 1.
Single soliton solution (57a): 3D graph with ; 2D graph with . The parameters are selected as .
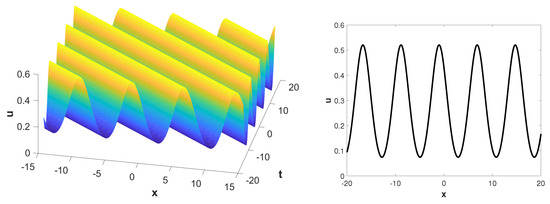
Figure 2.
Jacobi periodic solution (58a): 3D graph with ; 2D graph with . The parameters are selected as , .
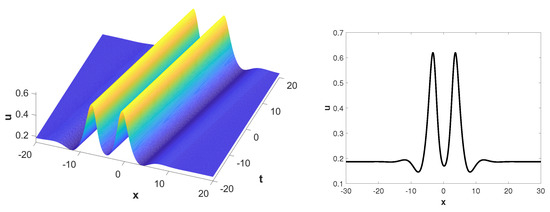
Figure 3.
The modulus of the Jacobi periodic solution (58b): 3D graph with ; 2D graph with . The parameters are selected as , .
6. Conclusions
The exact solutions of high-dimensional NPDEs have always been a hot topic in the field of mathematical physics. In this paper, the Lie group method is employed to derive four infinitesimals along with their corresponding symmetry algebras for sCDG-KP Equation (5). With the help of the one-dimensional optimal system and similarity reduction, sCDG-KP Equation (5) is reduced to nine classes of -dimensional NPDEs. Furthermore, by applying the unified algebraic method, various types of exact solutions are obtained, including soliton solutions, trigonometric function solutions, and Jacobi elliptic function solutions for sCDG-KP Equation (5).
Author Contributions
Conceptualization, M.Q. and M.Y.; methodology, M.Q. and Y.W.; software, M.Q.; validation, Y.W. and M.Y.; formal analysis, M.Q.; investigation, M.Q.; resources, Y.W. and M.Y.; data curation, M.Q.; writing—original draft preparation, M.Q.; writing—review and editing, Y.W. and M.Y.; visualization, M.Q.; supervision, Y.W.; project administration, Y.W. and M.Y.; funding acquisition, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by The National Natural Science Foundation of China (Nos. 12275172 and 11905124) and the Departmental Research Grant 2023-24 (MIT/DRG04/23-24) from the Education University of Hong Kong.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare that there are no conflicts of interest in relation to the publication of this work.
References
- Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin, German, 1991. [Google Scholar]
- Gu, C.H.; Hu, H.S.; Zhou, Z.X. Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry; Springer Science & Business Media: New York, NY, USA, 2004. [Google Scholar]
- Olver, P.J. Equivalence, Invariants and Symmetry; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations: A Beginner’s Guide; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Fan, E.G. Multiple travelling wave solutions of nonlinear evolution equations using a unified algebraic method. J. Phys. A Math. Gen. 2002, 35, 6853. [Google Scholar] [CrossRef]
- Lou, S.Y. Symmetries of the Kadomtsev-Petviashvili equation. J. Phys. A Math. Gen. 1993, 26, 4387. [Google Scholar] [CrossRef]
- Hu, X.R.; Chen, Y.; Huang, F. Symmetry analysis and explicit solutions of the (3+1)-dimensional baroclinic potential vorticity equation. Chin. Phys. B 2010, 19, 080203. [Google Scholar]
- Wang, G.W.; Liu, X.Q.; Zhang, Y.Y. Lie symmetry analysis to the time fractional generalized fifth-order KdV equation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2321–2326. [Google Scholar] [CrossRef]
- Sahoo, S.; Garai, G.; Saha Ray, S. Lie symmetry analysis for similarity reduction and exact solutions of modified KdV–Zakharov–Kuznetsov equation. Nonlinear Dyn. 2017, 87, 1995–2000. [Google Scholar] [CrossRef]
- Bansal, A.; Biswas, A.; Zhou, Q.; Babatin, M.M. Lie symmetry analysis for cubic–quartic nonlinear Schrödinger’s equation. Optik 2018, 169, 12–15. [Google Scholar] [CrossRef]
- Kumar, M.; Tiwari, A.K. Soliton solutions of BLMP equation by Lie symmetry approach. Comput. Math. Appl. 2018, 75, 1434–1442. [Google Scholar] [CrossRef]
- Biswas, A.; Vega-Guzman, J.; Bansal, A.; Kara, A.H.; Alzahrani, A.K.; Zhou, Q.; Belic, M.R. Optical dromions, domain walls and conservation laws with Kundu–Mukherjee–Naskar equation via traveling waves and Lie symmetry. Results Phys. 2020, 16, 102850. [Google Scholar] [CrossRef]
- Liu, F.Y.; Gao, Y.T.; Yu, X.; Li, L.Q.; Ding, C.C.; Wang, D. Lie group analysis and analytic solutions for a (2+1)-dimensional generalized Bogoyavlensky–Konopelchenko equation in fluid mechanics and plasma physics. Eur. Phys. J. Plus 2021, 136, 656. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K. Lie symmetry analysis, optimal system, exact solutions and dynamics of solitons of a (3+1)-dimensional generalised BKP–Boussinesq equation. Pramana-J. Phys. 2022, 96, 31. [Google Scholar] [CrossRef]
- Ali, M.R.; Ma, W.X.; Sadat, R. Lie symmetry analysis and invariant solutions for (2+ 1) dimensional Bogoyavlensky-Konopelchenko equation with variable-coefficient in wave propagation. J. Ocean Eng. Sci. 2022, 7, 248–254. [Google Scholar] [CrossRef]
- Paliathanasis, A. Symmetry analysis for the 2D aw-rascle traffic-flow model of multi-lane motorways in the Euler and Lagrange variables. Symmetry 2023, 15, 1525. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Jhangeer, A.; Raza, N. Symmetry and complexity: A Lie symmetry approach to bifurcation, chaos, stability and travelling wave solutions of the (3+1)-dimensional Kadomtsev-Petviashvili equation. Phys. Scr. 2023, 98, 115239. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Partial Differential Equations and Solitary Waves Theory; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersing media. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1970; Volume 192, pp. 753–756. [Google Scholar]
- Abbasbandy, S.; Zakaria, F.S. Soliton solutions for the fifth-order KdV equation with the homotopy analysis method. Nonlinear Dyn. 2008, 51, 83–87. [Google Scholar] [CrossRef]
- Salas, A.H.; Gómez S, C.A. Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math. Probl. Eng. 2010, 2010, 194329. [Google Scholar] [CrossRef]
- Wazwaz, A.M. One and two soliton solutions for seventh-order Caudrey-Dodd-Gibbon and Caudrey-Dodd-Gibbon-KP equations. Open Phys. 2012, 10, 1013–1017. [Google Scholar] [CrossRef]
- Hu, X.R.; Li, Y.Q.; Chen, Y. A direct algorithm of one-dimensional optimal system for the group invariant solutions. J. Math. Phys. 2015, 56, 053504. [Google Scholar] [CrossRef]
- Miao, Q.; Hu, X.R.; Chen, Y. ONEOptimal: A Maple package for generating one-dimensional optimal system of finite dimensional Lie algebra. Commun. Theor. Phys. 2014, 61, 160. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).