Semi-Separable Potentials as Solutions to the 3D Inverse Problem of Newtonian Dynamics

Abstract

We study the motion of a test particle in a conservative force-field. Our aim is to find three-dimensional potentials with symmetrical properties, i.e., $V(x,y,z)=P(x,y)+Q\left(z\right)$, or, $V(x,y,z)=P(x^2+y^2)+Q\left(z\right)$ and $V(x,y,z)=P(x,y)Q\left(z\right)$, where P and Q are arbitrary ${\mathcal{C}}^2$-functions, which are characterized as semi-separable and they produce a pre-assigned two-parametric family of orbits $f(x,y,z)$ = $c_1$, $g(x,y,z)$ = $c_2$ ($c_1$, $c_2$ = const) in 3D space. There exist two linear PDEs which are the basic equations of the Inverse Problem of Newtonian Dynamics and are satisfied by these potentials. Pertinent examples are presented for all the cases. Two-dimensional potentials are also included into our study. Families of straight lines is a special category of curves in 3D space and are examined separately.

1. Introduction

A dynamical system is a system whose state evolves with time over a state space according to a fixed rule. Examples of dynamical systems are the following ones: the growth of a population, a swinging pendulum, the motions of celestial bodies and so on. Mathematical methods for mechanical, electrical and biosystems were developed in [1]. Integrability [2], superintegrability [3], or, non-integrability [4] are some special properties of dynamical systems.

The inverse problem of dynamics, as formulated by [5], consists in looking for all potentials $V=V(x,y)$ which can produce a monoparametric family of planar orbits $f(x,y)=c$, traced in the $(x,y)$-Cartesian plane by a material point of unit mass with a preassigned energy dependence $\mathcal{E}=\mathcal{E}\left(f\right(x,y\left)\right)$ on the given family of orbits. The author produced a first-order partial differential equation, linear in the unknown function $V=V(x,y)$ whose coefficients depend on the family of orbits. Szebehely’s equation was later studied by many authors [6,7,8].

The three-dimensional inverse problem of dynamics, as described by [9], deals with the potentials $V=V(x,y,z)$ of $C^2$-class which produce a pre-assigned family of regular orbits given $f(x,y,z)=c_1,g(x,y,z)=c_2$ with a preasgned energy dependence $\mathcal{E}=\mathcal{E}\left(f\right(x,y,z),g(x,y,z\left)\right)$ on the given families of orbits. Before many years, several authors paid attention to this problem and studied different versions of it (see [10,11,12]). Especially, two-parametric families of straight lines (FSL) produced by three-dimensional potentials were studied in detail by [13]. The two free of energy PDEs of the three-dimensional inverse problem were found in [14,15]. Besides that, in [15], the authors constructed 3D homogeneous potentials of degree m producing homogeneous two-parametric families of orbits in 3D space and presented many examples. Other solvable cases of this problem were examined in [16,17]. In [18], the authors stated and solved a generalization of Dainelli and Joukovski problem and proposed a new method in order to solve the well-known Suslov’s problem. Inverse problems exist in many areas of Physics. More precisely, inverse problems for Schrödinger equation were studied by many authors in the past (e.g., [19]). An application of the inverse problem of dynamics in geometrical optics was given by [20]. Furthermore, ref. [21] approached the problem from the point of view of the general inverse problem of the calculus of variation. In [22] the authors presnted a direct method for solving inverse Sturm–Liouville problems Recently, integrable and superintegrable 3D Newtonian potentials were studied in [23] by using quadratic first integrals.

In this work we shall examine three-dimensional potentials of the form $V(x,y,z)=P(x,y)+Q\left(z\right)$, $V(x,y,z)=P(x^2+y^2)+Q\left(z\right)$ and $V(x,y,z)=P(x,y)Q\left(z\right)$ which are related to a two-parametric family of orbits $f(x,y,z)$ = $c_1$, $g(x,y,z)$ = $c_2$ ($c_1,c_2=const$). These potentials are common solutions of two linear PDEs which govern the Inverse Problem of dynamics; one of them is of first order and the second one is of second order.

The present paper has the following structure: In Section 2 we give the basic facts of the 3D Inverse Problem of Dynamics and we present the basic equations of this problem. Separable potentials have the general form $V=P\left(x\right)+Q\left(y\right)+R\left(z\right)$, or, $V=P\left(x\right)Q\left(y\right)R\left(z\right)$. Since the number of equations of the Inverse problem is two, i.e., Equations (9) and (11) in the text, and the functions $P\left(x\right),Q\left(y\right),R\left(z\right)$ are three, we choose semi-separable potentials of the form $V(x,y,z)=P(x,y)+Q\left(z\right)$, $V(x,y,z)=P(x^2+y^2)+Q\left(z\right)$ and $V(x,y,z)=P(x,y)Q\left(z\right)$ in order to handle the two equations of the Inverse problem. Thus, we start our survey with potentials $V(x,y,z)=P(x,y)+Q\left(z\right)$ and we develop a new methodology for this kind of potentials in Section 3. The second order PDE of the inverse problem becomes a linear second order PDE in the unknown function $P(x,y)$ and can be solved analytically under ceratin conditions. In Section 4 we work with potentials $V(x,y,z)=P(x^2+y^2)+Q\left(z\right)$. From the second order PDE we retrieve two linear O.D.Es in the unknown functions $P,Q$ respectively which are solvable. This technique help us to find the general solution for the potential V. Our results are connected with integrability/superintegrability of potentials which are under consideration.

In Section 5 we study the third class of potentials $V=P(x,y)Q\left(z\right)$. This class is more complicated than the previous ones. Now, the second order PDE becomes a non-linear PDE in the unknown function $P=P(x,y)$ and cannot be solved analytically by using the classical methods of the theory of PDEs. Thus, we look only for special solutions. We offer examples for all cases. The results are new and original. Special cases are studied in Section 6. Another category of potentials is the two-dimensional ones (Section 7). Two-parametric families of orbits produced by two-dimensional potentials were examined in [24]. Furthermore, an interesting case of curves in 3D space is a family of straight lines. As it was shown by [13], not any potentials, but only those satisfying two non-linear PDEs can produce a family of straight lines as orbits. We find appropriate potentials which correspond to the above cases in Section 8 and we are making some concluding comments in Section 9.

2. The Formulation of the 3D Inverse Problem

We consider the two-parametric family of orbits given

$$f(x,y,z)=c_1,g(x,y,z)=c_2,c_1,c_2=const.$$

(1)

Generally speaking, the two–parametric families of orbits written in the form (1) are studied in a three-dimensional frame. The most general question in Classical Mechanics is to find a potential function $V(x,y,z)$ such that the set of integral curves of the classical mechanical system

$$\ddot{x}=-\frac{\partial V}{\partial x},\ddot{y}=-\frac{\partial V}{\partial y},\ddot{z}=-\frac{\partial V}{\partial z},$$

(2)

contains the given family (1). Following [14,15,24], we define the vector $\overrightarrow{\delta }$ = $\nabla f\times \nabla g$ which is proportional to the velocity. Its components are

$${\delta }_1=f_y{g}_z-f_z{g}_y,{\delta }_2=f_z{g}_x-f_x{g}_z,{\delta }_3=f_x{g}_y-f_y{g}_x.$$

(3)

As it was shown by [14,15,24], the family of orbits (1) can be represented by two “slope functions”

$$\alpha =\alpha (x,y,z)and\beta =\beta (x,y,z),$$

(4)

given by the formulas

$$\alpha :=\frac{{\delta }_2}{{\delta }_1},\beta :=\frac{{\delta }_3}{{\delta }_1}.$$

(5)

On the other hand, if the pair of slope functions ($\alpha ,\beta$) is given in advance, then we can solve analytically the system of O.D.Es

$$\frac{dy}{dx}=\alpha (x,y,z,),\frac{dz}{dx}=\beta (x,y,z)$$

(6)

and find the two-parametric family of orbits in the form (1). The following notation is also introduced

$${\alpha }_0={\alpha }_x+\alpha {\alpha }_y+\beta {\alpha }_z,{\beta }_0={\beta }_x+\alpha {\beta }_y+\beta {\beta }_z,\Theta =1+{\alpha }^2+{\beta }^2.$$

(7)

and the subscripts denote partial derivatives w.r.t. the variables $x,y,z$. There are two basic equations for our problem (see e.g., [15], p. 346). Taking into account that ${\alpha }_0\ne$ 0, or, ${\beta }_0\ne$ 0, these equations read

$$\begin{array}{ccc}\hfill \alpha V_x-V_y& =& \frac{2{\alpha }_0}{\Theta }(\mathcal{E}-V),\hfill \\ \hfill \beta V_x-V_z& =& \frac{2{\beta }_0}{\Theta }(\mathcal{E}-V).\hfill \end{array}$$

(8)

The above Equation (8) include the energy-dependence $\mathcal{E}=\mathcal{E}(f,g)$. Proceeding more, ref. [15] eliminated the energy of the family of orbits from these two equations and obtained two new equations which include only the derivatives of the potential V and the set of slope functions $(\alpha ,\beta )$. These equations are the following ones

$$j_1{V}_x+j_2{V}_y+j_3{V}_z=0,$$

(9)

where

$$j_1=\alpha {\beta }_0-\beta {\alpha }_0,j_2=-{\beta }_0,j_3={\alpha }_0.$$

(10)

and

$$l_{11}{V}_{xx}+l_{12}{V}_{xy}+l_{13}{V}_{xz}+l_{22}{V}_{yy}+l_{23}{V}_{yz}+l_{01}{V}_x+l_{02}{V}_y+l_{03}{V}_z=0,$$

(11)

where

$$\begin{array}{c}{l}_{11}=\alpha \Theta {\alpha }_0,l_{12}=({\alpha }^2-1)\Theta {\alpha }_0,l_{13}=\alpha \beta \Theta {\alpha }_0,l_{22}=-\alpha \Theta {\alpha }_0,l_{23}=-\beta \Theta {\alpha }_0,\hfill \\ l_{01}=(\Theta +2){\alpha }_0^2+\alpha K,l_{02}=2\alpha {\alpha }_0^2-K,l_{03}=2\beta {\alpha }_0^2,\hfill \\ K=2(\alpha {\alpha }_0+\beta {\beta }_0){\alpha }_0-\Theta ({\alpha }_{0x}+\alpha {\alpha }_{0y}+\beta {\alpha }_{0z}).\hfill \end{array}$$

(12)

It is remarkable to say that if ${\alpha }_0=0,{\beta }_0\ne 0$, then we shall make use of another second-order PDE given in the paper of ([17], p. 9226). This PDE reads

$$m_{11}{V}_{xx}+m_{12}{V}_{xy}+m_{13}{V}_{xz}+m_{23}{V}_{yz}+m_{33}{V}_{zz}+m_{01}{V}_x+m_{02}{V}_y+m_{03}{V}_z=0,$$

(13)

where

$$\begin{array}{ccc}\hfill m_{11}& =& \tilde{n}\beta ,m_{12}=\tilde{n}\alpha \beta ,m_{13}=\tilde{n}({\beta }^2-1),m_{23}=-\tilde{n}\alpha ,m_{33}=-\tilde{n}\beta ,\hfill \\ \hfill m_{01}& =& 2+\beta {\tilde{n}}_0+\tilde{n}{\beta }_0,m_{02}=2\alpha ,m_{03}=2\beta -{\tilde{n}}_0\hfill \end{array}$$

(14)

and

$$\tilde{n}=\frac{\Theta }{{\beta }_0},{\tilde{n}}_0={\tilde{n}}_x+\alpha {\tilde{n}}_y+\beta {\tilde{n}}_z$$

(15)

The energy of family of orbits (1) is found to be [15]:

$$\mathcal{E}=\frac{\Theta }{2{\alpha }_0}(\alpha V_x-V_y)+V,$$

(16)

and the kinetic energy of the test particle is

$$T=\mathcal{E}-V.$$

(17)

Theorem 1.

If for the given family of orbits (1) the condition ${\alpha }_0={\beta }_0$ = 0 valids, the family of orbits is a family of straight lines [13] and this case will be studied in Section 8.

3. The Methodology for Our Problem

In this section we are interested in potentials of the form

$$V=P(x,y)+Q\left(z\right),$$

(18)

which are common solutions of the above two Equations (9) and (11) and $P,Q$ are arbitrary $C^2$-functions of their arguments. First of all, we find the first order derivatives of the potential function V with respect to $x,y,z$ respectively, i.e., $V_x=P_x$, $V_y=P_y$, $V_z=Q^{\prime }\left(z\right)$, where $Q^{\prime }\left(z\right)$ = $\frac{dQ}{dz}$. We insert them into (9) and get

$$j_1{P}_x+j_2{P}_y+j_3{Q}^{\prime }\left(z\right)=0$$

(19)

Setting $j_3\ne 0$, we find the expression for $Q^{\prime }\left(z\right)$. It is:

$$Q^{\prime }\left(z\right)={\kappa }_1{P}_x+{\kappa }_2{P}_y$$

(20)

where ${\kappa }_1=-\frac{j_1}{j_3},{\kappa }_2=-\frac{j_2}{j_3}$.

Now, we will work with the PDE (11). We obtain the derivatives of second order of the potential function V with respect to $x,y,z$ and we insert them into Equation (11). Thus, we get the linear second-order PDE

$$l_{11}{P}_{xx}+l_{12}{P}_{xy}+l_{22}{P}_{yy}+l_{01}{P}_x+l_{02}{P}_y+l_{03}{Q}^{\prime }\left(z\right)=0.$$

(21)

If we insert (20) into (21), then the PDE (21) reads

$$l_{11}{P}_{xx}+l_{12}{P}_{xy}+l_{22}{P}_{yy}+{\mu }_{01}{P}_x+{\mu }_{02}{P}_y=0,$$

(22)

where ${\mu }_{01}=l_{01}+{\kappa }_1{l}_{03}$ and ${\mu }_{02}=l_{02}+{\kappa }_2{l}_{03}$. Since the unknown function $P(x,y)$ in (22) depends only on two variables $x,y$, the corresponding coefficients $l_{11},l_{12},l_{22},{\mu }_{01},{\mu }_{02}$ must have the same property. Now, we can formulate the next

Theorem 2.

If the coefficients in (22) satisfy the differential conditions

$$\frac{\partial l_{11}}{\partial z}=\frac{\partial l_{12}}{\partial z}=\frac{\partial l_{22}}{\partial z}=\frac{\partial {\mu }_{01}}{\partial z}=\frac{\partial {\mu }_{02}}{\partial z}=0,$$

(23)

then we can find the general solution of (22), otherwise not.

Results

In this Section we present the first example.

Example 1.

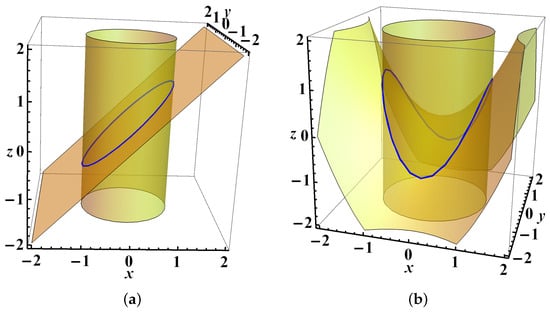
We study the two-parametric family of orbits (see Figure 1a)

$$f(x,y,z)=x^2+y^2=c_1,g(x,y,z)=\frac{z}{x}=c_2$$

(24)

which is represented by the pair

$$\alpha =-\frac{x}{y},\beta =\frac{z}{x}.$$

(25)

After some simplifications, the coefficients in (22) take the form

$$l_{11}=1,l_{12}=-\frac{x}{y}+\frac{y}{x},l_{22}=-1,{\mu }_{01}=\frac{3}{x},{\mu }_{02}=-\frac{3}{y}.$$

(26)

According to the Theorem 2, the coefficients (26) satisfy the condition (23). Then, the PDE (22) reads

$$xy{P}_{xx}+(y^2-x^2)P_{xy}-xy{P}_{yy}+3y{P}_x-3x{P}_y=0,$$

(27)

The discriminant of the characteristic equation of the PDE (27) is

$$\Delta ={(y^2-x^2)}^2+4x^2{y}^2=(x^2+y^2)>0.$$

(28)

So, the PDE (27) is hyperbolic and the characteristic roots are

$${\rho }_1=\frac{x}{y},{\rho }_2=-\frac{y}{x}.$$

(29)

Proceeding more, we solve the system

$$\frac{dy}{dx}+\frac{x}{y}=0,\frac{dy}{dx}-\frac{y}{x}=0$$

(30)

and we find the characteristic curves

$$y^2+x^2={\tilde{c}}_1,\frac{y}{x}={\tilde{c}}_2,$$

(31)

where ${\tilde{c}}_1,{\tilde{c}}_2=$ const. We make the transformation

$$\xi =y^2+x^2,\eta =\frac{y}{x},$$

(32)

and we estimate the first and second-order derivatives of the function P with respect to the new variables $\xi ,\eta$. After some straightforward algebra, the PDE (27) reads

$$\xi P_{\xi \eta }+P_{\eta }=0,$$

(33)

or, equivalently,

$$\frac{\partial }{\partial \xi }\left(\xi P_{\eta }\right)=0.$$

(34)

The general solution of (34) is

$$P(\xi ,\eta )=\frac{1}{\xi }\int T\left(\eta \right)d\eta +\Phi \left(\xi \right),$$

(35)

where $T,\Phi$ are arbitrary functions of their unique arguments respectively. We turn back to the old variables $x,y$ and the general solution (35) is written as

$$P(x,y)=\frac{1}{x^2+y^2}T\left(\frac{y}{x}\right)+\Phi (x^2+y^2).$$

(36)

Finally, we have to determine the function $Q=Q\left(z\right)$. We insert (36) into (20) and we check the following conditions

$$\frac{\partial Q^{\prime }\left(z\right)}{\partial x}=\frac{\partial Q^{\prime }\left(z\right)}{\partial y}=0.$$

(37)

The conditions (37) are satisfied if and only if

$$T\left(\frac{y}{x}\right)=d_0,d_0=const.,\frac{d\Phi \left(u\right)}{du}=1+\frac{d_0}{u^2},u=x^2+y^2,$$

(38)

or, equivalently,

$$\Phi \left(u\right)=u-\frac{d_0}{u},u=x^2+y^2.$$

(39)

By using the relations (36) and (39), we find

$$P(x,y)=x^2+y^2.$$

(40)

From (20), we have

$$Q^{\prime }\left(z\right)=\frac{dQ}{dz}=2z,$$

(41)

and the result is

$$Q\left(z\right)=z^2+d_1,d_1=const.$$

(42)

With the aid of (40) and (42), we obtain the potential

$$V(x,y,z)=x^2+y^2+z^2+d_1$$

(43)

which is integrable.

Remark 1.

If the coefficients in (26) depend implicitly on the variables $x,y,z$, then we cannot find the general solution of the PDE (27) because the unknown function $P(x,y)$ depends only on two variables $x,y$. In this case we can look only for special solutions.

4. Potentials of the Form $\mathit{V}(\mathit{x},\mathit{y},\mathit{z})=\mathit{P}({\mathit{x}}^{\mathbf{2}}+{\mathit{y}}^{\mathbf{2}})+\mathit{Q}\left(\mathit{z}\right)$

In this paragraph we shall deal with Equations (9) and (13) and study the second class of potentials

$$V=P(x^2+y^2)+Q\left(z\right),$$

(44)

where $P\left(u\right),u=x^2+y^2$ and $Q\left(z\right)$ are arbitrary functions of their arguments u and z respectively. At the first step, we find the derivatives: $V_x=2x{P}^{\prime }\left(u\right)Q$, $V_y=2y{P}^{\prime }\left(u\right)Q$, $V_z=Q^{\prime }\left(z\right)$, where $P^{\prime }\left(u\right)$=$\frac{dP}{du}$ and $Q^{\prime }\left(z\right)$=$\frac{dQ}{dz}$. We insert them into (9) and obtain

$$2(j_{1}x+j_{2}y)P^{\prime }\left(u\right)+j_3{Q}^{\prime }\left(z\right)=0.$$

(45)

If $j_3\ne$ 0, then we proceed as follows. From (45) we get

$$P^{\prime }\left(u\right)=\lambda Q^{\prime }\left(z\right),\lambda =-\frac{j_3}{2(j_{1}x+j_{2}y)}.$$

(46)

Since $P=P\left(u\right)$, it must be $\lambda =\lambda \left(z\right)$. Thus, we have

$$P^{\prime }\left(u\right)=\lambda \left(z\right)Q^{\prime }\left(z\right)=d_0=const.$$

(47)

From (47) we find the functions $P=P\left(u\right)$ and $Q=Q\left(z\right)$. It is:

$$P\left(u\right)=d_{0}u,Q\left(z\right)=\int \frac{d_0}{\lambda \left(z\right)}dz+d_1,d_1=const.$$

(48)

Next we proceed with the second order derivatives of the potential function (44) with respect to $u,z$ and we insert them into Equation (13). After that, we get the following expression

$$e_1{P}^{\prime }\left(u\right)+e_2{P}^{″}\left(u\right)+e_3{Q}^{\prime }\left(z\right)+e_4{Q}^{″}\left(z\right)=0.$$

(49)

where

$$\begin{array}{ccc}\hfill e_1& =& 2m_{11}+2x{m}_{01}+2y{m}_{02},e_2=4(x^2{m}_{11}+xy{m}_{12})\hfill \\ \hfill e_3& =& m_{03},e_4=m_{04}\hfill \end{array}$$

(50)

Theorem 3.

If the coefficients in (50) satisfy the following conditions:

$$\frac{\partial e_1}{\partial z}=\frac{\partial e_2}{\partial z}=0,\frac{\partial e_3}{\partial u}=\frac{\partial e_4}{\partial u}=0.$$

(51)

then we can retrieve solutions from (49), otherwise not.

Consequently, the Equation (49) can be rewritten in a more concise form:

$$e_1{P}^{\prime }\left(u\right)+e_2{P}^{″}\left(u\right)=-(e_3{Q}^{\prime }\left(z\right)+e_4{Q}^{″}\left(z\right))=b_0=const.$$

(52)

Thus, we have to solve two independent O.D.E.s namely

$$e_1{P}^{\prime }\left(u\right)+e_2{P}^{″}\left(u\right)=b_0,$$

(53)

and

$$e_3{Q}^{\prime }\left(z\right)+e_4{Q}^{″}\left(z\right)=-b_0.$$

(54)

The additon of these two solutions provides us with the result $V=P\left(u\right)+Q\left(z\right)$.

Remark 2.

If $j_3=$ 0, then we check the expression of ${\tilde{j}}_0=2(j_{1}x+j_{2}y)$. We distinguish two cases:

• ${\tilde{j}}_0=$ 0. Then, the relation (45) is satisfied identically.
• ${\tilde{j}}_0\ne$ 0. Then we have $P^{\prime }\left(u\right)=$0. This result leads to $P\left(u\right)=const.$ which is excluded from our study.

Results for the Second Case

In this paragraph we shall preseng two examples for this case.

Example 2.

We consider the family of orbits (see Figure 1b)

$$f(x,y,z)=x^2+y^2=c_1,g(x,y,z)=\frac{x^2-y^2}{z}=c_2$$

(55)

which is related to the pair

$$\alpha =-\frac{x}{y},\beta =\frac{4xz}{x^2-y^2}.$$

(56)

We will find a potential of the form (44) which produces the above family of orbits. For the given family of orbits (55), we have $j_3\ne$ 0 and

$$\lambda \left(z\right)=\frac{1}{8z}.$$

(57)

From (48) we find the functions $P=P\left(u\right)$ and $Q=Q\left(z\right)$. It is:

$$P=d_{0}u,Q\left(z\right)=4z^2.$$

(58)

and we replace them into (49). The last equation is satisfied only for $d_0$= 1. Thus, we obtain

$$V(x,y,z)=P(x^2+y^2)+Q\left(z\right)=x^2+y^2+4z^2.$$

(59)

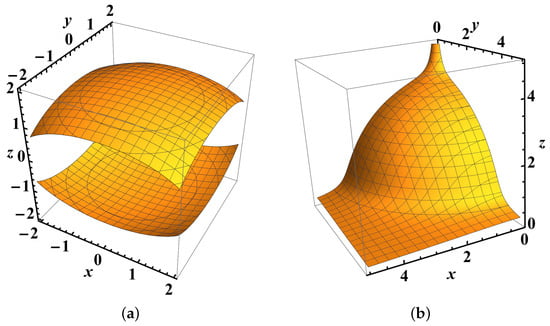
A 3D contour plot of the potential (59) is shown at Figure 2a.

Example 3.

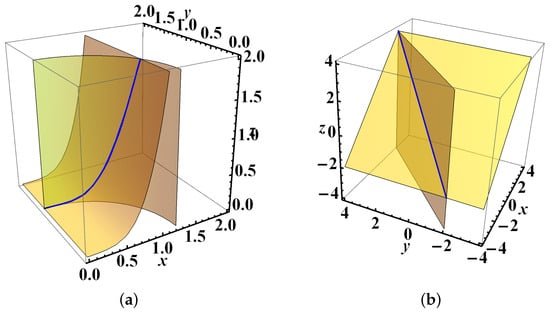
The following family of orbits is considered (see Figure 3a)

$$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=x^2+2y^2+3z^2=c_2.$$

(60)

The corresponding pair of slope functions $(\alpha ,\beta )$ is

$$\alpha =\frac{y}{x},\beta =-\frac{x^2+2y^2}{3xz}.$$

(61)

In this case we have ${\alpha }_0=0,{\beta }_0\ne 0$. But we can apply our theory because we deal with Equations (9) and (13). We shall find a potential of the form (44) which creates the above family of orbits. For the given family of orbits (55), we have

$$j_3=0and{\tilde{j}}_0=0.$$

(62)

Thus, the relation (45) is satisfied identically. Now, we proceed with the Equations (53) and (54). After some simplifications the coefficients in (52) take the form

$$e_1=1,e_2=\frac{1}{2}(x^2+y^2)=\frac{1}{2}u,e_3=-\frac{3}{8z},e_4=-\frac{1}{8}.$$

(63)

and we solve analytically O.D.Es. (53) and (54). The solution of the O.D.E. (53) is

$$P\left(u\right)=b_{0}u-\frac{d_1}{u}+d_2,d_1,d_2=const.$$

(64)

or, equivalently,

$$P(x^2+y^2)=b_0(x^2+y^2)-\frac{d_1}{x^2+y^2}+d_2,d_1,d_2=const.$$

(65)

and the solution of O.D.E. (54) is

$$Q\left(z\right)=b_0{z}^2-\frac{d_3}{2z^2}+d_4,d_3,d_4=const.$$

(66)

Thus, we obatin the result

$$V(x,y,z)=b_0(x^2+y^2+z^2)-\frac{d_1}{x^2+y^2}-\frac{d_3}{2z^2},$$

(67)

A 3D contour plot of the potential (67) is shown at Figure 2b. The energy of family of orbits (60) is given by

$$\mathcal{E}=-\frac{d_1(2+c_1^2)(1+2c_1^2)}{3{(1+c_1^2)}^2{c}_2}+\frac{9d_3(2+c_1^2)+2b_0(4+5c_1^2)c_2^2}{6(1+2c_1^2)c_2}.$$

(68)

The potential (67) is separable in cylindrical coordinates. Indeed, if we set ${\rho }^2=x^2+y^2,z=z$, then we get

$$V(\rho ,z)=(b_0{\rho }^2-\frac{d_1}{{\rho }^2})+(b_0{z}^2-\frac{d_3}{2z^2}).$$

(69)

Without loss of generality, we can omit the other additive constants in (67), or, in (69). As it was shown by ([3], p. 5669), the potential in (67) is minimally superintegrable because it admits four globally defined and single-valued integrals of motion. Other families of orbits generated by this potential are given at

Table 1. Families of orbits generated by the potential (67).

Families of Orbits	Pair $(\mathit{\alpha },\mathit{\beta })$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=x^2+y^2+2z^2=c_2$	$\alpha =\frac{y}{x},\beta =-\frac{x^2+y^2}{2xz}$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=x^2+16y^2+9z^2=c_2$	$\alpha =\frac{y}{x},\beta =-\frac{x^2+16y^2}{9xz}$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=x^2-16y^2+9z^2=c_2$	$\alpha =\frac{y}{x},\beta =-\frac{x^2-16y^2}{9xz}$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=x^2-16y^2-9z^2=c_2$	$\alpha =\frac{y}{x},\beta =\frac{x^2-16y^2}{9xz}$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=xy+z^2=c_2$	$\alpha =\frac{y}{x},\beta =-\frac{y}{z}$

. Additional results are presented at

Table 2. Families of orbits compatible with 3D potentials.

Families of Orbits	Potential $\mathit{V}(\mathit{x},\mathit{y},\mathit{z})$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=xz=c_2$	$V=k_0(x^2+y^2+z^2)+\frac{d_1}{2}{(x^2+y^2)}^2+\frac{1}{4}{z}^4$
$f(x,y,z)=\frac{y}{x}=c_1,g(x,y,z)=\frac{z}{\sqrt{x}}=c_2$	$V=k_0(x^2+y^2+\frac{1}{4}{z}^2)+2d_1\sqrt{x^2+y^2}-\frac{d_1}{2z^2}$

.

5. The Third Case: $\mathit{V}=\mathit{P}(\mathit{x},\mathit{y})\mathit{Q}\left(\mathit{z}\right)$

In this paragraph we shall examine potentials of the form

$$V=P(x,y)Q\left(z\right),$$

(70)

for the above two Equations (9) and (11), where $P(x,y)$ and $Q\left(z\right)$ are arbitrary functions of their arguments. At the beginning, we determine the derivatives: $V_x=P_{x}Q$, $V_y=P_{y}Q$, $V_z=P(x,y)Q^{\prime }\left(z\right)$, where $Q^{\prime }\left(z\right)$ = $\frac{dQ}{dz}$. We insert them into (9) and get

$$j_1{P}_{x}Q+j_2{P}_{y}Q+j_{3}P{Q}^{\prime }\left(z\right)=0$$

(71)

Putting $j_3\ne 0$, we find the expression for the ratio $\frac{Q^{\prime }\left(z\right)}{Q}$. It is:

$$\frac{Q^{\prime }\left(z\right)}{Q}=\frac{({\kappa }_1{P}_x+{\kappa }_2{P}_y)}{P}$$

(72)

where ${\kappa }_1=-\frac{j_1}{j_3},{\kappa }_2=-\frac{j_2}{j_3}$. Now, we concentrate on the second order PDE (11). We obtain the second order derivatives of the potential function V and we insert them into Equation (11). Then, we get the second-order PDE

$$(l_{11}{P}_{xx}+l_{12}{P}_{xy}+l_{22}{P}_{yy}+l_{01}{P}_x+l_{02}{P}_y)Q+(l_{13}{P}_x+l_{23}{P}_y+l_{03}P)Q^{\prime }\left(z\right)=0.$$

(73)

If we replace (72) into (73), then the non-linear PDE (73) reads

$$(l_{11}{P}_{xx}+l_{12}{P}_{xy}+l_{22}{P}_{yy}+l_{01}{P}_x+l_{02}{P}_y)P+(l_{13}{P}_x+l_{23}{P}_y+l_{03}P)({\kappa }_1{P}_x+{\kappa }_2{P}_y)=0.$$

(74)

Example 4.

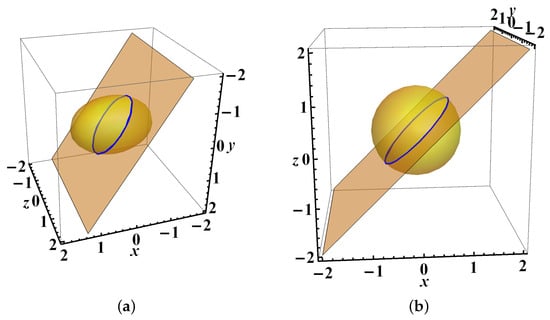
We take into account the family of orbits (circles, see Figure 3b)

$$f(x,y,z)=x^2+y^2+z^2=c_1,g(x,y,z)=\frac{z}{x}=c_2$$

(75)

and the pair is

$$\alpha =-\frac{x^2+z^2}{xy},\beta =\frac{z}{x}.$$

(76)

After some simplifications, the coefficients in (74) take the form

$$\left\{\begin{array}{c}{l}_{11}=1,l_{12}=-\frac{(x^2-xy+z^2)(x^2+xy+z^2)}{xy(x^2+z^2)},l_{13}=\frac{z}{x},\hfill \\ l_{22}=-1,l_{23}=\frac{yz}{x^2+z^2},\hfill \\ l_{01}=\frac{3x^2+z^2}{x(x^2+z^2)},{ł}_{02}=-\frac{3}{y},l_{23}=\frac{2z}{x^2+z^2}.\hfill \end{array}\right.$$

Since the PDE (74) is nonlinear, we find special solutions of the form

$$P(x,y)=M\left(u\right),u=x^2+y^2.$$

(77)

We replace (77) into (74), we take

$$\frac{4z^2{(x^2+z^2)}^2{(x^2+y^2+z^2)}^3}{x^5{y}^6}\left[{\left(M^{\prime }\left(u\right)\right)}^2-M\left(u\right)M^{″}\left(u\right)\right]=0,$$

(78)

where $M^{\prime }\left(u\right)$ = $\frac{dM}{du}$. The general solution of (78) is

$$M\left(u\right)=d_1{e}^u+d_2,d_1,d_2=const.$$

(79)

or, equivalently,

$$M(x^2+y^2)=d_1{e}^{x^2+y^2}+d_2,d_1,d_2=const.$$

(80)

Finally, we have to determine the ratio $R\left(z\right)=\frac{Q^{\prime }\left(z\right)}{Q\left(z\right)}$. We insert (80) into (72) and we check the following conditions

$$\frac{\partial R\left(z\right)}{\partial x}=\frac{\partial R\left(z\right)}{\partial y}=0.$$

(81)

The conditions (81) are satisfied if and only if

$$d_2=0$$

(82)

Thus, we have

$$\frac{Q^{\prime }\left(z\right)}{Q\left(z\right)}=2z,$$

(83)

and the result is

$$Q\left(z\right)=d_3{e}^{z^2},d_3=const.$$

(84)

With the aid of (77), (80) and (84), we find the potential

$$V(x,y,z)=d_3{e}^{x^2+y^2+z^2}$$

(85)

6. Special Cases

Up to now we considered that $j_3\ne$ 0 ($j_3$ is defined in (10)). In this paragraph we shall examine the case $j_3$ = 0. This leads to the result ${\alpha }_0$ = 0. Thus, we have to use the Equations (9) and (13). We choose potentials of the form

$$V=P(x,y)Q\left(z\right),$$

(86)

and we calculate the derivatives $V_x=P_{x}Q$, $V_y=P_{y}Q$, $V_z=P(x,y)Q^{\prime }\left(z\right)$, where $Q^{\prime }\left(z\right)$=$\frac{dQ}{dz}$. Then the PDE (6) reads

$$j_1{P}_x+j_2{P}_y=0$$

(87)

Now, we shall make use of the second order PDE (13). Working in a similar way as previously, we obtain the second order derivatives of the potential function V and we insert them into Equation (13). Thus, we get the second-order PDE

$$(m_{11}{P}_{xx}+m_{12}{P}_{xy}+m_{01}{P}_x+m_{02}{P}_y)Q+(m_{13}{P}_x+m_{23}{P}_y+m_{03}P)Q^{\prime }\left(z\right)+m_{33}{Q}^{″}\left(z\right)=0,$$

(88)

in which two independent functions, $P(x,y)$ and $Q\left(z\right)$, are involved. So, in this case, we have to find special solutions for the functions P and Q.

Example 5.

We study the two-parametric family of orbits (circles)

$$f(x,y,z)=x^2+y^2+z^2=c_1,g(x,y,z)=\frac{y}{x}=c_2$$

(89)

and the corresponding pair of slope functions is

$$\alpha =\frac{y}{x},\beta =-\frac{x^2+y^2}{xz}.$$

(90)

For this set of orbits, we have ${\alpha }_0=$ 0 which leads to $j_3=$ 0. After some simplifications, the Equation (87) takes the form

$$y{P}_x-x{P}_y=0$$

(91)

and has the general solution

$$P(x,y)=M(x^2+y^2)$$

(92)

where M is an arbitrary function of its argument $u=x^2+y^2$. Then we determine the coefficients in (88). They are

$$\left\{\begin{array}{c}{m}_{11}=\frac{x^2+y^2}{x},m_{12}=\frac{y(x^2+y^2)}{x^2}{m}_{13}=-\frac{(x^2+y^2-xz)(x^2+y^2+xz)}{x^{2}z},\hfill \\ m_{23}=\frac{yz}{x},m_{33}=-\frac{x^2+y^2}{x},\hfill \\ m_{01}=\frac{3x^2+y^2}{x^2},m_{02}=\frac{2y}{x},m_{03}=-\frac{3(x^2+y^2)}{xz}.\hfill \end{array}\right.$$

Among others, for the functions P and Q we select

$$P(x,y)={(x^2+y^2)}^k,Q\left(z\right)=z^s,k,s\in \mathbb{Z}$$

(93)

Under these circumstances, the relation (88) is satisfied if and only if

$$2+2k+s=0.$$

(94)

Thus, the potential function $V=V(x,y,z)$ is found to be

$$V(x,y,z)={(x^2+y^2)}^k{z}^s,s=-2-2k,$$

(95)

or, equivalently,

$$V(x,y,z)=\frac{1}{z^2}{\left(\frac{x^2+y^2}{z^2}\right)}^k.$$

(96)

7. Two-Dimensional Potentials

Two-dimensional potentials is another category of potentials and we obtain them if we set $Q\left(z\right)=$ 0 in (18), or, if we set $Q\left(z\right)=$ 1 in (33). In this case we have to face the problem from the beginning. More precisely, for the given family of orbits (1), we solve analytically the PDE (19) and we find the general solution $P(x,y)$. Then we insert it in (21) and we check if it is satisfied. We shall offer the following

Example 6.

We deal with the family of orbits (see Figure 4a)

$$f(x,y,z)=x^2+y^2=c_1,g(x,y,z)=\frac{z}{x^4}=c_2,$$

(97)

and

$$\alpha =-\frac{x}{y},\beta =\frac{4z}{x}.$$

(98)

The PDE (19) takes the form

$$x(x^2-2y^2)P_x-3y^3{P}_y=0.$$

(99)

The subsidiary system of (99) is

$$\frac{dx}{x(x^2-2y^2)}=\frac{dy}{-3y^3}=\frac{dP}{0}.$$

(100)

The first independent integral of (100) is:

$$P(x,y)={\tilde{c}}_1=const.$$

and the second one will be found if we solve the ODE

$$\frac{dy}{dx}=-\frac{3y^3}{x(x^2-2y^2)}.$$

(101)

By making the transformation $y=x\omega$, the O.D.E. (101) reads

$$\left(\frac{2{\omega }^2-1}{{\omega }^3+\omega }\right)d\omega =\frac{dx}{x}$$

(102)

and the general solution of (102) is

$$\frac{3}{2}log\left(\frac{1+{\omega }^2}{\omega }\right)=logx+log{\tilde{c}}_2,$$

(103)

or, equivalently,

$${\tilde{c}}_2=\frac{{(x^2+y^2)}^3}{x^6{y}^2}.$$

(104)

The general solution of (99) is $\mathcal{F}({\tilde{c}}_1,{\tilde{c}}_2)$ = 0, from which we take

$$P(x,y)=M\left(u\right),u=\frac{{(x^2+y^2)}^3}{x^6{y}^2}.$$

(105)

where M is an arbitrary function of its unique argument. Now, we insert (105) into (11) and we ascertain that the Equation (11) is satisfied if and only if

$$\frac{d^{2}M}{d{u}^2}=0,$$

(106)

which leads to the conclusion that $M\left(u\right)$ = $d_{1}u+d_2$, ($d_1,d_2=const$). Thus, the two-dimensional potential $V=P(x,y)$ is

$$V(x,y)=\frac{d_1{(x^2+y^2)}^3}{x^6{y}^2}+d_2.$$

(107)

Remark 3.

The potential found in (107) is two-dimensional and we can say that $V_z=0$. Thus, we have $\dot{z}=const.$ Consequently, the orbits cannot be closed. Furthermore, the projection of this orbit on the level $xy$ is a regular curve and it is determined by the system (97). A member of this family of orbits is shown at Figure 4a.

8. Families of Straight Lines

If ${\alpha }_0$ = 0 and ${\beta }_0$ = 0, then we have a two-parameter family of straight lines (FSL) in 3-D space under consideration. As it was shown by [13], not any potentials can produce two-parametric families of straight lines in 3-D space, but only those satisfying the following two necessary and sufficient differential conditions

$$\begin{array}{ccc}\hfill V_{xy}(V_x^2-V_y^2)& -& V_x{V}_y(V_{xx}-V_{yy})+V_z(V_x{V}_{yz}-V_y{V}_{xz})=0,\hfill \\ \hfill V_{xz}(V_x^2-V_z^2)& -& V_x{V}_z(V_{xx}-V_{zz})+V_y(V_x{V}_{yz}-V_z{V}_{xy})=0.\hfill \end{array}$$

(108)

If we replace (18) into (108), then we ascertain that the first of Equation (108) is satisfied when

• $\frac{\partial P}{\partial x}=\frac{\partial P}{\partial y},\frac{{\partial }^{2}P}{\partial x^2}=\frac{{\partial }^{2}P}{\partial y^2}$.
• $\frac{\partial P}{\partial x}=-\frac{\partial P}{\partial y},\frac{{\partial }^{2}P}{\partial x^2}=\frac{{\partial }^{2}P}{\partial y^2}$.

The Case I leads to the result that $P=P(x+y)$. But the second of Equation (108) is satisfied only if $P(x+y)$ = $x+y$ and $Q\left(z\right)$ = $d_{3}z$, where $d_3=const$. Thus, the potential is found to be $V(x,y,z)=x+y+d_{3}z$. Working in a similar way for the Case II, we obtain the following result: $V(x,y,z)=x-y+d_{3}z$. For the first result, the family of straight lines is

$$\alpha =\frac{V_y}{V_x}=1,\beta =\frac{V_z}{V_x}=d_3,$$

(109)

or, equivalently,

$$f(x,y,z)=y-x=c_1,g(x,y,z)=z-d_{3}x=c_2.$$

(110)

A member of the family of straight lines (110) is shown at Figure 4b. For the second result, the family of straight lines is

$$\alpha =\frac{V_y}{V_x}=-1,\beta =\frac{V_z}{V_x}=d_3,$$

(111)

or, equivalently,

$$f(x,y,z)=y+x=c_1,g(x,y,z)=z-d_{3}x=c_2.$$

(112)

Another choice is $P(x,y)=x^2+y^2$. The first of Equation (108) is satisfied identically but the second one is verified when

$$Q^{″}\left(z\right)=2$$

(113)

which means that $Q\left(z\right)=z^2+d_{3}z+d_4$, where $d_3,d_4=const$. Thus, the total expression for the potential is

$$V(x,y,z)=x^2+y^2+z^2+d_{3}z+d_4.$$

(114)

Similar results were obtained by [13,21].

9. Concluding Comments

In the present paper we studied semi-separable potentials as solutions of the 3D inverse problem of Newtonian dynamics. These potentials are: $V(x,y,z)=P(x,y)+Q\left(z\right)$, or, $V(x,y,z)=P(x^2+y^2)+Q\left(z\right)$ and $V(x,y,z)=P(x,y)Q\left(z\right)$ and are very useful in physical problems. Our aim was to find two-parametric families of spatial regular orbits $f(x,y,z)$ = $c_1$, $g(x,y,z)$ = $c_2$, ($c_1,c_2$ = const), which are generated by these potentials.

It is known that the two basic PDEs (9) and (11) combine potentials and families of orbits (Section 3) taking into account that at least one of $\{{\alpha }_0,{\beta }_0\}$ is different from zero. In the first case the second order PDE (11) is transformed to a linear second order PDE of a function P of two variables, i.e., $x,y$, and can be solved analytically by using the classical methods of the theory of PDEs. For the second case, we found three-dimensional integrable potentials. In the third case, the second order PDE (11) is transformed to a non-linear second order PDE of a function P of two variables, i.e., $x,y$, and cannot be solved analytically. Furthermore, special cases of the problem were also studied and useful results were obtained. The problem is more complicated now than the previous ones because we deal with two independent functions $P(x,y)$ and $Q\left(z\right)$ and we have to guess which the appropriate solutions are. Thus, we search special solutions in order to get a potential which generates the given family of orbits (1). Another category is the 2D potentials and were examined separately. Many simplifications can be made in this case because the function $Q\left(z\right)$ has a constant value. Families of straight lines is an interesting case of curves in 3D space and we studied potentials which produce them. Not any potentials but only those which satisfy the differential relations (108) in the text can produce a two-parametric family of straight lines.The examples are new and original and cover all the cases.