Modification of Intertwining Logistic Map and a Novel Pseudo Random Number Generator
Abstract
1. Introduction
- 1.
- A scheme of modifying the local structure of the Intertwining logic map, is proposed;
- 2.
- The new map is evaluated through methods and analyses, such as Scale index and Fuzzy entropy. The evaluation results show an improvement in the efficiency of software calculation and a reduction of the cost of hardware implementation while maintaining the complex dynamic behavior of the original map.
- 3.
- Based the new map, a novel pseudo random number generator (PRNG) is proposed;
- 4.
- The proposed PRNG is evaluated through methods and tests, such as statistical complexity measure and a test suite named NIST sp800-22. The evaluation results show that the proposed PRNG is safe and efficient.
2. Simple Intertwining Logistic
2.1. Processing for Transcendental Functions in the Map (1)
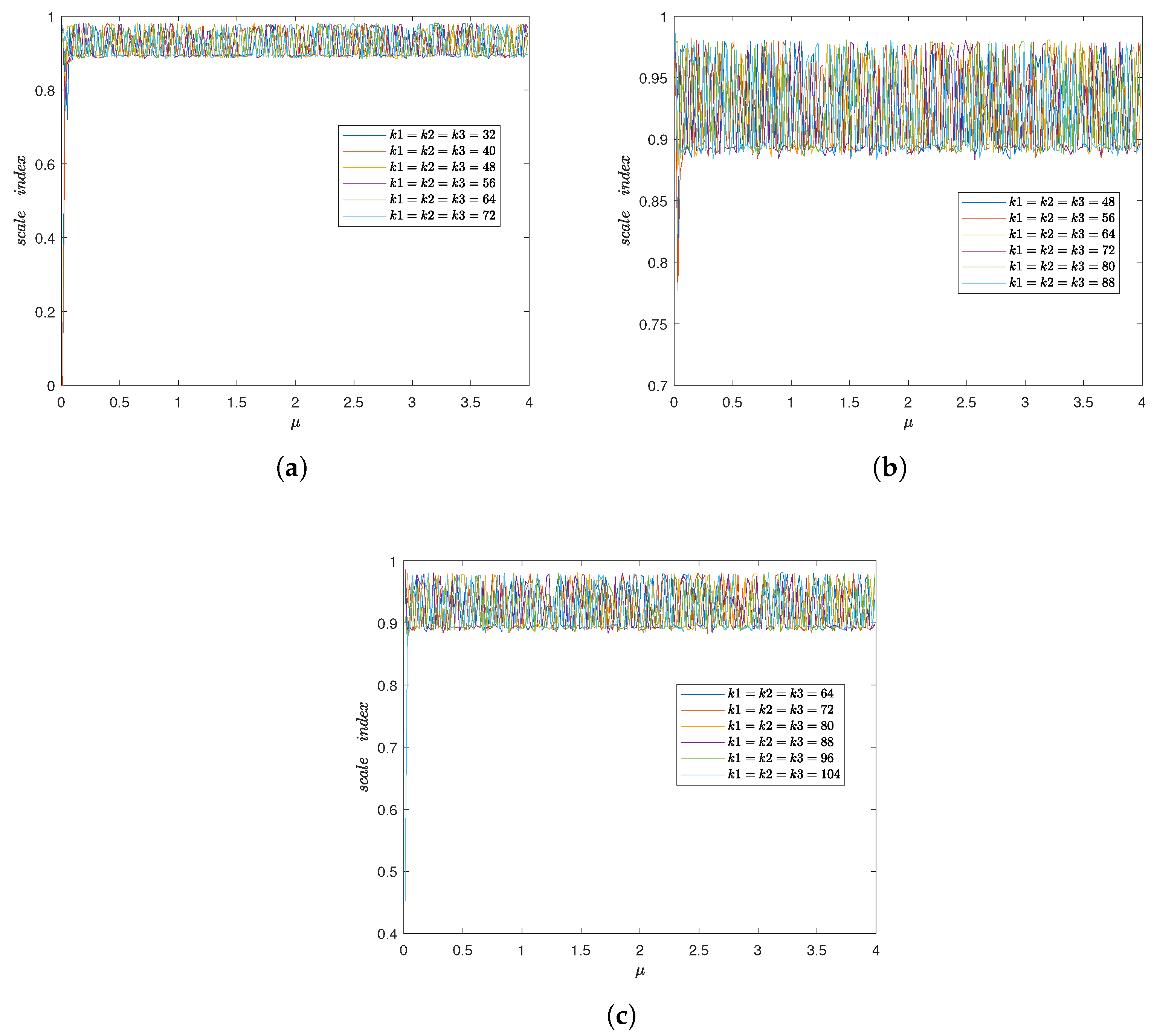
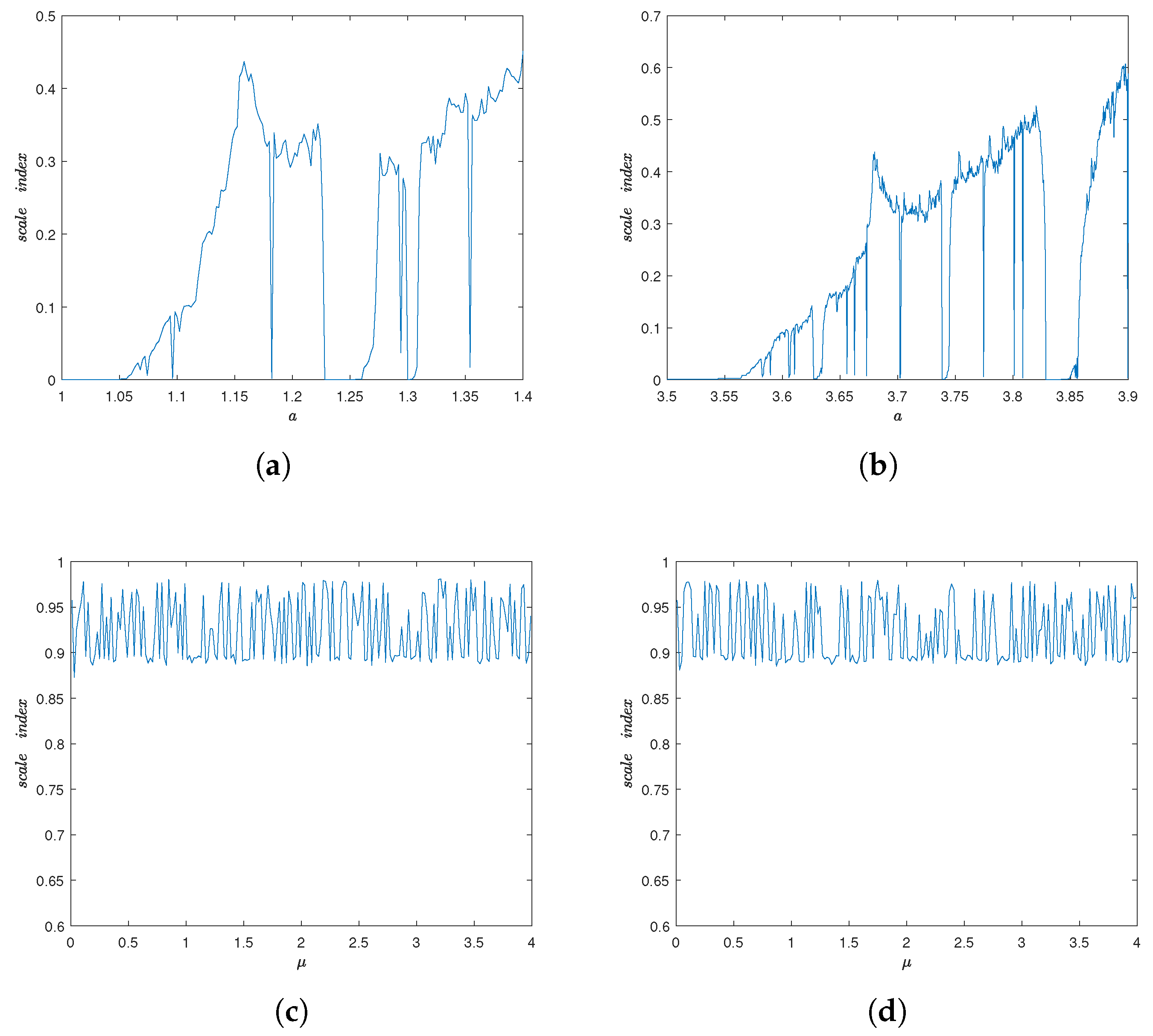
2.2. Degree of Non-Periodicity and Input Parameters Setting
2.3. The Proposed Map “Simple Intertwining Logistic”
2.4. Analysis of Computational Efficiency and Hardware Implementation
3. Chaotic Properties of Simple Intertwining Logistic
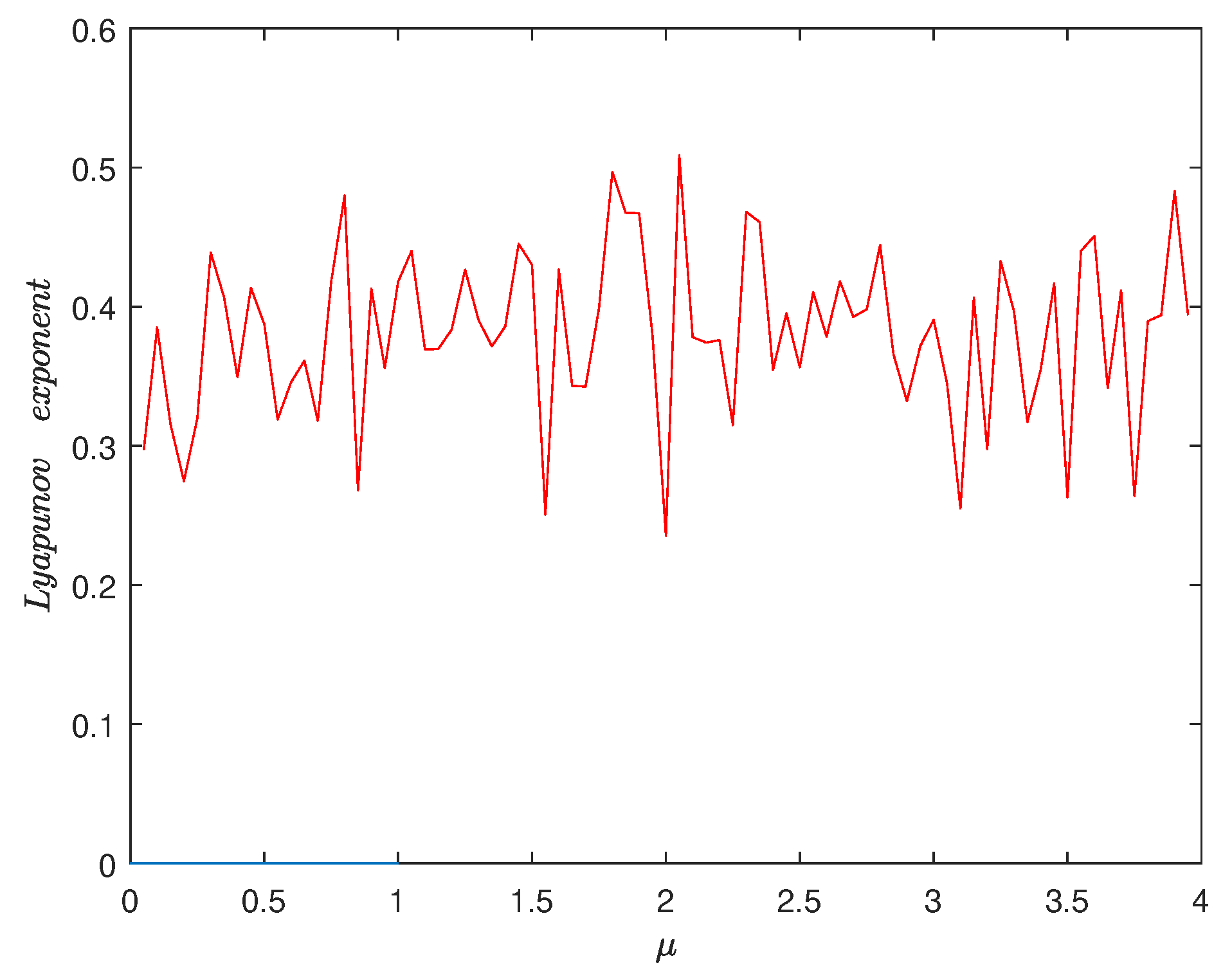
3.1. Lyapunov Exponent and Bifurcation Diagram
3.2. Comparison of the Non-Periodicity
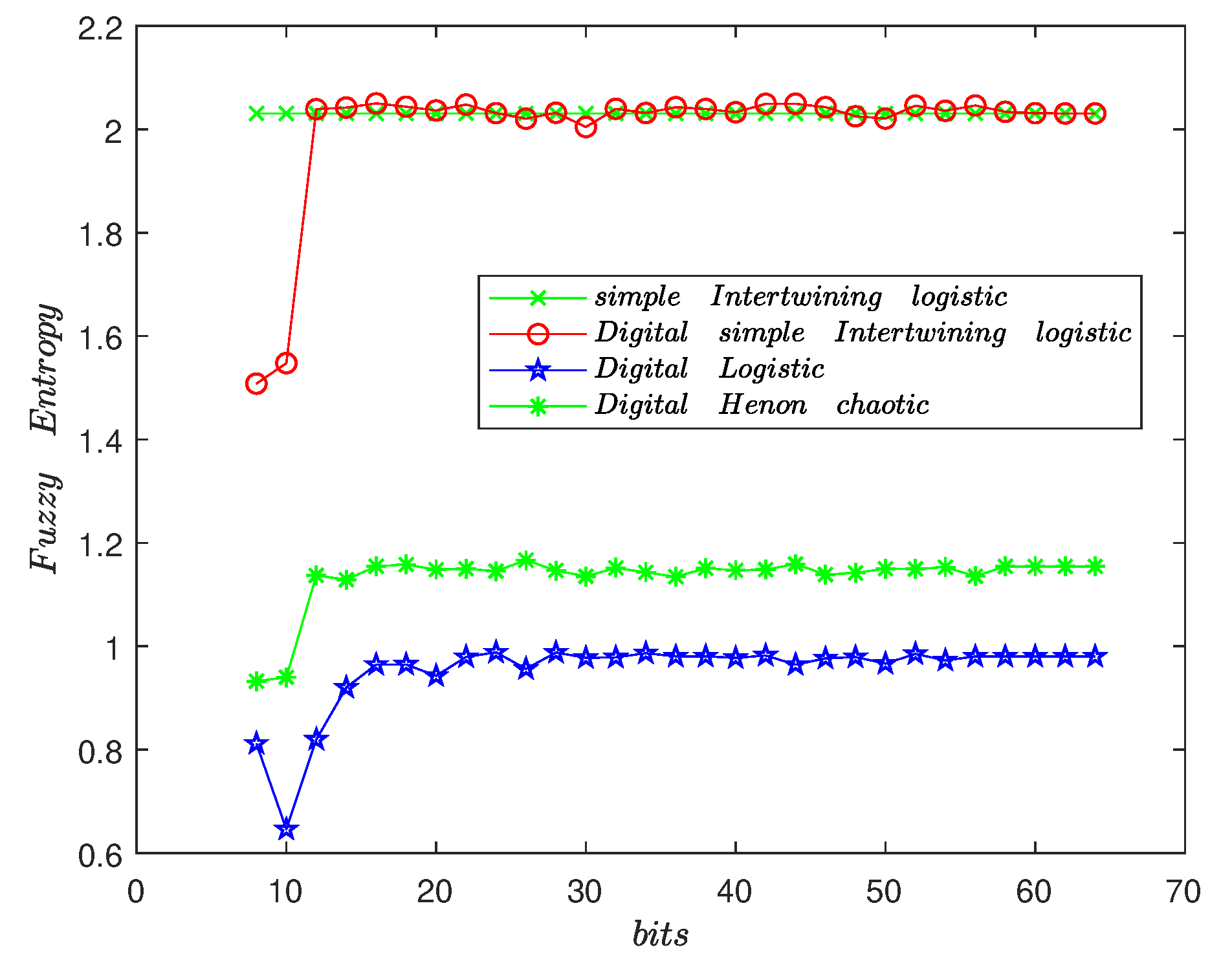
3.3. The Fuzzy Entropy of Chaotic Sequence with Finite Precision
4. The PRNG Based on Simple Intertwining Logistic
- 1.
- Import the keys: initialize and , which are the initialize arguments and control parameter. Set the required length of sequence with ;
- 2.
- To avoid transient effect, iterate the map Equation (2) 1000 times and the outputs are discarded.
- 3.
- A final number x based on is generated by the following equation:where ≪ is the shift operation, n start at 1000 and P is limited precision length in digital devices.
- 4.
- If the length of current generated sequence does not reach , return to the step 3, otherwise stop.
5. Analysis and Test of Security for the Proposed PRNG
5.1. Key Space Analysis
5.2. Correlation Analysis
- 1.
- Letandand two sequence with numbers are generated.
- 2.
- Letand a new is generated.
- 3.
- Letand another new is generated.
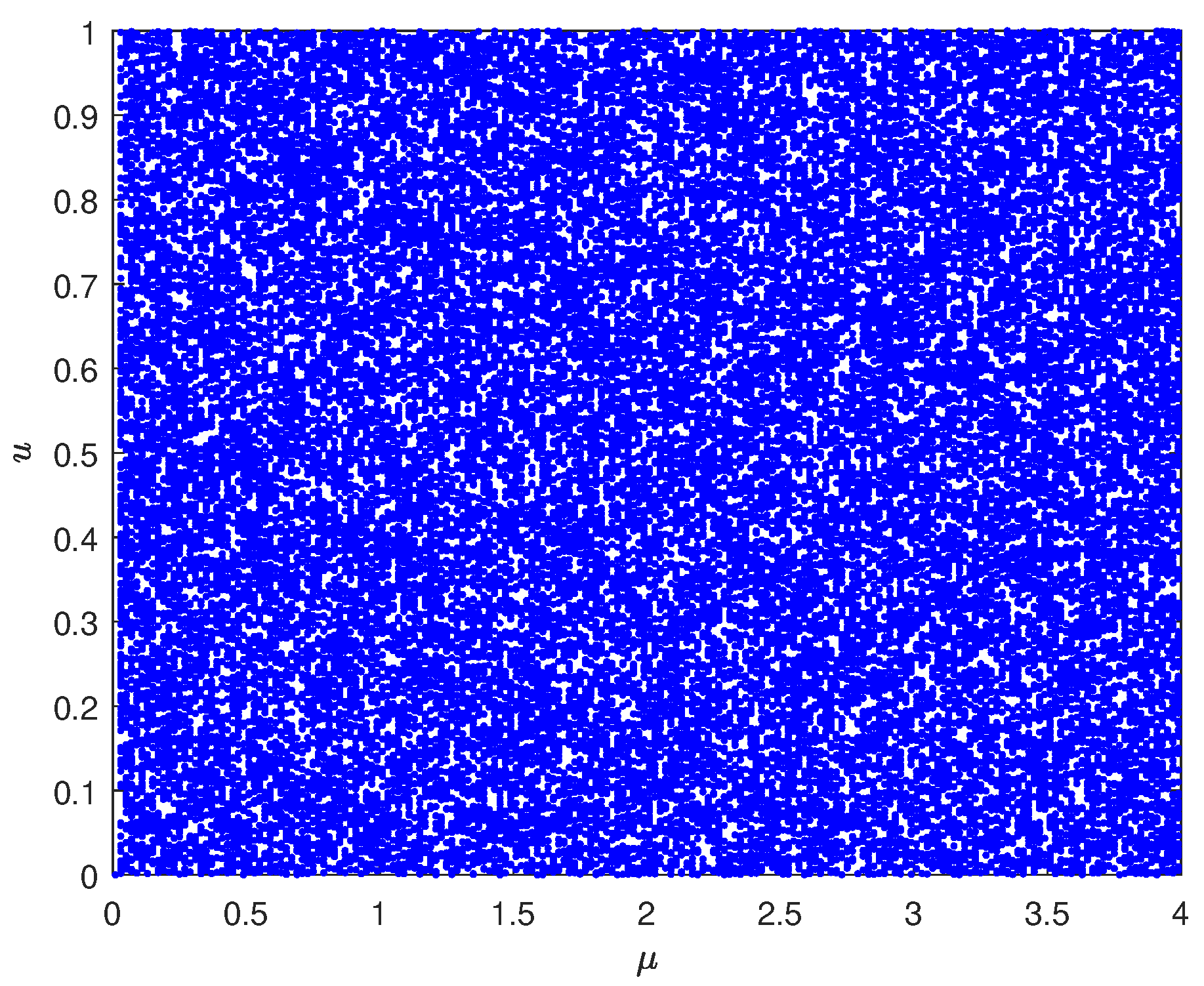
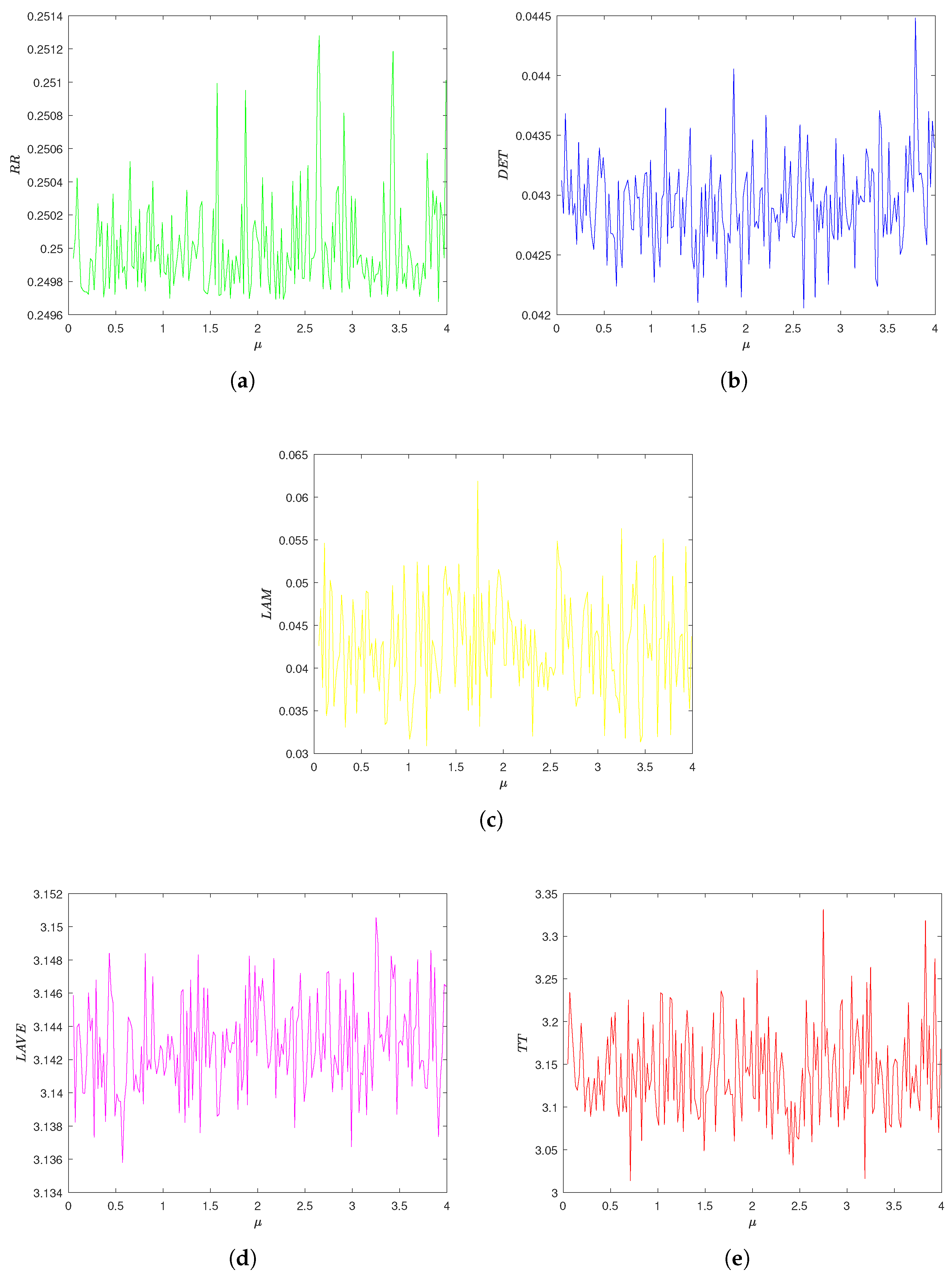
5.3. Recurrence Plots Analysis
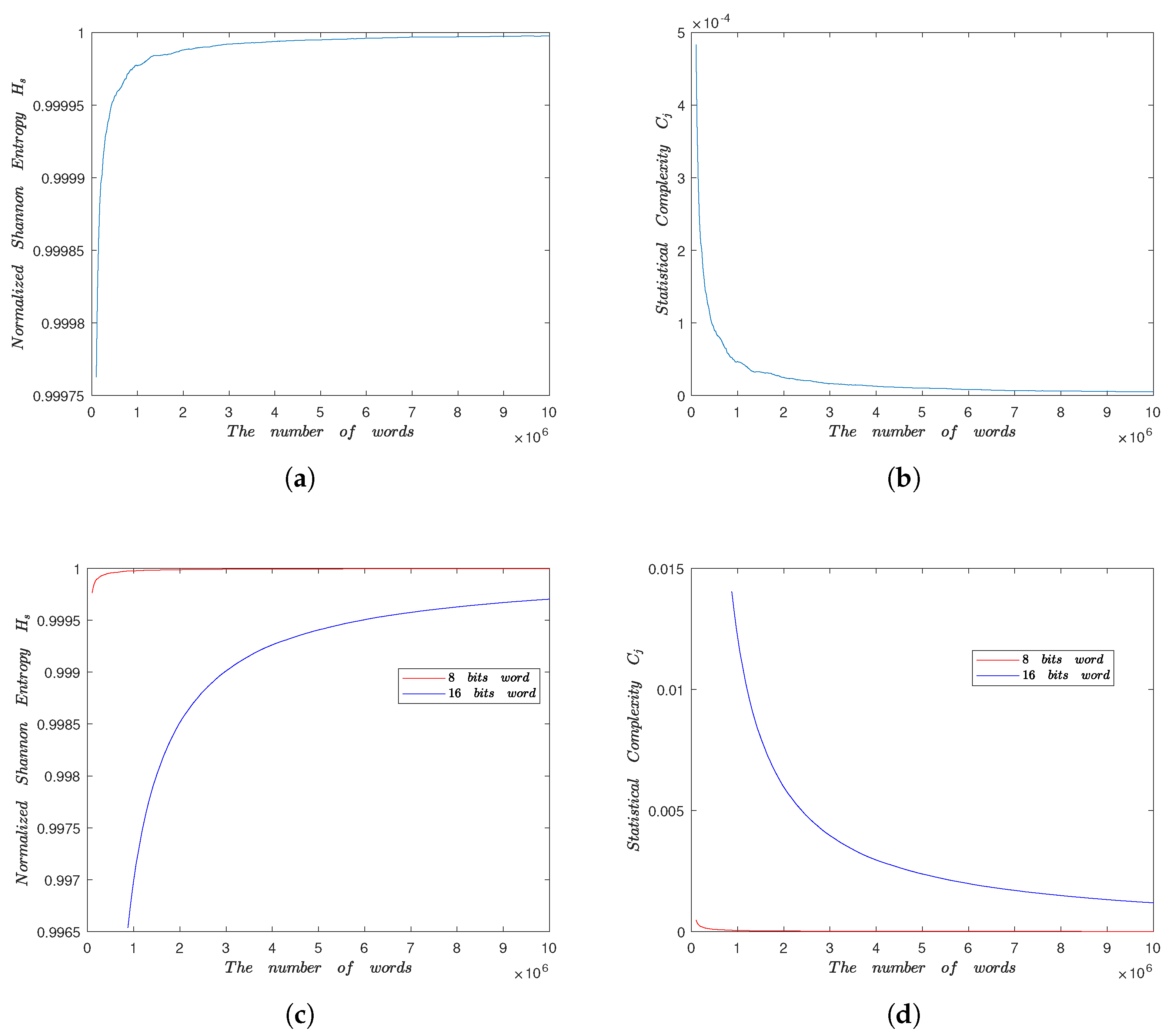
5.4. Information Entropy
5.5. Statistical Complexity Measure
5.6. Differential Attack
5.7. Randomness Analysis
5.7.1. NIST SP 800-22 Test
5.7.2. DIEHARD Test Suite
5.8. Analysis of Speed
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PRNG | Pseudo random number generator |
| CWT | Continuous Wavelet Transform |
| SCM | Statistical complexity measure |
| RP | Recurrence plot |
| RQA | Recurrence quantification analysis |
| BCR | Bit Change Rate |
References
- Lin, C.; Hu, G.; Chen, J.; Yan, J.; Tang, K. Novel design of cryptosystems for video/audio streaming via dynamic synchronized chaos-based random keys. Multimed. Syst. 2022, 28, 1793–1808. [Google Scholar] [CrossRef]
- Akhshani, A.; Akhavan, A.; Mobaraki, A.; Lim, S.C.; Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 101–111. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 26, 96–99. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. AES Proposal, Rijndael; Technical Report FIPS-197; National Institute of Standards and Technology: Charleston, SC, Canada, 2001. [Google Scholar]
- Meier, W. On the Security of the IDEA Block Cipher. In Proceedings of the Advances in Cryptology—EUROCRYPT ′93; Helleseth, T., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 371–385. [Google Scholar]
- Kwok, H.S.; Tang, W.K. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solitons Fractals 2007, 32, 1518–1529. [Google Scholar] [CrossRef]
- Jafari Barani, M.; Ayubi, P.; Yousefi Valandar, M.; Irani, B.Y. A new Pseudo random number generator based on generalized Newton complex map with dynamic key. J. Inf. Secur. Appl. 2020, 53, 102509. [Google Scholar] [CrossRef]
- Farri, E.; Ayubi, P. A blind and robust video watermarking based on IWT and new 3D generalized chaotic sine map. Nonlinear Dyn. 2018, 93, 1875–1897. [Google Scholar] [CrossRef]
- Bonny, T.; Nassan, W.A.; Vaidyanathan, S.; Sambas, A. Highly-secured chaos-based communication system using cascaded masking technique and adaptive synchronization. Multimed. Tools Appl. 2023, 82, 34229–34258. [Google Scholar] [CrossRef]
- Ren, J.; Ji’e, M.; Xu, S.; Yan, D.; Duan, S.; Wang, L. RC-MHM: Reservoir computing with a 2D memristive hyperchaotic map. Eur. Phys. J. Spec. Top. 2023, 232, 663–671. [Google Scholar] [CrossRef]
- Joshi, S.K. Chaos embedded opposition based learning for gravitational search algorithm. Appl. Intell. 2023, 53, 5567–5586. [Google Scholar] [CrossRef]
- Joshi, S.K. Synchronization of coupled oscillators in presence of disturbance and heterogeneity. Int. J. Dyn. Control 2021, 9, 602–618. [Google Scholar] [CrossRef]
- Baptista, M.S. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Shah, T.; Qureshi, A.; Usman, M. A Novel Color Image Encryption Scheme Based on Arnold’s Cat Map and 16-Byte S-box. Appl. Appl. Math. 2021, 16, 591–603. [Google Scholar]
- Matthews, R.A. On the Derivation of a “Chaotic” Encryption Algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Ma, J.; He, H. A pseudorandom number generator based on piecewise logistic map. Nonlinear Dyn. 2016, 83, 2373–2391. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, C.; Wang, G. A Novel S-Box Design Algorithm Based on a New Compound Chaotic System. Entropy 2019, 21, 1004. [Google Scholar] [CrossRef]
- Lv, X.; Liao, X.; Yang, B. A novel pseudo-random number generator from coupled map lattice with time-varying delay. Nonlinear Dyn. 2018, 94, 325–341. [Google Scholar] [CrossRef]
- Elrefaey, A.; Sarhan, A.; El-Shennawy, N. Parallel approaches to improve the speed of chaotic-maps-based encryption using GPU. J.-Real-Time Image Process. 2021, 18, 1897–1906. [Google Scholar] [CrossRef]
- Ayubi, P.; Setayeshi, S.; Rahmani, A.M. Chaotic Complex Hashing: A simple chaotic keyed hash function based on complex quadratic map. Chaos Solitons Fractals 2023, 173, 113647. [Google Scholar] [CrossRef]
- Alanazi, A.S.; Munir, N.; Khan, M.; Hussain, I. A novel design of audio signals encryption with substitution permutation network based on the Genesio-Tesi chaotic system. Multimed. Tools Appl. 2023, 82, 26577–26593. [Google Scholar] [CrossRef]
- Garrido, M.; Kallstrom, P.; Kumm, M.; Gustafsson, O. CORDIC II: A New Improved CORDIC Algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 186–190. [Google Scholar] [CrossRef]
- Li, P.; Jin, H.; Xi, W.; Xu, C.; Yao, H.; Huang, K. A Reconfigurable Hardware Architecture for Miscellaneous Floating-Point Transcendental Functions. Electronics 2023, 12, 233. [Google Scholar] [CrossRef]
- Richter, H.; Stein, G. On Taylor series expansion for chaotic nonlinear systems. Chaos Solitons Fractals 2002, 13, 1783–1789. [Google Scholar] [CrossRef]
- Kaltchev, D.; Dragt, A.J. Poincaré analyticity and the complete variational equations. Phys. D 2013, 242, 1–15. [Google Scholar] [CrossRef]
- Lombardi, L.; Antonini, G.; Ruehli, A.E. Analytical Evaluation of Partial Elements Using a Retarded Taylor Series Expansion of the Green’s Function. IEEE Trans. Microw. Theory Tech. 2018, 66, 2116–2127. [Google Scholar] [CrossRef]
- Kafetzis, I.; Moysis, L.; Volos, C. Assessing the chaos strength of Taylor approximations of the sine chaotic map. Nonlinear Dyn. 2023, 111, 2755–2778. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine Chaotification Model for Enhancing Chaos and Its Hardware Implementation. IEEE Trans. Ind. Electron. 2019, 66, 1273–1284. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Techreport, Special Publication (NIST SP); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Ye, G.; Huang, X. An efficient symmetric image encryption algorithm based on an intertwining logistic map. Neurocomputing 2017, 251, 45–53. [Google Scholar] [CrossRef]
- Raghuvanshi, K.K.; Kumar, S.; Kumar, S.; Kumar, S. Development of new encryption system using Brownian motion based diffusion. Multimed. Tools Appl. 2021, 80, 21011–21040. [Google Scholar] [CrossRef]
- Benítez, R.; Bolós, V.J.; Ramírez, M.E. A wavelet-based tool for studying non-periodicity. Comput. Math. Appl. 2010, 60, 634–641. [Google Scholar] [CrossRef]
- Bolós, V.J.; Benítez, R.; Ferrer, R. A New Wavelet Tool to Quantify Non-Periodicity of Non-Stationary Economic Time Series. Mathematics 2020, 8, 844. [Google Scholar] [CrossRef]
- Rüdisüli, M.; Schildhauer, T.; Biollaz, S.; Van Ommen, J. 18-Measurement, monitoring and control of fluidized bed combustion and gasification. In Fluidized Bed Technologies for Near-Zero Emission Combustion and Gasification; Scala, F., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2013; pp. 813–864. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic Analysis of Digital Chaotic Maps via State-Mapping Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, Y.; Liu, J.; Tang, S.; Harkin, J.; Cao, Y. Counteracting dynamical degradation of a class of digital chaotic systems via Unscented Kalman Filter and perturbation. Inf. Sci. 2021, 556, 49–66. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Algorithms, Key Size and Protocols Report. 2018. Available online: http://www.ecrypt.eu.org/csa/documents/D5.4-FinalAlgKeySizeProt.pdf (accessed on 10 October 2023).
- Pareek, N.K.; Patidar, V.; Sud, K.K. Diffusion substitution based gray image encryption scheme. Digit. Signal Process. 2013, 23, 894–901. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. (EPL) 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66 Pt 2, 26702. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Webber, C.L.; Zbilut, J.P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhao, Q. Novel pseudo-random number generator based on quantum random walks. Sci. Rep. 2016, 6, 20362. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Larrondo, H.A.; González, C.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive statistical complexity measure of pseudorandom number generators. Phys. A Stat. Mech. Its Appl. 2005, 356, 133–138. [Google Scholar] [CrossRef]
- Lamberti, P.W.; Martin, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic non-triviality measure. Phys. A Stat. Mech. Its Appl. 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Brown, R.G.; Eddelbuettel, D.; Bauer, D. Dieharder: A Random Number Test Suite. Available online: https://webhome.phy.duke.edu/~rgb/General/dieharder.php (accessed on 15 November 2023).
- Huang, X.; Liu, L.; Li, X.; Yu, M.; Wu, Z. A New Pseudorandom Bit Generator Based on Mixing Three-Dimensional Chen Chaotic System with a Chaotic Tactics. Complexity 2019, 2019, 6567198. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.; Li, X.; Yu, M.; Wu, Z. A New Two-Dimensional Mutual Coupled Logistic Map and Its Application for Pseudorandom Number Generator. Math. Probl. Eng. 2019, 2019, 7685359. [Google Scholar] [CrossRef]
- Krishnamoorthi, S.; Jayapaul, P.; Dhanaraj, R.K.; Rajasekar, V.; Balusamy, B.; Islam, S.H. Design of pseudo-random number generator from turbulence padded chaotic map. Nonlinear Dyn. 2021, 104, 1627–1643. [Google Scholar] [CrossRef]
- Alhadawi, H.S.; Zolkipli, M.F.; Ismail, S.M.; Lambić, D. Designing a pseudorandom bit generator based on LFSRs and a discrete chaotic map. Cryptologia 2019, 43, 190–211. [Google Scholar] [CrossRef]
| the proposed map | 0.021130440 | 0.211738380 | 2.152552600 | 21.714554600 |
| original map | 0.062234550 | 0.622838910 | 6.297382210 | 63.018479200 |
| 10,000 | 20,000 | ||||
|---|---|---|---|---|---|
| 7.8682369570 | 7.9330325313 | 7.9845058647 | 7.9998646492 | 7.9999855595 | |
| 7.8681921385 | 7.9291288733 | 7.9825195201 | 7.9998442316 | 7.9999858863 | |
| 7.8652402717 | 7.9228013409 | 7.9851102583 | 7.9998350428 | 7.9999845185 |
| Test Name | p-Value | Pass Rate | Result |
|---|---|---|---|
| Frequency | 0.350485 | 100/100 | Success |
| Block Frequency (m = 128) | 0.851383 | 100/100 | Success |
| Cumulative Sums (Forward) | 0.494392 | 100/100 | Success |
| Cumulative Sums (Reverse) | 0.213309 | 100/100 | Success |
| Runs | 0.319084 | 98/100 | Success |
| Longest Run of Ones | 0.171867 | 99/100 | Success |
| Rank | 0.946308 | 100/100 | Success |
| FFT | 0.637119 | 100/100 | Success |
| Non Overlapping | 0.816537 | 100/100 | Success |
| (m = 9, n = 8) | |||
| Overlapping Templates (m = 9) | 0.236810 | 99/100 | Success |
| Universal | 0.334538 | 98/100 | Success |
| Approximate Entropy (m = 10) | 0.437274 | 99/100 | Success |
| Random-Excursions (data3) | 0.330628 | 88/88 | Success |
| Random-Excursions Variant Serial (data5) | 0.534146 | 87/88 | Success |
| Serial Test 1 (m = 16) | 0.699313 | 98/100 | Success |
| Serial Test 2 (m = 16) | 0.834308 | 99/100 | Success |
| Linear complexity (M = 500) | 0.816537 | 99/100 | Success |
| Test Name | p-Value | Result (Assessment) |
|---|---|---|
| Birthday spacing | 0.94319333 | Passed |
| Overlapping permutation | 0.51435951 | Passed |
| Binary rank | 0.34466449 | Passed |
| Binary rank | 0.68760941 | Passed |
| Bitstream | 0.84946357 | Passed |
| OPSO | 0.41780931 | Passed |
| OQSO | 0.57576741 | Passed |
| DNA | 0.28379599 | Passed |
| Count ones str | 0.42594465 | Passed |
| Count ones byt | 0.14161743 | Passed |
| Parking Lot | 0.14887474 | Passed |
| 2DS spheres | 0.90080180 | Passed |
| 3DS spheres | 0.35141495 | Passed |
| Squeeze | 0.72469462 | Passed |
| Runs (up) | 0.91243702 | Passed |
| Runs (down) | 0.75463775 | Passed |
| Craps for no. of wins | 0.59335173 | Passed |
| Craps for throws/game | 0.56547058 | Passed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Ma, C. Modification of Intertwining Logistic Map and a Novel Pseudo Random Number Generator. Symmetry 2024, 16, 169. https://doi.org/10.3390/sym16020169
Zhao W, Ma C. Modification of Intertwining Logistic Map and a Novel Pseudo Random Number Generator. Symmetry. 2024; 16(2):169. https://doi.org/10.3390/sym16020169
Chicago/Turabian StyleZhao, Wenbo, and Caochuan Ma. 2024. "Modification of Intertwining Logistic Map and a Novel Pseudo Random Number Generator" Symmetry 16, no. 2: 169. https://doi.org/10.3390/sym16020169
APA StyleZhao, W., & Ma, C. (2024). Modification of Intertwining Logistic Map and a Novel Pseudo Random Number Generator. Symmetry, 16(2), 169. https://doi.org/10.3390/sym16020169





