Pulsar Kick: Status and Perspective
Abstract
1. Introduction
2. Mechanisms of Explaining Pulsar Kick
2.1. Asymmetric Neutrino Emission
2.2. Sterile Neutrino, Dark Matter, and Other New Physics Scenarios
2.2.1. Sterile Neutrino and Dark Matter
- The polytropic model: The isotropic neutrinosphere in the polytropic model is described by the following equations [51,52,53,54]where P denotes the pressure, F denotes the flux, G denotes Newton’s gravitational constant, , is the total density of matter, and denotes the luminosity of the proto-star. When the proto-star is assumed to be filled with relativistic nucleons of polytropic gas, the EoS can be written aswhere , , , and denote the adiabatic index, nucleon mass, temperature, and density of the core, respectively, and , . Using Equations (13) and (16), we can writewhere , , and denote the radius, density, and mass of the core of the proto-star. The quantity is given in Equation (9).The approximate solution of Equation (17) is obtained aswhere with . Also, by defining , and , , , we write Equation (18) asThe parameter is obtained by setting the condition , where is the radius of the star, and we obtainAlso, combining Equations (14) and (15), we can write the expression of the temperature profile in terms of density distribution aswhere the core luminosity is and . The solution of Equation (21) is obtained aswhereand is a polynomial function of x, given as
2.2.2. Majoron Emission
2.2.3. Neutrino Spin–Flavor Oscillation
2.2.4. Lorentz and CPT Violation
2.2.5. Massless Neutrino Framework
2.3. Hydrodynamic Instabilities
2.4. Other Mechanisms
- Chiral anisotropy conversion: Pulsar kicks can be accounted for by the anisotropic emission of neutrinos, which arises from their scattering with the background axial electron current—a result of the chiral separation effect [77]. Achieving a pulsar recoil requires anisotropy in either the magnetic field or density in momentum space. In this framework, a magnetic field strength of approximately can drive pulsar velocities exceeding .
- Evanescent proto-neutron star: If a CCSN results in a rapidly rotating proto-NS, it may subsequently cool and undergo fragmentation, forming a binary proto-NS system in a very close orbit [78]. In this scenario, the lighter companion could eventually be tidally disrupted, imparting a significant kick to the remaining proto-NS. This mechanism has the potential to generate kick velocities exceeding .
- Rocket effect: An asymmetry in the magnetic field configuration of a pulsar’s strong magnetic field could generate a small, continuous electromagnetic force. If the magnetic moment is misaligned with the pulsar’s rotation axis, this could lead to a “rocket effect,” exerting a gradual push on the pulsar [79]. However, a significant drawback of this mechanism is that it cannot achieve kick velocities as high as those produced by neutrino-driven or hydrodynamic processes.
3. Future Outlook
- Modified gravity: The physics of NS and compact objects has also been extensively studied in the framework of theories that generalized or modify the GR (see, for example [80,81,82], and for a review of extended theories of gravity, see [83]). Pulsar kick can be studied in these alternative theories of gravity.
- Modeling of proto-NS: Within the framework of relativistic mean field (RMF) theory, various constituents of SM or BSM particles can be incorporated, along with the effects of phase transitions [84]. These modifications to the proto-NS EoS can be explored in detail to analyze their impact on pulsar kicks.
- Modeling of magnetic field: The magnetic field of the proto-NS remains uncertain due to significant observational uncertainties. Nevertheless, various models have been proposed, and studying pulsar kicks within the context of these different models would be highly intriguing.
- Advanced simulations: More advanced simulations, supported by improved computational resources, will provide deeper insights into the mechanisms underlying pulsar kicks.
- New neutrino interaction: In addition to the neutrino interactions discussed earlier, exploring non-standard neutrino interactions, as well as the effects of neutrino decay and their interactions with DM, would be valuable. Conducting such studies with precise timing analyses could offer significant insights into the mechanisms of pulsar kicks.
4. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Pilkington, J.D.H.; Hewish, A.; Bell, S.J.; Cole, T.W. Observation of some further pulsated radio sources. Nature 1968, 218, 126–129. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of general relativity from timing the double pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M. Introduction to neutron stars. AIP Conf. Proc. 2015, 1645, 61–78. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Weih, L.R.; Hanauske, M.; Rezzolla, L. Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Mergers. Phys. Rev. Lett. 2020, 124, 171103. [Google Scholar] [CrossRef]
- Woltjer, L. X-Rays and Type I Supernova Remnants. Astrophys. J. 1964, 140, 1309–1313. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Afzal, A.; Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blanco-Pillado, J.J.; Blecha, L.; Boddy, K.K. The NANOGrav 15 yr Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 951, L11, Erratum in Astrophys. J. Lett. 2024, 971, L27. [Google Scholar] [CrossRef]
- Kouvaris, C.; Perez-Garcia, M.A. Can Dark Matter explain the Braking Index of Neutron Stars? Phys. Rev. D 2014, 89, 103539. [Google Scholar] [CrossRef]
- Hook, A.; Kahn, Y.; Safdi, B.R.; Sun, Z. Radio Signals from Axion Dark Matter Conversion in Neutron Star Magnetospheres. Phys. Rev. Lett. 2018, 121, 241102. [Google Scholar] [CrossRef]
- Fujiwara, M.; Hamaguchi, K.; Nagata, N.; Ramirez-Quezada, M.E. Vortex creep heating vs. dark matter heating in neutron stars. Phys. Lett. B 2024, 848, 138341. [Google Scholar] [CrossRef]
- Day, F.V.; McDonald, J.I. Axion superradiance in rotating neutron stars. J. Cosmol. Astropart. Phys. 2019, 10, 51. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Grippa, F.; Lambiase, G.; Poddar, T.K. Constraints on scalar and vector dark matter admixed neutron stars with linear and quadratic couplings. arXiv 2024, arXiv:2407.16386. [Google Scholar]
- Hobbs, G.; Lorimer, D.R.; Lyne, A.G.; Kramer, M. A Statistical study of 233 pulsar proper motions. Mon. Not. R. Astron. Soc. 2005, 360, 974–992. [Google Scholar] [CrossRef]
- Long, X.; Patnaude, D.J.; Plucinsky, P.P.; Gaetz, T.J. The Proper Motion of the Pulsar J1124–5916 in the Galactic Supernova Remnant G292.0+1.8. Astrophys. J. 2022, 932, 117. [Google Scholar] [CrossRef]
- Igoshev, A.P.; Chruslinska, M.; Dorozsmai, A.; Toonen, S. Combined analysis of neutron star natal kicks using proper motions and parallax measurements for radio pulsars and Be X-ray binaries. Mon. Not. R. Astron. Soc. 2021, 508, 3345–3364. [Google Scholar] [CrossRef]
- Burrows, A.; Hayes, J. An Origin for pulsar kicks in supernova hydrodynamics. AIP Conf. Proc. 1996, 366, 25–37. [Google Scholar] [CrossRef]
- Ayala, A.; Langarica, S.B.; Hernández-Ortiz, S.; Hernández, L.A.; Manreza-Paret, D. Lower bound for the neutrino magnetic moment from kick velocities induced at the birth of neutron stars. Int. J. Mod. Phys. E 2021, 30, 2150031. [Google Scholar] [CrossRef]
- Schmitt, A.; Shovkovy, I.A.; Wang, Q. Pulsar kicks via spin-1 color superconductivity. Phys. Rev. Lett. 2005, 94, 211101. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Wang, N.; Chen, W.C.; Li, X.D.; Liu, W.M.; Gao, Z.F. A strange star scenario for the formation of isolated millisecond pulsars. Astron. Astrophys. 2020, 633, A45. [Google Scholar] [CrossRef]
- Chu, Q.; Yu, S.; Lu, Y. Formation and evolution of binary neutron stars: Mergers and their host galaxies. Mon. Not. R. Astron. Soc. 2021, 509, 1557–1586. [Google Scholar] [CrossRef]
- Kusenko, A.; Mandal, B.P.; Mukherjee, A. Delayed pulsar kicks from the emission of sterile neutrinos. Phys. Rev. D 2008, 77, 123009. [Google Scholar] [CrossRef]
- Hansen, B.M.S.; Phinney, E.S. The Pulsar kick velocity distribution. Mon. Not. R. Astron. Soc. 1997, 291, 569. [Google Scholar] [CrossRef]
- Toscano, M.; Sandhu, J.S.; Bailes, M.; Manchester, R.N.; Britton, M.C.; Kulkarni, S.R.; Anderson, S.B.; Stappers, B.W. Millisecond pulsar velocities. Mon. Not. R. Astron. Soc. 1999, 307, 925. [Google Scholar] [CrossRef]
- Johnston, S.; Hobbs, G.; Vigeland, S.; Kramer, M.; Weisberg, J.M.; Lyne, A.G. Evidence for alignment of the rotation and velocity vectors in pulsars. Mon. Not. R. Astron. Soc. 2005, 364, 1397–1412. [Google Scholar] [CrossRef]
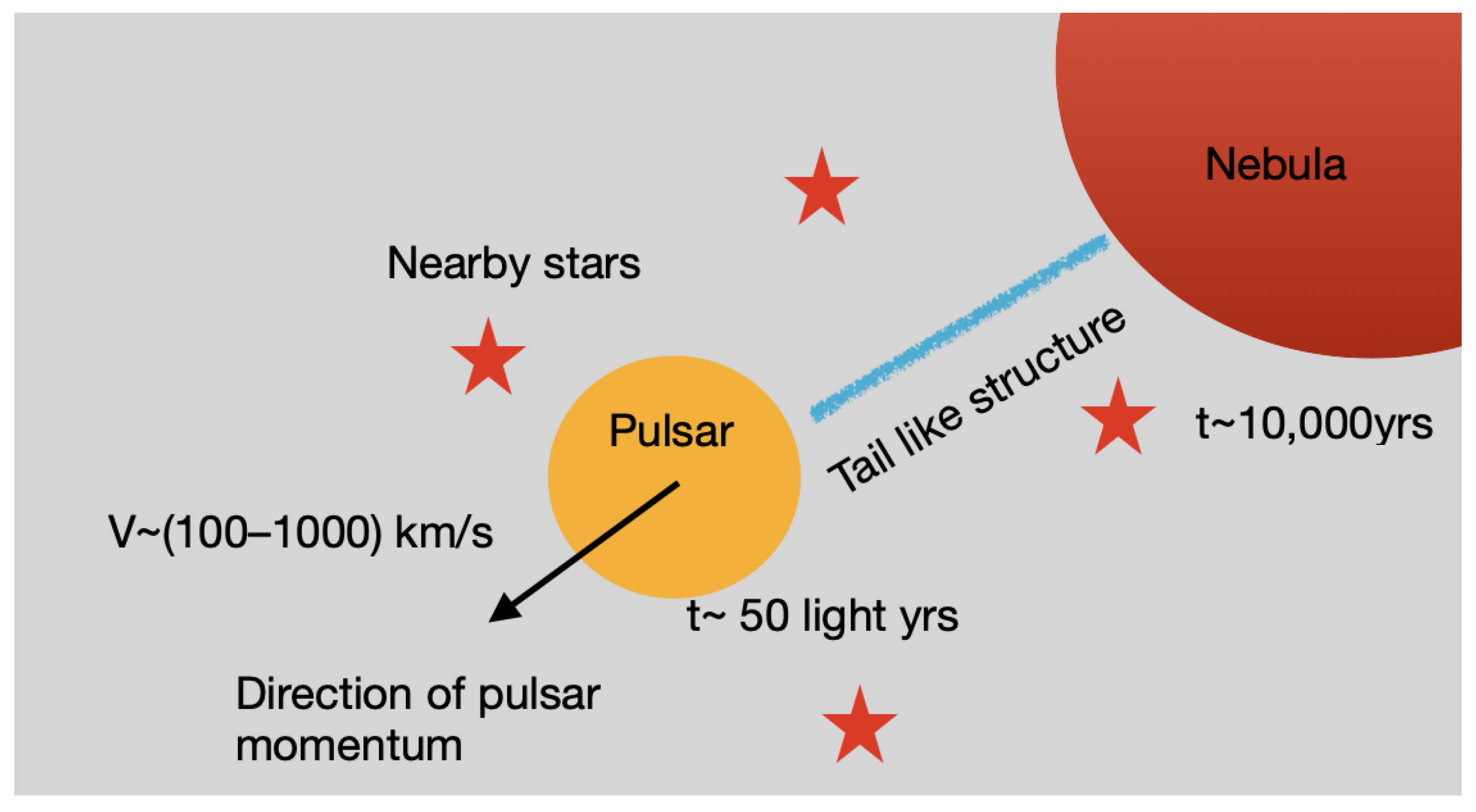
- Schinzel, F.K.; Kerr, M.; Rau, U.; Bhatnagar, S.; Frail, D.A. The Tail of PSR J0002+6216 and the Supernova Remnant CTB 1. Astrophys. J. Lett. 2019, 876, L17. [Google Scholar] [CrossRef]
- Landecker, T.L.; Routledge, D.; Reynolds, S.P.; Smegal, R.J.; Borkowski, K.J.; Seward, F.D. DA 530: A Supernova Remnant in a Stellar Wind Bubble. Astrophys. J. 1999, 527, 866. [Google Scholar] [CrossRef]
- Clark, C.J.; Wu, J.; Pletsch, H.J.; Guillemot, L.; Allen, B.; Aulbert, C.; Beer, C.; Bock, O.; Cuéllar, A.; Eggenstein, H.B.; et al. The Einstein@Home Gamma-ray Pulsar Survey. I. Search Methods, Sensitivity and Discovery of New Young Gamma-ray Pulsars. Astrophys. J. 2017, 834, 106. [Google Scholar] [CrossRef]
- Müller, B.; Tauris, T.M.; Heger, A.; Banerjee, P.; Qian, Y.Z.; Powell, J.; Chan, C.; Gay, D.W.; Langer, N. Three-Dimensional Simulations of Neutrino-Driven Core-Collapse Supernovae from Low-Mass Single and Binary Star Progenitors. Mon. Not. R. Astron. Soc. 2019, 484, 3307–3324. [Google Scholar] [CrossRef]
- Lai, D. Neutron star kicks and supernova asymmetry. arXiv 2003, arXiv:astro-ph/0312542. [Google Scholar]
- Nakamura, K.; Takiwaki, T.; Kotake, K. Long-term Simulations of Multi-Dimensional Core-collapse Supernovae: Implications for Neutron Star Kicks. Publ. Astron. Soc. Jpn. 2019, 71, 98. [Google Scholar] [CrossRef]
- Powell, J.; Müller, B. Three-dimensional core-collapse supernova simulations of massive and rotating progenitors. Mon. Not. R. Astron. Soc. 2020, 494, 4665–4675. [Google Scholar] [CrossRef]
- Burrows, A.; Hayes, J. Pulsar recoil and gravitational radiation due to asymmetrical stellar collapse and explosion. Phys. Rev. Lett. 1996, 76, 352–355. [Google Scholar] [CrossRef]
- Lai, D.; Goldreich, P. Growth of perturbation in gravitational collapse and accretion. Astrophys. J. 2000, 535, 402. [Google Scholar] [CrossRef]
- Nordhaus, J.; Brandt, T.D.; Burrows, A.; Livne, E.; Ott, C.D. Theoretical Support for the Hydrodynamic Mechanism of Pulsar Kicks. Phys. Rev. D 2010, 82, 103016. [Google Scholar] [CrossRef]
- Metlitski, M.A.; Zhitnitsky, A.R. Anomalous axion interactions and topological currents in dense matter. Phys. Rev. D 2005, 72, 045011. [Google Scholar] [CrossRef]
- Gessner, A.; Janka, H.T. Hydrodynamical Neutron-star Kicks in Electron-capture Supernovae and Implications for the CRAB Supernova. Astrophys. J. 2018, 865, 61. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A. Neutron Star Kicks and Implications for Their Rotation at Birth. Astrophys. J. 2023, 958, 130. [Google Scholar] [CrossRef]
- Lyne, A.G.; Lorimer, D.R. High birth velocities of radio pulsars. Nature 1994, 369, 127. [Google Scholar] [CrossRef]
- Kusenko, A.; Segre, G. Velocities of pulsars and neutrino oscillations. Phys. Rev. Lett. 1996, 77, 4872–4875. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.B.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Qian, Y.Z. Comment on ‘Pulsar velocities and neutrino oscillations’. Phys. Rev. Lett. 1997, 79, 2750–2751. [Google Scholar] [CrossRef]
- Kusenko, A.; Segre, G. Pulsar kicks from neutrino oscillations. Phys. Rev. D 1999, 59, 061302. [Google Scholar] [CrossRef]
- Janka, H.T.; Raffelt, G.G. No pulsar kicks from deformed neutrinospheres. Phys. Rev. D 1999, 59, 023005. [Google Scholar] [CrossRef]
- Barkovich, M.; D’Olivo, J.C.; Montemayor, R.; Zanella, J.F. Neutrino oscillation mechanism for pulsar kicks revisited. Phys. Rev. D 2002, 66, 123005. [Google Scholar] [CrossRef]
- Goldreich, P.; Weber, S.V. Homologously collapsing stellar cores. Astrophys. J. 1980, 238, 991–997. [Google Scholar] [CrossRef]
- Raffelt, G.G. Stars as Laboratories for Fundamental Physics: The Astrophysics of Neutrinos, Axions, and Other Weakly Interacting Particles; The University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Schinder, P.J.; Shapiro, S.L. Neutrino emission from a hot, dense, plane-parallel atmosphere in hydrostatic equilibrium. I. Astrophys. J. 1982, 259, 311–329. [Google Scholar] [CrossRef]
- Kusenko, A. Pulsar kicks from neutrino oscillations. Int. J. Mod. Phys. D 2004, 13, 2065–2084. [Google Scholar] [CrossRef]
- Barkovich, M.; D’Olivo, J.C.; Montemayor, R. Active sterile neutrino oscillations and pulsar kicks. Phys. Rev. D 2004, 70, 043005. [Google Scholar] [CrossRef]
- Lambiase, G.; Poddar, T.K. Pulsar kicks in ultralight dark matter background induced by neutrino oscillation. J. Cosmol. Astropart. Phys. 2024, 1, 69. [Google Scholar] [CrossRef]
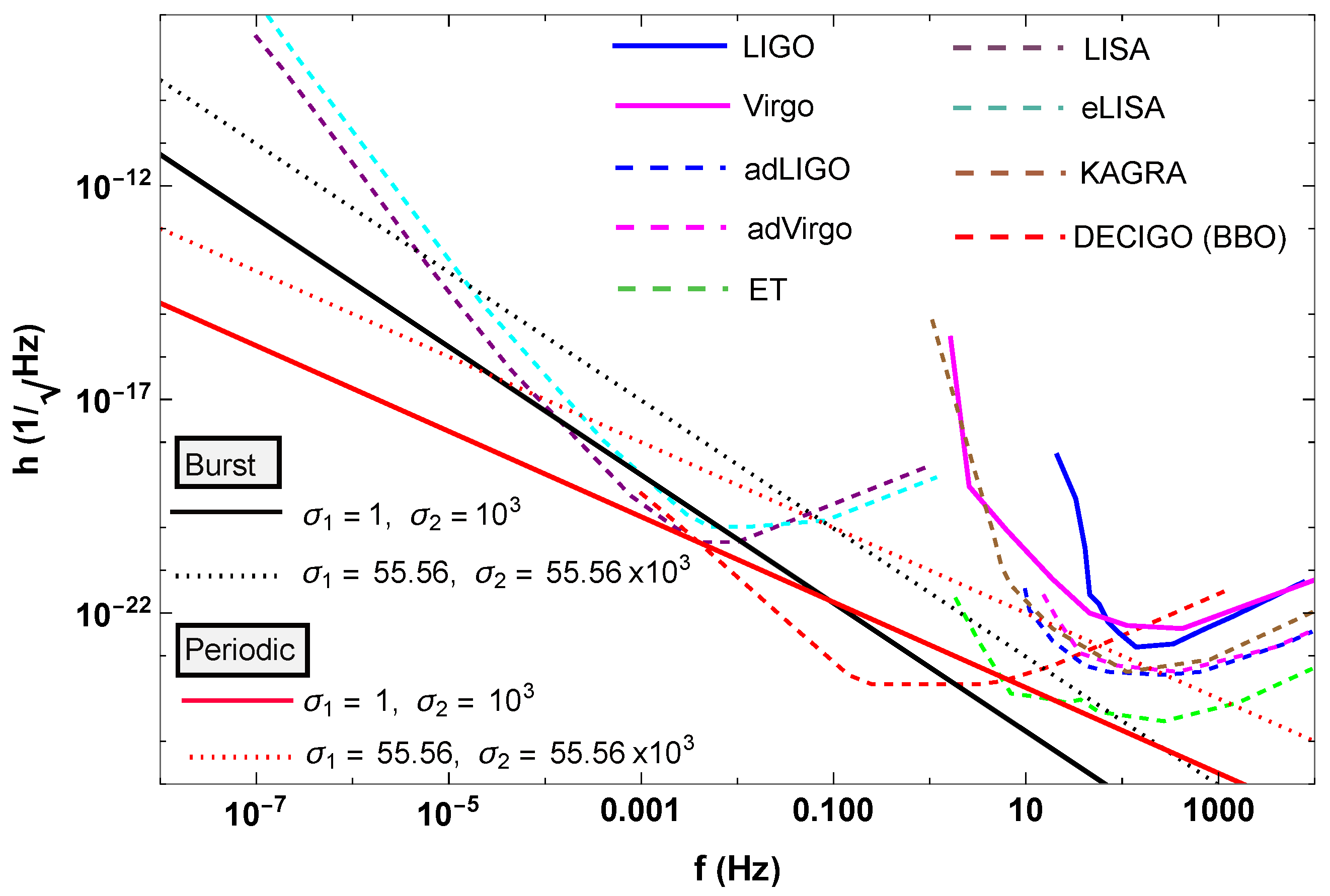
- Loveridge, L.C. Gravitational waves from a pulsar kick caused by neutrino conversions. Phys. Rev. D 2004, 69, 024008. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quant. Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
- Graham, P.W.; Hogan, J.M.; Kasevich, M.A.; Rajendran, S. Resonant mode for gravitational wave detectors based on atom interferometry. Phys. Rev. D 2016, 94, 104022. [Google Scholar] [CrossRef]
- Ruan, W.H.; Guo, Z.K.; Cai, R.G.; Zhang, Y.Z. Taiji program: Gravitational-wave sources. Int. J. Mod. Phys. A 2020, 35, 2050075. [Google Scholar] [CrossRef]
- Yagi, K.; Seto, N. Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries. Phys. Rev. D 2011, 83, 044011, Erratum in Phys. Rev. D 2017, 95, 109901. [Google Scholar] [CrossRef]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. J. Cosmol. Astropart. Phys. 2020, 3, 50. [Google Scholar] [CrossRef]
- Farzan, Y.; Gelmini, G.; Kusenko, A. Pulsar kicks from Majoron emission. Phys. Lett. B 2005, 621, 22–27. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Lanza, A.; Sciama, D.W. Resonant spin flavor precession of neutrinos and pulsar velocities. Phys. Rev. D 1997, 56, 6117–6124. [Google Scholar] [CrossRef]
- Ayala, A.; Bernal-Langarica, S.; Manreza-Paret, D. Estimate for the Neutrino Magnetic Moment from Pulsar Kick Velocities Induced at the Birth of Strange Quark Matter Neutron Stars. Universe 2024, 10, 301. [Google Scholar] [CrossRef]
- Lambiase, G. Pulsar kicks induced by spin flavor oscillations of neutrinos in gravitational fields. Mon. Not. R. Astron. Soc. 2005, 362, 867–871. [Google Scholar] [CrossRef]
- Lambiase, G. Effects of CPT and Lorentz invariance violation on pulsar kicks. Phys. Rev. D 2005, 71, 065005. [Google Scholar] [CrossRef]
- Horvat, R. Pulsar velocities due to a violation of the equivalence principle by neutrinos. Mod. Phys. Lett. A 1998, 13, 2379–2384. [Google Scholar] [CrossRef]
- Barkovich, M.; Casini, H.; D’Olivo, J.C.; Montemayor, R. Pulsar motions from neutrino oscillations induced by a violation of the equivalence principle. Phys. Lett. B 2001, 506, 20–26. [Google Scholar] [CrossRef]
- Casini, H.; D’Olivo, J.C.; Montemayor, R.; Urrutia, L.F. Neutrinos in a gravitational background: A Test for the universality of the gravitational interaction. Phys. Rev. D 1999, 59, 062001. [Google Scholar] [CrossRef]
- Scheck, L.; Kifonidis, K.; Janka, H.T.; Mueller, E. Multidimensional supernova simulations with approximative neutrino transport. 1. Neutron star kicks and the anisotropy of neutrino-driven explosions in two spatial dimensions. Astron. Astrophys. 2006, 457, 963. [Google Scholar] [CrossRef]
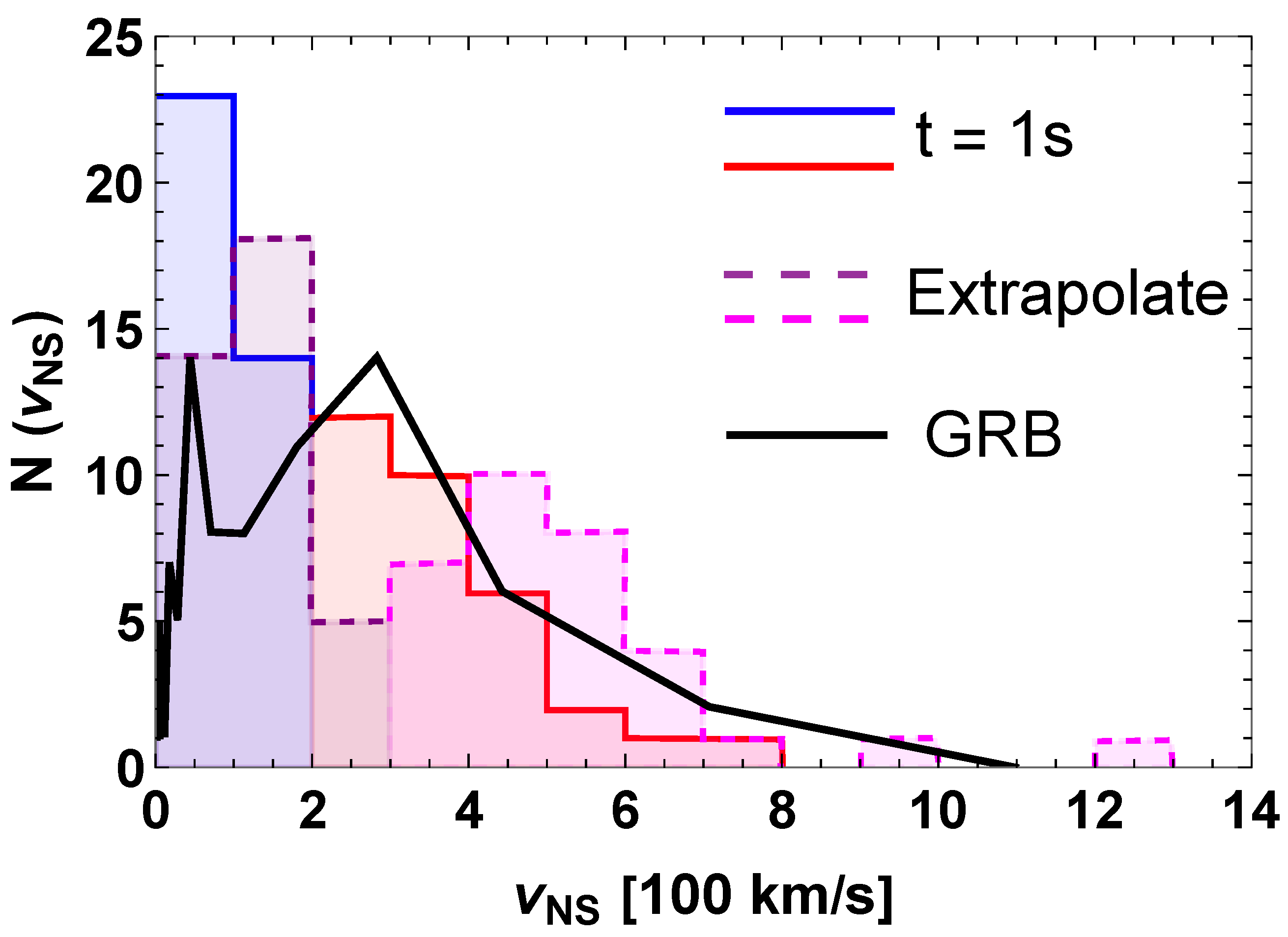
- Cui, X.H.; Wang, H.G.; Xu, R.X.; Qiao, G.J. Pulsar’s kicks and Gamma-ray bursts. Astron. Astrophys. 2007, 472, 1. [Google Scholar] [CrossRef]
- Holland-Ashford, T.; Lopez, L.A.; Auchettl, K.; Temim, T.; Ramirez-Ruiz, E. Comparing Neutron Star Kicks to Supernova Remnant Asymmetries. Astrophys. J. 2017, 844, 84. [Google Scholar] [CrossRef]
- Fukushima, K.; Yu, C. Pulsar Kick by the Chiral Anisotropy Conversion. arXiv 2024, arXiv:2401.04568. [Google Scholar]
- Colpi, M.; Wasserman, I. Formation of an evanescent proto–neutron star binary and the origin of pulsar kicks. Astrophys. J. 2002, 581, 1271–1279. [Google Scholar] [CrossRef]
- Agalianou, V.; Gourgouliatos, K.N. The rocket effect mechanism in neutron stars in supernova remnants. Mon. Not. R. Astron. Soc. 2023, 522, 5879–5891. [Google Scholar] [CrossRef]
- Cui, Y.X.; Yan, Z.; Numajiri, K.; Katsuragawa, T.; Nojiri, S. Compact star in a noninteger power model of f(R) gravity. Phys. Rev. D 2024, 110, 084028. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Further stable neutron star models from f(R) gravity. J. Cosmol. Astropart. Phys. 2013, 12, 40. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Maximal neutron star mass and the resolution of the hyperon puzzle in modified gravity. Phys. Rev. D 2014, 89, 103509. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Maruyama, T.; Yasutake, N.; Cheoun, M.K.; Hidaka, J.; Kajino, T.; Mathews, G.J.; Ryu, C.Y. Neutrino Emission from Magnetized Proto-Neutron Stars in Relativistic Mean Field Theory. Phys. Rev. D 2012, 86, 123003. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Fermi, E. Problems of Gravitational Stability in the Presence of a Magnetic Field. Astrophys. J. 1953, 118, 116, Erratum in Astrophys. J. 1955, 122, 208. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Chakrabarty, S.; Pal, S. The Quantizing magnetic field and quark - hadron phase transition in a neutron star. Phys. Rev. Lett. 1997, 79, 2176–2179. [Google Scholar] [CrossRef]
- Manka, R.; Zastawny-Kubica, M.; Brzezina, A.; Bednarek, I. Effects of the magnetic fields on the protoneutron star structure. arXiv 2002, arXiv:astro-ph/0202303. [Google Scholar]
- Wex, N.; Kalogera, V.; Kramer, M. Constraints on supernova kicks from the double neutron star system psr b1913+16. Astrophys. J. 2000, 528, 401. [Google Scholar] [CrossRef]
- Spruit, H.; Phinney, E.S. Birth kicks as the origin of pulsar rotation. Nature 1998, 393, 139–141. [Google Scholar] [CrossRef]
- Ng, C.Y.; Romani, R.W. Fitting pulsar wind tori. Astrophys. J. 2004, 601, 479–484. [Google Scholar] [CrossRef]
- Romani, R.W. Pulsar kicks: Spin and kinematic constraints. ASP Conf. Ser. 2005, 328, 337. [Google Scholar]
- Lai, D.; Chernoff, D.F.; Cordes, J.M. Pulsar jets: Implications for neutron star kicks and initial spins. Astrophys. J. 2001, 549, 1111. [Google Scholar] [CrossRef]
- Pavlov, G.G.; Kargaltsev, O.Y.; Sanwal, D.; Garmire, G.P. Variability of the vela pulsar-wind nebula observed with chandra. Astrophys. J. Lett. 2001, 554, L189. [Google Scholar] [CrossRef]
- Helfand, D.J.; Gotthelf, E.V.; Halpern, J.P. Vela pulsar and its synchrotron nebula. Astrophys. J. 2001, 556, 380–391. [Google Scholar] [CrossRef]
- Ng, C.Y.; Romani, R.W. Birth Kick Distributions and the Spin-Kick Correlation of Young Pulsars. Astrophys. J. 2007, 660, 1357–1374. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambiase, G.; Poddar, T.K. Pulsar Kick: Status and Perspective. Symmetry 2024, 16, 1649. https://doi.org/10.3390/sym16121649
Lambiase G, Poddar TK. Pulsar Kick: Status and Perspective. Symmetry. 2024; 16(12):1649. https://doi.org/10.3390/sym16121649
Chicago/Turabian StyleLambiase, Gaetano, and Tanmay Kumar Poddar. 2024. "Pulsar Kick: Status and Perspective" Symmetry 16, no. 12: 1649. https://doi.org/10.3390/sym16121649
APA StyleLambiase, G., & Poddar, T. K. (2024). Pulsar Kick: Status and Perspective. Symmetry, 16(12), 1649. https://doi.org/10.3390/sym16121649





