Practical Canonical Labeling of Multi-Digraphs via Computer Algebra

Abstract

Practical algorithms for computing canonical forms of multi-digraphs do not exist in the literature. This paper proposes two practical approaches for finding canonical forms, from the perspective of nD symbolic computation. Initially, the approaches turn the problem of finding canonical forms of multi-digraphs into computing canonical forms of indexed monomials in computer algebra. Then, the first approach utilizes the double coset representative method in computational group theory for canonicalization of indexed monomials and shows that finding the canonical forms of a class of multi-digraphs in practice has polynomial complexity of approximately $O\left({(k+p)}^2\right)$ or $O\left(k^{2.1}\right)$ by the computer algebra system (CAS) tool Tensor-canonicalizer. The second approach verifies the equivalence of canonicalization of indexed monomials and finding canonical forms of (simple) colored tripartite graphs. It is found that the proposed algorithm takes approximately $O\left({(k+2p)}^{4.803}\right)$ time for a class of multi-digraphs in practical implementation, combined with one of the best known graph isomorphism tools Traces, where k and p are the vertex number and edge number of a multi-digraph, respectively.

1. Introduction

The canonical labeling problem is to relabel a graph in such a way that all isomorphic graphs are identical after relabeling [1]. In other words, a canonical labeling of a graph is a unique representative of its isomorphism class, also called a canonical form [2], a canonical code [3], or an optimum code [4]. It is an approach used most frequently in practice to determine whether two graphs are isomorphic, since it overcomes the disadvantages of testing isomorphism directly for the problems of rejecting isomorphs from a graph database or identifying a graph. For instance, a large number of direct isomorphism tests are not required when we look up a given molecule in a database whose elements are all stored in their canonical forms. Instead, we only need to compute the canonical form of the given molecule [5]. Until now, no polynomial-time algorithm exists for either the isomorphism problem or calculating canonical forms of graphs (except for special classes of graphs).

In the literature, there are at least a few hundred algorithms for finding canonical forms of undirected graphs or specific graphs. For example, Babai showed that a canonical form can be constructed in quasipolynomial time [6], following Babai’s breakthrough on the quasipolynomial-time algorithm for graph isomorphism [7]. Huan et al. [8], Kuramochi et al. [9,10], He et al. [11], and Kashani et al. [12] computed canonical form via adjacency matrix. Arvind et al. [13] and Arnborg et al. [14] provided algorithms with complexity of $logn$ for partial 2- and 3-trees. The most successful approach in practice is the individualization-refinement paradigm, which was introduced by Parris et al. [15] and developed by Corneil et al. [16] and Arlazarov et al. [17]. It is utilized by virtually all modern competitive and efficient software tools (for canonical labeling or isomorphism), including nauty [18,19], Bliss [20,21], conauto [22,23], saucy [24], and Traces [25].

Among the above algorithms for computing canonical forms, no algorithm other than nauty accepts directed graphs. There are also other research works on finding canonical forms of (specific) simple directed graphs. For example, Hao [26] utilized k-mix-neighborhood subdigraphs to investigate canonical forms of simple directed graphs without loops. Wang [27] proposed a distributed algorithm for finding canonical forms of directed split-stars.

However, there are no (practical) algorithms for computing canonical forms of multi-digraphs in the literature. On the other hand, there is a natural connection between graphs and algebraic polynomials. Methods and techniques in computer algebra are used to investigate only undirected graphs or simple graphs in the literature. For example, polynomial ideals in a polynomial ring $\mathcal{K}[x_1,\dots ,x_n]$ are used to investigate basic problems in graph theory, such as graph coloring [28,29,30,31,32,33,34,35], S-packing k-coloring [36], independence number of graphs [37,38], and matching problem [39]. In these research works, the vertices of a graph are represented by the variables in $\mathcal{K}[x_1,\dots ,x_n]$, and the adjacency between vertices is represented by certain polynomials. Unfortunately, such representation is poorly suited for multi-digraphs since it is not easy to describe multi-edges and directions simultaneously. Moreover, there is no approach for using computer algebra to describe multi-digraphs in the literature. Although Ref. [40] reveals some relations between indexed monomials and digraphs, its motivation is to use digraphs to simplify indexed expressions, rather than to solve basic problems in graph theory. Therefore, it does not provide a method for describing multi-digraphs (for example, a multi-digraph corresponds to various indexed monomials in [40]). Then, there are the questions: How do we develop practical algorithms for computing canonical forms of multi-digraphs? Is it possible via computer algebra?

To address these questions, we describe multi-digraphs by indexed monomials (for the first time), propose two practical approaches for canonical labeling from the perspective of nD symbolic computation, and provide some results on the time complexity of the approaches for certain multi-digraphs. More precisely, we initially verify the equivalence of the two problems of finding canonical forms of multi-digraphs and canonicalization of indexed monomials in computer algebra. Then, the first approach computes the canonical forms of indexed monomials based on the double coset representative method in computational group theory and shows that the canonical forms of a class of multi-digraphs can be obtained in practice with polynomial complexity of approximate $O\left({(k+p)}^2\right)$ or $O\left(k^{2.1}\right)$ by the CAS tool Tensor-canonicalizer, where k is the vertex number, and p is the edge number. The second approach turns the problem of canonicalization of indexed monomials into the problem of finding canonical forms of (simple) colored tripartite graphs. It is shown that for a class of multi-digraphs with k vertices and p edges, practical implementation of the second approach is completed in approximately $O\left({(k+2p)}^{4.803}\right)$ time, with the graph isomorphism tool Traces.

2. Preliminaries

In this section, we first review some basic notions and notations regarding indexed monomials in computer algebra. Most of them are also presented in [41]. Then, some notations about graphs are also reviewed.

Definition 1. 

An indexed function is composed of four parts: function name, sequence of upper indices, sequence of lower indices, and  variables. An indexed monomial is the product of indexed functions and elements in $\mathcal{K}$, and  obeys the Einstein summation convention, where $\mathcal{K}$ is a field. The product of some indexed functions within an indexed monomial is called a sub-monomial. In an indexed monomial, a  free index occurs only once, and a dummy index occurs twice, as an upper index and a lower one, respectively. The F-degree of an indexed monomial is the number of indexed functions contained in the monomial.

Definition 2. 

If an indexed monomial with coefficient 1 cannot be divided into two sub-monomials without common dummy indices, it is called an elementary indexed monomial. If the indices of an indexed monomial are all dummy indices, we say that the monomial is fully contracted.

Any indexed monomial obeys rules that involve the renaming of dummy indices (Ren), and commutativity of multiplication (Com), defined as follows.

(1)

Renaming of dummy indices (Ren): Suppose m is an indexed monomial; $i_1,i_2,\dots ,i_s$ are some of its dummy indices; and $\mathcal{D}$ is the set of dummy indices of m. For  $j_l\notin \mathcal{D}\backslash \{i_1,i_2,\dots ,i_s\}$ ($l=1,\dots ,s$), let $m_1$ be the indexed monomial obtained by replacing $i_1,i_2,\dots ,i_s$ in m with $j_1,j_2,\dots ,j_s$, respectively. Then,

$$m-m_1=0.$$

(1)

(2)

Commutativity of multiplication (Com): Suppose $M_1$ and $M_2$ are two indexed functions of an indexed monomial m. Let $m_2$ be the indexed monomial obtained by exchanging the positions of $M_1,M_2$ in m. Then,

$$m-m_2=0.$$

(2)

Moreover, in this paper, the indexed monomials that are used to describe multi-digraphs also have the following properties called G-inner symmetries.

(1)

Suppose m is an indexed monomial that takes $\{i_1,i_2,\dots ,i_s\}$ as the upper (lower) index sequence of one indexed function, and $\sigma$ is an arbitrary permutation on $\{i_1,i_2,\dots ,i_s\}$. Let $m_3$ be the indexed monomial obtained by replacing the sequence $\{i_1,i_2,\dots ,i_s\}$ in m with the sequence $\{\sigma \left(i_1\right),\sigma \left(i_2\right),\dots ,\sigma \left(i_s\right)\}$. Then,

$$m-m_3=0.$$

(3)

(2)

Suppose ${F^{i_1,i_2,\dots ,i_s}}_{j_1,j_2,\dots ,j_q}$ is an indexed function of an indexed monomial m. Let $m_4$ be the indexed monomial obtained by replacing ${F^{i_1,i_2,\dots ,i_s}}_{j_1,j_2,\dots ,j_q}$ in m with ${F_{j_1,j_2,\dots ,j_q}}^{i_1,i_2,\dots ,i_s}$. Then,

$$m-m_4=0.$$

(4)

We refer to Ren, Com, and G-inner symmetries as monoterm properties (Mon) in this paper.

Two monomials m, $m^{\prime }$ being equivalent with respect to Mon means that $m-m^{\prime }$ belongs to the ideal generated by the left side of Equations (1)–(4) in the indexed polynomial ring. A canonical form of an indexed monomial m with respect to Mon is a unique representative of the indexed monomials that are equivalent to m with respect to Mon.

Remark 1. 

Theorem 3.10 in [42] proves that a canonical form of m with respect to Mon is the normal form of m with respect to a Gröbner basis in the ST-fundamental restricted ring. Proposition 2.8 and Corollary 3.3 in [42] show that each element in the Gröbner basis is in the form of $f-f_{mon}$, where f is an elementary indexed monomial in the restricted ring, and $f_{mon}$ is a unique representative of the elementary indexed monomials that can be rewritten as f by Mon. Therefore, by a direct computation, the canonical form of m with respect to Mon is also a unique representative of the indexed monomials that can be rewritten as m by Mon. In addition, in what follows, we do not distinguish between “two indexed monomials are equivalent with respect to Mon” and “one indexed monomial can be rewritten as another one by Mon”.

Example 1. 

$m={T^{abk}}_{ekl}{R_a^c}^l{H^e}_{cb}$ is an indexed monomial. ${T^{abk}}_{ekl},{R_a^c}^l,and{H^e}_{cb}$ are indexed functions. $a,b,c,e,k,l$ are all dummy indices. m is also an elementary indexed monomial and a fully contracted monomial. It obeys Ren, such as ${T^{abk}}_{ekl}{R_a^c}^l{H^e}_{cb}={T^{dbk}}_{gkl}{R_d^c}^l{H^g}_{cb}$.

Notation 1. 

(1)

In what follows, we sometimes write an indexed function in the form of ${F^{{\mathcal{I}}_1}}_{{\mathcal{I}}_2}$ as $F_{{\mathcal{I}}_2}^{{\mathcal{I}}_1}$ for simplicity, where F is an indexed function name, and ${\mathcal{I}}_1$ and ${\mathcal{I}}_2$ are index sequences.

(2)

$\mathcal{I}\mathcal{P}$ is used to denote the set of fully contracted monomials whose coefficients are 1 and whose indexed functions are in the form of ${T{(a,b)}^{{\mathcal{I}}_1}}_{{\mathcal{I}}_2}$ or ${T{(a,b)}_{{\mathcal{I}}_2}}^{{\mathcal{I}}_1}$ with $a= |{\mathcal{I}}_1|,b= |{\mathcal{I}}_2|$, where $T(a,b)$ is the indexed function name.

(3)

For an indexed monomial m, $\mathcal{F}\left(m\right)$ denotes the set of indexed functions contained in m.

(4)

Let $G=(V,E)$ denote a multi-digraph (whose vertices and edges are labelled $v_1,v_2,\dots$ and $e_1,e_2,\dots$, respectively). Let $\mathcal{G}$ denote the set of multi-digraphs.

(5)

$E(u,v)$ denotes the set of edges directed from u to v. For each vertex v, find the edges whose initial (resp. terminal) vertex is v, sort them by edge label in a lexicographical order, and obtain an index sequence denoted by $\overrightarrow{E}\left(v\right)$ (resp. $\overleftarrow{E}\left(v\right)$).

Definition 3. 

Two multi-digraphs $G=(V,E),G^{\prime }=(V^{\prime },E^{\prime })$ are isomorphic if there is a bijection ψ between V and $V^{\prime }$ such that $|E(u,v)|=|E(\psi \left(u\right),\psi \left(v\right))|$ for $u,v\in V$, in which case we write $G\cong G^{\prime }$, where $|·|$ denotes the element number of a set.

Definition 4. 

A canonical form of G is a function $C:\mathcal{G}\to \mathcal{G}$ such that $C\left(G\right)\cong G$, and $C\left(G\right)=C\left(G^{\prime }\right)$ for $G^{\prime }\cong G$. In other words, a canonical form of G is a unique representative of its isomorphism class.

3. The First Approach

As introduced in Section 1, we will provide two approaches for canonical labeling of multi-digraphs, and each of them generates some interesting results with regard to time complexity. This section presents the first one.

Proposition 1. 

Let $G=(V,E)$ be a multi-digraph. Then, G can be described by an indexed monomial in $\mathcal{I}\mathcal{P}$. In other words, there exists a mapping, denoted by δ, from $\mathcal{G}$ to $\mathcal{I}\mathcal{P}$.

Proof. 

First, define a function $\alpha :V\to \mathbb{N}\times \mathbb{N}$ by letting $\alpha \left(v\right)$ be the ordered pair ($|\overrightarrow{E}\left(v\right)|$, $|\overleftarrow{E}\left(v\right)|)$, where × refers to a Cartesian product.

Then, let $T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}$ be an indexed function whose function name is $T\left(\alpha \right(v\left)\right)$ and whose upper index sequence and lower index sequence are $\overrightarrow{E}\left(v\right)$ and $\overleftarrow{E}\left(v\right)$, respectively. Finally, let $\delta \left(G\right)$ be the indexed monomial ${\displaystyle \prod _{v\in V}}T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}$. It is clear that $\delta$ is a mapping from $\mathcal{G}$ to $\mathcal{I}\mathcal{P}$.  □

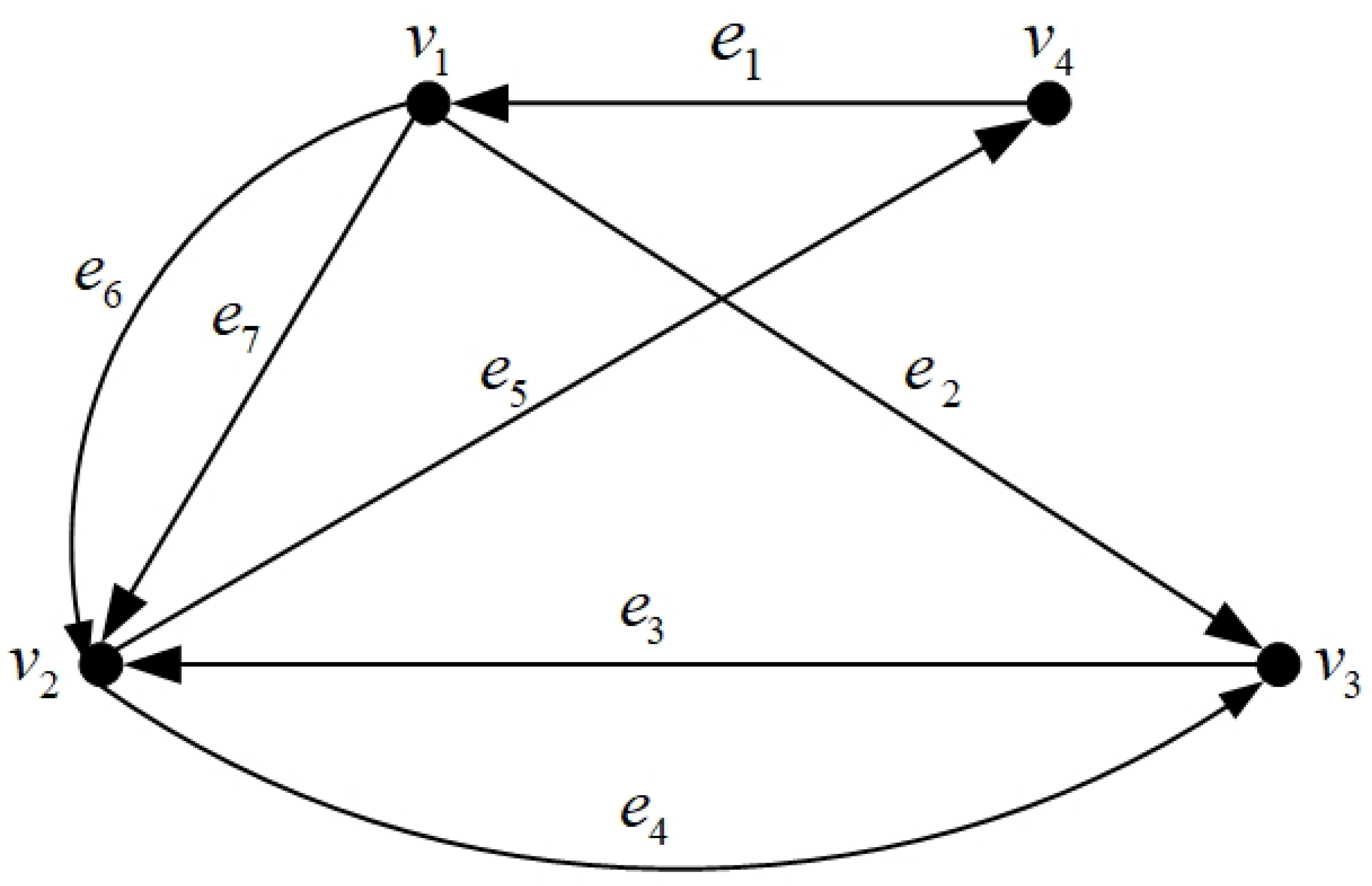
Example 2. 

Suppose $G=(V,E)$ is a multi-digraph, as shown in Figure 1.

$$\overrightarrow{E}\left(v_1\right)=\{e_2,e_6,e_7\},\overleftarrow{E}\left(v_1\right)=\left\{e_1\right\},\overrightarrow{E}\left(v_2\right)=\{e_5,e_4\},\overleftarrow{E}\left(v_2\right)=\{e_6,e_7,e_3\},$$

$$\overrightarrow{E}\left(v_3\right)=\left\{e_3\right\},\overleftarrow{E}\left(v_3\right)=\{e_2,e_4\},\overrightarrow{E}\left(v_4\right)=\left\{e_1\right\},\overleftarrow{E}\left(v_4\right)=\left\{e_5\right\}.$$

$$\alpha \left(v_1\right)=(3,1),\alpha \left(v_2\right)=(2,3),\alpha \left(v_3\right)=(1,2),\alpha \left(v_4\right)=(1,1).$$

Figure 1. An example of a multi-digraph.

Finally, $\delta \left(G\right)=T{(3,1)}_{e_1}^{e_2,e_6,e_7}T{(2,3)}_{e_6,e_7,e_3}^{e_5,e_4}T{(1,2)}_{e_2,e_4}^{e_3}T{(1,1)}_{e_5}^{e_1}$.

Corollary 1. 

δ in Proposition 1 induces a surjection (denoted by) $\widehat{\delta }$ from $\mathcal{G}$ to $\mathcal{I}\mathcal{P}$/∼, where ∼ is the equivalence relation defined as $m_1\sim m_2$ if and only if $m_1$ can be rewritten as $m_2$ by Mon.

Proof. 

Define $\widehat{\delta }$ as $\widehat{\delta }\left(G\right)=\left[\delta \left(G\right)\right]$, where $\left[\delta \right(G\left)\right]$ denotes the equivalence class containing $\delta \left(G\right)$.

Suppose $m^{\prime }$ is an element in $\left[m\right]$, satisfying the condition that the upper index sequence and lower index sequence are both sorted in lexicographical order, with $m\in \mathcal{I}\mathcal{P}$. Then, let the vertices of a multi-digraph $G^{\prime }$ be $v_1,v_2,\dots ,v_k$, and let $\overrightarrow{E}\left(v_i\right)$, $\overleftarrow{E}\left(v_i\right)$ be the upper index sequence and the lower index sequence of the ith indexed function of $m^{\prime }$, respectively, where k is the F-degree of $m^{\prime }$. It is clear that $\delta \left(G^{\prime }\right)=m^{\prime }$ according to the proof of Proposition 1. Hence, $\widehat{\delta }\left(G^{\prime }\right)=\left[m\right]$.  □

Proposition 2. 

$G_1$ and $G_2$ are isomorphic if and only if $\delta \left(G_1\right)$ and $\delta \left(G_2\right)$ are equivalent with respect to Mon.

Proof. 

Assume that $G_1\cong G_2$. Then, there exists a bijection $\psi$ between $V_1$ and $V_2$ such that $|E(u,v)|=|E(\psi \left(u\right),\psi \left(v\right))|$ for $u,v\in V_1$. Consequently, $\alpha \left(v\right)=\alpha \left(\psi \right(v\left)\right)$, $\overrightarrow{E}\left(v\right)$ (resp. $\overleftarrow{E}\left(v\right)$) can be rewritten as $\overrightarrow{E}\left(\psi \left(v\right)\right)$ (resp. $\overleftarrow{E}\left(\psi \left(v\right)\right)$) by exchanging positions of edge labels, and renaming the edge label, where $\alpha$ is defined in the proof of Proposition 1. In other words, ${\displaystyle \prod _{v\in V_1}}T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}$ can be rewritten as ${\displaystyle \prod _{\psi \left(v\right)\in V_2}}T{\left(\alpha \left(\psi \left(v\right)\right)\right)}_{\overleftarrow{E}\left(\psi \left(v\right)\right)}^{\overrightarrow{E}\left(\psi \left(v\right)\right)}$ by Ren, G-inner symmetries, and Com.

Conversely, assume that $\delta \left(G_1\right)={\displaystyle \prod _{v\in V_1}}T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}$ and $\delta \left(G_2\right)={\displaystyle \prod _{v\in V_2}}T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}$ are equivalent with respect to Mon. Then, there exists a bijection $\vartheta$ between $\mathcal{F}\left(\delta \left(G_1\right)\right)$ and $\mathcal{F}\left(\delta \left(G_2\right)\right)$, such that each indexed function $f=T{\left(\alpha \left(v\right)\right)}_{\overleftarrow{E}\left(v\right)}^{\overrightarrow{E}\left(v\right)}\in \mathcal{F}\left(\delta \left(G_1\right)\right)$ can be rewritten as $\vartheta \left(f\right)=T{\left(\alpha \left(v^{\prime }\right)\right)}_{\overleftarrow{E^{\prime }}\left(v\right)}^{\overrightarrow{E}\left(v^{\prime }\right)}$ by renaming the index and exchanging index positions. Define a mapping $\psi$ from $V_1$ to $V_2$, such that $\psi \left(v\right)=v^{\prime }$. It is clear that $G_1$ and $G_2$ are isomorphic under $\psi$.  □

The corollary below implies that finding canonical forms of multi-digraphs is equivalent to finding indexed monomials in $\mathcal{I}\mathcal{P}$, following immediately from Proposition 2 and the proof for Corollary 1.

Corollary 2. 

(1)

There is a bijection between $\mathcal{G}$/≈ and $\mathcal{I}\mathcal{P}$/∼, where ≈ is the equivalence relation defined as $G_1\approx G_2$ if and only if $G_1$ and $G_2$ are isomorphic, and ∼ is defined in Corollary 1.

(2)

The canonical form $G_{can}$ of a multi-digraph G can be obtained by letting the vertices of $G_{can}$ be $v_1,v_2,\dots ,v_k$, and $\overrightarrow{E}\left(v_i\right)$, $\overleftarrow{E}\left(v_i\right)$ be the upper index set and the lower index set of the ith indexed function of $m_{mon}$, respectively, where $m_{mon}$ is a canonical form of $\delta \left(G\right)$ with respect to Mon, and k is the F-degree of $m_{mon}$.

According to Corollary 2, we have the following Algorithm 1 for computing canonical forms of multi-digraphs.

Algorithm 1 Canonical form of a multi-digraph.

Input:  A multi-digraph G with vertex set $\{v_1,v_2,\dots ,v_k\}$ and edge set $\{e_1,e_2,\dots ,e_p\}$. Output:  Canonical form of G. Step 1.  For each vertex $v_i$, find the edges whose initial vertex is $v_i$, and sort them in a lexicographical order, obtaining an index sequence $\overrightarrow{E}\left(v_i\right)$. Then, sort the edges whose terminal vertex is $v_i$ in a lexicographical order, obtaining an index sequence $\overleftarrow{E}\left(v_i\right)$. Step 2.  Let $\alpha \left(v_i\right)$ be an ordered pair $(|\overrightarrow{E}\left(v_i\right)|,|\overleftarrow{E}\left(v_i\right)|)$, then obtain an indexed monomial $m={\displaystyle \prod _{v_i\in V}}T{\left(\alpha \left(v_i\right)\right)}_{\overleftarrow{E}\left(v_i\right)}^{\overrightarrow{E}\left(v_i\right)}$. Step 3.  Find the canonical form of m with respect to Ren, G-inner symmetries, and Com, denoted by $m_{mon}$. Step 4.  Let the vertices of a multi-digraph be $v_1,v_2,\dots ,v_k$, and the edges whose initial (resp. terminal) vertex is $v_i$ be the upper (resp. low) indices of the ith indexed function of $m_{mon}$. Output the multi-digraph.

Remark 2. 

It is clear that Step 1, Step 2, and Step 4 have polynomial complexity of at most $O\left({(k+p)}^2\right)$. The methods, algorithms and complexity for Step 3 are discussed below.

Canonicalization of indexed polynomials is a classical and important topic in computer algebra, as modern differential geometry and physics often involve the massive calculation of such polynomials. It is also a challenging problem since the ideal generated by the basic syzygies cannot be finitely generated, mainly due to the property of Ren. In particular, monoterm canonicalization of an indexed monomial (i.e., finding canonical form of an indexed monomial with respect to monoterm symmetries) is indispensable in polynomial canonicalization, as shown in [41,42,43]. Various efforts have been made to present methods and algorithms for monoterm canonicalization.

In the literature, the representative approaches for monoterm canonicalization of arbitrary indexed expressions include renaming reference [44,45,46], double coset representative [47,48], classification theory and undirected graph labelling [49], and digraph labelling [40]. For specific expressions such as Riemann tensor monomials and indexed differential monomials, representative methods include graph algebra extension [50] and the distance invariant method [51,52,53].

The double coset representative method turns the monoterm canonicalization problem into the problem of finding the canonical representative of a double coset in representation theory. For example, suppose m is a fully contracted indexed monomial with $2n$ dummy indices. First express m as a single tensor, denoted by T. Then, the property of Ren and metric symmetry (if it exists) can be described by a subgroup D of the direct product $H\otimes S_{2n}$, i.e., the action of D on (the indices of) T yields all the indexed monomials that are equivalent to T with respect to Ren and metric symmetry, where $S_{2n}$ is a symmetric group, and $H=\{-1,1\}$, which is used to indicate sign changes when applying symmetries to a monomial. Similarly, the other symmetries of T are described by a subgroup S of $H\otimes S_{2n}$. Consequently, the set of monomials equivalent to T is given by the action of $S\times D$ on T, where $S\times D$ is the double coset of S and D in $H\otimes S_{2n}$. Sort the indices of T in alphabetical order to get $T_0$, and let g be an element in $H\otimes S_{2n}$ satisfying the condition that the action of g on $T_0$ is T. Finally, the canonical form of m is obtained by the action of $\tilde{g}$ on T, where $\tilde{g}$ is the canonical representative of the double coset $S\times g\times D$ and can be found within $2n-1$ loops based on a base for S and strong generating sets for S and D. As illustrated in [48,50], the double coset representative method has exponential complexity in the worst case. The renaming reference method mainly splits the indices in classes, establishes the index order, and rename indices. It has factorial complexity. Other methods for arbitrary indexed expressions also present factorial complexity. In other words, the Butler–Portugal algorithm based on the double coset representative method [47] is the most efficient in theory. In practice, it is also the most efficient, since numerous experimental implementations show polynomial complexity in the number of indices in most common cases. Many popular CAS software packages based on the Butler–Portugal algorithm have also been developed, including the open-source Canon package [48] for Maple; xPerm package for Mathematica [54]; Cadabra [55] and SymPy [56], which are both standalone open-source; and Tensor-canonicalizer, which is based on the improved Butler–Portugal algorithm by Niehoff for Mathematica [57].

Among all these packages, Tensor-canonicalizer [57] performs the best in most common cases, especially in tensor calculus in higher dimensions. For example, while other software packages present nearly factorial complexity in practice for indexed monomials with total symmetry and contracted dummy indices, Tensor-canonicalizer is of polynomial complexity.

Therefore, we adopt Tensor-canonicalizer to find canonical forms of indexed monomials with respect to Mon.

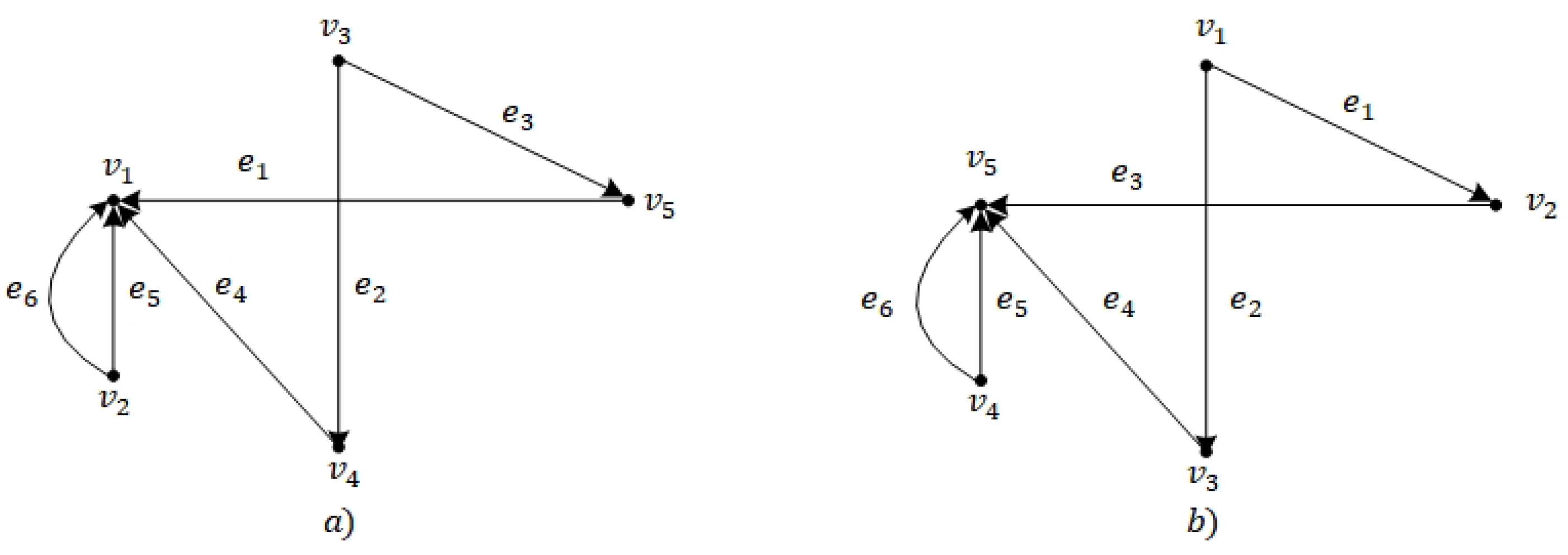
Example 3. 

Suppose $G=(V,E)$ is the multi-digraph shown in Figure 2a. Compute the canonical form of G as follows.

Figure 2. An example of computing canonical forms of multi-digraphs. (a) A multi-digraph G. (b) The canonical form of G.

Step 1.

G is described by the indexed monomial

$$m=T{(0,4)}_{e_1{e}_4{e}_5{e}_6}T{(2,0)}^{e_5,e_6}T{(2,0)}^{e_2,e_3}T{(1,1)}_{e_2}^{e_4}T{(1,1)}_{e_3}^{e_1}.$$

Step 2.

The canonical form of m is $T{(2,0)}^{e_1,e_2}{T{(1,1)}_{e_1}}^{e_3}{T{(1,1)}_{e_2}}^{e_4}T{(2,0)}^{e_5,e_6}T{(0,4)}_{e_3,e_4,e_5,e_6}$.

Step 3.

The canonical form of G is shown in Figure 2b, by Step 4 of Algorithm 1.

According to the analysis of experimental implementations in Ref. [57], we have the following conclusions.

Proposition 3. 

Suppose G is a multi-digraph with k indices and p edges. If for each vertex v, $|\overrightarrow{E}\left(v\right)|=|\overleftarrow{E}\left(v\right)|=2$, then finding the canonical form of G has polynomial complexity of approximately $O\left({(k+p)}^2\right)$ or $O\left(k^{2.1}\right)$ in practice.

Proof. 

According to Algorithm 1 or Corollary 1, $\widehat{\delta }\left(G\right)$ is in the form of

$$[{T(2,2)}_{\circ \circ }^{\circ \circ }T{(2,2)}_{\circ \circ }^{\circ \circ }\dots T{(2,2)}_{\circ \circ }^{\circ \circ }],$$

which has the same symmetries as Riemann tensor monomials. Section 5.2 in Ref. [57] shows that Tensor-canonicalizer can canonicalize contracted Riemann tensor monomials in polynomial time $O\left(k^{2.1}\right)$ in practice, which together with Remark 2 completes the proof.  □

4. The Second Approach

As illustrated in Section 3, we only need to consider monoterm canonicalization of indexed monomials in $\mathcal{I}\mathcal{P}$. In this section, another efficient method is proposed. It turns canonicalization of indexed monomials into finding canonical forms of tripartite graphs. First, the indexed monomials in $\mathcal{I}\mathcal{P}$ are described by simple colored undirected graphs. Then, the most efficient approach and the best known software Traces are applied to obtain some properties of time complexity in practice.

Notation 2. 

$G_s=(V_s,E_s)$ denotes a simple undirected graph. We use $(G_s,\pi )$ to denote a simple colored (undirected) graph, where π is a coloring of $G_s$, i.e., a surjection from $V_s$ to $\{1,2,\dots ,t\}$, and $t\le |V_s|$. ${\mathcal{G}}_{\mathrm{sc}}$ denotes the set of simple colored undirected graphs.

Definition 5. 

Suppose $(G_s,\pi ),(G_s^{\prime },{\pi }^{\prime })\in {\mathcal{G}}_{sc}$. They are isomorphic if there is a bijection ψ between $V_s$ and $V_s^{\prime }$ such that $\pi \left(v\right)=\pi \left(\psi \right(v\left)\right)$, and  $uv\in E_s$ if and only if $\psi \left(u\right)\psi \left(v\right)\in E_s^{\prime }$ for $u,v\in V_s$, in which case we write $(G_s,\pi )\cong (G_s^{\prime },{\pi }^{\prime })$.

Definition 6. 

A canonical form of $G_s$ is a function $C:{\mathcal{G}}_{\mathrm{sc}}\to {\mathcal{G}}_{\mathrm{sc}}$ such that $C\left((G_s,\pi )\right)\cong (G_s,\pi )$, and $C\left((G_s,\pi )\right)=C\left((G_s^{\prime },{\pi }^{\prime })\right)$ for $(G_s,\pi )\cong (G_s^{\prime },{\pi }^{\prime })$.

Proposition 4. 

Let m be an indexed monomial in $\mathcal{I}\mathcal{P}$. Then, m can be described by a simple colored undirected graph. In other words, there exists a mapping, denoted by ρ, from  $\mathcal{I}\mathcal{P}$ to ${\mathcal{G}}_{\mathrm{sc}}$.

Proof. 

Suppose $m={\displaystyle \prod _{i=1}^k}T{(a_i,b_i)}_{{\mathcal{I}}_{i_2}}^{{\mathcal{I}}_{i_1}}$. Then, $\rho \left(m\right)$ is constructed as follows. First, let the indexed function names (according to their appearance in m) be vertices $v_1,v_2,\dots ,v_k$, and  $\pi \left(v_i\right)=1$ for $1\le i\le k$. Secondly, let the upper indices of m be vertices $v_{k+1},\dots ,v_{k+l}$, the lower indices be vertices $v_{k+l+1},\dots ,v_{k+2l}$, $\pi \left(v_i\right)=2$ for $k+1\le i\le k+l$, and $\pi \left(v_i\right)=3$ for $k+l+1\le i\le k+2l$. An  edge $uv$ of $\rho \left(m\right)$ satisfies one of the following conditions: (1) $u,v$ correspond to an upper index and a lower index with the same name, (2) $u,v$ correspond to the indexed function name and one index of an indexed function, respectively.  □

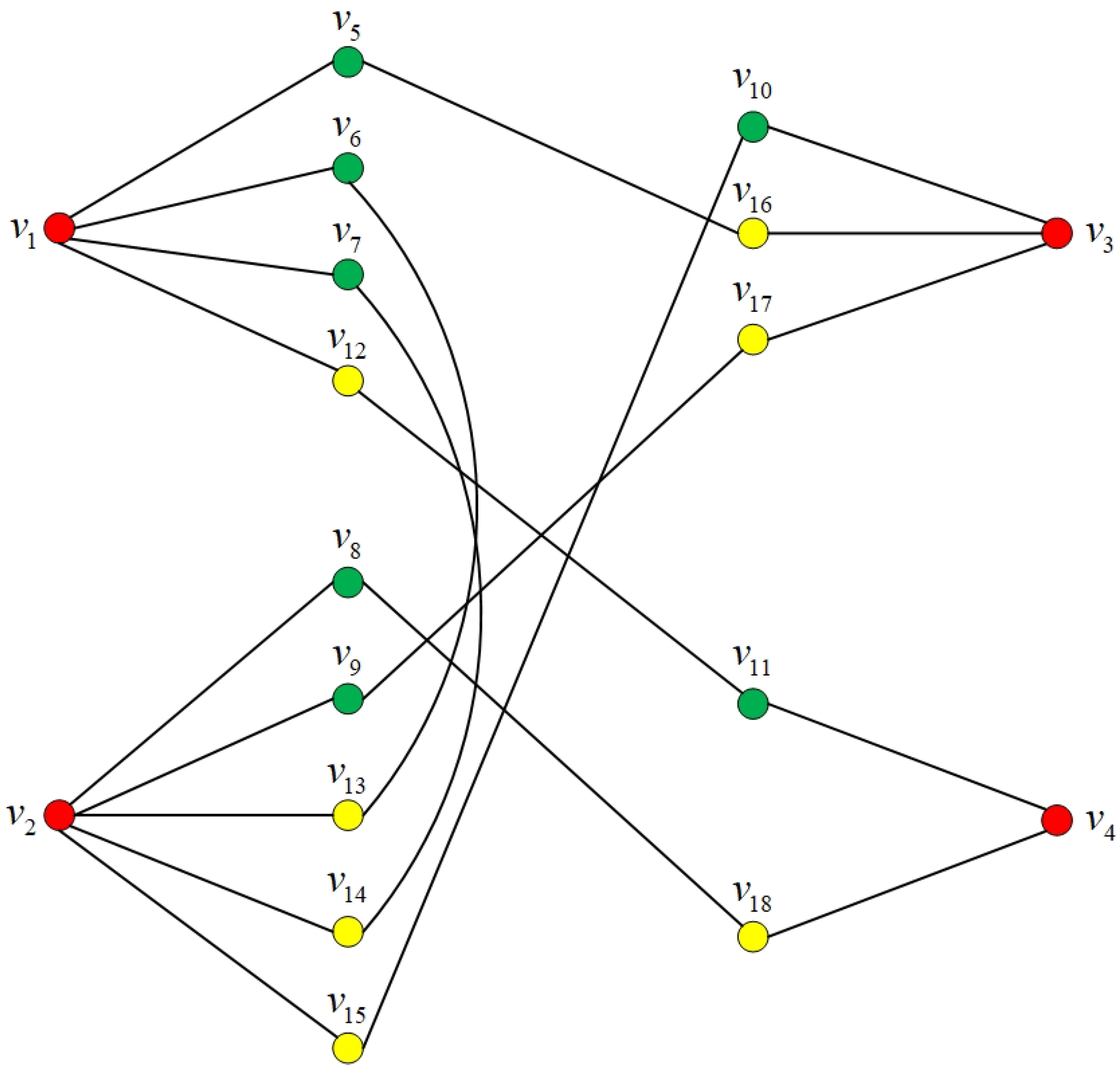
Example 4. 

Suppose $m=T{(3,1)}_{e_1}^{e_2,e_6,e_7}T{(2,3)}_{e_6,e_7,e_3}^{e_5,e_4}T{(1,2)}_{e_2,e_4}^{e_3}T{(1,1)}_{e_5}^{e_1}$, as given in Example 2.

First, let the vertices $v_1,v_2,v_3,v_4$ of the colored graph $\rho \left(m\right)$ represent the function names $T(3,1),T(2,3),T(1,2),T(1,1)$, respectively, $v_5,\dots ,v_{11}$ represent the upper indices $e_2,$ $e_6,$ $e_7,$ $e_5,$ $e_4,$ $e_3,$ $e_1$, and $v_{12},\dots ,v_{18}$ correspond to the lower indices $e_1,e_6,$ $e_7,e_3,$ $e_2,e_4,e_5$. Then, $\pi \left(v_1\right),\dots ,\pi \left(v_4\right)$ are 1, $\pi \left(v_5\right),\dots \pi \left(v_{11}\right)$ are 2, and $\pi \left(v_{12}\right),\dots ,\pi \left(v_{18}\right)$ are 3. The edges are

$$v_1{v}_5,v_1{v}_6,v_1{v}_7,v_1{v}_{12},v_2{v}_8,v_2{v}_9,v_2{v}_{13},v_2{v}_{14},v_2{v}_{15},$$

$$v_3{v}_{10},v_3{v}_{16},v_3{v}_{17},v_4{v}_{11},v_4{v}_{18},v_5{v}_{16},v_6{v}_{13},v_7{v}_{14},v_8{v}_{18},v_9{v}_{17},v_{10}{v}_{15},v_{11}{v}_{12}.$$

$\rho \left(m\right)$ is shown in Figure 3.

Figure 3. Graphical description of Example 4 (red = 1, green = 2, yellow = 3).

Remark 3. 

In the literature, Ref. [49] also uses an undirected graph to describe an indexed monomial. The graph takes each index of the indexed monomial as a vertex and has an extra vertex 1, which is adjacent to free indices. However, it does not take the indexed function names as vertices. The graphical description proposed in (the proof of) Proposition 4 integrates all the elements of an indexed monomial into a graph. What is more important, the proposed graphical representation can lead to some good properties, as shown in the following Propositions 6 and 7.

The following claim will verify the equivalence of finding canonical forms of indexed monomials and of colored graphs.

Proposition 5. 

Suppose $m,m^{\prime }\in \mathcal{I}\mathcal{P}$. Then, m and $m^{\prime }$ are equivalent with respect to Mon, if and only if $\rho \left(m\right)$ and $\rho \left(m^{\prime }\right)$ are isomorphic.

Proof. 

Assume that m and $m^{\prime }$ are equivalent. Then, there exists a bijection $\vartheta$ between $\mathcal{F}\left(m\right)$ and $\mathcal{F}\left(m^{\prime }\right)$ such that for each indexed function f, $\vartheta \left(f\right)$ can be rewritten as f by Ren (in one step), and then by G-inner symmetries and Com. Define a mapping $\psi$ from the vertex set of $\rho \left(m\right)$ to that of $\rho \left(m^{\prime }\right)$, such that either v and $\psi \left(v\right)$ represent the indexed function names of f and $\vartheta \left(f\right)$, respectively, or the index represented by v can be rewritten as the one represented by $\psi \left(v\right)$ via Ren, where $v\in \rho \left(m\right)$. It is clear that $\rho \left(m\right)$ and $\rho \left(m^{\prime }\right)$ are isomorphic under $\psi$.

Conversely, assume that $\rho \left(m\right)$ and $\rho \left(m^{\prime }\right)$ are isomorphic (under a bijection $\psi$). Suppose $v_{11},v_{12},v_{13}$ are vertices of $\rho \left(m\right)$ colored in $1,2,3$. Then, $v_{1i}{v}_{1j}$ is an edge of $\rho \left(m\right)$ if and only if $\psi \left(v_{1i}\right)\psi \left(v_{1j}\right)$ is an edge of $\rho \left(m^{\prime }\right)$, where $i,j\in \{1,2,3\}$. In other words, there exists a bijection $\omega$ between the index sets of m and $m^{\prime }$ such that $a,b$ are in the same indexed function if and only if $\omega \left(a\right)$ and $\omega \left(b\right)$ are in the same indexed function, and $(a,b)$ is a pair of dummy indices of m if and only if $\left(\omega \right(a),\omega (b\left)\right)$ is a pair of dummy indices of $m^{\prime }$. Therefore, m can be rewritten as $m^{\prime }$ by Mon.  □

By Proposition 5, the following corollary is straightforward.

Corollary 3. 

(1)

There is a bijection between ${\mathcal{G}}_{\mathrm{sc}}$/≈ and $\mathcal{I}\mathcal{P}$/∼, where ≈ is the equivalence relation defined as $G_s\approx G_s^{\prime }$, if and only if $G_s$ and $G_s^{\prime }$ are isomorphic, and ∼ is defined as a∼b if and only if a can be rewritten as b by Mon.

(2)

A canonical form of m can be obtained from $\rho {\left(m\right)}_{\mathrm{can}}$, a canonical form of $\rho \left(m\right)$, as follows: Sort the vertices of $\rho {\left(m\right)}_{\mathrm{can}}$ with the color 2 in a lexicographical order, and obtain a vertex sequence denoted by VS. Define a mapping ξ from VS to $\mathbb{N}$ by mapping the ith element in VS to i. ξ induces a mapping $\widehat{\xi }$ from the set of vertices with the color 3 to $\mathbb{N}$ such that $\widehat{\xi }\left(v^{\prime }\right)=\xi \left(v\right)$, where $v^{\prime }$ and v are adjacent, and $v,v^{\prime }$ are vertices with the colors 2 and 3 respectively. Then, $m_{mon}$ is ${\displaystyle \prod _i}T{(a_i,b_i)}_{{\mathcal{I}}_{2i}}^{{\mathcal{I}}_{1i}}$, satisfying the condition that $T(a_i,b_i)$ represents the ith element of the sequence of vertices with the color 1, ${\mathcal{I}}_{1i}$ and ${\mathcal{I}}_{2i}$ are subsequences of $\{1,2,\dots \}$, and  ${\xi }^{-1}\left(A\right)$ (resp. ${\widehat{\xi }}^{-1}\left(A\right)$) is adjacent to the vertex represented by $T(a_i,b_i)$, where A is in ${\mathcal{I}}_{1i}$ (resp. ${\mathcal{I}}_{2i}$).

Combining Proposition 4 and Corollary 3, we have the following method for finding canonical forms of multi-digraphs.

Remark 4. 

It is clear that Steps 2 and 4 have polynomial complexity of at most $O\left({(k+2p)}^2\right)$. Steps 1 and 5 have polynomial complexity $O\left({(k+p)}^2\right)$ by Remark 2. The methods and complexity of Step 3 for finding canonical forms of simple colored undirected graphs are discussed as follows.

The following proposition shows that we only need to consider canonical forms of simple colored tripartite graphs in Step 3 of Algorithm 2.

Algorithm 2 Another method for finding canonical forms of multi-digraphs.

Input:  A multi-digraph G, with k vertices and p edges. Output:  Canonical form of G. Step 1.  Apply Steps 1 and 2 of Algorithm 1, to get an indexed monomial m. Step 2.  Find the colored graph $\rho \left(m\right)$ to describe m. 2.1 Let the indexed function names of m (according to their appearance in m) be vertices $v_1,v_2,\dots ,v_k$, and  color them with 1. 2.2 Let the upper indices of m be vertices $v_{k+1},\dots ,v_{k+p}$, and color them with 2. Let the lower indices be vertices $v_{k+p+1},\dots ,v_{k+2p}$, and color them with 3. 2.3 If the vertices $u,v$ correspond to an upper index and a lower index with the same name, or they correspond to the indexed function name and one index of an indexed function, respectively, then let $uv$ be an edge. Step 3.  Compute a canonical form of $\rho \left(m\right)$, denoted by $\rho {\left(m\right)}_{\mathrm{can}}$. Step 4.  Obtain the canonical form $m_{mon}$ of m from $\rho {\left(m\right)}_{\mathrm{can}}$, as follows. 4.1 Sort the vertices of $\rho {\left(m\right)}_{\mathrm{can}}$ with the color 2 in a lexicographical order, and obtain a vertex sequence denoted by VS2. 4.2 Let $\xi$ be a mapping from VS2 to $\mathbb{N}$ by mapping the ith element in VS2 to i. 4.3 For each vertex v with the color 3, find the vertex $v^{\prime }$ with the color 2 which is adjacent to v, let $\widehat{\xi }$ be a mapping from the set of vertices with the color 3 to $\mathbb{N}$ such that $\widehat{\xi }\left(v^{\prime }\right)=\xi \left(v\right)$. 4.4 Obtain a vertex sequence, denoted by VS1, by sorting the vertices with the color 1 in a lexicographical order. Then, find the vertex set $S_{2i}$ (resp. $S_{3i}$) with the color 2 (resp. 3) that are adjacent to the ith element in VS1, and sort $\{\xi \left(v\right)|v\in S_{2i}\}$ (resp. $\{\widehat{\xi }\left(v\right)|v\in S_{3i}\}$) in ascending order to obtain ${\mathcal{I}}_{1i}$ (resp. ${\mathcal{I}}_{2i}$). 4.5 Let $m_{mon}$ be ${\displaystyle \prod _{i=1}^k}T{(a_i,b_i)}_{{\mathcal{I}}_{2i}}^{{\mathcal{I}}_{1i}}$, where $a_i,b_i$ are $|{\mathcal{I}}_{1i}|$ and $|{\mathcal{I}}_{2i}|$, respectively. Step 5.  Apply Step 4 of Algorithm 1 to get a multi-digraph.

Proposition 6. 

Suppose $m\in \mathcal{I}\mathcal{P}$. Then, $\rho \left(m\right)$ is a tripartite graph.

Proof. 

The vertex set of $\rho \left(m\right)$ can be divided into three disjoint subsets, consisting of vertices with the color 1, 2, and 3, respectively. According to Proposition 4, the two ends of an edge must have different colors. □

As mentioned in Section 1, the most successful approach in practice for finding canonical forms of graphs or solving the isomorphism problem is the individualization-refinement paradigm, which is utilized by virtually all modern competitive and efficient software tools, including nauty, Bliss, conauto, saucy, and Traces. Among the five tools, conauto and saucy do not perform canonical labeling. Nauty is the first highly efficient program that can handle structurally regular graphs with hundreds of vertices. Bliss is specially designed for large and sparse graphs. Traces, developed by Piperno et al. [25], made a major revision of the way the search tree is scanned. Mckay et al. [1] compared the performance of Traces with nauty, Bliss, saucy, and conauto, showing that for finding canonical forms, nauty is generally the fastest for small graphs and some easier families of graphs, while Traces is better for most of the difficult (colored) graph families. In particular, Traces is the fastest for tripartite graphs. Therefore, Algorithm 2 combined with these modern competitive tools, especially Traces, can provide an efficient approach for finding canonical forms of multi-digraphs, according to Remark 4.

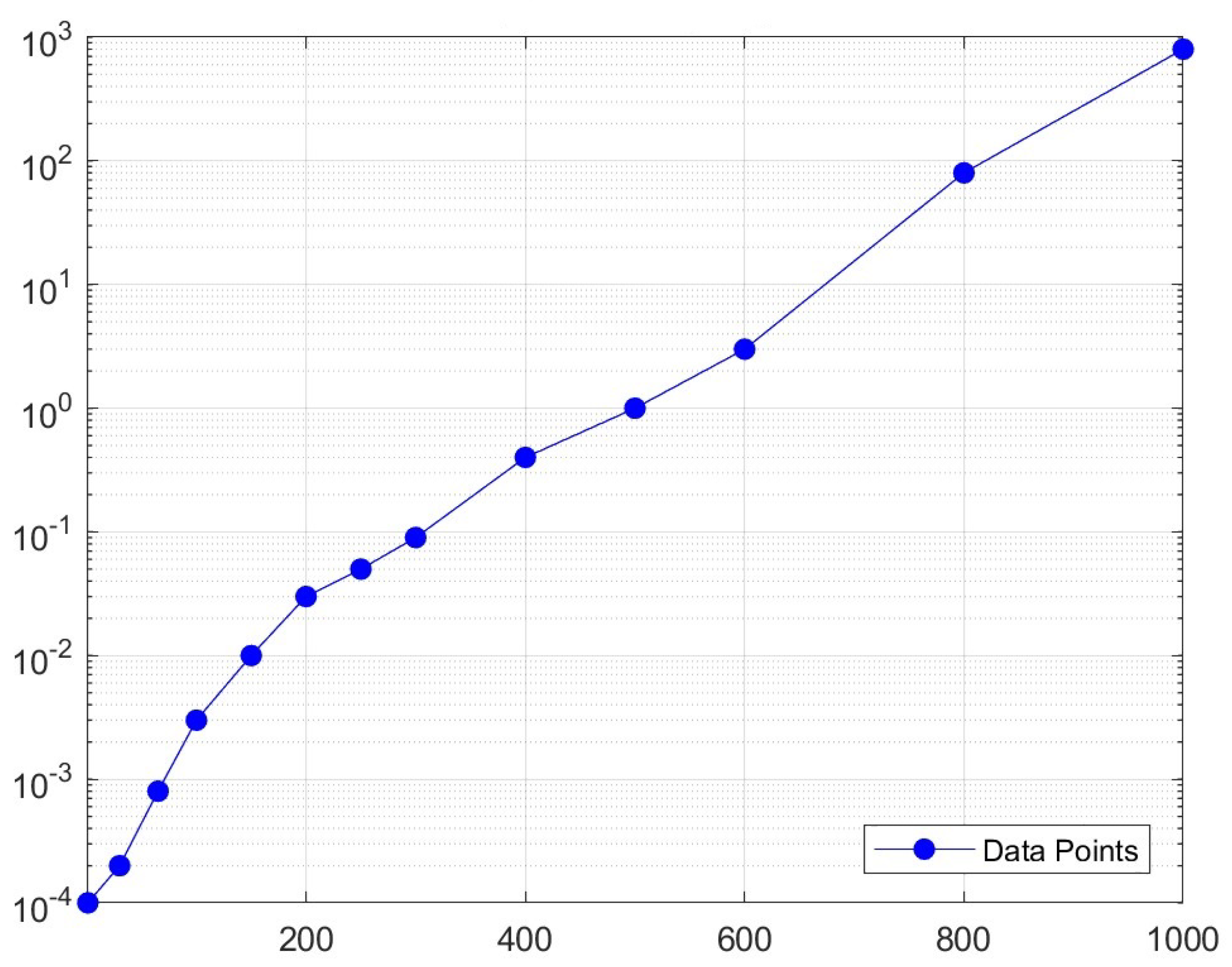
Remark 5. 

The experiments in [1] show that computing canonical forms of (non-disjoint) union of (small) tripartite graphs take polynomial time. We repeat such an experiment, and find that the time complexity is approximately $O\left(n^{4.803}\right)$, as shown in Figure 4.

Figure 4. Performance of computing canonical forms of (non-disjoint) union of tripartite graphs by Traces (horizontal: number of vertices; vertical: time in seconds).

By Remarks 4 and 5, the following conclusion is straightforward.

Proposition 7. 

For a multi-digraph G with k vertices and p edges, if $\rho \circ \delta \left(G\right)$ is a non-disjoint union of small tripartite graphs, then computing the canonical form of G takes approximately $O{(k+2p)}^{4.803}$ time in practice by Algorithm 2 and Traces, where $\rho ,\delta$ are defined in Propositions 4 and 1, respectively.

5. Conclusions and Future Work

This paper proposed a novel description of multi-digraphs as a class of indexed monomials, presented two efficient and practical approaches for computing canonical forms of multi-digraphs from the perspective of computer algebra, and explored some interesting results on complexity. Initially, we verified the equivalence of the two problems of finding canonical forms of multi-digraphs and of indexed monomials in $\mathcal{I}\mathcal{P}$. Then, the first approach employed the double coset representative method from computational group theory for canonicalization of indexed monomials and found that finding the canonical forms of a class of multi-digraphs in practice has polynomial complexity via Tensor-canonicalizer. The second approach turned canonicalization of indexed monomials into finding canonical forms of (colored) tripartite graphs. It was shown that the proposed algorithm combined with the Traces tool also takes polynomial time for computing canonical forms of a class of multi-digraphs.

In future work, ideals and syzygies in indexed polynomial rings will be used to investigate other basic problems in multi-digraphs, especially graph operations.