Codes with Weighted Poset Metrics Based on the Lattice of Subgroups of ${{\displaystyle \mathbb{Z}}}_{\mathit{m}}$

Abstract

By combining a lattice subgroup diagram of ${\mathbb{Z}}_m$ with a weighted poset metric, we introduce a new weighted coordinates poset metric for codes over ${\mathbb{Z}}_m$, called the $LS$-poset metric. When I is an ideal in a poset, the concept of I-perfect codes with an $LS$-poset metric is investigated. We obtain a Singleton bound for codes with the $LS$-poset metric and define MDS codes. When the poset in the poset metric is a chain, we provide sufficient conditions for a code with the $LS$-poset metric to be r-perfect for some $r\in \mathbb{N}$.

1. Introduction

Metrics play a central role in the design and operation of error-correcting codes. The distance between codewords, as defined by the metric, helps determine how errors are detected and corrected. By ensuring that codewords are sufficiently spaced apart (in terms of the chosen metric), coding schemes can detect errors and recover the original message with high reliability, even in the presence of noise during transmission.

The Hamming distance from 1950 (see [1]) and the Lee distance from 1958 (see [2]) are two metrics used to measure the difference between two codewords. They are both used to detect and correct errors in transmitted data, but they apply to different kinds of coding systems and have distinct characteristics. For the Hamming metric, it counts the number of positions in which two codewords differ. The Lee metric measures the shortest path between two codewords in the modular arithmetic space.

In 1995, the concept of poset metric codes over a finite field, ${\mathbb{F}}_q$, was introduced by Brualdi (see [3]). Over the past two decades, coding theory has seen significant developments through the study of codes in the poset metric. This generalization of classical coding metrics has opened up new avenues for research and applications, particularly in scenarios where traditional metrics like the Hamming or Lee distance are not sufficient to model the complexities of error patterns. We refer to [4,5,6,7,8] for some results on poset metric spaces such as packing radius, the existence of r-error-correcting codes, perfect codes, and groups of isometries. In 2018, the pomset metric was introduced by the authors in [9] to accommodate the Lee metric for codes over ${\mathbb{Z}}_m$. This metric is a further generalization of the poset metric and is based on the concept of pomsets, or partially ordered multisets. In both the poset and pomset metrics, the Singleton bound, MDS, and I-perfect property for codes are studied (see [10,11]).

Both the poset and pomset metrics are constructed based on the structure of posets. The structure of a poset serves as the foundation for defining these metrics, as it establishes the relationships and dependencies between the elements of the codeword positions.

In the present paper, we introduce a weighted poset metric based on the subgroups diagram of ${\mathbb{Z}}_m$. By using the poset of the power set of a multiset, we can effectively visualize the subgroup relationships in ${\mathbb{Z}}_m$. The poset captures the inclusion relationships between subgroups, while the multiset represents the different ways subgroups can be generated based on the divisors of m. This approach is especially powerful for cyclic groups where the subgroup structure is tightly related to the divisors of the group’s order.

Here is a concise summary of some well-known metrics specifically referenced for codes in this paper.

1.1. Hamming and Lee Metrics

Given two vectors $\mathbf{x}=(x_1,\dots ,x_n)$ and $\mathbf{y}=(y_1,\dots ,y_n)$, the Hamming distance from $\mathbf{x}$ to $\mathbf{y}$, denoted by $d_H(\mathbf{x},\mathbf{y})$, is defined to be the number of places at which $\mathbf{x}$ and $\mathbf{y}$ differ. For a vector $\mathbf{x}=(x_1,\dots ,x_n)$ over ${\mathbb{F}}_q$, the number of nonzero entries in $\mathbf{x}$ is called the Hamming weight of $\mathbf{x}$, denoted by $w_H\left(\mathbf{x}\right)$. In ${\mathbb{F}}_q^n$, the Hamming distance, $d_H(\mathbf{x},\mathbf{y})$, is given by the Hamming weight, $w_H(\mathbf{x}-\mathbf{y})$, and $d_H$ satisfies the properties of a metric (see [1]).

For two vectors $\mathbf{x}$ and $\mathbf{y}$ in ${\mathbb{Z}}_m^n$, the Lee distance between $\mathbf{x}$ and $\mathbf{y}$ is denoted by $d_L(\mathbf{x},\mathbf{y})$ and defined as

$${\displaystyle d_L(\mathbf{x},\mathbf{y}):=\sum _{i=1}^{n}min\left\{\right|x_i-y_i|,m-|x_i-y_i\left|\right\}.}$$

the Lee weight of $\mathbf{x}$ in ${\mathbb{Z}}_m^n$, denoted by $w_L\left(\mathbf{x}\right)$, is equivalent to the Lee distance between $\mathbf{x}$ and the zero vector. It was proved that the Lee distance, $d_L$, is a metric on ${\mathbb{Z}}_m^n$ (see [2,12]).

1.2. Poset Metrics

Let $P=(\left[n\right],{⪯}_P)$ be a poset on the set $\left[n\right]:=\{1,2,\dots ,n\}$ of coordinates of a vector in ${\mathbb{F}}_q^n$ (or ${\mathbb{Z}}_m^n$). For $I\subseteq \left[n\right]$, I is called an (order) ideal of P if $i\in I$, $j{⪯}_{P}i$ imply that $j\in I$. For a subset S of P, we denote $⟨S⟩$ as the smallest ideal containing S. Given a vector $\mathbf{x}=(x_1,\dots ,x_n)\in {\mathbb{F}}_q^n$, the support of $\mathbf{x}$ is $supp\left(\mathbf{x}\right)=\{i\in \left[n\right]:x_i\ne 0\}$. The poset weight of $\mathbf{x}$ is defined as

$$w_P\left(\mathbf{x}\right):=\left|⟨supp\left(\mathbf{x}\right)⟩\right|.$$

For $\mathbf{x},\mathbf{y}\in {\mathbb{F}}_q^n$, the poset distance between $\mathbf{x}$ and $\mathbf{y}$ is

$$d_P(\mathbf{x},\mathbf{y}):=w_P\left(\mathbf{x}-\mathbf{y}\right).$$

It was shown in [3] that $d_P$ is a metric on ${\mathbb{F}}_q^n$. Notice that the poset metric $d_P$ simplifies to the Hamming metric $d_H$ when the poset P is an antichain.

1.3. Pomset Metrics

1.3.1. Multisets and Pomsets

For given a nonempty set X and a map $\mathfrak{c}:X\to {\mathbb{N}}_0$, an mset M is considered as a pair $M=(X,\mathfrak{c})$. We write $a{\in }^{n}M$ (or $n/a\in M$), if $\mathfrak{c}\left(a\right)\ge n>0$, (i.e., a occurs in M at least n times).

An mset $M=(X,\mathfrak{c})$, drawn from $X=\{a_1,a_2,\dots ,a_t\}$, is represented as

$$M=\{k_1/a_1,k_2/a_2,\dots ,k_t/a_t\},$$

where $\mathfrak{c}\left(a_i\right)=k_i>0$ for $i=1,\dots ,t$. If $k/a\in M$, then $r/a\in M$ for all $1\le r\le k$. The cardinality of an mset $M=(X,\mathfrak{c})$ is defined as $\left|M\right|={\sum }_{x\in X}\mathfrak{c}\left(x\right)$.

For $m\in \mathbb{N}$, we denote ${\mathcal{M}}^m\left(X\right)$ as the (regular) mset of height m drawn from the set X, such that all elements of X occur with the same multiplicity m, i.e., $|{\mathcal{M}}^m\left(X\right)|=m|X|$. The mset space ${\left[X\right]}^m$ is the set of all msets drawn from X, such that no element in an mset occurs more than m times.

A submultiset (or submset) of an mset $M=(X,\mathfrak{c})$ is a multiset $S=(X,{\mathfrak{c}}_S)$, such that ${\mathfrak{c}}_S\left(x\right)\le \mathfrak{c}\left(x\right)$ for all $x\in X$. For an mset $M=(X,\mathfrak{c})$, the set $M^{*}=\{x\in X:\mathfrak{c}\left(x\right)>0\}$ is called the root set of M.

For two msets $M_1=(X,{\mathfrak{c}}_1)$ and $M_2=(X,{\mathfrak{c}}_2)$, we list some definitions of operations in msets [9] as follows:

• The addition(sum) of $M_1$ and $M_2$ is the mset $M_1\oplus M_2=(X,\mathfrak{s})$, where
  $\mathfrak{s}\left(x\right)={\mathfrak{c}}_1\left(x\right)+{\mathfrak{c}}_2\left(x\right)$ for all $x\in X$.
• The subtraction (difference) of $M_1$ from $M_2$ is the mset $M_2\ominus M_1=(X,\mathfrak{d})$, where
  $\mathfrak{d}\left(x\right)=max\{{\mathfrak{c}}_2\left(x\right)-{\mathfrak{c}}_1\left(x\right),0\}$ for all $x\in X$.
• The union of $M_1$ and $M_2$ is the mset $M_1\cup M_2=(X,\mathfrak{u})$, where
  $\mathfrak{u}\left(x\right)=max\{{\mathfrak{c}}_1\left(x\right),{\mathfrak{c}}_2\left(x\right)\}$ for all $x\in X$.
• The intersection of $M_1$ and $M_2$ is the mset $M_1\cap M_2=(X,\mathfrak{i})$, where
  $\mathfrak{i}\left(x\right)=min\{{\mathfrak{c}}_1\left(x\right),{\mathfrak{c}}_2\left(x\right)\}$ for all $x\in X$.

For $M_1,M_2\in {\left[X\right]}^m$, the mset sum $M_1\oplus M_2=(X,\mathfrak{s})\in {\left[X\right]}^m$, where $\mathfrak{s}\left(x\right)=min\{m,{\mathfrak{c}}_{M_1}\left(x\right)+{\mathfrak{c}}_{M_2}\left(x\right)\}$ for all $x\in X$. Given a submset $S=(X,\mathfrak{b})$ of an mset ${\mathcal{M}}^m\left(X\right)$, the complement of S is an mset $S^c=(X,{\mathfrak{b}}_c)\in {\left[X\right]}^m$, where ${\mathfrak{b}}_c\left(x\right)=m-\mathfrak{b}\left(x\right)$ for all $x\in X$.

For two msets $M_1,M_2$ drawn from a set X, we define the Cartesian product $M_1\times M_2$ by $M_1\times M_2:=\{rs/(r/x,s/y):r/x\in M_1,s/y\in M_2\}.$ A submset $R=(M\times M,\mathfrak{g})$ of $M\times M$ is said to be an mset relation on M if $\mathfrak{g}(r/x,s/y)=rs$.

An mset relation R on M is called a partially ordered mset relation (or pomset relation) R on M if the following properties are all satisfied:

(1)

[Reflexivity] $\forall m/x\in M,(m/x,m/x)\in R$;

(2)

[Antisymmetry] if $(m/x,n/y),(n/y,m/x)\in R\Rightarrow m=n,x=y$;

(3)

[Transitivity] if $(m/x,n/y),(n/y,k/z)\in R\Rightarrow (m/x,k/z)\in R$.

Notice that, if $(m/x,m/x)\in R$, then $(r/x,s/x)\in R$ for all $1\le r,s\le m$.

For given a poset $P=(X,{⪯}_P)$, we define the pomset relation ${\preccurlyeq }_P$ on ${\mathcal{M}}^m\left(X\right)$ having P-shape by

$${\preccurlyeq }_P:=\{m^2/(m/a,m/a),m^2/(m/a,m/b):\forall a,b\in X,a{⪯}_{P}b\}.$$

The pair $({\mathcal{M}}^m\left(X\right),{\preccurlyeq }_P)$ is known as a partially ordered multiset (pomset), denoted by $\mathbb{P}$.

The dual pomset of the pomset $\mathbb{P}=({\mathcal{M}}^m\left(X\right),{\preccurlyeq }_P)$, denoted by $\tilde{\mathbb{P}}$, is the pomset on $M^m\left(X\right)$ having $\tilde{P}$-shape, where $\tilde{P}$ is the dual poset of P. That is, $m/a{\preccurlyeq }_{P}m/b$ in $\mathbb{P}$ if and only if $m/b{\preccurlyeq }_{\tilde{P}}m/a$ in $\tilde{\mathbb{P}}$.

Let S be a submset of ${\mathcal{M}}^m\left(X\right)$ in a pomset $\mathbb{P}=({\mathcal{M}}^m\left(X\right),{\preccurlyeq }_P)$. An element $t/a\in S$ is said to be a maximal element in S if there is no element $k/c\in S(c\ne a)$, such that $t/a{\preccurlyeq }_{P}k/c$. An element $r/b\in S$ is said to be a minimal element in S if there is no element $k/c\in S(c\ne b)$, such that $k/c{\preccurlyeq }_{P}t/b$.

Let $\mathbb{P}=({\mathcal{M}}^k\left(\left[n\right]\right),{\preccurlyeq }_P)$ be the pomset of height k having P-shape, where the poset $P=(\left[n\right],{⪯}_P)$. An ideal in $\mathbb{P}$ is a submset $I\subseteq {\mathcal{M}}^k\left(\left[n\right]\right)$ with the property that if $j/b\in I$ and $i/a{\preccurlyeq }_{P}j/b(a\ne b)$ then $i/a\in I$. Given a submset S of ${\mathcal{M}}^k\left(\left[n\right]\right)$, we denote by $⟨S⟩$ the smallest ideal containing S.

An ideal I of ${\mathcal{M}}^k\left(\left[n\right]\right)$ is called an ideal with full count if $i/a\in I\Rightarrow k/a\in I$; otherwise, it is called an ideal with partial count.

Example 1. 

From the poset $P_1$, as in Figure 1, we consider the pomset ${\mathbb{P}}_1=({\mathcal{M}}^3\left(\left[4\right]\right),{\preccurlyeq }_{P_1})$. Let $I_1=\{3/1,3/4\}$ and $I_2=\{3/1,2/2,1/3\}$ be ideals with full count and partial count in ${\mathbb{P}}_1$, respectively. Then the complements $I_1^c=\{3/2,3/3\}$ and $I_2^c=\{1/2,2/3,3/4\}$ are ideals with full count and partial count in ${\tilde{\mathbb{P}}}_1$, respectively. Observe that $I_1\cap I_1^c=\varnothing$, whereas $I_2\cap I_2^c=\{1/2,1/3\}$.

Figure 1. The posets $P_1,P_2,P_3$.

Notice that if I is an ideal with full count in $\mathbb{P}=({\mathcal{M}}^k\left(\left[n\right]\right),{\preccurlyeq }_P)$, then $\{I,I^c\}$ is a partition of ${\mathcal{M}}^k\left(\left[n\right]\right)$, that is, $I\cap I^c=\varnothing$ and $I\cup I^c={\mathcal{M}}^k\left(\left[n\right]\right)$. However, for given any submset J of ${\mathcal{M}}^k\left(\left[n\right]\right)$, $J\oplus J^c={\mathcal{M}}^k\left(\left[n\right]\right)$.

1.3.2. Pomset Distance

In the space ${\mathbb{Z}}_m^n$ with the pomset $\mathbb{P}=({\mathcal{M}}^{\lfloor m/2\rfloor }\left(\left[n\right]\right),{\preccurlyeq }_P)$. For a vector $\mathbf{x}=(x_1,\dots ,x_n)\in {\mathbb{Z}}_m^n$, the support of $\mathbf{x}$ with respect to the Lee weight is defined to be

$${supp}_L\left(\mathbf{x}\right):=\{t/i:x_i\ne 0,\mathrm{and}t=min\{x_i,m-x_i\}\}.$$

The pomset weight of $\mathbf{x}\in {\mathbb{Z}}_m^n$ is defined to be $w_{\mathbb{P}}\left(\mathbf{x}\right):=\left|⟨{supp}_L\left(\mathbf{x}\right)⟩\right|$, and the pomset distance between two vectors $\mathbf{x},\mathbf{y}$ in ${\mathbb{Z}}_m^n$ is defined by $d_{\mathbb{P}}\left(\mathbf{x},\mathbf{y}\right):=w_{\mathbb{P}}\left(\mathbf{x}-\mathbf{y}\right)$. It is known that the pomset distance is a metric on ${\mathbb{Z}}_m^n$ (see [9]), and it is called a pomset metric. When the pomset is an antichain, there is no hierarchical structure to influence the weight calculation, making the pomset metric equivalent to the Lee metric in terms of how the weight of the codeword is computed.

2. Weighted Poset Metrics Based on the Lattice of Subgroups of ${{\displaystyle \mathbb{Z}}}_{\mathit{m}}$

The lattice of subgroups of ${\mathbb{Z}}_m$ can be effectively studied by leveraging the power set of a multiset of divisors. Here is how this provides insight into the hierarchical relationships between subgroups.

2.1. An Ordinal Product

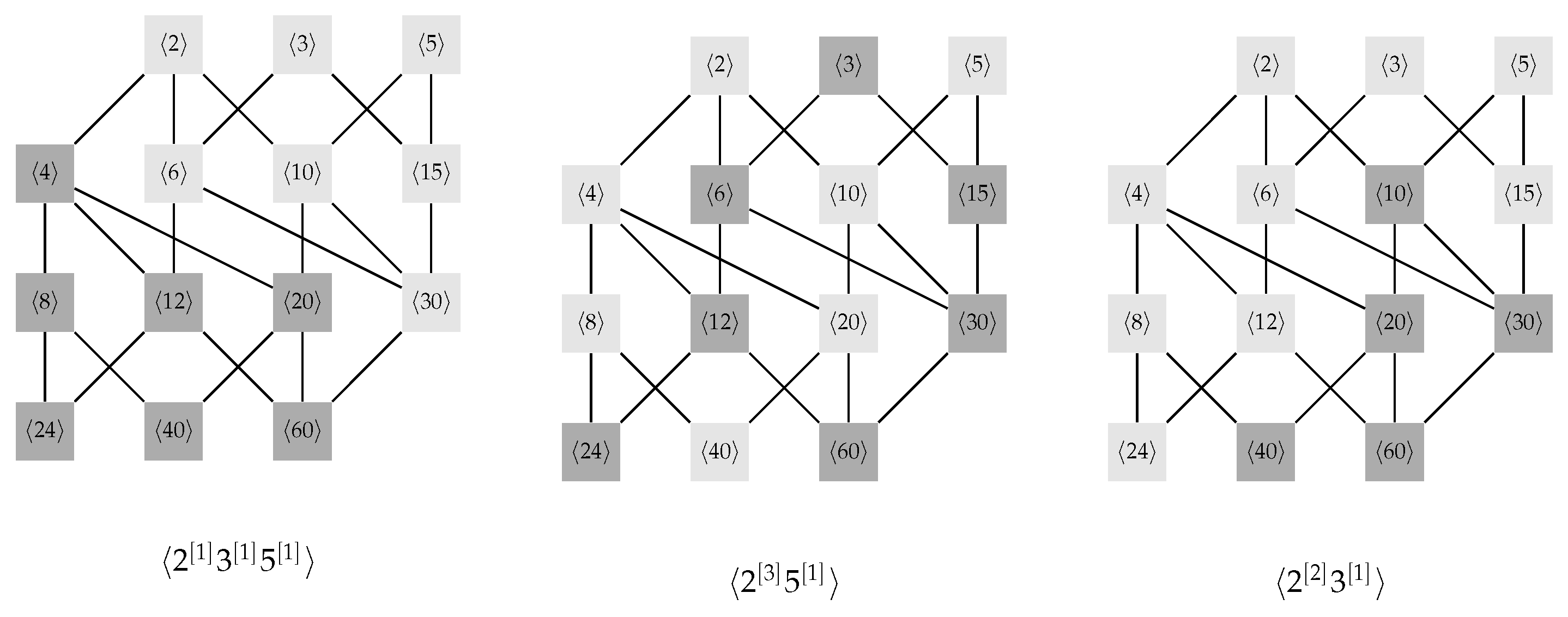
Let $A=\{n_1/a_1,n_2/a_2,\dots ,n_t/a_t\}$ be an mset with $A^{*}=\{a_1,a_2,\dots ,a_t\}$. Then ${\displaystyle \left|A\right|=\sum _{i=1}^t{n}_i}$. Let $\mathcal{P}\left(A\right)$ be the power set of the mset A. With a slight change of notation, we will use $a_{i_1}^{\left[t_{i_1}\right]}{a}_{i_2}^{\left[t_{i_2}\right]}\cdots a_{i_s}^{\left[t_{i_s}\right]}$ for the mset $\{t_{i_1}/a_{i_1},t_{i_2}/a_{i_2},\dots ,t_{i_s}/a_{i_s}\}\in \mathcal{P}\left(A\right)$. Here we let $\mathcal{P}\left(A\right):=\mathcal{P}\left(A\right)\setminus \{\varnothing \}$.

Note that we may write $a_i^{\left[0\right]}$ to indicate that $a_i$ does not appear. For ${\alpha }_1,{\alpha }_2\in \mathcal{P}\left(A\right)$, which ${\alpha }_1=a_1^{\left[l_1\right]}{a}_2^{\left[l_2\right]}\cdots a_t^{\left[l_t\right]}$ and ${\alpha }_2=a_1^{\left[h_1\right]}{a}_2^{\left[h_2\right]}\cdots a_t^{\left[h_t\right]}$, define the mset sum ${\alpha }_1\oplus {\alpha }_2=a_1^{\left[{\mathfrak{s}}_1\left(a_1\right)\right]}{a}_2^{\left[{\mathfrak{s}}_2\left(a_2\right)\right]}\cdots a_t^{\left[{\mathfrak{s}}_t\left(a_t\right)\right]}\in \mathcal{P}\left(A\right)$, where ${\mathfrak{s}}_i\left(a_i\right)=min\{n_i,l_i+h_i\}$ for all $i=1,\dots ,t$.

For each $\alpha =a_{i_1}^{\left[t_{i_1}\right]}{a}_{i_2}^{\left[t_{i_2}\right]}\cdots a_{i_s}^{\left[t_{i_s}\right]}\in \mathcal{P}\left(A\right)$ with $\alpha \ne A$, the dual of $\alpha$ is

$$\widehat{\alpha }=a_{i_1}^{[n_{i_1}-t_{i_1}]}{a}_{i_2}^{[n_{i_2}-t_{i_2}]}\cdots a_{i_s}^{[n_{i_s}-t_{i_s}]}\in \mathcal{P}\left(A\right),$$

which $\alpha \oplus \widehat{\alpha }=A$.

Under the submset relation ${\subseteq }_A$, $(\mathcal{P}\left(A\right),{\subseteq }_A)$ is a partially ordered set, denoted by ${\mathcal{P}}_A$. For each $\alpha \in \mathcal{P}\left(A\right)$, we denote $⟨\alpha ⟩$ the ideal in $\mathcal{P}\left(A\right)$ having $\alpha$ as its maximum element. It is clear that $⟨A⟩=\mathcal{P}\left(A\right)$. For example, let $a^{\left[1\right]}{b}^{\left[2\right]},b^{\left[3\right]}\in \mathcal{P}\left(a^{\left[2\right]}{b}^{\left[3\right]}\right)$. Then $⟨a^{\left[1\right]}{b}^{\left[2\right]}⟩=\{a^{\left[1\right]}{b}^{\left[2\right]},a^{\left[1\right]}{b}^{\left[1\right]},b^{\left[2\right]},a^{\left[1\right]},b^{\left[1\right]}\}$, and $⟨b^{\left[3\right]}⟩=\{b^{\left[3\right]},b^{\left[2\right]},b^{\left[1\right]}\}$.

Remark 1. 

For $\alpha =a_{i_1}^{\left[t_{i_1}\right]}{a}_{i_2}^{\left[t_{i_2}\right]}\cdots a_{i_s}^{\left[t_{i_s}\right]}\in \mathcal{P}\left(A\right)$, we have ${\displaystyle \left|\alpha \right|=\sum _{j=1}^s{t}_{i_j},and\left|⟨\alpha ⟩\right|=\prod _{j=1}^s(t_{i_j}+1)-1}$.

Given a poset $P=(\left[n\right],{⪯}_P)$, we define a relation $\gamma$ on $\left[n\right]\times \mathcal{P}\left(A\right)$ by

$$(i,\alpha )\gamma (j,\beta )\iff \left\{\begin{array}{c}i=j\mathrm{and}\alpha {\subseteq }_A\beta \hfill \\ i{⪯}_{P}j\mathrm{where}i\ne j\hfill \end{array}\right..$$

It is clear that $\left(\right[n]\times \mathcal{P}(A),\gamma )$ is a poset, denoted by $P\times {\mathcal{P}}_A$. By the property of any ideal in a poset that contains every element smaller than or equal to some of its elements, we have that, if $(i,\alpha )\in I$ and I is an ideal in $P\times {\mathcal{P}}_A$, then $\left\{i\right\}\times ⟨\alpha ⟩\subseteq I$.

An ideal I in $P\times {\mathcal{P}}_A=(\left[n\right]\times \mathcal{P}\left(A\right),\gamma )$ is called an ideal with full count if $(i,\alpha )\in I\Rightarrow (i,A)\in I$; otherwise, it is also called an ideal with partial count. Let $\mathcal{I}(P\times {\mathcal{P}}_A)$ be the set of all ideals in $P\times {\mathcal{P}}_A$. For $I\in \mathcal{I}(P\times {\mathcal{P}}_A)$, we denote

$$\begin{array}{cc}\hfill {\omega }_{I_f}:=& \{i\in [n]:(i,A)\in I\},\mathrm{and}\hfill \\ \hfill {\omega }_{I_p}:=& \{i\in [n]:(i,A)\notin I\mathrm{but}(i,\alpha )\in I\mathrm{for}\mathrm{some}\alpha \in \mathcal{P}(A\left)\right\}.\hfill \end{array}$$

Given an ideal with partial count I in $P\times {\mathcal{P}}_A$ and for $i\in {\omega }_{I_p}$, we let $\mathcal{A}(I;i):=\{\alpha \in \mathcal{P}(A):(i,\alpha )\in I\}$. An ideal I in $P\times {\mathcal{P}}_A$ is called normal if $\forall i\in {\omega }_{I_p}$, $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$. We denote by $\mathfrak{I}(P\times {\mathcal{P}}_A)$ the collections of normal ideals in $\mathcal{I}(P\times {\mathcal{P}}_A)$.

The dual poset with respect to P of $P\times {\mathcal{P}}_A$ is the poset $\tilde{P}\times {\mathcal{P}}_A$, where $\tilde{P}$ is the dual poset of P. Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. The complement of I, denoted by $I^{\mathfrak{C}}$, is a normal ideal in the dual poset $\tilde{P}\times {\mathcal{P}}_A$, which satisfies:

1.

${\omega }_{I_p^{\mathfrak{C}}}={\omega }_{I_p}$ and ${\omega }_{I_f^{\mathfrak{C}}}=\left[n\right]\setminus ({\omega }_{I_f}\cup {\omega }_{I_p})$;

2.

For $i\in {\omega }_{I_p^{\mathfrak{C}}}$, $\mathcal{A}(I^{\mathfrak{C}};i)=⟨{\widehat{\alpha }}_i⟩$, where $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$.

Example 2. 

Consider the poset $P_3=(\left[6\right],{⪯}_{P_3})$, as in Figure 1, and the mset $A=a^{\left[3\right]}{b}^{\left[2\right]}$. Let $I_1,I_2,I_3\in \mathcal{I}(P_3\times {\mathcal{P}}_A)$ be defined by

$$\begin{array}{cc}\hfill I_1& =\{1,2\}\times ⟨a^{\left[3\right]}{b}^{\left[2\right]}⟩\cup \left\{4\right\}\times ⟨a^{\left[2\right]}{b}^{\left[2\right]}⟩,\hfill \\ \hfill I_2& =\left\{1\right\}\times ⟨a^{\left[3\right]}{b}^{\left[2\right]}⟩,and{I}_3=\left\{1\right\}\times \left(⟨a^{\left[1\right]}{b}^{\left[2\right]}⟩\cup ⟨a^{\left[3\right]}⟩\right).\hfill \end{array}$$

We can see that $|I_1|=30$, $|I_2|=11$, and $|I_3|=7$. We have $I_1$ and $I_3$ as ideals with partial count, such that $I_1=⟨(4,a^{\left[2\right]}{b}^{\left[2\right]})⟩$ and $I_3=⟨\{(1,a^{\left[1\right]}{b}^{\left[2\right]}),(1,a^{\left[3\right]})\}⟩$, and $I_2$ is an ideal with full count, such that $I_2=⟨(1,a^{\left[3\right]}{b}^{\left[2\right]})⟩$. Clearly, $I_1$ and $I_2$ are normal, but $I_3$ is not normal. For the complements of $I_1$ and $I_2$, we have

$$\begin{array}{ccc}\hfill I_1^{\mathfrak{C}}& =\{3,5,6\}\times ⟨a^{\left[3\right]}{b}^{\left[2\right]}⟩\cup \left\{(4,a^{\left[1\right]})\right\},and{I}_2^{\mathfrak{C}}\hfill & \hfill =\{2,3,4,5,6\}\times ⟨a^{\left[3\right]}{b}^{\left[2\right]}⟩.\end{array}$$

For $\alpha =a_1^{\left[h_1\right]}{a}_2^{\left[h_2\right]}\cdots a_t^{\left[h_t\right]}\in \mathcal{P}\left(A\right)$, where the mset $A=a_1^{\left[n_1\right]}{a}_2^{\left[n_2\right]}\cdots a_t^{\left[n_t\right]}$ and $0\le h_i\le n_i$ for $1\le i\le t$, we define

$$\lfloor \alpha \rceil :=\left\{\begin{array}{cc}\left|\alpha \right|,\hfill & \mathrm{if}{h}_j=n_j=1\mathrm{for}\mathrm{some}j\in \{1,\dots ,t\},\hfill \\ \left|\alpha \right|+1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The following result is directly obtained.

Proposition 3. 

Given an mset $A=(A^{*},\mathfrak{c})$ and $\alpha \in \mathcal{P}\left(A\right)$, we have that

1. 

If $\lfloor \alpha \rceil =\left|\alpha \right|+1>2$, $\exists {\alpha }^{\prime }\in \mathcal{P}\left(A\right)$, such that ${\alpha }^{\prime }{\subseteq }_A\alpha$ and $\lfloor {\alpha }^{\prime }\rceil =|{\alpha }^{\prime }|+1=|\alpha |$.

2. 

If $\lfloor \alpha \rceil =\left|\alpha \right|>1$, $\exists {\alpha }^{\prime }\in \mathcal{P}\left(A\right)$, such that ${\alpha }^{\prime }{\subseteq }_A\alpha$ and $\lfloor {\alpha }^{\prime }\rceil =|{\alpha }^{\prime }|=|\alpha |-1$.

3. 

For ${\alpha }_1{\subseteq }_A{\alpha }_2\in \mathcal{P}\left(A\right)$, if $\lfloor {\alpha }_1\rceil =|{\alpha }_1|+1=|{\alpha }_2|=\lfloor {\alpha }_2\rceil$, then there is a unique $x\in {\alpha }_2^{*}\subseteq A^{*}$, such that $\mathfrak{c}\left(x\right)=1$.

4. 

If $\mathfrak{c}\left(x\right)>1$ for all $x\in A^{*}$, then there is no $\alpha \in \mathcal{P}\left(A\right)$, such that $\lfloor \alpha \rceil =1$.

Define a map ${\zeta }_A:\mathfrak{I}(P\times {\mathcal{P}}_A)\to \mathbb{N}$ by

$$\begin{array}{cc}\hfill {\zeta }_A\left(I\right)=& |{\omega }_{I_f}|·\lfloor A\rceil +\sum _{\begin{array}{c}i\in {\omega }_{I_p}\mathrm{such}\mathrm{that}\\ \mathcal{A}(I;i)=⟨{\alpha }_i⟩\mathrm{for}\mathrm{some}{\alpha }_i\in \mathcal{P}\left(A\right)\end{array}}\lfloor {\alpha }_i\rceil .\hfill \end{array}$$

(1)

Observe that ${\zeta }_A\left(I\right)\le \left|I\right|$ for all $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. Moreover, if $\left|A\right|=1$, then ${\zeta }_A\left(I\right)=\left|I\right|$ for all $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. For $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, let

$$\begin{array}{cc}\hfill {\mathsf{\Omega }}_{I_p}:=& \{\alpha \in \mathcal{P}\left(A\right):\mathcal{A}(I;i)=⟨\alpha ⟩\mathrm{and}\lfloor \alpha \rceil =|\alpha |\mathrm{for}i\in {\omega }_{I_p}\}\mathrm{and}\hfill \\ \hfill {\overline{\mathsf{\Omega }}}_{I_p}:=& \{\alpha \in \mathcal{P}\left(A\right):\mathcal{A}(I;i)=⟨\alpha ⟩\mathrm{and}\lfloor \alpha \rceil =|\alpha |+1\mathrm{for}i\in {\omega }_{I_p}\}.\hfill \end{array}$$

Then ${\zeta }_A\left(I\right)=\left|{\omega }_{I_f}\right|·\lfloor A\rceil +\left[{\mathsf{\Omega }}_{I_p}\right]$, where ${\displaystyle \left[{\mathsf{\Omega }}_{I_p}\right]=\sum _{\alpha \in {\mathsf{\Omega }}_{I_p}\cup {\overline{\mathsf{\Omega }}}_{I_p}}\lfloor \alpha \rceil }$.

With Proposition 3 and by deleting a maximal element of a normal ideal I in $P\times {\mathcal{P}}_A$, it gives a way to construct a normal ideal $J\subseteq I$. The next result is directly obtained.

Proposition 4. 

Consider an mset $A=(A^{*},\mathfrak{c})$ and the poset $P\times {\mathcal{P}}_A=(\left[n\right]\times \mathcal{P}\left(A\right),\gamma )$.

1. 

For each $0\le t\le n$, there exists an ideal J with full count, such that ${\zeta }_A\left(J\right)=t·\lfloor A\rceil$.

2. 

Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$ be such that ${\omega }_{I_p}\ne \varnothing$.

(2.1) 

If ${\mathsf{\Omega }}_{I_p}\ne \varnothing$, then for each $0\le t\le \left[{\mathsf{\Omega }}_{I_p}\right]$ there exists $J\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, such that $J\subseteq I$ and ${\zeta }_A\left(J\right)=\left|{\omega }_{I_f}\right|·\lfloor A\rceil +t$.

(2.2) 

If ${\mathsf{\Omega }}_{I_p}=\varnothing$, then for each $0\le t\le \left[{\mathsf{\Omega }}_{I_p}\right]$ with $t\ne 1$ there exists $J\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, such that $J\subseteq I$ and ${\zeta }_A\left(J\right)=\left|{\omega }_{I_f}\right|·\lfloor A\rceil +t$.

2.2. Supports and Weights

Suppose that $m=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\cdots p_k^{{\beta }_k}$, where $p_1,\dots ,p_k$ are distinct prime numbers and ${\beta }_1,\dots ,{\beta }_k$ are positive integers. By considering the mset $A=p_1^{\left[{\beta }_1\right]}{p}_2^{\left[{\beta }_2\right]}\cdots p_k^{\left[{\beta }_k\right]}$, we can see that the lattice of subgroups of ${\mathbb{Z}}_m$ and the poset structure of $\mathcal{P}\left(A\right)$ under ${\subseteq }_A$ are the same.

Let $\mathrm{Sub}\left({\mathbb{Z}}_m\right)$ be the set of all subgroups of ${\mathbb{Z}}_m$. The map $\psi :\mathrm{Sub}\left({\mathbb{Z}}_m\right)\to \mathcal{P}\left(A\right)$ defined by $\psi \left(H\right)={\alpha }_H=p_1^{\left[t_1\right]}{p}_2^{\left[t_2\right]}\cdots p_k^{\left[t_k\right]}$, where $\left|H\right|=p_1^{t_1}{p}_2^{t_2}\cdots p_k^{t_k}$ for $0\le t_i\le {\beta }_i$, is an order-isomorphism.

Let $P=(\left[n\right],{⪯}_P)$ be a poset. Given $\mathbf{x}=(x_1,\dots ,x_n)\in {\mathbb{Z}}_m^n$, we define the support of x associated with the lattice of subgroups of ${\mathbb{Z}}_m$ as

$${supp}_{LS}\left(\mathbf{x}\right):=\{(i,p_1^{\left[t_1\right]}{p}_2^{\left[t_2\right]}\cdots p_k^{\left[t_k\right]}):x_i\ne 0\mathrm{and}|⟨x_i⟩|=p_1^{t_1}{p}_2^{t_2}\cdots p_k^{t_k}\}$$

a subset of $\left[n\right]\times \mathcal{P}\left(A\right)$. By considering $⟨{supp}_{LS}\left(\mathbf{x}\right)⟩\in \mathfrak{I}(P\times {\mathcal{P}}_A)$ as the smallest ideal in $P\times {\mathcal{P}}_A$ containing ${supp}_{LS}\left(\mathbf{x}\right)$, the $LS$-poset weight of $\mathbf{x}\in {\mathbb{Z}}_m^n$ is defined to be $w_{LS}\left(\mathbf{x}\right):={\zeta }_A\left(⟨{supp}_{LS}\left(\mathbf{x}\right)⟩\right)$, and the $LS$-poset distance between $\mathbf{x},\mathbf{y}\in {\mathbb{Z}}_m^n$ is $d_{LS}(\mathbf{x},\mathbf{y}):=w_{LS}(\mathbf{x}-\mathbf{y})$. Now we prove that the $LS$-poset distance is a metric on ${\mathbb{Z}}_m^n$.

Theorem 5. 

Let $P=(\left[n\right],{⪯}_P)$ be a poset and $m=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\cdots p_k^{{\beta }_k}$, where $p_i$ are distinct primes. Under the poset $P\times {\mathcal{P}}_A$ with the mset $A=p_1^{\left[{\beta }_1\right]}{p}_2^{\left[{\beta }_2\right]}\cdots p_k^{\left[{\beta }_k\right]}$, the $LS$-poset distance $d_{LS}(·,·)$ is a metric on ${\mathbb{Z}}_m^n$.

Proof. 

It is clear that $d_{LS}(\mathbf{x},\mathbf{y})\ge 0$. As a group ${\mathbb{Z}}_m$, we have $d_{LS}(\mathbf{x},\mathbf{y})=0$ if $\mathbf{x}=\mathbf{y}$. Moreover, for any $x\in {\mathbb{Z}}_m$, $⟨x⟩=⟨-x⟩$, which implies that $d_{LS}(·,·)$ is symmetric. To show that the triangle inequality of $d_{LS}(·,·)$ holds, we let $a,b\in {\mathbb{Z}}_m$. By applying the fundamental theorem of finite cyclic groups, we assume that $⟨a⟩=⟨p_1^{t_1}{p}_2^{t_2}\cdots p_k^{t_k}⟩$ and $⟨b⟩=⟨p_1^{s_1}{p}_2^{s_2}\cdots p_k^{s_k}⟩$ for some nonnegative integers $t_i,s_i,$$(1\le i\le k)$. Then $\left|⟨a⟩\right|=p_1^{{\beta }_1-t_1}{p}_2^{{\beta }_2-t_2}\cdots p_k^{{\beta }_k-t_k}$ and $\left|⟨b⟩\right|=p_1^{{\beta }_1-s_1}{p}_2^{{\beta }_2-s_2}\cdots p_k^{{\beta }_k-s_k}$. Suppose that $⟨a+b⟩=⟨p_1^{r_1}{p}_2^{r_2}\cdots p_k^{r_k}⟩$ for some $r_i\ge 0$. It is clear that $⟨a+b⟩\subseteq H=⟨p_1^{min\{t_1,s_1\}}{p}_2^{min\{t_2,s_2\}}\cdots p_k^{min\{t_k,s_k\}}⟩$. Then ${\alpha }_{⟨a+b⟩}=p_1^{[{\beta }_1-r_1]}{p}_2^{[{\beta }_2-r_2]}\cdots p_k^{[{\beta }_k-r_k]}{\subseteq }_A{\alpha }_H=p_1^{[{\beta }_1-min\{t_1,s_1\}]}{p}_2^{[{\beta }_2-min\{t_2,s_2\}]}\cdots p_k^{[{\beta }_k-min\{t_k,s_k\}]}$. Observe that ${\displaystyle |{\alpha }_{⟨a+b⟩}|=\sum _{i=1}^k({\beta }_i-r_i)\le \sum _{i=1}^k[{\beta }_i-min\{t_i,s_i\}]=|{\alpha }_H|\le \sum _{i=1}^k[({\beta }_i-t_i)+({\beta }_i-s_i)]=|{\alpha }_{⟨a⟩}|+|{\alpha }_{⟨b⟩}|}$. If $|{\alpha }_{⟨a+b⟩}|<|{\alpha }_H|$, it follows that $\lfloor {\alpha }_{⟨a+b⟩}\rceil \le \lfloor {\alpha }_{⟨a⟩}\rceil +\lfloor {\alpha }_{⟨b⟩}\rceil$. Now, we suppose $|{\alpha }_{⟨a+b⟩}|=|{\alpha }_H|$. From ${\alpha }_{⟨a+b⟩}{\subseteq }_A{\alpha }_H$, this forces ${\alpha }_{⟨a+b⟩}={\alpha }_H$, which means $r_i=min\{t_i,s_i\}$ for all i. It is clear for the case $\lfloor {\alpha }_{⟨a+b⟩}\rceil =\left|{\alpha }_{⟨a+b⟩}\right|$. Next, assume that $\lfloor {\alpha }_{⟨a+b⟩}\rceil =\left|{\alpha }_{⟨a+b⟩}\right|+1$. It follows that, if ${\beta }_j=1$ for $j\in \{1,\dots ,k\}$, then $1=r_j=min\{t_j,s_j\}$, which implies $\lfloor {\alpha }_{⟨a⟩}\rceil =\left|{\alpha }_{⟨a⟩}\right|+1$ and $\lfloor {\alpha }_{⟨b⟩}\rceil =\left|{\alpha }_{⟨b⟩}\right|+1$. Consequently, $\lfloor {\alpha }_{⟨a+b⟩}\rceil \le \lfloor {\alpha }_{⟨a⟩}\rceil +\lfloor {\alpha }_{⟨b⟩}\rceil$. This completes the proof. □

The metric $d_{LS}(·,·)$ on ${\mathbb{Z}}_m^n$ is called as the $LS$-poset metric. Let C be a submodule of ${\mathbb{Z}}_m^n$ with the $LS$-poset metric $d_{LS}$. Then C is called an $LS$-poset code of length n over ${\mathbb{Z}}_m$. The minimum $LS$-poset distance $d_{LS}\left(C\right)$ is the smallest $LS$-poset distance between two distinct codewords of C. The dual of an $LS$-poset code C is defined as

$$C^{\perp }=\{\mathbf{v}\in {\mathbb{Z}}_m^n|\mathbf{u}·\mathbf{v}=u_1{v}_1+u_2{v}_2+\cdots +u_n{v}_n=0\mathrm{for}\mathrm{all}\mathbf{u}\in C\}.$$

To obtain more information on each element of ${\mathbb{Z}}_m\setminus \left\{0\right\}$, which is placed on the poset structure of $\mathcal{P}\left(A\right)$, we let

$${\mathcal{G}}_t:=\{x\in {\mathbb{Z}}_m\setminus \left\{0\right\}|\lfloor {\alpha }_{⟨x⟩}\rceil =t\}.$$

Example 6. 

Consider ${\mathbb{Z}}_{20}$ with the mset $A=2^{\left[2\right]}{5}^{\left[1\right]}$. We have the following table:

$\mathcal{P}\left(A\right)$	$\lfloor ·\rceil$	${\mathbb{Z}}_{20}\setminus \left\{0\right\}$
$5^{\left[1\right]}$	1	$4,8,12,16$
$2^{\left[1\right]}$	2	10
$2^{\left[1\right]}{5}^{\left[1\right]}$	2	$2,6,14,18$
$2^{\left[2\right]}$	3	$5,15$
$2^{\left[2\right]}{5}^{\left[1\right]}$	3	$1,3,7,9,11,13,17,19$

Recall some properties of the Euler $\varphi$-function as follows:

1.

If p is a prime, then $\varphi \left(p\right)=p-1$ and $\varphi \left(p^k\right)=p^k-p^{k-1}$ for all $k\in \mathbb{N}$.

2.

For $x,y\in \mathbb{N}$, if $gcd(x,y)=1$, then $\varphi \left(xy\right)=\varphi \left(x\right)\varphi \left(y\right)$.

Remark 2. 

Suppose $m=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\cdots p_k^{{\beta }_k}$, where $p_i$ are distinct primes. Consider the mset $A=p_1^{\left[{\beta }_1\right]}{p}_2^{\left[{\beta }_2\right]}\cdots p_k^{\left[{\beta }_k\right]}$. We have that

• If ${\beta }_i>1$ for all i, then ${\mathcal{G}}_1=\varnothing$ and $|{\mathcal{G}}_{\left|A\right|+1}|=\varphi \left(m\right)$.
• If ${\beta }_i=1$ for all i, then for $1\le t\le k$,

  $$|{\mathcal{G}}_t|=\sum _{\begin{array}{c}(s_1,\dots ,s_k)where\\ t={\sum }_i^k{s}_i,s_i\in \{0,1\}\end{array}}\varphi (p_1^{s_1}{p}_2^{s_2}\cdots p_k^{s_k}).$$

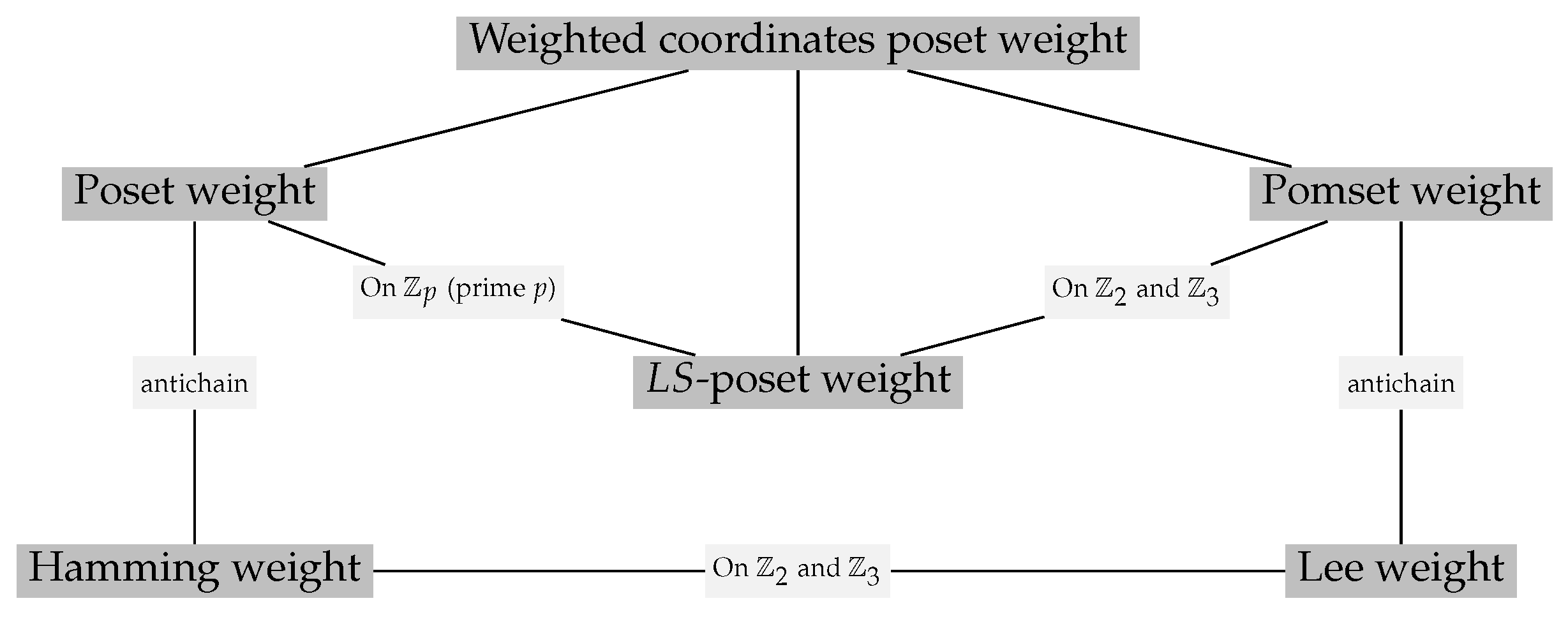
Example 7. 

In the space ${\mathbb{Z}}_{180}^4$, we consider the poset $P_1\times {\mathcal{P}}_A=(\left[4\right]\times \mathcal{P}\left(A\right),\gamma )$, where the mset $A=2^{\left[2\right]}{3}^{\left[2\right]}{5}^{\left[1\right]}$ and the poset $P_1=(\left[4\right],{⪯}_{P_1})$ is as shown in Figure 1. Consider the vector $(0,5,12,120)\in {\mathbb{Z}}_{180}^4$. We have

• (Poset weight) $w_{P_1}\left((0,5,12,120)\right)=\left|⟨\{2,3,4\}⟩\right|=4$.
• (Pomset weight) $w_{{\mathbb{P}}_1}\left((0,5,12,120)\right)=\left|⟨\{5/2,12/3,60/4\}⟩\right|=77.$
• ($LS$-poset weight)
  $w_{LS}\left((0,5,12,120)\right)={\zeta }_A⟨\{(2,2^{\left[2\right]}{3}^{\left[2\right]}),(3,3^{\left[1\right]}{5}^{\left[1\right]}),(4,3^{\left[1\right]})\}⟩=14.$

Notice that, for a space ${\mathbb{Z}}_p^n$ with prime p, the poset metric $d_P$ and the $LS$-poset metric $d_{LS}$ are the same, while the pomset metric $d_{\mathbb{P}}$ and the $LS$-poset metric $d_{LS}$ are equivalent when $p=2,3$. The diagram in Figure 2 illustrates these facts.

Figure 2. Weight relationship tree.

3. $\mathit{r}$-Balls and $\mathit{I}$-Balls

Let $\mathbf{u}$ be a vector in the space ${\mathbb{Z}}_m^n$ with $LS$-poset metric $d_{LS}$ and $r\in {\mathbb{N}}_0$. With the center at $\mathbf{u}$ and radius r, the r-ball and the r-sphere, respectively, are as follows:

$$\begin{array}{cc}\hfill B_{r,LS}\left(\mathbf{u}\right)& :=\{\mathbf{v}\in {\mathbb{Z}}_m^n|d_{LS}\left(\mathbf{u},\mathbf{v}\right)\le r\},\hfill \\ \hfill S_{r,LS}\left(\mathbf{u}\right)& :=\{\mathbf{v}\in {\mathbb{Z}}_m^n|d_{LS}\left(\mathbf{u},\mathbf{v}\right)=r\}.\hfill \end{array}$$

It is clear that ${\displaystyle |B_{r,LS}\left(\mathbf{u}\right)|=1+\sum _{i=1}^r\left|S_{i,LS}\left(\mathbf{u}\right)\right|}$.

Definition 1. 

Let C be a code of ${\mathbb{Z}}_m^n$ with $LS$-poset metric $d_{LS}$. Then C is said to be an r-perfect $LS$-poset code if the r-balls centered at the codewords of C are pairwise disjoint and their union is ${\mathbb{Z}}_m^n$.

Let $I^t\left(s\right)\in \mathfrak{I}(P\times {\mathcal{P}}_A)$ be such that ${\zeta }_A\left(I^t\left(s\right)\right)=t$ and $I^t\left(s\right)$ has exactly s maximal elements. We let ${\omega }_{I^t\left(s\right)}=\{i\in \left[n\right]|(i,\alpha )\mathrm{be}\mathrm{a}\mathrm{maximal}\mathrm{element}\mathrm{of}{I}^t\left(s\right)\mathrm{for}\mathrm{some}\alpha \in \mathcal{P}\left(A\right)\}$. Given a vector $\mathbf{v}=(v_1,\dots ,v_n)$ of ${\mathbb{Z}}_m^n$, we rewrite it as

$$\mathbf{v}:=({\mathbf{v}}_{\mathbf{1}}:{\mathbf{v}}_{\mathbf{2}}:\mathbf{0})=({\left\{v_i\right\}}_{i\in {\omega }_{I^t\left(s\right)}}:{\left\{v_i\right\}}_{i\in I^t{\left(s\right)}^{*}\setminus {\omega }_{I^t\left(s\right)}}:\mathbf{0}),$$

where, for each $i\in \left[n\right]$, $v_i$ is an element in ${\mathbb{Z}}_m$ satisfying:

(i) If $i\in {\omega }_{I^t\left(s\right)}$, then $v_i\in {\mathcal{G}}_{\lfloor {\alpha }_i\rceil }$,

  where $\mathcal{A}(I^t\left(s\right);i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$;

(ii) If $i\in I^t{\left(s\right)}^{*}\setminus {\omega }_{I^t\left(s\right)}$, then $v_i\in {\mathbb{Z}}_m$;

(iii) If $i\notin I^t{\left(s\right)}^{*}$, then $v_i=0$.

• Observe that $⟨{supp}_{LS}\left(\mathbf{v}\right)⟩=I^t\left(s\right)$. Now, letting ${\mathbb{A}}_{I^t\left(s\right)}$ be the collection of all vectors $\mathbf{v}$ in ${\mathbb{Z}}_m^n$, such that $⟨{supp}_{LS}\left(\mathbf{v}\right)⟩=I^t\left(s\right)$, we have

  $${\displaystyle |{\mathbb{A}}_{I^t\left(s\right)}|=m^{|I^t{\left(s\right)}^{*}\setminus {\omega }_{I^t\left(s\right)}|}·\prod _{i\in {\omega }_{I^t\left(s\right)}}\left|{\mathcal{G}}_{\lfloor {\alpha }_i\rceil }\right|.}$$

  Obviously, for two distinct ideals I and J in $\mathfrak{I}(P\times {\mathcal{P}}_A)$, ${\mathbb{A}}_I\cap {\mathbb{A}}_J=\varnothing$. Now, we denote by ${\mathcal{I}}^t\left(s\right)$ the set of all ideals $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, such that ${\zeta }_A\left(I\right)=t$, and I has exactly s maximal elements. Then the number of vectors in an r-ball with center $\mathbf{u}$ equals

  $$|B_{r,LS}\left(\mathbf{u}\right)|=1+\sum _{i=1}^r\sum _{j=1}^i\sum _{\begin{array}{c}I\in {\mathcal{I}}^i\left(j\right)\ne \varnothing \end{array}}\left|{\mathbb{A}}_I\right|.$$

  (2)

Given an ideal $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, the I-ball centered at $\mathbf{u}$ and the I-sphere centered at $\mathbf{u}$, respectively, are defined as

$$\begin{array}{cc}\hfill B_{I,LS}\left(\mathbf{u}\right)& :=\{\mathbf{v}\in {\mathbb{Z}}_m^n|⟨{supp}_{LS}\left(\mathbf{u}-\mathbf{v}\right)⟩\subseteq I\},\hfill \\ \hfill S_{I,LS}\left(\mathbf{u}\right)& :=\{\mathbf{v}\in {\mathbb{Z}}_m^n|⟨{supp}_{LS}\left(\mathbf{u}-\mathbf{v}\right)⟩=I\}.\hfill \end{array}$$

Definition 2. 

Let C be a code of ${\mathbb{Z}}_m^n$ with $LS$-poset metric $d_{LS}$ and I be an ideal in $P\times {\mathcal{P}}_A$. Then C is called an I-perfect $LS$-poset code if the I-balls centered at the codewords of C are pairwise disjoint and their union is ${\mathbb{Z}}_m^n$.

Under pomset metric $d_{\mathbb{P}}$ in ${\mathbb{Z}}_m^n$, it was shown in [11] that I-balls are no more linear subspaces of ${\mathbb{Z}}_m^n$ if I is an ideal with partial count in $\mathbb{P}=({\mathcal{M}}^{\lfloor m/2\rfloor }\left(\left[n\right]\right),{\preccurlyeq }_P)$. On the other hand, with the $LS$-poset metric, the I-ball centered at the zero vector is a submodule of ${\mathbb{Z}}_m^n$.

Proposition 8. 

Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. Then $B_{I,LS}\left(\mathbf{0}\right)$ is a submodule of ${\mathbb{Z}}_m^n$.

Proof. 

Clearly, if I is an ideal with full count in $P\times {\mathcal{P}}_A$, then $B_{I,LS}\left(\mathbf{0}\right)$ is a submodule of ${\mathbb{Z}}_m^n$ with dimension $|{\omega }_{I_f}|$. Now, suppose that I is an ideal with partial count. Then $|{\omega }_{I_p}|>0$. For each $i\in {\omega }_{I_p}$, let $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$. By considering $H_i$ as a subgroup of ${\mathbb{Z}}_m$, such that $\psi \left(H_i\right)={\alpha }_i$ for $i\in {\omega }_{I_p}$, for $\mathbf{u}=(u_1,\dots ,u_n),\mathbf{v}=(v_1,\dots ,v_n)\in B_{I,LS}\left(\mathbf{0}\right)$, we have $u_i,v_i\in H_i$ for all $i\in {\omega }_{I_p}$. It follows that $\mathbf{u}+\mathbf{v},c\mathbf{u}\in B_{I,LS}\left(\mathbf{0}\right)$ for $c\in {\mathbb{Z}}_m$. Hence, $B_{I,LS}\left(\mathbf{0}\right)$ is a submodule of ${\mathbb{Z}}_m^n$. □

For $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, let $B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$ denote the $I^{\mathfrak{C}}$-ball centered at $\mathbf{0}$ under the poset $\tilde{P}\times {\mathcal{P}}_A$.

Proposition 9. 

Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. Then the following statements hold:

1. 

For $\mathbf{u}\in {\mathbb{Z}}_m^n$, $B_{I,LS}\left(\mathbf{u}\right)=\mathbf{u}+B_{I,LS}\left(\mathbf{0}\right)$.

2. 

For $\mathbf{u},\mathbf{v}\in {\mathbb{Z}}_m^n$, $B_{I,LS}\left(\mathbf{u}\right)$ and $B_{I,LS}\left(\mathbf{v}\right)$ are either identical or disjoint. Moreover,

$B_{I,LS}\left(\mathbf{u}\right)=B_{I,LS}\left(\mathbf{v}\right)\iff {supp}_{LS}(\mathbf{u}-\mathbf{v})\subseteq I$.

3. 

$B_{I,LS}^{\perp }\left(\mathbf{0}\right)=B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$.

Proof. 

(1) Let $\mathbf{v}\in B_{I,LS}\left(\mathbf{u}\right)$. It follows that $\mathbf{u}-\mathbf{v}\in B_{I,LS}\left(\mathbf{0}\right)$, and $\mathbf{v}=\mathbf{u}+\left(\mathbf{v}-\mathbf{u}\right)\in \mathbf{u}+B_{I,{\mathbb{P}}_{\mathcal{C}}}\left(\mathbf{0}\right)$. For $\mathbf{w}\in B_{I,{\mathbb{P}}_{\mathcal{C}}}\left(\mathbf{0}\right)$, we have ${supp}_{LS}(\mathbf{u}-\left(\mathbf{u}+\mathbf{w}\right))={supp}_{LS}(-\mathbf{w})={supp}_{LS}\left(\mathbf{w}\right)\subseteq I$. Hence $\mathbf{u}+\mathbf{w}\in B_{I,LS}\left(\mathbf{u}\right)$.

(2) For each $i\in {\omega }_{I_f}\cup {\omega }_{I_p}$, we let $H_i$ be a subgroup of ${\mathbb{Z}}_m$, such that $\psi \left(H_i\right)={\alpha }_{H_i}\in \mathcal{P}\left(A\right)$, where $\mathcal{A}(I;i)=⟨{\alpha }_{H_i}⟩$. For $\mathbf{u}=(u_1,\dots ,u_n),\mathbf{v}=(v_1,\dots ,v_n)\in {\mathbb{Z}}_m^n$, suppose $\mathbf{w}=(w_1,\dots ,w_n)\in B_{I,LS}\left(\mathbf{u}\right)\cap B_{I,LS}\left(\mathbf{v}\right)$. We have ${supp}_{LS}(\mathbf{u}-\mathbf{w})\subseteq I$ and ${supp}_{LS}(\mathbf{v}-\mathbf{w})\subseteq I$. If $i\notin {\omega }_{I_f}\cup {\omega }_{I_p}$, then $u_i-w_i=w_i-v_i=0$, so $u_i-v_i=0$. For the case $i\in {\omega }_{I_f}\cup {\omega }_{I_p}$, we have $u_i-w_i,w_i-v_i\in H_i$, which implies $u_i-v_i\in H_i$. That is, $(i,{\alpha }_{⟨u_i-v_i⟩})\in I$ for all $i\in {\omega }_{I_f}\cup {\omega }_{I_p}$. Consequently, $\mathbf{u}-\mathbf{v}\in B_{I,LS}\left(\mathbf{0}\right)$, which means that $B_{I,LS}\left(\mathbf{u}\right)=B_{I,LS}\left(\mathbf{v}\right)$.

(3) If I is an ideal with full count in $P\times {\mathcal{P}}_A$, then $I^{\mathfrak{C}}$ is also an ideal with full count in $\tilde{P}\times {\mathcal{P}}_A$. Since ${\omega }_{I_f}\cap {\omega }_{I_f^{\mathfrak{C}}}=\varnothing$ and ${\omega }_{I_f}\cup {\omega }_{I_f^{\mathfrak{C}}}=\left[n\right]$, we derive the result.

Next, suppose that $m=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\cdots p_k^{{\beta }_k}$, where $p_i$ are distinct primes, and the mset $A=p_1^{\left[{\beta }_1\right]}{p}_2^{\left[{\beta }_2\right]}\cdots p_k^{\left[{\beta }_k\right]}$. Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$ be an ideal with partial count. From ${\omega }_{I_p}={\omega }_{I_p^{\mathfrak{C}}}$, for each $i\in {\omega }_{I_p}$, we let $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$, where ${\alpha }_i=p_1^{\left[t_{i_1}\right]}{p}_2^{\left[t_{i_2}\right]}\cdots p_k^{\left[t_{i_k}\right]}$, and let $H_i$ and $K_i$ be subgroups of ${\mathbb{Z}}_m$, such that $\psi \left(H_i\right)={\alpha }_i$ and $\psi \left(K_i\right)=\widehat{{\alpha }_i}$. Then $H_i=⟨p_1^{{\beta }_1-t_{i_1}}{p}_2^{{\beta }_2-t_{i_2}}\cdots p_k^{{\beta }_k-t_{i_k}}⟩$ and $K_i=⟨p_1^{t_{i_1}}{p}_2^{t_{i_2}}\cdots p_k^{t_{i_k}}⟩$. Let $\mathbf{x}=(x_1,\dots ,x_n)\in B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$ and $\mathbf{y}=(y_1,\dots ,y_n)\in B_{I,LS}\left(\mathbf{0}\right)$. Then ${\displaystyle \mathbf{x}·\mathbf{y}=\sum _{i\in {\omega }_{I_p}}{x}_i{y}_i}$, where, for each i, $x_i\in H_i$ and $y_i\in K_i$. It follows that $\mathbf{x}·\mathbf{y}$ is congruent to 0 modulo m. That is, $B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)\subseteq B_{I,LS}^{\perp }\left(\mathbf{0}\right)$. Now, we assume that there is $\mathbf{z}\in B_{I,LS}^{\perp }\left(\mathbf{0}\right)\setminus B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$. Since $\mathbf{z}·\mathbf{y}=0$ for all $\mathbf{y}\in B_{I,LS}\left(\mathbf{0}\right)$, we can, without loss of generality, write $\mathbf{z}=(0,\dots ,0,z_s,0,\dots ,0)$, where $s\in {\omega }_{I_p}$ and $z_s\notin K_s=⟨p_1^{t_{s_1}}{p}_2^{t_{s_2}}\cdots p_k^{t_{s_k}}⟩$. Then $z_s=y{p}_1^{r_{s_1}}{p}_2^{r_{s_2}}\cdots p_k^{r_{s_k}}$, where $gcd(y,p_j)=1$ and $0\le r_{s_j}<t_{s_j}$ for some $j\in \left[k\right]$. Choosing $\mathbf{w}=(w_1,\dots ,w_n)\in B_{I,LS}\left(\mathbf{0}\right)$, defined by $w_i=0$ for all $i\ne s$, and $w_s=p_1^{{\beta }_1-t_{s_1}}{p}_2^{{\beta }_2-t_{s_2}}\cdots p_k^{{\beta }_k-t_{s_k}}$, it follows that $\mathbf{z}·\mathbf{w}\neg \equiv 0$ modulo m, which is a contradiction. □

Example 10. 

Consider $120=2^3·3·5$ and the mset $A=2^{\left[3\right]}{3}^{\left[1\right]}{5}^{\left[1\right]}$. On $\mathcal{P}\left(A\right)$, we choose ${\alpha }_1=2^{\left[1\right]}{3}^{\left[1\right]}{5}^{\left[1\right]},{\alpha }_2=2^{\left[3\right]}{5}^{\left[1\right]},{\alpha }_3=2^{\left[2\right]}{3}^{\left[1\right]}$. The structure of each $⟨{\alpha }_i⟩$ when $i=1,2,3$, is demonstrated via the lattice of the nontrivial subgroup for ${\mathbb{Z}}_{120}$ (see in Figure 3) in which ${\widehat{\alpha }}_1=2^{\left[2\right]}$, ${\widehat{\alpha }}_2=3^{\left[1\right]}$, and ${\widehat{\alpha }}_3=2^{\left[1\right]}{5}^{\left[1\right]}$. Now let us consider the poset $P_1\times {\mathcal{P}}_A=(\left[4\right]\times \mathcal{P}\left(A\right),\gamma )$, where the poset $P_1=(\left[4\right],{⪯}_{P_1})$ is as shown in Figure 1. Let $I=⟨\{(2,{\alpha }_1),(3,{\alpha }_2),(4,{\alpha }_3)\}⟩\in \mathfrak{I}(P_1\times {\mathcal{P}}_A)$. Then I is an ideal with partial count. It is easy to see that $B_{I,LS}\left(\mathbf{0}\right)={\mathbb{Z}}_{120}\times ⟨4⟩\times ⟨3⟩\times ⟨10⟩$, whereas $B_{I,LS}^{\perp }\left(\mathbf{0}\right)=⟨0⟩\times ⟨30⟩\times ⟨40⟩\times ⟨12⟩$.

Figure 3. The lattice of nontrivial subgroups for ${\mathbb{Z}}_{120}$.

Observe that the I-ball centered at the zero vector can be considered as a direct product of cyclic subgroups of ${\mathbb{Z}}_m$. If m is a prime power, the following result is directly obtained.

Proposition 11. 

In the space ${\mathbb{Z}}_{q^{\beta }}^n$, let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$. Then

1. 

If $\beta =1$, then $|B_{I,LS}\left(\mathbf{0}\right)|=q^{\left|I\right|}$ and $|B_{I,LS}^{\perp }\left(\mathbf{0}\right)|=q^{n-\left|I\right|}$.

2. 

If $\beta >1$, then

• $|B_{I,LS}\left(\mathbf{0}\right)|=q^{\beta |{\omega }_{I_f}|+{\sum }_{i\in {\omega }_{I_p}}\left|{\alpha }_i\right|}$ and $|B_{I,LS}^{\perp }\left(\mathbf{0}\right)|=q^{\beta (n-|{\omega }_{I_f}\cup {\omega }_{I_p}\left|\right)+{\sum }_{i\in {\omega }_{I_p}}\left|{\widehat{\alpha }}_i\right|}$, where, for each $i\in {\omega }_{I_p}$, $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in \mathcal{P}\left(A\right)$.

From Propositions 8 and 9, the following theorem shows the existence of an I-perfect code with an $LS$-poset metric when I is an ideal with full count.

Theorem 12. 

For any ideal I with full count in $P\times {\mathcal{P}}_A$, we have

1. 

$B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$ is an I-perfect $LS$-poset code for the poset $P\times {\mathcal{P}}_A$.

2. 

$B_{I,LS}\left(\mathbf{0}\right)$ is an $I^{\mathfrak{C}}$-perfect $LS$-poset code for the poset $\tilde{P}\times {\mathcal{P}}_A$.

In the case of ideals I with partial count, the I-ball centered at the zero vector is not always I-perfect. The next lemma is a key for the existence of an I-perfect code with an $LS$-poset metric.

For each $i\in \left[n\right]$, let ${\mathbf{e}}_i=(e_1,\dots ,e_n)\in {\mathbb{Z}}_m^n$ be such that $e_j=0$ if $j\ne i$, and $e_i=1$.

Lemma 1. 

Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$ with ${\omega }_{I_p}\ne \varnothing$. For each $i\in {\omega }_{I_p}$, let $H_i$ be a nontrivial subgroup of ${\mathbb{Z}}_m$, such that $\mathcal{A}(I;i)=⟨{\alpha }_{H_i}⟩$. Then the following statements hold:

1. 

If there is $i\in {\omega }_{I_p}$, such that ${\alpha }_{H_i}^{*}=A^{*}$, then there is no I-perfect $LS$-poset code.

2. 

Suppose C is an I-perfect $LS$-poset code of ${\mathbb{Z}}_m^n$. Then, for each $i\in {\omega }_{I_p}$, there is a maximal subgroup $K_i$ of ${\mathbb{Z}}_m$, such that $A^{*}={\alpha }_{K_i}^{*}\dot{\cup }{\alpha }_{H_i}^{*}$. Moreover, ${\mathbf{e}}_i·C=K_i$ and $K_i+H_i={\mathbb{Z}}_m$.

Proof. 

(1) Suppose that ${\alpha }_{H_i}^{*}=A^{*}$. Choose $\mathbf{v}=(0,\dots ,0,v_i,0,\dots ,0)\in {\mathbb{Z}}_m^n$, where $v_i\notin H_i$. Then, ${\alpha }_{⟨v_i⟩}\notin ⟨{\alpha }_{H_i}⟩$. It follows that $\mathbf{v}\notin B_{I,LS}\left(\mathbf{0}\right)$. Suppose there is an I-perfect $LS$-poset code C of ${\mathbb{Z}}_m^n$. Then, $\mathbf{v}\in B_{I,LS}\left(\mathbf{c}\right)$ for some $\mathbf{c}=(c_1,\dots ,c_n)\in C$. That is, ${supp}_{LS}(\mathbf{c}-\mathbf{v})\subseteq I$. This implies that ${\alpha }_{⟨c_i-v_i⟩}\in ⟨{\alpha }_{H_i}⟩$, which means $0\ne c_i\in v_i+H_i$. From ${\alpha }_{H_i}^{*}=A^{*}$, there is $N_0\in \mathbb{N}$, such that $N_0{c}_i\ne 0$ and ${\alpha }_{⟨N_0{c}_i⟩}\in ⟨{\alpha }_{H_i}⟩$. Consequently, ${supp}_{LS}\left(N_0\mathbf{c}\right)\subseteq I$. As a submodule $B_{I,LS}\left(\mathbf{0}\right)$ of ${\mathbb{Z}}_m^n$, we have $\mathbf{0}\ne N_0\mathbf{c}\in B_{I,LS}\left(\mathbf{0}\right)$, which is a contradiction to the I-perfect of C.

(2) Suppose C is an I-perfect $LS$-poset code of ${\mathbb{Z}}_m^n$. Let $i\in {\omega }_{I_p}$. From (1), ${\alpha }_{H_i}^{*}\ne A^{*}$. Then there is a maximal subgroup $K_i$ of ${\mathbb{Z}}_m$, such that ${\alpha }_{K_i}^{*}\cap {\alpha }_{H_i}^{*}=\varnothing$. Let $0\ne x\in K_i$. Consider $\mathbf{v}=(0,\dots ,0,v_i=x,0,\dots ,0)\in {\mathbb{Z}}_m^n$. Then, $\mathbf{v}\notin B_{I,LS}\left(\mathbf{0}\right)$. We choose $\mathbf{c}=(c_1,\dots ,c_n)\in C$, such that $\mathbf{v}\in B_{I,LS}\left(\mathbf{c}\right)$. Since $B_{I,LS}\left(\mathbf{0}\right)\cap B_{I,LS}\left(\mathbf{c}\right)=\varnothing$, it follows that $c_i\ne 0$ and ${\alpha }_{⟨c_i⟩}\notin ⟨{\alpha }_{H_i}⟩$. Indeed, by proceeding as before, we have ${\alpha }_{⟨c_i⟩}^{*}\cap {\alpha }_{H_i}^{*}=\varnothing$. That is, $⟨c_i⟩\cap H_i=\left\{0\right\}$. Since ${supp}_{LS}\left(\mathbf{c}-\mathbf{v}\right)\subseteq I$, we have ${\alpha }_{⟨c_i-x⟩}\in ⟨{\alpha }_{H_i}⟩$, which means $⟨c_i-x⟩\subseteq H_i$. Then, $c_i-x=y$ for some $y\in H_i$. From ${\alpha }_{K_i}^{*}\cap {\alpha }_{H_i}^{*}=\varnothing$, we have $K_i\cap H_i=\left\{0\right\}$. Then there is $N\in \mathbb{N}$, such that $N\nmid |H_i|$ and $Nx\equiv 0$ modulo m. Thus, $N{c}_i\equiv Ny$ modulo m. These force $y=0$. Hence, $c_i=x$. That is, ${\mathbf{e}}_i·C=K_i$. Since C is I-perfect, by a similar technique, it can be shown that $K_i+H_i={\mathbb{Z}}_m$. □

Given an mset A, let ${\mathbb{E}}_A:=\{\alpha \in \mathcal{P}\left(A\right)|{\alpha }^{*}\cap {\widehat{\alpha }}^{*}=\varnothing \}$.

Theorem 13. 

Let $I\in \mathfrak{I}(P\times {\mathcal{P}}_A)$, with ${\omega }_{I_p}\ne \varnothing$. Then $B_{I,LS}^{\perp }\left(\mathbf{0}\right)$ is an I-perfect $LS$-poset code of ${\mathbb{Z}}_m^n$ if and only if, for each $i\in {\omega }_{I_p}$, $\mathcal{A}(I;i)=⟨{\alpha }_i⟩$ for some ${\alpha }_i\in {\mathbb{E}}_A$.

Proof. 

Suppose $B_{I,LS}^{\perp }\left(\mathbf{0}\right)$ is I-perfect. By Proposition 9(3), $B_{I,LS}^{\perp }\left(\mathbf{0}\right)=B_{I^{\mathfrak{C}},\widetilde{LS}}\left(\mathbf{0}\right)$. For the necessary condition, let $i\in {\omega }_{I_p}$. We have $\mathcal{A}(I;i)=⟨{\alpha }_{H_i}⟩$ and $\mathcal{A}(I^{\mathfrak{C}};i)=⟨{\widehat{\alpha }}_{H_i}⟩=⟨{\alpha }_{K_i}⟩$, where two subgroups $H_i,K_i$ are as in Lemma 1. Then ${\alpha }_{H_i}\in {\mathbb{E}}_A$.

For each $\alpha \in {\mathbb{E}}_A$, we have that ${\alpha }^{*}\cap {\widehat{\alpha }}^{*}=\varnothing$ and $\alpha \oplus \widehat{\alpha }=A$. These imply that ${\psi }^{-1}\left(\alpha \right)\cap {\psi }^{-1}\left(\widehat{\alpha }\right)=\left\{0\right\}$ and $|{\psi }^{-1}\left(\alpha \right)|·|{\psi }^{-1}\left(\widehat{\alpha }\right)|=m$. Hence, the converse is proved. □

Corollary 1. 

There is no I-perfect $LS$-poset code of ${\mathbb{Z}}_{q^{\beta }}^n$ if I is an ideal with partial count in $P\times {\mathcal{P}}_A$.

Example 14. 

In Example 10, we have ${\alpha }_2=2^{\left[3\right]}{5}^{\left[1\right]}\in {\mathbb{E}}_A$, with ${\widehat{\alpha }}_2=3^{\left[1\right]}$, but ${\alpha }_1,{\alpha }_3\notin {\mathbb{E}}_A$. Consider the poset $P_2=(\left[6\right],{⪯}_{P_2})$, as in Figure 1. In the space ${\mathbb{Z}}_{120}^6$ with the $LS$-poset metric, we let $I=⟨(4,2^{\left[3\right]}{5}^{\left[1\right]})⟩\in \mathfrak{I}(P_2\times {\mathcal{P}}_A)$ as an ideal with partial count. By Theorem 13, we have $B_{I,LS}^{\perp }\left(\mathbf{0}\right)=\left\{(0,0,0,x,y,z)\right|x\in ⟨40⟩={\psi }^{-1}\left(3^{\left[1\right]}\right),andy,z\in {\mathbb{Z}}_{120}\}$ is an I-perfect $LS$-poset code of ${\mathbb{Z}}_{120}^6$.

4. MDS $\mathit{LS}$-Poset Codes and Codes in Chain Poset Structure

Theorem 15. 

(Singleton Bound) Let $P\times {\mathcal{P}}_A$ be the poset on $\left[n\right]\times \mathcal{P}\left(A\right)$ and $C\subseteq {\mathbb{Z}}_m^n$ be an $LS$-poset code. Then

$$\begin{array}{cc}\hfill {log}_m\left|C\right|& {\displaystyle \le n-⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋}\hfill \end{array}$$

(3)

Proof. 

Choose $\mathbf{x},\mathbf{y}\in C$, such that $d_{LS}(\mathbf{x},\mathbf{y})=d_{LS}\left(C\right)$. Consider the ideal I generated by ${supp}_{LS}(\mathbf{x}-\mathbf{y})$. We have $d_{LS}\left(C\right)-1<{\zeta }_A\left(I\right)\le \lfloor A\rceil ·|{\omega }_{I_f}\cup {\omega }_{I_p}|$. From Proposition 4, there is a normal ideal J with full count of $P\times {\mathcal{P}}_A$, such that ${\displaystyle |{\omega }_{J_f}|=⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋}$. Then, ${\displaystyle {\zeta }_A\left(J\right)=⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋\lfloor A\rceil \le d_{LS}\left(C\right)-1}$. That is, there is no codeword $\mathbf{c}$ in C, such that ${supp}_{LS}\left(\mathbf{c}\right)\subseteq J$, and any two distinct codewords of C will not coincide in all positions $j\in \left[n\right]\setminus {\omega }_{J_f}$. These imply that $\left|C\right|\le m^{n-|{\omega }_{J_f}|}$. So, we have ${\displaystyle {log}_m\left|C\right|\le n-⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋}$. □

Definition 3. 

An $LS$-poset code C of length n over ${\mathbb{Z}}_m$ is said to be a maximum distance separable $LS$-poset code (or simply MDS $LS$-poset code) if it attains the Singleton bound, as in (3).

Theorem 16. 

In the space ${\mathbb{Z}}_m^n$ with the poset $P\times {\mathcal{P}}_A$, let $C\subseteq Z_m^n$ be an $LS$-poset code, such that $\left|C\right|=m^t$. Then C is an MDS $LS$-poset code if and only if C is an I-perfect $LS$-poset code for all ideals $I\in \mathcal{I}(P\times {\mathcal{P}}_A)$ with full count, such that $|{\omega }_{I_f}|=n-t$.

Proof. 

Let I be an ideal with full count in $P\times {\mathcal{P}}_A$, such that $|{\omega }_{I_f}|=n-t$. It is clear that $|B_{I,LS}\left(\mathbf{0}\right)|=m^{n-t}$. Suppose that C is an MDS $LS$-poset code. From (3), it follows that ${\displaystyle ⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋=n-t}$. Then, $d_{LS}\left(C\right)>{\zeta }_A\left(I\right)$, that is, $B_{I,LS}\left(\mathbf{x}\right)\cap B_{I,LS}\left(\mathbf{y}\right)=\varnothing$ for two distinct elements $\mathbf{x},\mathbf{y}\in C$. By $\left|C\right|=m^t$, we have C is I-perfect.

To show that C is MDS, we choose $\mathbf{c}\in C\setminus \left\{\mathbf{0}\right\}$, such that $w_{LS}\left(\mathbf{c}\right)=d_{LS}\left(C\right)$. Let $J=⟨{supp}_{LS}\left(\mathbf{c}\right)⟩$. Suppose ${\zeta }_A\left(J\right)\le \lfloor A\rceil (n-t)$. By Proposition 4, we can construct an ideal I with full count in $P\times {\mathcal{P}}_A$ containing J, such that ${\zeta }_A\left(I\right)=\lfloor A\rceil (n-t)$. But this would imply that $\mathbf{c}\in B_{I,LS}\left(\mathbf{0}\right)$, which is impossible since C is I-perfect. This forces that $d_{LS}\left(C\right)={\zeta }_A\left(J\right)>\lfloor A\rceil (n-t)$. Then ${\displaystyle ⌊\frac{d_{LS}\left(C\right)-1}{\lfloor A\rceil }⌋\ge n-t}$. By Theorem 15, we have C is MDS. □

Example 17. 

Let $A=2^{\left[3\right]}{3}^{\left[1\right]}{5}^{\left[1\right]}$ with $\lfloor A\rceil =5$. Consider $C_1=\left\{(0,0,x,y,z,w)\right|x,y,z,w\in {\mathbb{Z}}_{120}\}$, and $C_2=\left\{(0,0,0,x,y,z)\right|x,y,z\in {\mathbb{Z}}_{120}\}$.

• Under the poset $P_2\times {\mathcal{P}}_A$, where $P_2=(\left[6\right],{⪯}_{P_2})$, as in Figure 1, it is clear that $d_{LS}\left(C_1\right)=11$ and $d_{LS}\left(C_2\right)=16$. Then, $C_1$ and $C_2$ are MDS. Moreover, the poset $P_2\times {\mathcal{P}}_A$ has exactly one ideal $I=⟨\left\{\right(1,A),(2,A\left)\right\}⟩⟩$, such that ${\zeta }_A\left(I\right)=10$, and has exactly one ideal $J=⟨(3,A)⟩$, such that ${\zeta }_A\left(J\right)=15$. Clearly, $C_1$ and $C_2$ are I-perfect and J-perfect, respectively.
• Under the poset $P_3\times {\mathcal{P}}_A$, where $P_3=(\left[6\right],{⪯}_{P_3})$, as in Figure 1, it is clear that $d_{LS}\left(C_1\right)=1$ and $d_{LS}\left(C_2\right)=6$. Then, $C_1$ and $C_2$ are not MDS. In addition, there are two ideals $I_1=⟨(6,A)⟩$ and $I_2=⟨(4,A)⟩$, such that ${\zeta }_A\left(I_1\right)=10$ and ${\zeta }_A\left(I_2\right)=15$, in which $C_1$ is not $I_1$-perfect, and $C_2$ is not $I_2$-perfect.

Observe that, with the full count property of ideals in $P\times {\mathcal{P}}_A$, it was a main tool to study the MDS $LS$-poset code $C\subseteq {\mathbb{Z}}_m^n$, where $\left|C\right|=m^t$, $0\le t\le n$.

Next, we denote by ${\mathcal{C}}_n$ the chain poset $P=(\left[n\right],{⪯}_P)$, with $minP=1$. Observe that every ideal I with full count in ${\mathcal{C}}_n\times {\mathcal{P}}_A$ has a unique maximal element. Suppose $r=t\lfloor A\rceil \le n\lfloor A\rceil$ for some $t\in \mathbb{N}$. There is only one ideal I with full count, such that ${\zeta }_A\left(I\right)=t\lfloor A\rceil$. It follows that $B_{r,LS}\left(\mathbf{u}\right)=B_{I,LS}\left(\mathbf{u}\right)$ for all $\mathbf{u}\in {\mathbb{Z}}_m^n$.

The following results are some immediate consequences.

Proposition 18. 

In the space ${\mathbb{Z}}_m^n$ with the poset ${\mathcal{C}}_n\times {\mathcal{P}}_A$, given an ideal I with full count in ${\mathcal{C}}_n\times {\mathcal{P}}_A$, let C be an I-perfect $LS$-poset code of ${\mathbb{Z}}_m^n$. Then

1. 

C is an ${\zeta }_A\left(I\right)$-perfect $LS$-poset code.

2. 

C is an MDS $LS$-poset code.

Recall that the cardinality of an r-ball with center $\mathbf{u}\in {\mathbb{Z}}_m^n$, as in (2). By considering m as a prime power, we obtain the following result.

Proposition 19. 

In the space ${\mathbb{Z}}_{q^{\beta }}^n$ with the poset ${\mathcal{C}}_n\times {\mathcal{P}}_A$, if $\beta >1$, the cardinality of $B_{r,LS}\left(\mathbf{0}\right)$ is $q^{r-t}$, where $(t-1)(\beta +1)<r\le t(\beta +1)$ for $0<t\le n$.

Proof. 

As $A=q^{\left[\beta \right]}$, we have that the poset $(\mathcal{P}\left(A\right),{\subseteq }_A)$ becomes a chain. This implies that every ideal I in ${\mathcal{C}}_n\times {\mathcal{P}}_A$ contains a unique maximal element. Since $\beta >1$, $\lfloor A\rceil =\beta +1$. We write $r=(t-1)(\beta +1)+s+1$, where $0\le s\le \beta$. From (2), we have

$$\begin{array}{cc}\hfill |B_{r,LS}\left(\mathbf{0}\right)|& =1+\sum _{i=1}^r\left|{\mathbb{A}}_{I^i\left(1\right)}\right|\hfill \\ \hfill & =1+\sum _{j=0}^{t-2}{q}^{j\beta }[\varphi \left(q\right)+\varphi \left(q^2\right)+\cdots +\varphi \left(q^{\beta }\right)]+q^{(t-1)\beta }[\varphi \left(q\right)+\varphi \left(q^2\right)+\cdots +\varphi \left(q^s\right)]\hfill \\ \hfill & =1+\sum _{j=0}^{t-2}{q}^{j\beta }[q^{\beta }-1]+q^{(t-1)\beta }[q^s-1]\hfill \\ \hfill & =1+[q^{\beta }-1]\left({\displaystyle \frac{q^{(t-1)\beta }-1}{q^{\beta }-1}}\right)+q^{(t-1)\beta }[q^s-1]=q^{r-t}.\hfill \end{array}$$

□

From the above proposition, although $|B_{r,LS}\left(\mathbf{0}\right)|$ divides $q^{\beta n}$, by Corollary 1, there is no r-perfect $LS$-poset code of ${\mathbb{Z}}_{q^{\beta }}^n$ if $\beta +1$ does not divide r.

Next, we have thus established the sufficient condition of ideals with partial count in ${\mathcal{C}}_n\times {\mathcal{P}}_A$ for an $LS$-poset code of ${\mathbb{Z}}_m^n$ to be r-perfect.

Theorem 20. 

For $m=p_1^{{\beta }_1}{p}_2^{{\beta }_2}\cdots p_k^{{\beta }_k}$ with $k>1$, in the space ${\mathbb{Z}}_m^n$ with the poset ${\mathcal{C}}_n\times {\mathcal{P}}_A$, if there is a unique $p_i$, such that ${\beta }_i=1$, then there is an $(t\lfloor A\rceil +1)$-perfect $LS$-poset code of ${\mathbb{Z}}_m^n$ for $0\le t<n$.

Proof. 

By the assumption, we have $\lfloor A\rceil =\left|A\right|$, and $p_i^{\left[1\right]}$ is the unique element of $\mathcal{P}\left(A\right)$, such that $\lfloor p_i^{\left[1\right]}\rceil =1$. Let $0\le t<n$. By applying Proposition 4 (2.1), there is a unique ideal I with partial count in ${\mathcal{C}}_n\times {\mathcal{P}}_A$, such that ${\zeta }_A\left(I\right)=t\lfloor A\rceil +1$. Since $p_i^{\left[1\right]}\in {\mathbb{E}}_A$, by Theorem 13, it follows that $B_{I,LS}^{\perp }\left(\mathbf{0}\right)$ becomes an $(t\lfloor A\rceil +1)$-perfect $LS$-poset code. □

Example 21. 

In the space ${\mathbb{Z}}_{12}^3$ with the poset ${\mathcal{C}}_3\times {\mathcal{P}}_A$ and the mset $A=2^{\left[2\right]}{3}^{\left[1\right]}$, we consider $C=\{000,003,006,009\}$. Observe that $d_{LS}\left(C\right)=w_{LS}\left(006\right)=8$. Then we have $B_{7,LS}\left(000\right)={\mathbb{Z}}_{12}\times {\mathbb{Z}}_{12}\times ⟨4⟩$, $B_{7,LS}\left(003\right)={\mathbb{Z}}_{12}\times {\mathbb{Z}}_{12}\times (3+⟨4⟩)$, $B_{7,LS}\left(006\right)={\mathbb{Z}}_{12}\times {\mathbb{Z}}_{12}\times (6+⟨4⟩)$, and $B_{7,LS}\left(009\right)={\mathbb{Z}}_{12}\times {\mathbb{Z}}_{12}\times (9+⟨4⟩)$. We can see that C is an 7-perfect $LS$-poset code. Moreover, C is also an I-perfect $LS$-poset code when the ideal $I=⟨(3,3^{\left[1\right]})⟩$ with ${\zeta }_A\left(I\right)=7$.

In the space ${\mathbb{Z}}_{60}^3$ with the poset ${\mathcal{C}}_3\times {\mathcal{P}}_A$ and the mset $A=2^{\left[2\right]}{3}^{\left[1\right]}{5}^{\left[1\right]}$, let $D=\left\{\right(0,0,0),$ $(0,0,15),(0,0,30),(0,0,45)\}$. By Theorem 13, we can see that D is a J-perfect $LS$-poset code, where the ideal $J=⟨(3,3^{\left[1\right]}{5}^{\left[1\right]})⟩$, such that ${\zeta }_A\left(J\right)=10$. Observe that $d_{LS}\left(D\right)=w_{LS}(0,0,30)=10$. However, the space ${\mathbb{Z}}_{60}^3$ is not covered by the union of r-balls centered at the codewords of D for any $r<10$.

5. Discussion and Conclusions

The existence of codes over ${\mathbb{Z}}_m$ that are I-perfect under the pomset metric $d_{\mathbb{P}}$, where I is an ideal with partial count in $\mathbb{P}$, is determined by the necessary condition $2t+1|m-2t-1$ for some $t\in \mathbb{N}$ (see [11]). Meanwhile, the condition $m=pq$, where p and q are relatively prime, is required for the existence of J-perfect $LS$-poset codes, where J is a normal ideal with partial count in $P\times {\mathcal{P}}_A$ (as a consequence of Theorem 13). For example, in the space ${\mathbb{Z}}_6^2$ with the antichain poset structure, the code $C=\{00,03\}$ is I-perfect under $d_{\mathbb{P}}$, where $I=\{3/1,1/2\}$ of $\mathbb{P}$ (as seen in Example 4 of [11]). Additionally, C is also J-perfect under $d_{LS}$, where $J=\{(1,2^{\left[1\right]}{3}^{\left[1\right]}),(2,3^{\left[1\right]})\}$ of $P\times {\mathcal{P}}_A$. However, the code $D=\{00,02,04\}$ is $J^{\prime }$-perfect under $d_{LS}$, where $J^{\prime }=\{(1,2^{\left[1\right]}{3}^{\left[1\right]}),(2,2^{\left[1\right]})\}$ of $P\times {\mathcal{P}}_A$, but D does not satisfy the I-perfect condition for any ideal I with partial count in $\mathbb{P}$.

The main drawback of the $LS$-poset metric is that there are no J-perfect $LS$-poset codes over ${\mathbb{Z}}_{q^{\beta }}$ for a normal ideal J with partial count in $P\times {\mathcal{P}}_A$, where q is a prime and $\beta \in \mathbb{N}$. In contrast, for an odd prime q, the pomset metric guarantees the existence of I-perfect codes over ${\mathbb{Z}}_{q^{\beta }}$, where I is an ideal with partial count in $\mathbb{P}$. However, as shown in Example 7, the $LS$-poset weighted $w_{LS}$ of a vector in codes over ${\mathbb{Z}}_m$ has the advantage of not being excessively large, even when m is a large number.

As shown in Figure 2, for a given poset structure, the $LS$-poset metric and the poset metric are the same when m is a prime. For a non-prime power modulus m, this paper establishes the necessary and sufficient condition for the existence of I-perfect $LS$-codes for a given normal ideal I with partial count. Additionally, the relationship between MDS $LS$-poset codes and I-perfect $LS$-poset codes is explored. Finally, in case of the chain poset structure, we examine the existence of I-perfect and r-perfect $LS$-poset codes of ${\mathbb{Z}}_m^n$.