The Fundamental Difference Between Boolean Logic and Thermodynamic Irreversibilities, or, Why Landauer’s Result Cannot Be a Physical Principle
Abstract
1. Introduction
2. Landauer’s Arguments in Detail
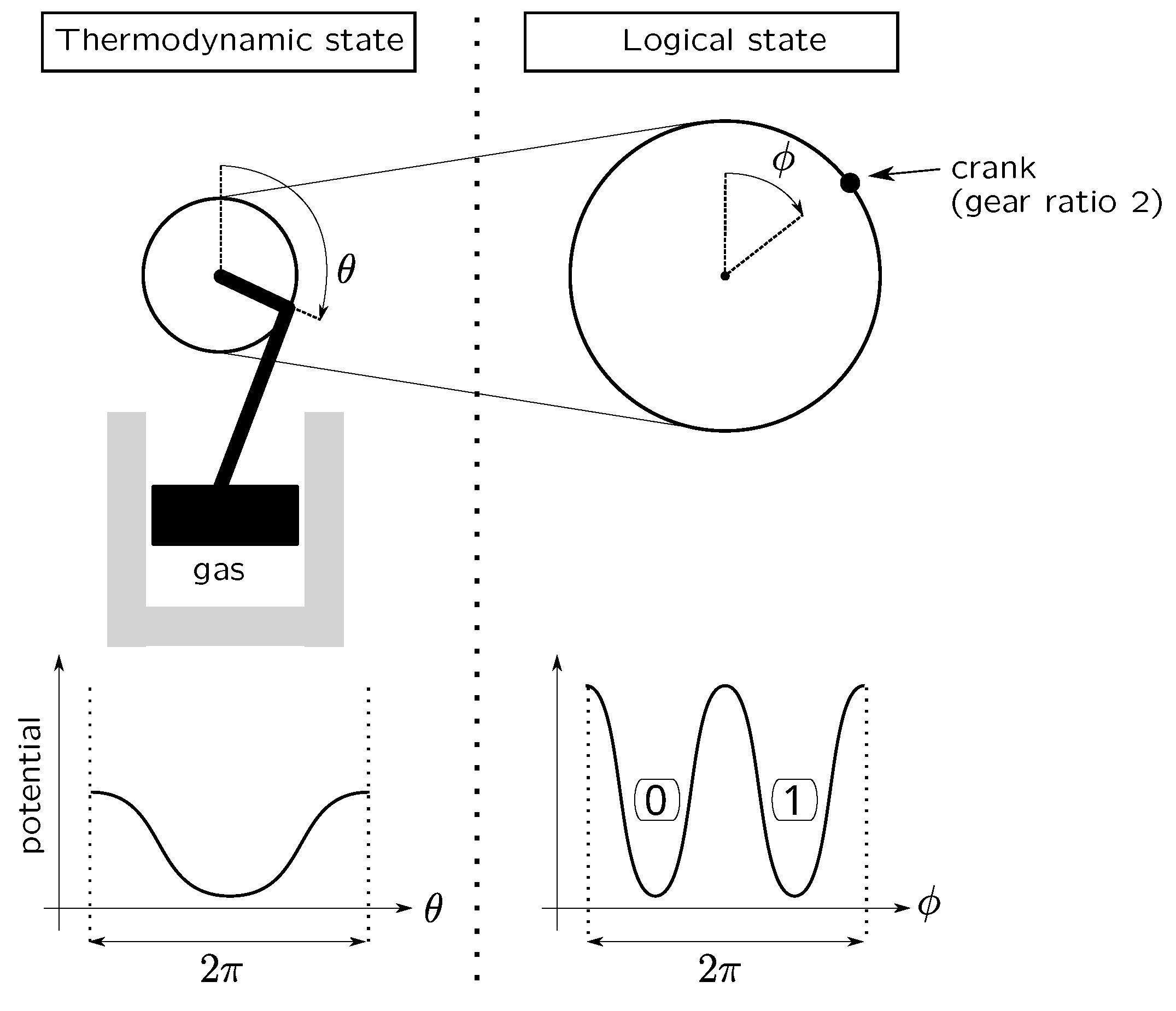
2.1. Minimum Requirements for a Hardware-Bit
- (1)
- The system must present two distinguishable configurations, namely, two logical states.
- (2)
- Configurations of the system must be lasting.
- (3)
- The system must allow the existence of a set of external interventions allowing it to be set in the logical state 0, namely, an erase procedure.
- (4)
- The erasure must have no side effect: only the bit to be erased is changed and nothing else.
2.2. Landauer Add-Ons and Result
- (i)
- One-to-one mapping: The system must present two distinct logical states to which two thermodynamic states of same internal energy and same entropy bijectively correspond.
- (ii)
- Uniqueness: the erase procedure must be unique regardless of the input value and must avoid a conditional statement.
- (iii)
- mandatory erasing scenario:
- The erasure divides into two steps.
- The first step is an expansion.The second is a compression by the same factor.
- The expansion of the phase space volume is at least by a factor of 2.
- The expansion is free and cannot be quasistatic.
- (a)
- Remove the partition (free expansion);
- (b)
- Use a piston to push the particle on the left side (reversible compression);
- (c)
- Put back the partition and remove the piston.
3. Irreversibilities
3.1. States Versus Path Properties
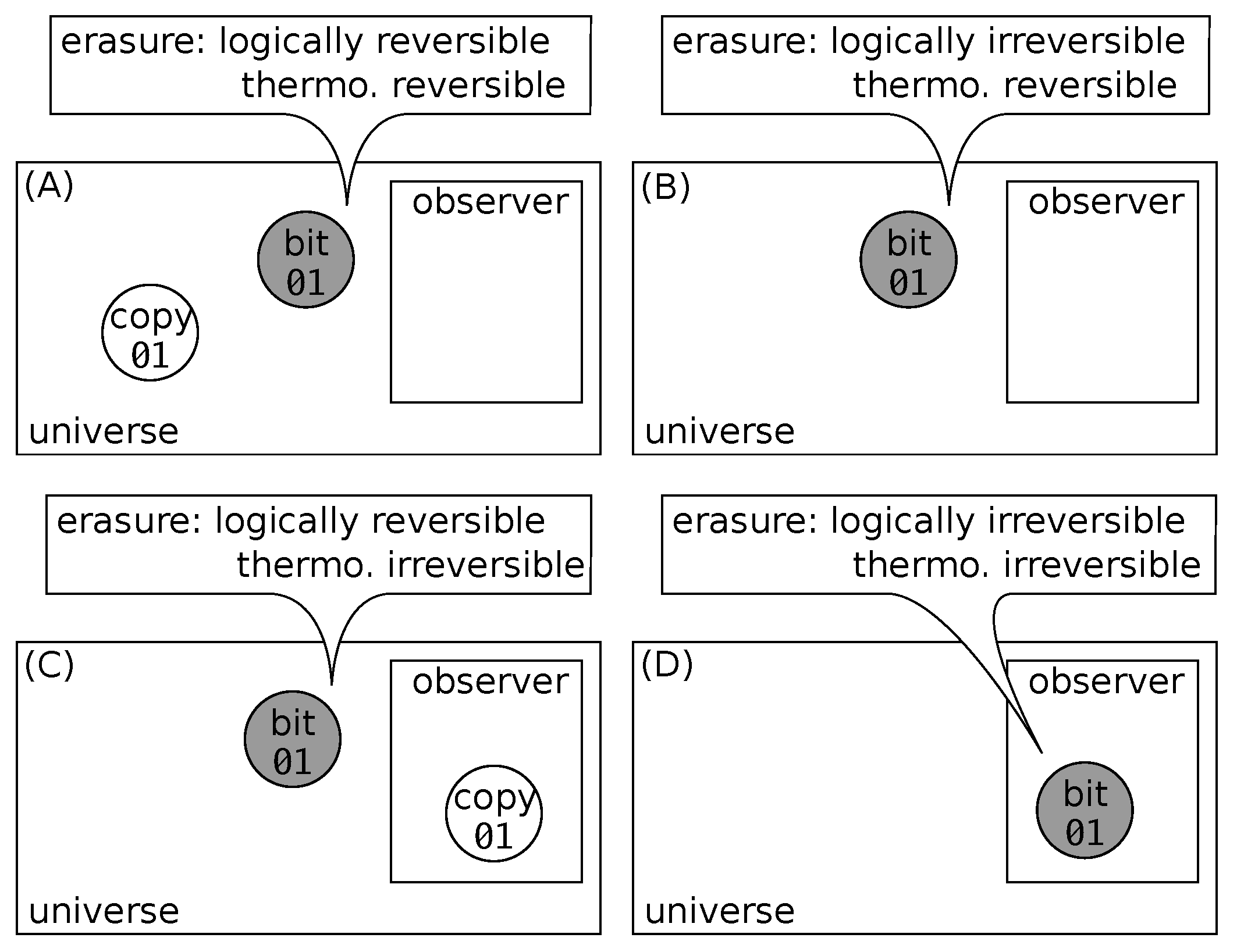
- Erase a bit of uncopied or original data, which is logically irreversible and results in loss of information;
- Erase a bit of copied data, which is logically reversible and leaves the information unchanged.
- Logical irreversibility is a property of the initial and final states of the overall system in relation with a loss of information:We cannot return the system to its initial logical state because we have no way of knowing where it came from.
- Thermodynamic irreversibility is a property of a particular path that connects two states:We cannot return the system to its initial thermodynamic state by the reverse path because it is impracticable in that direction, but other paths may exist.
3.2. Independence of the Two
3.3. Constraint of One-to-One Mapping
- Question: Can the same bit be erased and reused cyclically?
- Statement A: We are able to put the bit back to the same initial state.
- Statement B: The computer cycle is logically irreversible, meaning the bit cannot be returned to an initial state of which we do not know what it was.
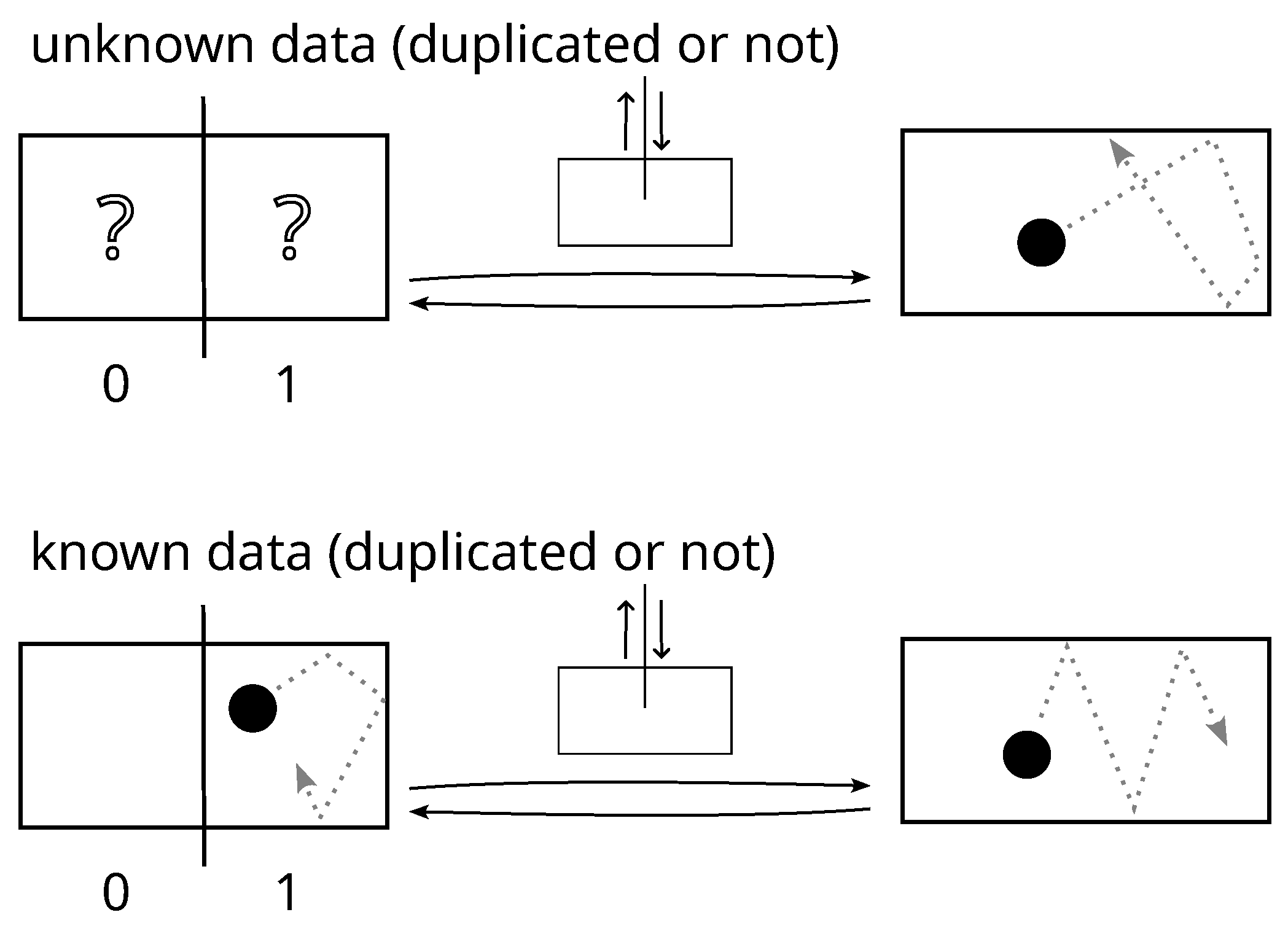
- (A)
- The bit-value is duplicated but unknown(the copy is not in the observer’s memory):
- The operation is logically reversible.
- The operation is thermodynamically reversible: after a cycle, the logical state is unknown but it was also unknown before; so, based on the observer’s knowledge, the initial state is restored.
- (B)
- The bit-value is not duplicated and is unknown(no copy anywhere):
- The operation is logically irreversible.
- The operation is thermodynamically reversible for the same reason as in the previous case.
- (C)
- The bit-value is duplicated and known(there is a copy that (or the original, or both) is in the observer’s memory):
- The operation is logically reversible.
- The operation is thermodynamically irreversible: based on the observer’s knowledge, the return of the partition is insufficient to systematically restore the initial state.
- (D)
- The bit-value is not duplicated but known(the original bit is in the observer’s memory):
- The operation is logically irreversible.
- The operation is thermodynamically irreversible for the same reason as in the previous case.
4. Erasure
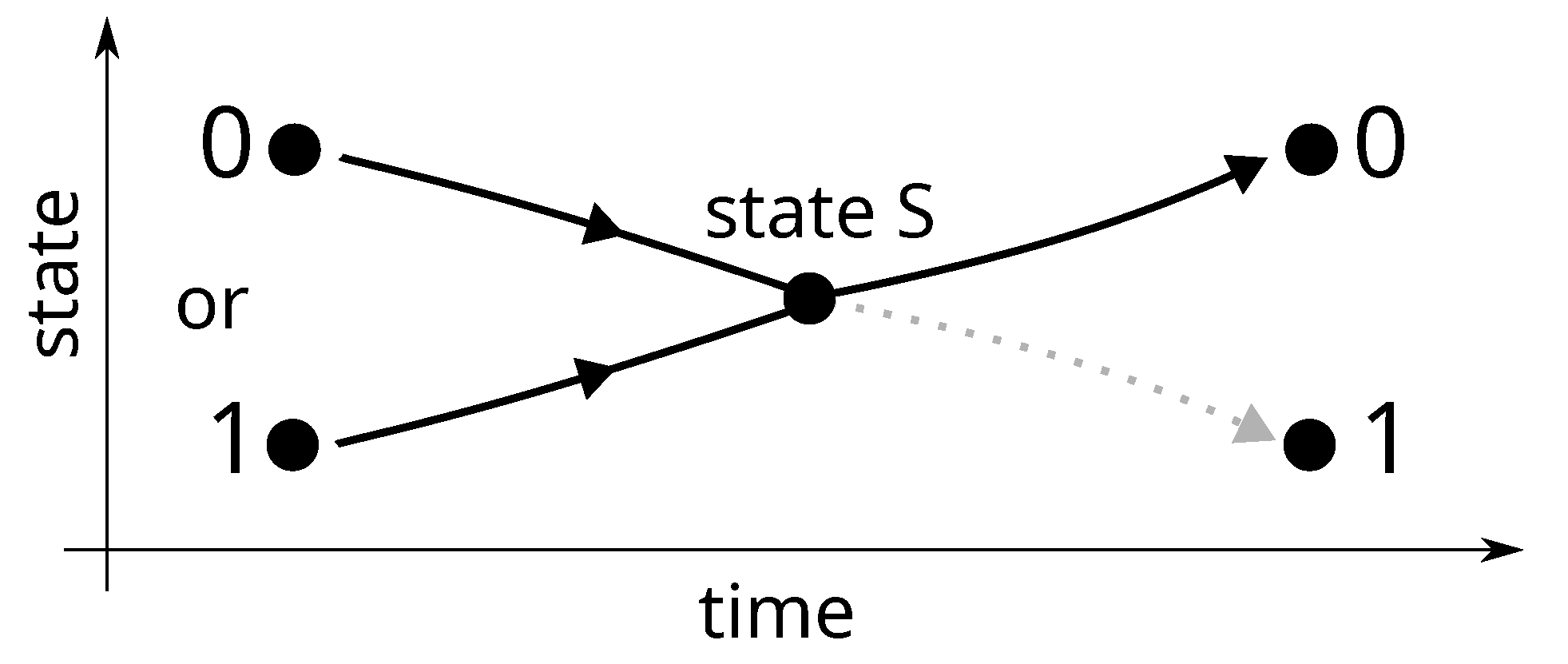
4.1. Constraint of Uniqueness
- If there exists a reversible compression path from state S to state 0, by symmetry, there is one from state S to state 1 (the choice of set to 0 to erase the bit is arbitrary; Landauer chose set to 1 [1]);
- If there is a reversible path from state S to state 1, then it can be used in the other direction for a reversible expansion from state 1 to state S.
- if the initial logical state is 0 then do nothing;
- else do: (1) the reversible expansion from state 1 to state S; then (2) the reversible compression from there to state 0.
4.2. Constraint of the Scenario
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Maxwell, J.C. Theory of Heat, 3rd ed.; Longmans, Green and Co.: London, UK, 1872. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Plenio, M.B.; Vitelli, V. The physics of forgetting: Landauer’s erasure principle and information theory. Contemp. Phys. 2001, 42, 25–60. [Google Scholar] [CrossRef]
- Frank, M.P. Physical Foundations of Landauer’s Principle. arXiv 2019, arXiv:1901.10327. [Google Scholar] [CrossRef]
- Bormashenko, E. The Landauer Principle: Re-Formulation of the Second Thermodynamics Law or a Step to Great Unification? Entropy 2019, 21, 918. [Google Scholar] [CrossRef]
- Herrera, L. Landauer Principle and General Relativity. Entropy 2020, 22, 340. [Google Scholar] [CrossRef]
- Georgescu, I. 60 years of Landauer’s principle. Nat. Rev. Phys. 2021, 3, 770. [Google Scholar] [CrossRef]
- Van Vu, T.; Saito, K. Finite-Time Quantum Landauer Principle and Quantum Coherence. Phys. Rev. Lett. 2022, 128, 010602. [Google Scholar] [CrossRef]
- Bormashenko, E. Landauer Bound in the Context of Minimal Physical Principles: Meaning, Experimental Verification, Controversies and Perspectives. Entropy 2024, 26, 423. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, B.; Ghosh, A.; Sen, S. Landauer’s principle and black hole area quantization. arXiv 2024, arXiv:2408.02077. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Paul, T.; SenGupta, S. Landauer principle in cosmology as the link to information theory. arXiv 2024, arXiv:2409.05009. [Google Scholar] [CrossRef]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef]
- Bérut, A.; Petrosyan, A.; Ciliberto, S. Information and thermodynamics: Experimental verification of Landauer’s Erasure principle. J. Stat. Mech. Theory Exp. 2015, 2015, P06015. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, T.; Rehan, K.; Zhou, F.; Liang, D.; Chen, L.; Zhang, J.; Yang, W.; Ma, Z.; Feng, M. Single-Atom Demonstration of the Quantum Landauer Principle. Phys. Rev. Lett. 2018, 120, 210601. [Google Scholar] [CrossRef]
- Proesmans, K.; Ehrich, J.; Bechhoefer, J. Finite-Time Landauer Principle. Phys. Rev. Lett. 2020, 125, 100602. [Google Scholar] [CrossRef]
- Giorgini, L.T.; Eichhorn, R.; Das, M.; Moon, W.; Wettlaufer, J.S. Thermodynamic cost of erasing information in finite time. Phys. Rev. Res. 2023, 5, 023084. [Google Scholar] [CrossRef]
- Binder, P. The Reversibility Paradox: Role of the Velocity Reversal Step. Int. J. Theor. Phys. 2023, 62, 200. [Google Scholar] [CrossRef]
- Oriols, X.; Nikolić, H. Three types of Landauer’s erasure principle: A microscopic view. Eur. Phys. J. Plus 2023, 138, 250. [Google Scholar] [CrossRef]
- Earman, J.; Norton, J.D. EXORCIST XIV: The Wrath of Maxwell’s Demon. Part II. From Szilard to Landauer and Beyond. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 1999, 30, 1–40. [Google Scholar] [CrossRef]
- Shenker, O.R. Logic and Entropy. 2000. Available online: https://philsci-archive.pitt.edu/115/ (accessed on 1 September 2024).
- Maroney, O. The (absence of a) relationship between thermodynamic and logical reversibility. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2005, 36, 355–374. [Google Scholar] [CrossRef]
- Norton, J.D. Eaters of the lotus: Landauer’s principle and the return of Maxwell’s demon. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2005, 36, 375–411. [Google Scholar] [CrossRef]
- Lairez, D. Thermodynamical versus Logical Irreversibility: A Concrete Objection to Landauer’s Principle. Entropy 2023, 25, 1155. [Google Scholar] [CrossRef]
- Lairez, D. On the Supposed Mass of Entropy and That of Information. Entropy 2024, 26, 337. [Google Scholar] [CrossRef]
- Lairez, D. Thermostatistics, Information, Subjectivity: Why Is This Association So Disturbing? Mathematics 2024, 12, 1498. [Google Scholar] [CrossRef]
- Quine, W.V. The Ways of Paradox, and Other Essays; Harvard University Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Bennett, C.H. The thermodynamics of computation - a review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Landauer, R. Information is Physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Lairez, D. Plea for the use of the exact Stirling formula in statistical mechanics. SciPost Phys. Lect. Notes 2023, 76. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the Equilibrium of Heterogeneous Substances: First [-Second] Part; Connecticut Academy of Arts and Sciences: New Haven, CT, USA, 1874. [Google Scholar] [CrossRef]
- Balian, R. From Microphysics to Macrophysics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar] [CrossRef]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behav. Sci. 1964, 9, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Whitelam, S. How to train your demon to do fast information erasure without heat production. Phys. Rev. E 2023, 108, 044138. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lairez, D. The Fundamental Difference Between Boolean Logic and Thermodynamic Irreversibilities, or, Why Landauer’s Result Cannot Be a Physical Principle. Symmetry 2024, 16, 1594. https://doi.org/10.3390/sym16121594
Lairez D. The Fundamental Difference Between Boolean Logic and Thermodynamic Irreversibilities, or, Why Landauer’s Result Cannot Be a Physical Principle. Symmetry. 2024; 16(12):1594. https://doi.org/10.3390/sym16121594
Chicago/Turabian StyleLairez, Didier. 2024. "The Fundamental Difference Between Boolean Logic and Thermodynamic Irreversibilities, or, Why Landauer’s Result Cannot Be a Physical Principle" Symmetry 16, no. 12: 1594. https://doi.org/10.3390/sym16121594
APA StyleLairez, D. (2024). The Fundamental Difference Between Boolean Logic and Thermodynamic Irreversibilities, or, Why Landauer’s Result Cannot Be a Physical Principle. Symmetry, 16(12), 1594. https://doi.org/10.3390/sym16121594







