1. Introduction
The Internet of Things (IoT) is facing increasingly complex and diverse security threats; security and privacy have become significant concerns [
1,
2]. Nowadays, when it comes to communication, IoT communication security mainly relies on asymmetric and symmetric cryptography systems. By using robust encryption algorithms and secure authentication mechanisms, the confidentiality and integrity of IoT device communications can be protected against unauthorized access and data tampering. Most cryptosystems rely on insurmountable combinatorial complexity, and their strength is traditionally related to their level of security bits.
In parallel development, quantum computers are emerging, which can quickly solve combinatorial problems with the help of superposition properties. Therefore, the development of quantum computing has begun to pose a real threat to the network security of the global digital infrastructure. Regarding cryptographic algorithms, quantum computing threatens the most popular public-key encryption systems [
3]. Public-key algorithms based on integer decomposition problems, elliptic curve discrete logarithm problems, or discrete logarithm problems can all be solved quickly using Shor’s algorithm [
4] on a sufficiently powerful quantum computer. According to the paper [
5], the 256-bit elliptic curve Diffie–Hellman (ECDH) and the 256-bit elliptic curve digital signature algorithm (ECDSA) are vulnerable to being broken by Shor’s algorithm on a sufficiently powerful quantum computer. In addition, quantum computers can use Grover’s algorithm [
6] to increase the speed of brute force cracking of symmetric passwords by approximately a quadratic factor [
7]. In recent years, more and more researchers have begun to study the security threats of quantum computers in different fields [
8,
9,
10,
11,
12].Therefore, studying how to ensure the security of IoT communications in a quantum computing environment has become an urgent issue that needs to be addressed.
In response to this issue, quantum communication technology has emerged as a potential solution and is gaining increasing attention. Quantum secure communication offers higher security compared to traditional encryption methods and can maintain communication confidentiality even against potential quantum computing attacks in the future. In 2022, Liu et al. [
13] applied quantum key distribution (QKD) technology to pre-distribute quantum keys to IoT devices, using these keys for encryption and decryption of sensitive IoT data. In 2023, Fu et al. [
14] proposed a scheme based on controlled remote quantum state preparation and quantum teleportation for multiple communication parties, leveraging nine-qubit entangled channels to enable secure communication among multiple devices in IoT systems. However, these solutions still face practical challenges, such as reliance on third-party controllers, which increase system complexity and operational overhead in IoT scenarios. Third-party controllers, often used for device authentication and communication coordination, can become single points of failure, compromising the network’s security and trustworthiness if breached. Additionally, they introduce latency and increase the resource demands on IoT devices, which are often constrained in terms of power and processing capabilities. Effective device authentication is critical in IoT to prevent unauthorized devices from forging identities, accessing sensitive data, and causing security risks. A decentralized approach to authentication is more aligned with the distributed nature of IoT, offering improved scalability and reduced operational burden while maintaining robust security.
To address the above challenges, this paper proposes an asymmetric bidirectional quantum communication scheme for IoT, integrating quantum identity authentication and quantum communication technologies. The scheme includes a device identity authentication module and an information transmission module. The authentication module uses the quantum no-cloning principle and measurement uncertainty to verify device identities, ensuring only legitimate devices participate in communication and preventing identity forgery and information leakage. The transmission module implements a bidirectional quantum teleportation scheme without relying on a third-party controller. Using six-qubit state as the quantum channel, device A transmits an unknown five-qubit entangled state to device B, while device B transmits an unknown three-qubit entangled state to device A. This integration enhances IoT communication security and quantum efficiency without adding complexity.
The rest of the paper is organized as follows. In
Section 2, we classify and introduce research on quantum teleportation and clarify challenges in introducing traditional bidirectional quantum teleportation (BQT) schemes into IoT. In
Section 3, we discuss the application scenarios of our scheme in IoT and describe it in detail.
Section 4 analyzes the security of the identity authentication module. In
Section 5, we experimentally verify the information transmission module.
Section 6 provides noise analysis of the scheme. Finally, we compared the scheme in
Section 6 and summarized the entire text in
Section 7.
2. Related Work
Quantum teleportation has a wide range of practical applications in quantum communication and quantum secret sharing. In 1993, Bennett et al. [
15] proposed the first quantum teleportation (QT) protocol for quantum teleportation using EPR particle pairs. Since then, multiple QT schemes have been proposed [
16,
17,
18,
19,
20,
21]. The difference between these QT schemes mainly lies in using different forms of quantum state channels. For example, Karlsson et al. [
16] used the Greenberger–Horne–Zeilinger (GHZ) state as a quantum channel to achieve communication between two parties, Man [
17] and Chen [
18] proposed a QT scheme based on the W state, and Cardoso et al. [
19] proposed a quantum teleportation scheme based on a GHZ-like state. Yang et al. [
20] proposed an efficient teleportation scheme for an unknown state to either one of two receivers via GHZ-like states. Shao [
21] proposed a scheme for quantum teleportation of a two-qubit entangled state using a four-qubit cluster state, etc.
With the deepening of research on quantum teleportation technology, different types of QT schemes have begun to appear, including controlled quantum teleportation, cyclic-controlled quantum teleportation, layered quantum teleportation, and bidirectional quantum teleportation (BQT).
Controlled quantum teleportation introduces a controller, and the sender sends the unknown quantum state to the receiver under supervision. Yuan et al. [
22] utilized a general three-qubit W state as a quantum channel and proposed a controlled quantum teleportation scheme under the control of a third party. Hu et al. [
23] proposed a controlled quantum teleportation scheme to achieve three-way quantum teleportation in a GHZ-like state.
Cyclic controlled quantum teleportation is a multi-party communication based on controlled quantum teleportation. Multiple participants use a maximally entangled state as a channel, impose different kinds of measurement operations and unitary transformation with the cooperation of a controller, ultimately achieving closed-loop cyclic communication. Zhou et al. [
24] proposed an asymmetric cyclic-controlled quantum teleportation protocol. Zarmehi et al. [
25] proposed an efficient cyclic-controlled quantum communication scheme.
Hierarchical quantum teleportation treats multiple receivers as agents of different levels. Different agents have different permissions to reconstruct secret quantum information, which can effectively prevent the problem of participant disloyalty. Zha et al. [
26] proposed a four-party hierarchical controlled quantum teleportation scheme based on an eight-qubit entangled state channel. Li et al. [
27] proposed a scheme for hierarchical quantum teleportation through four-qubit entangled states.
One of the most important subfields of QT is bidirectional quantum teleportation (BQT). In bidirectional quantum teleportation, two communicating parties can transmit qubits to each other, with users simultaneously acting as both senders and receivers. The bidirectional quantum teleportation protocol holds significant importance in quantum communication and quantum computing, garnering extensive attention from researchers. In 2013, by using cluster states of five qubits as quantum channel, Zha et al. [
28] proposed the first controlled BQT protocol, in which two participants, Alice and Bob, can transmit their unknown single-qubit state to each other with the help of supervisor Charlie. In 2016, also by using a cluster state of five qubits as a quantum channel, the author of [
29] proposed another different BQT protocol. This protocol is the first asymmetric BQT protocol, in which Alice can transmit a two-qubit entangled state to Bob, while Bob can transmit a single-qubit state to Alice. In 2018, Zadeh et al. [
30] proposed a new scheme of bidirectional quantum teleportation (BQT) making use of an eight-qubit entangled state as the quantum channel is presented. This protocol is based on the Controlled-NOT operation, appropriate single-qubit unitary operations, and single-qubit measurement. In 2022, Wang et al. [
31] proposed a new scheme to achieve bidirectional controlled quantum teleportation using a ten-qubit entangled state as a channel. This scheme studied the effects of amplitude-damping noise and phase-damping noise. Cao et al. [
32] proposed a bidirectional quantum teleportation protocol using a maximum six-qubit entangled state as a channel. Two-way controlled quantum transmission at different levels was achieved by selecting four appropriate agent measurement bases. Wang and Li [
33] proposed a bidirectional quantum teleportation scheme using a five-qubit entangled state as the quantum channel, minimizing the quantum and classical resources consumed during the communication process. In 2023, Yang et al. [
34] proposed a scheme that uses a cluster state of six qubits as a quantum channel to achieve controlled bidirectional quantum teleportation. The scheme’s feasibility was verified through data, and a security analysis was conducted on both external and internal attacks. Mandal et al. [
35] proposed a bidirectional quantum teleportation scheme that introduced Mentor to create a seven-qubit state between two parties and transmit single-qubit and three-qubit states to each other.
Most existing bidirectional quantum transmission (BQT) schemes require the involvement of a third-party controller to facilitate identity authentication and quantum communication. However, introducing a third party in IoT environments can undermine the trust relationship between communication devices. If the honesty and reliability of the third-party controller cannot be guaranteed, the security and confidentiality of the communication cannot be ensured. Furthermore, the inclusion of a third-party controller may introduce additional communication interference. Detecting and mitigating such interference would require more complex technologies and algorithms, increasing the complexity and overhead of IoT security systems.
To address these issues, our scheme eliminates the third-party verification mechanism and instead employs a unique device authentication module for identity verification. Additionally, we propose a bidirectional quantum transmission scheme in the information transmission module that does not rely on a third-party controller.
Section 3 provides a detailed description of this scheme.
3. Asymmetric Bidirectional Quantum Communication Scheme in IoT
3.1. Application Scenario
Quantum identity authentication and bidirectional quantum teleportation have significant application potential in IoT communication, particularly in the monitoring and control of industrial devices. With the advancement of industrial automation, sensors, actuators, and control systems in factories require real-time and secure data and command exchange. Our proposed scheme combines quantum identity authentication and bidirectional quantum communication technologies to provide a secure and reliable solution for device monitoring and control in industrial IoT.
In real-time monitoring, environmental data collected by sensors are securely transmitted to the control system via bidirectional quantum communication. Quantum identity authentication ensures that only authenticated devices can participate in communication, preventing unauthorized devices from accessing the network and guaranteeing the credibility of the data source. In command transmission, instructions generated by the control system are sent to actuators using bidirectional quantum communication. Before accepting the instructions, the actuator verifies the identity of the control system through quantum identity authentication, ensuring the authenticity and legitimacy of the commands. This prevents attackers from impersonating the control system and sending false instructions, thereby avoiding potential equipment damage or production accidents. In the feedback mechanism, actuators provide execution results or device status back to the control system. Quantum identity authentication again ensures the credibility of the feedback, allowing the control system to monitor device performance and make necessary adjustments and optimizations. This process creates a secure closed-loop system, where quantum identity authentication and bidirectional quantum communication ensure the confidentiality, integrity, and authenticity of data and commands throughout the transmission process, effectively mitigating security threats.
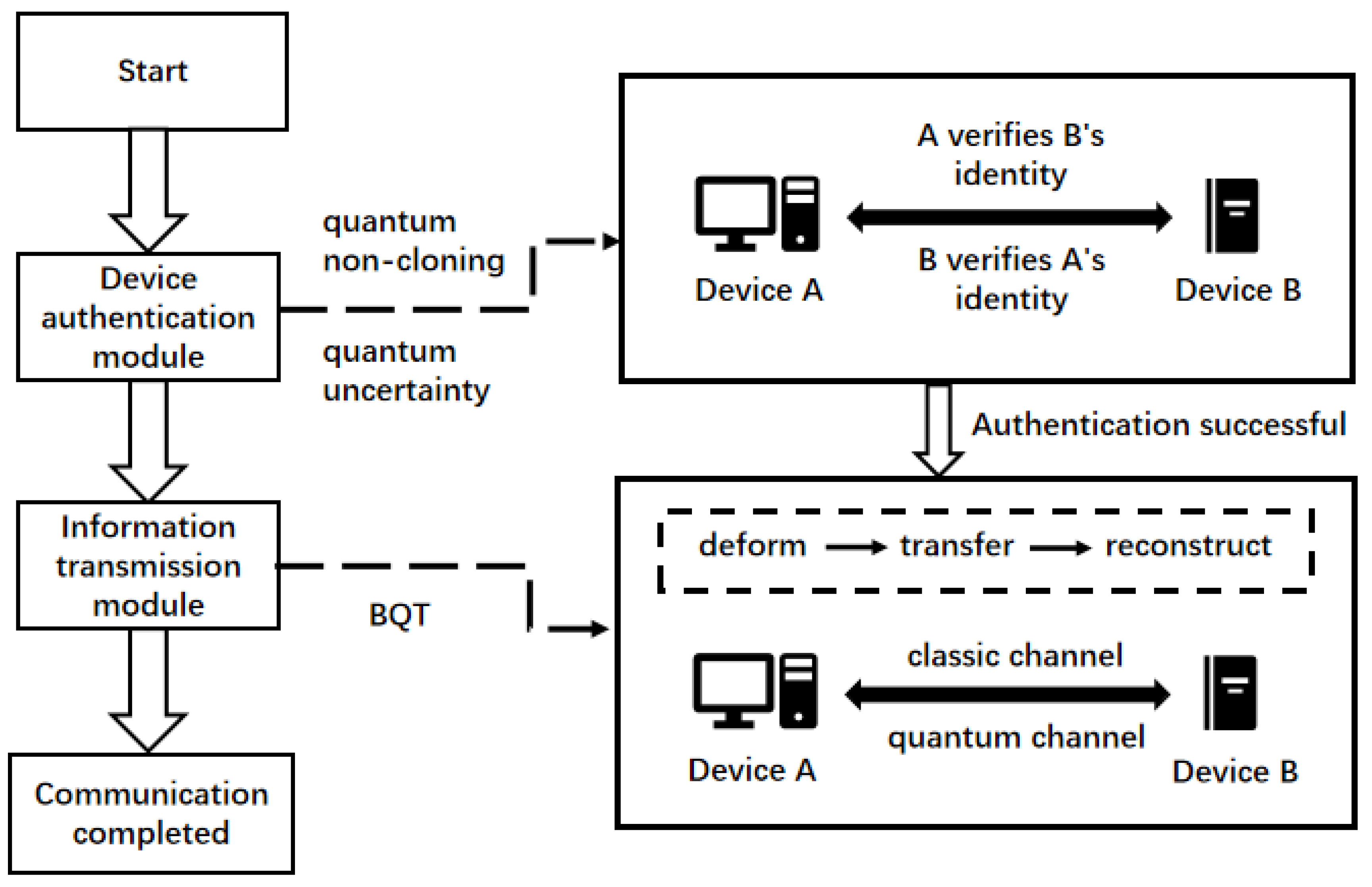
Based on the above application scenarios, our proposed scheme consists of a device identity authentication module and an information transmission module, which handle identity authentication and information exchange between Device A (e.g., sensors, actuators) and Device B (e.g., control systems), respectively. The overall process is illustrated in
Figure 1.
Section 3.2 and
Section 3.3 provide a detailed description of the quantum device identity authentication and information transmission processes, where Device A is represented as Alice and Device B as Bob.
3.2. Device Authentication Module
Implementing the identity authentication module on IoT devices requires consideration of hardware feasibility and resource constraints. Our authentication scheme can be realized by integrating a quantum random number generator (QRNG) and single-photon emission and detection modules into the devices. The QRNG provides true random numbers for basis and state bit selection, ensuring the security of the authentication process, while the single-photon emission and detection modules prepare and measure the required quantum states. These components can be miniaturized using micro-nano optics and integrated photonics technologies to meet the size and power consumption requirements of IoT devices, enabling the practical application of the authentication scheme in real-world devices.
Internal attacks mainly target the identity authentication stage of the communication parties. The device authentication module uses the quantum non-cloning principle and the quantum uncertainty principle to process the information of both communicating parties, compares it with the shared information pre-stored in the system to make a positive or negative judgment on the identity of the device.
The polarization state of a single photon is in a two-dimensional Hilbert space, and there are many orthogonal bases in this space. Generally, we only use two orthogonal bases ⊕ and ⊗, ⊕ is a linear polarization base composed of the vertical polarization state
and the horizontal polarization state
. ⊗ is the circular polarization base composed of
and
. According to the Heisenberg uncertainty principle and the quantum non-cloning principle, the measurement results of these two bases are incompatible. The quantum alphabet agreed upon by both communicating parties is shown in
Table 1.
First, Alice and Bob share a 2n-bit binary identity authentication string through the classic channel. Each bit of the string has a value of 0 or 1. Alice uses the first n bits of the identity authentication string to verify Bob’s identity, and Bob uses the last n bits to verify Alice’s identity.
(1) Alice verifies Bob’s identity
Step 1: Alice selects a physical noise source and generates an n-bit binary random sequence as the selected state bit string .
Step 2: Alice takes the first n bits of the identity authentication string as the selected base bit string, converts each bit of into a single photon polarization state, and then sends it to Bob.
Step 3: Bob selects the same basis based on the first n bits of the identity authentication string to measure the received photon state. He obtains a binary random sequence and then sends it to Alice.
Step 4: Alice compares the original selected bit string with Bob’s detection result sequence , then estimates the error. If the error is less than the preset security threshold, Alice believes Bob’s identity, and the authentication protocol continues. If the error exceeds the threshold, Bob’s identity is doubtful or the communication has been eavesdropped, and Alice needs to end the communication.
(2) Bob verifies Alice’s identity
Step 1: Alice takes the last n bits of the identity authentication string as the selection string.
Step 2: Alice selects a physical noise source to generate an n-bit binary random sequence as the selected base bit value, converts each bit of into a single-photon polarization state, and sends it to Bob.
Step 3: Bob uses the physical noise source to generate an n-bit random sequence as the selected base bit value sequence and then measures n single photons sent by Alice. Compare the measurement results with and record the mismatched positions. Bob sends these locations to Alice.
Step 4: Alice sends the corresponding values of these positions to Bob, who checks whether the corresponding values are the same as the values sent by Alice. If they are different, Bob believes Alice’s identity. If they are the same, Alice’s identity is in doubt or the communication has been eavesdropped, and Bob needs to end the communication.
At this point, the two-way identity authentication between device A and device B has been completed. We test the effectiveness of this scheme against identity forgery attacks in
Section 4.
3.3. Information Transmission Module
For the information transmission module, our bidirectional quantum teleportation scheme requires devices to have the capability to perform basic quantum operations. Specifically, devices need to receive and measure single-qubit states and execute essential quantum logic operations (such as CNOT gates). These functionalities can be achieved by integrating quantum communication modules based on integrated photonics into the devices. These modules utilize integrated optical components, such as waveguides, interferometers, and single-photon detectors, enabling the implementation of the information transmission scheme while adhering to the hardware constraints of IoT devices and without significantly increasing hardware complexity.
In this transmission scheme, Alice and Bob share a six-qubit channel, which is a six-qubit entangled state formed by intertwining three Bell states through quantum operations, specifically by applying swap gates. Alice has qubits 1, 3, and 6, Bob has qubits 2, 4, and 5, as shown in Equation (
1).
Alice wants to send an unknown five-qubit entangled state to Bob, as shown in Equation (
2).
At the same time, Bob also wants to send an unknown three-qubit entangled state to Alice, as shown in Equation (
3).
The steps for implementation are as follows:
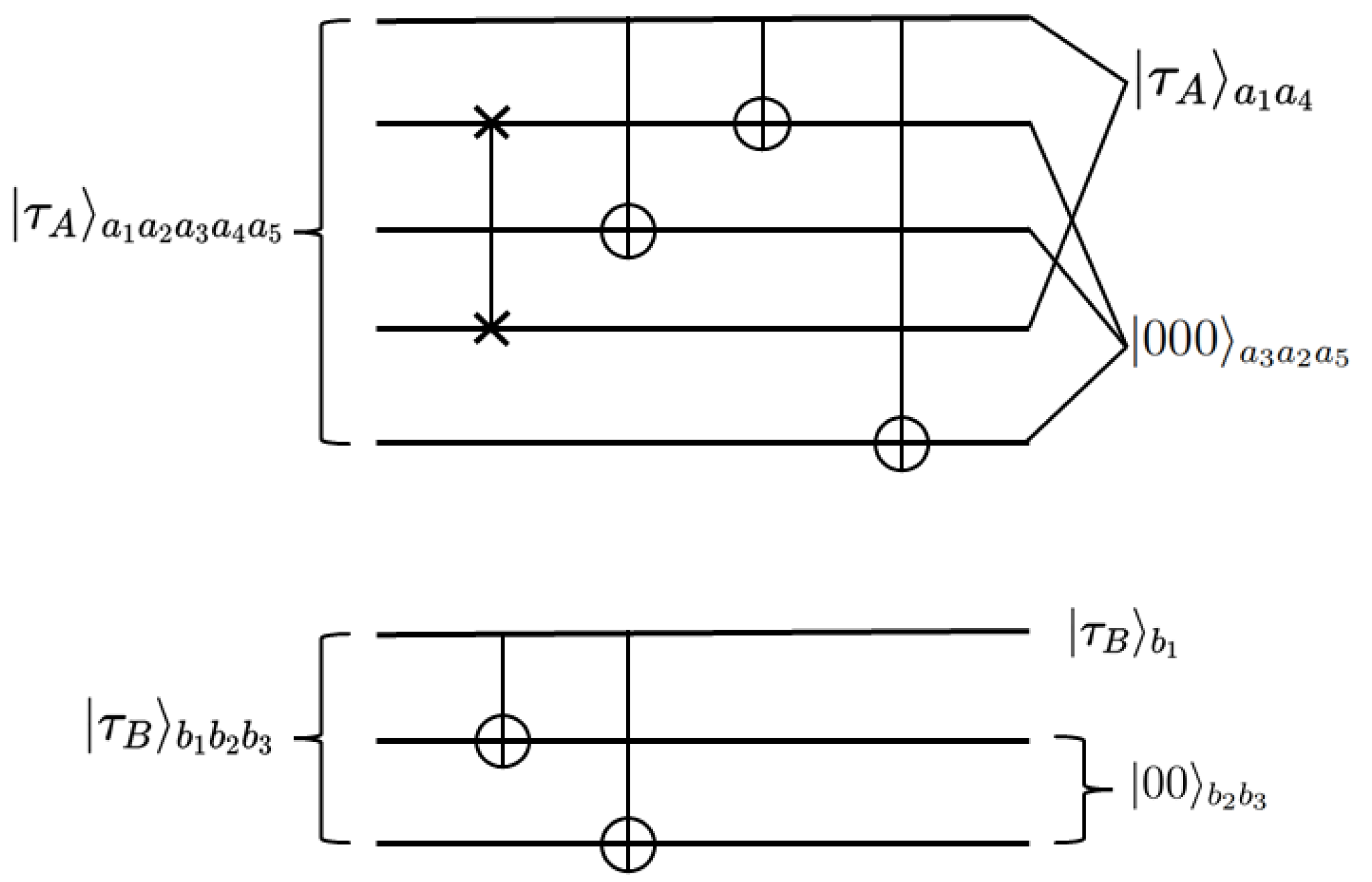
Before the communication between Alice and Bob, it is necessary to make some preparations for sending particles; all operations are applied to qubits based on their labels rather than their positions in the sequence. The specific operation can be seen in
Figure 2. Alice performs the swap gate operation on
and then performs the CNOT operation on the qubit pairs
, and
. Here,
is the controlling qubit, and
,
,
are target qubits. Finally,
is transformed into
and
.
Bob performs a CNOT operation on the qubit pair
and
with qubit
as control qubit and the qubits
,
as target qubits.
is transformed into
and
.
After the deformation operation is completed, only the first and fourth particles
carry information in the five-qubit entangled state, and only the first particle
carries information in the three-qubit entangled state. Now, we only need to entangle these three particles with the quantum channel to form a system state. The initial state of the whole system can be expressed as Equation (
6).
The flowing transmission process is shown in
Figure 3.
Alice performs the CNOT operation on qubit pairs (
) and (
). Here, the qubits
are the controlling qubits, and qubit 1 and qubit 3 are the target qubits. Bob applies the CNOT operation on qubit pair (
,2) with qubit
as the control qubit and qubit 2 as target qubit. After all operations are completed, the state of the whole system will be in the form of Equation (
7).
Alice and Bob perform Z-based single-quantum measurements on qubits 1, 3, and 2. After the measurements are completed, the remaining qubits collapse to one of the eight states with equal probability, as shown in
Table A1.
Alice and Bob utilize the classical channel to communicate their measurements to each other. Both parties apply the appropriate unitary operation to qubits 4, 5, and 6 according to
Table A2. The unitary operations performed by Alice and Bob are as follows:
After appropriate unitary operations are completed, the remaining qubits collapse into the form shown in Equation (
9):
Alice and Bob perform X-based single-quantum measurements on qubits
, and
. X-based measurement results are as follows:
After the measurement is completed, the remaining qubits collapse with the same probability, as shown in
Table A3.
In this step, Alice and Bob utilize the classical channel to communicate their measurements. Both parties apply the appropriate unitary operation to quantum bits 4, 5, and 6 according to
Table A4.
After the appropriate unitary operation is completed, all remaining qubits will be transformed into the form shown in Equation (
11):
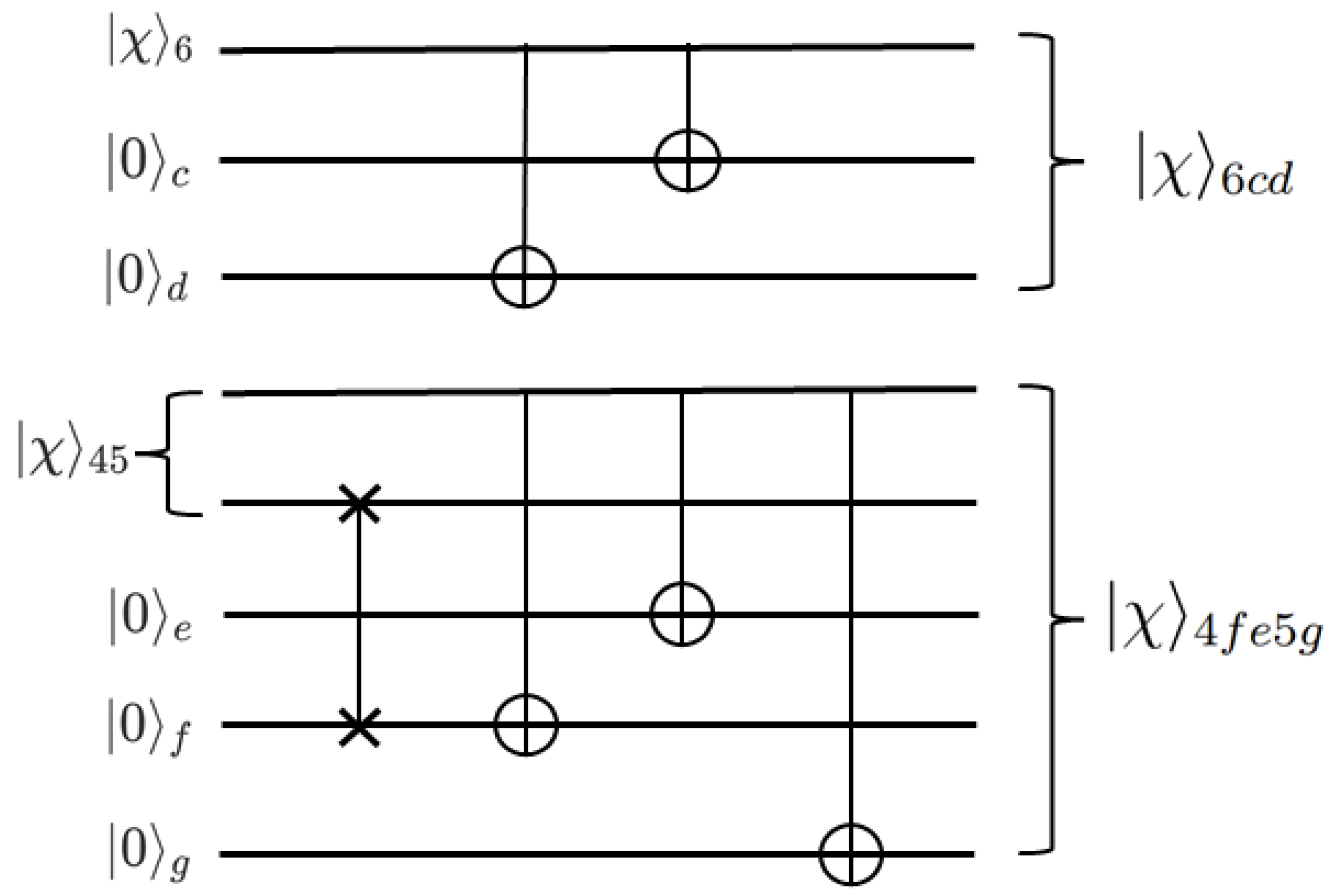
Then, Alice introduces two auxiliary qubits
for collapsed qubit 6; Bob introduces three auxiliary qubits
for collapsed quantum bits 4 and 5. After the arbitrary state particle transmission is completed, both parties need to repeat the transformation operation previously applied to the particle state. Alice performs a CNOT operation on the qubit pairs
and
with quantum bit 6 as control qubit and quantum bits
c,
d as target qubits; Bob performs a swap gate operation on qubits
, performs a CNOT operation on the qubit pairs
and
with quantum bit 4 as control bit and quantum bits
and
g as target bits. The result obtained is shown as Equation (
12), and the transmission target has been achieved. The reconstruction process can be seen in
Figure 4.
4. Security Analysis of Device Authentication Module
The two-way device authentication module has been introduced. Let us deduce whether it can prevent forged identity attacks effectively. For the sake of simplicity, ease of discussion, and to make it easier for readers to understand the process, we assume that . Thus, both communicating parties share a twelve-digit binary identity authentication string before communication. Only the communicating parties know the specific content of this ID string. At this time, the eavesdropper Eve tries to pretend to be the communicating party to communicate with the other party. This can be divided into the following two situations:
(1) Eve disguises herself as Bob to gain Alice’s trust
Alice first uses a physical noise source to generate a six-bit binary random sequence as the selected state bit string . Here, we assume and that Alice will take the first n bits of the ID string as the selected base bit value character. Based on the contents of the two strings, Alice generates the photon polarization state sequence and sends it to Eve for identity authentication. At this time, Eve receives the n-bit single photon polarization state from Alice. Eve does not know the specific content of , so it can only randomly select the measurement base. Assuming that Eve uses a random selection of the base bit value string , Eve will have a probability of nearly to select the wrong measurement base and obtain the wrong character. After measurement, Eve will obtain the binary random sequence and send it to Alice. Alice compares and , finds that the error is , which is much larger than the safety threshold. Alice will discover Eve’s disguised eavesdropping behavior and actively end the communication.
(2) Eve disguises herself as Alice to gain Bob’s trust
First, Eve needs to take the last n bits of the ID string as the selected bit value string, but Eve does not know the content of the ID string, so Eve can only use the random string , we assume . Then Eve selects a physical noise source to generate a selected base bit string , and we assume . Based on the contents of the two strings, Eve generates a photon polarization state sequence and sends it to Bob for identity authentication. After Bob receives the photon state sequence, he uses a physical noise source to generate an n-bit random sequence as the selected base bit value sequence. After measuring the n single photons sent by Alice, he can obtain the binary sequence . Bob compares the measurement results with and records the positions that do not match . In this case, the second and fifth positions do not match. Afterwards, Bob tells Eve to send the value of the corresponding position in . Since Eve does not have an ID string, it can only return the value [0,1] of the corresponding position of . The string of held by Bob corresponds to the value of the position, which is [1,1], and there are situations where the values are the same. At this time, Bob discovers Eve’s disguised eavesdropping behavior and actively ends the communication.
From the above protocol derivation, it can be known that the proposed two-way device authentication module can effectively prevent identity forgery attacks.
5. Experimental Verification of Information Transmission Module
We have theoretically verified the feasibility of this scheme and finally successfully achieved asymmetric bidirectional transmission of unknown quantum states. Next, we will use the IBM Quantum Experience (IBM QE) platform and Qiskit quantum programming language to verify the experimental process of our scheme. The IBM QE platform is a benchmark tool in the quantum computing field and has been extensively validated by the research community. Its use for proof-of-concept experiments is a standard practice in the development and evaluation of new quantum protocols. In addition, it is a cloud-based quantum computing platform developed by IBM. It provides researchers and developers with access to IBM’s quantum computers over the internet. The platform allows users to run quantum circuits and experiments, explore quantum algorithms, and gain hands-on experience with quantum computing. We will use specific data to verify the feasibility of the scheme. This experiment was conducted in an ideal environment that was free from noise.
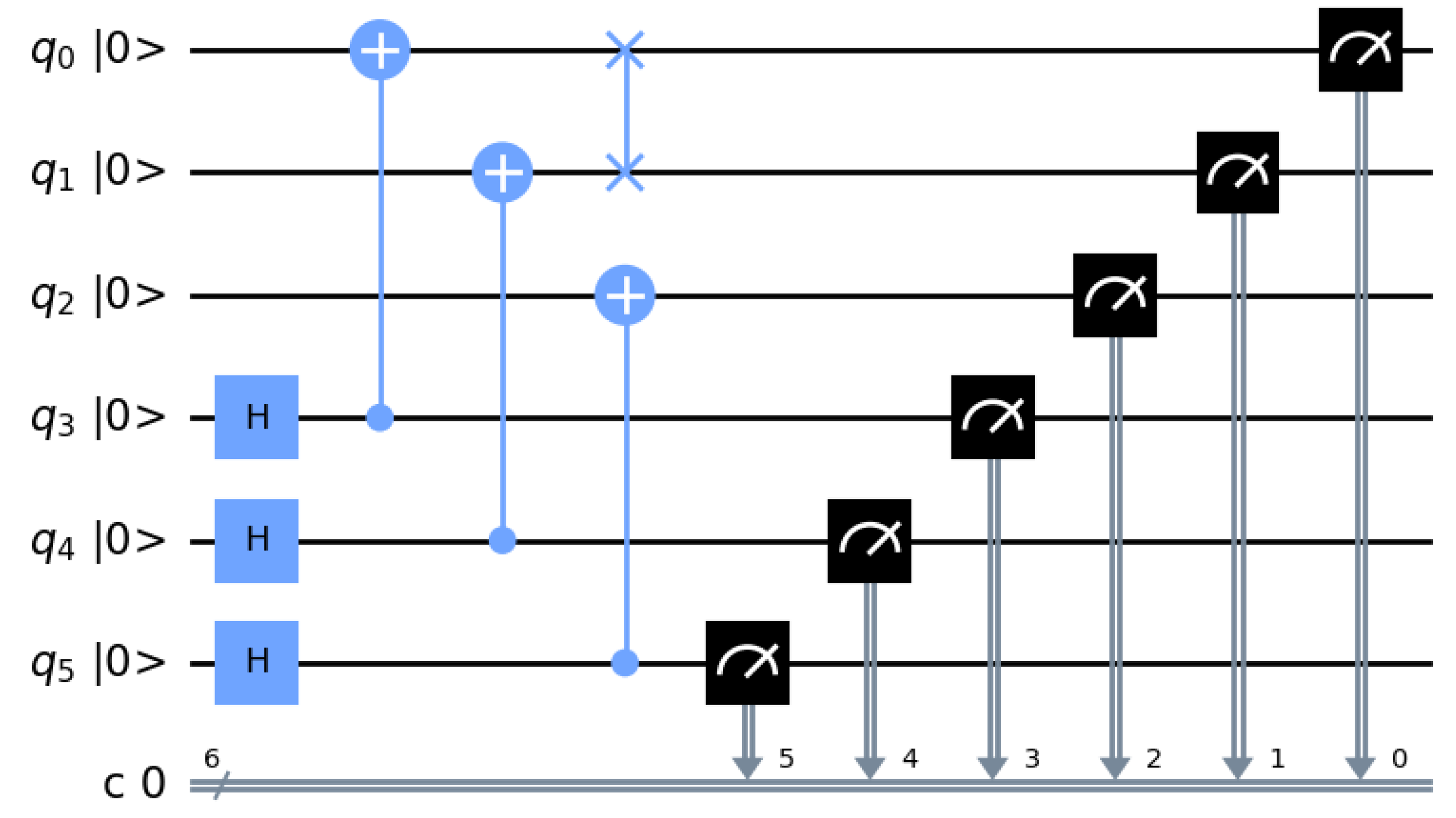
5.1. Quantum Channel Preparation
Before conducting the transmission experiment, we must prepare the quantum channel. The IBM Quantum Lab platform channel preparation circuit is shown in
Figure 5. In the leftmost part of the figure,
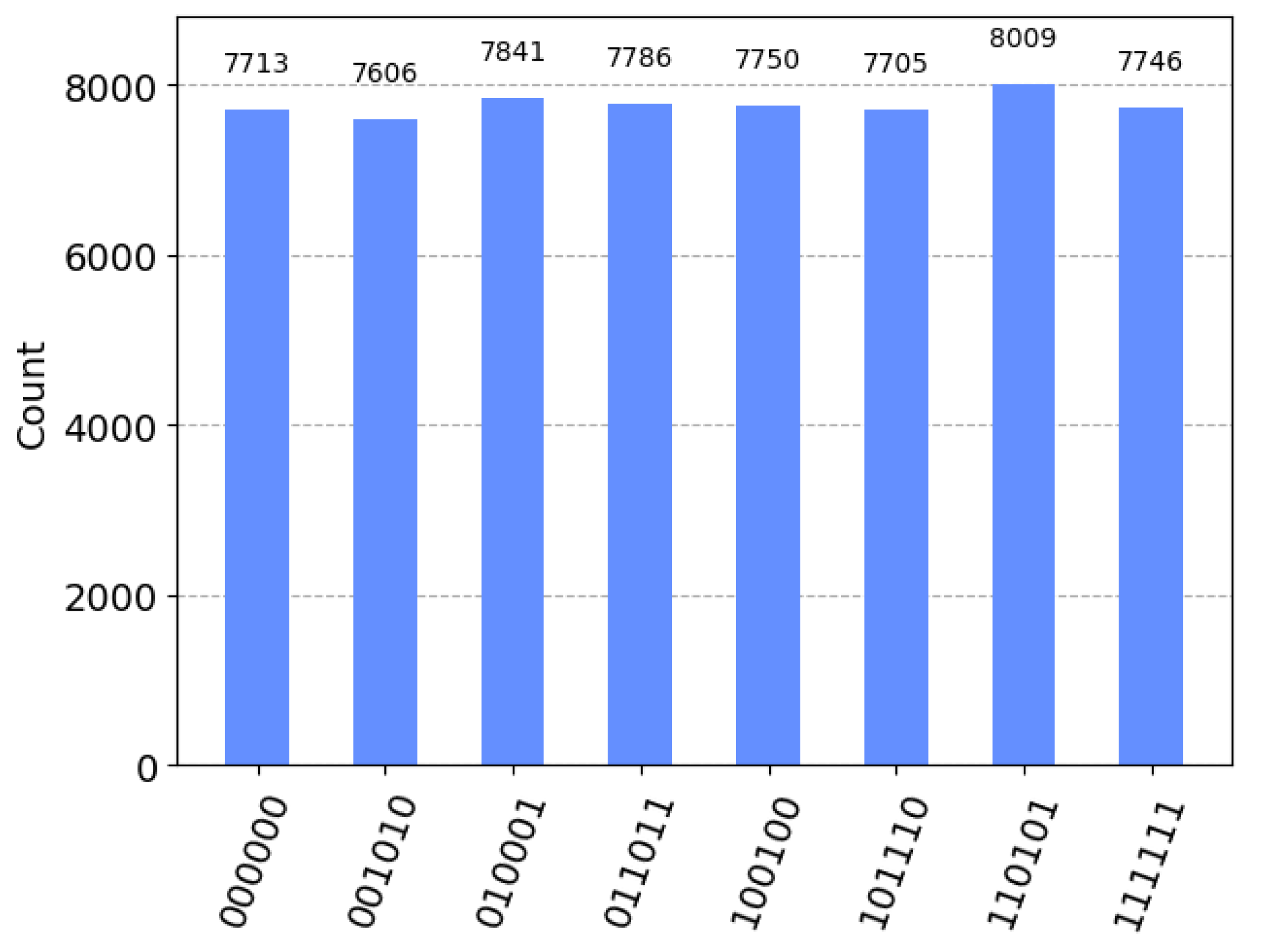
correspond to quantum bits 1, 2, 3, 4, 5, and 6, respectively. The histogram of the channel preparation results is shown in
Figure 6, we can successfully obtain the six-qubit Channel, and the probability of the eight collapsed states are all around
, so the preparation is successful.
5.2. Bidirectional Transmission Process
We have verified the feasibility of channel state preparation. Next, we use the IBM Quantum experimental platform to achieve bidirectional quantum teleportation based on Z-based measurement, X-based measurement, and unitary transformation. The entire process is shown in
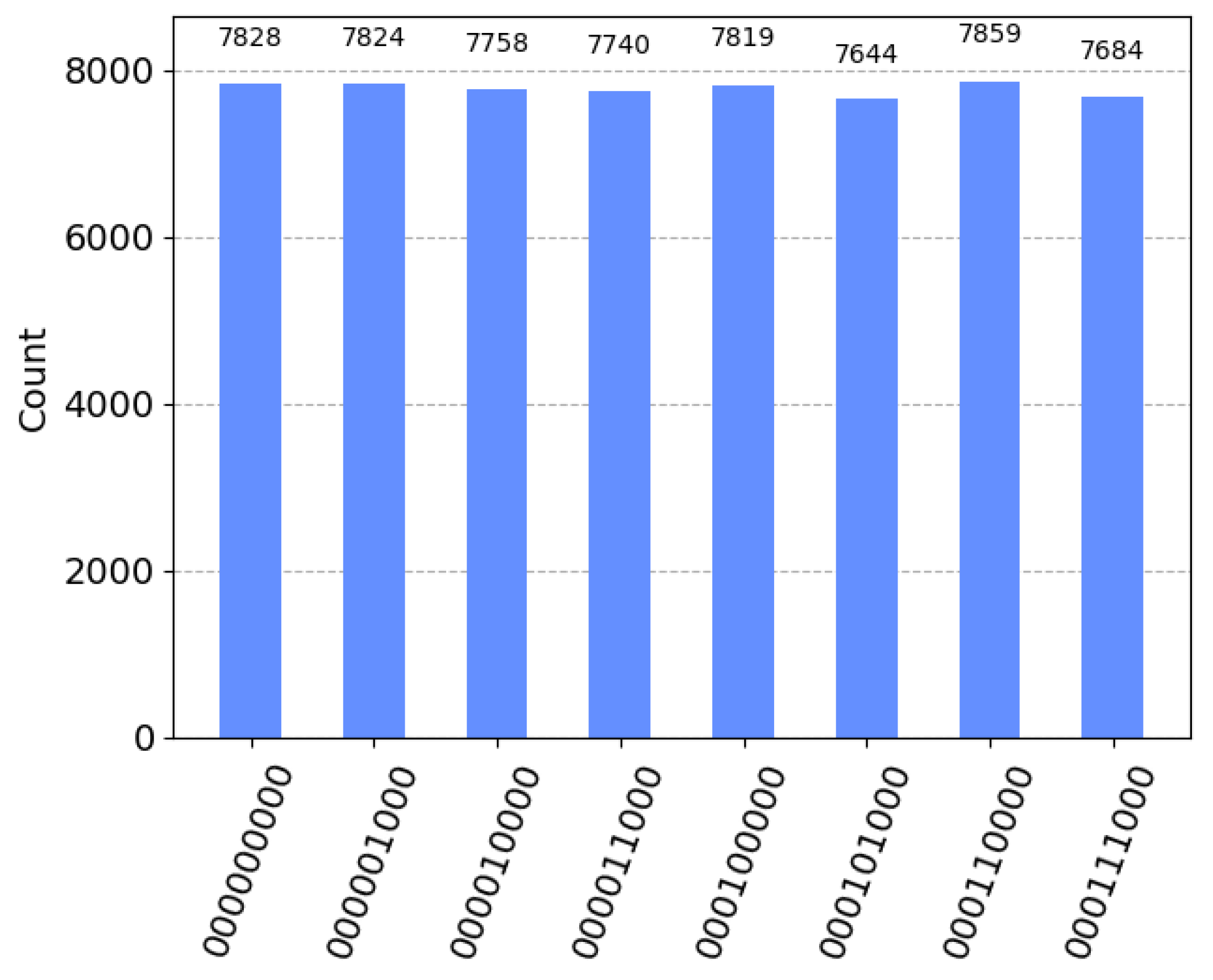
Figure 7, and a detailed explanation of each part is given in the figure name.
Figure 8 shows the frequency histogram of the quantum experimental circuit simulation results. It can be seen from the figure that particles
successfully collapsed onto particles
. Afterwards, Alice and Bob inform each other of their deformation operations through the classical channel. Both parties only need to add auxiliary quantum states and perform reverse operations, and then they can obtain the unknown five-qubit entangled state and the unknown three-qubit entangled state, respectively.
6. Impact of Quantum Noise on Bidirectional Quantum Communication Scheme
In practical IoT environments, quantum communication is inevitably affected by various quantum noise sources, primarily including bit-flip noise, phase-damping noise, and amplitude-damping noise. These types of noise arise from the interaction between quantum systems and their surrounding environment, significantly impacting the fidelity and reliability of quantum communication. By thoroughly studying the effects of these noise sources, we can design more robust communication protocols and implement appropriate error correction or noise mitigation measures to ensure the security and reliability of quantum information transmission.
Since the identity authentication module involves only local single-qubit measurements and the exchange of classical information, without requiring the transmission of quantum states through quantum channels, quantum channel noise does not affect the authentication process, and noise considerations are unnecessary. However, the information transmission module involves the transfer of quantum states through quantum channels, where quantum noise can interfere with the transmitted quantum states, leading to information loss or distortion. Therefore, it is crucial to analyze the potential impact of quantum noise in IoT environments on the information transmission module. In this chapter, we analytically derive the fidelities of the asymmetric bidirectional quantum communication Scheme in noisy environments including bit-flip noise, amplitude-damping noise, and phase-damping noise.
In a quantum noise environment, the pure input state is converted into a mixed state. It is more effective to represent the quantum state with a density operator than with a vector state. The density matrix corresponding to the six quantum channels
in the protocol is
. The effect of noise on the density matrix can be expressed as follows:
where
r represents the noise type, that is,
. If
indicates bit-flip noise, then
; if
indicates phase-damped noise, then
; if
indicates amplitude-damped noise, then
. The superscript numbers
indicate which particle the operator E acts on.
represents a quantum operation that converts
into
.
In order to reconstruct the original quantum state, Alice and Bob need to choose the appropriate unitary operation to transform their particles according to the classical information they received. Then, the density matrix
of the final quantum state is expressed as follows:
where
is the trace of particles
;
and
are the density matrices corresponding to quantum states
and
, respectively.
U represents a series of gate operations, measurement operations, and unitary operations performed in the bidirectional transmission process, and its expression is as follows:
In the formula, represent the three CNOT gate operations performed on particles with particles as control qubits in the scheme; , and represents the result of performing single-particle measurement on particles on the Z basis, and , and represent the result of single-particle measurement on the X basis for particles , and ; refers to the corresponding unitary operations performed by Alice and Bob in order to reconstruct the quantum state information sent by each other.
Section 3.3 has described the proposed bidirectional quantum teleportation scheme under ideal conditions, and the final output quantum state is
. After selecting the type of noise, we can obtain the output quantum state
under noise. Based on the above discussion, the fidelity under the influence of noise can be finally calculated as
Next, we discuss the impact of three noise environments.
6.1. Bit-Flip Noise
Bit-flip noise occurs when a qubit’s state randomly flips between and due to environmental interference. In IoT applications, devices are often deployed in challenging environments, such as industrial sites with strong electromagnetic interference or high-radiation areas, which increase the likelihood of bit-flip noise. This noise corrupts the information carried by qubits, leading to communication errors, reduced reliability, and potential security vulnerabilities exploitable by attackers.
The Kraus operator of bit-flip noise can be expressed as
In bit-flip noise, the quantum bit has a probability of 1-p remaining unchanged and a probability of p flipping. After the bit-flip noise operator is substituted into the quantum channel density matrix, the quantum state of the quantum channel will become a mixed state
. The communicating parties perform a series of operations on
, and the final output quantum state of the quantum system is
According to Equations (
16) and (
18), we can finally calculate that the fidelity of the scheme under bit-flip noise is
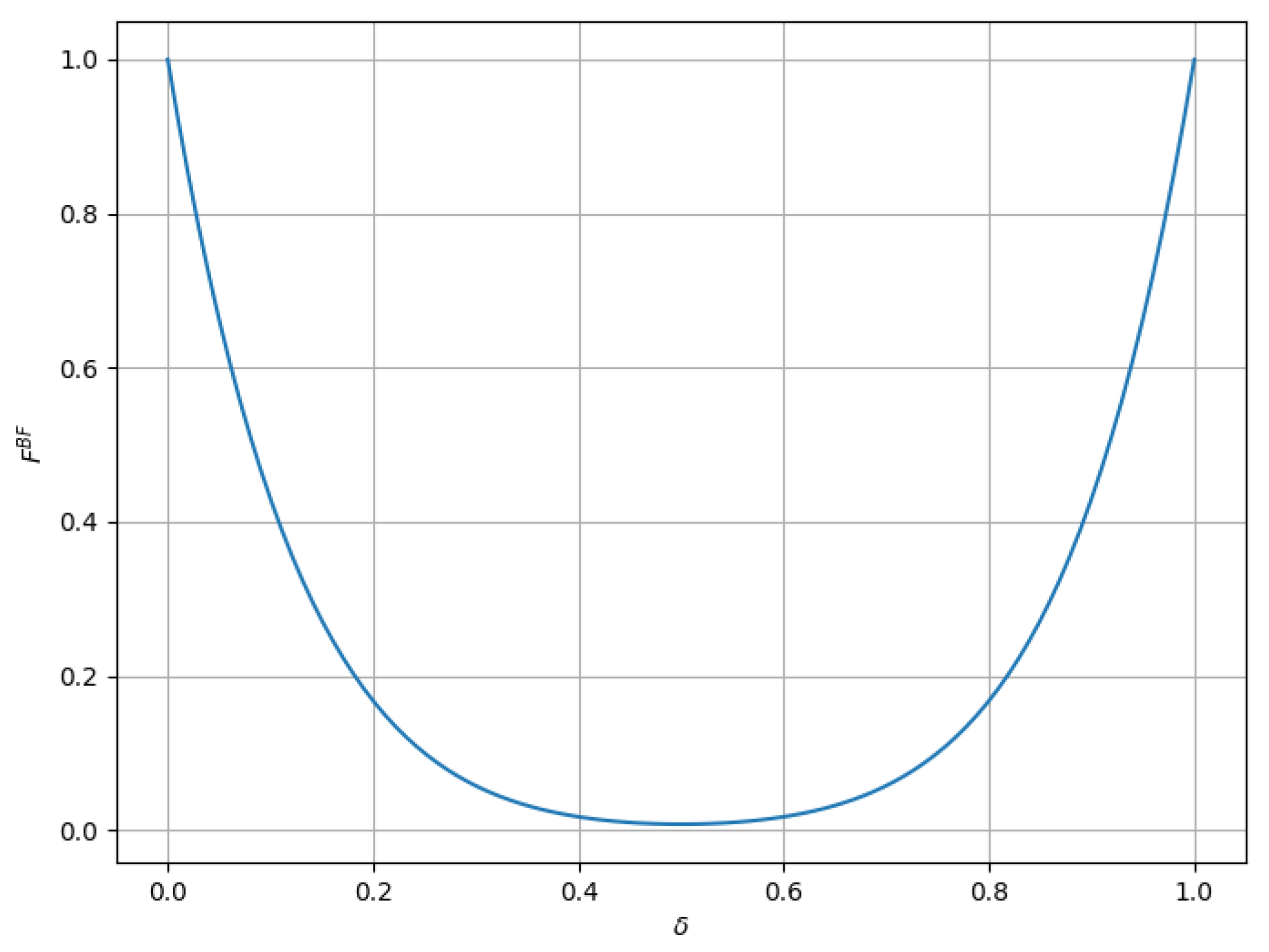
It can be seen from Equation (
19) that in bit-flip noise, the fidelity depends only on the decoherence rate
. As shown in
Figure 9, it can be observed from the change curve that the fidelity
of the output quantum state of the proposed BQT protocol first decreases and then increases with the increase in the decoherence rate, and
can reach 1 when
and
. When
, the fidelity
is the minimum.
6.2. Phase-Damping Noise
Phase-damping noise primarily affects the coherence of quantum bits, leading to the loss of phase information in quantum states. IoT devices may be deployed in environments with drastic temperature changes and frequent mechanical vibrations, such as outdoor sensor nodes or mobile devices. These environmental disturbances can cause phase decoherence in quantum systems, weakening the characteristics of quantum superposition and entanglement. The Kraus operator of phase-damped noise can be expressed as
where
in the formula represents the intensity of the noise. After the bit-flip noise operator is substituted into the quantum channel density matrix, the quantum state of the quantum channel will become a mixed state
. The communicating parties perform a series of operations on
, and the final output quantum state of the quantum system is
According to Equations (
16) and (
21), we can finally calculate that the fidelity of the BQT solution in a phase-damped noise environment is
From Equation (
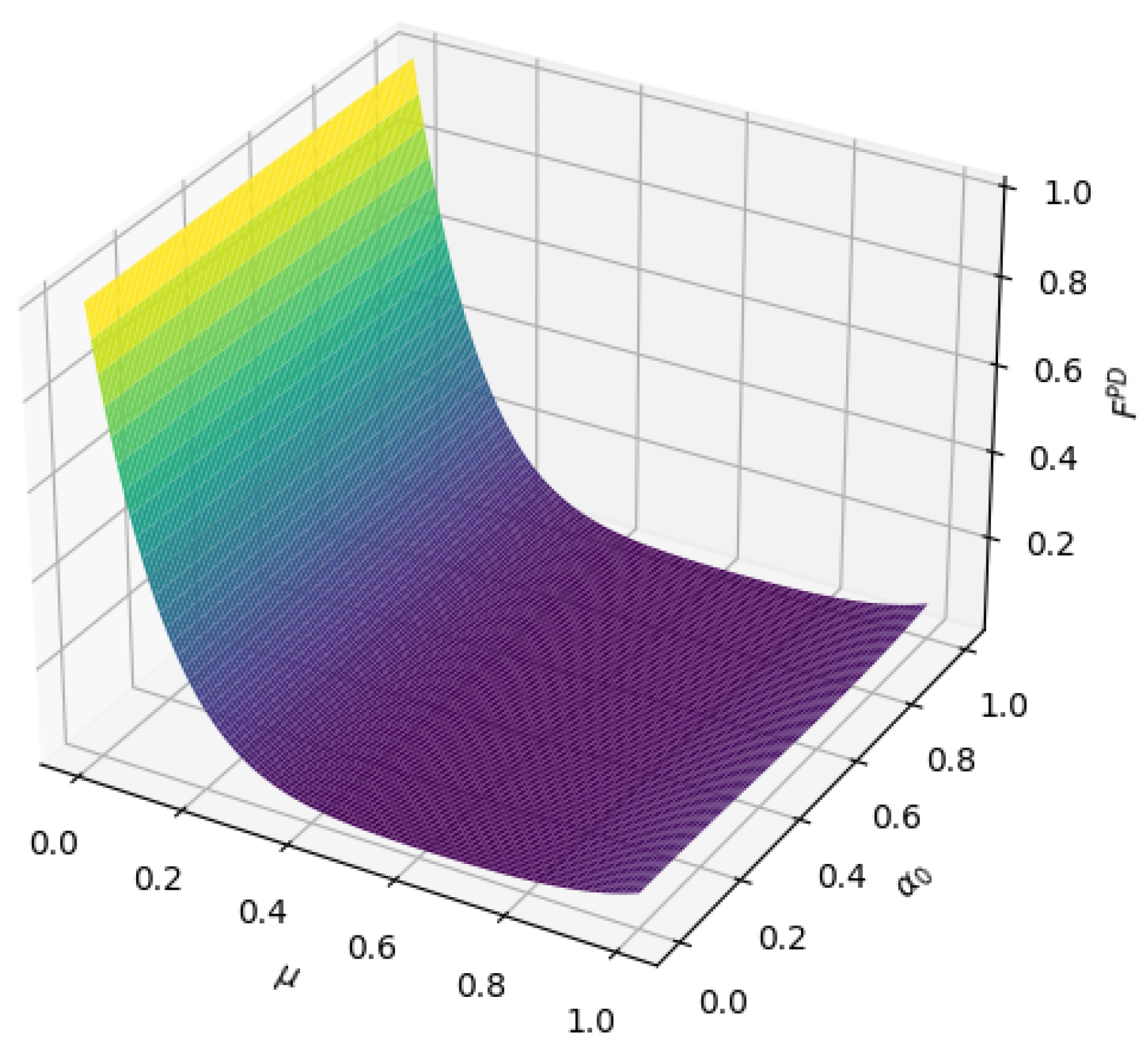
22), we can see that in phase-damped noise, the fidelity of this scheme depends on the amplitude parameter and decoherence rate of the transmitted quantum state. From
Figure 10, we can see that the fidelity
of the protocol output quantum state generally decreases with the increase in the decoherence rate
.
6.3. Amplitude-Damping Noise
Amplitude-damping noise arises from energy exchange between a quantum system and its environment. In IoT environments, devices may be affected by thermal noise, photon loss, and other disturbances, particularly during high-temperature operations or fiber optic transmission, where amplitude-damping noise is more pronounced. This noise leads to the attenuation of quantum signals, reducing the probability of the quantum bit remaining in the excited state, thereby decreasing the success rate of quantum communication and impacting the efficiency and reliability of the communication. The Kraus operator of amplitude-damped noise can be expressed as
where
is the error probability caused by the amplitude-damping noise of the qubit. In the presence of quantum noise, the pure state input is converted into a mixed state. The density matrix of the resulting state obtained by executing the scheme is
According to Equations (
16) and (
24), we can finally calculate that the fidelity of the scheme in the amplitude-damped noise environment is
From Equation (
25), we can see that in amplitude-damped noise, the fidelity depends on the amplitude parameter and decoherence rate of the transmitted quantum state.
Figure 11 shows the change process of the fidelity
. When the noise intensity in
Figure 11a is 1, the larger the amplitude parameter, the higher the fidelity, which is close to 1; from
Figure 11b,c, we can see that the fidelity of the output quantum state decreases with the increase in the decoherence rate, but when the decoherence rate and the amplitude parameter of the transmitted quantum state are in a specific combination, it also shows an upward trend.
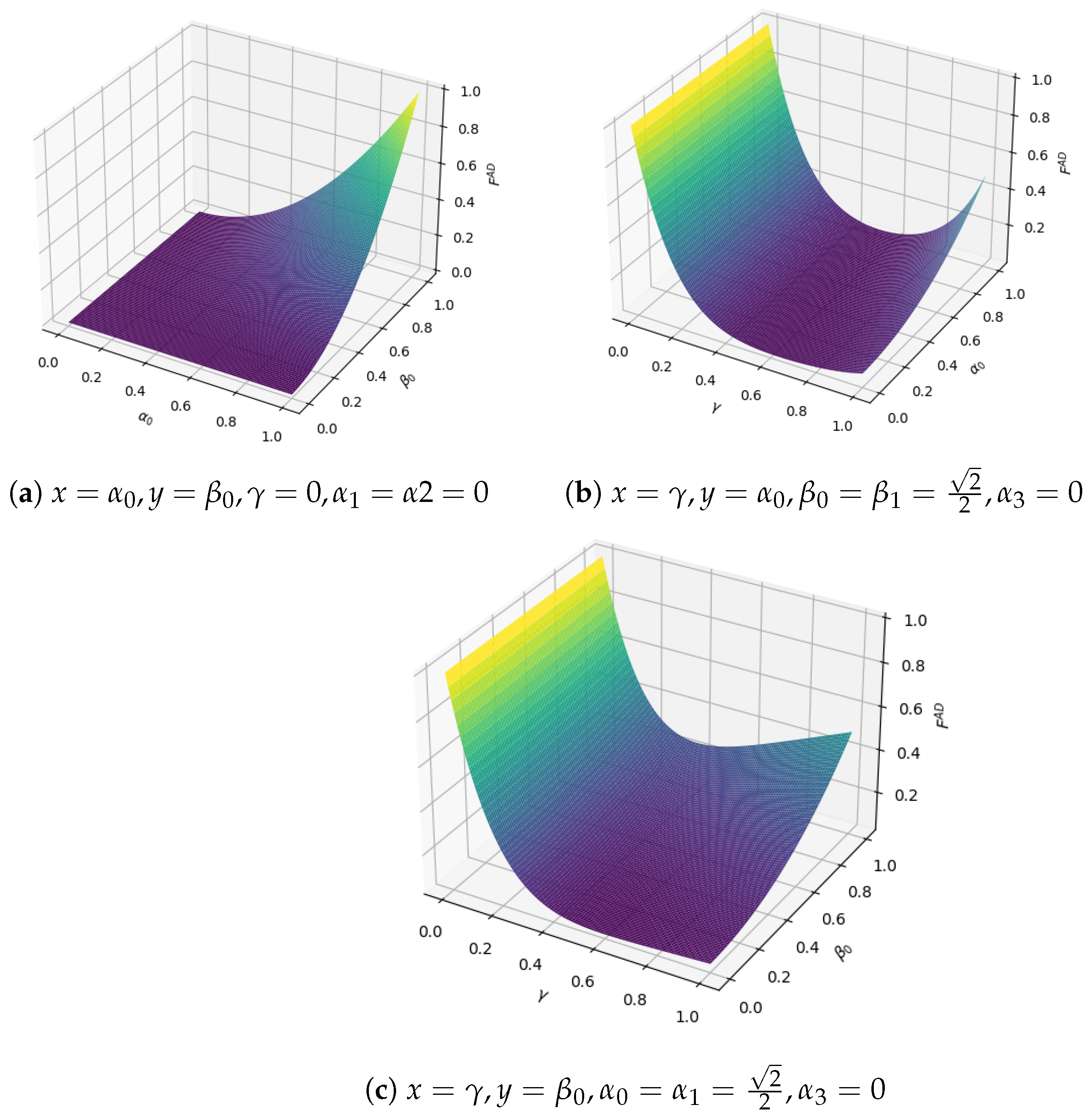
6.4. Noise Comparison Analysis
From the above analysis, in the phase-damped noise and amplitude-damped noise environments, the fidelity of the output quantum state is determined by the decoherence rate and the amplitude parameters of the transmitted quantum state. However, in the bit-flip noise and depolarization noise environments, the fidelity of the output quantum state depends only on the decoherence rate. In order to compare the trend of the output quantum state fidelity changing with the decoherence rate in the three noise environments, let
. Then the fidelity in the three noise environments is, respectively,
Figure 12 shows the trend of the fidelity of the output quantum state with the decoherence rate in three different noise environments. We can see that in the bit-flip noise and phase-damping noise environments, the curves of the fidelity of the output quantum state with the decoherence rate are almost overlapping in the interval
. However, the fidelity
of the output quantum state under bit-flip noise first decreases and then increases with the increase in the decoherence rate. When
or
,
reaches the maximum value of 1, and when
,
takes the minimum value. Under a high decoherence rate, the fidelity of PD control has a slight upward trend with the increase in decoherence rate, and the fidelity of AD control is relatively stable. When p is greater than 0.844, the fidelity in the PD environment exceeds that of AD.
In summary, our scheme is designed with full consideration of the bit-flip noise, phase-damping noise, and amplitude-damping noise present in IoT environments, effectively mitigating their impact on quantum state transmission. By carefully selecting and adjusting the amplitude parameters of the transmitted quantum states, the communicating parties can reduce the negative effects of noise, significantly enhancing the fidelity and reliability of communication. This not only facilitates the implementation of more efficient and secure quantum data transmission protocols but also demonstrates the robustness of our bidirectional quantum communication scheme against noise in IoT environments, providing a solid theoretical foundation for its deployment in practical IoT applications.
7. Comparison and Analysis
In this section, to reflect our scheme’s superiority, we compare it with the papers [
36,
37] from four aspects: quantum resource consumption, classical resource consumption, operation complexity, and inherent efficiency. While resource consumption is similar to other schemes, this scheme does not require the participation of a third party. It can transmit more quantum state information using only simple single quantum measurements. This scheme has lower operational complexity and higher inherent efficiency.
In terms of operational complexity, to achieve bidirectional asymmetric transmission, the paper [
36] needs to perform a GHZ-state measurement and a Bell-state measurement. In order to realize bidirectional teleportation of a three-qubit entangled state and arbitrary single-qubit state, the paper [
37] needs to perform a GHZ-state measurement, a Bell-state measurement, and a single-qubit measurement, respectively. In our scheme, only simple von Neumann measurements and single quantum measurements based on Z-basis are performed in the entire process to achieve bidirectional quantum state teleportation. Therefore, this scheme has lower operational complexity.
In terms of actual efficiency, the formula for calculating transmission efficiency
of quantum teleportation schema is defined as follows:
In the formula, is the number of quantum states transmitted in both directions, is the number of quantum states required to construct a quantum channel, is the number of auxiliary quantum states that need to be introduced to reconstruct information, and c is the consumed classical bits number.
Paper [
36] is a bidirectional quantum teleportation scheme based on two GHZ states, so the channel consumption quantum number is 6. During the transmission process, communication parties must perform GHZ-state and Bell-state measurements. This scheme consumes five classical bits and ultimately transmits four qubits. According to the above formula, the inherent efficiency can be calculated as
.
Paper [
37] is an asymmetric two-way transmission scheme based on six quantum entangled states, so the channel consumption quantum number is 6. The communication process requires a GHZ-state measurement, a Bell-state measurement, and a single-qubit measurement. This scheme consumes six classic bits and ultimately transmits four qubits. According to the above formula, the inherent efficiency can be calculated as
.
This scheme also uses a six-qubit state as a channel. During the transmission process, the communicating parties must perform three X-based and three Z-based measurements. The number of classical bits consumed by the classic scheme is 6, and 8 qubits of information are ultimately transmitted. According to the above formula, the inherent efficiency can be calculated as .
The required resources and inherent efficiency of each scheme are shown in
Table 2.
Therefore, this paper cannot only transmit more quantum state information but also has the advantages of lower operational complexity and higher inherent efficiency.
8. Conclusions
This paper proposes an asymmetric bidirectional quantum communication scheme tailored for IoT, addressing the trust issues and system complexity introduced by third-party controllers in traditional bidirectional quantum transmission schemes. We designed a unique device identity authentication module that leverages the quantum no-cloning principle and measurement uncertainty to achieve inter-device authentication without relying on third parties. In the information transmission module, we employed a bidirectional quantum transmission scheme without a third-party controller, utilizing the six-qubit state as the quantum channel. This enables Device A to transmit an unknown five-qubit entangled state to Device B while Device B transmits an unknown three-qubit entangled state to Device A.
Through experimental validation, we demonstrated the feasibility of the proposed scheme and conducted a security analysis of the identity authentication module, showing its effectiveness against identity spoofing attacks. Additionally, we analyzed the impact of quantum noise on the scheme, and the results indicate strong robustness in practical environments. Compared with the existing schemes, our approach offers significant advantages in terms of resource consumption and efficiency, reducing operational complexity and enhancing intrinsic efficiency.
This study provides an effective solution for quantum secure communication in IoT. Future work will focus on optimizing the scheme’s performance and exploring applications in larger-scale quantum networks. However, the proposed scheme has limitations, including reliance on idealized quantum channels, challenges in scalability for large networks, and the difficulty of implementing the scheme on resource-constrained IoT devices. Addressing these issues will require robust error correction, scalable architectures, and efficient hardware integration. Future research could also explore hybrid quantum–classical approaches to expand the scheme’s applicability in diverse IoT scenarios.