Breather Bound States in a Parametrically Driven Magnetic Wire
Abstract
1. Introduction
2. The Theoretical Model
3. The Numerical Framework
4. Dynamical Indicators
5. Results
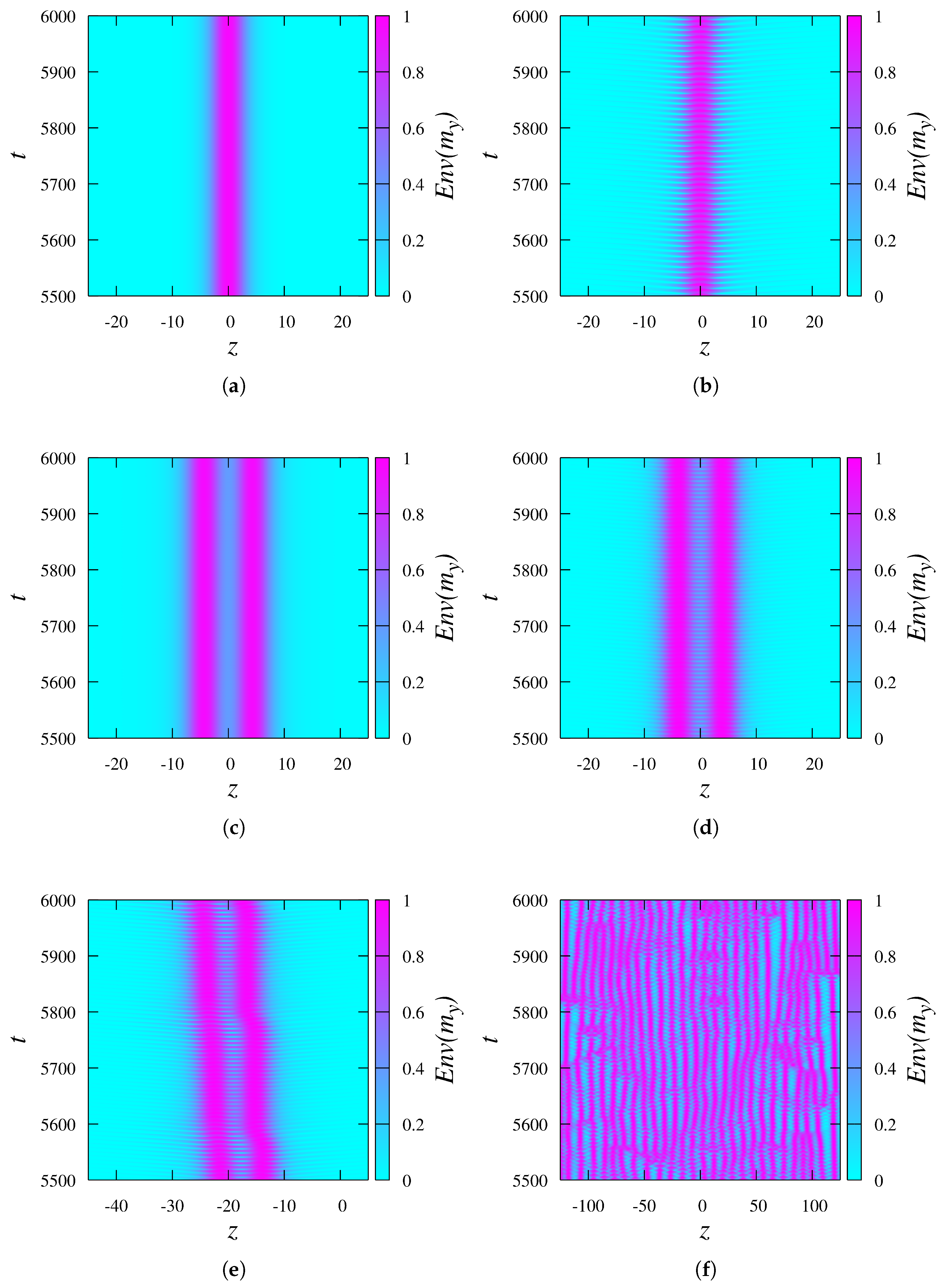
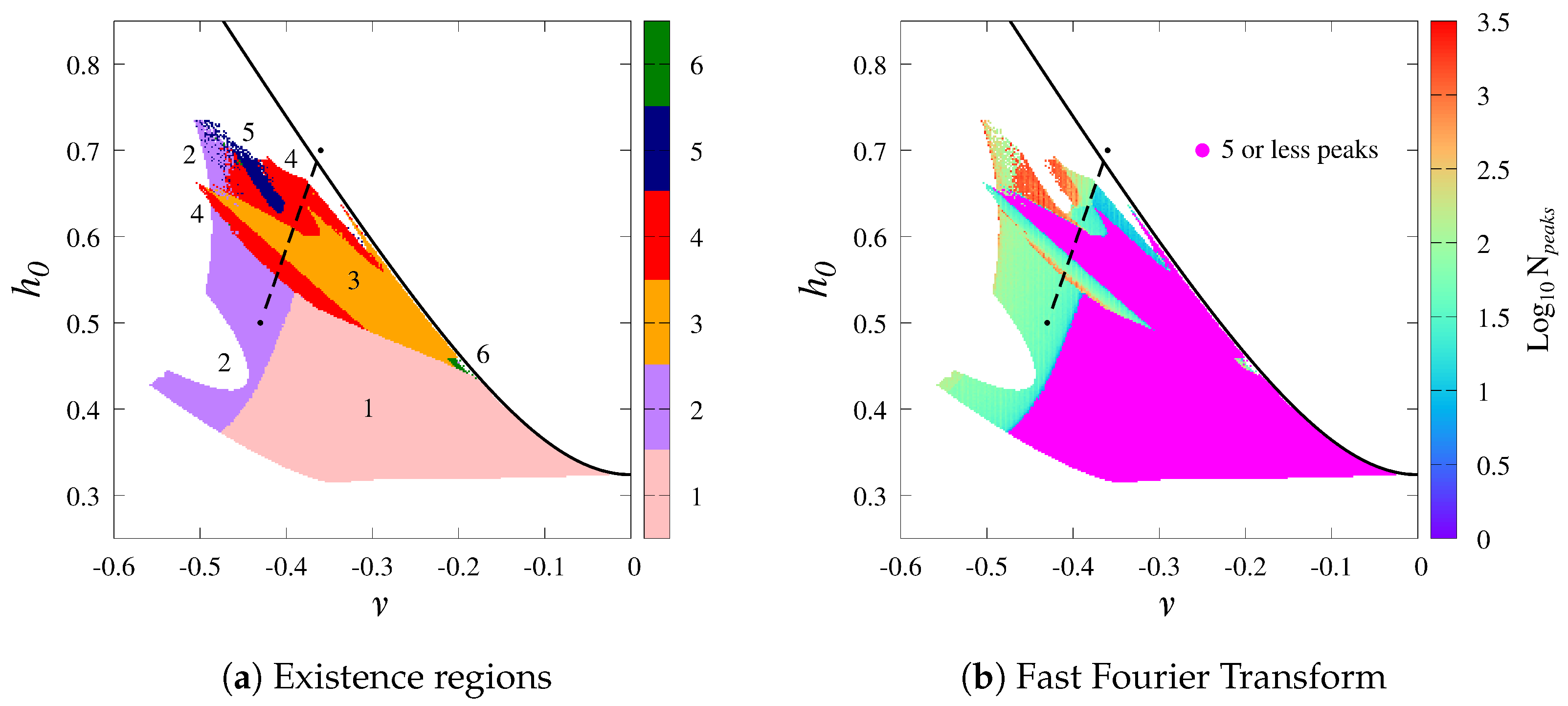
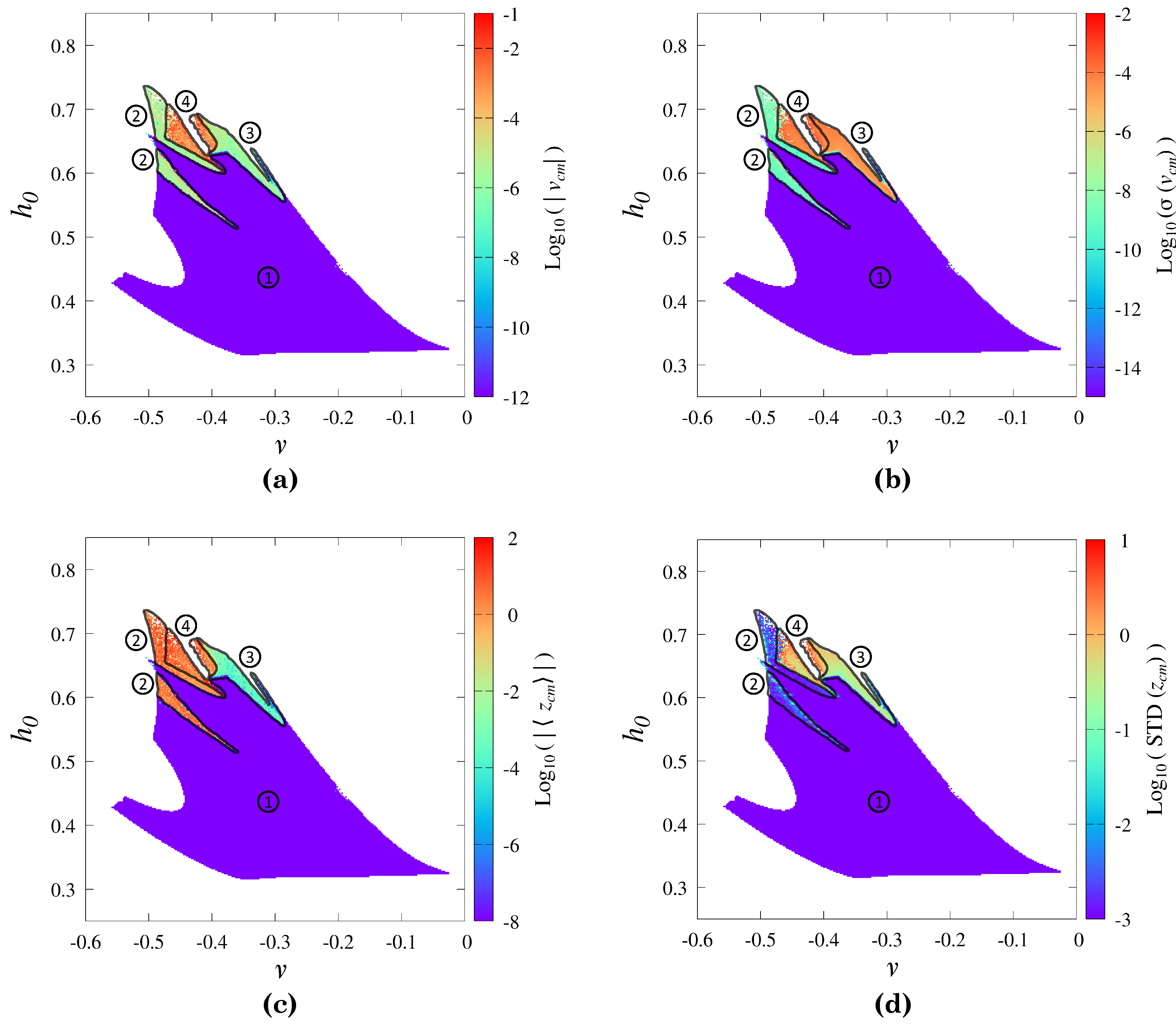
5.1. Existence Regions
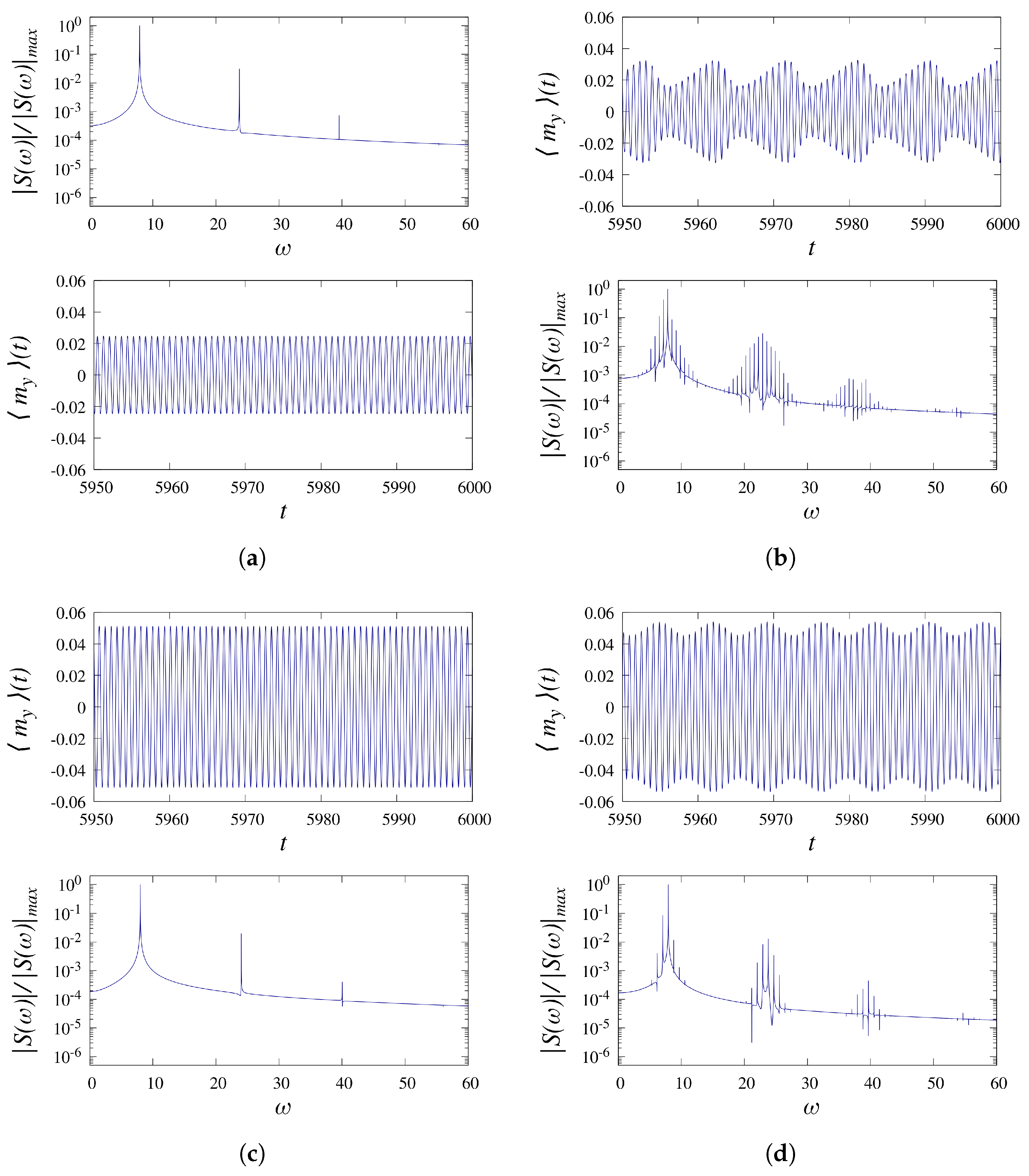
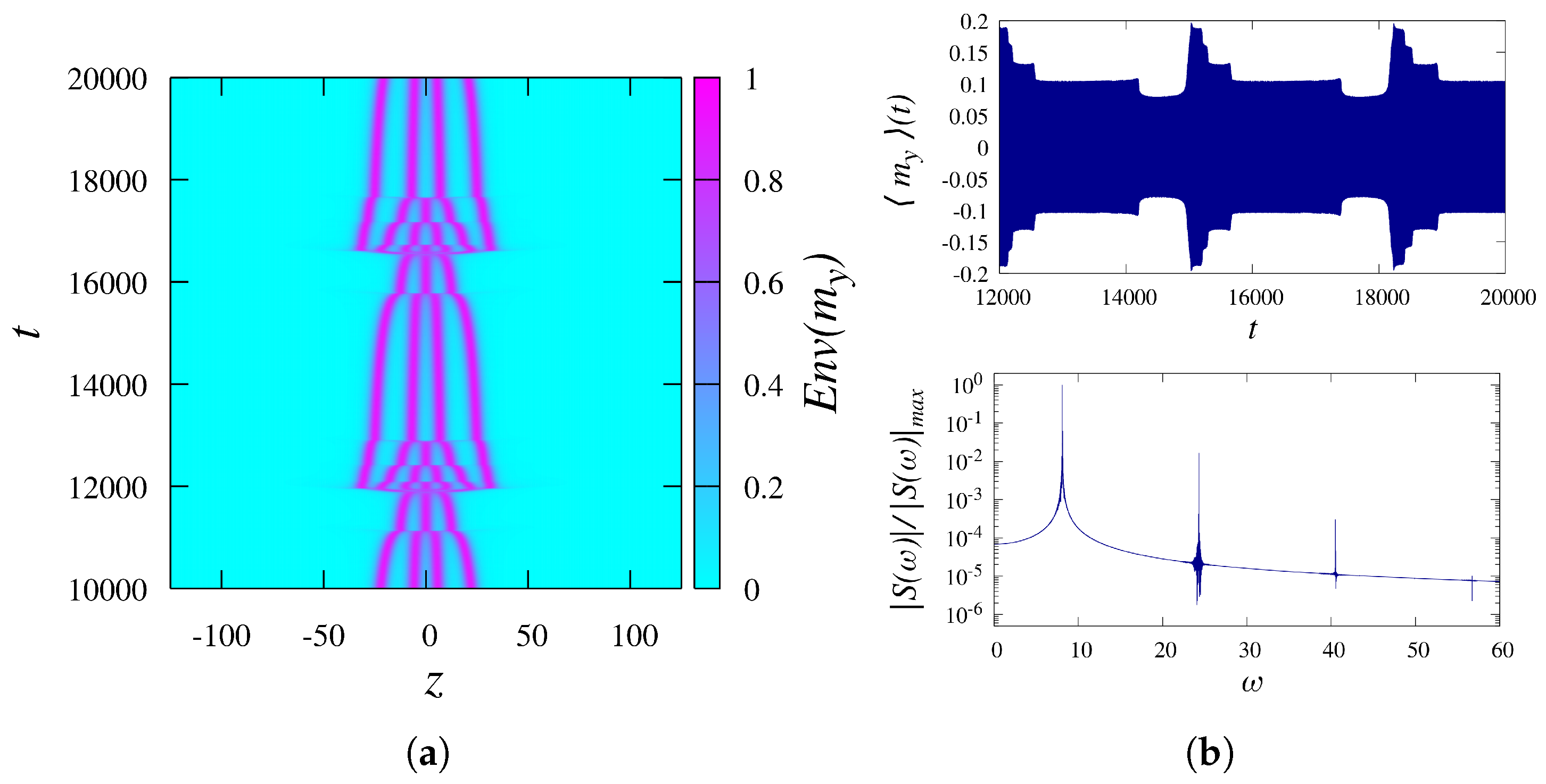
5.2. The Power Spectral Density
5.3. The Center-of-Mass (CM) Drift of Solitons
5.4. The Micromagnetic Energy
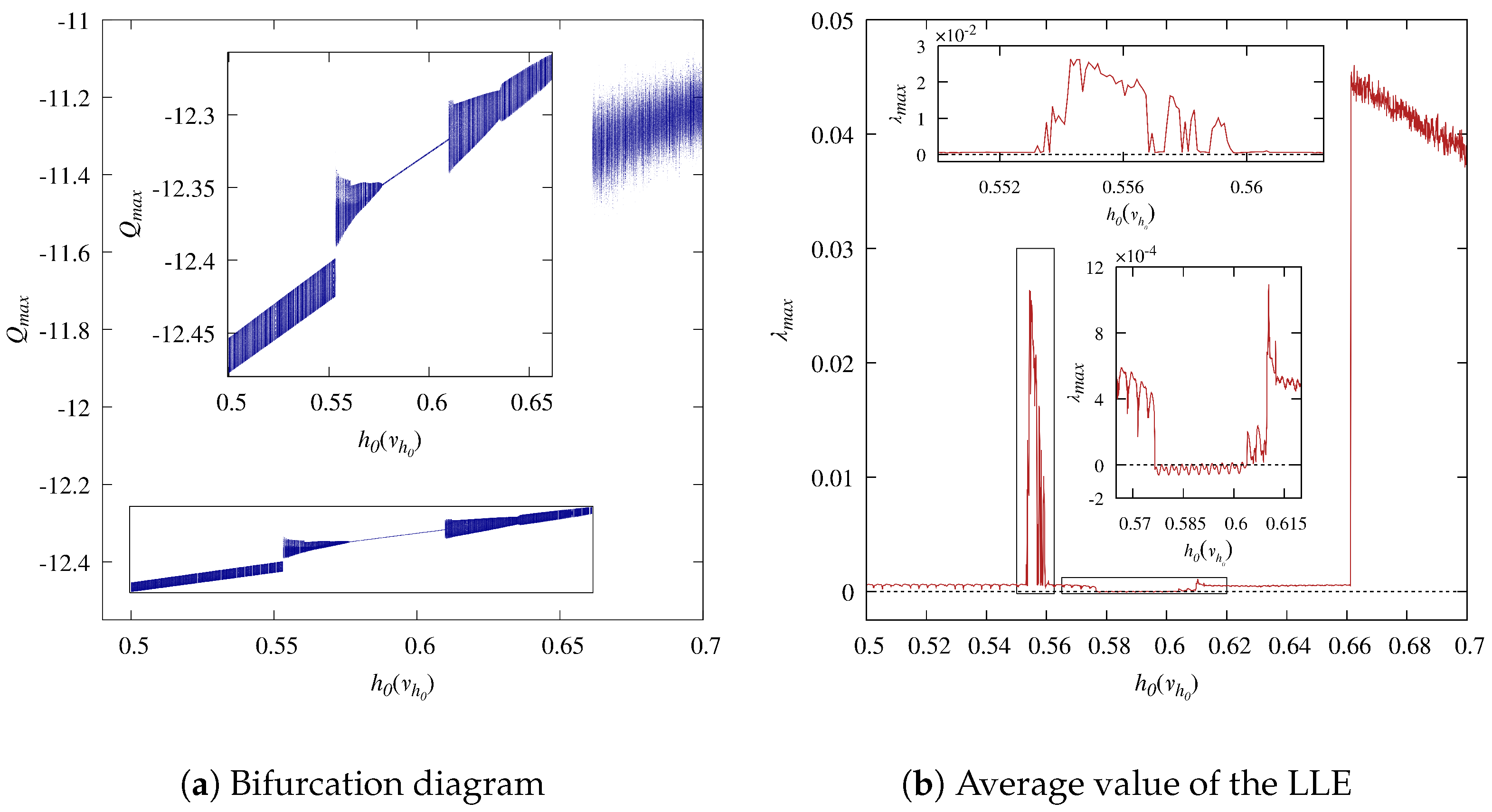
5.5. The Largest Lyapunov Exponent (LLE)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LLG | Landau–Lifshitz–Gilbert |
| PSD | Power Spectral Density |
| LLE | Largest Lyapunov Exponent |
| CM | Center of Mass |
References
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Rosanov, N.N. Spatial Hysteresis and Optical Patterns; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Lugiato, L.A.; Lefever, R. Spatial Dissipative Structures in Passive Optical Systems. Phys. Rev. Lett. 1987, 58, 2209–2211. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.; Alexander, O.; Skryabin, D. Multistability and coexisting soliton combs in ring resonators: The Lugiato-Lefever approach. Opt. Express 2017, 25, 11550–11555. [Google Scholar] [CrossRef] [PubMed]
- Miles, J.W. Parametrically excited solitary waves. J. Fluid Mech. 1984, 148, 451–460. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Bogdan, M.M.; Korobov, V.I. Stability Diagram of the Phase-Locked Solitons in the Parametrically Driven, Damped Nonlinear Schrödinger Equation. Europhys. Lett. 1991, 15, 113. [Google Scholar] [CrossRef]
- Faraday, M. XVII. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 1831, 31, 299–340. [Google Scholar]
- Scott, A.C. A nonlinear Klein-Gordon equation. Am. J. Phys. 1969, 37, 52–61. [Google Scholar] [CrossRef]
- Coullet, P.; Frisch, T.; Sonnino, G. Dispersion-induced patterns. Phys. Rev. E 1994, 49, 2087. [Google Scholar] [CrossRef]
- Clerc, M.; Coulibaly, S.; Laroze, D. Interaction law of 2D localized precession states. Europhys. Lett. 2010, 90, 38005. [Google Scholar] [CrossRef]
- Barashenkov, I.; Zemlyanaya, E.; Van Heerden, T. Time-periodic solitons in a damped-driven nonlinear Schrödinger equation. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83, 056609. [Google Scholar] [CrossRef]
- Alexeeva, N.; Barashenkov, I.; Tsironis, G. Impurity-induced stabilization of solitons in arrays of parametrically driven nonlinear oscillators. Phys. Rev. Lett. 2000, 84, 3053. [Google Scholar] [CrossRef] [PubMed]
- Barashenkov, I.; Zemlyanaya, E. Stable complexes of parametrically driven, damped nonlinear Schrödinger solitons. Phys. Rev. Lett. 1999, 83, 2568. [Google Scholar] [CrossRef]
- Zemlyanaya, E.V.; Alexeeva, N. Oscillating solitons of the driven, damped nonlinear Schrödinger equation. Theor. Math. Phys. 2009, 159, 870–876. [Google Scholar] [CrossRef]
- Barashenkov, I.; Zemlyanaya, E. Soliton complexity in the damped-driven nonlinear Schrödinger equation: Stationary to periodic to quasiperiodic complexes. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83, 056610. [Google Scholar] [CrossRef]
- Urzagasti, D.; Laroze, D.; Clerc, M.G.; Coulibaly, S.; Pleiner, H. Two-soliton precession state in a parametrically driven magnetic wire. J. Appl. Phys. 2012, 111, 07D111. [Google Scholar] [CrossRef]
- Shchesnovich, V.; Barashenkov, I. Soliton–radiation coupling in the parametrically driven, damped nonlinear Schrödinger equation. Physica D Nonlinear Phenom. 2002, 164, 83–109. [Google Scholar] [CrossRef]
- Arnold, V.I. Geometrical Methods in the Theory of Ordinary Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 250. [Google Scholar]
- Clerc, M.G.; Coulibaly, S.; Laroze, D. Parametrically Driven Instability in Quasi-Reversal Systems. Int. J. Bifurc. Chaos 2009, 19, 3525–3532. [Google Scholar] [CrossRef]
- Okamura, A.; Konno, H. Resonant Breakup of Soliton in Parametrically Driven Nonlinear Schrödinger Equation. J. Phys. Soc. Jpn. 1989, 58, 1930–1933. [Google Scholar] [CrossRef]
- Denardo, B.; Galvin, B.; Greenfield, A.; Larraza, A.; Putterman, S.; Wright, W. Observations of localized structures in nonlinear lattices: Domain walls and kinks. Phys. Rev. Lett. 1992, 68, 1730–1733. [Google Scholar] [CrossRef]
- Bondila, M.; Barashenkov, I.V.; Bogdan, M.M. Topography of attractors of the parametrically driven nonlinear Schrödinger equation. Physica D Nonlinear Phenom. 1995, 87, 314–320. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Smirnov, Y.S. Existence and stability chart for the ac-driven, damped nonlinear Schrödinger solitons. Phys. Rev. E 1996, 54, 5707–5725. [Google Scholar] [CrossRef] [PubMed]
- Cabanas, A.; Vélez, J.; Pérez, L.; Díaz, P.; Clerc, M.; Laroze, D.; Malomed, B. Dissipative structures in a parametrically driven dissipative lattice: Chimera, localized disorder, continuous-wave, and staggered states. Chaos Solitons Fractals 2021, 146, 110880. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Cross, S.; Malomed, B.A. Multistable pulselike solutions in a parametrically driven Ginzburg-Landau equation. Phys. Rev. E 2003, 68, 056605. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Malomed, B.A. Solitary Pulses and Periodic Waves in the Parametrically Driven Complex Ginzburg-Landau Equation. J. Phys. Soc. Jpn. 2003, 72, 1360–1365. [Google Scholar] [CrossRef]
- Reyes, L.; Pérez, L.; Pedraja-Rejas, L.; Díaz, P.; Mendoza, J.; Bragard, J.; Clerc, M.; Laroze, D. Characterization of Faraday patterns and spatiotemporal chaos in parametrically driven dissipative systems. Chaos Solitons Fractals 2024, 186, 115244. [Google Scholar] [CrossRef]
- León, A.O.; Clerc, M.G.; Coulibaly, S. Traveling pulse on a periodic background in parametrically driven systems. Phys. Rev. E 2015, 91, 050901. [Google Scholar] [CrossRef]
- Leon, A.O.; Berríos-Caro, E.; León, A.; Clerc, M.G. Faraday kinks connecting parametric waves in magnetic wires. Commun. Nonlinear Sci. Numer. Simul. 2024, 131, 107841. [Google Scholar] [CrossRef]
- Moille, G.; Leonhardt, M.; Paligora, D.; Englebert, N.; Leo, F.; Fatome, J.; Srinivasan, K.; Erkintalo, M. Parametrically driven pure-Kerr temporal solitons in a chip-integrated microcavity. Nat. Photonics 2024, 18, 617–624. [Google Scholar] [CrossRef]
- Bogdan, M.; Charkina, O. Structure of soliton bound states in the parametrically driven and damped nonlinear systems. Low Temp. Phys. 2022, 48, 1062–1070. [Google Scholar] [CrossRef]
- Shaukat, M.I.; Qasymeh, M.; Eleuch, H. Spatial solitons in an electrically driven graphene multilayer medium. Sci. Rep. 2022, 12, 10931. [Google Scholar] [CrossRef]
- Cabanas, A.M.; Rivas, R.; Pérez, L.M.; Vélez, J.A.; Díaz, P.; Clerc, M.G.; Pleiner, H.; Laroze, D.; Malomed, B.A. A quasi-periodic route to chaos in a parametrically driven nonlinear medium. Chaos Solitons Fractals 2021, 151, 111089. [Google Scholar] [CrossRef]
- Urzagasti, D.; Laroze, D.; Pleiner, H. Two-dimensional localized chaotic patterns in parametrically driven systems. Phys. Rev. E 2017, 95, 052216. [Google Scholar] [CrossRef]
- Urzagasti, D.; Laroze, D.; Pleiner, H. Localized chaotic patterns in weakly dissipative systems. Eur. Phys. J. Spec. Top. 2014, 223, 141–154. [Google Scholar] [CrossRef]
- Marín, J.F.; Riveros-Ávila, R.; Coulibaly, S.; Taki, M.; Gordillo, L.; García-Ñustes, M.A. Drifting Faraday patterns under localised driving. Commun. Phys. 2023, 6, 63. [Google Scholar] [CrossRef]
- Barbosa, A.; Sena, J.P.; Kacem, N.; Bouhaddi, N. An artificial intelligence approach to design periodic nonlinear oscillator chains under external excitation with stable damped solitons. Mech. Syst. Signal Process. 2023, 205, 110879. [Google Scholar] [CrossRef]
- Dileep, K.; Murugesh, S. Emergent soliton-like solutions in the parametrically driven 1-D nonlinear Schrödinger equation. Phys. Scr. 2023, 98, 045228. [Google Scholar] [CrossRef]
- Parra-Rivas, P.; Mas Arabi, C.; Leo, F. Dissipative localized states and breathers in phase-mismatched singly resonant optical parametric oscillators: Bifurcation structure and stability. Phys. Rev. Res. 2022, 4, 013044. [Google Scholar] [CrossRef]
- Englebert, N.; De Lucia, F.; Parra-Rivas, P.; Arabí, C.M.; Sazio, P.J.; Gorza, S.P.; Leo, F. Parametrically driven Kerr cavity solitons. Nat. Photonics 2021, 15, 857–861. [Google Scholar] [CrossRef]
- Diamantidis, S.; Horikis, T.P.; Karachalios, N.I. Exciting extreme events in the damped and AC-driven NLS equation through plane-wave initial conditions. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 053103. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Houri, S. Generation and propagation of topological solitons in a chain of coupled parametric-micromechanical-resonator arrays. Phys. Rev. Appl. 2021, 15, 034091. [Google Scholar] [CrossRef]
- Mertens, F.G.; Quintero, N.R. Empirical stability criteria for parametrically driven solitons of the nonlinear Schrödinger equation. J. Phys. A Math. Theor. 2020, 53, 315701. [Google Scholar] [CrossRef]
- Barashenkov, I.; Chernyavsky, A. Stable solitons in a nearly PT-symmetric ferromagnet with spin-transfer torque. Physica D Nonlinear Phenom. 2020, 409, 132481. [Google Scholar] [CrossRef]
- Urra, H.; Marín, J.F.; Páez-Silva, M.; Taki, M.; Coulibaly, S.; Gordillo, L.; García-Ñustes, M.A. Localized Faraday patterns under heterogeneous parametric excitation. Phys. Rev. E 2019, 99, 033115. [Google Scholar] [CrossRef]
- Edri, Y.; Meron, E.; Yochelis, A. Spatial asymmetries of resonant oscillations in periodically forced heterogeneous media. Physica D Nonlinear Phenom. 2020, 410, 132501. [Google Scholar] [CrossRef]
- Ferré, M.A.; Clerc, M.G.; Coulibally, S.; Rojas, R.G.; Tlidi, M. Localized structures and spatiotemporal chaos: Comparison between the driven damped sine-Gordon and the Lugiato-Lefever model. Eur. Phys. J. D 2017, 71, 172. [Google Scholar] [CrossRef]
- Clerc, M.G.; Garcia-Ñustes, M.A.; Zárate, Y. Propagative phase shielding solitons in inhomogeneous media. Physica D Nonlinear Phenom. 2014, 269, 86–93. [Google Scholar] [CrossRef]
- Bertotti, G.; Mayergoyz, I.D.; Serpico, C. Nonlinear Magnetization Dynamics in Nanosystems; Elsevier Series in Electromagnetism; Elsevier: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Scholz, W.; Batra, S. Micromagnetic modeling of ferromagnetic resonance assisted switching. J. Appl. Phys. 2008, 103, 07F539. [Google Scholar] [CrossRef]
- Lakshmanan, M. The fascinating world of the Landau-Lifshitz-Gilbert equation: An overview. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1280–1300. [Google Scholar] [CrossRef]
- Montoya, E.A.; Perna, S.; Chen, Y.J.; Katine, J.A.; d’Aquino, M.; Serpico, C.; Krivorotov, I.N. Magnetization reversal driven by low dimensional chaos in a nanoscale ferromagnet. Nat. Commun. 2019, 10, 543. [Google Scholar] [CrossRef]
- Bragard, J.; Vélez, J.; Riquelme, J.; Pérez, L.; Hernández-García, R.; Barrientos, R.; Laroze, D. Study of type-III intermittency in the Landau–Lifshitz-Gilbert equation. Phys. Scr. 2021, 96, 124045. [Google Scholar] [CrossRef]
- Alvarez, L.F.; Pla, O.; Chubykalo, O. Quasiperiodicity, bistability, and chaos in the Landau-Lifshitz equation. Phys. Rev. B 2000, 61, 11613. [Google Scholar] [CrossRef]
- Perez, L.M.; Bragard, J.; Mancini, H.; Gallas, J.A.; Cabanas, A.M.; Suarez, O.J.; Laroze, D. Effect of anisotropies on the magnetization dynamics. Netw. Heterog. Media 2015, 10, 209–221. [Google Scholar]
- Smith, R.K.; Grabowski, M.; Camley, R. Period doubling toward chaos in a driven magnetic macrospin. J. Magn. Magn. Mater. 2010, 322, 2127–2134. [Google Scholar] [CrossRef]
- Vélez, J.; Bragard, J.; Pérez, L.; Cabanas, A.; Suarez, O.; Laroze, D.; Mancini, H. Periodicity characterization of the nonlinear magnetization dynamics. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 093112. [Google Scholar] [CrossRef] [PubMed]
- Ferona, A.M.; Camley, R.E. Nonlinear and chaotic magnetization dynamics near bifurcations of the Landau-Lifshitz-Gilbert equation. Phys. Rev. B 2017, 95, 104421. [Google Scholar] [CrossRef]
- Smith, R.K.; Grabowski, M.; Camley, R. Nonlinear behavior in magnetic transients. J. Magn. Magn. Mater. 2009, 321, 3472–3477. [Google Scholar] [CrossRef]
- Sementsov, D. Chaotic magnetization dynamics in single-crystal thin-film structures. Crystallogr. Rep. 2009, 54, 98–105. [Google Scholar]
- Botha, A.; Shukrinov, Y.M.; Tekić, J.; Kolahchi, M. Chaotic dynamics from coupled magnetic monodomain and Josephson current. Phys. Rev. E 2023, 107, 024205. [Google Scholar] [CrossRef]
- Shen, L.; Shen, K. Skyrmion-based chaotic oscillator driven by a constant current. Phys. Rev. B 2024, 109, 014422. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Tsunegi, S.; Nakajima, K.; Taniguchi, T. Computational capability for physical reservoir computing using a spin-torque oscillator with two free layers. Phys. Rev. B 2023, 107, 054406. [Google Scholar] [CrossRef]
- Unikandanunni, V.; Medapalli, R.; Asa, M.; Albisetti, E.; Petti, D.; Bertacco, R.; Fullerton, E.E.; Bonetti, S. Inertial spin dynamics in epitaxial cobalt films. Phys. Rev. Lett. 2022, 129, 237201. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, R.; Cherkasskii, M.; Jiang, R.; Mondal, R.; Etesamirad, A.; Tossounian, A.; Ivanov, B.A.; Barsukov, I. Spin Inertia and Auto-Oscillations in Ferromagnets. Phys. Rev. Lett. 2024, 132, 246701. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Novosad, V.; Fradin, F.; Pearson, J.; Tiberkevich, V.; Slavin, A.; Bader, S. From chaos to selective ordering of vortex cores in interacting mesomagnets. Nat. Commun. 2012, 3, 1330. [Google Scholar] [CrossRef]
- Pivano, A.; Dolocan, V. Chaotic dynamics of magnetic domain walls in nanowires. Phys. Rev. B 2016, 93, 144410. [Google Scholar] [CrossRef]
- Guslienko, K.Y.; Heredero, R.H.; Chubykalo-Fesenko, O. Nonlinear gyrotropic vortex dynamics in ferromagnetic dots. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 82, 014402. [Google Scholar] [CrossRef]
- Ovcharov, R.V.; Hamdi, M.; Ivanov, B.A.; Åkerman, J.; Khymyn, R.S. Antiferromagnetic droplet soliton driven by spin current. Appl. Phys. Lett. 2024, 124, 172406. [Google Scholar] [CrossRef]
- d’Aquino, M.; Perna, S.; Pancaldi, M.; Hertel, R.; Bonetti, S.; Serpico, C. Micromagnetic study of inertial spin waves in ferromagnetic nanodots. Phys. Rev. B 2023, 107, 144412. [Google Scholar] [CrossRef]
- Gareeva, Z.; Guslienko, K. Nutation excitations in the gyrotropic vortex dynamics in a circular magnetic nanodot. Nanomaterials 2023, 13, 461. [Google Scholar] [CrossRef]
- Fert, A.; Reyren, N.; Cros, V. Magnetic skyrmions: Advances in physics and potential applications. Nat. Rev. Mater. 2017, 2, 17031. [Google Scholar] [CrossRef]
- Jiang, S.; Chung, S.; Ahlberg, M.; Frisk, A.; Khymyn, R.; Le, Q.T.; Mazraati, H.; Houshang, A.; Heinonen, O.; Åkerman, J. Magnetic droplet soliton pairs. Nat. Commun. 2024, 15, 2118. [Google Scholar] [CrossRef]
- Garcia-Sanchez, F.; Sampaio, J.; Reyren, N.; Cros, V.; Kim, J. A skyrmion-based spin-torque nano-oscillator. New J. Phys. 2016, 18, 075011. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, G.; Liu, K.; Zang, J.; Te Velthuis, S.G.; Hoffmann, A. Skyrmions in magnetic multilayers. Phys. Rep. 2017, 704, 1–49. [Google Scholar] [CrossRef]
- Deng, Z.L.; Shi, T.; Krasnok, A.; Li, X.; Alù, A. Observation of localized magnetic plasmon skyrmions. Nat. Commun. 2022, 13, 8. [Google Scholar] [CrossRef] [PubMed]
- Kosevich, A.M.; Ivanov, B.; Kovalev, A.S. Magnetic solitons. Phys. Rep. 1990, 194, 117–238. [Google Scholar] [CrossRef]
- Mohseni, S.M.; Sani, S.; Persson, J.; Nguyen, T.A.; Chung, S.; Pogoryelov, Y.; Muduli, P.; Iacocca, E.; Eklund, A.; Dumas, R.; et al. Spin torque–generated magnetic droplet solitons. Science 2013, 339, 1295–1298. [Google Scholar] [CrossRef]
- Roessli, B.; Schefer, J.; Petrakovskii, G.; Ouladdiaf, B.; Boehm, M.; Staub, U.; Vorotinov, A.; Bezmaternikh, L. Formation of a magnetic soliton lattice in copper metaborate. Phys. Rev. Lett. 2001, 86, 1885. [Google Scholar] [CrossRef]
- Rothos, V.; Mylonas, I.; Bountis, T. Dissipative soliton dynamics of the Landau–Lifshitz–Gilbert equation. Theor. Math. Phys. 2023, 215, 622–635. [Google Scholar] [CrossRef]
- Clerc, M.G.; Coulibaly, S.; Laroze, D. Localized states beyond the asymptotic parametrically driven amplitude equation. Phys. Rev. E 2008, 77, 056209. [Google Scholar] [CrossRef]
- Clerc, M.G.; Coulibaly, S.; Laroze, D. Nonvariational Ising-Bloch Transition in Parametrically Driven Systems. Int. J. Bifurc. Chaos 2009, 19, 2717–2726. [Google Scholar] [CrossRef]
- Clerc, M.G.; Coulibaly, S.; Laroze, D. Localized states and non-variational Ising–Bloch transition of a parametrically driven easy-plane ferromagnetic wire. Physica D Nonlinear Phenom. 2010, 239, 72–86. [Google Scholar] [CrossRef]
- Urzagasti, D.; Laroze, D.; Clerc, M.G.; Pleiner, H. Breather soliton solutions in a parametrically driven magnetic wire. Europhys. Lett. 2013, 104, 40001. [Google Scholar] [CrossRef][Green Version]
- Aharoni, A. Introduction to the Theory of Ferromagnetism; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Laroze, D.; Bragard, J.; Suarez, O.J.; Pleiner, H. Characterization of the Chaotic Magnetic Particle Dynamics. IEEE Trans. Magn. 2011, 47, 3032–3035. [Google Scholar] [CrossRef]
- Laroze, D.; Becerra-Alonso, D.; Gallas, J.A.C.; Pleiner, H. Magnetization Dynamics Under a Quasiperiodic Magnetic Field. IEEE Trans. Magn. 2012, 48, 3567–3570. [Google Scholar] [CrossRef]
- Kibler, B.; Chabchoub, A.; Bailung, H. Peregrine Soliton and Breathers in Wave Physics: Achievements and Perspectives; Frontiers Research Topics; Frontiers Media SA: Lausanne, Switzerland, 2022. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in FORTRAN; The Art of Scientific Computing; Cambridge University Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Urzagasti, D.; Aramayo, A.; Laroze, D. Soliton–antisoliton interaction in a parametrically driven easy-plane magnetic wire. Phys. Lett. A 2014, 378, 2614–2618. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Sano, M.; Sawada, Y. Measurement of the Lyapunov spectrum from a chaotic time series. Phys. Rev. Lett. 1985, 55, 1082. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Sriram, M. A comparative study of computation of Lyapunov spectra with different algorithms. Physica D Nonlinear Phenom. 2000, 139, 72–86. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Geist, K.; Parlitz, U.; Lauterborn, W. Comparison of different methods for computing Lyapunov exponents. Prog. Theor. Phys. 1990, 83, 875–893. [Google Scholar] [CrossRef]
- Pati, N. Spiral organization of quasi-periodic shrimp-shaped domains in a discrete predator–prey system. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 083126. [Google Scholar] [CrossRef]
- Mazanik, A.; Botha, A.; Rahmonov, I.; Shukrinov, Y.M. Hysteresis and chaos in anomalous Josephson junctions without capacitance. Phys. Rev. Appl. 2024, 22, 014062. [Google Scholar] [CrossRef]
- Bazzani, A.; Giovannozzi, M.; Montanari, C.; Turchetti, G. Performance analysis of indicators of chaos for nonlinear dynamical systems. Phys. Rev. E 2023, 107, 064209. [Google Scholar] [CrossRef] [PubMed]
- Field, R.J.; Freire, J.G.; Gallas, J.A. Quint points lattice in a driven Belousov–Zhabotinsky reaction model. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 053124. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, Y. Multiple tori intermittency routes to strange nonchaotic attractors in a quasiperiodically-forced piecewise smooth system. Nonlinear Dyn. 2024, 112, 6329–6338. [Google Scholar] [CrossRef]
- Nieto, A.R.; Zotos, E.E.; Seoane, J.M.; Sanjuán, M.A.F. Measuring the transition between nonhyperbolic and hyperbolic regimes in open Hamiltonian systems. Nonlinear Dyn. 2020, 99, 3029–3039. [Google Scholar] [CrossRef]
- Bernal, J.D.; Seoane, J.M.; Vallejo, J.C.; Huang, L.; Sanjuán, M.A.F. Influence of the gravitational radius on asymptotic behavior of the relativistic Sitnikov problem. Phys. Rev. E 2020, 102, 042204. [Google Scholar] [CrossRef]
- Daza, A.; Wagemakers, A.; Sanjuán, M.A.F. Unpredictability and basin entropy. Europhys. Lett. 2023, 141, 43001. [Google Scholar] [CrossRef]
- Yin, X.; Xu, L.; Yang, L. Evolution and interaction of soliton solutions of Rossby waves in geophysical fluid mechanics. Nonlinear Dyn. 2023, 111, 12433–12445. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, C.J.; Ortega-Piwonka, I.; Malomed, B.A.; Urzagasti, D.; Pedraja-Rejas, L.; Díaz, P.; Laroze, D. Breather Bound States in a Parametrically Driven Magnetic Wire. Symmetry 2024, 16, 1565. https://doi.org/10.3390/sym16121565
Castro CJ, Ortega-Piwonka I, Malomed BA, Urzagasti D, Pedraja-Rejas L, Díaz P, Laroze D. Breather Bound States in a Parametrically Driven Magnetic Wire. Symmetry. 2024; 16(12):1565. https://doi.org/10.3390/sym16121565
Chicago/Turabian StyleCastro, Camilo José, Ignacio Ortega-Piwonka, Boris A. Malomed, Deterlino Urzagasti, Liliana Pedraja-Rejas, Pablo Díaz, and David Laroze. 2024. "Breather Bound States in a Parametrically Driven Magnetic Wire" Symmetry 16, no. 12: 1565. https://doi.org/10.3390/sym16121565
APA StyleCastro, C. J., Ortega-Piwonka, I., Malomed, B. A., Urzagasti, D., Pedraja-Rejas, L., Díaz, P., & Laroze, D. (2024). Breather Bound States in a Parametrically Driven Magnetic Wire. Symmetry, 16(12), 1565. https://doi.org/10.3390/sym16121565





