The Application of Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings
Abstract
1. Introduction
- (1)
- If , then is called nonexpansive mapping. Let denote the fixed point set of .
- (2)
- If , , then is called contractive mapping.
- (1)
- If there exists such that , then is called accretive operator.
- (2)
- For any , if , then is called m-accretive operator.
- (3)
- For any , if , then is called the resolvent of m-accretive operator .
2. Preliminaries
3. Results
- (i)
- ;
- (ii)
- , , ;
- (iii)
- , .
- Step 1: Show the boundedness of and .
- Step 2: Show that .
- Step 3: Show that .
- Step 4: Show that .
- Step 5: Show that .
- Step 6: Show that .
- Step 7: Show that .
- Step 8: Show that .
- Step 9: Show that .
- Step 10: Show that .
- Step 11: Show that .
- (i)
- ;
- (ii)
- ,,;
- (iii)
- ,;
- (iv)
- .
- (i)
- ;
- (ii)
- , , ;
- (iii)
- , ;
- (iv)
- .
- Step 1: Show the boundedness of and .
- Step 2: Show that .
- Step 3: Show that .
- Step 4: Show that .
- Step 5: Show that .
- Step 6: Show that .
- Step 7: Show that .
- Step 8: Show that .
- Step 9: Show that .
- Step 10: Show that .
- Step 11: Show that .
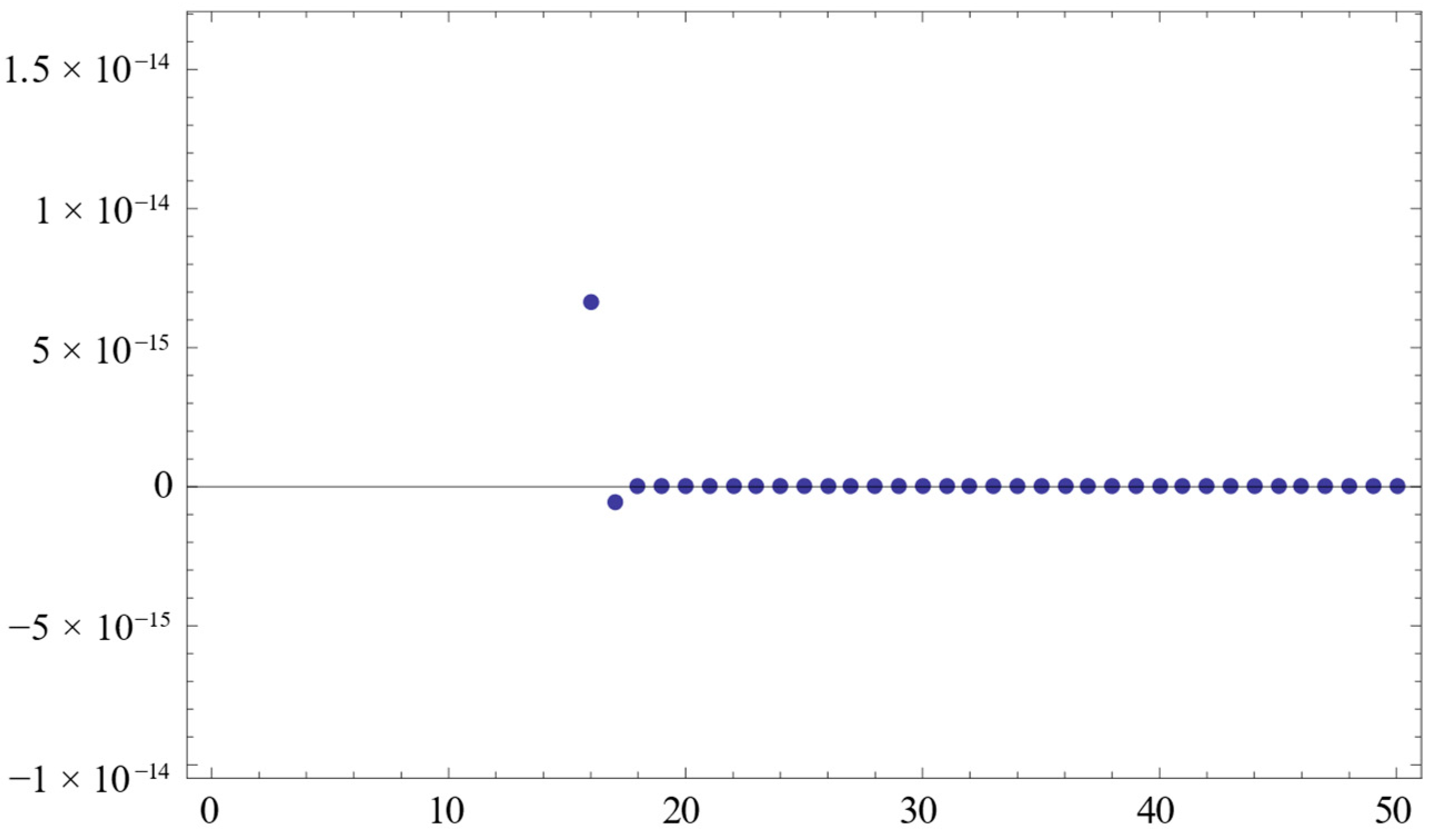
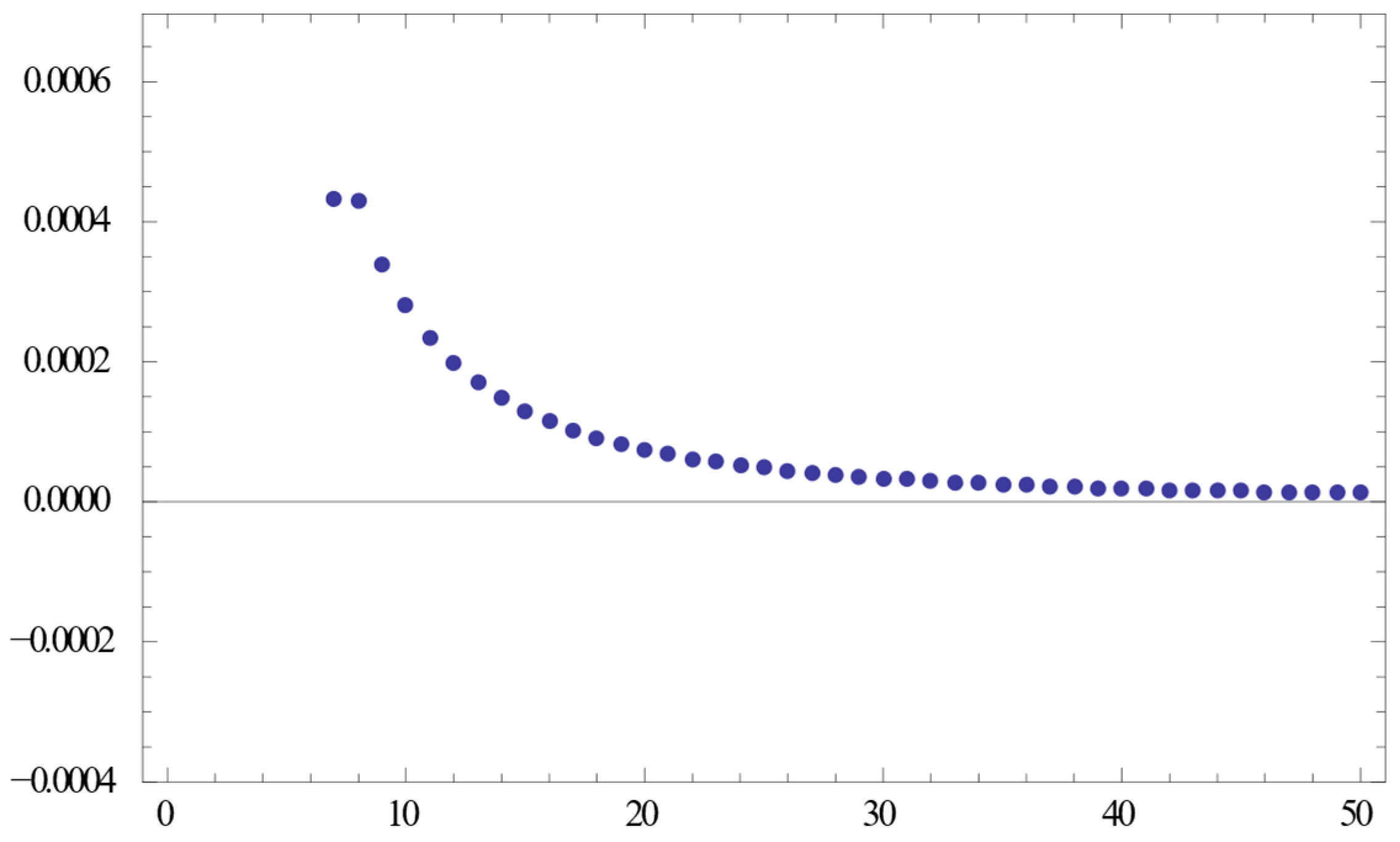
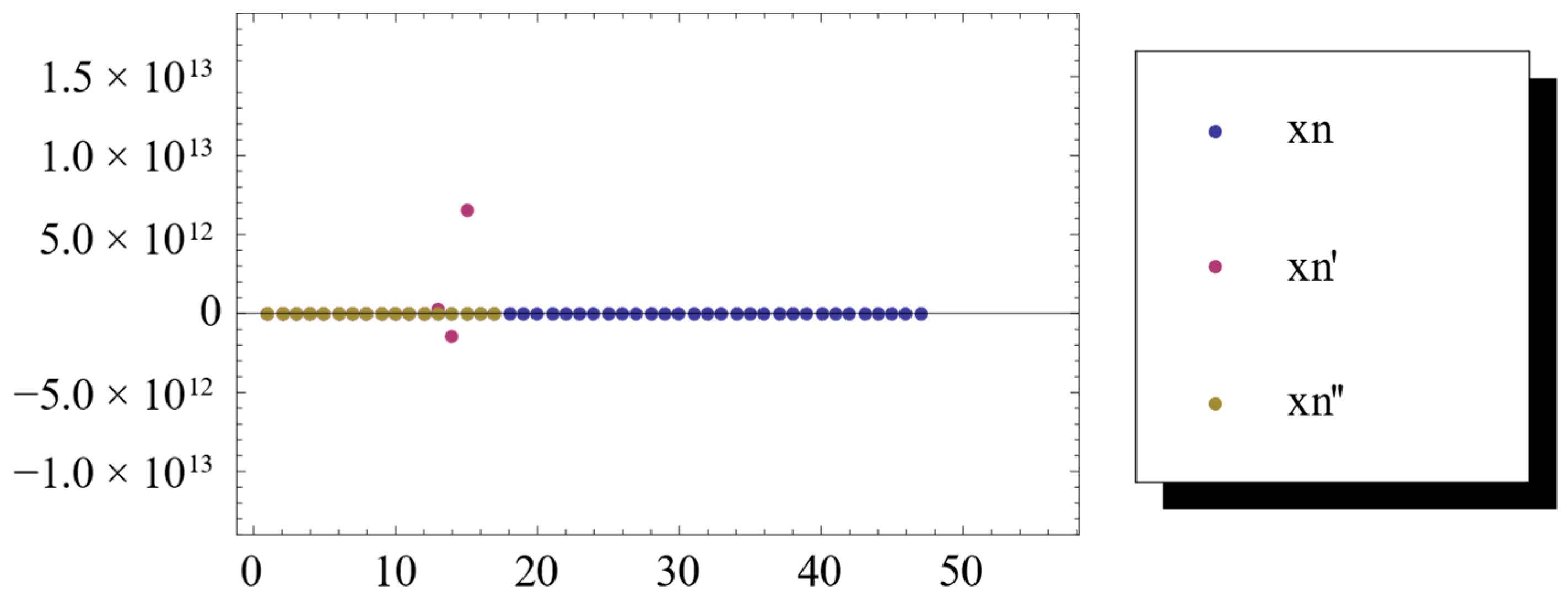
4. Numerical Examples
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, S.S.; Lee, H.W.J.; Chan, C.K. Strong convergence theorems by viscosity approximation methods for accretive mappings and nonexpansive mappings. J. Appl. Math. Inform. 2009, 27, 59–68. [Google Scholar]
- Jung, J.S.; Cho, Y.J.; Zhou, H.Y. Iterative processes with mixed errors for nonlinear equations with perturbed m-accretive operators in Banach spaces. Appl. Math. Comput. 2002, 133, 389–406. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation methods for fixed points problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Qin, X.L.; Cho, S.Y.; Wang, L. Iterative algorithms with errors for zero points of m-accretive Operators. Fixed Point Theory Appl. 2013, 2013, 148. [Google Scholar] [CrossRef]
- Reich, S. Approximating zeros of accretive operators. Proc. Am. Math. Soc. 1975, 51, 381–384. [Google Scholar] [CrossRef]
- Reich, S. On fixed point theorems obtained from existence theorems for differential equations. J. Math. Anal. Appl. 1976, 54, 26–36. [Google Scholar] [CrossRef]
- Auzinger, W.; Frank, R. Asymptotic error expansions for stiff equations: An analysis for the implicit midpoint and trapezoidal rules in the strongly stiff case. Numer. Math. 1989, 56, 469–499. [Google Scholar] [CrossRef]
- Bader, G.; Deuflhard, P. A semi-implicit mid-point rule for stiff systems of ordinary differential equations. Numer. Math. 1983, 41, 373–398. [Google Scholar] [CrossRef]
- Deuflhard, P. Recent progress in extrapolation methods for ordinary differential equations. SIAM Rev. 1985, 27, 505–535. [Google Scholar] [CrossRef]
- Schneider, C. Analysis of the linearly implicit mid-point rule for differential-algebra equations. Electron. Trans. Numer. Anal. 1993, 1, 1–10. [Google Scholar]
- Somalia, S. Implicit midpoint rule to the nonlinear degenerate boundary value problems. Int. J. Comput. Math. 2002, 79, 327–332. [Google Scholar] [CrossRef]
- Van Veldhuxzen, M. Asymptotic expansions of the global error for the implicit midpoint rule (stiff case). Computing 1984, 33, 185–192. [Google Scholar] [CrossRef]
- Hammad, H.A.; ur Rehman, H.; De la Sen, M. Accelerated modified inertial Mann and viscosity algorithms to find a fixed point of α—Inverse strongly monotone operators. AIMS Math. 2021, 6, 9000–9019. [Google Scholar] [CrossRef]
- Hammad, H.A.; ur Rehman, H.; Kattan, D.A. Strong convergence for split variational inclusion problems under hybrid algorithms with applications. Alex. Eng. J. 2024, 87, 350–364. [Google Scholar] [CrossRef]
- Jung, J.S. Strong convergence of an iterative algorithm for accretive operators and nonexpansive mappings. J. Nonlinear Sci. Appl. 2016, 9, 2394–2409. [Google Scholar] [CrossRef]
- Li, D.F. On nonexpansive and accretive operators in Banach spaces. J. Nonlinear Sci. Appl. 2017, 10, 3437–3446. [Google Scholar] [CrossRef]
- Xu, H.K.; Alghamdi, M.A.; Shahzad, N. The viscosity technique for the implicit midpoint rule of nonexpansive mappings in Hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Luo, P.; Cai, G.; Shehu, Y. The viscosity iterative algorithms for the implicit midpoint rule of nonexpansive mappings in uniformly smooth Banach spaces. J. Inequal. Appl. 2017, 2017, 154. [Google Scholar] [CrossRef] [PubMed]
- Ke, Y.F.; Ma, C.F. The generalized viscosity implicit rules of nonexpansive mappings in Hilbert spaces. Fixed Point Theory Appl. 2015, 2015, 190. [Google Scholar] [CrossRef]
- Zhang, H.C.; Qu, Y.H.; Su, Y.F. Strong convergence theorems for fixed point problems for nonexpansive mappings and zero point problems for accretive operators using viscosity implicit midpoint rules in Banach spaces. Mathematics 2018, 6, 257. [Google Scholar] [CrossRef]
- Zhang, H.C.; Qu, Y.H.; Su, Y.F. The generalized viscosity implicit midpoint rule for nonexpansive mappings in Banach space. Mathematics 2019, 7, 512. [Google Scholar] [CrossRef]
- Filali, D.; Ali, F.; Akram, M.; Dilshad, M. A Novel Fixed-Point Iteration Approach for Solving Troesch’s Problem. Symmetry 2024, 16, 856. [Google Scholar] [CrossRef]
- Reich, S. On the asymptotic behavior of nonlinear semigroups and the range of accretive operators. J. Math. Anal. Appl. 1981, 79, 113–126. [Google Scholar] [CrossRef]
- Barbu, V. Nonlinear Semigroups and Differential Equations in Banach Spaces; Editura Academiei Republicii Socialiste Romania; Springer: Dordrecht, The Netherlands, 1976; Volume 2, pp. 1–6. [Google Scholar]
- Liu, L.S. Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 1995, 194, 114–125. [Google Scholar] [CrossRef]
- Reich, S. Strong convergence theorems for resolvents of accretive operators in Banach spaces. J. Math. Anal. Appl. 1980, 75, 287–292. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H. The Application of Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings. Symmetry 2024, 16, 1528. https://doi.org/10.3390/sym16111528
Zhang H. The Application of Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings. Symmetry. 2024; 16(11):1528. https://doi.org/10.3390/sym16111528
Chicago/Turabian StyleZhang, Huancheng. 2024. "The Application of Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings" Symmetry 16, no. 11: 1528. https://doi.org/10.3390/sym16111528
APA StyleZhang, H. (2024). The Application of Generalized Viscosity Implicit Midpoint Rule for Nonexpansive Mappings. Symmetry, 16(11), 1528. https://doi.org/10.3390/sym16111528





