Quantitative Analysis of Magnetic Force of Axial Symmetry Permanent Magnet Structure Using Hybrid Boundary Element Method
Abstract
1. Introduction
2. Methodology
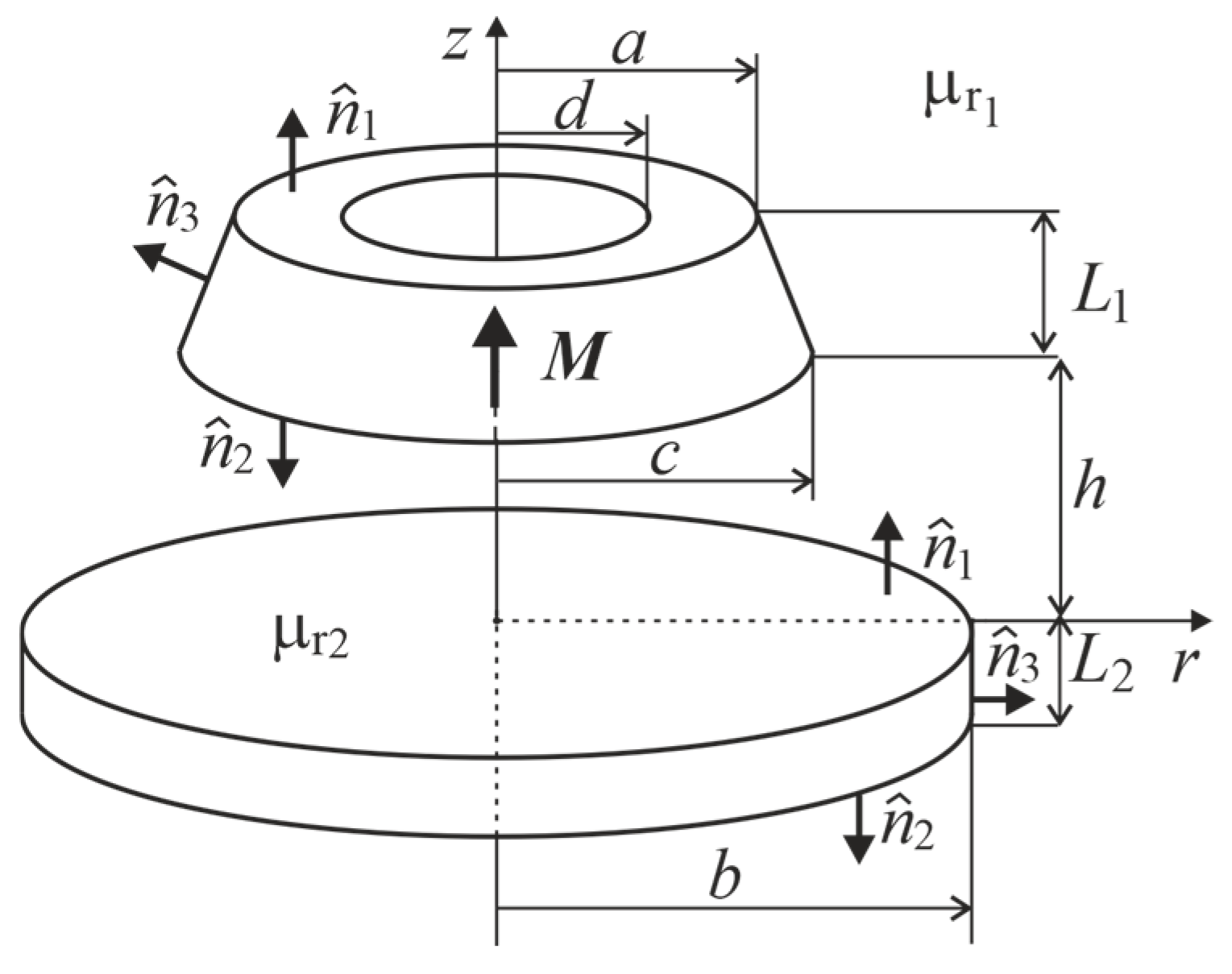
2.1. Problem Statement
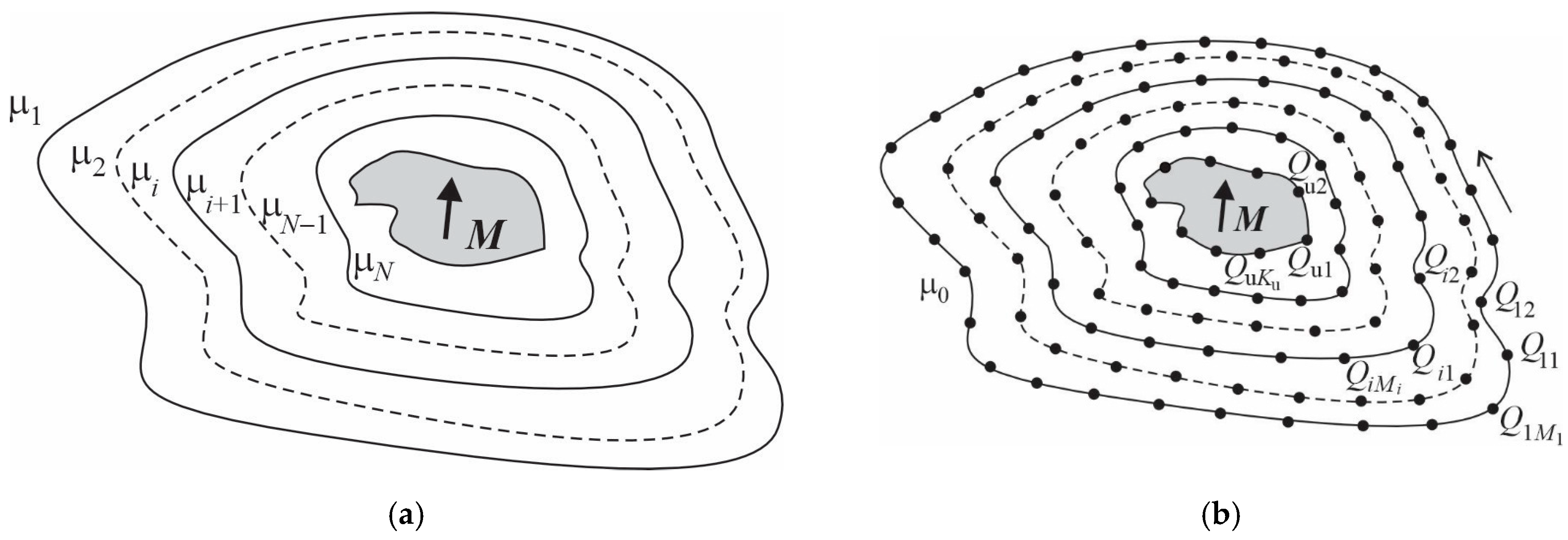
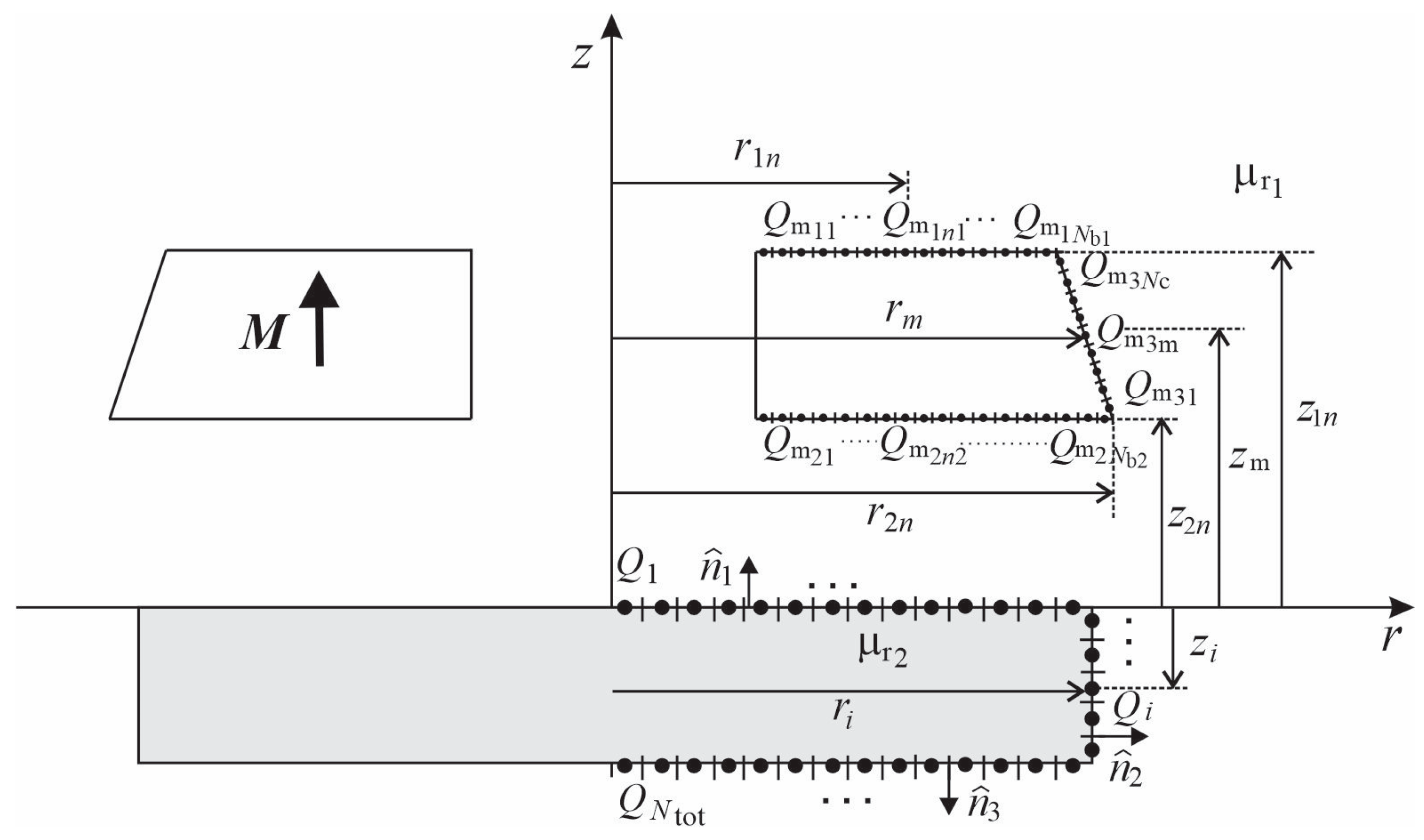
2.2. Determination of Magnetic Charges
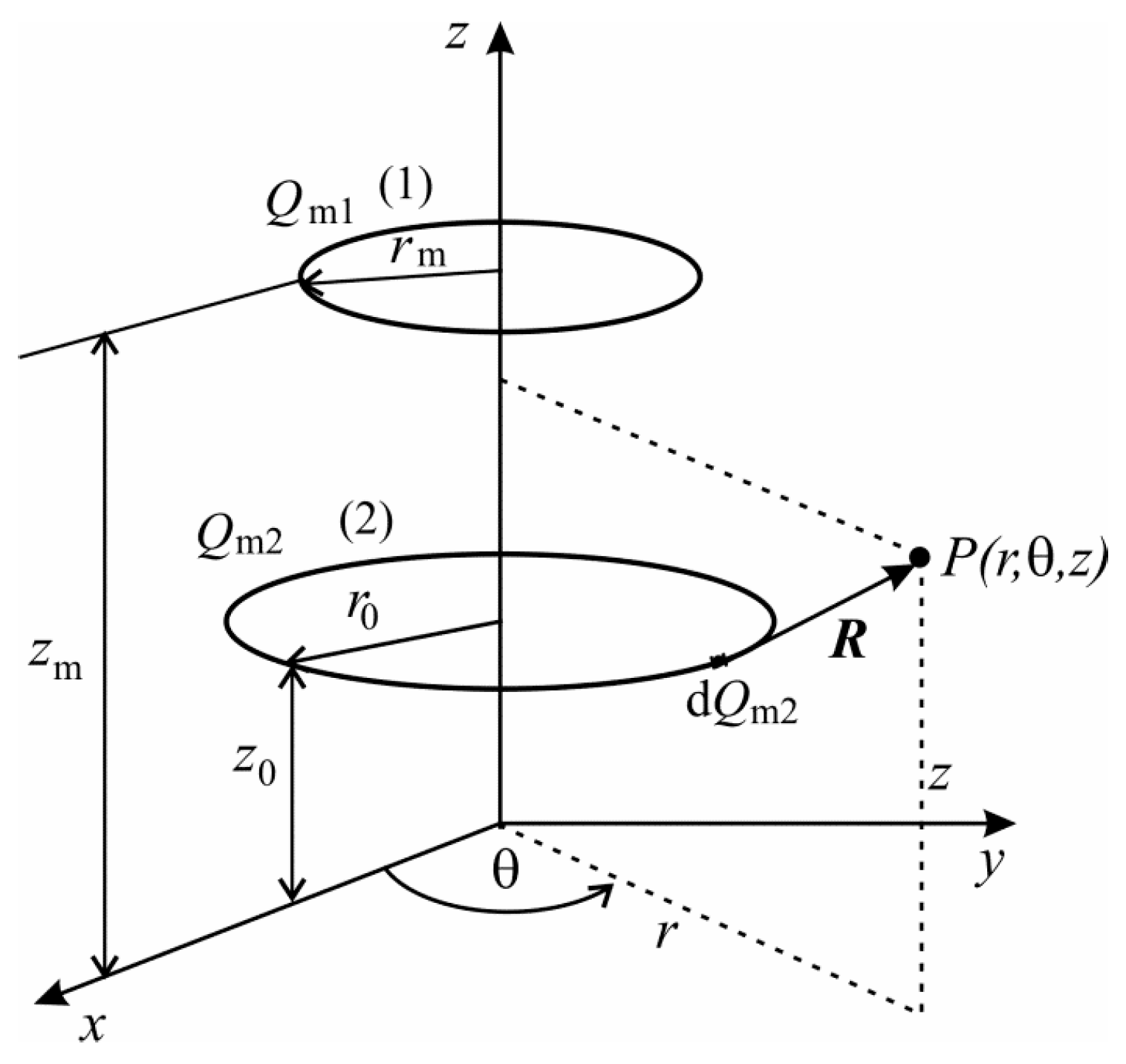
2.3. Force Calculation
3. Numerical Results
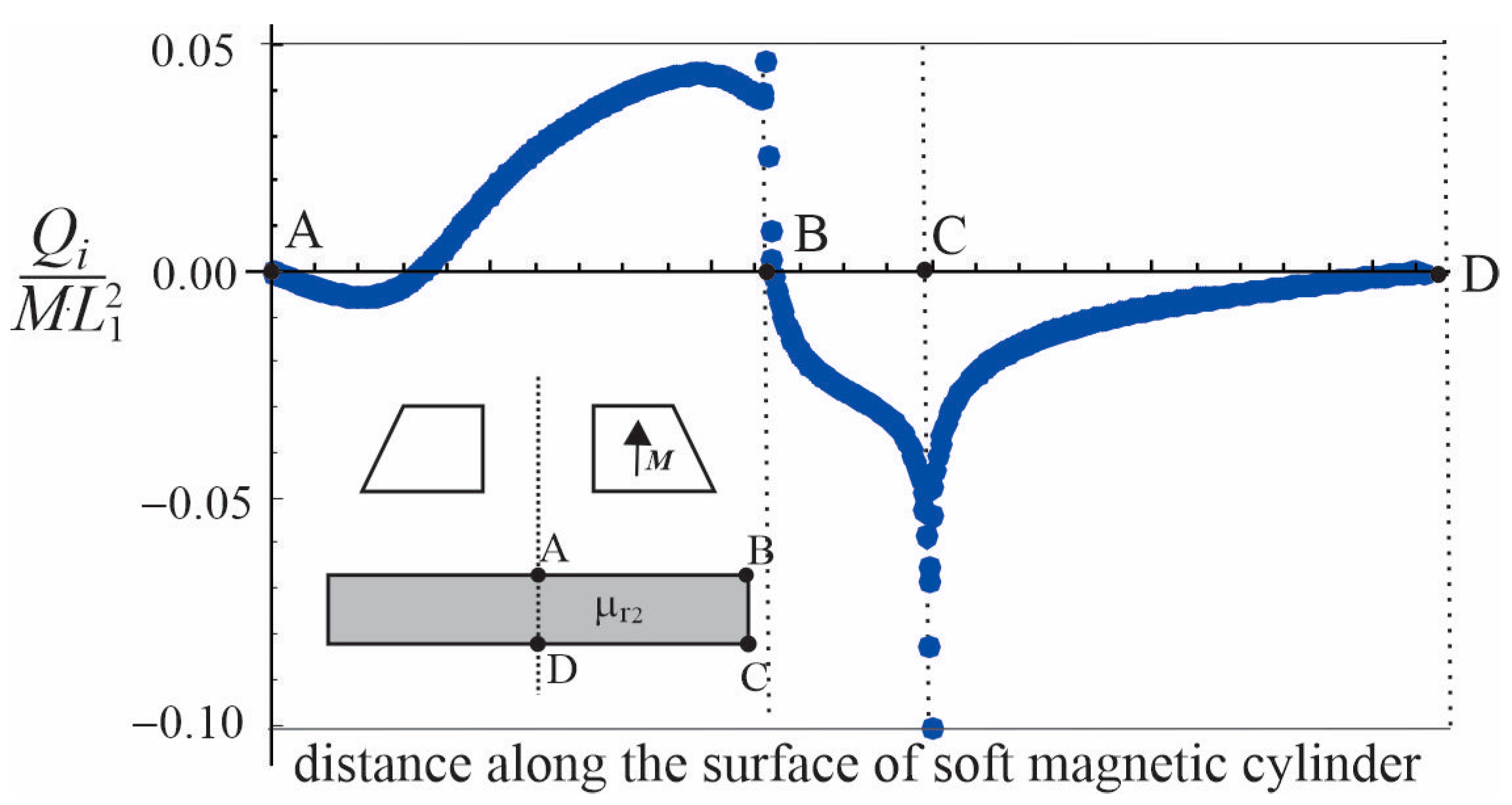
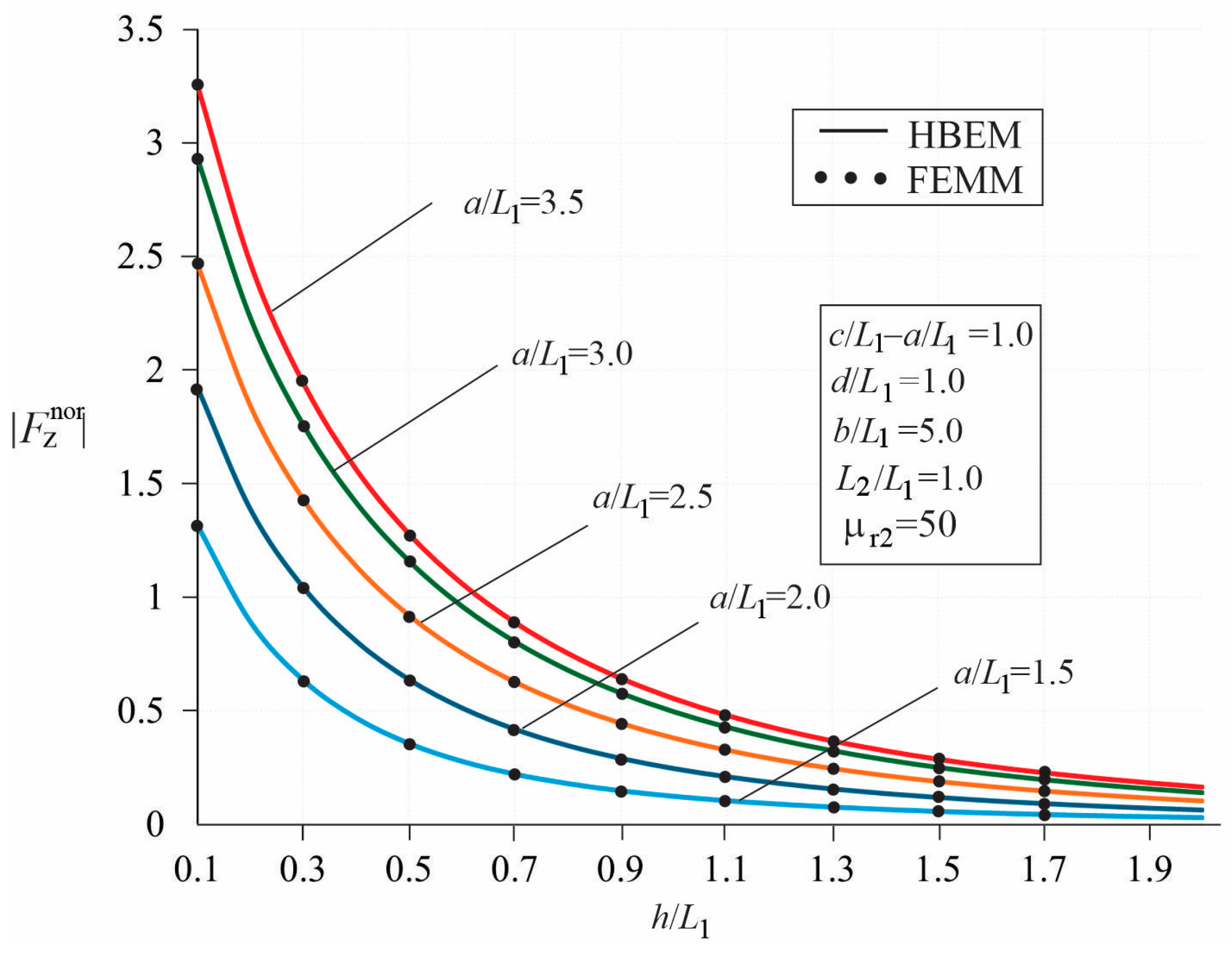
3.1. Comparison with FEMM
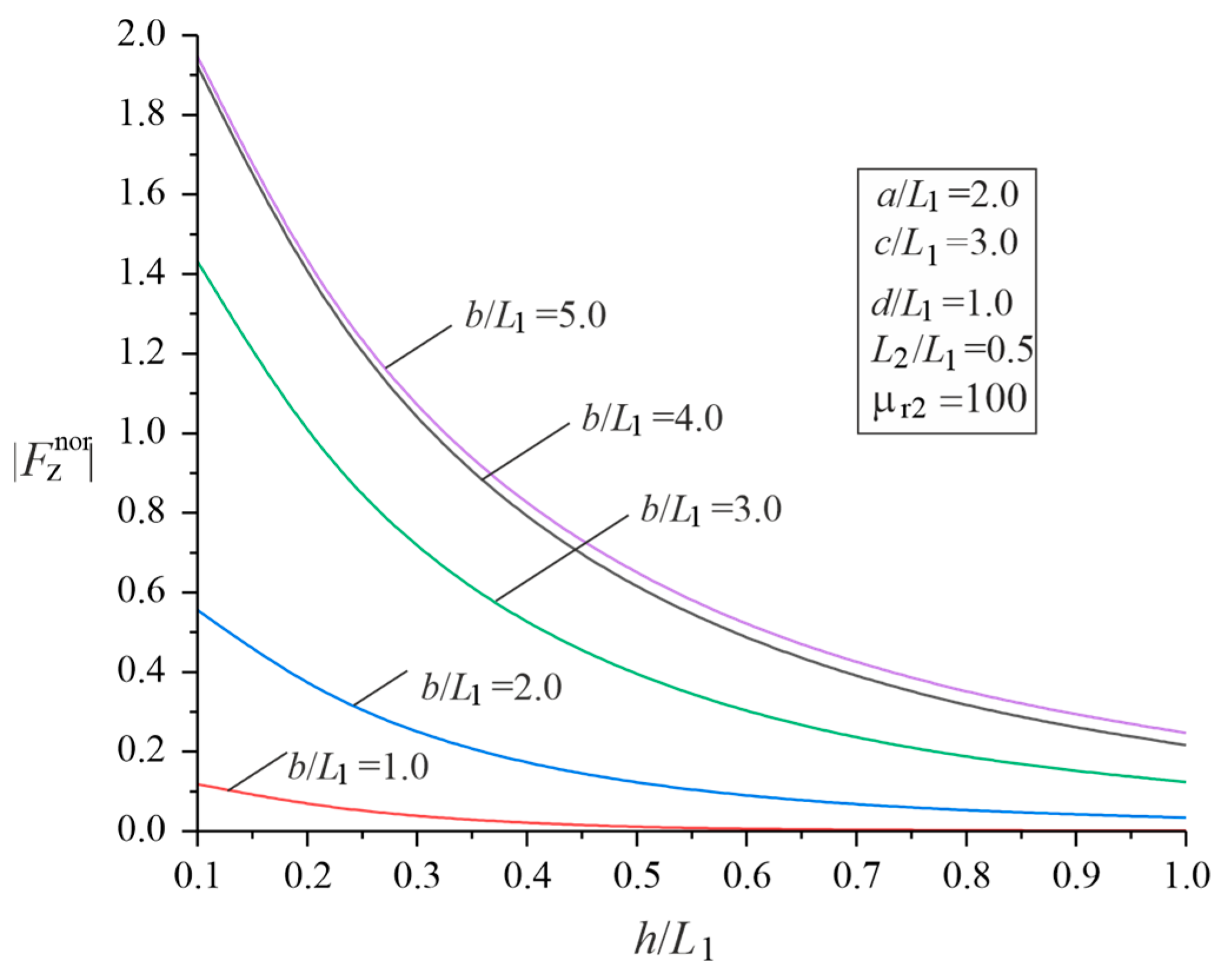
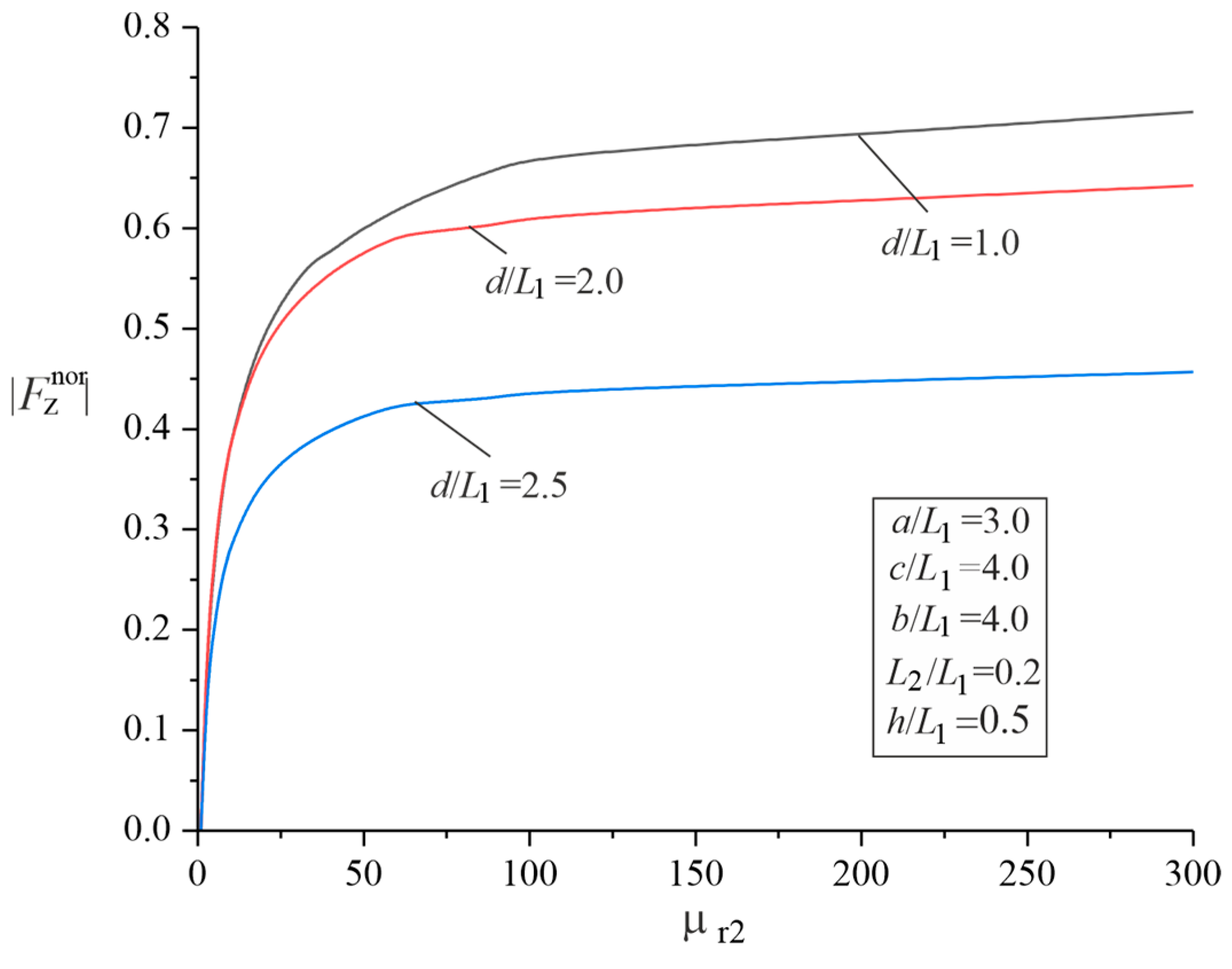
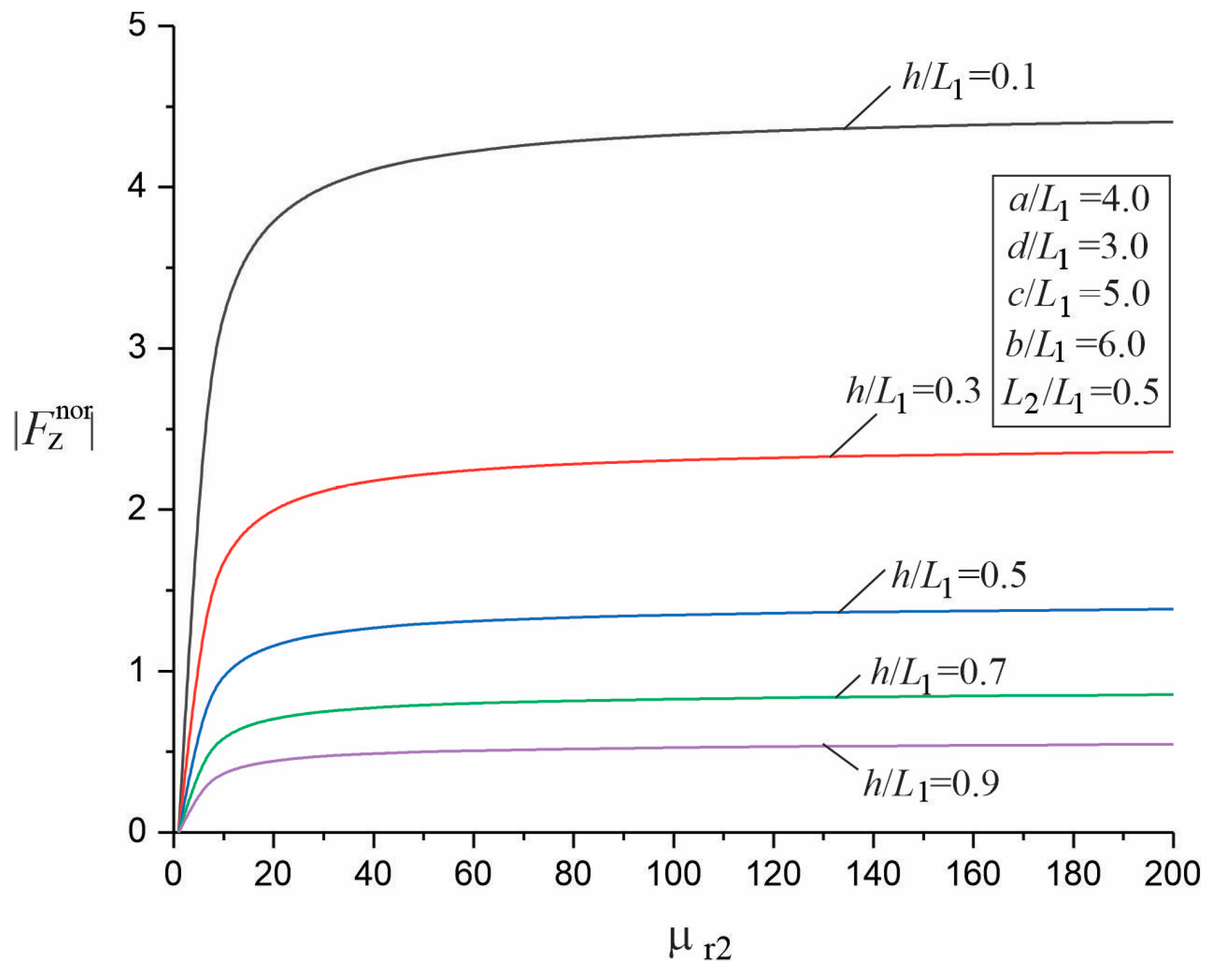
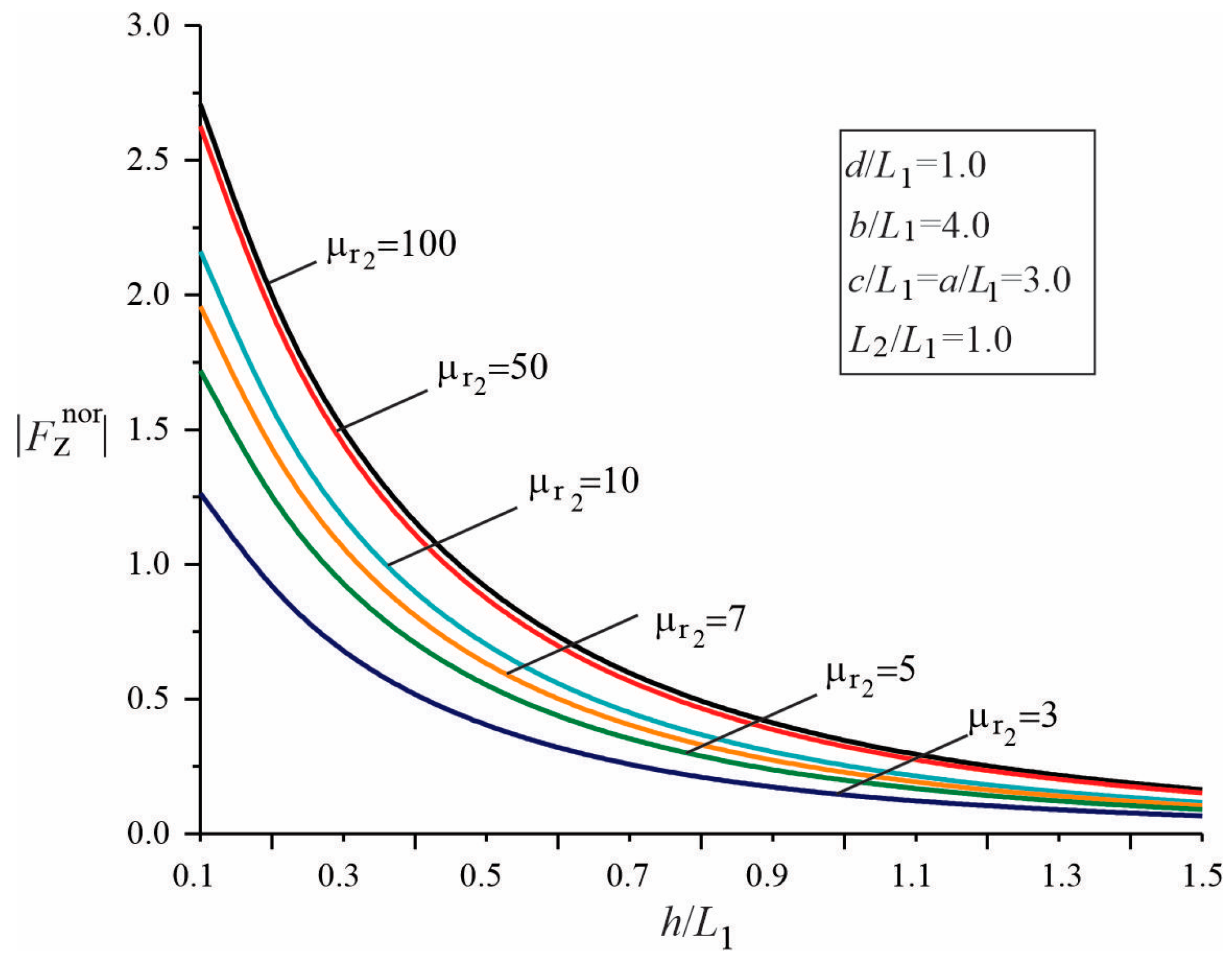
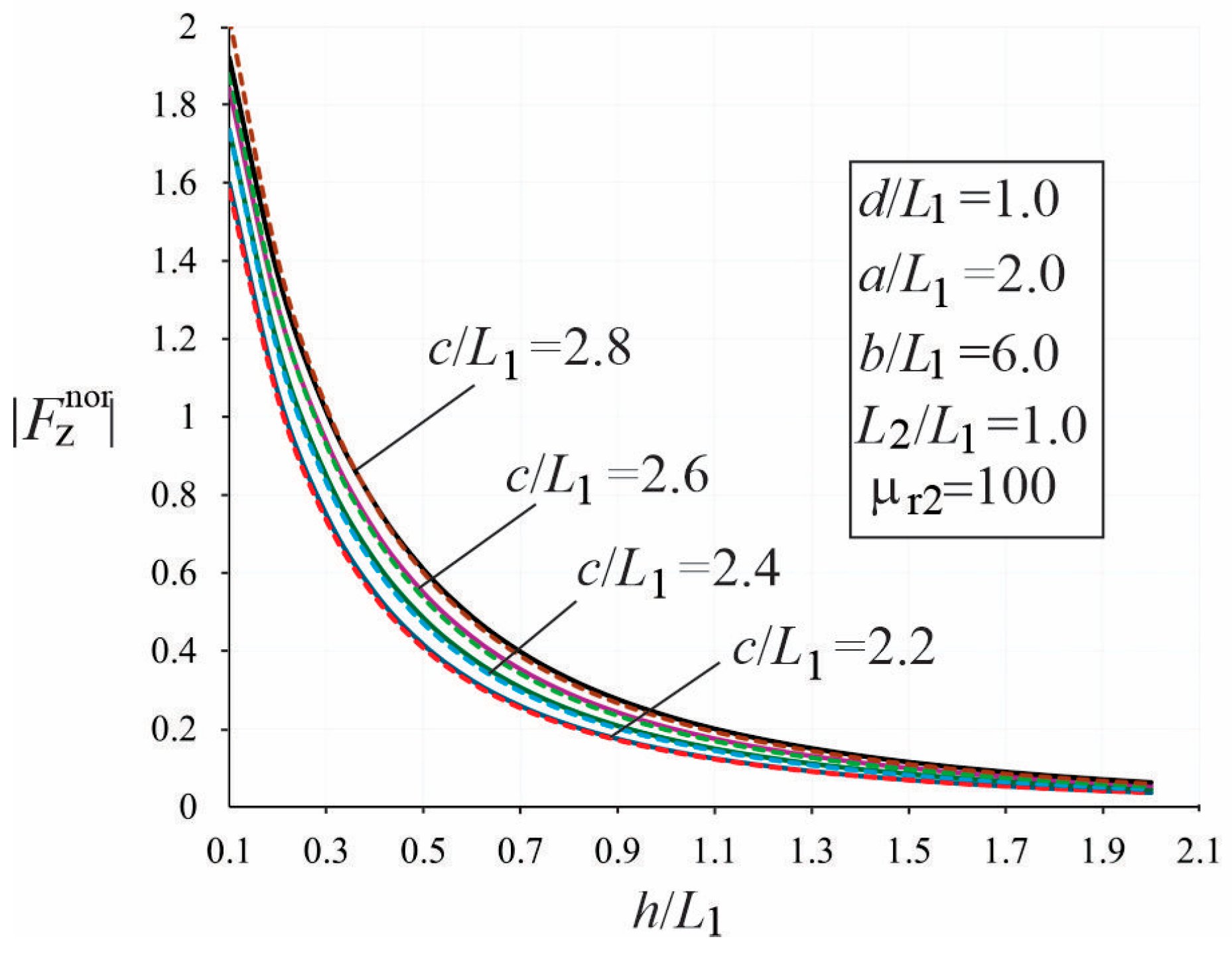
3.2. Parametric Studies of the Force
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cavallaro, S.P.; Venturini, S.; Bonisoli, E. Nonlinear dynamics of a horizontal rotor with asymmetric magnetic supports. Int. J. Non-Linear Mech. 2024, 165, 104764. [Google Scholar] [CrossRef]
- Bernad, S.I.; Bernad, E. Magnetic Forces by Permanent Magnets to Manipulate Magnetoresponsive Particles in Drug-Targeting Applications. Micromachines 2022, 13, 1818. [Google Scholar] [CrossRef] [PubMed]
- Nemoianu, I.V.; Dragomirescu, C.G.; Manescu, V.; Dascalu, M.I.; Paltanea, G.; Ciuceanu, R.M. Self-Organizing equilibrium patterns of multiple permanent magnets floating freely under the action of a central attractive magnetic force. Symmetry 2022, 14, 795. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Jiao, S.; Zhang, X.; Li, M. Optimization design and parameter analysis of a wheel with array magnets. Symmetry 2023, 15, 962. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V. Force and stiffness of passive magnetic bearings using permanent magnets. Part 1: Axial magnetization. IEEE Trans. Magn. 2009, 45, 2996–3002. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V. Force and stiffness of passive magnetic bearings using permanent magnets. Part 2: Radial magnetization. IEEE Trans. Magn. 2009, 45, 3334–3342. [Google Scholar] [CrossRef]
- Earnshaw, S. On the nature of the molecular forces which regulate the constitution of the luminiferous ether. Trans. Camb. Philos. Soc. 1842, 7, 97–112. [Google Scholar]
- Vučković, A.N.; Raičević, N.B.; Ilić, S.S.; Aleksić, S.R. Interaction magnetic force calculation of radial passive magnetic bearing using magnetization charges and discretization technique. Int. J. Appl. Electromagn. Mech. 2013, 43, 311–323. [Google Scholar] [CrossRef]
- Robertson, W.S.; Cazzolato, B.S.; Zander, A.C. A Simplified force equation for coaxial cylindrical magnets and thin coils. IEEE Trans. Magn. 2011, 47, 2045–2049. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, G.; Gong, K.; Li, Y. The numeric calculation for cylindrical magnet’s magnetic flux intensity. Int. J. Appl. Electromagn. Mech. 2012, 40, 227–235. [Google Scholar] [CrossRef]
- Rakotoarison, H.L.; Yonnet, J.P.; Delinchant, B. Using Coulombian approach for modeling scalar potential and magnetic field of a permanent magnet with radial polarization. IEEE Trans. Magn. 2007, 43, 1261–1264. [Google Scholar] [CrossRef]
- Vučković, A.N.; Ilić, S.S.; Aleksić, S.R. Interaction magnetic force calculation of ring permanent magnets using Ampere’s microscopic surface currents and discretization technique. Electromagnetics 2012, 32, 117–134. [Google Scholar] [CrossRef]
- Beleggia, M.; Vokoun, D.; Graef, M.D. Forces between a permanent magnet and a soft magnetic plate. IEEE Magn. Lett. 2012, 3, 0500204. [Google Scholar] [CrossRef]
- Akoun, G.; Yonnet, J.P. 3D analytical calculation of the forces exerted between two cuboidal magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar] [CrossRef]
- Furlani, E.P.; Reznik, S.; Kroll, A. A three-dimensional field solution for radially polarized cylinders. IEEE Trans. Magn. 1995, 31, 844–851. [Google Scholar] [CrossRef]
- Vučković, A.N.; Perić, M.T.; Ilić, S.S.; Raičević, N.B.; Vučković, D.M. Interaction magnetic force of cuboidal permanent magnet and soft magnetic bar using hybrid boundary element method. ACES J. 2021, 36, 1492–1498. [Google Scholar] [CrossRef]
- Hart, S.; Hart, K.; Selvaggi, J.P. Analytical expressions for the magnetic field from axially magnetized and conically shaped permanent magnets. IEEE Trans. Magn. 2020, 56, 7. [Google Scholar] [CrossRef]
- O’Connell, J.L.G.; Robertson, W.S.P.; Cazzolato, B.S. Analytic magnetic fields and semi-analytic forces and torques due to general polyhedral permanent magnets. IEEE Trans. Magn. 2020, 56, 7400208. [Google Scholar] [CrossRef]
- Vučković, A.; Vučković, D.; Perić, M.; Raičević, N. Magnetic force calculation between truncated cone-shaped permanent magnet and soft magnetic cylinder using hybrid boundary element method. In Stochastic Processes, Statistical Methods, and Engineering Mathematics; Springer Proceedings in Mathematics & Statistics; Springer International Publishing: Cham, Switzerland, 2022; Chapter 32; pp. 719–733. ISSN 2194-1009. ISBN 978-3-031-17819-1. [Google Scholar]
- Raičević, N.B.; Aleksić, S.R.; Ilić, S.S. A hybrid boundary element method for multilayer electrostatic and magnetostatic problems. Electromagnetics 2010, 30, 507–524. [Google Scholar] [CrossRef]
- Perić, M.T.; Ilić, S.S.; Aleksić, S.R.; Raičević, N.B. Characteristic parameters determination of different striplines configurations using HBEM. ACES J. 2013, 28, 858–865. [Google Scholar]
- Vučković, A.; Vučković, D.; Perić, M.; Raičević, N. Influence of the magnetization vector misalignment on the magnetic force of permanent ring magnet and soft magnetic cylinder. Int. J. Appl. Electromagn. Mech. 2021, 26, 417–430. [Google Scholar] [CrossRef]
- Vučković, A.N.; Raičević, N.B.; Perić, M.T. Radially magnetized ring permanent magnet modelling in the vicinity of soft magnetic cylinder. Saf. Eng. 2018, 8, 33–37. [Google Scholar] [CrossRef]
- Raičević, N.B.; Ilić, S.S.; Aleksić, S.R. Application of new hybrid boundary element method on the cable terminations. In Proceedings of the 14th International IGTE’10 Symposium, Graz, Austria, 20–22 September 2010; pp. 56–61. [Google Scholar]
- Perić, M.T.; Ilić, S.S.; Aleksić, S.R.; Raičević, N.B. Application of Hybrid boundary element method to 2D microstrip lines analysis. Int. J. Appl. Electromagn. Mech. 2013, 42, 179–190. [Google Scholar] [CrossRef]
- Ilić, S.S.; Raičević, N.B.; Aleksić, S.R. Application of new hybrid boundary element method on grounding systems. In Proceedings of the 14th International IGTE’10 Symposium, Graz, Austria, 20–22 September 2010; pp. 160–165. [Google Scholar]
- Raičević, N.B.; Ilić, S.S. One hybrid method application on complex media strip lines determination. In Proceedings of the 3rd International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Metamaterials, London, UK, 30 August–4 September 2009; pp. 698–700. [Google Scholar]
- Rovers, J.M.M.; Jansen, J.W.; Lomonova, E.A. Modeling of relative permeability of permanent magnet material using magnetic surface charges. IEEE Trans. Magn. 2013, 49, 2913–2919. [Google Scholar] [CrossRef]
- Meeker, Software Package FEMM 4.2. Available online: http://www.femm.info/wiki/Download (accessed on 2 March 2007).



| NS | 50 | 100 | 200 | 300 | 400 | 500 | 600 | |
|---|---|---|---|---|---|---|---|---|
| N | ||||||||
| 50 | 0.2982 | 0.2980 | 0.2979 | 0.2979 | 0.2979 | 0.2979 | 0.2979 | |
| 100 | 0.2977 | 0.2974 | 0.2973 | 0.2973 | 0.2973 | 0.2973 | 0.2973 | |
| 200 | 0.2973 | 0.2970 | 0.2969 | 0.2969 | 0.2969 | 0.2969 | 0.2969 | |
| 300 | 0.2971 | 0.2968 | 0.2968 | 0.2968 | 0.2967 | 0.2967 | 0.2967 | |
| 400 | 0.2970 | 0.2967 | 0.2967 | 0.2967 | 0.2966 | 0.2966 | 0.2966 | |
| 500 | 0.2969 | 0.2967 | 0.2966 | 0.2966 | 0.2966 | 0.2966 | 0.2966 | |
| 600 | 0.2969 | 0.2966 | 0.2966 | 0.2965 | 0.2965 | 0.2965 | 0.2965 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vučković, A.; Vučković, D.; Perić, M.; Ranđelović, B.M. Quantitative Analysis of Magnetic Force of Axial Symmetry Permanent Magnet Structure Using Hybrid Boundary Element Method. Symmetry 2024, 16, 1495. https://doi.org/10.3390/sym16111495
Vučković A, Vučković D, Perić M, Ranđelović BM. Quantitative Analysis of Magnetic Force of Axial Symmetry Permanent Magnet Structure Using Hybrid Boundary Element Method. Symmetry. 2024; 16(11):1495. https://doi.org/10.3390/sym16111495
Chicago/Turabian StyleVučković, Ana, Dušan Vučković, Mirjana Perić, and Branislav M. Ranđelović. 2024. "Quantitative Analysis of Magnetic Force of Axial Symmetry Permanent Magnet Structure Using Hybrid Boundary Element Method" Symmetry 16, no. 11: 1495. https://doi.org/10.3390/sym16111495
APA StyleVučković, A., Vučković, D., Perić, M., & Ranđelović, B. M. (2024). Quantitative Analysis of Magnetic Force of Axial Symmetry Permanent Magnet Structure Using Hybrid Boundary Element Method. Symmetry, 16(11), 1495. https://doi.org/10.3390/sym16111495







