Analysis of COVID-19’s Dynamic Behavior Using a Modified SIR Model Characterized by a Nonlinear Function
Abstract
1. Introduction
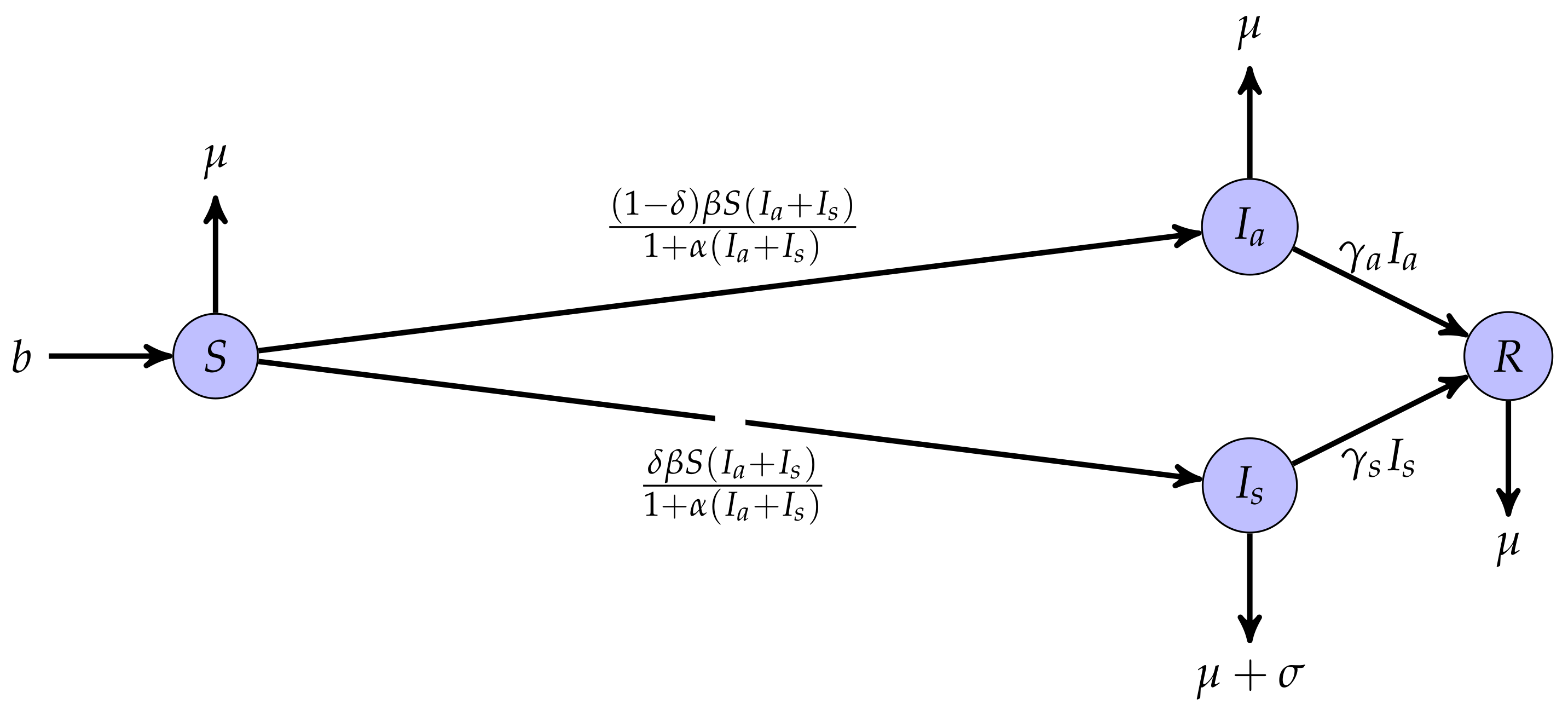
2. Formulation of COVID-19 Mathematical Model
- 1.
- Symmetrical assumption: In this model, the capacity for virus transmission is identical for infected individuals, whether symptomatic or asymptomatic. Thus, groups (asymptomatic individuals) and (symptomatic individuals) are treated identically, following a common path to recovery with different transmission rates ( for asymptomatic individuals and for symptomatic individuals).
- 2.
- Asymmetrical assumption: The response to the virus varies among individuals; some develop symptoms, while others remain asymptomatic, creating an asymmetry in transmission. A certain percentage of the susceptible population develops symptoms (), while another percentage becomes asymptomatic ().
- 3.
- Natural mortality: Natural mortality affects all compartments of the model and represents a shared biological constant. Unlike the symmetrical and asymmetrical assumptions, this mortality does not distinguish between individuals based on their infectious status but reflects a universal biological reality.
3. Results
3.1. Principal Properties of the Model
3.1.1. Analysis of the Positivity of the Solutions
3.1.2. Invariant Domain
3.2. Asymptotic Stability Relating to the Disease-Free Equilibrium
3.2.1. Determination of the Basic Reproduction Number
3.2.2. Local Asymptotic Stability of the Disease-Free Equilibrium
- Since and according to the value of , we consider the following three scenarios: if , then and ; if , then and ; and if , then with both and where denotes the real part of a complex number. In summary, system (3) has a disease-free equilibrium () that is asymptotically stable if and only if is strictly less than 1. □
3.2.3. Global Asymptotic Stability of the Disease-Free Equilibrium
3.3. Asymptotic Stability of the Endemic Equilibrium
3.3.1. Local Asymptotic Stability of the Endemic Equilibrium
3.3.2. Global Asymptotic Stability of the Endemic Equilibrium
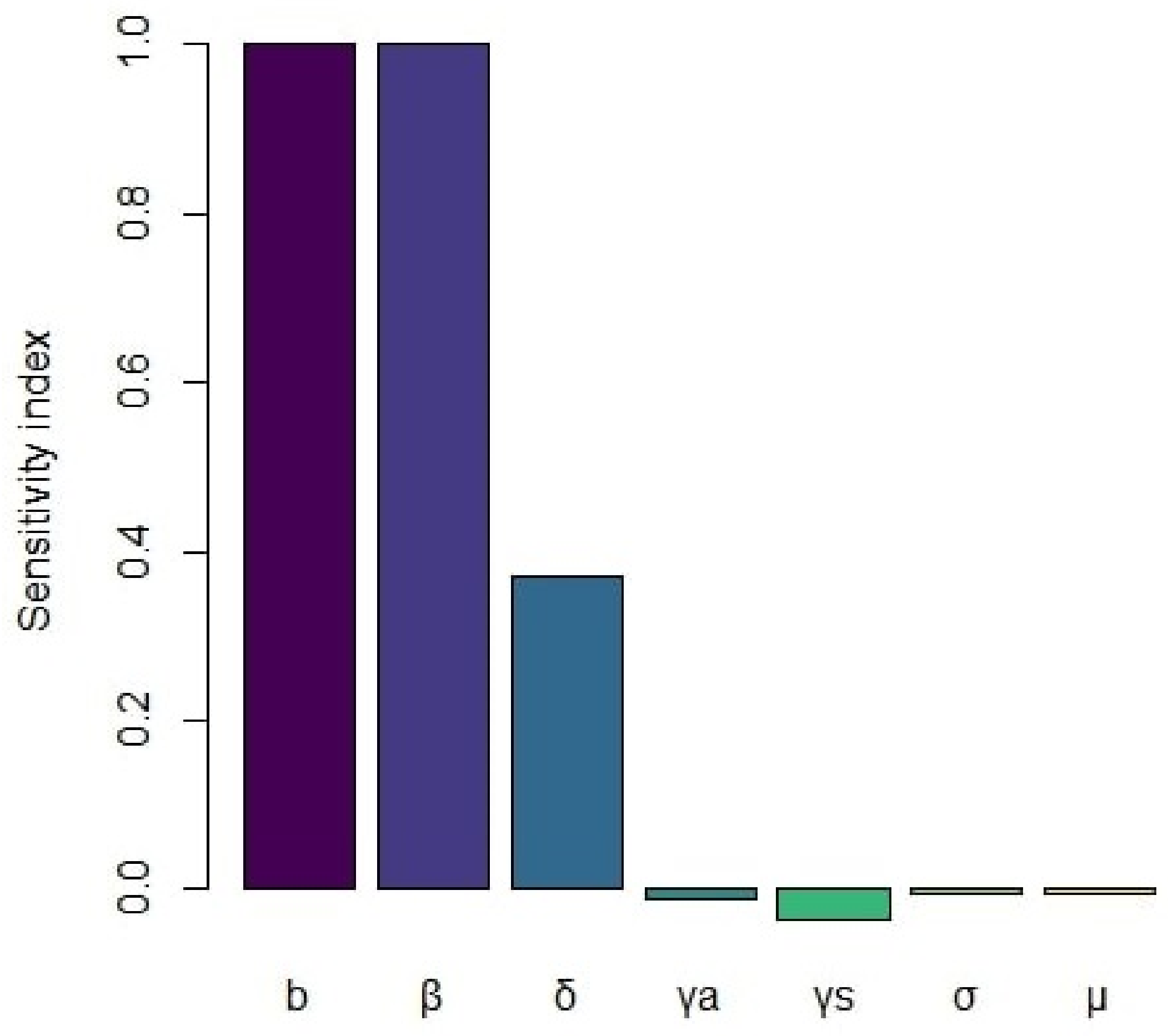
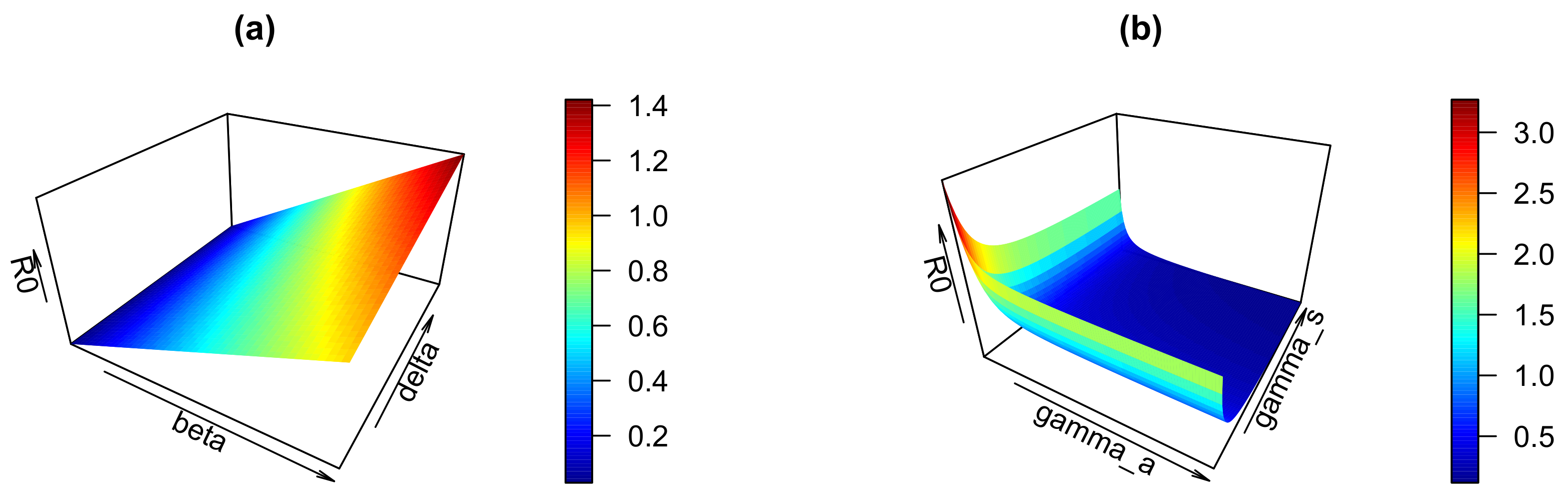
4. Sensitivity of the Basic Reproduction Number
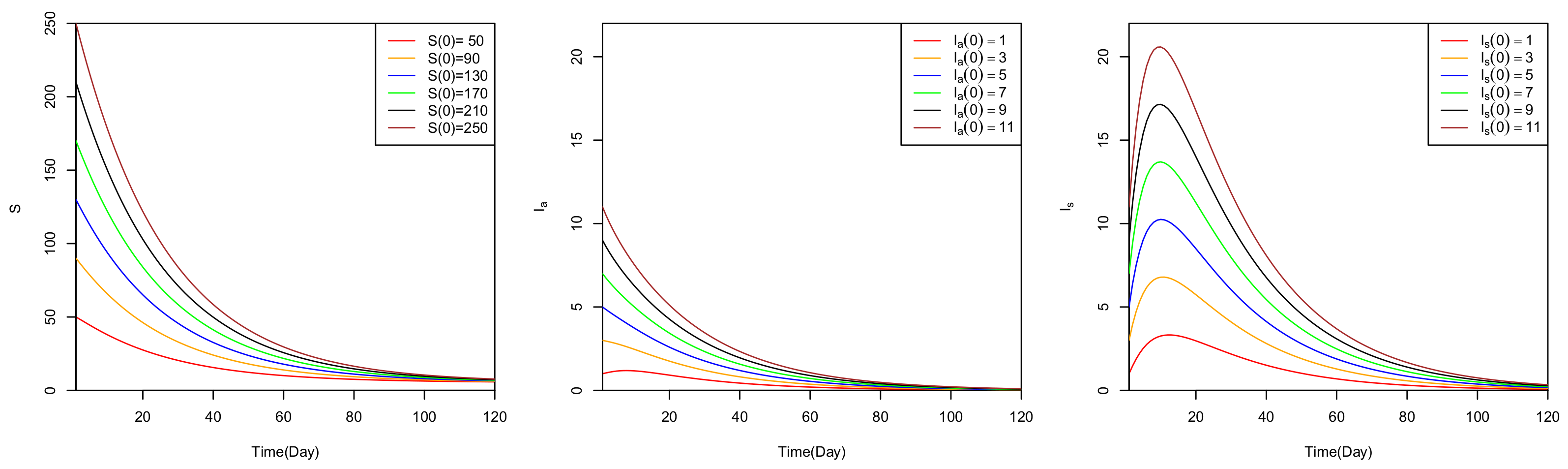
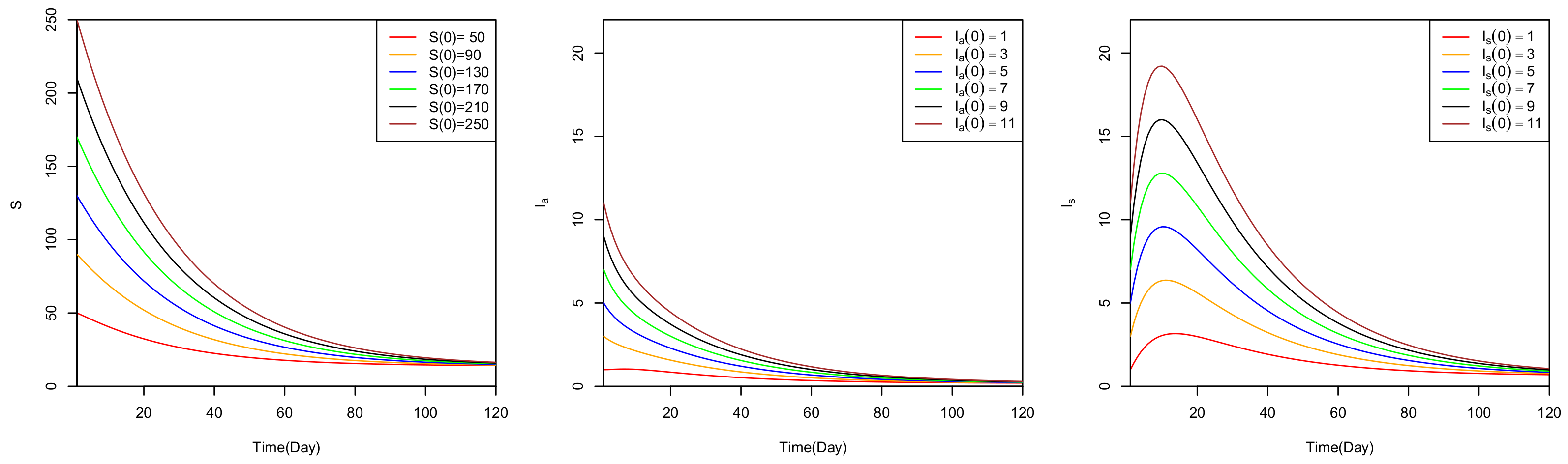
5. Numerical Analysis
6. Discussion
7. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Li, H.; Wu, Y. Dynamics of SCIR Modeling for COVID-19 with Immigration. Complexity 2022, 2022. [Google Scholar] [CrossRef]
- Lei, C.; Li, H.; Zhao, Y. Dynamical behavior of a reaction-diffusion SEIR epidemic model with mass action infection mechanism in a heterogeneous environment. Discret. Contin. Dyn. Syst.-B 2024, 29, 3163–3198. [Google Scholar] [CrossRef]
- Shao, P.; Shateyi, S. Stability Analysis of SEIRS Epidemic Model with Nonlinear Incidence Rate Function. Mathematics 2021, 9, 2644. [Google Scholar] [CrossRef]
- Li, T.; Zhang, F.; Liu, H.; Chen, Y. Threshold dynamics of an SIRS model with nonlinear incidence rate and transfer from infectious to susceptible. Appl. Math. Lett. 2017, 70, 52–57. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Maini, P.K. Non-linear incidence and stability of infectious disease models. Math. Med. Biol. J. IMA 2005, 22, 113–128. [Google Scholar] [CrossRef]
- Korobeinikov, A. Global Properties of Infectious Disease Models with Nonlinear Incidence. Bull. Math. Biol. 2007, 69, 1871–1886. [Google Scholar] [CrossRef]
- Korobeinikov, A. Lyapunov Functions and Global Stability for SIR and SIRS Epidemiological Models with Non-Linear Transmission. Bull. Math. Biol. 2006, 68, 615–626. [Google Scholar] [CrossRef]
- Feng, Z.; Thieme, H.R. Endemic Models with Arbitrarily Distributed Periods of Infection I: Fundamental Properties of the Model. SIAM J. Appl. Math. 2000, 61, 803–833. [Google Scholar] [CrossRef]
- Cerón Gómez, M.; Mondragon, E.I.; Molano, P.L. Global stability analysis for a model with carriers and non-linear incidence rate. J. Biol. Dyn. 2020, 14, 409–420. [Google Scholar] [CrossRef]
- Askar, S.; Ghosh, D.; Santra, P.; Elsadany, A.A.; Mahapatra, G. A fractional order SITR mathematical model for forecasting of transmission of COVID-19 of India with lockdown effect. Results Phys. 2021, 24, 104067. [Google Scholar] [CrossRef]
- Alshammari, F.S.; Khan, M.A. Dynamic behaviors of a modified SIR model with nonlinear incidence and recovery rates. Alex. Eng. J. 2021, 60, 2997–3005. [Google Scholar] [CrossRef]
- Ali, A.; Alshammari, F.S.; Islam, S.; Khan, M.A.; Ullah, S. Modeling and analysis of the dynamics of novel coronavirus (COVID-19) with Caputo fractional derivative. Results Phys. 2021, 20, 103669. [Google Scholar] [CrossRef] [PubMed]
- Awais, M.; Alshammari, F.S.; Ullah, S.; Khan, M.A.; Islam, S. Modeling and simulation of the novel coronavirus in Caputo derivative. Results Phys. 2020, 19, 103588. [Google Scholar] [CrossRef]
- Basnarkov, L. SEAIR Epidemic spreading model of COVID-19. Chaos Solitons Fractals 2021, 142, 110394. [Google Scholar] [CrossRef] [PubMed]
- Prem Kumar, R.; Basu, S.; Ghosh, D.; Santra, P.K.; Mahapatra, G.S. Dynamical analysis of novel COVID-19 epidemic model with non-monotonic incidence function. J. Public Aff. 2021, 22, e2754. [Google Scholar] [CrossRef]
- Abbasi, Z.; Zamani, I.; Mehra, A.H.A.; Shafieirad, M.; Ibeas, A. Optimal Control Design of Impulsive SQEIAR Epidemic Models with Application to COVID-19. Chaos Solitons Fractals 2020, 139, 110054. [Google Scholar] [CrossRef]
- Basu, S.; Prem Kumar, R.; Santra, P.; Mahapatra, G.; Elsadany, A. Preventive control strategy on second wave of COVID-19 pandemic model incorporating lock-down effect. Alex. Eng. J. 2022, 61, 7265–7276. [Google Scholar] [CrossRef]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [CrossRef]
- Avila-Ponce de León, U.; Pérez, Á.G.; Avila-Vales, E. An SEIARD epidemic model for COVID-19 in Mexico: Mathematical analysis and state-level forecast. Chaos Solitons Fractals 2020, 140, 110165. [Google Scholar] [CrossRef]
- Engbert, R.; Rabe, M.M.; Kliegl, R.; Reich, S. Sequential Data Assimilation of the Stochastic SEIR Epidemic Model for Regional COVID-19 Dynamics. Bull. Math. Biol. 2020, 83, 1. [Google Scholar] [CrossRef]
- Gralinski, L.E.; Menachery, V.D. Return of the Coronavirus: 2019-nCoV. Viruses 2020, 12, 135. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, D.; Santra, P.K.; Mahapatra, G.S.; Elsonbaty, A.; Elsadany, A.A. A discrete-time epidemic model for the analysis of transmission of COVID19 based upon data of epidemiological parameters. Eur. Phys. J. Spec. Top. 2022, 231, 3461–3470. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Huang, M. An SIHR epidemic model of the COVID-19 with general population-size dependent contact rate. AIMS Math. 2020, 5, 6714–6725. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A.; Alzahrani, E.; Fatmawati. The dynamics of COVID-19 with quarantined and isolation. Adv. Differ. Equations 2020, 2020, 425. [Google Scholar] [CrossRef]
- Kuddus, M.A.; Rahman, A. Analysis of COVID-19 using a modified SLIR model with nonlinear incidence. Results Phys. 2021, 27, 104478. [Google Scholar] [CrossRef]
- Prem Kumar, R.; Santra, P.; Mahapatra, G. Global stability and analysing the sensitivity of parameters of a multiple-susceptible population model of SARS-CoV-2 emphasising vaccination drive. Math. Comput. Simul. 2023, 203, 741–766. [Google Scholar] [CrossRef]
- Kumar, R.P.; Basu, S.; Santra, P.; Ghosh, D.; Mahapatra, G. Optimal control design incorporating vaccination and treatment on six compartment pandemic dynamical system. Results Control Optim. 2022, 7, 100115. [Google Scholar] [CrossRef]
- Richard, Q.; Alizon, S.; Choisy, M.; Sofonea, M.T.; Djidjou-Demasse, R. Age-structured non-pharmaceutical interventions for optimal control of COVID-19 epidemic. PLoS Comput. Biol. 2021, 17, e1008776. [Google Scholar] [CrossRef]
- Ram, V.; Schaposnik, L.P. A modified age-structured SIR model for COVID-19 type viruses. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]
- Pal, D.; Ghosh, D.; Santra, P.K.; Mahapatra, G.S. Mathematical Analysis of a COVID-19 Epidemic Model by Using Data Driven Epidemiological Parameters of Diseases Spread in India. Biophysics 2022, 67, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Ghosh, D.; Santra, P.K.; Mahapatra, G.S. Mathematical modeling and analysis of COVID-19 infection spreads in India with restricted optimal treatment on disease incidence. BIOMATH 2021, 10. [Google Scholar] [CrossRef]
- Saldaña, F.; Flores-Arguedas, H.; Camacho-Gutiérrez, J.A.; Barradas, I. Modeling the transmission dynamics and the impact of the control interventions for the COVID-19 epidemic outbreak. Math. Biosci. Eng. 2020, 17, 4165–4183. [Google Scholar] [CrossRef] [PubMed]
- Silva, P.C.; Batista, P.V.; Lima, H.S.; Alves, M.A.; Guimarães, F.G.; Silva, R.C. COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fractals 2020, 139, 110088. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Z. Transmission dynamics, global stability and control strategies of a modified SIS epidemic model on complex networks with an infective medium. Math. Comput. Simul. 2021, 188, 23–34. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math. Biosci. Eng. 2020, 17, 2708–2724. [Google Scholar] [CrossRef]
- Day, M. COVID-19: Four fifths of cases are asymptomatic, China figures indicate. BMJ 2020, 369, m1375. [Google Scholar] [CrossRef]
- He, D.; Zhao, S.; Lin, Q.; Zhuang, Z.; Cao, P.; Wang, M.H.; Yang, L. The relative transmissibility of asymptomatic COVID-19 infections among close contacts. Int. J. Infect. Dis. 2020, 94, 145–147. [Google Scholar] [CrossRef]
- Tomochi, M.; Kono, M. A mathematical model for COVID-19 pandemic—SIIR model: Effects of asymptomatic individuals. J. Gen. Fam. Med. 2020, 22, 5–14. [Google Scholar] [CrossRef]
- Ahmed, I.; Modu, G.U.; Yusuf, A.; Kumam, P.; Yusuf, I. A mathematical model of Coronavirus Disease (COVID-19) containing asymptomatic and symptomatic classes. Results Phys. 2021, 21, 103776. [Google Scholar] [CrossRef]
- Kuhl, E. Computational Epidemiology: Data-Driven Modeling of COVID-19; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Ottaviano, S.; Sensi, M.; Sottile, S. Global stability of SAIRS epidemic models. Nonlinear Anal. Real World Appl. 2022, 65, 103501. [Google Scholar] [CrossRef]
- Essak, A.A.; Boukanjime, B. Global stability of an SAIRS epidemic model with vaccinations, transient immunity and treatment. Nonlinear Anal. Real World Appl. 2023, 73, 103887. [Google Scholar] [CrossRef]
- Ying, L.; Tang, X. COVID-19: Is it safe now? Study of asymptomatic infection spread and quantity risk based on SAIR model. Chaos Solitons Fractals X 2021, 6, 100060. [Google Scholar] [CrossRef]
- Mwalili, S.; Kimathi, M.; Ojiambo, V.; Gathungu, D.; Mbogo, R. SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC Res. Notes 2020, 13, 352. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Zhao, Z.; Liu, F.; Zhang, K.; Wu, A.; Nie, X. Understanding Dynamics of Pandemic Models to Support Predictions of COVID-19 Transmission: Parameter Sensitivity Analysis of SIR-Type Models. IEEE J. Biomed. Health Inform. 2022, 26, 2458–2468. [Google Scholar] [CrossRef]
- Hale, J. Ordinary Differential Equations; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 1969; p. 384. [Google Scholar]
- Birkhoff, G.; Rota, G.C. Ordinary Differential Equations, 4th ed.; Wiley: Hoboken, NJ, USA, 1991; p. 416. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.; Metz, J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–381. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- La Salle, J.P. The Stability of Dynamical Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1976. [Google Scholar] [CrossRef]
- La Salle, J.; Lefschetz, S.; Alverson, R.C. Stability by Liapunov’s Direct Method With Applications. Phys. Today 1962, 15, 59. [Google Scholar] [CrossRef]

| Parameter | Description |
|---|---|
| b | Rate of population recruitment |
| Rate of disease transmission from susceptible individuals (S) to infected compartments ( and ) | |
| Constant of saturation reflecting psychological or inhibitory effects on the transmission of infection | |
| Rate of susceptible individuals who develop symptoms of the disease | |
| Rate of recovery from the asymptomatic population to the recovered population | |
| Rate of recovery from the symptomatic population to the recovered population | |
| Mortality rate attributed to COVID-19 | |
| Rate of natural mortality |
| Parameter | Value | Source |
|---|---|---|
| b | 0.05 | Assumed |
| 0.024 | Assumed | |
| 0.9 | Assumed | |
| 0.7 | [46] | |
| 0.25 | Assumed | |
| 0.14 | Assumed | |
| 0.023 | Assumed | |
| 0.01 | Assumed |
| Parameter | Sensitivity Index |
|---|---|
| b | +1 |
| +1 | |
| −0.0116 | |
| −0.0344 | |
| +0.372 | |
| −0.005 | |
| −0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habott, F.; Ahmedou, A.; Mohamed, Y.; Sambe, M.A. Analysis of COVID-19’s Dynamic Behavior Using a Modified SIR Model Characterized by a Nonlinear Function. Symmetry 2024, 16, 1448. https://doi.org/10.3390/sym16111448
Habott F, Ahmedou A, Mohamed Y, Sambe MA. Analysis of COVID-19’s Dynamic Behavior Using a Modified SIR Model Characterized by a Nonlinear Function. Symmetry. 2024; 16(11):1448. https://doi.org/10.3390/sym16111448
Chicago/Turabian StyleHabott, Fatimetou, Aziza Ahmedou, Yahya Mohamed, and Mohamed Ahmed Sambe. 2024. "Analysis of COVID-19’s Dynamic Behavior Using a Modified SIR Model Characterized by a Nonlinear Function" Symmetry 16, no. 11: 1448. https://doi.org/10.3390/sym16111448
APA StyleHabott, F., Ahmedou, A., Mohamed, Y., & Sambe, M. A. (2024). Analysis of COVID-19’s Dynamic Behavior Using a Modified SIR Model Characterized by a Nonlinear Function. Symmetry, 16(11), 1448. https://doi.org/10.3390/sym16111448






