The Singularity of Three Kinds of New Tricyclic Graphs

Abstract

A graph G is singular if its adjacency matrix is singular. The starting vertices of two paths $P_{b_1}$ and $P_{b_2}$ are simultaneously bound to the ending vertex of the path $P_{s_1}$, and the ending vertices of the paths $P_{b_1}$ and $P_{b_2}$ are bound to the starting vertex of path $P_{s_2}$. Meanwhile, the starting vertex of the path $P_{s_1}$ is bound to a vertex of the cycle $C_{a_1}$, and the ending vertex of the path $P_{s_2}$ is bound to a vertex of the cycle $C_{a_2}$. Thus, the resulting graph is written as $\xi (a_1,a_2,b_1,b_2,s_1,s_2)$. This is denoted by $\zeta (a_1,a_2,b_1,b_2,s)=\xi (a_1,a_2,b_1,b_2,1,s)$ and $\epsilon (a_1,a_2,b_1,b_2)=\zeta (a_1,a_2,b_1,b_2,1)$, which are referred to as the $\xi$-graph, $\zeta$-graph and $\epsilon$-graph for short, respectively. It is known that there are 15 kinds of tricyclic graphs. The purpose of this paper is to study the necessary and sufficient conditions for $\xi$-graphs, $\zeta$-graphs and $\epsilon$-graphs to be singular graphs. We analyzed the structure of the elementary spanning subgraphs of the graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$. By calculating the determinant of the adjacency matrix of the graph G, the necessary and sufficient conditions for the determinant of the graph G to be zero is obtained, and so the necessary and sufficient conditions for graph $\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ to be singular are obtained. As the corollaries, the necessary and sufficient conditions for graphs $\zeta (a_1,a_2,b_1,b_2,s)$ and $\epsilon (a_1,a_2,b_1,b_2)$ to be singular are also obtained.

1. Introduction

Only the finite and undirected simple graphs are considered in this article. Let G be a graph with n vertices; then, its adjacency matrix $A\left(G\right)$ is represented as follows: $A\left(G\right)={\left(a_{ij}\right)}_{n\times n}$, where $a_{ij}=1$ if the vertex i and vertex j are adjacent; otherwise, $a_{ij}=0$. Apparently, $A\left(G\right)$ is a real symmetric matrix with elements 0 or 1 whose eigenvalues are all real numbers. The eigenvalues of $A\left(G\right)$ are the eigenvalues of graph G, and the set of n eigenvalues of G is said to be the spectrum of graph G. The number of non-zero eigenvalues and zero eigenvalues in the spectrum of G are called the rank of G and the nullity of G, respectively, which are denoted by $r\left(G\right)$ and $\eta \left(G\right)$, $r\left(G\right)+\eta \left(G\right)=n$.

In chemistry, a conjugated hydrocarbon molecule can be represented by a graph, which is called the molecular graph of the molecule. The nullity (or rank) of a molecular graph has many potential applications in chemistry [1]. For instance, the nullity of a graph equal to 0 is a necessary condition for the stability of the chemical properties of the molecule, which represents [2]. In 1957, Collatz and Sinogowitz [3] had proposed to characterize the singular graphs by the graph nullity greater than zero. As is known to all, a graph is singular if 0 is one of its eigenvalues, that is, $\eta \left(G\right)>0$. Thus, the problem by Collatz and Sinogowitz is equivalent to the problem of characterizing all singular graphs, which is a very hard problem. In order to study this issue, many people investigate the relationship between the nullity of a graph and its structure by means of the structural characteristics of singular graphs. The nullity set and the graphs with extremal nullity of the trees [4], the unicyclic graphs [5,6], the bicyclic graphs [7,8,9] and the tricyclic graphs [10] is determined by researchers. The authors [9] studied some lower bounds for the nullity of graphs. The graphs on n vertices with nullity $n-4$ and $n-5$ are characterized [10,11,12]. The authors [13] proved that the nullity of the line graph of a tree is at most one.

Singular graphs have many equivalent definitions; for example, a graph G is singular when and only when the kernel space of $A\left(G\right)$ is not null space; a graph G is singular when and only when the homogeneous system of linear equations $AX=0$ with $A\left(G\right)$ as the coefficient has a non-zero solution. From this perspective, necessary and sufficient conditions are given [14] for a graph to be singular in terms of admissible induced subgraphs. Some methods are provided [15] for constructing singular graphs from others of smaller order; furthermore, some sufficient conditions are given for a graph to be singular. The singular graph of line graphs of trees are characterized [16]. The authors [17] studied the singular graphs in fullerenes. The authors [18] characterized singular Cayley graphs over cyclic groups and proved that vertex transitive graphs with prime order are non-singular. A graph G is singular if $A\left(G\right)$ is a singular matrix; that is, the determinant of $A\left(G\right)$ is zero. From this point of view, the authors [19,20] gave the necessary and sufficient conditions for the singularity of several classes of tricyclic graphs and the probability of singular graphs occurring in these graph classes. Recent studies have also shown that singular graphs are related to other fields of mathematics, such as the representation theory of finite groups, combinatorial mathematics, algebraic geometry, and so on (see [18,21,22,23,24]).

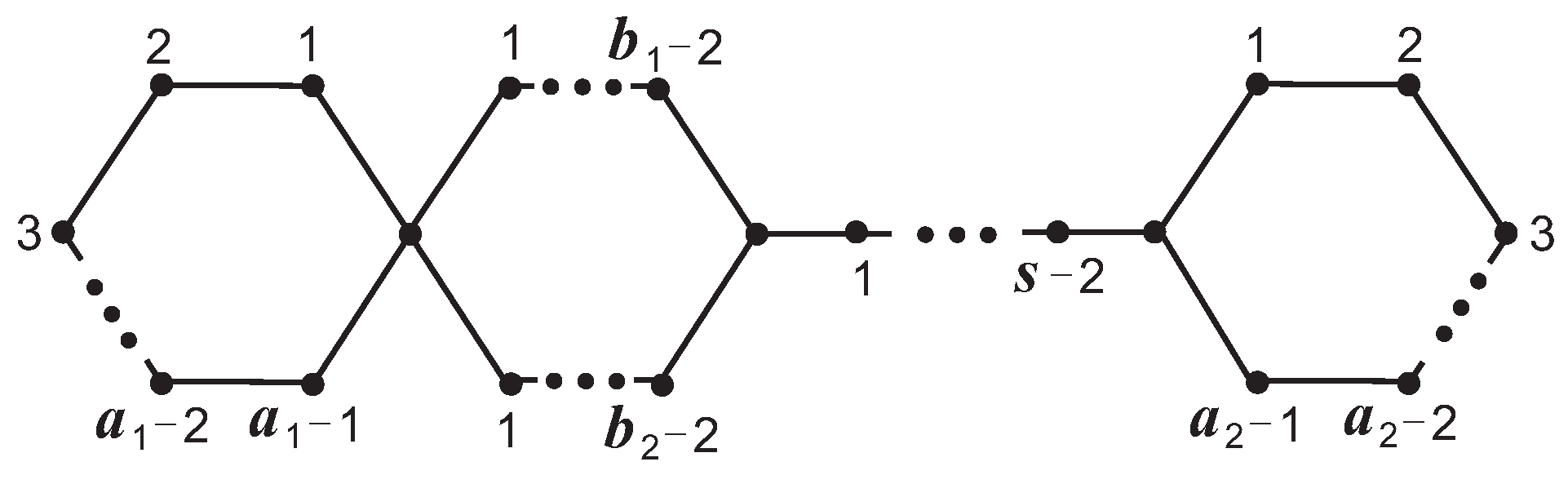
Let $P_n$, $C_n$ and $K_n$ denote the path, cycle and complete graph with n vertices, respectively. The starting vertices of two paths $P_{b_1}$ and $P_{b_2}$ are simultaneously bound to the ending vertex of the path $P_{s_1}$, and the ending vertices of the paths $P_{b_1}$ and $P_{b_2}$ are bound to the starting vertex of path $P_{s_2}$. Meanwhile, the starting vertex of the path $P_{s_1}$ is bound to a vertex of the cycle $C_{a_1}$, and the ending vertex of the paths $P_{s_2}$ is bound to a vertex of the cycle $C_{a_2}$. Thus, the resulting graph is denoted by $\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ (see Figure 1), which is abbreviated as the $\xi$-graph. In Figure 1, the cycle $C_{a_1}$ and the cycle $C_{a_2}$ are called the cycles on both sides, and the cycle $C_{b_1+b_2-2}$ is said to be the middle cycle. 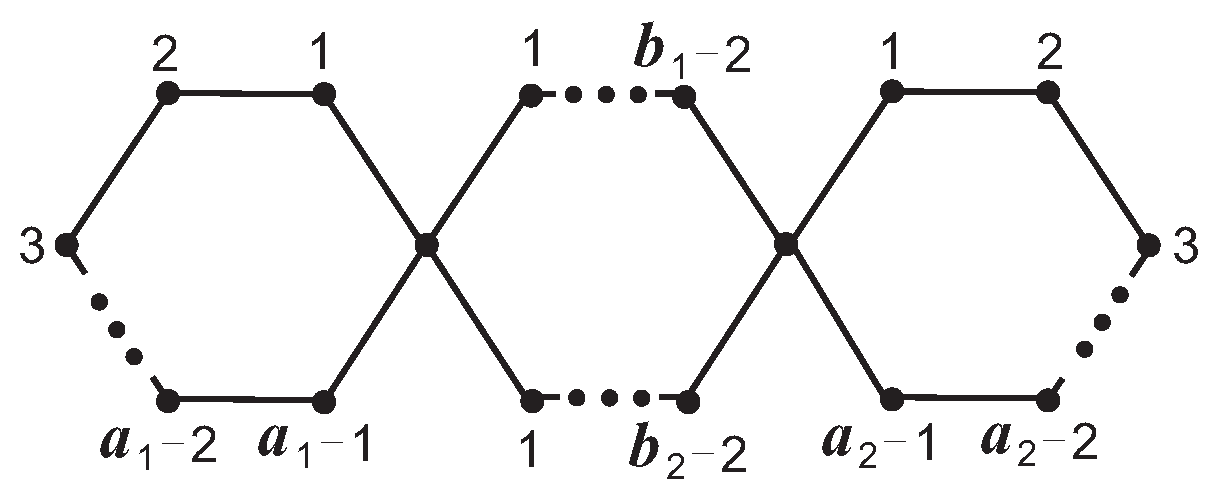Let $\zeta (a_1,a_2,b_1,b_2,s)=\xi (a_1,a_2,b_1,b_2,1,s)$ (see Figure 2), which is the $\zeta$-graph for short. Let $\epsilon (a_1,a_2,b_1,b_2)=\zeta (a_1,a_2,b_1,b_2,1)$ (see Figure 3), which is referred to as the $\epsilon$-graph.

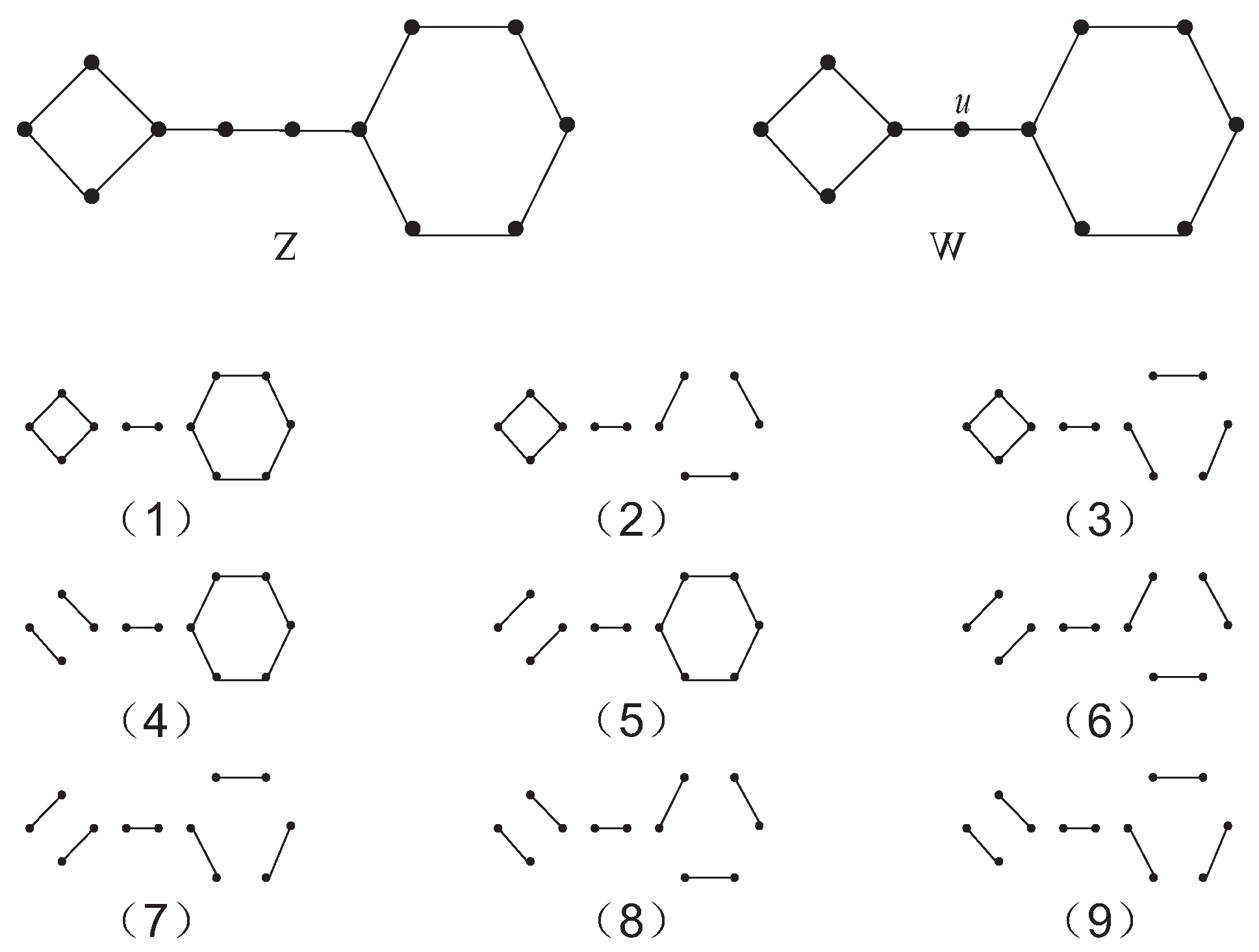
Tricycle graphs can be categorized into 15 kinds according to the induced subgraphs (see Figure 4). In [19], we have given the necessary and sufficient conditions of tricycle graphs including the induced subgraphs (1)–(4) and the probability of singular graphs occurring in these graph classes. In [20], we have given the necessary and sufficient conditions of tricycle graphs including the induced subgraphs (5) and (6) and the probability of singular graphs occurring in these graph classes. The purpose of this paper is to study the necessary and sufficient conditions for tricycle graphs including the induced subgraphs (7)–(9).

For two graphs G and H, $G\cup H$ denoted the disjoiont union of G and H, and $mG$ stands for the disjoint union of m copies of G; especially, $m{P}_2$ stands for the disjoint union of the m isolated edge. The vertex of degree 1 is called the pendant vertex, and the vertex adjacent to the pendant vertex is called the quasi-pendant vertex. For the notations and terms which are not defined above, please refer to [1].

2. Preliminaries

Lemma 1

([1]). Suppose $G=G_1\cup G_2\cup \cdots \cup G_t$, where $G_i$$(i=1,2,\dots ,t)$ are connected components of G; then, $\eta \left(G\right)={\displaystyle \sum _{i=1}^t}\eta \left(G_i\right)$. Equivalently, G is non-singular if and only if each $G_i(i=1,2,\dots ,t)$ is non-singular.

Lemma 2

([1]). If graph G has a pendant vertex, graph H is obtained by deleting the pendant vertex and the quasi-pendant vertex adjacent to it from G; then, $\eta \left(G\right)=\eta \left(H\right)$. Equivalently, G is singular if and only if H is singular.

Example 1.

As shown in Figure 5, we deleted the pendant verttices and quasi-pendant vertices $u_1$, $u_2$; $v_1$, $v_2$ in turn on the graph X, and the resulting graph is $\xi (6,6,4,4,3,4)$. We deleted the pendant vertices and quasi-pendant vertices $u_1$, $u_2$; $v_1$, $v_2$; $w_1$, $w_2$ in turn on graph Y, and the resulting graph is $\xi (3,5,4,4,3,4)$. By Lemma 2, graph X is singular if and only if $\xi (6,6,4,4,3,4)$ is singular, and graph Y is singular if and only if $\xi (3,5,4,4,3,4)$ is singular.

The subgraph of graph G in which each component is an isolated edge or cycle is called an elementary subgraph (or a Sachs subgraph) of graph G. The elementary subgraph containing all vertices of G is termed an elementary spanning subgraph (or a spanning Sachs subgraph). An elementary spanning subgraph only composed of isolated edges is said to be a perfect matching of graph G. Of course, if a graph has perfect matching, the number of vertices on the graph must be even.

Lemma 3

([1]). Let G be a graph with n vertices and let its adjacency matrix be $A\left(G\right)$; then,

$$det\left(A\left(G\right)\right)={(-1)}^n\sum _{H\in \mathcal{H}}{(-1)}^{p\left(H\right)}{2}^{c\left(H\right)},$$

where $\mathcal{H}$ denotes the set of elementary spanning subgraphs of graph G, $p\left(H\right)$ denotes the number of components in graph H, and $c\left(H\right)$ denotes the number of cycles in graph H.

We use the following example to illustrate the structure of elementary spanning subgraphs of a graph.

Example 2.

As shown in Figure 6, there exists one elementary spanning subgraph of graph Z with two cycles: $C_4\cup C_6\cup P_2$ (see (1)). There exist two elementary spanning subgraphs of graph Z with cycle: $C_4$; they are $C_4\cup 4P_2$ (see (2) and (3)). There exist two elementary spanning subgraphs of graph Z with cycle: $C_6$; they are $C_6\cup 3P_2$ (see (4) and (5)). There exist four perfect matchings of Z (see (6)–(9)). By Lemma 3,

$$det\left(A\left(Z\right)\right)={(-1)}^{12}[{(-1)}^3\times 2^2+{(-1)}^5\times 2\times 2+{(-1)}^4\times 2\times 2+{(-1)}^6\times 4]=0.$$

Thus, Z is a singular graph.

There exists no elementary spanning subgraph of graph W with two cycles, $C_4\cup C_6$; otherwise, vertex u does not match. There exists no elementary spanning subgraph of graph W with one cycle, $C_4$ or $C_6$, because the number of remaining vertices after $C_4$ or $C_6$ is removed is odd, and they do not form a perfect matching. There exists no elementary spanning subgraph that does not include cycles (the perfect matchings); this is because the number of vertices in graph W is odd. Thus, W is a singular graph.

3. Main Theorems and Proofs

For convenience, we define $a=\{a_1,a_2\}$, $b=\{b_1,b_2\}$ and $s=\{s_1,s_2\}$, and we say a is odd (resp. even) if both $a_1$ and $a_2$ are odd (resp. even), one of a is odd if exactly one of $a_1$ or $a_2$ is odd, and at least one of a is odd if at least one of $a_1$ and $a_2$ is odd. There are similar conventions for b and s. A graph that is determined to be singular or non-singular only by the parity of the parameters on the graph is called a singularity-determined graph. Otherwise, the graph is called a singularly-indeterminate graph.

Theorem 1.

The graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ (see Figure 1) is determined to be non-singular if one of the following is satisfied:

(1) 

a is odd, b is even, and at least one of s is even.

(2) 

a is odd and one of b is even.

Proof. 

(1) (i) When s is even, there exists one elementary spanning subgraph of graph G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (because by removing the cycles $C_{a_1}$ and $C_{a_2}$, the remaining vertices can form two kinds of perfect matchings). There exist no elementary spanning subgraphs of G with one cycle. There exists one perfect matching of G.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}=0,$$

which is contradictious. Thus, G is non-singular.

(ii) When one of s is even, let us assume that $s_1$ is even and $s_2$ is odd. Then, there exists no elementary spanning subgraph of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$, and there exists one elementary spanning subgraph of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exists no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2=0,$$

which is impossible. Thus, G is non-singular.

(2) Let us assume that $b_1$ is even and $b_2$ is odd.

(i) When s is even, there exists one elementary spanning subgraph of graph G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exists no elementary spanning subgraph of G with two cycles. There exist two elementary spanning subgraphs of graph G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ and $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exists no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2=0,$$

which is impossible. Thus, G is non-singular.

(ii) When one of s is odd, let us assume that $s_1$ is even and $s_2$ is odd. In this case, there exists no elementary spanning subgraph of G with three cycles. There exist two elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$, and $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. G has no elementary spanning subgraph with one cycle; it contains one perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}=0,$$

which is impossible. Thus, G is non-singular.

(iii) When s is odd, there exists no elementary spanning subgraph of G with three and two cycles; there exist three elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$, $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$, and $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$. There exists no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2=0,$$

which is impossible. Thus, G is non-singular. □

Theorem 2.

The graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ is determined to be singular if one of the following is satisfied:

(1) 

a is even, b is even, and one of s is even.

(2) 

a is even, one of b is even, and s is odd.

(3) 

a is even, b is odd, and at least one of s is odd.

(4) 

one of a is even, b is odd, at least one of s is odd and the $s_i(i=1,2)$ connected to exactly an even cycle is odd.

Proof. 

It is easy to verify those in above cases there are no elementary spanning subgraphs in the graph G. According to Lemma 3, G is singular. □

Theorem 3.

If one of a is odd, one of b is odd, one of s is odd and the $s_i(i=1,2)$ connecting the even cycles is even, then the graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ is singular if and only if the length of the even cycles is a multiple of 4 or the lengths of the two odd cycles do not have congruence with respect to module 4.

Proof. 

Let us assume that $a_1,b_1,s_1$ are even and $a_2,b_2,s_2$ are odd. Then, there exists no elementary spanning subgraph of G with three cycles. There exist two elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$, and $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two), $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}{P}_2$ (two). There exists no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2^2=0;$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{s_1+s_2-3}{2}}}$, then

$${(-1)}^{{\displaystyle \frac{b_1+b_2-3}{2}}}+{(-1)}^{{\displaystyle \frac{a_2-1}{2}}}-{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2-3}{2}}}-{(-1)}^{{\displaystyle \frac{a_1+a_2-1}{2}}}=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{b_1+b_2-3}{2}}}+{(-1)}^{{\displaystyle \frac{a_2-1}{2}}})=0,$$

when and only when $4|a_1$ or $a_2\not\equiv b_1+b_2-2$ (mod 4). □

Theorem 4.

If a is odd, b is even, and s is odd, then the graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ is singular if and only if $a_1\equiv a_2$ (mod 4), $b_1\equiv b_2$ (mod 4).

Proof. 

There exists no elementary spanning subgraph of G with three cycles; there exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$; there exists one elementary spanning subgraph of G with one cycle: $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$. It contains two perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 2=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$, then

$${(-1)}^{{\displaystyle \frac{a_1+a_2}{2}}+2}\times 2+{(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}+1}+1=0,$$

when and only when $a_1\equiv a_2$ (mod 4), $b_1\equiv b_2$ (mod 4). □

Theorem 5. 

(1) If a is even, b is even and s is odd. (2) One of a is even, b is even, at least one of s is odd and the $s_i(i=1,2)$ connecting the even cycles is odd; then, the graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ is singular if and only if the length of at least one of the cycles on both sides is a multiple of 4.

Proof. 

(1) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two), $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two). There exist four perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 4=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$, then

$${(-1)}^{{\displaystyle \frac{a_1+a_2}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+{(-1)}^{{\displaystyle \frac{a_2}{2}}+1}+1=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{a_2}{2}}}-1)=0,$$

if and only if $4|a_1$ or $4|a_2$.

(2) Let us assume that $a_1$ is even, $a_2$ is odd and $s_1$ is odd.

(i) When $s_2$ is even, there are no elementary spanning subgraphs of G with three cycles. There is no elementary spanning subgraph of G with two cycles. There exists one elementary spanning subgraph of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exist two perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 2=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$, then

$${(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+1=0,$$

when and only when $4|a_1$.

(ii) When $s_2$ is odd, there is no elementary spanning subgraph of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exists no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}}$, then

$${(-1)}^{{\displaystyle \frac{a_1}{2}}+2}-1=0,$$

if and only if $4|a_1$. □

Theorem 6.

With the exception of the scenarios covered by Theorems 1–5, the graph $G=\xi (a_1,a_2,b_1,b_2,s_1,s_2)$ is singular if and only if the graph G contains at least one cycle whose length is a multiple of 4.

Proof. 

$\left|V\left(G\right)\right|=a_1+a_2+b_1+b_2+s_1+s_2-6$. Combining the parity of $a_1,a_2,b_1,b_2,s_1,$$s_2$ and the symmetry of the graph $\xi (a_1,a_2,b_1,b_2,s_1,s_2)$, there are 30 cases (see

Table 1. The classification table of the proof of Theorem 6.

${\mathit{a}}_{\mathbf{1}},{\mathit{a}}_{\mathbf{2}},{\mathit{b}}_{\mathbf{1}},{\mathit{b}}_{\mathbf{2}},{\mathit{s}}_{\mathbf{1}},{\mathit{s}}_{\mathbf{2}}$	M	${\mathit{a}}_{\mathbf{1}},{\mathit{a}}_{\mathbf{2}},{\mathit{b}}_{\mathbf{1}},{\mathit{b}}_{\mathbf{2}},{\mathit{s}}_{\mathbf{1}},{\mathit{s}}_{\mathbf{2}}$	M	${\mathit{a}}_{\mathbf{1}},{\mathit{a}}_{\mathbf{2}},{\mathit{b}}_{\mathbf{1}},{\mathit{b}}_{\mathbf{2}},{\mathit{s}}_{\mathbf{1}},{\mathit{s}}_{\mathbf{2}}$	M
(1) $e,e,e,e,e,e$		(11) $e,o,e,e,e,o$		(21) $e,o,o,o,o,o$	*
(2) $e,e,e,e,e,o$	*	(12) $e,o,e,e,o,e$	*	(22) $o,o,e,e,e,e$	*
(3) $e,e,e,e,o,o$	*	(13) $e,o,e,e,o,o$	*	(23) $o,o,e,e,e,o$	*
(4) $e,e,e,o,e,e$		(14) $e,o,e,o,e,e$		(24) $o,o,e,e,o,o$	*
(5) $e,e,e,o,e,o$		(15) $e,o,e,o,e,o$	*	(25) $o,o,e,o,e,e$	*
(6) $e,e,e,o,o,o$	*	(16) $e,o,e,o,o,e$		(26) $o,o,e,o,e,o$	*
(7) $e,e,o,o,e,e$		(17) $e,o,e,o,o,o$		(27) $o,o,e,o,o,o$	*
(8) $e,e,o,o,e,o$	*	(18) $e,o,o,o,e,e$		(28) $o,o,o,o,e,e$
(9) $e,e,o,o,o,o$	*	(19) $e,o,o,o,e,o$		(29) $o,o,o,o,e,o$
(10) $e,o,e,e,e,e$		(20) $e,o,o,o,o,e$	*	(30) $o,o,o,o,o,o$

). In Table 1, e means that the corresponding parameter is even, o means that the corresponding parameter is odd, M means the Mark, and * means that this case has been dealt with in the previous theorem.

In Table 1, Cases (22), (23), (25), (26) and (27) are dealt with in Theorem 1; Cases (2), (6), (8), (9), (20) and (21) are dealt with in Theorem 2; Case (15) is dealt with in Theorem 3; Case (24) is dealt with in Theorem 4; Cases (3), (12) and (13) are dealt with in Theorem 5. The unprocessed cases are verified below in the order of the table.

(1) There exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist six elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two), $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$ (two), and $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exist twelve elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four), $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four), and $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$ (four). It contains eight perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^3+{(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^3$$

$$+{(-1)}^{{\displaystyle \frac{a_1+s_1+s_2-4}{2}}+2}\times 2^3+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^3$$

$$+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 8=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2-2}{2}}+3}+{(-1)}^{{\displaystyle \frac{a_1+a_2}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2-2}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2-2}{2}}+2}$$

$$+{(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+{(-1)}^{{\displaystyle \frac{a_2}{2}}+1}+{(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}+1}+1=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{a_2}{2}}}-1)({(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}}-1)=0,$$

which holds when and only when $4|a_1$, $4|a_2$ or $4\left|\right(b_1+b_2-2)$.

(4) There exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$ (two) and $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exist four elementary spanning subgraphs of G with one cycle: $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$ (four). It contains four perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^3$$

$$+{(-1)}^{{\displaystyle \frac{a_1+s_1+s_2-4}{2}}+2}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2^3=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+a_2}{2}}+3}+{(-1)}^{{\displaystyle \frac{a_1}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_2}{2}}+2}-1=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{a_2}{2}}}-1)=0,$$

which holds when and only when $4|a_1$ or $4|a_2$.

(5) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two) and $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two). It contains four perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 4=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+a_2}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+{(-1)}^{{\displaystyle \frac{a_2}{2}}+1}+1=0,$$

which holds when and only when $4|a_1$ or $4|a_2$.

(7) There exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist six elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two), $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$ (two), $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exist twelve elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four), $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four), and $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$ (four). It contains eight perfect matchings.

Similar to case (1), it is concluded that G is singular when and only when $4|a_1$, $4|a_2$ or $4\left|\right(b_1+b_2-2)$.

(10) There exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two) and $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exist four elementary spanning subgraphs of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four). There is no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^3$$

$$+{(-1)}^{{\displaystyle \frac{a_1+s_1+s_2-4}{2}}+2}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^3=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+b_1+b_2-2}{2}}+3}+{(-1)}^{{\displaystyle \frac{a_1}{2}}+2}+{(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}+2}-1=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}}-1)=0,$$

when and only when $4|a_1$ or $4\left|\right(b_1+b_2-2)$.

(11) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two) and $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$ (two). It contains four perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 4=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+b_1+b_2-2}{2}}+2}+{(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+{(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}+1}+1=0,$$

which holds when and only when $4|a_1$ or $4\left|\right(b_1+b_2-2)$.

(14) In this case, there exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with two cycles: $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exists one elementary spanning subgraph of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. It contains two perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{a_1+s_1+s_2-4}{2}}+2}\times 2^3$$

$$+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 2=0,$$

multiplying both sides by ${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2-2}{2}}+3}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2-2}{2}}+2}\times 2^2$$

$$+{(-1)}^{{\displaystyle \frac{a_1}{2}}+1}+1=0,$$

when and only when

$$({(-1)}^{{\displaystyle \frac{a_1}{2}}}-1)({(-1)}^{{\displaystyle \frac{a_2+b_1+b_2-2}{2}}}\times 2^2+1)=0,$$

when and only when $4|a_1$.

(16) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two). There is no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2=0,$$

when and only when

$${(-1)}^{{\displaystyle \frac{a_1}{2}}}-1=0,$$

when and only when $4|a_1$.

(17) There are no elementary spanning subgraphs of G with three cycles. There is no elementary spanning subgraphs of G with two cycles. There exists one elementary spanning subgraph of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. It contains two perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 2=0,$$

when and only when $4|a_1$.

(18) There exists one elementary spanning subgraph of G with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two) and $C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+s_1+s_2-4}{2}}{P}_2$ (two). There exist four elementary spanning subgraphs of G with one cycle: $C_{a_2}\cup {\displaystyle \frac{a_1+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (four). There exists no perfect matching.

Similar to case (10), it is concluded that G is singular when and only when $4|a_1$ or $4\left|\right(b_1+b_2-2)$.

(19) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. There exist four elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$ (two) and $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$ (two). It contains four perfect matchings.

Similar to case (11), it is concluded that G is singular when and only when $4|a_1$ or $4\left|\right(b_1+b_2-2)$.

(28) There exists one elementary spanning subgraph with three cycles: $C_{a_1}\cup C_{a_2}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{s_1+s_2-4}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with two cycles: $C_{a_1}\cup C_{a_2}\cup {\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There are no elementary spanning subgraphs of G with one cycle. There exists no perfect matching.

Acoeding to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{s_1+s_2-4}{2}}+3}\times 2^3+{(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}+2}\times 2^3=0,$$

multipling the above by ${(-1)}^{{\displaystyle \frac{b_1+b_2+s_1+s_2-6}{2}}}$ yields that

$${(-1)}^{{\displaystyle \frac{b_1+b_2-2}{2}}+3}+1=0,$$

which holds when and only when $4\left|\right(b_1+b_2-2)$.

(29) There are no elementary spanning subgraphs of G with three cycles. There exists one elementary spanning subgraph of G with two cycles: $C_{a_1}\cup C_{b_1+b_2-2}\cup {\displaystyle \frac{a_2+s_1+s_2-4}{2}}{P}_2$. There exist two elementary spanning subgraphs of G with one cycle: $C_{a_1}\cup {\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}{P}_2$. There is no perfect matching.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_2+s_1+s_2-4}{2}}+2}\times 2^2+{(-1)}^{{\displaystyle \frac{a_2+b_1+b_2+s_1+s_2-6}{2}}+1}\times 2^2=0,$$

when and only when $4\left|\right(b_1+b_2-2)$.

(30) There are no elementary spanning subgraphs of G with three cycles. There are no elementary spanning subgraphs of G with two cycles. There exists one elementary spanning subgraph of G with one cycle: $C_{b_1+b_2-2}\cup {\displaystyle \frac{a_1+a_2+s_1+s_2+s_3-4}{2}}{P}_2$. There exist two perfect matchings.

According to Lemma 3, G is singular when and only when

$${(-1)}^{{\displaystyle \frac{a_1+a_2+s_1+s_2-4}{2}}+1}\times 2+{(-1)}^{{\displaystyle \frac{a_1+a_2+b_1+b_2+s_1+s_2-6}{2}}}\times 2=0,$$

when and only when $4\left|\right(b_1+b_2-2)$. □

Note 1.

Theorem 5 cannot be merged into Theorem 6. Because under the conditions of Theorem 5, it is also possible that the length of the middle cycle $b_1+b_2-2$ is a multiple of 4, but it is irrelevant with the singularity of the graph.

Comparing Theorems 1–6, for the graph $G=\zeta (a_1,a_2,b_1,b_2,s)=\xi (a_1,a_2,b_1,b_2,1,s)$ (see Figure 2), we have the following corollaries.

Corollary 1.

The graph $G=\zeta (a_1,a_2,b_1,b_2,s)$ is singular if one of the following is satisfied:

(1) 

a is even, b is even, and s is even.

(2) 

a is even, one of b is even, and s is odd.

(3) 

At least one of a is even and b is odd.

(4) 

One a is odd, one b is odd, s is even, and the length of the even cycles is a multiple of 4 or the lengths of the two odd cycles do not have congruence with respect to module 4.

(5) 

a is odd, b is even, s is odd, and $a_1\equiv a_2$ (mod 4), $b_1\equiv b_2$ (mod 4).

(6) 

a is even, b is even, and s is odd, and the lengths of at least one of the cycles on both sides is a multiple of 4.

(7) 

Except for the cases (1)–(6) and the following (i)–(ii), there exists at least one cycle in the graph G whose length is a multiple of 4.

(i) 

a is odd, b is even, and s is even;

(ii) 

a is odd, and one of b is even.

Comparing Corollary 1, for the graph $G=\epsilon (a_1,a_2,b_1,b_2)=\zeta (a_1,a_2,b_1,b_2,1)$ (see Figure 3), we have the following corollary.

Corollary 2.

The graph $G=\epsilon (a_1,a_2,b_1,b_2)$ is singular if one of the following is satisfied:

(1) 

a is even, and at least one b is odd.

(2) 

a is odd, b is even, and $a_1\equiv a_2$ (mod 4), $b_1\equiv b_2$ (mod 4).

(3) 

At least one of a is even, b is even, and the length of at least one of the cycles on both sides is a multiple of 4.

(4) 

Except the cases (1)–(3) and the following (i), there exists at least one cycle in the graph G whose length is a multiple of 4.

(i) 

a is odd, and one of b is even.

4. Discussion

In article [20], the singularity identification methods of unicyclic graphs, bicyclic graphs, and some tricycle graphs are given. For example, a cycle $C_n$ is singular if and only if $4|n$. It is known that a connected graph G is a tree, unicyclic graph, bicyclic graph and a tricycle graph if and only if $\left|E\right(G\left)\right|=\left|V\right(G\left)\right|-1,\left|V\right(G\left)\right|,\left|V\right(G\left)\right|+1$ and $\left|V\right(G\left)\right|+2$, respectively. Tricycle graphs can be categorized into 15 kinds according to the induced subgraphs. Tricycle graphs containing $\xi$-graphs, $\zeta$-graphs and $\epsilon$-graphs as their induced subgraphs are denoted as $\mathcal{T}\left(\xi \right)$, $\mathcal{T}\left(\zeta \right)$ and $\mathcal{T}\left(\epsilon \right)$, respectively. Using Lemma 2 repeatedly, that is, deleting the pendant vertex and quasi-pendant vertex on the graph, and then using Lemmas 1 and 2, Theorems 1–6, Corollaries 1 and 2 and the conclusions concerning the singularity of the bicyclic graphs in the article [20], one can identify the singular graph in $\mathcal{T}\left(\xi \right)$, $\mathcal{T}\left(\eta \right)$ and $\mathcal{T}\left(\epsilon \right)$. For example, we can now answer the singularity of graphs X and Y in Example 1, by Theorem 2(1), $\xi (6,6,4,4,3,4)$ is singular; thus, X is singular. By Theorem 1(1), $\xi (3,5,4,4,3,4)$ is non-singular; thus, Y is non-singular. A similar work can be performed for tricycle graphs including the induced subgraphs (10)–(15) (see Figure 4); if all this work is completed, we can give an algorithm for quickly checking out singular graphs.

5. Conclusions

By analyzing the structure of elementary spanning subgraphs of the xi graphs, and applying the formula $det\left(A\left(G\right)\right)={(-1)}^n{\sum }_{H\in \mathcal{H}}{(-1)}^{p\left(H\right)}{2}^{c\left(H\right)},$ we have established the necessary and sufficient conditions which render $det\left(A\right(G\left)\right)=0$ in the xi graphs, that is, the necessary and sufficient conditions that the xi graph is singular. We have also given the corollaries in which the necessary and sufficient conditions are that the zeta graphs and the varepsilon graphs are singular. We expect similar arguments to work for the yet to be handled for cases of tricyclic graphs (10)–(15) (see Figure 4). If all this work is completed, these arguments are simple enough to program and check the singularity of a given tricycle graph on a computer.