Abstract
Diabetes is becoming more and more dangerous, and the effects continue to grow due to the population’s ignorance of the seriousness of this phenomenon. The studies that have been carried out have not been able to follow the phenomenon more precisely, which has led to the use of the fractional derivative tool, which has a very great capability to study real problems and phenomena but is somewhat limited on nonlinear models. In this work, we will develop a new fractional derivative model of a diabetic population, the Takagi–Sugeno fractional fuzzy model, which will enable us to study the phenomenon with these nonlinear terms in order to obtain greater precision in the results. We will study the existence and uniqueness of the solution using the Lipschizian theorem and then turn to the new fuzzy model, which leads us to four dynamical systems. The interpretation results show the quality of fuzzy membership in tracking the malleable phenomena of nonlinear terms existing in the system.
1. Introduction
In recent years, the calculation of fractional derivatives has been the subject of much research. In fact, this notion is not new: it was born 300 years ago with the question of the derivative proposed by Hospital [1,2,3]. But the most important thing about this fractional derivative is that it grows exponentially, and different types of this derivative have been proposed in the literature. For example, Caputo’s derivative is the most popular, along with Riemann–Liouville fractional derivative, Atangana–Baleanu fractional derivative, Hilfer fractional derivatives, Riesz–Caputo fractional derivative and others [2]. Recently, the fractional derivative has been applied in various fields, in particular biology, economics, engineering and science [4,5,6,7,8,9,10,11]. Indeed, the fractional calculus is introduced into network systems owing to its positive memory and hereditary characteristic in describing the model [12,13]. In our research paper, we focus on the field of biology, in particular on the phenomenon of diabetes and its effects on people [14]. Diabetes is a chronic disease that is one of the challenges of the medical future. Artificial intelligence has been the optimal solution for better understanding the disease and monitoring patients progressively [15]. It is characterized by chronic metabolic dysfunction, leading to high blood sugar levels and subsequent damage to vital organs, including nerves, kidneys, eyes, blood vessels and the heart. As we know and as the statistics show, this disease is growing exponentially around the world, and particularly in Morocco [15]. There are several reasons for this increase in diabetes, which we will discuss in the next section. The aim of using this type of derivative to model real-world phenomena is to study them accurately. What is more, this type of derivative is best suited to dynamic systems. Several studies have been carried out to reduce the negative effects of type 2 diabetes [16,17,18,19]. Among these studies, we can mention and extract a few that focus on the general population and the different external variants that are directly linked to the growth of this disease: for example, the environment, problems linked to people’s genetics, food and other reasons. Mathematical models of the diabetic population have been the subject of several research papers [17,20]. Each of these models focuses on different people’s situations, but in general, the most popular compartments are pre-diabetic patients, uncomplicated diabetics and diabetics with complications. Despite the tools we presented earlier, we find that some criteria cannot be known precisely. We have therefore proposed in this paper to take the parameters as imprecise parameters, and we use fuzzy numbers as imprecise parameters. In addition, all real dynamic systems are represented by nonlinear differential equations, as linear systems cannot be used to model physical, electrical and biological phenomena due to their complex and discontinuous behavior [21]. These nonlinear differential equations are highly complex to solve. This problem is solved by a method widely used in the literature: the multi-model approach [21]. For this purpose, we used a universal approximation based on this approach, namely Takagi–Sugeno fractional fuzzy models [22]. Since their introduction in 1985, Takagi–Sugeno (T-S) type fuzzy models have met widespread success in the scientific community [23]. Most studies of phenomena using the concept of fuzzy sets aim to track the evolution of phenomena. This technique can be used to costruct a system with multiple processes based on data or the kernel model [22]. Takagi and Sugeno [22] propose a system with IF–THEN fuzzy rules, which describe the local linear input–output relations of a nonlinear system. There are two types of discrete and nonlinear systems, each with its own rules. For discrete systems, the ith rules of T-S fuzzy models have the form DFS (discrete fuzzy system), and for nonlinear systems, the ith rules of T-S fuzzy models have the form CFS (continuous fuzzy system) [22]. In the forthcoming research discussed earlier in this article, the majority of researchers will be turning to artificial intelligence not only to study diabetes but also to refine the monitoring and surveillance of this disease with increasing precision. As mentioned, we plan to use fractional differential equations with different values to track the evolution of the disease. In addition, we will adopt the concept of “fuzzy logic”, an advanced and promising branch of applied mathematics and artificial intelligence, to process phenomena with greater precision [24]. In this paper, we will explore the robust fuzzy technique. Basically, most existing mathematical models in the literature use models either with fuzziness and ordinary differential equations, or they use fractional differential equations without fuzziness. Our study used nonlinear fractional models with fuzzy terms for a precise study of the diabetes phenomenon. We propose a fuzzy fracionary model and mathematically demonstrate the transformation of the nonlinear model to a linear model using fuzzy terms.
This paper is organized as follows: in Section 2, we present related work in which we describe the various techniques and models published in the literature to reduce the negative effect of diabetic phenomena as well as certain diseases. In Section 3, we present some preliminaries of the fractional derivative used in this paper. Section 4 presents the proposed fractional dynamic system with the Takagi–Sugeno (T-S) type fuzzy model, in which we will prove the existence and uniqueness of the solution and other criteria. Section 5 contains the simulation part of the proposed system with both operators plus the description of the result. Finally, in Section 6, we summarize our paper in a short conclusion.
2. Related Work
As we mentioned earlier, there are several works that study the phenomenon of diabetes in different situations and with different techniques. Examples include simple modeling in linear and nonlinear deferential equations, in different types of fractional differential equations, and some studies use the fuzzy membership technique. Here, we present the most important studies published recently in the literature. Among the works on nonlinear dynamical systems and genetic algorithms is that of Goharimanesh et al. [25], who proposed the use of a fractional-order PID controller. A new study was made by Nasir [14], who proposed a dynamic system controlled with delay. He carried out all the studies on this system, including stability, sensitivity and optimal control. Jagdev Singh et al. [26] carried out a specific study of a deterministic dynamical system with the Caputo–Fabrizio fractional derivative of the phenomenon of diabetes and its complications. For the study of their model, several methods were used, including the homotopy analysis method, the Laplace transform and the Padé approximation to exercise the analytical solution and other methods as well as simulations to demonstrate the theoretical results found. The work carried out by [27] focuses on just two types of patients: diabetics without complications and diabetics with complications. Then, the authors proposed a dynamic system of fractional order with a study of stability, demonstrating the feasibility of the solution by utilization of the method of homotopic decomposition (HDM). In studies on fractional dynamic systems, the Atangana–Baleanu Caputo (ABC) operator is also present. Yadav et al. [3] used this operator to study the phenomenon; the proposed system is in the form of a specific study on diabetes with complications. A general study has also been carried out, starting with the well-defined system through to numerical simulations. Kouidere’s work treats the phenomenon of diabetes and its effect on tuberculosis as a dynamic fractional syetem. They proposed a system with two comparisons, one for diabetic patients and the other for non-diabetic patients. A general study was also made of optimal control strategies [28]. A system that used the the Atangana–Baleanu Caputo (ABC) operator is also proposed but this time with a combined dynamic fractionary control model between the COVID-19 co-infected population and diabetic patients. A general study was also made of optimal control strategies [29]. Certainly, studies on the phenomenon of diabetes are numerous, even at the fractional level, and even at the in-depth level in the form of a dynamic model that superimposes a system of insulin, glucose and growth hormone on the organism. This time, they used an in-depth model with a global study of stability, observability and controllability [30]. A thorough system also using the Atangana–Baleanu Caputo (ABC) operator is given in [31], a nabla fractional difference dynamic system has been proposed, and there was also a general study on the system and its stability. A number of methods have also been taken into consideration for the proposed model, such as the non-singular Mittag–Leffler function and the fixed-point method. A dynamic mathematical model with fractional-order delay has been proposed by Balakrishnan in [32]. The proposed model is well defined and well studied, and the authors have also studied the local stability of the equilibrium points. An optimal control model has also been proposed with the objective of balancing glucose level and treatment over a finite period of time.
3. Preliminary of the Fractional Calculations
Fracionary derivatives offer a precesion of deep study for the phenomena. In this section, we present a sneak preview of the theory of fracionary culcules, which we will use in our part of the dynamic system and optimal control characterizations.
Definition 1.
The Riemann–Liouville fractional integrals of order of a function are given by
The left Riemann–Liouville fractional derivative
The right Riemann–Liouville fractional derivative
Definition 2.
Let , where represents the space of absolutely continuous functions on , and .
The left Caputo fractional derivative is defined by
and
The right Caputo fractional derivative is defined by
The Laplace transform of the Caputo fractional derivative (CFD) is given by
where is the Laplace transform defined by
Definition 3.
A two parameter Mittag–Leffler function is defined by
The Mittag–Leffler function satisfies the following equation:
Definition 4.
The Laplace transform of Mittag–Leffler function is defined by
4. Knowledge Mathematics Representation Model
4.1. Fractional Diabetes Model
In this section, we begin by presenting Kouidere’s diabetic population dynamics system [33]. This model is based on the pre-diabetic population and their development toward the diabetic population without and with complications.
where
- : total number of people with pre-diabetes.
- : number of people with pre-diabetes due to the negative influence of socio-environmental factors.
- : number of people with uncomplicated diabetes.
- : number of people with diabetes with complications.
Various parameters have been taken into account in this model, providing a more global view of the diabetes phenomenon. Note that N is the sum of all the compartments in the proposed model in a time t. As we have already shown in this section, this model is based on pre-diabetic patients, and and present the incidence of this type of patient. denotes the size of the population of diabetics and pre-diabetics at time t, where
- denotes the incidence of pre-diabetes.
- represents the natural mortality rate.
- signifies the probability of developing diabetes.
- denotes the probability of a diabetic person developing a complication.
- expresses the probability of developing diabetes at the stage of complications.
- is the rate at which complications are cured.
- represents the rate at which patients with complications become severely disabled.
- is the mortality rate due to complications.
Theorem 1.
4.2. Existence and Uniqueness
Let
where and
The following result proves the existence and uniqueness solution of (9).
Theorem 2.
For the fractional-order system of differential (9) with initial condition , there exists a unique solution for all .
Proof.
For the system (9) to have a unique solution, we need to prove that the function g is Lipschitzian:
So, we have
and
Or
Then,
Or, from the previous calculus, we have this inequality
Then, we have this expression
Finally,
Or
Thus, it follows that the function g is uniformly Lipschitz continuous. We can conclude the uniqueness and existence of the system (9) with the initial state . □
4.3. Fractional Takagi–Sugeno Fuzzy Model
Given a fractional nonlinear system, T-S [21] is interested in transforming the system into the following form:
Model Rule i:
If is and …and is ,
Here, is the fuzzy set and r is the number of model rules; is the state vector, is the disturbance, is the output vector, is the square matrix with real elements and is the premise variable vector whose elements are the functions of states.
Note that is the solution of the ith rule.
After defuzzification, the solution of the fracional nonlinear system is given by
where .
4.4. Fractional T-S Fuzzy of Our Model
Let us now define the new model proposed in this paper. In general, our contribution consists of simplifying the nonlinear term in the two compartments, which makes the model less complex to simulate and facilitates the study of phenomena.
From this fractional model, and through a straightforward transformation to matrix form, we find the following model.
We add a simple notion to the model, and then we have this expression
where
To acquire membership functions, we should calculate the minimum and maximum values of and .
From the maximum and minimum values, and can be represented by
where .
Therefore, the membership functions , , and can be calculated as
We name the membership functions , , and “Positive”, “Negative”, “Big”, and “Small”, respectively. Then, the nonlinear system (10) is represented by the following fuzzy model. We have noted the following about the model rule by MR:
- MR 1: If is “Positive” and is “Big”, therefore, .
- MR 2: If is “Positive” and is “Small”, therefore, .
- MR 3: If is “Negative” and is “Big”, therefore, .
- MR 4: If is “Negative” and is “Small”, therefore, .
where
Let be the solution of the ith linear system , so the solution on our system was
Through the recent research presented earlier in this article, most researchers are trying to use artificial intelligence to study diabetes, but more than that, they are trying to track the disease and monitor it more and more accurately. As we have already mentioned, we have tried to use fractional differential equations to track the disease with different alpha values, and we have also used the term fuzzy as one of the successful and advanced branches of applied mathematics and artificial intelligence to deal with phenomena more precisely. The following section presents practically all the theoretical results obtained, using graphs created with Matlab and new artificial intelligence tools.
5. Numerical Simulation
In this section, we show the numerical result of the problem with a different value. In the given model, various parameters play crucial roles in describing the dynamics of pre-diabetes and its associated complications. The natural death rate, denoted by , is set at 0.02. The mortality rate due to complications, represented by , is established at 0.001. The likelihood of developing diabetes, captured by , is specified as 0.2. Additionally, the probability of a diabetic person developing complications, denoted by , is assigned a value of 0.5. The probability of developing diabetes at the stage of complications, denoted by , is set at 0.1. The effective contact rate, symbolized by , is established as 0.8, while the probability of a diabetic person developing through behavioral factors, indicated by , is also set at 0.8. Furthermore, the model includes two factors contributing to the incidence of pre-diabetes: denotes the incidence through genetic factors, and represents the incidence through behavioral factors. Together, these parameters form a comprehensive framework for understanding the dynamics of pre-diabetes and its associated complications in the model.
The initial state of each compartment is given by the following values: , , and .
The weights in the objective functional are estimated to be , and .
Solving the problem using the TS-Fuzzy fractional method allows us to track the phenomenon more precisely. The two nonlinear terms add a complixity to the model (11), and to remedy this problem, we proposed using the TS-Fuzzy method, which allows us to make the model linear; i.e., we transformed the nonlinear model into four linear models thanks to the four fuzzy membershping, and each membershping gives us a linear model. From Figure 1, we notice that the linear and nonlinear models are similar, and this is because we have no fuzzy membership terms added in Equation (11). To solve the model, we used the Runge–Kutta method for different values of , and we found the results given in the following paragraph.
Figure 1.
Description of this research paper.
The simulations show the effectiveness of the proposed method for dealing with the nonlinear case. Figure 1 and Figure 2, which represent the compartments of pre-diabetic and pre-diabetic patients as a result of the negative impact of the socioenvironment factor, respectively, and which do not contain any nonlinear terms, show that nothing changes. On the other hand, the two remaining compartments, which do have nonlinear terms, show that the difference between the linear and nonlinear cases can be seen in Figure 3 and Figure 4, which demonstrate the quality of the fuzzy term we have proposed.
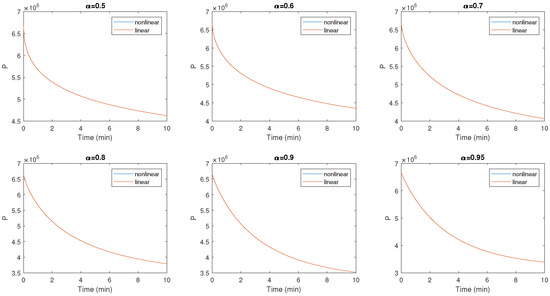
Figure 2.
Evolution of the number of people with pre-diabetes given by the nonlinear model and the linear model for different values of .
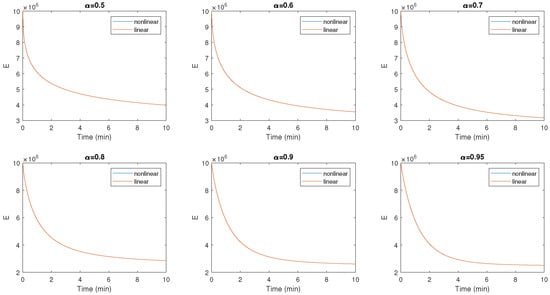
Figure 3.
Evolution of the number of people with pre-diabetes given by the nonlinear model and the linear model for different values of .
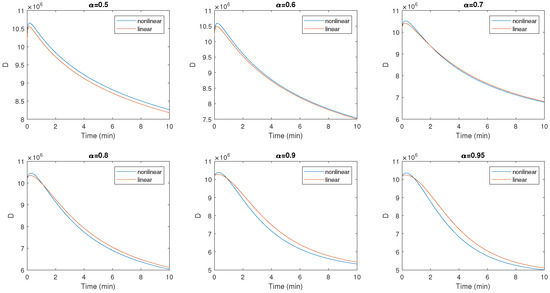
Figure 4.
Evolution of the numbers of diabetics without complications given by the nonlinear model and the linear model for different values of .
Figure 2 and Figure 3 illustrate the dynamic effects observed for a range of values ( 0.50, 0.60, 0.70, 0.80, 0.90, 1). Notably, when considering fractional order, pre-diabetic populations show a downward trend. However, as approaches 1, a significant decrease in these populations is observed. This suggests that an increase in parameters leads to a decrease in pre-diabetic populations. The results highlight the influence of on the dynamics of diabetic populations.
Figure 4 and Figure 5 represent the most difficult case to deal with, that of diabetic patients with complications, as it is influenced by several factors. The figure illustrates the presence of exponential growth in the diabetic population with complications over time, whatever the fractional orders used. Still using the same strategy as the previous compartments, we studied this compartment with different values of , and these are the parameters that we will use previously. Consequently, the fractional dimension plays an essential role in the type 2 diabetes model simulation experiments given in this paper. This work uses the fractional order derivative with fuzzy membership to study the behavior of the diabetes model. The influence of fractional order is clearly visible in the simulation results, and the fuzzy enhancement we proposed, to simplify terms that contain multiplication and furthermore add complexity to the model, shows its effectiveness, as shown in the figures.
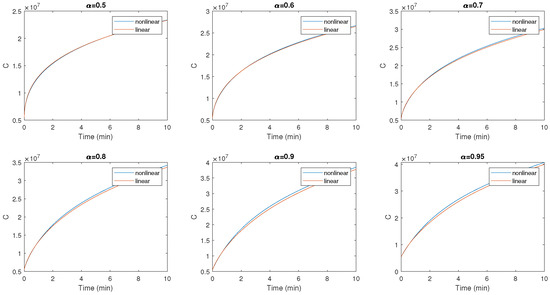
Figure 5.
Evolution of the numbers of diabetics with complications given by the nonlinear model and the linear model for different values of .
Consequently, we have found that the use of a fuzzy control simplifies the complexity of the model and, in future work, we will work on the optimal control problem, but this time, we will introduce a model controlled by three controls. Taking into account what we have gained in this paper, and based on these results, we will start to try to control the disease by fuzzy controls to reduce the negative effect of diabetes.
6. Conclusions
The proposed approach involves the development of a novel fractional derivative model, specifically the Takagi–Sugeno fractional fuzzy model, to study the diabetic population. This model is chosen for its capability to handle real-world problems and phenomena albeit with some limitations in dealing with nonlinear models. The aim is to enhance precision in the study of diabetes by incorporating nonlinear terms. The study involves the exploration of the existence and uniqueness of the solution using the Lipschitzian theorem. Subsequently, the focus shifts to the newly introduced fuzzy model, resulting in the formulation of four dynamical systems. The interpretation of results indicates that the fuzzy membership quality effectively tracks the adaptable nature of phenomena associated with nonlinear terms within the system.
In the future, we will extend the constant coefficients of the model to variable functions in order to obtain additional information on the dynamics of the diabetic population in Morocco. In addition, we will consider a spatial variable to introduce the geographical effect into the model.
Author Contributions
Conceptualization, E.O.A. and E.M.K.; methodology, E.-z.M.; writing—original draft preparation, E.-z.M., E.O.A. and A.A.; writing—review and editing, E.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of National Education, Professional Training, Higher Education and Scientific Research (MENFPESRS) and the Digital Development Agency (DDA) of Morocco (No. Alkhawarizmi/2020/23).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Syam, M.I.; Al-Refai, M. Fractional differential equations with Atangana–Baleanu fractional derivative: Analysis and applications. Chaos Solitons Fractals X 2019, 2, 100013. [Google Scholar] [CrossRef]
- Sweis, H.; Shawagfeh, N.; Arqub, O.A. Fractional crossover delay differential equations of Mittag-Leffler kernel: Existence, uniqueness, and numerical solutions using the Galerkin algorithm based on shifted Legendre polynomials. Results Phys. 2022, 41, 105891. [Google Scholar] [CrossRef]
- Yadav, P.; Jahan, S.; Shah, K.; Peter, O.J.; Abdeljawad, T. Fractional-order modelling and analysis of diabetes mellitus: Utilizing the Atangana-Baleanu Caputo (ABC) operator. Alex. Eng. J. 2023, 81, 200–209. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Shaikh, A.; Tassaddiq, A.; Nisar, K.S.; Baleanu, D. Analysis of differential equations involving Caputo-Fabrizio fractional operator and its applications to reaction-diffusion equations. Adv. Differ. Equ. 2019, 2019, 178. [Google Scholar] [CrossRef]
- Shaikh, A.S.; Nisar, K.S. Transmission dynamics of fractional order Typhoid fever model using Caputo Fabrizio operator. Chaos Solitons Fractals 2019, 128, 355–365. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Baleanu, D. Two analytical methods for time-fractional nonlinear coupled Boussinesq-Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn. 2016, 85, 699–715. [Google Scholar] [CrossRef]
- Shah, N.A.; Asogwa, K.K.; Mahsud, Y.; Lee, S.R.; Kang, S.; Chung, J.D.; Ishtiaq, M. Effect of generalized thermal transport on MHD free convection flows of nanofluids: A generalized Atangana-Baleanu derivative model. Case Stud. Therm. Eng. 2022, 40, 102480. [Google Scholar] [CrossRef]
- Rauf, A.; Batool, F.; Shah, N.A.; Chung, J.D. The influence of fractional time-derivative on the helical flows of generalized multi-layer immiscible second grade fluids in a cylindrical domain. Ain Shams Eng. J. 2023, 14, 102145. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023111. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; El Ouissari, A.; Palade, V.; Charroud, A.; Olaru, A.; Baïzri, H.; Chellak, S.; Cheggour, M. Multi-objective optimization for controlling the dynamics of the diabetic population. Mathematics 2023, 11, 2957. [Google Scholar] [CrossRef]
- Shen, M.; Wang, C.; Wang, Q.G.; Sun, Y.; Zong, G. Synchronization of Fractional Reaction-Diffusion Complex Networks with Unknown Couplings. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4503–4512. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Wen, D.; Shen, M.; Li, L.; Zhang, Z. Novel passivity and dissipativity criteria for discrete-time fractional generalized delayed Cohen–Grossberg neural networks. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107960. [Google Scholar] [CrossRef]
- Nasir, H. A time-delay model of diabetic population: Dynamics analysis, sensitivity, and optimal control. Phys. Scr. 2021, 96, 115002. [Google Scholar] [CrossRef]
- Saliha, C.; Hicham, B. Genetic algorithms for optimal control of a continuous model of a diabetic population. In Proceedings of the 2022 IEEE 3rd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Fez, Morocco, 1–2 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discret. Contin. Dyn. Syst. Ser. 2020, 13, 709–722. [Google Scholar] [CrossRef]
- El Ouissari, A.; El Moutaouakil, K. Genetic algorithm applied to fractional optimal control of a diabetic patient. Ufa Math. J. 2023, 15, 129–147. [Google Scholar] [CrossRef]
- Abdellatif, E.O.; Karim, E.M.; Hicham, B.; Saliha, C. Intelligent local search for an optimal control of diabetic population dynamics. Math. Model. Comput. Simul. 2022, 14, 1051–1071. [Google Scholar] [CrossRef]
- El Ouissari, A.; El Moutaouakil, K. Intelligent optimal control of nonlinear diabetic population dynamics system using a genetic algorithm. Syst. Res. Inf. Technol. 2024, 134–148. [Google Scholar]
- El Moutaouakil, K.; Bouhanch, Z.; Ahourag, A.; Aberqi, A.; Karite, T. OPT-FRAC-CHN: Optimal Fractional Continuous Hopfield Network. Symmetry 2024, 16, 921. [Google Scholar] [CrossRef]
- Mehran, K. Takagi-Sugeno Fuzzy Modeling for Process Control. In Industrial Automation, Robotics and Artificial Intelligence (EEE8005); School of Electrical, Electronic and Computer Engineering, Newcastle University: Newcastle upon Tyne, UK, 2008. [Google Scholar]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 0-471-32324-1. [Google Scholar]
- Guelton, K. Modèles Flous de Type Takagi-Sugeno: Des Origines à la Problématique Actuelle de leur Commande à Base de Signaux Echantillonnés. In Rencontres Francophones sur la Logique Floue et ses Applications (LFA); Sète: Cépaduès-Editions, France, 2020. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Goharimanesh, M.; Lashkaripour, A.; Abouei Mehrizi, A. Fractional order PID controller for diabetes patients. J. Comput. Appl. Mech. 2015, 46, 69–76. [Google Scholar]
- Singh, J.; Kumar, D.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 231. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093111. [Google Scholar] [CrossRef] [PubMed]
- El Moutaouakil, K.; El Ouissari, A.; Hicham, B.; Saliha, C.; Cheggour, M. Multi-objectives optimization and convolution fuzzy C-means: Control of diabetic population dynamic. RAIRO-Oper. Res. 2022, 56, 3245–3256. [Google Scholar] [CrossRef]
- Omame, A.; Nwajeri, U.K.; Abbas, M.; Onyenegecha, C.P. A fractional order control model for Diabetes and COVID-19 co-dynamics with Mittag-Leffler function. Alex. Eng. J. 2022, 61, 7619–7635. [Google Scholar] [CrossRef]
- Farman, M.; Ahmad, A.; Zehra, A.; Nisar, K.S.; Hincal, E.; Akgul, A. Analysis and controllability of diabetes model for experimental data by using fractional operator. Math. Comput. Simul. 2024, 218, 133–148. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Rajchakit, G.; Jirawattanapanit, A.; Priya, B. Stability analysis for Nabla discrete fractional-order of Glucose–Insulin Regulatory System on diabetes mellitus with Mittag-Leffler kernel. Biomed. Signal Process. Control 2023, 80, 104295. [Google Scholar] [CrossRef]
- Balakrishnan, G.P.; Chinnathambi, R.; Rihan, F.A. A fractional-order control model for diabetes with restraining and time-delay. J. Appl. Math. Comput. 2023, 69, 3403–3420. [Google Scholar] [CrossRef]
- Kouidere, A.; Khajji, B.; Balatif, O.; Rachik, M. A multi-age mathematical modeling of the dynamics of population diabetics with effect of lifestyle using optimal control. J. Appl. Math. Comput. 2021, 67, 375–403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).