Abstract
This study treats the problem of Finite Time Stability Analysis (FTSA) and Finite Time Feedback Control (FTFC), using a Linear Matrix Inequalities Approach (LMIA). It specifically focuses on Takagi–Sugeno fuzzy Time Delay Fractional-Order Systems (TDFOS) that include nonlinear perturbations and interval Time Varying Delays (ITVDs). We consider the case of the Caputo Tempered Fractional Derivative (CTFD), which generalizes the Caputo Fractional Derivative (CFD). Two main results are presented: a two-step procedure is provided, followed by a more relaxed single-step procedure. Two examples are presented to show the reduction in conservatism achieved by the proposed methods. The first is a numerical example, while the second involves the FTFC of an inverted pendulum, which exhibits both symmetrical dynamics for small angular displacements and asymmetrical dynamics for larger deviations.
1. Introduction
Over the past few decades, a lot of work has been conducted to push the boundaries of advanced stability analysis for different types of symmetrical and asymmetrical systems, from simpler models to highly complex ones [1,2]. The main challenges in setting up the design conditions are often related to the specific class of stability analysis involved. In the literature, stability analysis typically falls into two categories: asymptotic stability analysis and Finite Time Stability Analysis (FTSA). It is important to note that FTSA is far more complex than asymptotic stability because it ensures the system’s states converge within a finite time, rather than over an infinite time horizon. On the other hand, the complexity of the class of system considered can make the design conditions much more difficult. Indeed, a system may be more complicated than another due to a variety of factors. In this study, we focus on three main factors: the nonlinear dynamic, the presence of a time delay, particularly an Interval Time Varying Delay (ITVD), and finally the fractional-order derivative particulary Caputo Tempered Fractional Derivative (CTFD), which is more general than the standard Caputo Fractional Derivative (CFD). The next sections provide the state-of-the-art of results related to these factors.
Since its creation by Takagi and Sugeno in 1985 [3], nonlinear systems can be effectively represented by a set of local linear models seamlessly integrated by the membership function, the Takagi–Sugeno fuzzy model. So, using the Linear Matrix Inequalities Approach (LMIA), a vast number of studies have been conducted to address stability analyses and the control of a broader range of systems described by the Takagi–Sugeno fuzzy model (e.g., [4,5]). It is widely recognized that time delay is a common phenomenon in various systems. In 2000, Takagi–Sugeno fuzzy models were expanded by Cao and Franck [6] to address nonlinear systems with time delays. There has been a surge in research activity on stability analyses and the control of delayed Takagi–Sugeno fuzzy models (e.g., [7,8,9]).
In recent years, the study of Fractional-Order Systems (FOS) has attracted increasing interest. Various types of fractional derivatives have appeared in the literature, such as the Caputo Fractional Derivative (CFD) [10,11] and the Caputo Tempered Fractional Derivative (CTFD) [12]. It is well known that the CTFD involves the exponential function, which has distinct properties and applications in fractional calculus. Stability results for FOS obtained using the CTFD are often superior compared to those obtained using the standard CFD [13]. Since their introduction, significant efforts have been made to provide advanced stability analysis methods for FOS, resulting in a variety of new techniques. For example, Chen et al., in [14], studied the stability of FOS with multiple orders. Chen et al., in [15], investigated the asymptotic stability of a class of neural networks’ FOS. Ben Makhlouf, in [16], presented the partial practical stability of FOS depending on a small parameter. Some other results have appeared regarding investigations of the analysis and control problems presented by Time Delay Fractional-Order Systems (TDFOS). The issue of sliding mode control for linear TDFOS is investigated in [17]. Using an integral inequality, He et al. [18] delved into the problem of asymptotic stability for various classes of differential TDFOS. Ben Makhlouf, in [19], studied the FTSA of nonlinear TDFOS using a fixed point approach. Naifar et al., in [19], presented the quasiuniform stability of FOS neural networks with mixed delay using the generalized Gronwall inequality. Thanh et al., in [20], studied the FTSA of FOS with ITVD. Phat et al., in [21], proved the FTSA of singular TDFOS. The problem of event-triggered control is treated in [18]. Based on LMIA and Mittag–Leffler function, sufficient conditions, which can be solved via the LMI Toolbox, were proposed in [20] to study the FTSA of a fractional-order linear system with ITVD. The CFD was considered in this work.
Motivated by the work presented in [20], we provide a more general version of the given LMIs conditions. In this concept, the proposed results allow for a lot more flexibility when it comes to resolving these LMIs, making solutions easier to find.
Inspired by the discussions above, this study explores the FTSA and the FTFC problems of Takagi–Sugeno TDFOS with nonlinear perturbations via LMIA. Cases of both CFD and CTFD are considered. The main highlights of this paper are as follows:
- Takagi–Sugeno fuzzy modeling is extensively employed for approximating nonlinear dynamics, including FOS. Recent papers have extended the modeling approach of FOS to include time-varying delay using the CFD. However, there are no studies dealing with the combination of CTFD and delayed Takagi–Sugeno fuzzy models in the literature. This work presents the first investigation of the class of delayed Takagi–Sugeno fuzzy models with a tempered derivative.
- This paper investigates the finite time stability problem of Takagi–Sugeno fuzzy TDFOS with CTFD. This problem is more challenging than the asymptotic stability problem for two reasons. Firstly, finite time stability is sensitive to initial conditions. Indeed, the stability is guaranteed for a restricted region of initial conditions, which requires stricter constraints compared to asymptotic stability. Secondly, the convergence of the system state is imposed onto to a ball centered at the origin within a finite time.
- The FTSA and FTFC results can be directly derived from the class of FOS with CFD as corollaries of the results obtained for the case of CTFD. This offers a unified framework that permits the seamless transition between CTFD and CFD.
- In [20], the LMI conditions depend on a specific positive scalar, which is the upper bound of the delay. The proposed results provide greater flexibility in resolving these LMIs. In fact, this upper bound can be any positive scalar.
- Two means of FTSA and FTFC are developed. In the first one, two stages are proposed in the analysis. LMIs are firstly solved and a minimizing problem, containing a Mittag–Leffler function, is then adressed. In the second way, the previous two stages are solved in only one stage, which allows us to reduce the conservatism.
The remainder of this paper is organized as follows: Section 2 covers the preliminaries, providing the necessary definitions for CTFD and finite time stability. In addition, the Takagi–Sugeno fuzzy TDFOS is presented. In Section 3, we present the FTSA of the considered model; this is followed by Section 4, where we address the FTFC. Section 5 illustrates our theoretical findings through two examples, and finally, Section 6 concludes the paper.
Notations: .
2. Preliminaries
The purpose of this section is to provide some basic information about tempered fractional calculus.
Definition 1
([13]). Let and . The tempered fractional integral of order δ of v is given by
where is the Riemann–Liouville fractional integral of order δ.
Definition 2
([13]). Let and . The CTFD of order δ of v is given by
where
If , then the Caputo tempered fractional derivative of order δ for is given by:
Definition 3
([11]). The Mittag–Leffler function is given by
where , , .
If , we consider .
Lemma 1
([13]). Let , and an absolutely continuous function ; therefore,
Lemma 2
([13]). Consider the system
where and . The solution of the system is as follows: (2)
Lemma 3
([21]). Let , , and a function be non-decreasing. Then,
implies
In the following, let us consider the Takagi-=Sugeno TDFOS:
The model rule is as follows: . If is and is , then
with , , , and , . , and representing the state, the control input, and the nonlinear perturbations, respectively.
Assumption 1.
Assume that and , such that , verifying the Lipschitz condition given below:
Consider the following feedback controller:
The model rule is as follows: . If is and ⋯ and is then
where are feedback gains.
Using the fuzzy blending, (7) and (9) are expressed as follows:
where
It is clear that
In the rest, is used to denote . Combining (10) and (11), we get
Definition 4
Lemma 4
([22]). For the given matrices and , we have
This is satisfied for any .
For the sake of brevity, we use and instead of and , respectively.
3. FTSA for Takagi–Sugeno TDFOS
In this section, we consider (13) with :
Theorem 1.
Proof.
Let
Using Lemma 1, we can obtain
Based on Lemma 4, we have
Combining (20) and (21), we obtain
based on inequality (8), where .
The inequality (16) implies that
Let
Using (6) and (22), we can obtain
From Lemma 9 in [23], we can obtain the following:
Therefore,
For , we can obtain
Therefore,
Let ,
Then,
It follows from Lemma 3 that
Thus,
Hence, if
and
therefore,
Then, the FOS is FTS with respect to . □
Remark 1.
Theorem 2.
Thw following two steps should be confirmed:
Step 1: For a given , there are with and , such that the following LMIs are satisfied:
Step 2: For the given and , minimize subject to (17);
then, the FOS (15) is FTS with respect to ,
Proof.
Remark 2.
The two-step method, proposed in Theorem 2, is too conservate. In order to relax this result, we propose, in the next Theorem, conditions which can be solved by the LMI Toolbox in only one step.
Theorem 3.
For a given , if the following one step is confirmed:
Proof.
The one-step result is obtained by bounding P. □
When considering Takagi–Sugeno TDFOS with CFD and without perturbations,
we derive the following two-step and one-step corollaries:
4. FTFC Takagi–Sugeno TDFOS
Now, we consider the system presented in (13).
Theorem 4.
Proof.
Consider the Lyapunov function as presented in (19). Following a similar approach as in the proof of Theorem 1, we obtain:
then, the FTS of the closed-loop system (13) is ensured if
and (17) are satisfied.
By pre- and post-multiplying (37) by in which , we can obtain
where .
Similarly to FTSA results, we can obtain the following FTFC results:
Theorem 5.
The following two steps should be confirmed:
Step 1: For a given , there are , with and , such that LMIs (33) are satisfied.
Proof.
Theorem 6.
For a given , the following step should be completed:
Proof.
By bounding X within and , the problem can be solved in a single step. Indeed, and . □
Remark 3.
All previous results can be applied to linear TDFOS when , .
5. Illustrative Examples
5.1. Example 1
In order to demonstrate the advantage of our results compared to [20], we consider a linear FOS without control , in which
The ITVD is . It is clear that and .
Case 1: (The CFD case) and without perturbations .
The design procedure that provides the minimum of involving LMIs conditions that can be obtained in one step is better that the two-step approach for two main reasons. The first one is the reduction in computational effort. Indeed, when the LMI problem and the minimization problem are solved simultaneously, the interaction between the two problems is handled automatically, avoiding the requirement of multiple recalculations. The second reason is the reduction in conservatism. In fact, when the two problems are solved together, the optimization problem can consider both simultaneously, leading to a possibly more integrated optimal solution. Table 1 lists the comparison results regarding the minimum allowed , which was obtained in this paper using the theorem of Thanh et al. [20] and Corollaries 1 and 2. This demonstrates not only the advantage of the one-step result but also the importance of selecting a specific positive scalar , which must not be equal to .

Table 1.
Comparison results of the minimum for the CFD case without perturbations.
Case 2: (The CTFD case) and with perturbations , .
According to (18), we get for .
Our objective is to calculate the minimum allowable , c and , such that the system is stable within a finite time.
Table 2 lists the comparison results regarding the minimum allowed via Theorems 2 and 3. It can be seen in this table that the one-step process produces better results than the two-step process.

Table 2.
Comparison results of the minimum for CTFD case.
The time evolution of is shown in Figure 1 for the initial condition
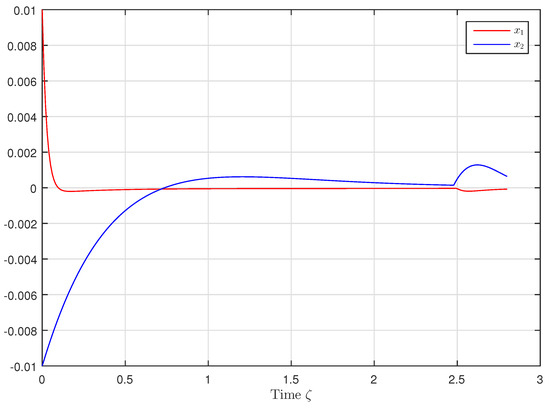
Figure 1.
Time evolution of .
5.2. Example 2: Application to an Inverted Pendulum
The nonlinear dynamics of the inverted pendulum system are modeled using a two-rule Takagi–Sugeno fuzzy model [24]. The first rule describes the symmetrical dynamics, where the angular displacement is about 0, while the second rule captures the asymmetrical dynamics, with the angular displacement of about . The overall Takagi–Sugeno fuzzy model with perturbed delay and CTFD is as follows:
where
We chose the ITVD and the initial conditions provided in Example 1, where Figure 2 shows the time evolution of without control. It demonstrates that the open-loop system is not finite-time-stable, as the states diverge over time.
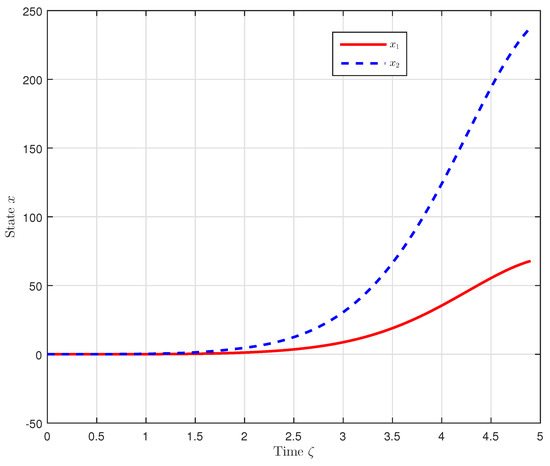
Figure 2.
Time evolution of without control.
Now, our objective is to design an FTFC. Therefore, by solving LMIs in Theorem 6, we can obtain: The minimum of is and the gains are as follows:
Figure 3 shows the time evolution of with FTFC. It illustrates that the FTFC successfully prevents divergence. It is clear that and converge within s to a small ball.
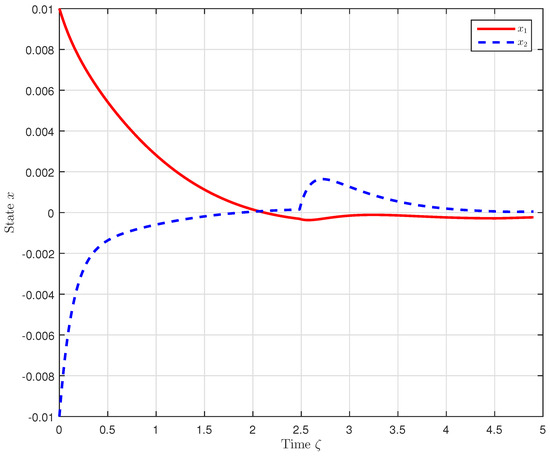
Figure 3.
Time evolution of with FTFC.
6. Conclusions
This paper investigates the FTSA and FTFC challenges of using Takagi–Sugeno TDFOS with ITVD. By utilizing the Linear Matrix Inequalities Approach (LMIA), we establish conditions that account for nonlinear perturbations. Two methods are introduced: the first is presented in two steps, while the second is achieved in just one step. These conditions are solved using the LMI toolbox. The updated results are presented as straightforward corollaries for CFD and linear models. To highlight the effectiveness of these results, two illustrative examples are provided. Future research will explore the FTSA problem of singular Takagi–Sugeno TDFOS, which is significantly more challenging than that used for regular systems, as it affects both the regularity and the impulse-free issues. Additionally, improvements can be made by investigating challenges such as uncertainties and sensor faults. In future work, we will study the FTSA and FTFC of impulsive fractional-order time delay systems.
Author Contributions
H.G.: Writing—review and editing, Investigation. M.T.: Conceptualization, Writing—review and editing, Investigation. L.M.: Software, Visualization. A.B.M.: Methodology and Validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Saud University through Researchers Supporting Project number (RSPD2024R685), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
No underlying data were collected or produced in this study.
Acknowledgments
The authors acknowledge ”Researchers Supporting Project number (RSPD2024R685), King Saud University, Riyadh, Saudi Arabia”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, B. Finite-time stability analysis and stabilization by bounded linear time-varying feedback. Automatica 2020, 121, 109191. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Q.; Tang, X.; Sun, L.; Deng, P.; Liu, H. Dynamic stability analysis of jointed rock slopes using the combined finite-discrete element method (FDEM). Comput. Geotech. 2023, 160, 105556. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Fuzzy Syst. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Kim, E.; Lee, H. New approaches to relaxed quadratic stability condition of fuzzy control systems. IEEE Trans. Fuzzy Syst. 2000, 8, 523–534. [Google Scholar]
- Nguyen, A.-T.; Campos, V.; Guerra, T.-M.; Pan, J.; Xie, W. Takagi–Sugeno fuzzy observer design for nonlinear descriptor systems with unmeasured premise variables and unknown inputs. Int. J. Robust Nonlinear Control 2021, 31, 8353–8372. [Google Scholar] [CrossRef]
- Cao, Y.-Y.; Franck, P.M. Analysis and synthesis of nonlinear time-delay system via fuzzy control approach. IEEE Trans. Fuzzy Syst. 2000, 8, 200–211. [Google Scholar]
- Gassara, H.; ElHajjaji, A.; Chaabane, M. Observer-based robust H∞ reliable control for uncertain TS fuzzy systems with state time delay. IEEE Trans. Fuzzy Syst. 2010, 18, 1027–1040. [Google Scholar] [CrossRef]
- Yanga, F.; Guana, S.; Wang, D. Quadratically convex combination approach to stability of T–S fuzzy systems with time-varying delay. J. Frankl. Inst. 2014, 351, 3752–3765. [Google Scholar] [CrossRef]
- Mátyás, A.; Nagy, Z.; Lendek, Z. Stabilization of time-delay nonlinear systems using Takagi-Sugeno fuzzy models. Fuzzy Sets Syst. 2024, 480, 108861. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. The fractional non-polynomial spline method: Precision and modeling improvements. Math. Comput. Simul. 2024, 218, 512–525. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Li, C.; Deng, W.; Zhao, L. Well-posedness and numerical algorithm for the tempered fractional differential equations. Discret. Contin. Dyn. Syst.-Ser. B 2019, 24, 1989–2015. [Google Scholar] [CrossRef]
- Deng, J.; Ma, W.; Deng, K.; Li, Y. Tempered Mittag-Leffler Stability of Tempered Fractional Dynamical Systems. Math. Probl. Eng. 2020, 2020, 7962542. [Google Scholar] [CrossRef]
- Chen, L.; Guo, W.; Gu, P.; Lopes, A.M.; Chu, Z.; Chen, Y.Q. Stability and Stabilization of Fractional-Order Uncertain Nonlinear Systems With Multiorder. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 576–580. [Google Scholar] [CrossRef]
- Chen, L.; Gu, P.; Lopes, A.M.; Chai, Y.; Xu, S.; Ge, S. Asymptotic Stability of Fractional-Order Incommensurate Neural Networks. Neural Process. Lett. 2023, 55, 5499–5513. [Google Scholar] [CrossRef]
- Makhlouf, A.B. Partial practical stability for fractional-order nonlinear systems. Math. Methods Appl. Sci. 2022, 45, 5135–5148. [Google Scholar] [CrossRef]
- Yousefi, M.; Binazadeh, T. Delay-independent sliding mode control of time-delay linear fractional order systems. Trans. Inst. Meas. Control 2016, 40, 1212–1222. [Google Scholar] [CrossRef]
- Huong, D.C. Event-triggered H∞ control for fractional-order time-delay systems. Asian J. Control 2024. [Google Scholar] [CrossRef]
- Makhlouf, A.B. A novel finite time stability analysis of nonlinear fractional-order time delay systems: A fixed point approach. Asian J. Control 2022, 24, 3580–3587. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N. Improved approach for finite-time stability of nonlinear fractional-order systems with interval time-varying delay. IEEE Trans. Circ. Sys. II Exp. Bri. 2019, 66, 1356–1360. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N.; Niamsup, P. New finite-time stability analysis of singular fractional differential equations with time-varying delay. Fract. Calc. Appl. Anal. 2020, 23, 504–519. [Google Scholar] [CrossRef]
- Shi, G.; Zou, Y.; Wang, C. An algebraic approach to robust H∞ control via state feedback. Syst. Control Lett. 1992, 18, 365–370. [Google Scholar] [CrossRef]
- Choi, S.K.; Kang, B.; Koo, N. Stability for Caputo Fractional Differential Systems. Abstr. Appl. Anal. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Q.-G.; Lee, T.H.; He, Y.; Chen, B. Design of observer based H∞ for fuzzy time-delay systems. IEEE Trans. Fuzzy Syst. 2008, 16, 534–543. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).