3.1. The Soliton Near-Field
In this work, we consider a particular development of the dBB theory, namely, the DS theory proposed originally by de Broglie in 1925 [
16,
17]. This theory, we will show, can bring new insights concerning the issue of nonlocality. Moreover, it is important to mention that de Broglie strongly modified his theory in 1927 and in the 1950s [
6,
11] in collaboration with Vigier [
47]. It is often this last version that is mentioned in the literature, i.e., when it is not completely ignored (for useful reviews about the DS approach, see [
48,
49]). The DS theory, inspired by Einstein’s early works on photons, is based on the idea to describe particles as moving singularities of a classical scalar field theory (by a singularity, we mean that the field is infinite at the position of the particle). De Broglie first considered [
16,
17] that each particle is a point-like moving clock pulsating at its Compton frequency
(in the rest of this work, we will use the relativistic conventions
). This actually means that the particle has internal properties. If this particle is at rest in the laboratory frame, the clock ‘generates’ an extended stationary field surrounding the singularity. When the particle is in motion, this field guides the particles and interacts with obstacles. De Broglie hoped [
17] that the interaction between this wave-like field, the particle, and its environment could explain wave–particle duality (associated with interference fringes) and the stationary orbits required in the Bohr atomic model.
The fundamental scalar field
used by de Broglie is outside the singularities at space-time point
, a solution of a basic linear and local field equation, i.e.,
The simplest oscillating solution associated with the pulsation
defined in the rest frame
of the singularity is the monopolar (spherically symmetric) field:
with
being the radial distance to the singularity (particle) located at the spacial origin, and
being a constant. Remarkably, when this monopole field is studied from a different Lorentz frame
where the field singularity moves at the velocity
v (along the
x-direction), the relativistically invariant scalar
u-fields now reads
with
and
. What is beautiful here is that the (scalar relativistic invariant) phase wave
involved in
u is actually a plane wave solution of the linear Klein–Gordon equation
. It is easily shown that the particle (clock) is synchronized with the
-wave and therefore the
u-field during its motion. The whole picture is interesting because, on the one hand, it is inherently classical and relativistic, i.e., in the same sense as Maxwell theory or general relativity are classical and relativistic (the
u-field propagates in space-time with the particle). On the other hand, this approach suggests that wave–particle duality and more generally quantum mechanics is just a sophisticated version of classical physics involving oscillating and moving point sources coupled to a field. In order to prove this hypothesis, de Broglie hoped to be able to calculate trajectories of the singularities in complex environments involving external potentials like the Coulomb potential or the double slit barrier. In the DS approach, the
u-field should be able to influence the motion of the particle singularities in such a way as to reproduce quantum mechanics. We stress that in 1927 de Broglie used the linear Klein–Gordon equation instead of the simple Equation (
5) but this does not simplify the analysis [
6,
49].
Clearly, this picture with trajectories guided by a wave is linked to the dBB pilot-wave theory discussed before. In the 1920s, de Broglie could not develop this DS program mathematically (see the discussion in [
49]) and it is mostly for this reason that he switched to the simpler dBB pilot-wave approach. The problem of course is that, in the dBB theory, the nature of the guiding field is more obscure and more ‘epistemic’. In the end, the dBB theory was developed in the configuration space, not in the 3D physical space, and therefore the initial intuition of the DS project was lost. Importantly, de Broglie also abandoned in 1928 the pilot-wave theory because he felt the theory was unable to explain the strong form of nonlocality involved in quantum mechanics (in 1928, that issue was related to the difficulty for understanding the mysterious concept of ‘wave function collapse’ or ‘reduction’ in terms of Einstein’s special relativity prohibiting faster-than-light communication [
8]). Moreover, in 1952, de Broglie together with Vigier [
11,
47] and a few collaborators went back to the DS program and tried to show that singularities or solitonic solutions of some unknown wave equations are following the paths or trajectories predicted by the dBB theory in the configuration space. The most important modification they suggested was, in analogy with general relativity, to consider nonlinear wave equations for the
u-field in order to remove the mathematical singularities at the particle positions. In such an approach, particles are becoming ‘solitons’, i.e., localized solitary ‘bunched’ waves propagating as a whole without dispersion. However, nonlinear wave equations are even more difficult to solve than linear wave equations with moving singularities. Apart from that point, they could not define a precise nonlinear wave equation that could implement the DS goals. Moreover, the most problematic point is perhaps that de Broglie underestimated the impact of nonlocality in the DS theory. Indeed, the dBB approach is nonlocal in the configuration space. How could a nonlinear but local classical field theory defined in the 4D relativistic space-time reproduce and justify the nonlocality of the dBB theory? Following some old intuitions going back to Einstein, they suggested that nonlocality existed only in the interacting regime when the particles were not separated too much [
50,
51]. Furthermore, Bell’s theorem came out in 1965 and de Broglie could not assimilate and accept the lesson of this central result [
52,
53]. (That was not the case of Vigier, who stopped working on the DS project for a while and moved to alternative nonlocal and stochastic hidden variables approaches à la Bohm or Nelson [
54]).
In the present research (discussed in more detail in [
18] following a related article [
55]), we are taking seriously the idea of a particle–soliton but at the same time we are going back to the old 1925 ideas sketched in Equations (
5)–(
7). What we find motivating is the deep time-symmetry of this old picture. Indeed, it is visible that the field Equation (
6) is a solution of the wave equation
involving a source term. Equation (
6) is actually the time-symmetric solution, i.e., the half-sum of retarded and advanced radiating waves:
What actually inspired de Broglie was the work of Tetrode and Page [
56,
57,
58] (later rediscovered by Fokker [
59] and Wheeler with Feynman [
19]) on the time-symmetric electrodynamics in which action-at-a-distance is mediated by the half-sum of retarded and advanced electromagnetic waves emitted by electrons and protons. Page [
57,
58] suggested that the time-symmetric field could explain why electrons orbits in Bohr’s atoms do not radiate, and this was one of the initial crux of de Broglie’s attempt in 1925 [
16,
17]. Interestingly, de Broglie abandoned this idea in 1926 and never went back to it even after his former student Costa de Beauregard rediscovered a sequel of the idea in 1942 [
40] in order to solve the EPR paradox! After this work [
40], many retrocausal and time-symmetric theories were developed in order to explain the violations of Bell’s inequalities (see for example [
41,
43,
44] and the interesting retrocausal dBB theory [
45,
46]). All this clearly motivates the present work.
Here, we start from the de Broglie DS and postulate the following nonlinear wave equation for the
u-field [
18]:
where
is a covariant derivative involving the electromagnetic potential four-vector
and
e is an electric charge. The nonlinear function we consider [
18] is the simple ‘Lane–Emden’ fifth power law, where
is a (nondimensional) coupling constant (which can be positive or negative) and
is a length that will define the typical radius of our soliton. Importantly, this nonlinearity allows us to define explicit analytical solitons (at least in the near-field of the particle, i.e., for distances
R to the center such that
). This equation is clearly different from the quantum linear Klein–Gordon equation
involving the standard relativistic wave function
for scalar (spin 0) particle. We stress that if the field decays sufficiently, we can, in the far-field of the soliton, approximate Equation (
9) by the linear equation
. This property is fundamental since it allows us to develop a simplified approach for describing the soliton if
(as shown in
Section 3.2).
In order to find a solution to Equation (
9), we use the polar form
and obtain after separation the following:
Equation (10a) is generally named the (nonlinear) dBB Hamilton–Jacobi equation, and Equation (10b) is reminiscent of the electric current conservation. This defines a hydrodynamical representation of the nonlinear Klein–Gordon equation. Similarly, we can define a hydrodynamical representation for the field
solution of the linear Klein–Gordon equation:
with
being the so called quantum potential [
6,
9,
11] used in the pilot-wave theory. We solve the pair of Equation (10) in the region where the soliton profile is supposed to be well peaked (i.e., near the center or soliton ‘core’ surrounding a mean trajectory
labeled by the proper time
along the path). For this, we assume with de Broglie the so-called ‘phase-harmony condition’ [
6,
11]:
To every regular solution of the linear Klein–Gordon equation corresponds a localized solution of Equation (9) having locally the same phase , but with an amplitude involving a generally moving soliton centered on the path and which represents the particle.
In other words, this phase-locking condition forces the two waves
u and
to vibrate locally in unison. We thus consider a Taylor expansion of the phase
in the vicinity of
in a space-like hyperplane crossing
and defining a local instantaneous rest frame for the particle center (this hyperplane
is defined by the condition
with
). We assume:
where
is a new collective coordinate introduced to increase the number of degrees of freedom. As shown in [
18,
55], we can define the fluid velocities
and
in the regions where
. The velocity
is associated with the dBB pilot-wave interpretation of 1927 [
6] and de Broglie postulated that the particle is guided by the
-wave:
This formula is non-ambiguous, at least in the regime
avoiding tachyonic trajectories, and we limit our analysis to that case in the main text of this article. However, the tachyonic or superluminal regime can be self-consistently described in the dBB pilot-wave approach and is discussed in the context of our DS proposal in
Appendix A. Moreover, from our DS theory and Equation (
12), we deduce [
18,
55]
and similarly
,
. The whole picture is actually self-consistent if the soliton central trajectory
is identified with the dBB pilot-wave trajectory given by Equation (
13). We thus have
justifying the guidance postulate of de Broglie. In other words, we show that it is always possible to find locally a first-order matching
,
. The two phase waves
and
S of the two fields
u and
are thus connected along the curve
and this is the core of the DS or phase-harmony approach. We stress that from the dBB dynamics Equations (11a) and (11b) and the guidance formula, we obtain the second-order relativistic ‘Newton’ law already found by de Broglie in 1927 [
60]
with
the Maxwell tensor field at point
. The varying de Broglie mass
(i.e., varying quantum potential
) is central in order to recover the non-classical features of quantum mechanics specific of the dBB pilot-wave theory.
An important relation is obtained from the hydrodynamical conservation Equation (10b) and the phase-harmony Equation (
12) constraint:
The first two equalities concern fluid deformation and compressibility, where we introduce an infinitesimal co-moving 3D fluid volume
(defined in the local rest frame
associated with
) driven by the fluid motion. In particular, we see that if the soliton is undeformable, we must have
, and thus from the last equality in Equation (
16), we obtain
. Moreover, if this soliton is undeformable, we must also have
, and thus from Equation (
16),
must hold along the trajectory
. This is conflicting with the dBB theory imposing a varying
along particle trajectories. We conclude that we will have to relax the natural assumption of undeformability (i.e.,
,
) in order to develop a self-consistent DS theory reproducing the dBB trajectories, i.e., agreeing with quantum predictions.
In order to find the soliton profile
f, we rewrite Equation (10b) in the rest frame
near the soliton center (in the Fermi limit
where we have
[
18,
55]) and obtain the partial differential equation for the soliton profile for points
x belonging to
and localized near
:
with
[
18,
55]. Furthermore, in the near-field, if we suppose the soliton core size
to be much smaller than the Compton wavelength
, we can use the stronger approximation
which is known as the Lane–Emden equation [
18]. This equation admits the spherically symmetrical exact solution:
which is parametrized by the constant
and has the dilation invariance
. Far away from the soliton ‘core’, i.e., if
, this field has the asymptotic monopolar limit
. In this limit, it is justified to use instead Poisson’s equation
for a point-like source with effective ‘scalar-charge’
. We will come back to the asymptotic field later, but for the moment we stress that Equation (
19) is an approximate equation keeping its general validity if the motion of the soliton is not varying too fast (as justified in [
55]) and we thus physically interpret the parameter
as a new collective coordinate for the soliton. More precisely, we now assume that during its motion, the soliton typical extension
changes (adiabatically) with time
and we write
or equivalently
where
defines the dynamics concerning the radius (the proper time
is chosen arbitrarily to correspond to an initial point
along the trajectory).
In order to fix the
-dynamics, we use the local conservation law for a fluid element located at the soliton center Equation (
16):
and we have by integration
defining a constant of motion along a given trajectory. Furthermore, from Equation (
19),
and
(a more rigorous justification is given in [
18]). And we deduce:
Moreover, from Equations (
16) and (
22), we deduce
which, together with Equation (
22), defines the complete deformation/compression of the soliton near-field.
At this stage, it is useful to summarize our main findings. Starting from the picture of a deformable soliton, we introduced some collective coordinates to describe its approximate structure and evolution. The central idea is to consider that the soliton is strongly peaked near a main trajectory in space-time
and that we can solve the nonlinear equation in the near-field. The phase
reduces to a function
along the trajectory. We were then able to show, after including the deformation of the soliton
, how the motion of the soliton can follow a dBB path with dynamical Equation (
15). The soliton thus acts as a dBB particle guided by the phase
of a solution of the linear Klein–Gordon equation. In other words, the DS theory recovers the dBB pilot-wave from a more fundamental field. The idea we followed was, in agreement with de Broglie and also Einstein, to remove the strangeness of the quantum potential by showing how to rederive it from a classical but nonlinear field theory.
We stress that the model developed here for a subluminal soliton can be extended to the superluminal or tachyonic sector. This is presented briefly in
Appendix A. While it could, at first look, be curious to derive superluminal motions from a purely local DS theory, respecting the principle of special relativity, we cannot a priori forbid such a regime since the dBB pilot-wave theory for a point-like particle obeying the Klein-Gordon theory predicts that, in some cases, such a particle can reach the speed of light and even cross the light cone (i.e., if and only if the mass
vanishes while the particle crosses the light cone as it was already predicted by de Broglie in 1927 [
7,
11]). In the context of the DS theory, trying to reproduce the dBB pilot-wave predictions, the existence of tachyonic waves is reminiscent of the so called ‘X-waves’ observed in optics, where a region of a wave-packet is allowed to propagate faster than the speed of light in vacuum if and only if this cannot be used to transfer information or energy, i.e., similar to a phase-wave (see [
61] for an illuminating discussion on this non-signaling constraint on X-waves). Since the tachyonic dBB motions are generally associated with evanescent or transient
-fields localized in finite space-time regions, there is no way to violate no-signaling. Using the DS theory, the solutions we obtain also involve some ‘X-waves’, which can only have a physical meaning in transient regions. Therefore, altogether, the picture obtained from the DS theory is consistent even in the tachyonic regime.
3.2. The Soliton Far-Field
The previous theory developed for the near-field can be used to define the mid-field and far-field of the soliton i.e., if we do not neglect the mass term
in Equation (
17). We consider first the case of an uniform motion where
and search for a spherical solution of
As shown in [
18], if we can assume
(i.e., a very small soliton), Equation (
24) admits the solution
which is an interpolation between the near-field Equation (
19) and the far-field de Broglie monopolar solution
obtained if
. Such a far-field is a solution of the inhomogeneous d’Alembert equation
with
.
Two remarks can be made here: First, note that the coefficient and the frequency of the soliton are not determined univocally by the theory. The soliton admits a continuous frequency spectrum corresponding to a continuous mass spectrum . Hence, it means that the present theory would have to be completed to fix the mass of the particle. Moreover, assume that the mass is fixed. In the context of the dBB pilot-wave theory (which in our DS approach defines the soliton trajectory), it corresponds to a situation where from Equation (11a) (i.e., ). This is associated with a guiding plane wave , which in the rest frame reads . Yet, the dBB pilot-wave theory can also generate constant masses different from if the quantum potential is constant but different from zero. This is, for example, the case if the guiding field solution of the linear Klein–Gordon equation reads (corresponding to a 1-dimensional stationary wave along the spatial x direction with pulsation and k the wave vector along the x direction) or (corresponding to a 1-dimensional evanescent wave along the spatial x direction with pulsation ).
The second remark concerns the structure of the far-field and its description by an inhomogeneous d’Alembert equation. It is clear from the general structure of Equation (
9) that the nonlinearity of the wave equation can be neglected in the far-field since
, and therefore we can use a linearized approximation
far away from the soliton core. More precisely, as shown in [
18], the far-field of the Lane–Emden soliton with core trajectory
satisfies the equation:
The second line is written in the laboratory frame, where at a time
t the soliton core behaves as a point-like particle with position
and velocity
(here we assume the trajectory being time-like).
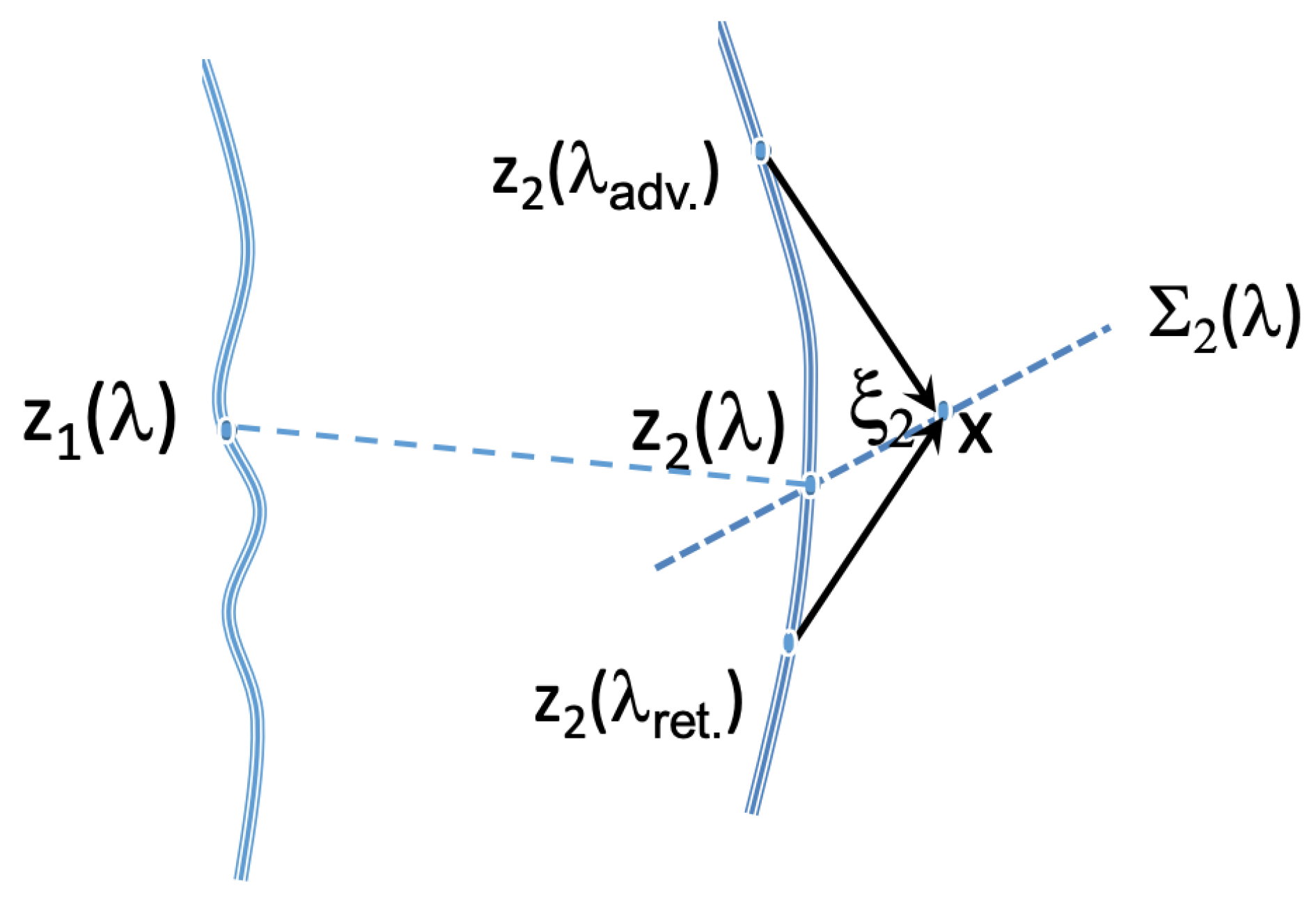
The general solution of Equation (
27) reads
where
is a solution of the homogeneous equation
, and the propagator
satisfies
. As it is well known, the choice of the propagator is not univocal; only the total field
has a physical unambiguous and absolute meaning. That means that we can have different representations of the field given by Equation (
28) by changing of propagator. The most common propagators are the retarded (respectively advanced) one
(respectively
) associated with radiation in the forward (respectively in the backward) light cone with apex at point
. Advanced waves correspond to anticausal features associated with ‘conspiratorial’ absorptions by sources (i.e., violating the second law of thermodynamics) and are therefore often not used. Moreover, this is actually related to the boundary conditions that are the most adapted in order to analyze the specific problem considered. Indeed, we can always write an arbitrary solution of Equation (
28) equivalently as
or
, and the different free fields are thus not independent. As an example, a typical (in the thermodynamical sense) causal field is generally written after Sommerfeld as a pure radiative field with boundary conditions
. This in turn leads to the free ‘outcoming’ field
, which is indeed non-singular.
As explained in the previous
Section 3.1, in 1925 de Broglie [
16,
17] considered a time-symmetric field in analogy with works in classical time-symmetric electrodynamics [
19,
56,
57,
59]. Therefore, it seems natural to use such time-symmetric description in connection with Equation (
28). We first write
with
being a free wave solution of the homogeneous equation and the time-symmetric source term
. We then assume the boundary condition
(i.e.,
). The
u-field of Equation (
28) now reads:
with
the time-symmetric propagator. In the absence of an external field (i.e.,
) this propagator reads:
(with
). In the presence of an external electromagnetic field
, the propagator reads
where we introduce
(using the operator
), which defines the reflected part of the propagator resulting from the interaction of the vacuum solution
with the potential
A. Therefore, the
u-field splits as
Inserting Equation (
30) into Equation (
29) leads to [
18]:
with
and where the retarded proper time
(respectively, advanced proper time
) corresponds to the point
(respectively,
) belonging to the trajectory
, in which
u-radiation propagating along the forward light cone (respectively, backward light cone) is reaching the point
x. This
u-field is clearly reminiscent from the retarded and advanced Lienard–Wiechert potentials in classical electrodynamics and has several remarkable properties. Most importantly, near the singularity
, i.e., for points located at a distance
from the singularity in the space-like (rest frame) hyperplane
, we have approximately [
18]:
From this, we deduce at the lowest order
and we recover the asymptotic soliton near-field (i.e., for
but still in the near-field
) discussed in the
Section 3.1. Furthermore, for a uniform motion with
,
,
,
,
, Equation (
34) leads to
, which is the field associated with the de Broglie stationary monopole discussed above. Therefore, the time-symmetric far-field matches the near-field.
An important feature of this theory concerns the phase of the singular far-field when
r tends to zero. Indeed, from Equation (
34) we deduce in the absence of an external field:
which can be compared with the Taylor expansion
and shows that the first-order term vanishes:
Yet, by definition
in
, and consequently
is parallel (i.e., proportional) to
. In other words, since
, we recover, in the absence of an external field
, the DS guidance formula Equation (
14)
. This result is robust, and in [
18] we showed that it survives in the presence of an external electromagnetic field when the full propagator Equation (
31) must be considered near the singularity. More precisely, we then have
and we deduce
implying
Therefore, as before, we recover the guidance formula, i.e.,
Some remarks are important concerning this formula:
First, recovering the guidance formula was expected since de Broglie already gave a general derivation for the
u-field in 1926–1927 [
6]. As reviewed in [
49], de Broglie’s deduction is based on the conservation law Equation (10b) written as
where
is the 3-velocity of the
—fluid and
. Near the singularity, de Broglie assumed
, where
F is a regular function and
is the singularity trajectory. De Broglie’s assumption is indeed satisfied by our singular field
in a reference frame where the singularity is practically at rest (i.e.,
). From the property
we thus deduce:
which implies (near the singularity) the guidance formula
Using covariant relativistic notations, this is mathematically equivalent to Equations (
38) and (
39).
Moreover, and this constitutes our second remark, the guidance formula is not obvious to satisfy since it requires a well-defined gradient
for points near the singularity. In our theory based on a time-symmetric construction, this is automatically fulfilled but this would not be the case if we instead assumed a pure retarded
or advanced
field. Indeed, instead of Equation (
37), we obtain:
with the minus (respectively, plus) sign for a pure retarded (respectively, advanced) wave. We deduce
, which implies a phase discontinuity on the singularity. Watched in the instantaneous rest frame
, this condition reads in the absence of an external field:
which is clearly reminiscent of the retarded (respectively, advanced) singular field
In other words, only the time-symmetric monopole
removes the phase discontinuity associated with retarded or advanced waves resulting from an unadapted selection of the propagator
.
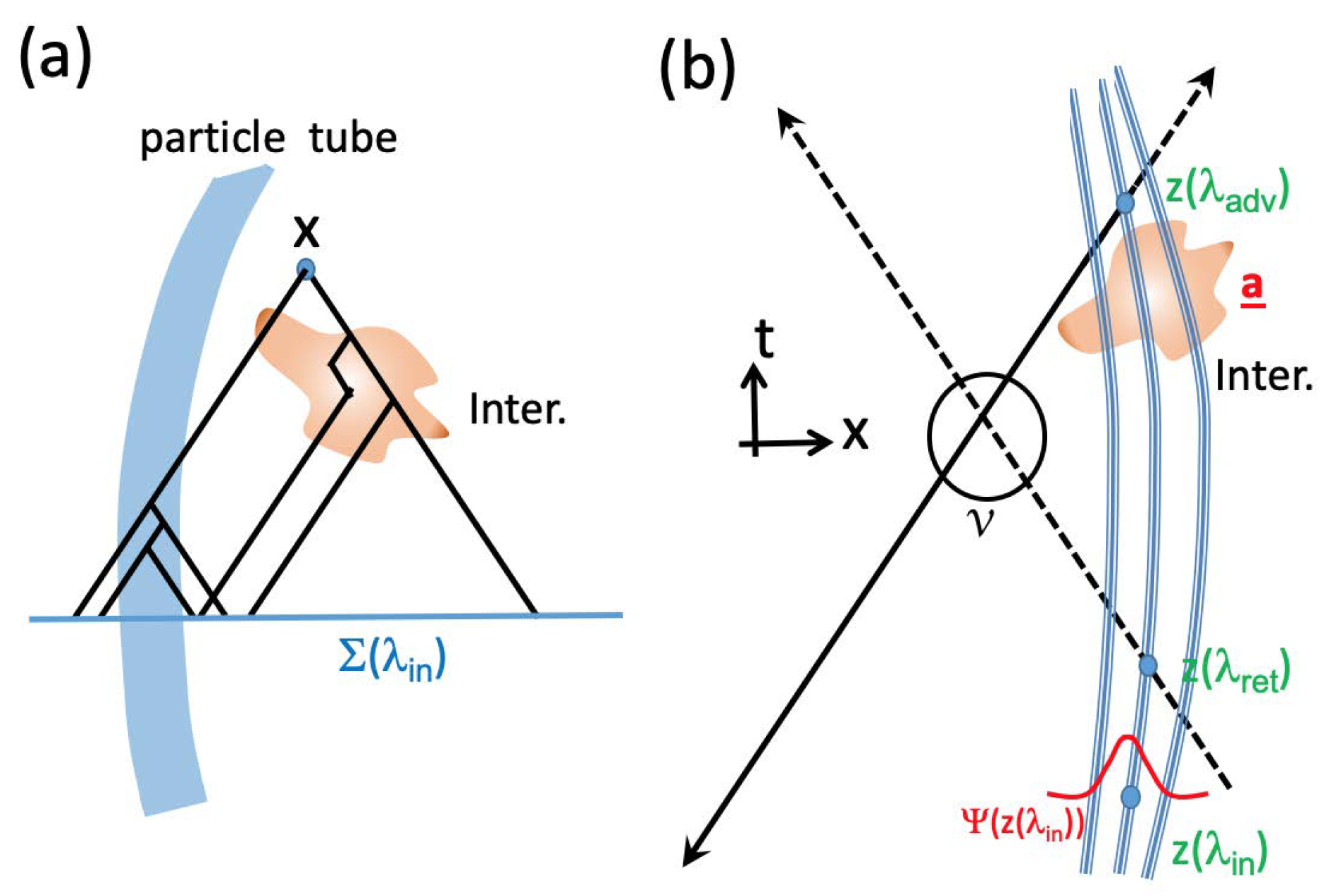
Regarding the guidance formula derived here from the far-field, we stress that it a priori only concerns the
u-field containing a singularity or a soliton, not the
-field, which is much more regular and smooth and has a statistical interpretation, e.g., in the dBB pilot-wave theory. However, as discussed in
Section 3.1, the soliton near-field used in our DS theory requires the phase-harmony condition Equation (
12) near the core of the particle, and this imposes a first-order contact between the two phase functions
and
S of the
u and
fields:
,
along the curve
. This idea is of course applicable to the singular field considered in this subsection. Therefore, we can here also assume a first-order contact
,
and obtain the full guidance formula needed in the DS theory:
In other words, using a first-order contact (and not a second-order contact, i.e., imposing also
as originally assumed by de Broglie and Vigier [
6,
11,
47]) allows us to develop a self-consistent DS model in both the near-field and far-field.
3.3. ‘Justifying’ the Wave Equation for the -Guiding Field
The present theory for the
u-field left a priori unconstrained or undetermined concerns (i) the precise form of the wave equation for
, and (ii) the physical nature of this
-field. First consider point (i): the mathematical form of the wave equation for the
-field. In our theory [
18], we assumed that the
-field obeys the linear Klein–Gordon equation. This choice can be approximately justified.
For this purpose, we start with the phase-harmony relation Equation (
12) defining the phase
in the vicinity of the soliton-core trajectory
characterized by the phase
. We do not have to assume here that the soliton is coupled to an external physical wave
with phase
S guiding the soliton. Indeed, it is enough to show that, from
obtained from our wave equation for
u, we can construct a wave equation for a
-field having the properties of the linear Klein–Gordon equation. The method goes back to Vigier and Régnier [
47,
62,
63]. We assume that the soliton trajectory
exists and the phase is given in its vicinity by the phase-harmony condition Equation (
12). Now, we consider a statistical ensemble of solitons and impose a local conservation law
where
plays the role of a density for the statistical fluid in the configuration space of the particle with path
. We thus define a wave field given by
and this allows us to rewrite Equation (
46) as
with
. After transformation, Equation (
48) reads
or equivalently
. Now, the real part
is left unconstrained by this procedure and this leads to the general condition
with
a function of
z, and finally implies:
Clearly, if we separate the real and imaginary part in the wave Equation (
51), we recover Equation (
46) and obtain the generalized Hamilton–Jacobi equation
with
the quantum potential. In order to close our ‘derivation’ of the wave equation, we now consider the semiclassical regime where
and this implies
. In order to recover classical physics for a particle of mass
in an external field
, we impose
and this leads to the linear Klein–Gordon equation
We can also justify the choice
on physical ground: If we assume that in the remote past the soliton has a uniform inertial motion defining in the rest frame a pulsation
, we can identify this motion with
in Equation (
52). Consequently, in order to fulfill the first-order contact hypothesis, we impose
.
The previous reasoning motivates the choice for a guiding field obeying a linear Klein–Gordon equation but clearly does not impose it. This shows that the choice of a guiding -field is not here dictated only by physical reasoning but also by practical features associated with the simplicity of a linear wave equation compared to a nonlinear one.
This in turn leads us to point (ii): What is the physical meaning of the
-field? Indeed, since we are here proposing a minimal model with only a single fundamental
u-field, the
-field cannot be a fundamental independent field interacting with the
u-field (such a different approach has been developed by us in [
55]). Here, we suggest to interpret the
-field as the natural extension of the action
introduced in the old Hamilton–Jacobi equation for a point-like particle. Here, the wave
is seen as a mathematical tool for describing the motion of the soliton with trajectory
and is clearly similar to the role played by
obeying
in the old classical theory. Moreover, in the classical Hamilton–Jacobi theory, the 3D configuration space, with vectors
, defines the set of all possible positions and trajectories for the point-like particle and must be distinguished from the 3D physical space with vector
where the extended soliton is evolving. In the DS theory developed here, the complex wave function
defines a generalization of the Hamilton–Jacobi function adapted to the dynamics of a soliton and
z defines a configuration space for the center of the soliton.
At the philosophical level, we stress that there is an old debate between advocates of the dBB pilot-wave or ‘Bohmian’ mechanics concerning the physical status of the wave function
. De Broglie always emphasized that, for him, the wave function
is not a fundamental of ‘objective’ field but instead a ‘subjective’ probabilistic field [
11]. Quite similarly, Dürr, Goldstein, and Zanghì [
64] wrote that the wave function
is not a physical external agent acting on the particle but better a mathematical (nomological) object used for describing the quantum law of particle (similar to the Hamiltonian function
in classical mechanics). A physical point clearly in favor of this view is the absence of retroaction of the particle on the
-wave in the dBB theory. An objection often made against this nomological view is that, in classical mechanics, the Hamiltonian function is given, whereas the wave function depends on the choice of initial conditions. However, we can easily counter the objection: The problem is not actually the nomological view itself but instead the comparison with the Hamiltonian. As we saw, and in agreement with de Broglie, the good comparison concerns
and
S, i.e., the wave function and the action in the old Hamilton–Jacobi theory. Indeed,
and
S are both dependent on initial conditions, are defined in the configuration space, can evolve in time, and are used to classify ensembles of possible particle trajectories
z. However, we can also perhaps justify the psychological resistance against the nomological view by the non-intuitive features observed in the dBB theory. For example, as already pointed out by de Broglie in 1930 [
8] concerning interference in the double-hole experiment, it looks as if the dynamical motion of the single particle (going through one hole) is affected by alternative motions (going through the second hole) which did not occur but were potentially possible. In classical physics, this does not happen and possible trajectories coming from each hole are just crossing each other, i.e., the particles going through one hole are completely unaffected by the presence of the second hole not crossed. In the DS approach, this non-intuitive aspect of the pilot-wave dynamics is explained by the existence of the
u-field associated with an extended physical phenomena surrounding the soliton core and involving the whole environment of the wave. In other words, the
-dynamics is just an effective description of the soliton core motion
that in practice is neglecting an important part of the
u-wave propagation associated with the retarded and advanced contributions focused on the soliton.