Abstract
In this work, we review and extend a version of the old attempt made by Louis de Broglie for interpreting quantum mechanics in realistic terms, namely, the double solution. In this theory, quantum particles are localized waves, i.e., solitons, that are solutions of relativistic nonlinear field equations. The theory that we present here is the natural extension of this old work and relies on a strong time-symmetry requiring the presence of advanced and retarded waves converging on particles. Using this method, we are able to justify wave–particle duality and to explain the violations of Bell’s inequalities. Moreover, the theory recovers the predictions of the pilot-wave theory of de Broglie and Bohm, often known as Bohmian mechanics. As a direct consequence, we reinterpret the nonlocal action-at-a-distance in the pilot-wave theory. In the double solution developed here, there is fundamentally no action-at-a-distance but the theory requires a form of superdeterminism driven by time-symmetry.
1. Preamble
One hundred years ago, the genius of Louis de Broglie gave birth to quantum wave mechanics that we celebrate in this Special Issue of the journal Symmetry. The consequences of de Broglie’s insights [,,,,], particularly his understanding in 1923 of the great generality of wave–particle duality that applies to every kind of material particles (i.e., not only limited to particles of light as postulated by Einstein in 1905), paved the way for modern quantum mechanics and all its physical and technological implications. Moreover, de Broglie’s intuition was based on a realistic and deterministic picture in which particles follow trajectories in space-time. His view contrasts, and even conflicts, with the usual description of quantum mechanics, associated with the Bohr–Heisenberg ‘Copenhagen interpretation’, in which such a spatio-temporal and causal representation of the world is abandoned and considered as impossible.
It is well known that de Broglie proposed a realistic approach of quantum mechanics, namely, the pilot-wave theory, which he defended in 1927 at the fifth Solvay conference [,]. It is also well known that he soon abandoned it because he felt his theory too paradoxical and too preliminary []. He thus accepted and publicly advocated for 20 years the Copenhagen interpretation and returned to his realistic approach only in 1951–1952 after David Bohm rediscovered a version of the pilot-wave theory (the theory is known as the de Broglie Bohm (dBB) theory [,] or Bohmian mechanics). What is much less known, and rarely discussed, is that de Broglie actually hoped to develop a different approach, namely, the double solution (DS) theory presented in detail in a publication in 1927 [] and defended later in the 1950s []. Contrarily to the dBB pilot-wave theory, the DS proposal is written not in the configuration space for N particles but in the 4-dimensional space-time. The DS theory involves particles having undulatory but localized structures in space-time, whereas the dBB theory involves point-like particles moving in the abstract configuration space with dimensions. De Broglie considered DS as much closer to Einstein’s perspective, where particles are identified with localized solutions of nonlinear field equations (e.g., like in the general theory of gravitation or in the nonlinear electrodynamical theory of Mie, Born, and Infeld [,,]). For de Broglie, like for Einstein, the particle must be a concentrated amount of energy, i.e., a ‘soliton’ or solitary wave (what Einstein called a ‘bunch-like’ field), moving in space-time and following a main trajectory. de Broglie’s intuition, already discussed in his PhD thesis [], was to assume that a particle is an oscillating soliton or pulse acting as a kind of quantum clock moving in space-time. The relativistic properties of this clock connected with those of the soliton field solution of the nonlinear wave equation were expected to account for all the observed quantum phenomena, e.g., including wave–particle dualism, quantum entanglement, and spin properties. In particular, the central part of the soliton (hereafter, the ‘core’) was assumed to be guided by a much weaker propagating field oscillating in phase with the core of the soliton. Originally, and partly inspired by an older proposal by Einstein where the photon was defined as a moving singularity of the electromagnetic field [], the DS theory considered a singular field diverging at the position of the point-like particle []). De Broglie expected that the trajectories predicted by the DS approach would be equivalent to those given by the dBB pilot-wave theory, which is known to reproduce standard quantum mechanics (at least in the non-relativistic limit).
Interestingly, a preliminary version of the DS theory using a scalar wave equation was already proposed by de Broglie in 1925 [,], i.e., before Schrödinger actually developed his famous wave equation. However, this older theory of de Broglie has been curiously forgotten by historians and physicists (even by de Broglie himself who never mentioned it again). When de Broglie went back to the DS approach in the 1950s and 1960s, it was the 1927 version that was considered and further developed, not his early work of 1925! However, we believe that the earlier version contains a deeper and forgotten truth which must be exploited. It is the aim of the present article to pay a tribute to the remarkable intuitions of de Broglie concerning his historical DS approach of 1925. Here, to celebrate de Broglie’s insights, we review and partially extend a recent proposal we presented concerning this old and forgotten DS theory []. This new development of de Broglie’s ideas constitutes, we believe, the logical and natural completion of his early 1925 work. In fact, one of the central ideas of the original double solution approach was to accept a strong time-symmetry of the fundamental field constituting the soliton [,]. This strong time-symmetry is actually similar to the one later developed by Wheeler and Feynman [,] in their famous electrodynamics, namely the ‘absorber theory’ that involves a half sum of retarded and advanced fields. De Broglie realized already in 1925 [,] that such a time-symmetric field could be central to justify wave–particle duality and the stability of the non-radiating Bohr’s orbits in atoms. Not surprisingly, time-symmetry can be used to avoid some paradoxical consequences of Bell’s theorem [] concerning the nonlocality of quantum mechanics. Here, we will show indeed that our time-symmetric version of the de Broglie DS can interpret the nonlocality of quantum mechanics as resulting from a much deeper nonlinear but local dynamics involving a time-symmetric field (i.e., involving a half sum of retarded and advanced fields). In turn, we show that this approach in the four-dimensional space-time exactly recovers the dBB interpretation of de Broglie and Bohm for the entangled motions of quantum particles in the configuration space. Therefore, the DS model we propose here is able to recover quantum mechanics for spinless particles coupled to external fields. Altogether, this work also brings new insights in the context of quantum hydrodynamic analogs [,] or related mechanical proposals made by the author and collaborators [,].
The structure of the article is as follows: In Section 2, we review the content of Bell’s theorem and the challenge it puts on the notion of locality, causality, and statistical independence. As we stress, Bell’s theorem and the possibility to explain or decipher ‘spooky’ action-at-a-distance involved in the dBB pilot-wave theory constitutes the central motivation for this work. The key idea will be to use time-symmetric fields linked to the ideas of superdeterminism and retrocausality. In Section 3, we give a precise description of the the time-symmetric DS theory involving a nonlinear wave equation for solitons (this work extends a previous related analysis []). In particular, we stress the role of the ‘phase-harmony’ condition and explain how to recover Bohmian mechanics and the famous ‘guidance formula’ out of this theory. In Section 4, we discuss the many-body problem involving N entangled solitons. We show how these N solitons or singularities are driven by a Schrödinger or Klein–Gordon linear pilot-wave-field , allowing us to recover the consequences of the dBB pilot-wave theory. Finally, in Section 5, we discuss how our model evades the usual nonlocality of the standard dBB pilot-wave theory and replaces it with a superdeterministic link driven by the time-symmetry of our fundamental de Broglie nonlinear field.
2. Motivations: The Nonlocality Conundrum
Bell’s theorem [] is probably one of the most important results in the Physics of the XXth century. Briefly stated, it shows that any explanations of quantum mechanics involving or not involving hidden variables must be ‘nonlocal’. Actually, this is an oversimplification since the theorem involves several fundamental axioms concerning locality, causality, and statistical independence that must be fulfilled in order to derive the famous Bell’s inequalities.
Let us review that issue briefly. Starting with a pair of entangled particles 1 and 2 prepared in a source S and subsequently (space-like) separated in two remote regions A and B, Bell considers the joint quantum probability for observing particle 1 with the property and particle 2 with the property (e.g., associated with spin observables), granted that the settings of the measuring apparatus in region A and B are prepared as and , respectively. Assuming the existence of hidden variables or, more generally, beables in order to describe quantum mechanics, we can write
where the first equality means that the experimental probability is recovered by summing over the different actualizations of the variables (Bell beables) associated with the particles, and the second equality is just an application of the mathematical definition of conditional probabilities. In his derivation, Bell further assumed that:
The two Equations (2) and (3) are not controversial and are associated with the notion of local causality already advocated by Einstein. The idea is that, by assuming that observers Alice and Bob in regions A and B are choosing ‘freely’ at the last moments the setting directions and , it must (according to the principle of Einstein’s special relativity) be impossible to have faster-than-light (tachyonic) propagation of any physical influence from A to B or B to A affecting the ‘independent’ measurements. The measurements performed by Alice and Bob must therefore only depend on the local properties or and on the shared hidden variable associated with the ‘preparation at the source’ (common past) of the two entangled particles. The last Equation (4) is even more obvious and natural and states that the hidden variables prepared at the source S must be independent of the settings and because the choice was made freely at the last moment after the preparation of the entangled pair at the source. Relaxing this statistical independence assumption would a priori lead to a superdeterministic and conspiratorial Universe that seems to conflict with the goal and methodology of science.
With all these natural hypotheses, Bell proved that a specific statistical property written and depending on different possible choices of the settings at A and at B must be bound: . The problem is that quantum mechanics predictions and experiments show in some cases that Bell’s inequalities are violated up to the value . In other words, the theorem reveals a logical contradiction arising from the simultaneous supposed validity of quantum mechanics and the existence of locally causal, statistically independent hidden variables. Something must be wrong, and assuming quantum mechanics is true, this implies that at least one of Bell’s hypotheses must be abandoned. Furthermore, assuming the existence of hidden variables (i.e., assuming a strong form of realism that refuses a bare operationalist/positivist approach) implies necessarily that we must relax at least one of the conditions 2–4. In this context, it is useful to note that the historical experiments of Aspect et al. [] closed the ‘locality loophole’ using periodical switching devices, and subsequent experiments [] used ‘genuine’ quantum-random-number generators (i.e., single photons sources) assuming no-superdeterminism. The ‘detection loophole’ can be closed in some cases [], and some tests also excluded ‘tachyonic loopholes’ (with some assumptions), leading to the lower limit for the velocity of nonlocal information of ~50,000 times the velocity of light []. (The tests assume that the signal is propagating in the future and cannot refute the dBB theory that involves necessarily signals traveling forward or backward in time in different reference frames [].) Moreover, recently closing the ‘freedom of choice’ loophole was realized using switching devices monitored by photons emitted ~10 billion years ago by quasars [,,,]. Assuming that there is no nonlocality (i.e., no instantaneous or tachyonic action-at-a-distance, including dBB connections), this lets the conspiratorial or super/hyper deterministic loophole as the only serious remaining loophole. Indeed, such ‘Cosmic Bell’ correlations seem to imply that everything should be fine-tuned and conspiratorially correlated from more or less the Big Bang time in order to reproduce quantum predictions [,]. (Note, moreover, that cosmic inflation is supposed to save causality without superdeterminism by providing an explanation for the homogeneity of the cosmological microwave background.)
Moreover, Bell understood very well from the start [] that de Broglie in 1927 [,] and Bohm in 1952 [,] already developed a rigorous, deterministic, and explicitly nonlocal hidden variable theory. In this dBB approach, the particles are point-like objects guided by the entangled wave function, creating a nonlocal link between the particles. That is, in the dBB pilot-wave theory, the two apparently natural relations Equations (2) and (3) do not hold true ( is now associated with the spatial coordinates of the particles in the remote past at the emission time by the source S). This means that some kind of instantaneous action-at-a-distance exists between the particles and therefore the measurements are not really independent (even if this cannot be used to send ‘macroscopic’ faster-than-light signals). Bell’s following Bohm therefore acknowledged this remarkable and elegant dBB theory that is curiously in tension with the spirit of special relativity but that nevertheless ‘peacefully’ hides the tachyonic effects at the microscopic level of the hidden variables in such a way as to reproduce exactly the statistical prediction of quantum mechanics. Importantly, the dBB theory assumes statistical independence, and as a consequence, Equation (4) still holds true. Moreover, not everyone is pleased with the nonlocality of the dBB theory entailing necessarily a preferred reference frame or space-time foliation looking like a reminiscence of the prerelativistic era and its ‘Aether’ substratum []. Yet, the dBB theory is devoid of any logical contradiction involving tachyonic signals (i.e., influencing its own past to create a forbidden causal loop or paradox []), and the theory can also be generalized by associating a hidden variable to the preferred foliation of space-time specifying the particle dynamics (i.e., in order to recover a democracy and symmetry between the different foliations without introducing an Aether []). Nevertheless, the dBB theory still looks odd and counterintuitive.
For these reasons and others, many authors have attempted different approaches like Everett’s Many-Worlds interpretation []. Indeed, it is sometimes claimed that Everett’s theory is not in tension with special relativity because the theory avoids the ‘single-world’ picture associated with hidden variables theories. However, it can be shown that such an unfounded statement is based on overlooking the status of probability that cannot be defined unambiguously in the Many-Worlds theory []. Therefore, in the following, we will not consider such attempts. Other alternatives to the dBB action-at-a-distance concern superdeterminism and retrocausality. Ontological models based on superdeterminism have been, for example, recently discussed in [,,], but all these approaches are often rejected on a philosophical ground, i.e., judged as conspiratorial or ‘fine-tuned’. Retrocausality or backward-in-time causality has also been seriously considered to evade the conclusions of Bell’s theorem [,,,,,,]. The idea goes back at least to Costa de Beauregard in the 1940s [] and is linked to the work of Wheeler and Feynman on time-symmetric classical electrodynamics [,] (de Beauregard idea was developped during the war around 1942–1947 but Costa de Beauregard waited for the approval of de Broglie which came after the publication by Wheeler and Feynman []). This approach is directly linked to the present proposal inspired by the work of de Broglie in 1925 [,] also involving time-symmetric fields. Interestingly, while de Broglie could not know in 1925 the result of Bell’s theorem, it is clear that the time-symmetric DS approach of de Broglie is strongly pushing in the direction of a justification of Bell’s inequality without action-at-a-distance. That was the central motivation for the present study concerning the DS theory.
3. The Time-Symmetric Double Solution Program
3.1. The Soliton Near-Field
In this work, we consider a particular development of the dBB theory, namely, the DS theory proposed originally by de Broglie in 1925 [,]. This theory, we will show, can bring new insights concerning the issue of nonlocality. Moreover, it is important to mention that de Broglie strongly modified his theory in 1927 and in the 1950s [,] in collaboration with Vigier []. It is often this last version that is mentioned in the literature, i.e., when it is not completely ignored (for useful reviews about the DS approach, see [,]). The DS theory, inspired by Einstein’s early works on photons, is based on the idea to describe particles as moving singularities of a classical scalar field theory (by a singularity, we mean that the field is infinite at the position of the particle). De Broglie first considered [,] that each particle is a point-like moving clock pulsating at its Compton frequency (in the rest of this work, we will use the relativistic conventions ). This actually means that the particle has internal properties. If this particle is at rest in the laboratory frame, the clock ‘generates’ an extended stationary field surrounding the singularity. When the particle is in motion, this field guides the particles and interacts with obstacles. De Broglie hoped [] that the interaction between this wave-like field, the particle, and its environment could explain wave–particle duality (associated with interference fringes) and the stationary orbits required in the Bohr atomic model.
The fundamental scalar field used by de Broglie is outside the singularities at space-time point , a solution of a basic linear and local field equation, i.e.,
The simplest oscillating solution associated with the pulsation defined in the rest frame of the singularity is the monopolar (spherically symmetric) field:
with being the radial distance to the singularity (particle) located at the spacial origin, and being a constant. Remarkably, when this monopole field is studied from a different Lorentz frame where the field singularity moves at the velocity v (along the x-direction), the relativistically invariant scalar u-fields now reads
with and . What is beautiful here is that the (scalar relativistic invariant) phase wave involved in u is actually a plane wave solution of the linear Klein–Gordon equation . It is easily shown that the particle (clock) is synchronized with the -wave and therefore the u-field during its motion. The whole picture is interesting because, on the one hand, it is inherently classical and relativistic, i.e., in the same sense as Maxwell theory or general relativity are classical and relativistic (the u-field propagates in space-time with the particle). On the other hand, this approach suggests that wave–particle duality and more generally quantum mechanics is just a sophisticated version of classical physics involving oscillating and moving point sources coupled to a field. In order to prove this hypothesis, de Broglie hoped to be able to calculate trajectories of the singularities in complex environments involving external potentials like the Coulomb potential or the double slit barrier. In the DS approach, the u-field should be able to influence the motion of the particle singularities in such a way as to reproduce quantum mechanics. We stress that in 1927 de Broglie used the linear Klein–Gordon equation instead of the simple Equation (5) but this does not simplify the analysis [,].
Clearly, this picture with trajectories guided by a wave is linked to the dBB pilot-wave theory discussed before. In the 1920s, de Broglie could not develop this DS program mathematically (see the discussion in []) and it is mostly for this reason that he switched to the simpler dBB pilot-wave approach. The problem of course is that, in the dBB theory, the nature of the guiding field is more obscure and more ‘epistemic’. In the end, the dBB theory was developed in the configuration space, not in the 3D physical space, and therefore the initial intuition of the DS project was lost. Importantly, de Broglie also abandoned in 1928 the pilot-wave theory because he felt the theory was unable to explain the strong form of nonlocality involved in quantum mechanics (in 1928, that issue was related to the difficulty for understanding the mysterious concept of ‘wave function collapse’ or ‘reduction’ in terms of Einstein’s special relativity prohibiting faster-than-light communication []). Moreover, in 1952, de Broglie together with Vigier [,] and a few collaborators went back to the DS program and tried to show that singularities or solitonic solutions of some unknown wave equations are following the paths or trajectories predicted by the dBB theory in the configuration space. The most important modification they suggested was, in analogy with general relativity, to consider nonlinear wave equations for the u-field in order to remove the mathematical singularities at the particle positions. In such an approach, particles are becoming ‘solitons’, i.e., localized solitary ‘bunched’ waves propagating as a whole without dispersion. However, nonlinear wave equations are even more difficult to solve than linear wave equations with moving singularities. Apart from that point, they could not define a precise nonlinear wave equation that could implement the DS goals. Moreover, the most problematic point is perhaps that de Broglie underestimated the impact of nonlocality in the DS theory. Indeed, the dBB approach is nonlocal in the configuration space. How could a nonlinear but local classical field theory defined in the 4D relativistic space-time reproduce and justify the nonlocality of the dBB theory? Following some old intuitions going back to Einstein, they suggested that nonlocality existed only in the interacting regime when the particles were not separated too much [,]. Furthermore, Bell’s theorem came out in 1965 and de Broglie could not assimilate and accept the lesson of this central result [,]. (That was not the case of Vigier, who stopped working on the DS project for a while and moved to alternative nonlocal and stochastic hidden variables approaches à la Bohm or Nelson []).
In the present research (discussed in more detail in [] following a related article []), we are taking seriously the idea of a particle–soliton but at the same time we are going back to the old 1925 ideas sketched in Equations (5)–(7). What we find motivating is the deep time-symmetry of this old picture. Indeed, it is visible that the field Equation (6) is a solution of the wave equation involving a source term. Equation (6) is actually the time-symmetric solution, i.e., the half-sum of retarded and advanced radiating waves:
What actually inspired de Broglie was the work of Tetrode and Page [,,] (later rediscovered by Fokker [] and Wheeler with Feynman []) on the time-symmetric electrodynamics in which action-at-a-distance is mediated by the half-sum of retarded and advanced electromagnetic waves emitted by electrons and protons. Page [,] suggested that the time-symmetric field could explain why electrons orbits in Bohr’s atoms do not radiate, and this was one of the initial crux of de Broglie’s attempt in 1925 [,]. Interestingly, de Broglie abandoned this idea in 1926 and never went back to it even after his former student Costa de Beauregard rediscovered a sequel of the idea in 1942 [] in order to solve the EPR paradox! After this work [], many retrocausal and time-symmetric theories were developed in order to explain the violations of Bell’s inequalities (see for example [,,] and the interesting retrocausal dBB theory [,]). All this clearly motivates the present work.
Here, we start from the de Broglie DS and postulate the following nonlinear wave equation for the u-field []:
where is a covariant derivative involving the electromagnetic potential four-vector and e is an electric charge. The nonlinear function we consider [] is the simple ‘Lane–Emden’ fifth power law, where is a (nondimensional) coupling constant (which can be positive or negative) and is a length that will define the typical radius of our soliton. Importantly, this nonlinearity allows us to define explicit analytical solitons (at least in the near-field of the particle, i.e., for distances R to the center such that ). This equation is clearly different from the quantum linear Klein–Gordon equation involving the standard relativistic wave function for scalar (spin 0) particle. We stress that if the field decays sufficiently, we can, in the far-field of the soliton, approximate Equation (9) by the linear equation . This property is fundamental since it allows us to develop a simplified approach for describing the soliton if (as shown in Section 3.2).
In order to find a solution to Equation (9), we use the polar form and obtain after separation the following:
Equation (10a) is generally named the (nonlinear) dBB Hamilton–Jacobi equation, and Equation (10b) is reminiscent of the electric current conservation. This defines a hydrodynamical representation of the nonlinear Klein–Gordon equation. Similarly, we can define a hydrodynamical representation for the field solution of the linear Klein–Gordon equation:
with being the so called quantum potential [,,] used in the pilot-wave theory. We solve the pair of Equation (10) in the region where the soliton profile is supposed to be well peaked (i.e., near the center or soliton ‘core’ surrounding a mean trajectory labeled by the proper time along the path). For this, we assume with de Broglie the so-called ‘phase-harmony condition’ [,]:
where is a new collective coordinate introduced to increase the number of degrees of freedom. As shown in [,], we can define the fluid velocities and in the regions where . The velocity is associated with the dBB pilot-wave interpretation of 1927 [] and de Broglie postulated that the particle is guided by the -wave:
This formula is non-ambiguous, at least in the regime avoiding tachyonic trajectories, and we limit our analysis to that case in the main text of this article. However, the tachyonic or superluminal regime can be self-consistently described in the dBB pilot-wave approach and is discussed in the context of our DS proposal in Appendix A. Moreover, from our DS theory and Equation (12), we deduce [,] and similarly , . The whole picture is actually self-consistent if the soliton central trajectory is identified with the dBB pilot-wave trajectory given by Equation (13). We thus have
justifying the guidance postulate of de Broglie. In other words, we show that it is always possible to find locally a first-order matching , . The two phase waves and S of the two fields u and are thus connected along the curve and this is the core of the DS or phase-harmony approach. We stress that from the dBB dynamics Equations (11a) and (11b) and the guidance formula, we obtain the second-order relativistic ‘Newton’ law already found by de Broglie in 1927 []
with the Maxwell tensor field at point . The varying de Broglie mass (i.e., varying quantum potential ) is central in order to recover the non-classical features of quantum mechanics specific of the dBB pilot-wave theory.
In other words, this phase-locking condition forces the two waves u and to vibrate locally in unison. We thus consider a Taylor expansion of the phase in the vicinity of in a space-like hyperplane crossing and defining a local instantaneous rest frame for the particle center (this hyperplane is defined by the condition with ). We assume:To every regular solution of the linear Klein–Gordon equation corresponds a localized solution of Equation (9) having locally the same phase , but with an amplitude involving a generally moving soliton centered on the path and which represents the particle.
An important relation is obtained from the hydrodynamical conservation Equation (10b) and the phase-harmony Equation (12) constraint:
The first two equalities concern fluid deformation and compressibility, where we introduce an infinitesimal co-moving 3D fluid volume (defined in the local rest frame associated with ) driven by the fluid motion. In particular, we see that if the soliton is undeformable, we must have , and thus from the last equality in Equation (16), we obtain . Moreover, if this soliton is undeformable, we must also have , and thus from Equation (16), must hold along the trajectory . This is conflicting with the dBB theory imposing a varying along particle trajectories. We conclude that we will have to relax the natural assumption of undeformability (i.e., , ) in order to develop a self-consistent DS theory reproducing the dBB trajectories, i.e., agreeing with quantum predictions.
In order to find the soliton profile f, we rewrite Equation (10b) in the rest frame near the soliton center (in the Fermi limit where we have [,]) and obtain the partial differential equation for the soliton profile for points x belonging to and localized near :
with [,]. Furthermore, in the near-field, if we suppose the soliton core size to be much smaller than the Compton wavelength , we can use the stronger approximation
which is known as the Lane–Emden equation []. This equation admits the spherically symmetrical exact solution:
which is parametrized by the constant and has the dilation invariance . Far away from the soliton ‘core’, i.e., if , this field has the asymptotic monopolar limit . In this limit, it is justified to use instead Poisson’s equation for a point-like source with effective ‘scalar-charge’ . We will come back to the asymptotic field later, but for the moment we stress that Equation (19) is an approximate equation keeping its general validity if the motion of the soliton is not varying too fast (as justified in []) and we thus physically interpret the parameter as a new collective coordinate for the soliton. More precisely, we now assume that during its motion, the soliton typical extension changes (adiabatically) with time and we write
or equivalently
where defines the dynamics concerning the radius (the proper time is chosen arbitrarily to correspond to an initial point along the trajectory).
In order to fix the -dynamics, we use the local conservation law for a fluid element located at the soliton center Equation (16): and we have by integration defining a constant of motion along a given trajectory. Furthermore, from Equation (19), and (a more rigorous justification is given in []). And we deduce:
Moreover, from Equations (16) and (22), we deduce
which, together with Equation (22), defines the complete deformation/compression of the soliton near-field.
At this stage, it is useful to summarize our main findings. Starting from the picture of a deformable soliton, we introduced some collective coordinates to describe its approximate structure and evolution. The central idea is to consider that the soliton is strongly peaked near a main trajectory in space-time and that we can solve the nonlinear equation in the near-field. The phase reduces to a function along the trajectory. We were then able to show, after including the deformation of the soliton , how the motion of the soliton can follow a dBB path with dynamical Equation (15). The soliton thus acts as a dBB particle guided by the phase of a solution of the linear Klein–Gordon equation. In other words, the DS theory recovers the dBB pilot-wave from a more fundamental field. The idea we followed was, in agreement with de Broglie and also Einstein, to remove the strangeness of the quantum potential by showing how to rederive it from a classical but nonlinear field theory.
We stress that the model developed here for a subluminal soliton can be extended to the superluminal or tachyonic sector. This is presented briefly in Appendix A. While it could, at first look, be curious to derive superluminal motions from a purely local DS theory, respecting the principle of special relativity, we cannot a priori forbid such a regime since the dBB pilot-wave theory for a point-like particle obeying the Klein-Gordon theory predicts that, in some cases, such a particle can reach the speed of light and even cross the light cone (i.e., if and only if the mass vanishes while the particle crosses the light cone as it was already predicted by de Broglie in 1927 [,]). In the context of the DS theory, trying to reproduce the dBB pilot-wave predictions, the existence of tachyonic waves is reminiscent of the so called ‘X-waves’ observed in optics, where a region of a wave-packet is allowed to propagate faster than the speed of light in vacuum if and only if this cannot be used to transfer information or energy, i.e., similar to a phase-wave (see [] for an illuminating discussion on this non-signaling constraint on X-waves). Since the tachyonic dBB motions are generally associated with evanescent or transient -fields localized in finite space-time regions, there is no way to violate no-signaling. Using the DS theory, the solutions we obtain also involve some ‘X-waves’, which can only have a physical meaning in transient regions. Therefore, altogether, the picture obtained from the DS theory is consistent even in the tachyonic regime.
3.2. The Soliton Far-Field
The previous theory developed for the near-field can be used to define the mid-field and far-field of the soliton i.e., if we do not neglect the mass term in Equation (17). We consider first the case of an uniform motion where and search for a spherical solution of
As shown in [], if we can assume (i.e., a very small soliton), Equation (24) admits the solution
which is an interpolation between the near-field Equation (19) and the far-field de Broglie monopolar solution
obtained if . Such a far-field is a solution of the inhomogeneous d’Alembert equation with .
Two remarks can be made here: First, note that the coefficient and the frequency of the soliton are not determined univocally by the theory. The soliton admits a continuous frequency spectrum corresponding to a continuous mass spectrum . Hence, it means that the present theory would have to be completed to fix the mass of the particle. Moreover, assume that the mass is fixed. In the context of the dBB pilot-wave theory (which in our DS approach defines the soliton trajectory), it corresponds to a situation where from Equation (11a) (i.e., ). This is associated with a guiding plane wave , which in the rest frame reads . Yet, the dBB pilot-wave theory can also generate constant masses different from if the quantum potential is constant but different from zero. This is, for example, the case if the guiding field solution of the linear Klein–Gordon equation reads (corresponding to a 1-dimensional stationary wave along the spatial x direction with pulsation and k the wave vector along the x direction) or (corresponding to a 1-dimensional evanescent wave along the spatial x direction with pulsation ).
The second remark concerns the structure of the far-field and its description by an inhomogeneous d’Alembert equation. It is clear from the general structure of Equation (9) that the nonlinearity of the wave equation can be neglected in the far-field since , and therefore we can use a linearized approximation far away from the soliton core. More precisely, as shown in [], the far-field of the Lane–Emden soliton with core trajectory satisfies the equation:
The second line is written in the laboratory frame, where at a time t the soliton core behaves as a point-like particle with position and velocity (here we assume the trajectory being time-like).
The general solution of Equation (27) reads
where is a solution of the homogeneous equation , and the propagator satisfies . As it is well known, the choice of the propagator is not univocal; only the total field has a physical unambiguous and absolute meaning. That means that we can have different representations of the field given by Equation (28) by changing of propagator. The most common propagators are the retarded (respectively advanced) one (respectively ) associated with radiation in the forward (respectively in the backward) light cone with apex at point . Advanced waves correspond to anticausal features associated with ‘conspiratorial’ absorptions by sources (i.e., violating the second law of thermodynamics) and are therefore often not used. Moreover, this is actually related to the boundary conditions that are the most adapted in order to analyze the specific problem considered. Indeed, we can always write an arbitrary solution of Equation (28) equivalently as or , and the different free fields are thus not independent. As an example, a typical (in the thermodynamical sense) causal field is generally written after Sommerfeld as a pure radiative field with boundary conditions . This in turn leads to the free ‘outcoming’ field , which is indeed non-singular.
As explained in the previous Section 3.1, in 1925 de Broglie [,] considered a time-symmetric field in analogy with works in classical time-symmetric electrodynamics [,,,]. Therefore, it seems natural to use such time-symmetric description in connection with Equation (28). We first write with being a free wave solution of the homogeneous equation and the time-symmetric source term . We then assume the boundary condition (i.e., ). The u-field of Equation (28) now reads:
with the time-symmetric propagator. In the absence of an external field (i.e., ) this propagator reads:
(with ). In the presence of an external electromagnetic field , the propagator reads
where we introduce (using the operator ), which defines the reflected part of the propagator resulting from the interaction of the vacuum solution with the potential A. Therefore, the u-field splits as
Inserting Equation (30) into Equation (29) leads to []:
with and where the retarded proper time (respectively, advanced proper time ) corresponds to the point (respectively, ) belonging to the trajectory , in which u-radiation propagating along the forward light cone (respectively, backward light cone) is reaching the point x. This u-field is clearly reminiscent from the retarded and advanced Lienard–Wiechert potentials in classical electrodynamics and has several remarkable properties. Most importantly, near the singularity , i.e., for points located at a distance from the singularity in the space-like (rest frame) hyperplane , we have approximately []:
From this, we deduce at the lowest order and we recover the asymptotic soliton near-field (i.e., for but still in the near-field ) discussed in the Section 3.1. Furthermore, for a uniform motion with , , , , , Equation (34) leads to , which is the field associated with the de Broglie stationary monopole discussed above. Therefore, the time-symmetric far-field matches the near-field.
An important feature of this theory concerns the phase of the singular far-field when r tends to zero. Indeed, from Equation (34) we deduce in the absence of an external field:
which can be compared with the Taylor expansion and shows that the first-order term vanishes:
Yet, by definition in , and consequently is parallel (i.e., proportional) to . In other words, since , we recover, in the absence of an external field , the DS guidance formula Equation (14) . This result is robust, and in [] we showed that it survives in the presence of an external electromagnetic field when the full propagator Equation (31) must be considered near the singularity. More precisely, we then have and we deduce
implying
Therefore, as before, we recover the guidance formula, i.e.,
Some remarks are important concerning this formula:
First, recovering the guidance formula was expected since de Broglie already gave a general derivation for the u-field in 1926–1927 []. As reviewed in [], de Broglie’s deduction is based on the conservation law Equation (10b) written as where is the 3-velocity of the —fluid and . Near the singularity, de Broglie assumed , where F is a regular function and is the singularity trajectory. De Broglie’s assumption is indeed satisfied by our singular field in a reference frame where the singularity is practically at rest (i.e., ). From the property we thus deduce:
which implies (near the singularity) the guidance formula
Using covariant relativistic notations, this is mathematically equivalent to Equations (38) and (39).
Moreover, and this constitutes our second remark, the guidance formula is not obvious to satisfy since it requires a well-defined gradient for points near the singularity. In our theory based on a time-symmetric construction, this is automatically fulfilled but this would not be the case if we instead assumed a pure retarded or advanced field. Indeed, instead of Equation (37), we obtain:
with the minus (respectively, plus) sign for a pure retarded (respectively, advanced) wave. We deduce , which implies a phase discontinuity on the singularity. Watched in the instantaneous rest frame , this condition reads in the absence of an external field:
which is clearly reminiscent of the retarded (respectively, advanced) singular field
In other words, only the time-symmetric monopole removes the phase discontinuity associated with retarded or advanced waves resulting from an unadapted selection of the propagator .
Regarding the guidance formula derived here from the far-field, we stress that it a priori only concerns the u-field containing a singularity or a soliton, not the -field, which is much more regular and smooth and has a statistical interpretation, e.g., in the dBB pilot-wave theory. However, as discussed in Section 3.1, the soliton near-field used in our DS theory requires the phase-harmony condition Equation (12) near the core of the particle, and this imposes a first-order contact between the two phase functions and S of the u and fields: , along the curve . This idea is of course applicable to the singular field considered in this subsection. Therefore, we can here also assume a first-order contact , and obtain the full guidance formula needed in the DS theory:
In other words, using a first-order contact (and not a second-order contact, i.e., imposing also as originally assumed by de Broglie and Vigier [,,]) allows us to develop a self-consistent DS model in both the near-field and far-field.
3.3. ‘Justifying’ the Wave Equation for the -Guiding Field
The present theory for the u-field left a priori unconstrained or undetermined concerns (i) the precise form of the wave equation for , and (ii) the physical nature of this -field. First consider point (i): the mathematical form of the wave equation for the -field. In our theory [], we assumed that the -field obeys the linear Klein–Gordon equation. This choice can be approximately justified.
For this purpose, we start with the phase-harmony relation Equation (12) defining the phase in the vicinity of the soliton-core trajectory characterized by the phase . We do not have to assume here that the soliton is coupled to an external physical wave with phase S guiding the soliton. Indeed, it is enough to show that, from obtained from our wave equation for u, we can construct a wave equation for a -field having the properties of the linear Klein–Gordon equation. The method goes back to Vigier and Régnier [,,]. We assume that the soliton trajectory exists and the phase is given in its vicinity by the phase-harmony condition Equation (12). Now, we consider a statistical ensemble of solitons and impose a local conservation law
where plays the role of a density for the statistical fluid in the configuration space of the particle with path . We thus define a wave field given by
and this allows us to rewrite Equation (46) as
with . After transformation, Equation (48) reads
or equivalently . Now, the real part is left unconstrained by this procedure and this leads to the general condition
with a function of z, and finally implies:
Clearly, if we separate the real and imaginary part in the wave Equation (51), we recover Equation (46) and obtain the generalized Hamilton–Jacobi equation
with the quantum potential. In order to close our ‘derivation’ of the wave equation, we now consider the semiclassical regime where and this implies . In order to recover classical physics for a particle of mass in an external field , we impose and this leads to the linear Klein–Gordon equation
We can also justify the choice on physical ground: If we assume that in the remote past the soliton has a uniform inertial motion defining in the rest frame a pulsation , we can identify this motion with in Equation (52). Consequently, in order to fulfill the first-order contact hypothesis, we impose .
The previous reasoning motivates the choice for a guiding field obeying a linear Klein–Gordon equation but clearly does not impose it. This shows that the choice of a guiding -field is not here dictated only by physical reasoning but also by practical features associated with the simplicity of a linear wave equation compared to a nonlinear one.
This in turn leads us to point (ii): What is the physical meaning of the -field? Indeed, since we are here proposing a minimal model with only a single fundamental u-field, the -field cannot be a fundamental independent field interacting with the u-field (such a different approach has been developed by us in []). Here, we suggest to interpret the -field as the natural extension of the action introduced in the old Hamilton–Jacobi equation for a point-like particle. Here, the wave is seen as a mathematical tool for describing the motion of the soliton with trajectory and is clearly similar to the role played by obeying in the old classical theory. Moreover, in the classical Hamilton–Jacobi theory, the 3D configuration space, with vectors , defines the set of all possible positions and trajectories for the point-like particle and must be distinguished from the 3D physical space with vector where the extended soliton is evolving. In the DS theory developed here, the complex wave function defines a generalization of the Hamilton–Jacobi function adapted to the dynamics of a soliton and z defines a configuration space for the center of the soliton.
At the philosophical level, we stress that there is an old debate between advocates of the dBB pilot-wave or ‘Bohmian’ mechanics concerning the physical status of the wave function . De Broglie always emphasized that, for him, the wave function is not a fundamental of ‘objective’ field but instead a ‘subjective’ probabilistic field []. Quite similarly, Dürr, Goldstein, and Zanghì [] wrote that the wave function is not a physical external agent acting on the particle but better a mathematical (nomological) object used for describing the quantum law of particle (similar to the Hamiltonian function in classical mechanics). A physical point clearly in favor of this view is the absence of retroaction of the particle on the -wave in the dBB theory. An objection often made against this nomological view is that, in classical mechanics, the Hamiltonian function is given, whereas the wave function depends on the choice of initial conditions. However, we can easily counter the objection: The problem is not actually the nomological view itself but instead the comparison with the Hamiltonian. As we saw, and in agreement with de Broglie, the good comparison concerns and S, i.e., the wave function and the action in the old Hamilton–Jacobi theory. Indeed, and S are both dependent on initial conditions, are defined in the configuration space, can evolve in time, and are used to classify ensembles of possible particle trajectories z. However, we can also perhaps justify the psychological resistance against the nomological view by the non-intuitive features observed in the dBB theory. For example, as already pointed out by de Broglie in 1930 [] concerning interference in the double-hole experiment, it looks as if the dynamical motion of the single particle (going through one hole) is affected by alternative motions (going through the second hole) which did not occur but were potentially possible. In classical physics, this does not happen and possible trajectories coming from each hole are just crossing each other, i.e., the particles going through one hole are completely unaffected by the presence of the second hole not crossed. In the DS approach, this non-intuitive aspect of the pilot-wave dynamics is explained by the existence of the u-field associated with an extended physical phenomena surrounding the soliton core and involving the whole environment of the wave. In other words, the -dynamics is just an effective description of the soliton core motion that in practice is neglecting an important part of the u-wave propagation associated with the retarded and advanced contributions focused on the soliton.
4. The Many-Body Problem
The previous model based on a local but nonlinear wave equation can be extended to the case of many non-interacting solitons coupled to external electromagnetic fields []. The idea is to find the multisoliton solution of Equation (9). Moreover, an explicit and analytical formula for describing such a system is not known and would require to consider the coupling between solitons. Therefore, we instead assume that the far-field of a given soliton is decaying quickly with the distance to the center. Here, we work in the approximation where the perturbation near the location of the jth soliton , and associated with the u-field created by a different soliton labeled by the index i, is small enough and can be neglected compared to the near-field of the jth soliton itself (i.e., if ). Physically this makes sense if the various solitons are separated by distances (this will be true in general if the soliton typical extension is very small compared to the Compton wavelength and other characteristic lengths of the system).
In the near-field of the jth soliton with trajectory , we can apply the method described in Section 3.1. In particular, using the phase-harmony condition, we can define for points x in the local hyperplane the phase if :
For example, for a single soliton, the local hyperplane is defined by the condition with and is the soliton center velocity. is a collective coordinate measuring the deformation of the N solitons. In this discussion, is a common evolution parameter for the moving points along the various trajectories . Therefore, defines a ‘common time’ for the N synchronized particles. We stress that Equation (54) concerns points x contained in the local hyperplane of the jth soliton with trajectory . This means that, for a different soliton, let us say the , we need an equivalent equation (this explains why is labeled by the soliton number j or k: ). We have thus N local expansions to consider in this approach, each one corresponding to a different soliton solution of the same nonlinear equation. Mathematically, this means that in Equation (54), i.e., that the phase is locally conditioned on the knowledge of the N synchronized trajectories once the hyperplane for the jth particle is defined. This operation is geometrically x-dependent and unambiguous at least for points located not too far from the particle trajectories (see Figure 1).
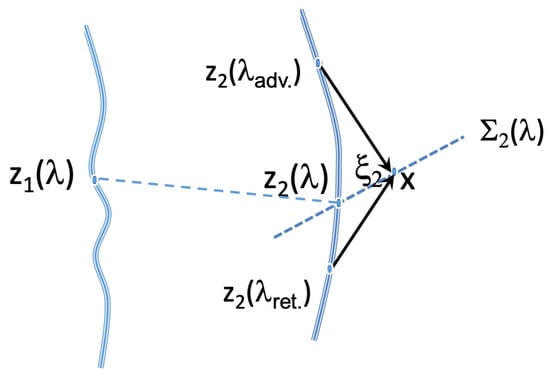
Figure 1.
Determination of the space-like hyperplane for a system of two particles 1 and 2 with synchronized trajectories , . For a point x located near the trajectory , the hyperplane is defined by the relation . Once the corresponding point is unambiguously defined, the value of fixes the entangled position associated with the other particle. Also shown are retarded and advanced positions of particle 2 used in the description of the u-field.
Moreover, nothing has been said yet about the choice of the action function . In the context of the dBB pilot-wave theory, it is natural to introduce the wave function solution of the set of N coupled Klein–Gordon equations: with and being the 4-gradient operator for the jth particle. Using the polar representation, we can write
with being a quantum potential. In the context of the relativistic dBB theory, the particle velocity for the jth particle is supposed to be
Once the initial conditions are given, this set of coupled equations can be integrated to obtain N coupled (i.e., entangled) trajectories for the N particles. We stress that Equation (56) is general and valid whatever the sign of (in particular if the particle is moving faster than light as explained in Appendix A).
An important feature of dBB trajectories obtained here is that they can be used to compute the wave function knowing . More precisely, we have:
where Equation (57a) is deduced from the N conservation rules (i.e., Equation (55b)) and the definition , and similarly Equation (57b) from the definition (i.e., equivalent to a Lagrangian for the N dBB particles) and Equation (56).
Moreover, we point out that, contrarily to what occurs in the nonrelativistic regime (i.e., based on the many-body Schrödinger equation), the dBB trajectories obtained here from the set of N coupled Klein–Gordon equations is in general not able to reproduce all statistical predictions of standard quantum mechanics for every time (the theory is said to be not statistically transparent). Indeed, we in general a priori do not know how (and we do not know if it is even possible) to combine the N partial conservation laws (i.e., Equation (55b)) into a single ‘master’ equation defining a probabilistic conservation law for the N-paths. Of course, in the non-relativistic regime, the situation is easier since Equation (55b) reduces to . In this non-relativistic regime, we can introduce a single common time such that and we deduce
which recovers the standard Bohmian probability law for the many-body Schrödinger equation with the definition . Here, defines the density of probability in the configuration space in agreement with Born’s rule. However, despite the present limitations, it is possible to show (and the mathematical details will not be given here but in a subsequent publication) that the relativistic dBB trajectories given by Equation (56) are asymptotically statistically transparent. This means that such N paths can be used to recover statistical predictions of quantum mechanics in scattering processes where interactions between particles and fields are well localized in space-time and where particles can be considered as initially independent (i.e., unentangled). With such restrictions, the theory is physically satisfying for all practical purposes. In the following, we will not consider this problem anymore and accept the physical relevance of Equation (56) for founding a self-consistent dBB theory.
Going back to our DS theory and to Equation (54), we now have a set of N synchronized dBB trajectories used to define local rest frames and hyperplanes . The general method developed in Section 3.1 is thus applicable. In particular, using fluid conservation Equation (16) allows us to determine the N deformation coefficients obeying to the set of coupled equations
that generalizes for N solitons the results of Equations (23) and (A9) deduced for a single soliton. In order to complete the description, we need to evaluate the amplitude of the u-field for points such as in the hyperplane . For example, for and Equation (54), we have locally and this amplitude obeys to a nonlinear equation generalizing Equation (17), i.e.,
As in Section 3.1, the integration of this equation leads to
with the radial distance to the jth soliton center, and where we have:
if we assume and (see Appendix A). This analysis completes our description of the N-solitons near-field.
The description of the N-solitons far-field can be achieved similarly by generalization of the method developed in Section 3.2. In the far-field regime, the u-field obeys a linear equation except along singular lines corresponding to the N trajectories . The field at point x reads where is a solution of Equation (27). Therefore, we have:
where defines a coupling constant for each individual singularity. The solution of Equation (63) we consider reads:
with being the time-symmetric Green propagator given by Equation (31).
The picture we obtain in the far-field is thus the following:
(i) Starting from the dBB pilot-wave theory for N relativistic scalar particles, we define N generally entangled particles trajectories guided by the wave function .
(ii) To each trajectory we associate a moving singularity term in the linear but inhomogeneous Equation (63).
(iii) The solutions we consider are the N time-symmetric fields whose sum is given by Equation (64) and which depend on the time-symmetric propagator .
The consistency of the whole picture, as explained before for the near-field, relies on the assumption that the N solitons are non-interacting, i.e., that we neglect the effect of soliton on soliton for any pair . Relaxing this condition could, for example, imply that we take into account the electromagnetic interaction between solitons and this would ultimately require a development of quantum electrodynamics for solitons (with particle and antiparticle creation). A second possibility for extending the theory could be to include the interaction of solitons when we cannot neglect the perturbation compared to . In this regime, new effects could potentially appear going beyond the usual predictions of quantum mechanics (i.e., beyond the guidance formula of the dBB theory). This coupling between solitons should depend on the sign of the coupling constants for soliton i (i.e., not necessarily equal to a common coupling constant as it was assumed in this work). This clearly opens interesting perspectives for future works.
An important feature of this DS approach is that we started from a local but nonlinear equation for the u-field and nevertheless we were able to find solitonic solutions driven by a phase , which in general implies nonlocal action-at-a-distance between the (dBB) trajectories. Is that not a contradiction after all? As we analyzed in [], the fundamental aspect of this theory is the time-symmetry associated with the half sum of advanced and retarded waves in the far-field. As we will now discuss, this explains how to remove contradictions and even to justify and explain the dBB nonlocality as an effective feature of our nonlinear dynamics involving time-symmetric fields.
5. Discussion: Superdeterminism and Effective Nonlocality à La Bohm
The present DS theory, with its underlying time-symmetry, has some remarkable consequences for discussing the nature of causality in quantum mechanics. Indeed, in the standard dBB pilot-wave theory, the first-order guidance formula for the set of coordinates (local beables) at time t leads to trajectories requiring the knowledge of the initial positions and a time . As it is has been often emphasized, this Bohmian evolution is strongly contextual and also presupposes a preferred space-time foliation. Nevertheless, this dBB theory preserves some natural features already visible in the old classical dynamics, namely, the knowledge of the past state is necessary and sufficient to predict the future evolution of the system. In this Cauchy problem, the integration of the guidance formula, i.e., for the Schrödinger or Klein–Gordon equations, is thus naturally obtained once we know the physical state defined along a space-like hypersurface located in the past. In our DS theory, we preserved the validity of the dBB theory but the trajectories are used to guide solitons having time-symmetric profiles in space-time. Indeed, because of the presence of the time-symmetric Green propagator in Equation (64), the moving solitons (i.e., moving singularities in the far-field approximation) emit natural retarded waves into the future time direction, but also more exotic advanced waves ‘propagating’ into the past direction. The direct consequence is that any space-like hypersurface contains information about physical interactions acting upon the particle in the future of that surface. It is not difficult to see that this information coming from the future and affecting the initial state can be interpreted as a form of superdeterminism associated with the retrocausal waves emitted by the particles in the future. This superdeterminism and retrocausality impact discussions of problems involving one or more particles.
5.1. Problems Involving a Single Particle: Empty Waves and the Perrin Objection to DS
As an illustration, consider the case of a single dBB particle interacting with a 50/50 beam splitter as studied for example in [] (see Figure 2a).
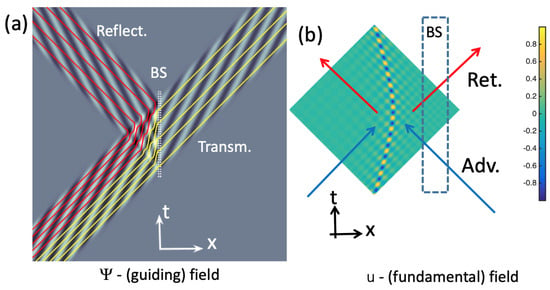
Figure 2.
(a) A typical one-dimensional scattering experiment with a Schrödinger wave-packet impinging on a 50/50 beam splitter (BS) and the dBB particle trajectories associated (details in []). Half of the trajectories are reflected (red curves) and half transmitted (yellow curves). (b) A typical u time-symmetric field guided by an idealized reflected dBB trajectory of (a) (see the model in [] for more technical details). We added an idealized BS to compare with Figure 2a. The arrows indicate the presence of retarded (in red color) and advanced components (in blue color) propagating forward and backward in time from any points of the dBB main trajectory.
As explained in [], the -wave-packet associated with an incident particle (represented by a quasi monochromative wave in Figure 2a) is impinging on the beam splitter represented by an external field strongly localized in space and also potentially in time. The system is tuned in order to have 50% of the incident particles being reflected and 50% being transmitted. In the dBB pilot-wave theory, this implies that half of the possible trajectories will be reflected or transmitted and that the exact outcome of the experiment depends precisely on the initial condition (i.e., position) of the particle in the incident beam. Since this initial coordinate is unknown, i.e., ‘hidden’, to the observer, the result is described by probability (see [] for a discussion) in agreement with Born’s rule of standard quantum mechanics. Moreover, in the dBB theory, one sometimes questions the role of the empty channel not chosen by the particle. If we suppose as an example that the dBB particle is reflected, then a -wave guides the particle in the reflected branch but an ‘empty wave’ must propagate in the non-occupied transmission channel or branch. The existence of this empty wave is a priori inferred from the fact that we could (i.e., by adding mirrors and a second beam splitter in the two paths of the reflected and transmitted -waves) create an interferometer where the influence of the wave propagating in the empty channel is required in order to recover the observed results. Already in 1930 [], de Broglie considered this issue as problematic for the pilot-wave theory since the empty wave should carry energy and this has never directly been detected despite many attempts (see [] for a discussion and [] for an attempt to reactualize the debate). Of course, we can use a ‘nomological’, more neutral picture as de Broglie [,] or Dürr, Goldstein, and Zanghì did [] (see also the more complete analysis conducted by Allori [,]) and refuse to attribute a physical content to the empty wave. However, the problem survives in the DS theory developed by de Broglie in the 1950s where the soliton was expected to lose (i.e., radiate) progressively its energy after interacting with several beam splitters [,]. This problem is known as the Perrin objection [] and it was considered as a fatal flaw for the DS problem in the 1950–1960s. The issue was never clarified in the old DS approach.
In our DS time-symmetric theory, the situation is very different because of the time-symmetry involved. Consider for example a typical reflected dBB trajectory from Figure 2a i.e., associated with the motion of the soliton core. The u-field of such a soliton is computed in Figure 2b for a simplified model []. In agreement with Equation (29) involving , this u-field is the half-sum of retarded and advanced contributions . Furthermore, the advanced field ‘propagates’ backward in time and this is even before the particle crosses the beam splitter. Therefore, in the remote past, i.e., before the interaction time of the particle with the beam splitter, there is an advanced field . Such field is emitted by the particle singularity at a later time, i.e., after the interaction with the beam splitter. This advanced field carries to the past an information and energy on the future interaction, something which is strongly retrocausal and conspiratorial. Indeed, if we watch the time evolution normally, i.e., from past to future, what we see is a fine-tuned u-field converging on the particle and arriving precisely at the good moment in order to fulfill the wave equation and preserve the energy conservation. From the point of view of normal causality going from past to future, this is a form of superdeterminism.
Furthermore, the presence of radiated and advanced u-field components propagating in the remote future or past preserves the stability of the soliton at the same time as it preserves energy conservation. The old paradox associated with empty waves carrying and dissipating the corpuscle energy is therefore resolved in our time-symmetric DS approach []. In other words, Perrin’s objection to the DS theory [] is solved in our time-symmetric approach.
The situation is actually very general. Consider, as shown in Figure 3, one single dBB particle scattered by an external classical potential located in a finite space-time region. Lets call such a dBB trajectory crossing the interaction region. First, we note that the classical field can be impacted by actions coming from his past and we know from standard relativistic causality that such actions must be included in the past light cone (hereafter denoted as ) having its apex on the interaction zone. For example, if the external classical field can be switched or modified, we can always imagine an external parameter characterizing the mechanical or electromagnetic devices or settings associated with the external field and that must be located in the relativistic causal past, i.e., in the backward light cone . Note that since the interaction region has a finite space-time extension, we should rigorously consider several past light cones with apexes in the interaction zone. Moreover, we can always find a configuration in which the dBB positions belonging to the trajectory and located before the interaction zone are causally independent from the external field and thus from (this was clearly the case in the example of Figure 2). This will naturally occur when the wave-packet associated with the incident wave function defined before the interaction zone is not initially overlapping or physically interacting with the devices characterized by the parameter . (Ultimately, if the parameter characterizes a light pulse coming from the past along the light cone , there is no possibility—even in principle—to imagine an interaction between the strongly localized wave function and the mechanical or electromagnetic device ).
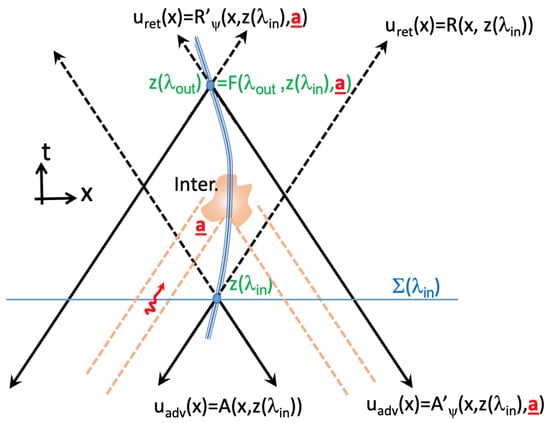
Figure 3.
A generic dBB trajectory passing through an interaction zone where a classical (electromagnetic) field is characterized by the external settings . The settings can be modified by information (red arrow) traveling from the past. The causal zone of influence is limited by the past light cones (orange color) having their apexes in the interaction volume. As explained in the main text, the dBB motion after the interaction will depend on the initial condition and the settings . Moreover, the retarded (respectively, advanced) u-waves emitted by the particle transfer the information very far away from the interaction zone. In particular, the advanced waves transfer information concerning to points belonging to the hypersurface , i.e., located before the interaction zone. This can be interpreted as a retrocausal and superdeterministic feature of the DS theory.
Now, if we consider the point , we can calculate with Equation (29) the u-field emitted into the past, which is a function of the point x and the position : . Note that x cannot be arbitrary since information is constrained to propagate along the past light cone where and . Similarly, we can compute the u-field radiated in the far future: (see Figure 3) with similar constraints along the future light cone. These fields are causally independent from , as they should be. However, the situation drastically changes after the interaction of the dBB particle with the external field. The position belonging to the dBB trajectory after the interaction is indeed a function of the initial position and external field:
Obviously, the retarded and advanced fields emitted by the singularity in the far future or past will be functions of these parameters. Most importantly for us, the advanced field emitted into the past reads
where we use Equation (65) and the constraints , to remove the dependency over . Crucially, now depends on . Therefore, along a space-like hyperplane containing (see Figure 3), the field which is located outside the limit provided by the intersection between and will depend on parameters such as even though is necessarily independent from these variables. In other words, the description of the field is superdeterministic and retrocausal! It is interesting to add that the total field along will in general also contain a retarded contribution coming from points of the trajectory located much earlier than (not shown in Figure 3). The u-field sum of retarded and advanced components is thus in general a very complicated mathematical object which strongly depends on the full particle history.
5.2. Causality and Superdeterminism
At this stage, it is useful to give a very general discussion about causality in our DS approach. Here, the u-field at point x is the solution of the nonlinear Equation (9), which equivalently reads
with the linear operator . Using the Green theorem, the formal solution reads
where is the Green propagator in vacuum ( is a three-dimensional scalar elementary volume belonging to the boundary at point y, and is the outwardly oriented unit four-vector at point y such that ). If we consider the retarded Green function , the integral in Equation (67) can be pushed to the infinity and the surface integral along the boundary includes only a contribution from a space-like hyperplane located in the remote past (i.e., at ). We thus have
with the incident field . Using recursively Equation (69) will allow us to express the total field at a point x as a functional
which depends on the incident fields defined in the whole past light cone hypervolume with apex at point x (see Figure 4a). Moreover, using the definition of , we can restrict this definition to points y located in the region of located between x and the past hypersurface . We can also rewrite Equation (70) as
which is a new functional depending only of the fields and derivatives along the part of the hyperplane included in the past light cone .
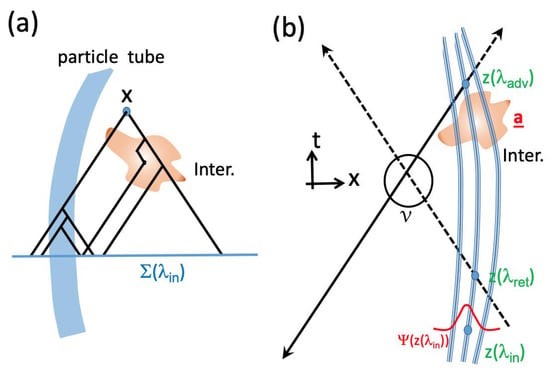
Figure 4.
(a) A typical Cauchy problem where the u-field at point x is expressed as a functional of the incident field and retarded field emitted in the backward light cone . Here, we show some typical scattering rays in the presence of a particle tube (associated with a region of strong nonlinearity) and an interacting field. (b) Defining the probability in the four-dimensional volume requires the knowledge of retarded and advanced u-fields emitted by the soliton during its dBB motion. The dBB statistical distribution associated with the initial wave function will weight this otherwise completely deterministic property defined in volume . Advanced and retarded contributions to the u-field lead to a mere violation of Bell’s local causality which involves only past light cones.
This naturally defines the Cauchy problem where the knowledge of initial conditions of the fields and derivatives on is necessary and sufficient to compute (in principle algorithmically) the field at the apex of . However, in the present theory, the evolution Equation (67) is strongly nonlinear, and nonlinear equations are hard to solve. It would be difficult to guess (by inserting some input fields by hand) what would be the final solution and in particular if this would lead to a stable soliton. What we showed is that the theory admits self-consistent solitonic solutions having a time-symmetric structure . As we already explained in Section 3.2, we can always equal this solution to the natural Cauchy solution Equation (69) written as if we put . But now, because of the presence of advanced fields in its definition, computed in will depend on the future field at point x. Generally speaking, systems of equations involving retrocausal links can lead to mathematical inconsistencies due to causal loops. Here, however, we find a family of self-consistent solitons driven by dBB trajectories guided by a -field solution of the linear Klein–Gordon or Schrödinger equation. The self-consistency means that if we use the u-field computed from our solitons to define the input fields variables needed in Equations (70) and (71), we could in principle check that the u-field at position x can be precisely recomputed to give the input field that is required. Therefore, we obtain a kind of algorithmic causal loop! But this is a self-consistent causal loop, unlike the infamous ‘grandfather paradox’ where a grandson acting backward in time kills his grandfather long before his own birth and thus prohibits his existence.
At an even more philosophical level, this leads to interesting questions if we try to identify the whole Universe with a kind of computer which is calculating algorithmically the u-field at any position x as a function (or functional) of its causal past (i.e., the past included in the light cone ). We see that the Cauchy approach going traditionally from past to future would not be a good or efficient one without knowing already in advance the solitonic solutions of our nonlinear equations. At a cosmological level, i.e., with the Big Bang, this would even require a fine tuning or conspiratorial scenario. Moreover, in a block Universe picture taking seriously the symmetry of nature between space and time dimensions, the fact to use self-consistent and time-symmetric fields is not ridiculous and can solve the problem. Clearly, however, it leads to interesting questions concerning causality, superdeterminism, and free will.
One of the questions concerns the concept of probability in our DS theory. Consider, for example, the case sketched in Figure 4b where a particle interacts with an external field characterized as before by a parameter . Knowing the initial dBB position distribution , given by the wave function and Born’s rule, will allow us to define the probability for the field to have some specified values in the four-dimensional volume . Writing in this probability, we have
where the integration is conducted over the dBB particle distribution , and where the Dirac distribution is functional (required because the theory is deterministic) and where depends as before on the history of the dBB particle. In particular, the u-field in region can clearly depend on the position of the particle in the future light cone with apex at point x due to the presence of advanced wave components (see Figure 4b). The probability therefore violates the local causality requirement of Bell. Interestingly, this also violates the idea of the usual dBB theory that a probability cannot depend on future events (Lucien Hardy and Squires called this the principle of outcome independence from later measurements: POILM [,]). Moreover, POILM concerned the dBB pilot-wave theory and observables associated with the particle presence at point z. Here, we are considering the u-field at points in the context of the DS theory. Furthermore, it is not required to consider as a standard quantum observable in the sense that the detection of a particle implies that the core of the soliton (with a highly nonlinear and peaked u-field) is crossing the region . This is not the case in the example discussed here where only a weak linear far-field is supposed to reach the region . is better interpreted as a probability concerning (hidden) beables or ontic states of the quantum system described by the DS theory.
An important application concerns the case where, instead of the volume , we consider a part of the Cauchy hypersurface (i.e., ) associated with the causal past of the particle. We thus have
which shows that the incident field needed to apply the Cauchy problem in Equation (71) is itself associated with a probability distribution deduced from the dBB distribution . Ultimately, using Equation (71), the u-field near the particle singularity: is itself associated with a probability as it should be in order for the DS and dBB theory to be self-consistent.
A central point in our analysis is that we obtained two different alternative descriptions of the u-field: (A) On one side, we have the usual Cauchy description involving past information dispatched over the hyper-surface (see Equations (70) and (71)) in order to compute the future field. This description would be very difficult to use in practice for a nonlinear field. (B) On the other side, we have the time-symmetric description used in the present work leading to Equation (28) or Equation (64) in the far-field (the near-field being described by Equations (19) and (61)). This new description relies on the knowledge of dBB particle paths , which are expressed as functions of the initial dBB coordinates . By integration, we have . Importantly, these dBB trajectories are not dependent on future events as it was clearly analyzed by Hardy and Squires in [] (see also []) with POILM. This is exactly what is happening in the example of Equation (65), which depends on the parameter only after the interaction of the particle with the external field. By inserting these expressions for into given by Equation (64), we thus obtain formulas like Equation (66) for the u-field, which most generally would read:
where the retarded field and the advanced field depend in general on the particle histories and interactions and constrained by the Hardy/Squires dBB causality principle POILM. In the end, the time-symmetric field of Equation (74) with the dBB input variables is rigorously equivalent to the Cauchy description of Equation (71). However, the time-symmetric description requires much less local hidden variables or beables for its description since ultimately it requires only the dBB coordinates and not the full knowledge of the fields over the Cauchy hypersurface.
5.3. Bell’s Theorem: How to Remove the ‘Spookiness’ from the dBB Pilot-Wave Theory
The previous analysis applies to the last problem that we must discuss here, namely, Bell’s theorem and nonlocality. Indeed, it is remarkable that our local DS theory, as shown in Section 4, allows for a description of N solitons involving a —function associated with N entangled dBB particles. Indeed, is associated with the Klein–Gordon equation, which admits solutions having a strong nonlocal character in the sense that these solutions can be used to violate some Bell’s inequalities. The dBB trajectories obtained with the guidance formula Equation (56) are thus strongly correlated and the particles, characterized by the varying masses acting as relativistic quantum potential, are submitted to nonlocal instantaneous forces, i.e., actions-at-a-distance. Altogether, this violates the conditions of local-causality and or statistical independence defined by Bell and presented in Section 2. To recap once more: The DS theory is relativistically local (even though nonlinear), whereas the dBB pilot-wave theory is nonlocal and requires a preferred foliation (as discussed for example in []) or synchronization (as discussed in Section 4). There is thus a clear tension between the dBB pilot-wave theory and the DS theory developed here. How can we solve this apparent contradiction?
The central idea to solve this dilemma is to take seriously the time-symmetric u-field of our DS theory. Indeed, from Equation (64), we deduce that the solitons or singularities emit advanced waves that propagate backward in time and can in turn carry information from the future to the past. This retrocausal link can be used to define the incident u-field along a past Cauchy surface . In turn, we have a way to decipher the mysterious nonlocal link between particles using time-symmetry to justify a form of superdeterminism and removing the spookiness of action-at-a-distance present in the old dBB pilot-wave theory.
To be more precise, consider for example, as shown in Figure 5, two entangled particles forming an EPR pair (systems of spinless Klein–Gordon particles having this property are discussed in []). We suppose that the two entangled particles are sent to observers Alice and Bob located in remote labs where fields act locally on the separated particles. The settings (respectively, ) associated with the external fields acting on particle 1 (respectively, 2) are for example monitored or driven by random optical signals coming from remote stars or quasars as in [,,,] (see Figure 5). Alice’s and Bob’s operations on particle 1 and 2 lead to measurements of dichotomic observables and that can take values .
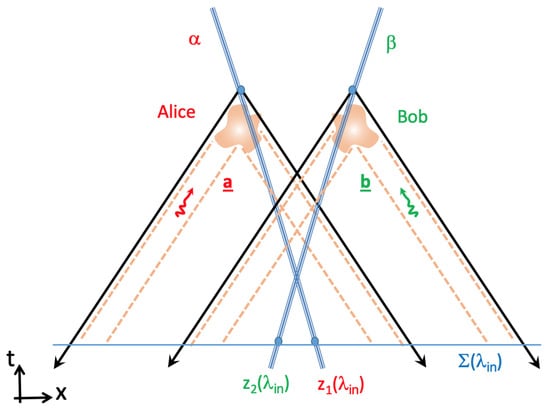
Figure 5.
Bell’s scenario involving two dBB particles associated with solitons. The information coming from the remote past and located along the space-like Cauchy hyperplane contains macroscopic classical information for changing the settings , of the external fields used by observers Alice and Bob. In the time-symmetric DS theory, we also have advanced wave converging on the two dBB particles. These advanced waves can be seen as superdeterministic signals bringing information about the settings , and located in the regions belonging to the past lights cones with apexes in the interaction regions (in particular in the overlap of the black light cones, which is central in the derivation of Bell’s theorem). This in turn explains the effective (but clearly not fundamental) nonlocal action-at-a-distance which is driven by our time symmetric u-field and which leads to Bell’s correlations between observables and associated with the two dBB particles.
In classical physics assuming local causality, but also in the dBB theory using POILM [,], the particles detected cannot know in advance the settings and operations realized by Alice and Bob. This is a natural assumption, and in classical physics or the dBB quantum framework approaches, we generally refuse superdeterminism or retrocausality (see, however, [,] for alternative versions of the dBB theory that we are not considering). In other words, we generally assume the validity of condition 4 of Section 2, i.e., for the beables . In order to explain the observed violations of Bell’s inequalities [,,] a Bohmian invokes action-at-a-distance. More precisely, the dBB particles crossing the interaction zones of Alice and Bob are coupled by a nonlocal link defined in the phase of the wave function for the EPR pair. It is this nonlocal link that produces the instantaneous action-at-a-distance between the particles and which in turn violates at least one of the two local-causality conditions 2 and 3 of Section 2. In other words, following the dBB pilot-wave theory, we will have in the interaction zones and after:
In this Bell–EPR experiment, the dBB trajectories are thus nonlocally dependent on both settings .
Moreover, in our DS theory, we can find a different (and better) explanation without ‘spookiness’ i.e., where the nonlocality is not fundamental but derived. Indeed, in the present DS approach the u-field of the two singularities reads:
In particular, this time-symmetric field can be used to compute the advanced waves propagating along the backward light cones with apexes in the interaction zones of Alice and Bob. These waves carry precisely in the overlap of the two past light cones the physical information on both settings that were supposed not to exist in the standard dBB theory. Therefore, along a Cauchy surface and more precisely in the overlap of such a surface with the region included in the past light cones, we have an information about both settings , i.e., about events occurring in the future of the solitons with respect to .
The situation is even more explicit if we consider the outcomes which read in the dBB theory:
and depend nonlocally on the settings and the local beables . These are the quantities involved in the Alice and Bob joint measurements leading to the violation of Bell inequalities. Once more, for a Bohmian, the situation is clearly demonstrating the necessary nonlocal link based on an instantaneous action-at-a-distance. However, in the present DS theory, we have alternatively after using Equation (71):
which define Cauchy functionals requiring the knowledge of field variables defined on the hypersurface (and associated with the intersection of the light cone regions with apexes on detector settings of particles 1 and 2 with the Cauchy hyperplane ). This causal region is the only one which is physically relevant for evaluating observables and . In this description there is no nonlocal link; fundamentally, everything is local and obeys to Equation (9). Moreover, the advanced wave contribution to the time-symmetric solution Equation (76) allows us to compute retrocausally the fields on the hypersurface . Since the advanced field depends through Equation (75) on the input variables and the parameters , we have a superdeterministic theory.
In other words, Equations (77) and (78) are alternative but equivalent descriptions of the observables . In the DS theory based on the u-field, the nonlocality of the dBB pilot-wave theory is not fundamental. Rather, it constitutes and effective description which ignores the time-symmetric motion of the u-wave and focuses only on the entangled motion of the solitons cores. If we ignore the u-waves and only watch the dBB trajectories, we miss the causal information associated with advanced and retarded components of the u-field that are converging on the particles. If we alternatively watch the motion of the u-field and apply a Cauchy-like perspective where the time is flowing from past to future, we will see a superdeterministic theory where the incident field on the hypersurface depends on the future states through the parameters . Somebody with access to this initial u-field would thus conclude a conspiratorial scenario where the field is fine-tuned exactly in the precise way to reproduce the dBB nonlocal motions and the predictions of quantum mechanics, e.g., the Bell inequalities violations. In our time-symmetric DS framework, the most complete description is thus to watch the problem from a block-Universe perspective in which the presence of advanced and retarded waves is fully appreciated.
In the recent debates concerning quantum foundations and the Bell theorem, superdeterminism has been often neglected or considered as an ‘absurd’ solution that would bring into question the whole science methodology assuming statistical independence (for interesting exceptions and attempts, see, however, [,,,,,,]). This could a priori question the values of ‘free choice’ performed by agents like Alice and Bob. Importantly, the methodology assuming statistical independence is well established but only for macroscopic phenomena. For example, it plays a fundamental role in medical and clinical tests relying on fair statistical sampling. If statistical independence was not true, that could of course undermine the whole scientific enterprise at large macroscopic scale []. However, we are here considering quantum experiments where hidden variables and beables can violate some macroscopical intuitions. Therefore, relaxing statistical independence is a priori not worse than invoking spooky action-at-a-distance. In a local Universe, preserving the results of classical relativity superdeterminism can thus appear as the best alternative.
As we have shown, the DS theory developed initially by de Broglie and pushed here to its logical conclusion requires time-symmetric fields, and this ultimately justifies a form of superdeterminism to recover the guidance formula of the dBB theory. This superdeterminism is, however, not like the one of a magician on the stage using tricks to fool or dupe the public and create an illusion. The fine-tuning needed in our theory is not so contingent as for the magician since it is needed to justify the existence and stability of the time-symmetric solitons. Indeed, the nonlinearity of the DS theory forces us to assume a time-symmetric u-field, and in turn this time-symmetry is essential to explain why the superdeterministic initial conditions defined along the Cauchy hyperplane located in the past is caused by the properties of the solitons recorded in the future. Furthermore, there is no question concerning free choice or free will here and this for at least two reasons. First, like classical and Bohmian mechanics, the DS theory is fully deterministic and in such frameworks the concept of free will is necessarily an illusion, even if very persistent (we will not here enter the philosophical debate existing between incompatibilists and compatibilists concerning free will and determinism). Second, we should not forget that our theory agrees with the dBB pilot-wave theory concerning the predictions and statistics of quantum events. In an experiment like the one proposed before with an EPR pair, we naturally suppose that the -wave functions associated with the two observers, i.e., and , factorize from the EPR state before the interactions and measurements in the remote labs. It implies that the dBB trajectories associated with the observers and the pair of particles are not correlated and the sub-systems are statistically independent. The DS theory will in general involve advanced fields that in the usual time direction (i.e., from past to future) are converging from the remote past with information about settings . This superdeterministic information will converge on the particles and observers only during and after the interactions. Before these convergences, the observers were not influenced by any superdeterministic information and their actions were no less and no more free than in Newtonian mechanics. In the end, everything is consistent with the dBB theory interpreting the observer journeys through nonlocal links manifesting during the interactions, but this is just an effective way to see the problem when you ignore the u-field.
To conclude this long story, it is useful to note once again that nonlinear field equations admitting solitons are extremely difficult to solve and these studies are still in their infancy. The general methodological message of the present study is therefore that we should perhaps not be so astonished that new features require relinquishing prejudices about causality and time-symmetry. Progress in science is often made by abandoning prejudices. This is specially true since our theory is fundamentally relativistic and requires taking seriously the symmetry existing between space and time. This was clearly the path followed by de Broglie in 1925 when he attempted to explain quantum mechanics using the DS theory. Here, by taking this path seriously, we developed a complete DS theory able to reproduce a large set of quantum features associated with the Klein–Gordon relativistic equation. The DS theory in turn explains wave–particle dualism and recovers the predictions of the dBB pilot-wave theory for relativistic particles in external electromagnetic fields. The DS theory also explains the nonlocality and the action-at-a-distance of the dBB pilot-wave theory as an effective description. Fundamentally there is, however, no such ‘spooky’ action-at-a-distance entering into conflict with special relativity. The DS theory, thanks to time-symmetry, is local but superdeterministic.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. The Tachyonic Regime for Solitons
As it is well known, the dBB theory for the Klein–Gordon equation leads to some paradoxical features already discussed in 1927 [,] in the regime where . In this regime, the mass becomes imaginary and this implies a faster-than-light, i.e., tachyonic, motion for the particle guided by the -wave. However, contrarily to some old claims (see for example []), the dBB pilot-wave theory can be developed self-consistently even in the regime where . For this purpose, it is enough to generalize Equation (13) as
where is a parameter evolving along the particle trajectory. If , this must be used with corresponding to a time-like motion. However, if we must take associated with a space-like, i.e., tachyonic regime for the particle.
In the case of a space-like motion with , we can use the parameter , i.e., along the trajectory. Similarly, since , we can introduce , i.e., . These definitions correspond to a continuation in the complex plane of the subluminal formula defined in Equation (13). We thus have
i.e., in agreement with Equation (A1). It is important to note that along a dBB trajectory a subluminal segment (with ) is necessarily separated from a superluminal segment (with ) by a critical point where the mass vanishes, i.e., . This explains why, in the dBB theory, a particle can cross the light cone. In general, tachyonic sectors are confined to finite regions of space-time and are associated with evanescent -fields or occur in interference zones near fringes minima, as already shown by de Broglie []. Moreover, this also explains why tachyonic motions are not problematic from the causal point of view, since the tachyonic solutions are not observed in the the far-field, i.e., remotely from interference zones or strong scattering potentials.
In the context of the DS theory developed here, we need to define a hyperplane locally orthogonal to the trajectory. In the time-like subluminal regime, this space-like hyperplane is defined by the condition with that corresponds to the local inertial rest frame following the particle motion . In the tachyonic regime, we can similarly define a local hyperplane by the condition with but is not space-like. In order to physically interpret this hyperplane, we consider a laboratory frame where the particle is at time t moving with a velocity along the spacial direction. We thus define a generalized Lorentz transformation , (with ), , . The hyperplane corresponds to Const. Equivalently, we can define a Lorentz frame moving with the subluminal velocity along the spacial direction and introduce coordinates , , , . Interestingly, we see that, comparing the coordinates, the spacial coordinate corresponds to the time , and conversely, the time corresponds to the spacial coordinates . These equivalent sets of new coordinates characterize the hyperplane by = Const. Hence, the DS approach developed in Section 3.1 is easily extended to the tachyonic case. First, we can, similarly to Equation (12), define in the hyperplane the phase-harmony condition
From this, we recover the guidance formula Equation (14)
with , and from the continuity equation, we generalize Equation (16) as
The soliton profile is determined in the hyperplane by the equation:
which admits in the near-field the solution
The parameter is introduced in order to remove the singularity that would otherwise appear on the hyperboloids . We stress that this mathematical expression is reminiscent of X-type superluminal waves discussed in optics []. Moreover, for practical reasons it is possible to neglect the role of . Indeed, if we consider a continuous dBB trajectory, the subliminal and superluminal regions are separated by critical points where . But as we showed in Section 3.1, a soliton starting from a subluminal path coming from past infinity (i.e., ) is characterized by a coefficient , which is vanishing at the critical point. In other words, from Equations (19) and (21), we deduce , when we approach the critical point from the subluminal side. On the the other side, i.e., in the tachyonic regime, we must by continuity also impose that in Equation (A7) near the critical point. Therefore, the singular hyperboloids would be located at infinity and are not physical. For this reason, we can fairly assume as a sufficient approximation for describing the soliton near-field.
Ultimately, using the fluid conservation law Equations (10b) and (A5), we easily obtain the general evolution of and along the trajectory involving tachyonic and subluminal segments:
where we assume the asymptotic values and . In particular, in the subliminal regime, we recover Equation (23), and in the superluminal regime, we have .
References
- De Broglie, L. Ondes et quanta. C. R. Acad. Sci. 1923, 177, 507–510. [Google Scholar]
- De Broglie, L. Quanta de lumière, diffraction et interférences. C. R. Acad. Sci. 1923, 177, 548–560. [Google Scholar]
- De Broglie, L. Les quanta, la théorie cinétique des gaz et le principe de Fermat. C. R. Acad. Sci. 1927, 177, 630–632. [Google Scholar]
- De Broglie, L. Sur la définition générale de la correspondance entre onde et mouvement. C. R. Acad. Sci. 1927, 179, 39–40. [Google Scholar]
- De Broglie, L. Recherches Sur la théorie des Quanta; Faculté des Sciences de Paris: Paris, France, 1924; pp. 22–128. [Google Scholar]
- De Broglie, L. La mécanique ondulatoire et la structure atomique de la matière et du rayonnement. J. Phys. Radium 1927, 8, 225–241. [Google Scholar] [CrossRef]
- Bacciagaluppi, G.; Valentini, A. Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- De Broglie, L. Introduction à l’étude de la Mécanique Ondulatoire; Hermann: Paris, France, 1930. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “Hidden” Variables. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe; Routledge: London, UK, 1993. [Google Scholar]
- De Broglie, L. Une Tentative D’interprétation Causale et Non Linéaire de la Mécanique Ondulatoire: La Théorie de la Double Solution; Gauthier-Villars: Paris, France, 1956. [Google Scholar]
- Einstein, A.; Rosen, N. The particle problem in the general theory of relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
- Mie, G. Grundlagen einer Theorie der Materie. Ann. Phys. 1912, 99, 1–40. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Einstein, A. Über entwicklung unserer anschauungen über das wesen und die konstitution der strahlung. Physikalische Zeitschrift 1909, 10, 817–825. [Google Scholar] [CrossRef]
- De Broglie, L. Sur la fréquence propre de l’électron. C. R. Acad. Sci. 1925, 180, 498–500. [Google Scholar]
- De Broglie, L. Ondes et Mouvements; Gauthier-Villars: Paris, France, 1926. [Google Scholar]
- Drezet, A. A time-symmetric soliton dynamics à la de Broglie. Found. Phys. 2023, 53, 72. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Interaction with the absorber as the mechanism of radiation. Rev. Mod. Phys. 1945, 17, 157–181. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Classical electrodynamics in terms of direct interparticle action. Rev. Mod. Phys 1949, 21, 425–433. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Couder, Y.; Fort, E. Single-particle diffraction and interference at a macroscopic scale. Phys. Rev. Lett. 2006, 97, 154101. [Google Scholar] [CrossRef] [PubMed]
- Bush, J.W. The new wave of pilot-wave theory. Phys. Today 2015, 68, 47–53. [Google Scholar] [CrossRef]
- Drezet, A.; Jamet, P.; Bertschy, D.; Ralko, A.; Poulain, C. Mechanical analog of quantum bradyons and tachyons. Phys. Rev. E 2020, 102, 052206. [Google Scholar] [CrossRef]
- Jamet, P.; Drezet, A. A mechanical analog of Bohr’s atom based on de Broglie’s double-solution approach. Chaos 2021, 31, 103120. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental tests of realistic local theories via Bell’s theorem. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; Zeilinger, A. Violation of Bell’s inequality under strict Einstein locality conditions. Phys. Rev. Lett. 1998, 81, 5039–5043. [Google Scholar] [CrossRef]
- Hansen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Salart, D.; Baas, A.; Branciard, C.; Gisin, N.; Zbinden, H. Testing the speed of ‘spooky action at a distance’. Nature 2008, 454, 861–864. [Google Scholar] [CrossRef] [PubMed]
- Drezet, A. Lorentz-invariant, retrocausal, and deterministic hidden variables. Found. Phys. 2019, 49, 1166–1199. [Google Scholar] [CrossRef]
- Rauch, D.H.; Steiner, J.; Hochrainer, A.; Gallicchio, J.; Friedman, A.S.; Leung, C.; Liu, B.; Bulla, L.; Ecker, S.; Steinlechner, F.; et al. Cosmic Bell test using random measurement from high-redshift quasars. Phys. Rev. Lett. 2018, 121, 080403. [Google Scholar] [CrossRef]
- Handsteiner, J.; Steiner, J.; Friedman, A.S.; Rauch, D.; Gallicchio, J.; Liu, B.; Hosp, H.; Kofler, J.; Bricher, D.; Fink, M.; et al. Cosmic Bell test: Measurement settings from milky way stars. Phys. Rev. Lett. 2017, 118, 060401. [Google Scholar] [CrossRef]
- Gallicchio, J.; Friedman, A.S.; Kaiser, D. Testing Bell’s inequality with comsic photons: Closing the independence loophole. Phys. Rev. Lett. 2014, 112, 110405. [Google Scholar] [CrossRef]
- Arndt, M.; Aspelmeyer, M.; Zeilinger, A. How to extend quantum experiments. Fortschr. Phys. 2009, 57, 1153–1162. [Google Scholar] [CrossRef]
- ’t Hooft, G. Entangled quantum states in a local deterministic theory. arXiv 2009, arXiv:0908.3408. [Google Scholar]
- Everett, H., III. ‘Relative State’ formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Drezet, A. An elementary proof that Everett’s quantum multiverse is nonlocal: Bell-locality and branch-symmetry in the many-worlds interpretation. Symmetry 2023, 15, 1250. [Google Scholar] [CrossRef]
- Palmer, T. Superdeterminism without conspiracy. arXiv 2023, arXiv:2308.11262. [Google Scholar]
- Ciepielewski, G.; Okon, E.; Sudarsky, D. On superdeterministic rejections of settings independence. Br. J. Philos. Sci. 2023, 74, 435–467. [Google Scholar] [CrossRef]
- Costa de Beauregard, O. A response to the argument directed by Einstein, Poldosky and Rosen against the Bohrian interpretation of quantum phenomena. C. R. Acad. Sci. 1953, 236, 1632–1634. [Google Scholar]
- Costa de Beauregard, O. Time symmetry and the Einstein paradox. Nuovo Cimento Soc. Ital. Fis. 1977, 42B, 41–64. [Google Scholar] [CrossRef]
- Costa de Beauregard, O. Lorentz and CPT invariances and the Einstein-Podolsky-Rosen correlations. Phys. Rev. Lett. 1983, 50, 867–869. [Google Scholar] [CrossRef]
- Cramer, J.G. The transactional interpretation of quantum mechanics. Rev. Mod. Phys. 1986, 58, 647–687. [Google Scholar] [CrossRef]
- Aharonov, Y.; Gruss, E.Y. Two-time interpretation of quantum mechanics. arXiv 2005, arXiv:quant-ph/0507269. [Google Scholar]
- Sutherland, R.I. Causally symmetric Bohm model. Stud. Hist. Philos. Mod. Phys. 2008, 39, 782–805. [Google Scholar] [CrossRef]
- Sen, I. A local ψ-epistemic retrocausal hidden-variable model of Bell correlations with wavefunctions in physical space. Found. Phys. 2019, 49, 83. [Google Scholar] [CrossRef]
- Vigier, J.-P. Structure des Micro-Objets dans L’interprétation Causale de la Théorie de la Théorie des Quanta; Gauthier-Villars: Paris, France, 1956. [Google Scholar]
- Fargue, D. Permanence of the corpuscular appearance and non linearity of the wave equation. In The Wave-Particle Dualism; Diner, S., Fargue, D., Lochak, G., Selleri, F., Eds.; D. Reidel Publishing: Dordrecht, The Netherlands, 1984; pp. 149–172. [Google Scholar]
- Drezet, A. The guidance theorem of de Broglie. Ann. Fond. Broglie 2021, 46, 65–85. [Google Scholar]
- Andrade e Silva, J. La théorie des systèmes de particules dans l’interprétation causale de la mécanique ondulatoire. Ann. L’Institut Henri Poincaré 1960, 16, 289–359. [Google Scholar]
- De Broglie, L.; Andrade e Silva, J. La Réinterprétation de la Mécanique Ondulatoire. Première Partie: Principes généraux; Gauthier-Villars: Paris, France, 1971. [Google Scholar]
- De Broglie, L. Sur la réfutation du théorème de Bell. C. R. Acad. Sci. 1974, 278, 721–722. [Google Scholar]
- Bell, J.S. Locality in quantum mechanics: Reply to critics. Epistemological Letters 1975, 11, 2–6. [Google Scholar]
- Vigier, J.P. Jean-Pierre Vigier and the Stochastic Interpretation of Quantum Mechanics; Jeffers, S., Lehnert, B., Abramson, N., Chebortarev, L., Eds.; Apeiron: Montreal, QC, Canada, 2000. [Google Scholar]
- Drezet, A. Quantum solitodynamics: Non-linear wave mechanics and pilot-wave theory. Found. Phys. 2023, 53, 31. [Google Scholar] [CrossRef]
- Tetrode, H. Über den wirkungszusammenhang der welt. Eine erweiterung der klassischen dynamic. Z. Phys. 1922, 10, 317–328. [Google Scholar] [CrossRef]
- Page, L. A generalization of electrodynamics with applications to the structure of the electron and to non-radiating orbits. Phys. Rev. 1921, 18, 292–302. [Google Scholar] [CrossRef]
- Page, L. Advanced potentials and their application to atomic models. Phys. Rev. 1924, 24, 296–305. [Google Scholar] [CrossRef]
- Fokker, A.D. Ein invarianter variationssatz für die bewegung mehrerer electrischer massenteilshen. Z. Phys. 1929, 58, 386–389. [Google Scholar] [CrossRef]
- De Broglie, L. Corpuscules et ondes Ψ. C. R. Acad. Sci. 1927, 185, 1118–1119. [Google Scholar]
- Saari, P. Superluminal Localized Waves of Electromagnetic Field in Vacuo. In Time’s Arrows, Quantum Measurement and Superluminal Behavior; Mugnai, D., Ranfagni, A., Schulman, L.S., Eds.; Scientific Monographs: Physics Sciences Series; Italian CNR Publisher: Rome, Italy, 2001; pp. 37–48. [Google Scholar]
- Vigier, J.P. Mécanique ondulatoire dans l’espace de configuration. C. R. Acad. Sci. 1952, 235, 1372–1375. [Google Scholar]
- Régnier, A. Sur la conservation de la cahrge. C. R. Acad. Sci. 1952, 235, 1370–1372. [Google Scholar]
- Dürr, D.; Goldstein, S.; Zanghì, N. Bohmian mechanics and the meaning of the wave function. In Experimental Metaphysics—Quantum Mechanical Studies for Abner Shimony; Cohen, R.S., Horne, M., Stachel, J., Eds.; Volume One, (Boston Studies in the Philosophy of Science 193); Kluwer Academic Publishers: Boston, MA, USA, 1997. [Google Scholar]
- Drezet, A. Justifying Born’s rule Pα=|Ψα|2 using deterministic chaos, decoherence, and the de Broglie-Bohm quantum theory. Entropy 2021, 23, 1371. [Google Scholar] [CrossRef] [PubMed]
- Selleri, F. Die Debatte um die Quantentheorie; Vieweg+Teubner Verlag Wiesbaden, Springer: Cham, Switzerland, 1983. [Google Scholar]
- Croca, J.R.; Castro, P.; Gatta, M.; Moreira, R.N. Proposed experiments to clarify the real nature of the quantum waves. Found. Phys. 2023, 53, 14. [Google Scholar] [CrossRef]
- Allori, V.; Goldstein, S.; Tumulka, R.; Zanghì, N. Predictions and primitive ontology in quantum foundations: A study of examples. Br. J. Philos. Sci. 2014, 65, 323–352. [Google Scholar] [CrossRef]
- Allori, V. Wave-functionalism. Synthese 2021, 199, 12271–12293. [Google Scholar] [CrossRef]
- Hardy, L.; Squires, E. On the violation of Lorentz-invariance in deterministic hidden-variable interpretations of quantum mechanics. Phys. Lett. A 1992, 168, 169–173. [Google Scholar] [CrossRef]
- Brans, C.H. Bell’s theorem does not eliminate fully causal hidden variables. Int. J. Theor. Phys. 1988, 27, 219–226. [Google Scholar] [CrossRef]
- ’t Hooft, G. Free will in the theory of everything. arXiv 2017, arXiv:1709.02874. [Google Scholar]
- ’t Hooft, G. Ontology in quantum mechanics. arXiv 2021, arXiv:2107.14191. [Google Scholar]
- Vervoort, L. Bell’s theorem two neglected solutions. Found. Phys. 2013, 6, 769–791. [Google Scholar] [CrossRef][Green Version]
- Goldstein, S.; Norsen, T.; Tausk, D.V.; Zanghi, N. Bell’S Theorem. Scholarpedia 2011, 6, 8378. [Google Scholar] [CrossRef]
- Kyprianidis, A. Particle trajectories in relativistic quantum mechanics. Phys. Lett. A 1985, 111, 111–116. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).