Binary Bipolar Soft Points and Topology on Binary Bipolar Soft Sets with Their Symmetric Properties

Abstract

The aim of this paper is to give an interesting connection between two mathematical approaches to vagueness: binary bipolar soft sets and binary bipolar soft topology. The binary bipolar soft points are defined using binary bipolar soft sets. The binary bipolar soft set will be the binary bipolar soft union of its binary bipolar soft points. Moreover, the notion of binary bipolar soft topological spaces over two universal sets and a parameter set is proposed. Some topological properties of binary bipolar soft sets, such as binary bipolar soft open, binary bipolar soft closed, binary bipolar soft closure, binary bipolar soft interior, and binary bipolar soft boundary, are introduced. Some important properties of these classes of binary bipolar soft sets are investigated. Furthermore, the symmetry relation is compared between binary bipolar soft topology and binary soft topology on a common universe set. Finally, some results and counterexamples are demonstrated to explain this work.

1. Introduction

For formal modeling, reasoning, and computing, most traditional tools are characterized by being crisp, deterministic, and precise. However, many complex problems exist in the domains of economics, engineering, the environment, social science, medical science, and so on. Therefore, traditional methods based on cases may not be suitable for solving or modeling these issues. Based on this, a set of theories has been proposed to tackle these problems. Molodtsov [1] introduced a new concept, namely soft set. In [1,2], Molodtsov successfully applied the soft theory in several directions, such as smoothness of functions, game theory, operations research, Riemann integration, Perron integration, probability, theory of measurement, etc.

In 2013, Shabir and Naz [3] explained that the bipolar soft set structure has clearer and more general results than the soft set structure. They came up with the fuzzy bipolar soft sets and bipolar fuzzy soft sets and established some algebraic structures of these two classes of bipolar soft sets. They presented an application of fuzzy bipolar soft sets in decision-making problems [4]. Based on Dubois and Prada [5], decision making is constructed on two sides, namely positive and negative. Bipolarity is significant for characterization between positive and negative information to differentiate between reasonable and unreasonable events. Shabir and Bakhtawar [6] introduced the concept of bipolar soft topological spaces and studied some of their properties. Fadel and Dzul-Kifli [7] defined the concept of bipolar soft topological spaces via bipolar soft sets and some properties. Öztürk [8,9] presented more properties and operations on bipolar soft sets, and the bipolar soft points are introduced.

Subsequently, a number of definitions, operations, and applications on bipolar soft sets and bipolar soft structures have been investigated. For instance, Dizman and Öztürk [10] introduced fuzzy bipolar soft topological spaces via fuzzy bipolar soft sets. Abdullah et al. [11] proposed a bipolar fuzzy soft set, which is a new idea of bipolar soft set and they introduced some basic operations and an application of bipolar fuzzy soft set into decision-making problems. They gave an algorithm to solve decision-making problems by using a bipolar fuzzy soft set. Al-Shami [12] defined some ordinary points on bipolar soft sets and presented an application of optimal choices by applying the idea of bipolar soft sets. Karaaslan and Karataş [13] redefined the concept of the bipolar soft set and bipolar soft set operations and presented a decision-making method with application. Karaaslana et al. [14] defined normal bipolar soft subgroups. Mahmood [15] defined a novel approach towards bipolar soft sets and discussed an application on decision-making problems. Wang et al. [16], and Rehman and Mahmood [17] combined some generalizations of fuzzy sets and bipolar soft sets. They investigated applications in decision-making problems. Hussain [18] defined and discussed binary soft connected spaces in binary soft topological spaces. He proposed an application of a decision-making problem by using the approach of rough sets. Sathiyaseelan et al. [19] presented symmetric matrices on inverse soft expert sets and investigated their applications.

Yet, studies conducted on the limit point concept were required by mathematicians to bring about more developments in mathematics. Musa and Asaad [20] introduced the concept of the bipolar hypersoft set as a combination of a hypersoft set with a bipolarity setting and investigated some of its basic operations. They also discussed some topological notions in the frame of bipolar hypersoft setting [21]. In 2022, Saleh et al. [22,23] studied bipolar soft generalized topological spaces and defined the basic notions of bipolar soft topological properties with the investigation of a number of their symmetric properties.

Correspondingly, in 2016, the concept of the binary soft set was first defined by Açıkgöz and Taş in [24], where they introduced the binary soft set on two initial universal sets and proposed some of their properties. After that, Benchalli et al. [25] presented some related basic properties, which are defined over two initial universal sets with suitable parameters, and they defined the binary soft topological spaces with some of their properties. Recently, in 2023, Naime and Orhan [26] defined a new concept of bipolar soft sets over two universal sets and a parameter set, namely binary bipolar soft sets, which is an extension of bipolar soft sets and binary soft sets. They presented some operations on binary bipolar soft sets, such as complement, union, intersection, AND, and OR, and they investigated their basic properties.

The following sections in our work are organized in the following manner: Section 2 provides the essential conceptual framework concerning symmetry categories of sets, including soft sets, bipolar soft sets, and binary soft sets, to familiarize the reader with the underlying principles. After that, in Section 3, our main idea is to define the binary bipolar soft points using binary bipolar soft sets and some of their properties. Section 4 introduces the binary bipolar soft topological spaces using binary bipolar soft sets, which is an extension of the bipolar soft topological spaces and binary soft topological spaces, accompanied by an exploration of the associated topological operators binary bipolar soft closure, binary bipolar soft interior and binary bipolar soft boundary. Some results and counterexamples are given to explain this work. Section 5 serves as the concluding section of our presentation.

2. Preliminaries

Throughout this paper, we recall some notions in bipolar soft sets via binary bipolar soft sets, and we will give some preliminary information about binary bipolar soft sets, binary soft topological spaces, and bipolar soft topological spaces.

2.1. Bipolar Soft Sets

This subsection investigates the concepts of bipolar soft set operations. Let ℧ be an initial universe set and ℜ be a set of parameters. Let $\mathrm{\Psi }$ ⊆ ℜ and $\mathbb{P}(\mho )$ denote the collection of all subsets of ℧. The set of all bipolar soft sets over ℧ with $\mathrm{\Psi }$ will be denoted by $\mathbb{BSS}{(\mho )}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. Let $\mathrm{\Psi }=\left\{{\xi }_1,{\xi }_2,...,{\xi }_n\right\}$ be a subset of ℜ.

Definition 1. 

The Not set of Ψ is denoted by $\neg \mathrm{\Psi }=\{\neg {\xi }_1,\neg {\xi }_2,...,\neg {\xi }_n\}$, where $\neg {\xi }_i=$ Not ${\xi }_i$ for each i.

The following definitions can be found in [3].

Definition 2. 

A triple $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is called a bipolar soft set on ℧, denoted by $\mathbb{BSS}$, where $\widehat{\aleph }$ and $\check{\aleph }$ are mappings defined by $\widehat{\aleph }:\mathrm{\Psi }⟶2^{\mathrm{\Psi }}$ and $\check{\aleph }:\neg \mathrm{\Psi }⟶2^{\mathrm{\Psi }}$ such that $\widehat{\aleph }\left(\xi \right)$∩$\check{\aleph }(\neg \xi )=\varphi$ for each $\xi \in \mathrm{\Psi }$ and $\neg \xi \in \neg \mathrm{\Psi }$.

Definition 3. 

The $\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be a $\mathbb{BS}$ subset of $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ if $\widehat{\aleph }\left(\xi \right)\subseteq \widehat{\gimel }\left(\xi \right)$ and $\check{\gimel }(\neg \xi )\subseteq \check{\aleph }(\neg \xi )$ for each $\xi \in \mathrm{\Psi }$.

Definition 4. 

The complement of a $\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is denoted by ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ $=({\widehat{\aleph }}^c,{\check{\aleph }}^c,\mathrm{\Psi })$ where ${\widehat{\aleph }}^c\left(\xi \right)=\check{\aleph }(\neg \xi )$ and $\check{\aleph }{(\neg \xi )}^c=\widehat{\aleph }\left(\xi \right)$ for each $\xi \in \mathrm{\Psi }$.

Definition 5. 

A $\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be an absolute $\mathbb{BSS}$ denoted by $(\widehat{\mho },\mathrm{\Phi },\mathrm{\Psi })$ with the property that for each $\xi \in \mathrm{\Psi }$, $\widehat{\mho }\left(\xi \right)=\mho$ and $\mathrm{\Phi }(\neg \xi )=\varphi$.

Definition 6. 

A $\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be a null $\mathbb{BSS}$ is denoted by $(\mathrm{\Phi },\check{\mho },\mathrm{\Psi })$ with the property that for each $\xi \in \mathrm{\Psi }$, $\mathrm{\Phi }\left(\xi \right)=\varphi$ and $\check{\mho }(\neg \xi )=\mho$.

Definition 7. 

The restricted intersection of two $\mathbb{BSS}s$ $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ on the common universe ℧ is the $\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ ${\tilde{\sqcap }}_{\mathbb{R}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_1)$, where for each $\xi \in \mathrm{\Psi }$, $\widehat{\nabla }\left(\xi \right)=\widehat{\aleph }\left(\xi \right)\cap \widehat{\gimel }\left(\xi \right)$ and $\check{\nabla }(\neg \xi )=\check{\aleph }(\neg \xi )\cup \check{\gimel }(\neg \xi )$.

Definition 8. 

The extended intersection of two $\mathbb{BSS}s$ $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ on the common universe ℧ is the $\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cup {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\tilde{\sqcap }$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_1)$, where

$$\widehat{\nabla }\left(\xi \right)=\left\{\begin{array}{cc}\widehat{\aleph }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2,\hfill \\ \widehat{\gimel }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_2-{\mathrm{\Psi }}_1,\hfill \\ \widehat{\aleph }\left(\xi \right)\cap \widehat{\gimel }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2\hfill \end{array}\right.$$

and

$$\check{\nabla }(\neg \xi )=\left\{\begin{array}{cc}\check{\aleph }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1-\neg {\mathrm{\Psi }}_2,\hfill \\ \check{\gimel }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_2-\neg {\mathrm{\Psi }}_1,\hfill \\ \check{\aleph }(\neg \xi )\cup \check{\gimel }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1\cap \neg {\mathrm{\Psi }}_2.\hfill \end{array}\right.$$

Definition 9. 

The restricted union of two $\mathbb{BSS}s$ $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ on the common universe ℧ is the $\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ ${\tilde{\bigsqcup }}_{\mathbb{R}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_1)$, where for each $\xi \in \mathrm{\Psi }$, $\widehat{\nabla }\left(\xi \right)=\widehat{\aleph }\left(\xi \right)\cup \widehat{\gimel }\left(\xi \right)$ and $\check{\nabla }(\neg \xi )=\check{\aleph }(\neg \xi )\cap \check{\gimel }(\neg \xi )$.

Definition 10. 

The extended union of two $\mathbb{BSS}s$ $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ on the common universe ℧ is the $\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cup {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\tilde{\bigsqcup }$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$, where [3]

$$\widehat{\nabla }\left(\xi \right)=\left\{\begin{array}{cc}\widehat{\aleph }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2,\hfill \\ \widehat{\gimel }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_2-{\mathrm{\Psi }}_1,\hfill \\ \widehat{\aleph }\left(\xi \right)\cup \widehat{\gimel }\left(\xi \right),\hfill & \xi \in {\mathrm{\Psi }}_1\cup {\mathrm{\Psi }}_2\hfill \end{array}\right.$$

and

$$\check{\nabla }(\neg \xi )=\left\{\begin{array}{cc}\check{\aleph }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1-\neg {\mathrm{\Psi }}_2,\hfill \\ \check{\gimel }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_2-\neg {\mathrm{\Psi }}_1,\hfill \\ \check{\aleph }(\neg \xi )\cap \check{\gimel }(\neg \xi ),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1\cap \neg {\mathrm{\Psi }}_2.\hfill \end{array}\right.$$

Shabir and Naz [3] introduced bipolar soft topological spaces ($\mathbb{BSTS}s$) $(\mho ,\widehat{\widehat{\Im }},\mathrm{\Psi },\neg \mathrm{\Psi })$, where $\widehat{\widehat{\Im }}$ is the collection of $\mathbb{BSS}s$ over ℧ containing $(\widehat{\mho },\mathrm{\Phi },\mathrm{\Psi })$ and $(\mathrm{\Phi },\widehat{\mho },\mathrm{\Psi })$, the $\mathbb{BS}$ union of any member of $\mathbb{BSS}s$ in $\widehat{\widehat{\Im }}$ belongs to $\widehat{\widehat{\Im }}$, and the $\mathbb{BS}$ intersection of any two $\mathbb{BSS}s$ in $\widehat{\widehat{\Im }}$ belongs to $\widehat{\widehat{\Im }}$. The members of $\widehat{\widehat{\Im }}$ are said to be $\mathbb{BS}$ open sets in ℧. The $\mathbb{BSS}$ is said to be $\mathbb{BS}$ closed in ℧ if its relative complement ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ belongs to $\widehat{\widehat{\Im }}$.

2.2. Binary Bipolar Soft Sets

This subsection investigates the concepts of binary soft set operations and binary bipolar soft set operations. In 2016, Açıkgöz and Taş [24] introduced the binary soft set theory and investigated some of its related operations. After that, in 2017, Benchalli et al. [25] defined a topology on $\mathcal{B}\mathbb{SS}$, namely binary soft topological space ($\mathcal{B}\mathbb{STS}$), where ${\widehat{\Im }}_{\Delta }$ is the collection of $\mathcal{B}\mathbb{SS}s$ over ${\mho }_1$ and ${\mho }_2$, which contains a null $\mathcal{B}\mathbb{SS}$ and an absolute $\mathcal{B}\mathbb{SS}$, and it is closed under finite $\mathcal{B}\mathbb{S}$ intersections and closed under $\mathcal{B}\mathbb{S}$ unions.

The following definitions can be found in [26]. Let ${\mho }_1$ and ${\mho }_2$ be two initial universe sets and ℜ be a set of parameters. Let $\mathbb{P}\left({\mho }_1\right)$ and $\mathbb{P}\left({\mho }_2\right)$ denote the power set of ${\mho }_1$ and ${\mho }_2$, respectively. Let $\mathrm{\Psi }\subseteq \Re$.

Definition 11. 

A triple $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is called a binary bipolar soft set $\left(\mathcal{B}\mathbb{BSS}\right)$ over $\mathbb{P}\left({\mho }_1\right)$ and $\mathbb{P}\left({\mho }_2\right)$, where $\widehat{\aleph }$ and $\check{\aleph }$ are mappings defined by $\widehat{\aleph }:\mathrm{\Psi }⟶\mathbb{P}\left({\mho }_1\right)\times \mathbb{P}\left({\mho }_2\right)$ and $\check{\aleph }:\neg \mathrm{\Psi }⟶\mathbb{P}\left({\mho }_1\right)\times \mathbb{P}\left({\mho }_2\right)$ such that $\widehat{\mathtt{X}},\check{\mathtt{X}}$ $\subseteq {\mho }_1$, $\widehat{\mathtt{Y}},\check{\mathtt{Y}}$ $\subseteq {\mho }_2$ and $\widehat{\aleph }\left(\xi \right)$∩$\check{\aleph }(\neg \xi )=$ $(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})\cap (\check{\mathtt{X}},\check{\mathtt{Y}})$ $=\varphi$ for each $\xi \in \mathrm{\Psi }$.

Definition 12. 

The $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ is said to be a $\mathcal{B}\mathbb{BS}$ subset of $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ if ${\mathrm{\Psi }}_1\subseteq {\mathrm{\Psi }}_2$, ${\widehat{\mathtt{X}}}_{\mathtt{1}}\subseteq {\widehat{\mathtt{X}}}_{\mathtt{2}}$ and ${\widehat{\mathtt{Y}}}_{\mathtt{1}}\subseteq {\widehat{\mathtt{Y}}}_{\mathtt{2}}$ such that $\widehat{\aleph }\left(\xi \right)(=({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}}))\subseteq \widehat{\gimel }\left(\xi \right)(=({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}}))$ and $\check{\gimel }(\neg \xi )(=({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}}))\subseteq \check{\aleph }(\neg \xi )(=({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}}))$ for each $\xi \in \mathrm{\Psi }$. This relationship is denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$. Similarly, $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ is said to be a $\mathcal{B}\mathbb{BS}$ superset of $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ if $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ is a $\mathcal{B}\mathbb{BS}$ subset of $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\widetilde{\tilde{⊒}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$.

Definition 13. 

Two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ over universes ${\mho }_1$ and ${\mho }_2$ are said to be equal $\mathcal{B}\mathbb{BSS}$s if $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ is a $\mathcal{B}\mathbb{BS}$ subset of $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ is a $\mathcal{B}\mathbb{BS}$ subset of $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$.

Definition 14. 

The complement of a $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is denoted by ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ $=({\widehat{\aleph }}^c,{\check{\aleph }}^c,\mathrm{\Psi })$ where ${\widehat{\aleph }}^c:\mathrm{\Psi }⟶\mathbb{P}\left({\mho }_1\right)\times \mathbb{P}\left({\mho }_2\right)$ and ${\check{\aleph }}^c:\neg \mathrm{\Psi }⟶\mathbb{P}\left({\mho }_1\right)\times \mathbb{P}\left({\mho }_2\right)$ are mapping given by ${\widehat{\aleph }}^c\left(\xi \right)=({\mho }_1-\widehat{\mathtt{X}},{\mho }_2-\widehat{\mathtt{Y}})=(\check{\mathtt{X}},\check{\mathtt{Y}})=\check{\aleph }(\neg \xi )$ and ${\check{\aleph }}^c(\neg \xi )=({\mho }_1-\check{\mathtt{X}},{\mho }_2-\check{\mathtt{Y}})=(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})$ $=\widehat{\aleph }\left(\xi \right)$ for each $\xi \in \mathrm{\Psi }$.

Definition 15. 

A $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be absolute $\mathcal{B}\mathbb{BSS}$ is denoted by $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ with the property that for each $\xi \in \mathrm{\Psi }$, $\widehat{\widehat{\mho }}\left(\xi \right)=({\mho }_1,{\mho }_2)$ and $\mathrm{\Phi }(\neg \xi )=(\varphi ,\varphi )$.

Definition 16. 

A $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be a null $\mathcal{B}\mathbb{BSS}$ is denoted by $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ with the property that for each $\xi \in \mathrm{\Psi }$, $\mathrm{\Phi }\left(\xi \right)=(\varphi ,\varphi )$ and $\widehat{\widehat{\mho }}(\neg \xi )=({\mho }_1,{\mho }_2)$.

Definition 17. 

The difference of two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ over universes ${\mho }_1$ and ${\mho }_2$ is the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },\mathrm{\Psi })$ $=(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\setminus }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, where $\widehat{\nabla }\left(\xi \right)=({\widehat{\mathtt{X}}}_{\mathtt{1}}-{\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{1}}-{\widehat{\mathtt{Y}}}_{\mathtt{2}})$ and $\check{\nabla }(\neg \xi )=$ $({\check{\mathtt{X}}}_{\mathtt{1}}-{\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{1}}-{\check{\mathtt{Y}}}_{\mathtt{2}})$ for each $\xi \in \mathrm{\Psi }$.

Definition 18. 

The restricted intersection of two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ over universes ${\mho }_1$ and ${\mho }_2$ is the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2)$ with ${\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2\ne \varphi$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ ${\tilde{\tilde{\sqcap }}}_{\mathbb{R}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$, where for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$, $\widehat{\nabla }\left(\xi \right)=\widehat{\aleph }\left(\xi \right)\cap \widehat{\gimel }\left(\xi \right)$ and $\check{\nabla }(\neg \xi )=\check{\aleph }(\neg \xi )\cup \check{\gimel }(\neg \xi )$ such that $\widehat{\aleph }\left(\xi \right)=({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}})$, $\check{\aleph }(\neg \xi )=({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}})$ for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$ and $\widehat{\gimel }\left(\xi \right)=({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}})$, $\check{\gimel }(\neg \xi )=({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}})$ for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$.

Definition 19. 

The extended intersection of two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ over universes ${\mho }_1$ and ${\mho }_2$ is the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cup {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$, where for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$

$$\widehat{\nabla }\left(\xi \right)=\left\{\begin{array}{cc}({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}}),\hfill & \xi \in {\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2,\hfill \\ ({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \xi \in {\mathrm{\Psi }}_2-{\mathrm{\Psi }}_1,\hfill \\ ({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}})\cap ({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2\hfill \end{array}\right.$$

and

$$\check{\nabla }(\neg \xi )=\left\{\begin{array}{cc}({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1-\neg {\mathrm{\Psi }}_2,\hfill \\ ({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_2-\neg {\mathrm{\Psi }}_1,\hfill \\ ({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}})\cup ({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1\cap \neg {\mathrm{\Psi }}_2.\hfill \end{array}\right.$$

Definition 20. 

The restricted union of two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ over universes ${\mho }_1$ and ${\mho }_2$ is the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2)$ with ${\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2\ne \varphi$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ ${\tilde{\tilde{\bigsqcup }}}_{\mathbb{R}}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$, where for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$, $\widehat{\nabla }\left(\xi \right)=\widehat{\aleph }\left(\xi \right)\cup \widehat{\gimel }\left(\xi \right)$ and $\check{\nabla }(\neg \xi )=\check{\aleph }(\neg \xi )\cap \check{\gimel }(\neg \xi )$ such that $\widehat{\aleph }\left(\xi \right)=({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}})$, $\check{\aleph }(\neg \xi )=({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}})$ for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$ and $\widehat{\gimel }\left(\xi \right)=({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}})$, $\check{\gimel }(\neg \xi )=({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}})$ for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$.

Definition 21. 

The extended union of two $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ and $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$ on the universes ${\mho }_1$ and ${\mho }_2$ is the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\nabla },\check{\nabla },{\mathrm{\Psi }}_1\cup {\mathrm{\Psi }}_2)$, denoted by $(\widehat{\aleph },\check{\aleph },{\mathrm{\Psi }}_1)$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },{\mathrm{\Psi }}_2)$, where for each $\xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2$,

$$\widehat{\nabla }\left(\xi \right)=\left\{\begin{array}{cc}({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}}),\hfill & \xi \in {\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2,\hfill \\ ({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \xi \in {\mathrm{\Psi }}_2-{\mathrm{\Psi }}_1,\hfill \\ ({\widehat{\mathtt{X}}}_{\mathtt{1}},{\widehat{\mathtt{Y}}}_{\mathtt{1}})\cup ({\widehat{\mathtt{X}}}_{\mathtt{2}},{\widehat{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \xi \in {\mathrm{\Psi }}_1\cap {\mathrm{\Psi }}_2\hfill \end{array}\right.$$

and

$$\check{\nabla }(\neg \xi )=\left\{\begin{array}{cc}({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1-\neg {\mathrm{\Psi }}_2,\hfill \\ ({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_2-\neg {\mathrm{\Psi }}_1,\hfill \\ ({\check{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}})\cap ({\check{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}}),\hfill & \neg \xi \in \neg {\mathrm{\Psi }}_1\cap \neg {\mathrm{\Psi }}_2.\hfill \end{array}\right.$$

3. Binary Bipolar Soft Points

In this section, we present the binary bipolar soft points and some related properties.

Definition 22. 

A $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be binary bipolar soft point $\left(\mathcal{B}\mathbb{BSP}\right)$ if there exists $({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}})$, $({\widehat{\mathtt{x}}}_{\mathtt{2}},{\widehat{\mathtt{y}}}_{\mathtt{2}})$ ∈ $({\mho }_1,{\mho }_2)$ (it possible to $({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}})$ = $({\widehat{\mathtt{x}}}_{\mathtt{2}},{\widehat{\mathtt{y}}}_{\mathtt{2}})$) and $\xi \in \mathrm{\Psi }$ such that

$$\widehat{\aleph }\left(\eta \right)=\left\{\begin{array}{cc}\left\{({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}})\right\},\hfill & \eta =\xi ,\hfill \\ (\varphi ,\varphi ),\hfill & \eta \ne \xi \hfill \end{array}\right.$$

and

$$\check{\aleph }\left({\eta }^{\prime }\right)=\left\{\begin{array}{cc}({\mho }_1,{\mho }_2)\setminus \{({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}}),({\widehat{\mathtt{x}}}_{\mathtt{2}},{\widehat{\mathtt{y}}}_{\mathtt{2}})\},\hfill & {\eta }^{\prime }=\xi ,\hfill \\ ({\mho }_1,{\mho }_2),\hfill & {\eta }^{\prime }\ne \xi .\hfill \end{array}\right.$$

We denote ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$ by the $\mathcal{B}\mathbb{BSP}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, where $\widehat{\mathtt{X}}=({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}})$ and $\widehat{\mathtt{Y}}=({\widehat{\mathtt{x}}}_{\mathtt{2}},{\widehat{\mathtt{y}}}_{\mathtt{2}})$ in $({\mho }_1,{\mho }_2)$. The collection of $\mathcal{B}\mathbb{BSP}s$ is denoted by $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$.

Definition 23. 

Let ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$, ${\xi }_{(\widehat{{\mathtt{X}}^{\prime }},\widehat{{\mathtt{Y}}^{\prime }})}^{\prime }$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. Then, ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$ and ${\xi }_{(\widehat{{\mathtt{X}}^{\prime }},\widehat{{\mathtt{Y}}^{\prime }})}^{\prime }$ are called different $\mathcal{B}\mathbb{BSP}s$, denoted by ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$≠${\xi }_{({\widehat{\mathtt{X}}}^{\prime },{\widehat{\mathtt{Y}}}^{\prime })}^{\prime }$ if $\widehat{\mathtt{X}}=(\widehat{\mathtt{x}},\widehat{\mathtt{y}})\ne ({\widehat{\mathtt{x}}}^{\prime },{\widehat{\mathtt{y}}}^{\prime })=\widehat{\mathtt{Y}}$ or $\xi \ne {\xi }^{\prime }$.

Definition 24. 

Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSS}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$ and ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. Then, ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$ is said to be contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ if $\widehat{\mathtt{X}}=({\widehat{\mathtt{x}}}_{\mathtt{1}},{\widehat{\mathtt{y}}}_{\mathtt{1}})$ $\in \widehat{\aleph }\left(\xi \right)$ and $\widehat{\mathtt{Y}}=({\widehat{\mathtt{x}}}_{\mathtt{2}},{\widehat{\mathtt{y}}}_{\mathtt{2}})$ $\in ({\mho }_1,{\mho }_2)\setminus \check{\aleph }(\neg \xi )$. It is denoted by ${\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}$ $\tilde{\tilde{\in }}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Proposition 1. 

Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSS}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. Then, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the $\mathcal{B}\mathbb{BS}$ union of its $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. That is,

$$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })=\widetilde{\tilde{⨆}} \{{\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}:{\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})} \tilde{\tilde{\in }} (\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\}.$$

Proof. 

It is sufficient to show the following:

For each $\xi \in \mathrm{\Psi }$,

$$\widehat{\aleph }\left(\xi \right)={\tilde{\tilde{\bigsqcup }}}_{{\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}\tilde{\tilde{\in }}(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}\left\{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})\right\},$$

and for each $\neg \xi \in \neg \mathrm{\Psi }$,

$$\check{\aleph }(\neg \xi )={\tilde{\tilde{\sqcap }}}_{{\xi }_{(\widehat{\mathtt{X}},\widehat{\mathtt{Y}})}\tilde{\tilde{\in }}(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}\{({\mho }_1,{\mho }_2)\setminus (\widehat{\mathtt{X}},\widehat{\mathtt{Y}})\},$$

Since the proof of these two equalities are easy and hence it is completed. □

Example 1. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}$ and ${\mho }_2=\{{\lambda }_1,{\lambda }_2\}$ be two universe sets and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$ be a set of parameters. The $\mathcal{B}\mathbb{BSS}$

$$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })=\{({\xi }_1,(\{{\kappa }_1,{\kappa }_3\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\})),({\xi }_2,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_3\},\left\{{\lambda }_2\right\}))\}.$$

We can write this $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ as a $\mathcal{B}\mathbb{BS}$ union of its $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$,

$$\begin{gathered} (\widehat{\aleph },\check{\aleph },\mathrm{\Psi })=\widetilde{\tilde{⨆}}\{{{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_1,{\lambda }_2),}{{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_3,{\lambda }_2)},{{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_3,{\lambda }_2)},{{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_1,{\lambda }_2)},{{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_2,{\lambda }_1)}, \\ {{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_3,{\lambda }_1)},{{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_3,{\lambda }_1)},{{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_2,{\lambda }_1)}\}, \end{gathered}$$

where ${{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_1,{\lambda }_2)}$, ${{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_3,{\lambda }_2)}$, ${{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_3,{\lambda }_2)}$, ${{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_1,{\lambda }_2)}$, ${{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_2,{\lambda }_1)}$, ${{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_3,{\lambda }_1)}$, ${{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_3,{\lambda }_1)}$, ${{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_2,{\lambda }_1)}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BS}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$ and defines as

$$\begin{array}{cc}\hfill {{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_1,{\lambda }_2)}& =\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_2,{\kappa }_3\},\left\{{\lambda }_1\right\})),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\},\hfill \\ \hfill {{\xi }_1}_{({\kappa }_1,{\lambda }_2),({\kappa }_3,{\lambda }_2)}& =\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\})),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\},\hfill \\ \hfill {{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_3,{\lambda }_2)}& =\{({\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\})),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\},\hfill \\ \hfill {{\xi }_1}_{({\kappa }_3,{\lambda }_2),({\kappa }_1,{\lambda }_2)}& =\{({\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\})),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\},\hfill \\ \hfill {{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_2,{\lambda }_1)}& =\{({\xi }_1,(\varphi ,\varphi ),({\mho }_1,{\mho }_2)),({\xi }_2,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_3\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill {{\xi }_2}_{({\kappa }_2,{\lambda }_1),({\kappa }_3,{\lambda }_1)}& =\{({\xi }_1,(\varphi ,\varphi ),({\mho }_1,{\mho }_2)),({\xi }_2,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill {{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_3,{\lambda }_1)}& =\{({\xi }_1,(\varphi ,\varphi ),({\mho }_1,{\mho }_2)),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill {{\xi }_2}_{({\kappa }_3,{\lambda }_1),({\kappa }_2,{\lambda }_1)}& =\{({\xi }_1,(\varphi ,\varphi ),({\mho }_1,{\mho }_2)),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\}))\}.\hfill \end{array}$$

Proposition 2. 

Let $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ be a family of $\mathcal{B}\mathbb{BSS}s$. Then,

1. 

${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ ${\tilde{\tilde{\sqcap }}}_{i\in I}$ $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ if and only if ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ for each $i\in I$. That is, $\widehat{\mathtt{X}}\in {\widehat{\aleph }}_i\left(\xi \right)$ and $\widehat{\mathtt{Y}}\in ({\mho }_1,{\mho }_2)\setminus {\check{\aleph }}_i(\neg \xi )$ for every $i\in I,\xi \in \mathrm{\Psi }$, $\neg \xi \in \neg \mathrm{\Psi }$.

2. 

${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ if and only if there exists $i\in I$, such that ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$. That is, there exists $i\in I$, such that $\widehat{\mathtt{X}}\in {\widehat{\aleph }}_i\left(\xi \right)$ and $\widehat{\mathtt{Y}}\in ({\mho }_1,{\mho }_2)\setminus {\check{\aleph }}_i(\neg \xi )$ for every $\xi \in \mathrm{\Psi }$ and $\neg \xi \in \neg \mathrm{\Psi }$.

Proof. 

Straightforward. □

Proposition 3. 

Let $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSS}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. Then, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2$, $\mathrm{\Psi })$ if and only if for each ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ implies that ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$.

Proof. 

Suppose ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ is an arbitrary $\mathcal{B}\mathbb{BSP}$ and $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$. Then, $\widehat{\mathtt{X}}$∈${\widehat{\aleph }}_1\left(\xi \right)$⊆${\widehat{\aleph }}_2\left(\xi \right)$ and $\widehat{\mathtt{Y}}$∈$({\mho }_1,{\mho }_2)\setminus {\check{\aleph }}_1(\neg \xi )$⊆$({\mho }_1,{\mho }_2)\setminus {\check{\aleph }}_2(\neg \xi )$ for all $\xi \in \mathrm{\Psi }$ and $\neg \xi \in \neg \mathrm{\Psi }$. Therefore, ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$. □

Proposition 4. 

Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSS}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$ and ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$. If the $\mathcal{B}\mathbb{BSP}$ ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ belongs to $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, then the $\mathcal{B}\mathbb{SP}$ ${\xi }_{\widehat{\mathtt{X}}}$ also belongs to the $\mathcal{B}\mathbb{SS}$ $(\widehat{\aleph },\mathrm{\Psi })$.

Proof. 

Obvious. □

4. Topology on Binary Bipolar Soft Sets

In this section, we introduce the concept of binary bipolar soft topological spaces over two universal sets and a set of parameters. We investigate some topological structures of binary bipolar soft sets such as binary bipolar soft open, binary bipolar soft closed, binary bipolar soft closure, binary bipolar soft interior, and binary bipolar soft boundary.

Definition 25. 

Let ${\widehat{\widehat{\Im }}}_{\oslash }$ be a collection of $\mathcal{B}\mathbb{BSS}$s over ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\widehat{\Im }}}_{\oslash }$ is said to be a binary bipolar soft topology, denoted by $\mathcal{B}\mathbb{BST}$, on ${\mho }_1$ and ${\mho }_2$ if

Ax.1. 

$(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$.

Ax.2. 

The $\mathcal{B}\mathbb{BS}$ union of any member of $\mathcal{B}\mathbb{BSS}$s in ${\widehat{\widehat{\Im }}}_{\oslash }$ belongs to ${\widehat{\widehat{\Im }}}_{\oslash }$.

Ax.3. 

The $\mathcal{B}\mathbb{BS}$ intersection of any two $\mathcal{B}\mathbb{BSS}$s in ${\widehat{\widehat{\Im }}}_{\oslash }$ belongs to ${\widehat{\widehat{\Im }}}_{\oslash }$.

The quintuple $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is called a binary bipolar soft topological space ($\mathcal{B}\mathbb{BSTS}$) over ${\mho }_1$ and ${\mho }_2$.

Example 2. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}$ and ${\mho }_2=\{{\lambda }_1,{\lambda }_2\}$ be two universe sets and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$ be a set of parameters. Let ${\widehat{\widehat{\Im }}}_{\oslash }=\{(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi }),(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi }),({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi }),({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })\}$, where

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\})),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })& =\{({\xi }_1,(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\}))\}.\hfill \end{array}$$

Therefore, $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$.

Example 3. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}$ and ${\mho }_2=\{{\lambda }_1,{\lambda }_2\}$ be two universe sets and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$ be a set of parameters. Let ${\widehat{\widehat{\Im }}}_{\oslash }=\{(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi }),(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi }),({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi }),({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })\}$, where

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\})),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_2\right\})\},\hfill \\ \hfill ({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_1\right\})\}.\hfill \end{array}$$

Hence, $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is not a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$ because $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\notin }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$.

Definition 26. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, then the members of ${\widehat{\widehat{\Im }}}_{\oslash }$ are said to be $\mathcal{B}\mathbb{BS}$ open sets in ${\mho }_1$ and ${\mho }_2$. The $\mathcal{B}\mathbb{BSS}$ is said to be $\mathcal{B}\mathbb{BS}$ closed in ${\mho }_1$ and ${\mho }_2$ if its relative complement ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ is belong to ${\widehat{\widehat{\Im }}}_{\oslash }$.

Definition 27. 

Let ${\mho }_1$ and ${\mho }_2$ be the two initial universe sets and Ψ be a set of parameters. If ${\widehat{\widehat{\Im }}}_{\oslash }$ $=\{(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })\}$, then ${\widehat{\widehat{\Im }}}_{\oslash }$ is called the $\mathcal{B}\mathbb{BS}$ indiscrete space over ${\mho }_1$ and ${\mho }_2$. If ${\widehat{\widehat{\Im }}}_{\oslash }$ is the collection of all $\mathcal{B}\mathbb{BSS}$s, which can be defined over ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\widehat{\Im }}}_{\oslash }$ is called the $\mathcal{B}\mathbb{BS}$ discrete space over ${\mho }_1$ and ${\mho }_2$.

Proposition 5. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. Then, the following properties hold:

1. 

$(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ and $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ are $\mathcal{B}\mathbb{BS}$ closed sets.

2. 

The $\mathcal{B}\mathbb{BS}$ union of any two $\mathcal{B}\mathbb{BS}$ closed sets is $\mathcal{B}\mathbb{BS}$ closed.

3. 

The arbitrary $\mathcal{B}\mathbb{BS}$ intersection of $\mathcal{B}\mathbb{BS}$ closed sets is $\mathcal{B}\mathbb{BS}$ closed.

Proof. 

It is obvious. □

Theorem 1. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ and $({\mho }_1,{\mho }_2,{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be $\mathcal{B}\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$, then $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$.

Proof. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ and $({\mho }_1,{\mho }_2,{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$

Ax.1.

Clearly $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash }$.

Ax.2.

Let $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ be a family of $\mathcal{B}\mathbb{BSS}$s in ${\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash }$, Then, $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ and $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{J}}}_{\oslash }$ for each $i\in I$, so ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ and ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{J}}}_{\oslash }$. Thus, ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash }$.

Ax.3.

Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ be two $\mathcal{B}\mathbb{BSS}$s in ${\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash }$. Then, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{J}}}_{\oslash }$. Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{J}}}_{\oslash }$. Therefore, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash }$. Hence, $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\sqcap }}{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$.

□

Remark 1. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ and $({\mho }_1,{\mho }_2,{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be $\mathcal{B}\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$, then $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash }\tilde{\tilde{\bigsqcup }}{\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ may not be $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$ in general.

Example 4. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3,{\kappa }_4\}$ and ${\mho }_2=\{{\lambda }_1,{\lambda }_2,{\lambda }_3\}$ be two universe sets and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$ be a set of parameters. Let ${\widehat{\widehat{\Im }}}_{\oslash }$ $=\{(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi }),(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi }),({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })\}$ and ${\widehat{\widehat{J}}}_{\oslash }$ $=\{(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })\}$ where $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ and $({\widehat{\aleph }}_2$, ${\check{\aleph }}_2$, $\mathrm{\Psi })$ are $\mathcal{B}\mathbb{BSS}$s over ${\mho }_1$ and ${\mho }_2$ defined as

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })& =\left\{\left({\xi }_1,(\{{\kappa }_1,{\kappa }_3\},\left\{{\lambda }_2\right\}),(\{{\kappa }_2,{\kappa }_4\},\{{\lambda }_1,{\lambda }_3\}),({\xi }_2,(\{{\kappa }_2,{\kappa }_3\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\})\right)\right\},\hfill \\ \hfill ({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })& =\left\{\left({\xi }_1,(\{{\kappa }_1,{\kappa }_2\},\{{\lambda }_1,{\lambda }_2\}),(\left\{{\kappa }_4\right\},\left\{{\lambda }_3\right\}),({\xi }_2,(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_2,{\kappa }_3\},\{{\lambda }_1,{\lambda }_3\})\right)\right\}.\hfill \end{array}$$

Then, ${\widehat{\widehat{\Im }}}_{\oslash }$ and ${\widehat{\widehat{J}}}_{\oslash }$ are $\mathcal{B}\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$. Now, ${\widehat{\widehat{\Im }}}_{\oslash }$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{J}}}_{\oslash }$ $=\{(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi }),({\widehat{\aleph }}_2$, ${\check{\aleph }}_2,\mathrm{\Psi }\left)\right\}$ is not $\mathcal{B}\mathbb{BSTS}$ because $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2$, $\mathrm{\Psi })$ $=\left\{\right({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_2\right\})$, $(\{{\kappa }_2,{\kappa }_4\},\{{\lambda }_1,{\lambda }_3\})),({\xi }_2,(\varphi ,\varphi ))$, $(\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}$, ${\mho }_2\left)\right)\}$ $\tilde{\tilde{\notin }}$ $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash }$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{J}}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$.

Theorem 2. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ $=\{(\widehat{\aleph },\mathrm{\Psi }):$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }\}$ is $\mathcal{B}\mathbb{STS}$ over ${\mho }_1$ and ${\mho }_2$.

Proof. 

Suppose that $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. Then,

Ax.1.

$(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ implies that $(\mathrm{\Phi },\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$, also $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ implies that $(\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$.

Ax.2.

Let $\{({\widehat{\aleph }}_i,\mathrm{\Psi })$ $:i\in I\}$ belong to $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$. Since $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ for all $i\in I$, then ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Thus, ${\tilde{\bigsqcup }}_{i\in I}({\widehat{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$.

Ax.3.

Let $({\widehat{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$. Since $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\widehat{\Im }}}_{\oslash }$, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Therefore, $({\widehat{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\sqcap }$ $({\widehat{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$

Hence, ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ defines a $\mathcal{B}\mathbb{STS}$ over ${\mho }_1$ and ${\mho }_2$. □

Theorem 3. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\Im }}_{\oslash (\neg \xi )}$ $=\{(\check{\aleph },\mathrm{\Psi }):$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }\}$ is $\mathcal{B}\mathbb{STS}$ over ${\mho }_1$ and ${\mho }_2$.

Proof. 

Similar to Theorem 2. □

Remark 2. 

The following example shows that the converse of Theorems 2 and 3 are not true.

Example 5. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3,{\kappa }_4\}$, ${\mho }_2=\{{\lambda }_1,{\lambda }_2,{\lambda }_3\}$ and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$. Suppose that

$$\begin{gathered} {\widehat{\widehat{\Im }}}_{\oslash } =\{(\mathrm{\Phi },\mathrm{\Psi }),(\widehat{\widehat{\mho }},\mathrm{\Psi }),({\widehat{\aleph }}_1,\mathrm{\Psi }),({\widehat{\aleph }}_2,\mathrm{\Psi }),({\widehat{\aleph }}_3,\mathrm{\Psi })\}\mathit{and} \\ \neg {\widehat{\widehat{\Im }}}_{\oslash }=\{(\widehat{\widehat{\mho }},\neg \mathrm{\Psi }),(\mathrm{\Phi },\neg \mathrm{\Psi }),({\check{\aleph }}_1,\neg \mathrm{\Psi }),({\check{\aleph }}_2,\neg \mathrm{\Psi }),({\check{\aleph }}_3,\neg \mathrm{\Psi })\}, \end{gathered}$$

are two $\mathcal{B}\mathbb{STS}s$ defined on ${\mho }_1$ and ${\mho }_2$, where

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_2\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_2,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\})),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_3\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_3,\mathrm{\Psi })& =\{({\xi }_1,(\{{\kappa }_1,{\kappa }_2\},\{{\lambda }_1,{\lambda }_2\})),({\xi }_2,(\{{\kappa }_1,{\kappa }_3\},\{{\lambda }_1,{\lambda }_3\}))\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill ({\check{\aleph }}_1,\neg \mathrm{\Psi })& =\{(\neg {\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\check{\aleph }}_3\right\})),(\neg {\xi }_2,(\left\{{\kappa }_2\right\},\left\{{\check{\aleph }}_2\right\}))\},\hfill \\ \hfill ({\check{\aleph }}_2,\neg \mathrm{\Psi })& =\{(\neg {\xi }_1,(\left\{{\kappa }_4\right\},\left\{{\check{\aleph }}_3\right\})),(\neg {\xi }_2,\left(\left\{{\kappa }_4\right\}\right),\left\{{\check{\aleph }}_2\right\})\},\hfill \\ \hfill ({\check{\aleph }}_3,\neg \mathrm{\Psi })& =\{(\neg {\xi }_1,(\{{\kappa }_3,{\kappa }_4\},\left\{{\check{\aleph }}_3\right\})),(\neg {\xi }_2,(\{{\kappa }_2,{\kappa }_4\},\left\{{\check{\aleph }}_2\right\}))\}.\hfill \end{array}$$

Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$ $=\{(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$, $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$, $({\widehat{\aleph }}_3,{\check{\aleph }}_3,\mathrm{\Psi })\}$, where $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ and $({\widehat{\aleph }}_3,{\check{\aleph }}_3,\mathrm{\Psi })$ defined as follows:

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_2\right\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_3\right\})),({\xi }_2,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_2\right\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_4\right\},\left\{{\lambda }_3\right\})),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_3\right\}),(\left\{{\kappa }_4\right\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_3,{\check{\aleph }}_3,\mathrm{\Psi })& =\{({\xi }_1,(\{{\kappa }_1,{\kappa }_2\},\{{\lambda }_1,{\lambda }_2\}),(\{{\kappa }_3,{\kappa }_4\},\left\{{\lambda }_3\right\})),({\xi }_2,(\{{\kappa }_1,{\kappa }_3\},\{{\lambda }_1,{\lambda }_3\}),\hfill \\ \hfill & (\{{\kappa }_2,{\kappa }_4\},\left\{{\lambda }_2\right\})\left)\right\}.\hfill \end{array}$$

Hence, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $=\{({\xi }_1,(\{{\kappa }_1,{\kappa }_2\},\{{\lambda }_1,{\lambda }_2\}),(\varphi ,\left\{{\lambda }_3\right\})),({\xi }_2,(\{{\kappa }_1,{\kappa }_3\}$,$\{{\lambda }_1$, ${\lambda }_3\left\}\right),$ $(\varphi ,\left\{{\lambda }_2\right\})\left)\right\}$ $\tilde{\tilde{\notin }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$ is not $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$.

However, the following theorem shows that the converse of Theorem 2 is true under some conditions.

Theorem 4. 

Let $(\mho ,\widehat{\Im },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{STS}$ over ${\mho }_1$ and ${\mho }_2$. Then, the collection ${\widehat{\widehat{\Im }}}_{\oslash }$ consisting of $\mathcal{B}\mathbb{BSS}$s $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ such that $(\widehat{\aleph },\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ and $\check{\aleph }(\neg \xi )$ $=(\check{\mathtt{X}},\check{\mathtt{Y}})$ $=({\mho }_1,{\mho }_2)\setminus \widehat{\aleph }\left(\xi \right)=({\mho }_1,{\mho }_2)\setminus (\widehat{\mathtt{X}},\widehat{\mathtt{Y}})=({\mho }_1\setminus \widehat{\mathtt{X}},{\mho }_2\setminus \widehat{\mathtt{Y}})$ for all $\neg \xi \in \neg \mathrm{\Psi }$ defines a $\mathcal{B}\mathbb{BSS}$ topology on ${\mho }_1$ and ${\mho }_2$.

Proof. 

Ax.1.

Since $(\mathrm{\Phi },\mathrm{\Psi })$, $(\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$, then $\mho (\neg \xi )=({\mho }_1,{\mho }_2)\setminus \mathrm{\Phi }\left(\xi \right)=({\mho }_1,{\mho }_2)\setminus (\varphi ,\varphi )=({\mho }_1,{\mho }_2)$ and hence $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Also, $\mho (\neg \xi )=({\mho }_1,{\mho }_2)\setminus \widehat{\widehat{\mathfrak{A}}}\left(\xi \right)=(\varphi ,\varphi )$, thus $(\tilde{\tilde{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$.

Ax.2.

Let $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Then, $\{({\widehat{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ and ${\check{\aleph }}_i(\neg \xi )=({\mho }_1,{\mho }_2)\setminus {\widehat{\aleph }}_i\left(\xi \right)$ $=({\mho }_1\setminus \widehat{\mathtt{X}},{\mho }_2\setminus \widehat{\mathtt{Y}})$. Now, since ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ is a $\mathcal{B}\mathbb{S}$ topology, then ${\tilde{\bigsqcup }}_{i\in I}({\widehat{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$. Let $(\widehat{\aleph },\mathrm{\Psi })={\tilde{\bigsqcup }}_{i\in I}({\widehat{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$, thus $\check{\aleph }(\neg \xi )$ $=(\check{\mathtt{X}},\check{\mathtt{Y}})$ $=({\mho }_1,{\mho }_2)\setminus \left({\cup }_{i\in I}{\widehat{\aleph }}_i\left(\xi \right)\right)$ $=({\mho }_1\setminus {\cup }_{i\in I}{\widehat{\mathtt{X}}}_{\mathtt{i}},{\mho }_2\setminus {\cup }_{i\in I}{\widehat{\mathtt{Y}}}_{\mathtt{i}})$ $=({\cap }_{i\in I}{\check{\mathtt{X}}}_{\mathtt{i}},{\cap }_{i\in I}{\check{\mathtt{Y}}}_i)$ $={\cap }_{i\in I}({\check{\mathtt{X}}}_{\mathtt{i}},{\check{\mathtt{Y}}}_{\mathtt{i}})$ $={\cap }_{i\in I}{\check{\aleph }}_i(\neg \xi )$. Therefore, ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$.

Ax.3.

Let $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Then, $({\widehat{\aleph }}_1,\mathrm{\Psi })$,$({\widehat{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ and ${\check{\aleph }}_1(\neg \xi )=({\mho }_1,{\mho }_2)\setminus {\widehat{\aleph }}_1\left(\xi \right)$ $=({\mho }_1\setminus {\widehat{\mathtt{X}}}_{\mathtt{1}},{\mho }_2\setminus {\widehat{\mathtt{Y}}}_{\mathtt{1}})$ so ${\check{\aleph }}_2(\neg \xi )=({\mho }_1,{\mho }_2)\setminus {\widehat{\aleph }}_2\left(\xi \right)$ $=({\mho }_1\setminus {\widehat{\mathtt{X}}}_{\mathtt{2}},{\mho }_2\setminus {\widehat{\mathtt{Y}}}_{\mathtt{2}})$. Now, since ${\widehat{\Im }}_{\oslash \left(\xi \right)}$ is a $\mathcal{B}\mathbb{S}$ topology, $({\widehat{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\sqcap }$ $({\widehat{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$. Let $(\widehat{\aleph },\mathrm{\Psi })=$ $(\widehat{F_1},\mathrm{\Psi })$ $\tilde{\sqcap }$ $({\widehat{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\in }$ ${\widehat{\Im }}_{\oslash \left(\xi \right)}$, hence $\check{\aleph }(\neg \xi )$ $=(\check{\mathtt{X}},\check{\mathtt{Y}})$ $=({\mho }_1,{\mho }_2)\setminus \widehat{\aleph }\left(\xi \right)$ $=({\mho }_1\setminus ({\widehat{\mathtt{X}}}_{\mathtt{1}}\cap {\widehat{\mathtt{X}}}_{\mathtt{2}}),{\mho }_2\setminus ({\widehat{\mathtt{Y}}}_{\mathtt{1}}\cap {\widehat{\mathtt{Y}}}_{\mathtt{2}}))$ $=({\check{\mathtt{X}}}_{\mathtt{1}}\cup {\check{\mathtt{Y}}}_{\mathtt{1}},{\widehat{\mathtt{X}}}_{\mathtt{2}}\cup {\widehat{\mathtt{Y}}}_{\mathtt{2}})$ $={\check{\aleph }}_1(\neg \xi )\cup {\check{\aleph }}_2(\neg \xi )$. Therefore, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. The proof is completed.

□

Theorem 5. 

If $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, then $({\mho }_1,{\widehat{\widehat{\Im }}}_{{\mho }_1},\mathrm{\Psi },\neg \mathrm{\Psi })$ and $({\mho }_2,{\widehat{\widehat{\Im }}}_{{\mho }_2},\mathrm{\Psi },\neg \mathrm{\Psi })$ are $\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$, respectively.

Proof. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$ and by Definition 4, we have $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$, $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ in ${\widehat{\widehat{\Im }}}_{{\mho }_{\oslash }}$ with $\mho =({\mho }_1,{\mho }_2)$, then $(\mathrm{\Phi },{\widehat{\widehat{\mho }}}_1,\mathrm{\Psi })$, $({\widehat{\widehat{\mho }}}_1,\mathrm{\Phi },\mathrm{\Psi })$ in ${\widehat{\widehat{\Im }}}_{{{\mho }_1}_{\oslash }}$ and $(\mathrm{\Phi },{\widehat{\widehat{\mho }}}_2,\mathrm{\Psi })$, $({\widehat{\widehat{\mho }}}_2,\mathrm{\Phi },\mathrm{\Psi })$ in ${\widehat{\widehat{\Im }}}_{{{\mho }_2}_{\oslash }}$. So, let $\{({\widehat{\mathtt{X}}}_{\mathtt{i}},{\check{\mathtt{X}}}_{\mathtt{i}},\mathrm{\Psi }):i\in I\}$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_1}_{\oslash }}$ and $\{({\widehat{\mathtt{Y}}}_{\mathtt{i}},{\check{\mathtt{Y}}}_{\mathtt{i}},\mathrm{\Psi }):i\in I\}$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_2}_{\oslash }}$, where $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $=(({\widehat{\mathtt{X}}}_{\mathtt{i}},{\widehat{\mathtt{Y}}}_{\mathtt{i}})$, $({\check{\mathtt{X}}}_{\mathtt{i}},{\check{\mathtt{Y}}}_{\mathtt{i}}),\mathrm{\Psi })$ then $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{\mho }_{\oslash }}$, from ${\widehat{\widehat{\Im }}}_{{\mho }_{\oslash }}$ is a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, thus ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{\mho }_{\oslash }}$. Therefore, ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{X}}_i,{\check{X}}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_1}_{\oslash }}$ and ${\tilde{\tilde{\bigsqcup }}}_{i\in I}({\widehat{Y}}_i,{\check{Y}}_i,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_2}_{\oslash }}$. Now, let $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$, $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{\mho }_{\oslash }}$. Then, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_1}_{\oslash }}$, thus $({\widehat{\mathtt{X}}}_{\mathtt{1}},{\check{\mathtt{X}}}_{\mathtt{1}},\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\mathtt{X}}}_{\mathtt{2}},{\check{\mathtt{X}}}_{\mathtt{2}},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_1}_{\oslash }}$ and $({\widehat{\mathtt{Y}}}_{\mathtt{1}},{\check{\mathtt{Y}}}_{\mathtt{1}},\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\mathtt{Y}}}_{\mathtt{2}},{\check{\mathtt{Y}}}_{\mathtt{2}},\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{{{\mho }_2}_{\oslash }}$. Hence, $({\mho }_1,{\widehat{\widehat{\Im }}}_{{\mho }_1},\mathrm{\Psi },\neg \mathrm{\Psi })$ and $({\mho }_2,{\widehat{\widehat{\Im }}}_{{\mho }_2},\mathrm{\Psi },\neg \mathrm{\Psi })$ are $\mathbb{BSTS}s$ over ${\mho }_1$ and ${\mho }_2$, respectively. □

Definition 28. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$ over universe sets ${\mho }_1$ and ${\mho }_2$. Then, the $\mathcal{B}\mathbb{BS}$ closure of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, denoted by ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, is the intersection of all $\mathcal{B}\mathbb{BS}$ closed sets, which contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the smallest $\mathcal{B}\mathbb{BS}$ closed set over ${\mho }_1$ and ${\mho }_2$, which contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Theorem 6. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ be $\mathcal{B}\mathbb{BSS}s$ over universe sets ${\mho }_1$ and ${\mho }_2$. Then

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $=(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ $=(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$.

2. 

$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ implies ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set and contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

3. 

$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set if and only if $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

4. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$cl({\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

5. 

$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ implies ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

6. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

7. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

Proof. 

• Follows directly from Definitions 26 and 28.
• Let $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ be a family of $\mathcal{B}\mathbb{BS}$ closed sets containing ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Then, from Definition 28,

  $${\widehat{\widehat{\Im }}}_{\oslash }\text{-}cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })={\tilde{\tilde{\sqcap }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })\dots (\mathrm{i})$$
  Since $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$ is a $\mathcal{B}\mathbb{BS}$ closed set for each $i\in I$, it implies that ${\tilde{\tilde{\sqcap }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$ is also $\mathcal{B}\mathbb{BS}$ closed set by Proposition 5. Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set by (i). Now, to prove that $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, we have for each $i\in I$, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $\{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi }):i\in I\}$, implying $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\tilde{\tilde{\sqcap }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$, using (i) to obtain ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set and contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.
• Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BS}$ closed set, to prove $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ a $\mathcal{B}\mathbb{BS}$ closed and from Part (2), $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Thus, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set containing $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the smallest $\mathcal{B}\mathbb{BS}$ closed set containing $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is smaller than $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ that is ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Conversely, if $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is $\mathcal{B}\mathbb{BS}$ closed, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.
• Since ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set, by Part (3), it implies that ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl({\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.
• Suppose $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, then $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, Since ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set containing $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. But, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the smallest $\mathcal{B}\mathbb{BS}$ closed containing $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is smaller than ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.
• Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.
  Then, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ and
  ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$, by Part (5). Therefore,
  ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$.
  Also, from the $\mathcal{B}\mathbb{BS}$ closure property, we obtain $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. But, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ is the smallest $\mathcal{B}\mathbb{BS}$ closed set containing $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ is the smallest than ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.
• Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, by Part (5) ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

□

Remark 3. 

The next example shows that the equality of Part (7) in Theorem 6 does not hold in general.

Example 6. 

Let ${\widehat{\widehat{\Im }}}_{\oslash }$ be defined as in Example 2. If $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ and $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ are two $\mathcal{B}\mathbb{BSS}s$ defined as

$$\begin{array}{cc}\hfill ({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })& =\left\{({\xi }_1,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\{{\kappa }_1,{\kappa }_3\},\left\{{\lambda }_2\right\}))\right\},\hfill \\ \hfill ({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })& =\{({\xi }_2,(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})\}.\hfill \end{array}$$

Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$=$(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, while ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\gimel }}_2,{\check{\gimel }}_2$, $\mathrm{\Psi }\left)\right)$ $=(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$  ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$

Definition 29. 

Let $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$ of a $\mathcal{B}\mathbb{BSTS}$ $({\mho }_1,{\mho }_2$, ${\widehat{\widehat{\Im }}}_{\oslash }$, $\mathrm{\Psi },\neg \mathrm{\Psi })$ over ${\mho }_1$ and ${\mho }_2$. Then, we associate pointwise the $\mathcal{B}\mathbb{BS}$ closure of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ over ${\mho }_1$ and ${\mho }_2$ is denoted by ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ and defined as ${\widehat{\widehat{\Im }}}_{\oslash }$-${(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })}_{\xi }$ $={\widehat{\widehat{\Im }}}_{\oslash }$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$, where ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$ is the $\mathcal{B}\mathbb{BS}$ closure of ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$ in $({\mho }_1,{\mho }_2$, ${\widehat{\widehat{\Im }}}_{\oslash }$, $\mathrm{\Psi },\neg \mathrm{\Psi })$ for each $\xi \in \mathrm{\Psi }$.

Theorem 7. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)},\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$ over universe sets on ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$

Proof. 

For any parameter $\xi \in \mathrm{\Psi }$, ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$ is the smallest $\mathcal{B}\mathbb{BS}$ closed set in $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)},\mathrm{\Psi },\neg \mathrm{\Psi })$, which contains ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$. Then, if ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-${(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })}_{\xi }$ $=(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set in $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)},\mathrm{\Psi },\neg \mathrm{\Psi })$ containing ${(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$. This implies that ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-${(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })}_{\xi }$ $={\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}_{\xi }$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$(cl(\widehat{\aleph },\check{\aleph })$, $\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash \left(\xi \right)}$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. □

Theorem 8. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$ over ${\mho }_1$ and ${\mho }_2$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Proof. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, if ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set, thus ${\widehat{\widehat{\Im }}}_{\oslash }$-${(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })}^c$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Conversely, if ${\widehat{\widehat{\Im }}}_{\oslash }$-${(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })}^c$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set containing $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. By Theorem 7, and from the definition of $\mathcal{B}\mathbb{BS}$ closure of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, any $\mathcal{B}\mathbb{BS}$ closed set, which contains $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ will contains ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Thus, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$(cl(\widehat{\aleph },\check{\aleph }),\mathrm{\Psi })$. □

Definition 30. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. Let ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}({\mho }_1$, ${\mho }_2{)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$, the $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is said to be binary bipolar soft neighborhood set of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$, denoted by the $\mathcal{B}\mathbb{BS}$ neighborhood of $\mathcal{B}\mathbb{BSP}$ ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ if there exists a $\mathcal{B}\mathbb{BS}$ open set $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ such that

$${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}} \tilde{\tilde{\in }} (\widehat{\gimel },\check{\gimel },\mathrm{\Psi }) \widetilde{\tilde{⊑}} (\widehat{\aleph },\check{\aleph },\mathrm{\Psi }).$$

That is $\widehat{\mathtt{X}}$ ∈ $\widehat{\gimel }\left(\xi \right)$ ⊆ $\widehat{\aleph }\left(\xi \right)$ and $\widehat{\mathtt{Y}}$ ∈ $({\mho }_1,{\mho }_2)\setminus \check{\gimel }(\neg \xi )$ ⊆ $({\mho }_1,{\mho }_2)\setminus \check{\aleph }(\neg \xi )$, for each $\xi \in \mathrm{\Psi }$ and $\neg \xi \in \neg \mathrm{\Psi }$.

Theorem 9. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. Then

1. 

Each ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$ has a $\mathcal{B}\mathbb{BS}$ neighborhood set.

2. 

The intersection of two $\mathcal{B}\mathbb{BS}$ neighborhood sets of $\mathcal{B}\mathbb{BSP}$ ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ is a $\mathcal{B}\mathbb{BS}$ neighborhood.

3. 

Every $\mathcal{B}\mathbb{BS}$ superset of a $\mathcal{B}\mathbb{BS}$ neighborhood set of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ is a $\mathcal{B}\mathbb{BS}$ neighborhood of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$.

Proof. 

• Clearly from ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ $\widetilde{\widehat{⊑}}$ $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$.
• Let ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$, if $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ and $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ are $\mathcal{B}\mathbb{BS}$ neighborhood sets of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$. Then, there exist two $\mathcal{B}\mathbb{BS}$ open sets $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$, $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ such that ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ and ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$. Since $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Therefore, ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$. Hence, $({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ neighborhood of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$.
• Let ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $\mathcal{B}\mathbb{BSP}{({\mho }_1,{\mho }_2)}_{(\mathrm{\Psi },\neg \mathrm{\Psi })}$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\nabla },\check{\nabla },\mathrm{\Psi })$. Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is $\mathcal{B}\mathbb{BS}$ neighborhood of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$, then ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ with $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$. Therefore, ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\nabla },\check{\nabla },\mathrm{\Psi })$. Hence, $(\widehat{\nabla },\check{\nabla },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ neighborhood of ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$.

□

Definition 31. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. A $\mathcal{B}\mathbb{BSP}$ ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ is said to be binary bipolar soft interior point of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, denoted by the $\mathcal{B}\mathbb{BS}$ interior point if there exists a $\mathcal{B}\mathbb{BS}$ open set $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$ such that ${\xi }_{\widehat{\mathtt{X}},\widehat{\mathtt{Y}}}$ $\tilde{\tilde{\in }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ for each $\xi \in \mathrm{\Psi }$ and $\neg \xi \in \neg \mathrm{\Psi }$.

The $\mathcal{B}\mathbb{BS}$ interior set of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, denoted by ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, is the union of all $\mathcal{B}\mathbb{BS}$ open sets contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Theorem 10. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be $\mathcal{B}\mathbb{BSS}$. Then, the following properties hold:

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the largest $\mathcal{B}\mathbb{BS}$ open set over ${\mho }_1$ and ${\mho }_2$, which contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

3. 

$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is $\mathcal{B}\mathbb{BS}$ open if and only if $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $={\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Proof. 

• Obvious from Definition 31.
• From Part (1) and Definition 31.
• Suppose that $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is $\mathcal{B}\mathbb{BS}$ open. Then, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ but from Part (2), ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is the largest $\mathcal{B}\mathbb{BS}$ open set contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $={\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Conversely, if $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $={\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, then $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set from Part (1).

□

Theorem 11. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ be $\mathcal{B}\mathbb{BSS}s$. Then, the following properties hold:

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $=(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ $=(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int({\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

3. 

$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ implies ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

4. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.

5. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$.

Proof. 

• Obvious.
• Since ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set. Then, by Theorem 10 (3), ${\widehat{\widehat{\Im }}}_{\oslash }$-$int({\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.
• Suppose $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, thus ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ and from ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is the largest $\mathcal{B}\mathbb{BS}$ open contained in $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.
• Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. From (3), ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Implies ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Also, from ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$, which implies
  ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. But ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is the largest $\mathcal{B}\mathbb{BS}$ open set contained in $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$.
• Since $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$. Then, by (3), ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$.

□

Remark 4. 

The following example shows the equality of Theorem 11 (5) does not hold in general.

Example 7. 

Let ${\widehat{\widehat{\Im }}}_{\oslash }$ be defined as in Example 2. If $({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ and $({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$ are $\mathcal{B}\mathbb{BSS}s$ defined as

$$\begin{array}{cc}\hfill ({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })& =\left\{({\xi }_1,({\mho }_1,{\mho }_2),(\varphi ,\varphi ))\right\},\hfill \\ \hfill ({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })& =\left\{({\xi }_2,({\mho }_1,{\mho }_2),(\varphi ,\varphi ))\right\}.\hfill \end{array}$$

Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int({\widehat{\gimel }}_2,{\check{\gimel }}_2,\mathrm{\Psi })$=$(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$, while ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(({\widehat{\gimel }}_1,{\check{\gimel }}_1,\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $({\widehat{\gimel }}_2$, ${\check{\gimel }}_2,\mathrm{\Psi }\left)\right)$ $=(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel }$, $\check{\gimel },\mathrm{\Psi })$    ${\widehat{\widehat{\Im }}}_{\oslash }$-$int\left(\right(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi }))$.

Theorem 12. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$ over ${\mho }_1$ and ${\mho }_2$. Then

1. 

$({\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }){)}^c$=${\widehat{\widehat{\Im }}}_{\oslash }$-$int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$.

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$=$({\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }){)}^c$.

Proof. 

• Let $\mathrm{\Sigma }=\{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }):(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })$, ${({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })}^c$ $\tilde{\tilde{\in }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$, $i\in I\}$, then

  $$\begin{array}{cc}\hfill {({\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))}^c& ={\left[{\tilde{\tilde{\sqcap }}}_{i\in I}({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })\right]}^c\hfill \\ \hfill & =\left[{\tilde{\tilde{\bigsqcup }}}_{i\in I}{({\widehat{\aleph }}_i,{\check{\aleph }}_i,\mathrm{\Psi })}^c\right]\hfill \\ \hfill & ={\widehat{\widehat{\Im }}}_{\oslash }-int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c.\hfill \end{array}$$
• Similar to Part (1).

□

Definition 32. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. A binary bipolar soft boundary set of $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, denoted by $\mathcal{B}\mathbb{BS}$ boundary and defined as ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$.

Remark 5. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. For any $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, we have

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$bd{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$=${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Theorem 13. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. For any $\mathcal{B}\mathbb{BSS}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$, we have

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\setminus }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\setminus }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Proof. 

• We start the proof by using Definition 32

  $$\begin{array}{cc}\hfill {\widehat{\widehat{\Im }}}_{\oslash }-bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })& ={\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{\widehat{\widehat{\Im }}}_{\oslash }-cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c\hfill \\ \hfill & ={\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{({\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))}^c\hfill \\ \hfill & ={\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\setminus }}{\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\hfill \end{array}$$
• By using Remark 5, we have

  $$\begin{array}{cc}\hfill (\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\setminus }}{\widehat{\widehat{\Im }}}_{\oslash }-bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })& =(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{({\widehat{\widehat{\Im }}}_{\oslash }-bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))}^c\hfill \\ \hfill & =(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}\left({\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\bigsqcup }}{\widehat{\widehat{\Im }}}_{\oslash }-int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c\right)\hfill \\ \hfill & ={\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\bigsqcup }}(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })\widetilde{\tilde{⊒}}{\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }).\hfill \end{array}$$

□

Remark 6. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. Then, in general

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$≠$(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\setminus }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

2. 

$(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$≠${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Example 8. 

Let ${\mho }_1=\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}$ and ${\mho }_2=\{{\lambda }_1,{\lambda }_2\}$ be two universe sets and $\mathrm{\Psi }=\{{\xi }_1,{\xi }_2\}$ be a set of parameters. Let $\widehat{\widehat{\tau }}=\{(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi }),(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi }),({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi }),({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi }),({\widehat{\aleph }}_3,{\check{\aleph }}_3,\mathrm{\Psi })\}$, where

$$\begin{array}{cc}\hfill ({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\})),({\xi }_2,(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}),(\{{\kappa }_1,{\kappa }_2\},\left\{{\lambda }_1\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_2,{\check{\aleph }}_2,\mathrm{\Psi })& =\{({\xi }_1,(\varphi ,\left\{{\lambda }_1\right\}),(\{{\kappa }_2,{\kappa }_3\},\left\{{\lambda }_2\right\})),({\xi }_2,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}))\},\hfill \\ \hfill ({\widehat{\aleph }}_3,{\check{\aleph }}_3,\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_3\right\},{\mho }_2),(\varphi ,\varphi )),({\xi }_2,(\{{\kappa }_1,{\kappa }_3\},{\mho }_2),(\varphi ,\varphi ))\}\hfill \end{array}$$

If we take a $\mathcal{B}\mathbb{BSS}s$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ as

$$\begin{array}{cc}\hfill (\widehat{\gimel },\check{\gimel },\mathrm{\Psi })& =\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\}.\hfill \end{array}$$

Then, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })=$ $(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int{(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })}^c$ $={({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })}^c$, so ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $={({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })}^c$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl{(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })}^c$ $=(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd{(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })}^c$ $={({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })}^c$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\widehat{\widehat{\mho }},\mathrm{\Psi })$ $\ne \{({\xi }_1,(\varphi ,\varphi ),(\{{\kappa }_1,{\kappa }_3\},{\mho }_2)),({\xi }_2,(\varphi ,\varphi ),({\mho }_1,{\mho }_2))\}$ = $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\setminus }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Also, $(\widehat{\widehat{\mho }},\mathrm{\Phi },\mathrm{\Psi })$ ≠ $\left\{\right({\xi }_1,(\{{\kappa }_1,{\kappa }_3\},{\mho }_2)$, $(\varphi ,\varphi ))$, $({\xi }_2,({\mho }_1,{\mho }_2)$, $(\varphi ,\varphi )\left)\right\}$ $={\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ $\tilde{\tilde{\bigsqcup }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Theorem 14. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. If $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set, then $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ are disjoint $\mathcal{B}\mathbb{BSS}$.

Proof. 

Suppose that $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set. By Theorem 13 (2), ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }){)}^c$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $({\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }){)}^c$. Hence, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ are disjoint $\mathcal{B}\mathbb{BSS}$. □

Theorem 15. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$. If $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$.

Proof. 

Suppose that $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set. Then, ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. □

Theorem 16. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BSS}$. If $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is both a $\mathcal{B}\mathbb{BS}$ open and $\mathcal{B}\mathbb{BS}$ closed set, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$.

Proof. 

Suppose that $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ open set. By Theorem 14, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ and ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ are disjoint $\mathcal{B}\mathbb{BSS}$. So, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$. Now, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ is a $\mathcal{B}\mathbb{BS}$ closed set. By Theorem 14, ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\widetilde{\tilde{⊑}}$ $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Therefore, $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$=${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$. Hence, ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$. □

Remark 7. 

The converse of Theorems 14–16 in general is not hold.

Example 9. 

Consider ${\widehat{\widehat{\Im }}}_{\oslash }$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ in Example 8. Clearly, ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ and $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ are disjoint $\mathcal{B}\mathbb{BSS}$, but $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is not $\mathcal{B}\mathbb{BS}$ open.

If we take $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $=\{({\xi }_1,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\left\{{\kappa }_2\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}))\}$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $={({\widehat{\aleph }}_1,{\check{\aleph }}_1,\mathrm{\Psi })}^c$ $\widetilde{\tilde{⊑}}$ $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ but $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is not $\mathcal{B}\mathbb{BS}$ closed.

Again, if we take $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $=\{({\xi }_1,(\varphi ,\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\})),({\xi }_2,(\left\{{\kappa }_1\right\},\left\{{\lambda }_1\right\}),(\left\{{\kappa }_3\right\},\left\{{\lambda }_2\right\}))\}$, then ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$, but $(\widehat{\gimel },\check{\gimel },\mathrm{\Psi })$ is neither $\mathcal{B}\mathbb{BS}$ closed nor $\mathcal{B}\mathbb{BS}$ open.

Theorem 17. 

Let $({\mho }_1,{\mho }_2,{\widehat{\widehat{\Im }}}_{\oslash },\mathrm{\Psi },\neg \mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSTS}$ over ${\mho }_1$ and ${\mho }_2$, and $(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ be a $\mathcal{B}\mathbb{BSS}$. Then,

1. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$.

2. 

${\widehat{\widehat{\Im }}}_{\oslash }$-$int{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c$ $\tilde{\tilde{\sqcap }}$ ${\widehat{\widehat{\Im }}}_{\oslash }$-$bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })$ $=(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi })$.

Proof. 

• We start the proof by using Definition 32

  $$\begin{array}{cc}\hfill & {\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{\widehat{\widehat{\Im }}}_{\oslash }-bd(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\hfill \\ & ={\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}\left[{\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{\widehat{\widehat{\Im }}}_{\oslash }-cl{(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })}^c\right]\hfill \\ \hfill & ={\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{\widehat{\widehat{\Im }}}_{\oslash }-cl(\widehat{\aleph },\check{\aleph },\mathrm{\Psi })\tilde{\tilde{\sqcap }}{({\widehat{\widehat{\Im }}}_{\oslash }-int(\widehat{\aleph },\check{\aleph },\mathrm{\Psi }))}^c\hfill \\ \hfill & =(\mathrm{\Phi },\check{\aleph },\mathrm{\Psi }).\hfill \end{array}$$
• Similar to Part (1).

□

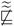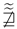5. Conclusions and Future Research

In this work, binary bipolar soft points using binary bipolar soft sets have been defined, and their properties have been given. The binary bipolar soft set is the binary bipolar soft union of its binary bipolar soft points. In addition, we continue studying the essential ideas in the frame bipolar soft topological spaces over two initial universal sets ${\mho }_1$ and ${\mho }_2$ with a set of parameters $\mathrm{\Psi }$, namely binary bipolar soft topological spaces, which are related to binary bipolar soft sets. Some topological concepts such as $\mathcal{B}\mathbb{BS}$ open (closed), $\mathcal{B}\mathbb{BS}$ closure, $\mathcal{B}\mathbb{BS}$ interior and $\mathcal{B}\mathbb{BS}$ boundary have been discussed. The comparison among binary bipolar soft topological space, binary soft topological space, and bipolar soft topological space have been presented, and the converse holds under special conditions. According to the obtained results, many classical properties of these concepts are still valid for $\mathcal{B}\mathbb{BSTS}$ structures. In forthcoming works, we will add some other concepts of binary bipolar soft topological properties such as binary bipolar soft continuous mappings, binary bipolar soft compactness, binary bipolar soft connectedness, and binary bipolar soft separation axioms in terms of binary bipolar soft open sets and binary bipolar soft points. We extend this work to define some types of symmetrical soft sets such as N-soft sets [27,28,29], N-hypersoft sets [30], N-bipolar soft sets [31], and fuzzy N-soft sets [17,32,33,34]. Furthermore, we can introduce the concepts as defined in [35,36,37,38] by using the binary bipolar soft sets.