1. Introduction
Using 5G technology for wireless communication can make it easier to send a lot of data quickly. It has the potential to overcome problems like limited bandwidth, access issues, and delays. This means that future technologies, like “5G and Beyond”, could let us send data at speeds of hundreds of Megabits per second with very short delays, less than 1 millisecond. As a consequence, it will make it possible to connect simultaneously billions of devices and it can also lead to the creation of entirely new and innovative applications that we haven’t seen before [
1]. Examples of where these new applications could be used cover a wide range of areas. This includes things like mobile health, self-driving cars, manufacturing and entertainment, education, smart grids, big data analysis, smart cities and homes, aerospace, ocean exploration, emergency response, and mobile platforms, among others [
1]. As can be verified from the literature, a base station (BS) can transmit data with up to a radius of approximately 200ms while using 5G mmWave technology [
2]. So far, the experimental evidence suggests that deploying base stations (BSs) with a radius of at least 200 m can solve the coverage issue in outdoor areas by utilizing direct line-of-sight communication. However, it is important to note that opting for smaller radius values would mean needing a significantly larger number of base stations to ensure complete coverage for users [
2,
3]. In particular, note that any pair of BSs can be connected by using cables to form the backbone network structure. Consequently, it is necessary to adapt current infrastructures [
4]. This will be essential for the deployment of future 5G-based networks to manage the increasing demand for data usage and broader coverage, as recommended in [
2,
5].
In this article, the problem of achieving the minimum backbone connectivity cost while simultaneously maximizing user coverage using 5G mmWave technology is considered. For this purpose, let us consider
to be an input graph instance with a set of nodes (BSs)
and a set of edges (or connection links)
. Thus, it is assumed that
G represents a wired or wireless backbone network. Also, let
represent a set of users to be covered by
G. Note that mmWave technology has been considered in the literature as an important candidate solution for 5G networks due to its low latency. Nevertheless, there remain some practical problems to overcome before using this technology for real network applications. A serious one is that millimeter waves cannot cover large radial transmission distances. Consequently, in this article, the main contributions are to propose mixed-integer programming models to deal with this problem. In particular, our models allow the determination of which of the nodes of
G should be active and connected at the lowest connectivity cost while simultaneously maximizing the total number of covered users. More precisely, two flow-based models, a Miller–Tucker–Zemlin-based one and an exponential one, are proposed [
6]. In general, these models mainly differ in the way a set of constraints forms a spanning tree backbone. In our research article, we consider scenarios where network nodes remain stationary, which is a common characteristic of sensor networks, for instance, or in catastrophic scenarios where it might be required to set up a wireless network communication rapidly, such as in earthquakes or pandemic situations. If a particular user is not covered, they will disconnect from the backbone network, as occurs, for example, on rural highways. This underpins our assertion that the novel models we introduce have direct applicability to wireless networks. This assumption aligns well with the prevalent conditions in sensor network deployments. However, we recognize the more intricate scenario involving mobile BSs and users, capable of traversing various application domains. Note that even in dynamic scenarios, our proposed models retain their utility, offering an alternative avenue to derive optimal network configurations. This optimization task is facilitated by considering optimization tools such as the CPLEX solver, an industry-leading solution in the realm of operations research [
7]. Its efficacy is underscored by its inclusion of exact approaches like branch and cut (B&C) and Benders algorithms, aspects well-documented in the literature [
7,
8]. Within the context of wireless sensor networks (WSNs), a myriad of applications has been explored in the existing body of work. It is also observed that additional metrics such as users’ and BS’s mobility, quality of service requisites, and security provisions will certainly lead to future modeling approaches. Nevertheless, our models and algorithms address the pivotal issue of distance—both between BSs and users and among BSs themselves. This treatment is rooted in the understanding that many metrics are contingent on distance, often exhibiting degradation as distances increase. Note that even when both BSs and users are in motion, our models and algorithms remain efficient, consistently yielding near-optimal solutions remarkably, as demonstrated through our numerical experiments. This adaptability positions them not only as practical tools but also as a benchmark for the development of novel and more efficient algorithmic approaches. While they may not be amenable to exact solutions within a one-hour CPU time limit in certain cases, the extensive use of rigorous upper and lower bounds ensures that the solutions attained are indeed near-optimal. Our contribution, therefore, lies not just in the solutions themselves but in the robust methodology employed to ascertain their quality. In summary, the contributions outlined in our novel models exhibit a remarkable degree of generality, making them adaptable to a range of contexts, contingent upon the specific application domain. This flexibility underscores their value as a versatile toolset for addressing diverse wireless network scenarios. Finally, in a situation where the BSs and users move, there are always alternative ways of finding feasible solutions faster. For this purpose, our second algorithm uses an iteration parameter
MaxIter which allows it to run for a predefined number of iterations. The latter can be handled efficiently to find good solutions, as is seen from the velocities reported in the last two figures, where the algorithm reaches near-objective values very fast. Since all our models are solved with the CPLEX solver using its branch and cut and its automatic Bender decomposition algorithmic options, a set of complete and sparse connected input graphs to form the backbone network is considered. So, the assumption is that the positions of all users and base stations BSs are randomly distributed within a square area. Additionally, the assumption is made that in an outdoor setting, all users and base stations BSs can communicate using a direct line-of-sight channel. For this purpose, the maximum CPU time limit allowed for the CPLEX solver is arbitrarily set to be at most one hour when solving each of the instances, and also the CPLEX Mipgap option is set to be zero and less than one percent [
7]. Finally, an efficient local search meta-heuristic algorithm is proposed that allows for finding tight solutions in significantly low CPU time when compared to the proposed models either for small- or large-sized instances of the problem. As far as we know, our proposed models and solution approaches are new to the literature and therefore enrich the existing literature to deal with the problem from a management point of view. Note that our proposed models allow us to incorporate a new aspect to the problem which is considering the distance between users and base stations BSs, and the optimal connectivity between all BSs. Finally, we mention that our proposed models could cover all users when the maximum user coverage metric becomes more relevant than considering the connectivity cost of the backbone network. Total coverage could also be ensured by using a larger amount of candidate sites for the BSs to be activated in the network.
Consequently, a direct comparison with other methods is not straightforward as the modeling and algorithmic approaches are completely new. From the literature, only one article was found to be as close as possible to the connectivity problem, where a flow-based formulation is proposed. In this article, that flow model is adapted to our new more intricate problem. Unfortunately, its performance in terms of obtaining optimal solutions when compared to our new proposed models is poor. Moreover, all our proposed models allow us to determine the optimal number of BSs and which of them should be active to form the backbone network structure. This consideration also takes into account the characteristics of 5G mmWave technology. It is worth noting that the literature has not yet explored the aspect of wireless networks with random deployments, such as sensor networks. Note that the rationale behind employing the CPLEX solver primarily rests on its exceptional, unique, and potent algorithmic capabilities, as evidenced by its success in tackling challenging optimization problems in the literature [
7]. Finally, we mention that this work corresponds to a larger version of the article presented at the IEEE conference [
9].
The organization of the article is as follows. In
Section 2, first, some recent studies from the literature that are closer to the optimal network planning problem considered in this article are reviewed. Then, in
Section 3, the optimization problem at hand is briefly explained, and each proposed mathematical formulation is presented in detail. Subsequently, in
Section 4, the algorithmic approaches used to solve the optimization problem are presented and explained. More precisely, an exact algorithm that consists of adding sub-tour elimination constraints to our exponential model until the optimal solution is obtained without cycles is presented. Then, how the Bender decomposition algorithm finds the optimal solutions and the automatic Benders CPLEX version as well are briefly explained [
7]. Finally, in this section, we introduce and clarify the proposed meta-heuristic. Moving forward to
Section 5, we carry out extensive numerical experiments, presenting and discussing the results obtained from the proposed models and algorithms. The comparison is based on factors such as CPU time and the optimal or best solutions achieved. Lastly, in
Section 6, we conclude the article while discussing insights for potential future research.
2. Related Work
The BS placement problem using 5G mmWaves for outdoor areas has not been investigated so far with sufficient depth in the literature. Some recently published works using mmWaves technology which are closely related to this network planning problem can be described as follows. In [
10], the authors utilize mmWave radar technology to unobtrusively detect human falls. To this end, they collect data from healthy young volunteers with the radar mounted on the side wall or overhead of an experimental room. They consider a set of features that are manually extracted from the data and apply multilayer perceptron, random forest, k-nearest neighbor, and support vector machine classifiers on the features. Subsequently, they devise a convolutional neural network and conclude from their numerical results that the development of a hidden monitoring system for fall detection using mmWave radar is feasible. Finally, the authors mention that the optimal placement of the radars is unknown, and consequently, they locate them intuitively. Similarly, in [
11], the authors propose a novel 3D geometry-based framework for deploying mmWave base stations in urban environments and also provide a solution for the optimum deployment of passive metallic reflectors to extend the radial coverage to non-line-of-sight areas. Specifically, they formulate their network planning problem as two independent optimization problems to maximize the coverage area, and minimize the deployment cost, while ensuring a desired quality-of-service level. Finally, they test the efficacy of their approach by using a generic map. The study conducted by the authors concludes that their network planning approach, utilizing mmWave technology, effectively reduces the need for passive metallic reflectors in non-line-of-sight areas, consequently lowering deployment costs. In [
12], the authors investigate the practicality of relaying and caching in mmWave-based networks, assuming the coexistence of base stations and relay nodes (RNs). Their findings suggest that increasing the number of RNs and expanding the cache size in mmWave networks presents a more cost-effective solution compared to simply increasing BS density for similar backhaul off-loading performance. Another work [
13], explores advanced computational geometry concepts for placing numerous mmWave wall-mounted BSs in large urban areas. The authors assert that their study is the first to use mmWave cells on buildings, and their approach enables accurate modeling for small-cell mmWave-based networks, providing gigabit capacities for densely populated urban areas.
In addition to the mentioned works, recent publications on network planning issues for future communication networks include references [
6,
14]. In the specific case of [
14], the authors tackle the broader challenge of maximizing user coverage while adhering to facility location and radial distance constraints in the context of 5G/6G wireless communication networks. They propose mixed-integer linear programming models, drawing inspiration from the classical p-median problem in optimization literature. Notably, the authors introduce non-overlapping radial distance constraints for various pairs of base stations (BSs). Their experiments involve solving instances with up to 100 antennas and 1000 users. The study concludes that incorporating a larger number of radius values enhances the flexibility and accuracy of solutions, albeit at a higher computational cost. In a similar vein, in [
6] the author proposes generic and novel mixed-integer linear programming models for the p-median problem while imposing ring, tree, and star backbone topology constraints on the facility locations. The author also mentions that the proposed models find applications in wired and wireless network design, computer networks, transportation, water supply, and electrical networks, to name a few. The author further proposes a variable neighborhood search meta-heuristic for each network backbone structure. Finally, the author concludes, based on substantial numerical experiments, that the ring models are harder to solve with CPLEX than the tree and star ones. Ultimately, the proposed meta-heuristics in [
6] proved to be highly efficient as they allowed better feasible solutions to be obtained compared to CPLEX, and with significantly less computational effort. Other related works can be consulted in references [
2,
15,
16] and in references therein. As can be observed from these previous works, none of them takes into account the radial transmission distance limitation of 5G mmWave technology so far. Consequently, the proposed mathematical models in this article change in structure significantly to deal with the network planning problem from a management point of view.
To conclude this section, it is mentioned that we observe only a few works in the literature that are directly related to the network planning problem using 5G mmWave technology. Consequently, our work will contribute to providing a new dimension of the problem, i.e., taking into account optimal connectivity. Since the objective function of our proposed models contains conflicting objectives, i.e., maximizing user coverage and minimizing backbone connectivity cost simultaneously, a weighting parameter ∈ is introduced to balance the degree of importance of each objective. Finally, it is mentioned that the direct implication for the mmWave networks is to at least find very good solutions, including optimal configurations.
5. Results and Discussion
In this section, substantial numerical experiments are conducted to compare the performances of the proposed models
,
,
,
, and the proposed algorithms. To this end, a Python code is implemented using the CPLEX solver [
7]. In particular, the models
,
, and
are solved with both the branch and cut and the Benders decomposition options of the solver. Note that model
has no continuous variables and, consequently, Benders approach cannot be applied [
8]. In particular, for solving the models
,
, and
, the CPLEX solver is used with default options. The maximum CPU time is limited to at most one hour. Consequently, if a particular reported objective value is obtained in 3600 s or more, it means that the solver is reporting the best solution obtained in one hour. Otherwise, it corresponds to an optimal solution to the problem. Note that the optimization problems of this type are NP-hard due to their discrete nature. Thus, both algorithms used by the CPLEX solver have exponential complexity [
7]. The numerical experiments were performed on an Intel(R) 64-bit core (TM) i5-8400 CPU 2.81 GHz with 16 G of RAM under Windows 10. Randomly sparse and complete input graphs were generated. In the latter, it was assumed that all active BSs can be connected using cables, for instance. Whilst for the sparse graphs it was assumed that the radial transmission range between BSs was 300 ms. The dimensions of the graphs in terms of the number of nodes and the number of users were
and
, respectively. Finally, it was assumed that each user could connect to an active BS if and only if the user was located inside a radial transmission range of at most 200 ms. Each of the coordinates for the nodes and users was generated within a square area of 1 km
according to a uniform distribution function. Thus, each entry of the input distance matrix
D was computed using these coordinates.
In
Table 1 and
Table 2, numerical results are reported for the models
and
, respectively. In particular,
Table 1 reports numerical results for the sparse graphs. Whereas
Table 2 reports numerical results for the complete ones. In both tables, the legends are the same. In columns 1 and 2, the instance number and the density of the graph are presented. The latter is computed by dividing the number of edges by the total number of edges of a complete graph having the same number of nodes. Column 3 reports the weighing parameter
. Next, columns 4–6 and 7–9 report the best objective value obtained, the number of branch and bound nodes, and the CPU time in seconds for model
when solved with the branch and cut and Benders algorithms, respectively. Similarly, columns 10–12 and 13–15 report the same information for
.
In
Table 1, from the sparse graph results, it is mainly observed that, in general,
outperforms
. First, one can note that the best solutions obtained with
are the optimal ones for all the instances when using
nodes, either using B&C or Benders algorithms. On the other hand, it is observed that
does not optimally solve the instances with the B&C algorithm. However, it can solve all the instances optimally using Benders algorithm. These observations can be confirmed by looking at the columns of the CPU times and the number of branching nodes. Subsequently, one can see that none of the graphs composed of
nodes can be solved optimally in one hour of CPU time. The latter shows that the graph instances become significantly harder to solve when
n grows. Finally, it is observed that for the value of
, the problem is solved easily with any of the models and methods. In particular, for the complete graph instances reported in
Table 2, it is possible to observe similar trends. More precisely, one can see that
can solve all the instances optimally for
with both methods. It is also observed that none of the instances can be solved optimally in one hour of CPU time for
nodes. Furthermore, it is observed that
obtains the optimal solutions for all the instances for
with Benders approach. The latter cannot be achieved with the pure B&C method. Lastly, it is seen that all the graph instances are solved optimally and very rapidly for the value of
, which is the optimization problem without taking into account the connectivity cost of the backbone. Ultimately, from both
Table 1 and
Table 2, one can observe that the increase in users, going from 500 to 1000, does not have a significant impact on the performance when solving the problem. In
Table 3 and
Table 4, numerical results are reported for models
and
. In particular,
Table 3 and
Table 4 report numerical results for the sparse and complete graphs, respectively. In both tables, the legends are the same. More precisely, in columns 1–3, the instance number, the density of the graph, and the value of the parameter
are presented. Next, columns 4–6 and 7–9 report the best objective function value obtained, the number of branch and bound nodes, and the CPU time in seconds for model
when using the B&C and Benders algorithmic approaches, respectively. Finally, columns 10–13 report the best objective function value obtained with Algorithm 1, the CPU time in seconds required to obtain that solution, the number of iterations of Algorithm 1, and the gap which is obtained by subtracting the best objective value obtained with
with the best objective value obtained with the remaining models and dividing this quotient by the latter value. The gap is finally multiplied by 100 to present percentages. Note that the objective values obtained with models
,
, and
are lower bounds as they are feasible or in the best case optimal solutions, while the values obtained with
are in the best case the optimal solutions or upper bounds since they are solved iteratively without including all sub-tour elimination constraints within each iteration of Algorithm 1.
From
Table 3, for the sparse graphs, one can see that
cannot solve any of the instances with a certificate of optimality with any of the algorithms since the CPU time values are larger than one hour. Again, the exception occurs for the graphs using
, which are easily solved with any of the methods. For
, it is not possible to ensure that the objective values correspond to the optimal solutions because they are not obtained in less than one hour. However, in the case of model
, recall that the objective values are upper bounds. Consequently, one can ensure that the graph instances having zero gaps report the optimal solutions. This is because these upper bounds are equal to the lower bounds obtained with one or more of the remaining models. This also ensures that the lower bounds obtained with the other models correspond to optimal solutions. For the complete graph instances in
Table 4, one observes similar trends. One can see that only one graph instance is solved optimally in less than one hour. However, it is again mentioned that for model
the graph instances having zero gaps report the optimal solutions. The argument is the same as for the sparse graphs presented in
Table 3, i.e., the upper bounds are equal to the lower bounds.
To conclude, from the numerical results presented in
Table 1,
Table 2,
Table 3 and
Table 4 one can mainly observe that model
has a slightly better performance than the rest of the models when using the pure B&C approach of the CPLEX solver, at least for the reported instances.
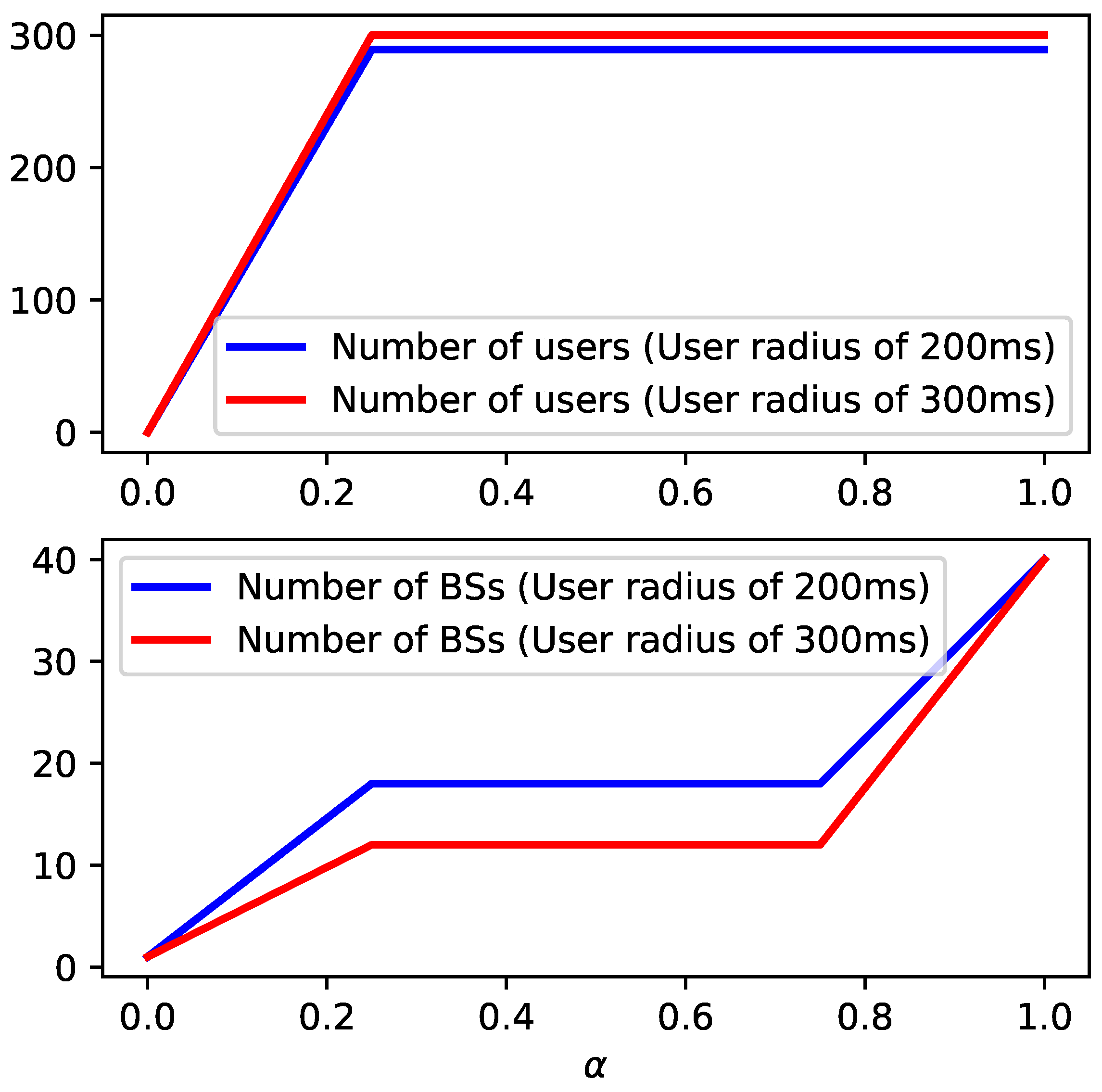
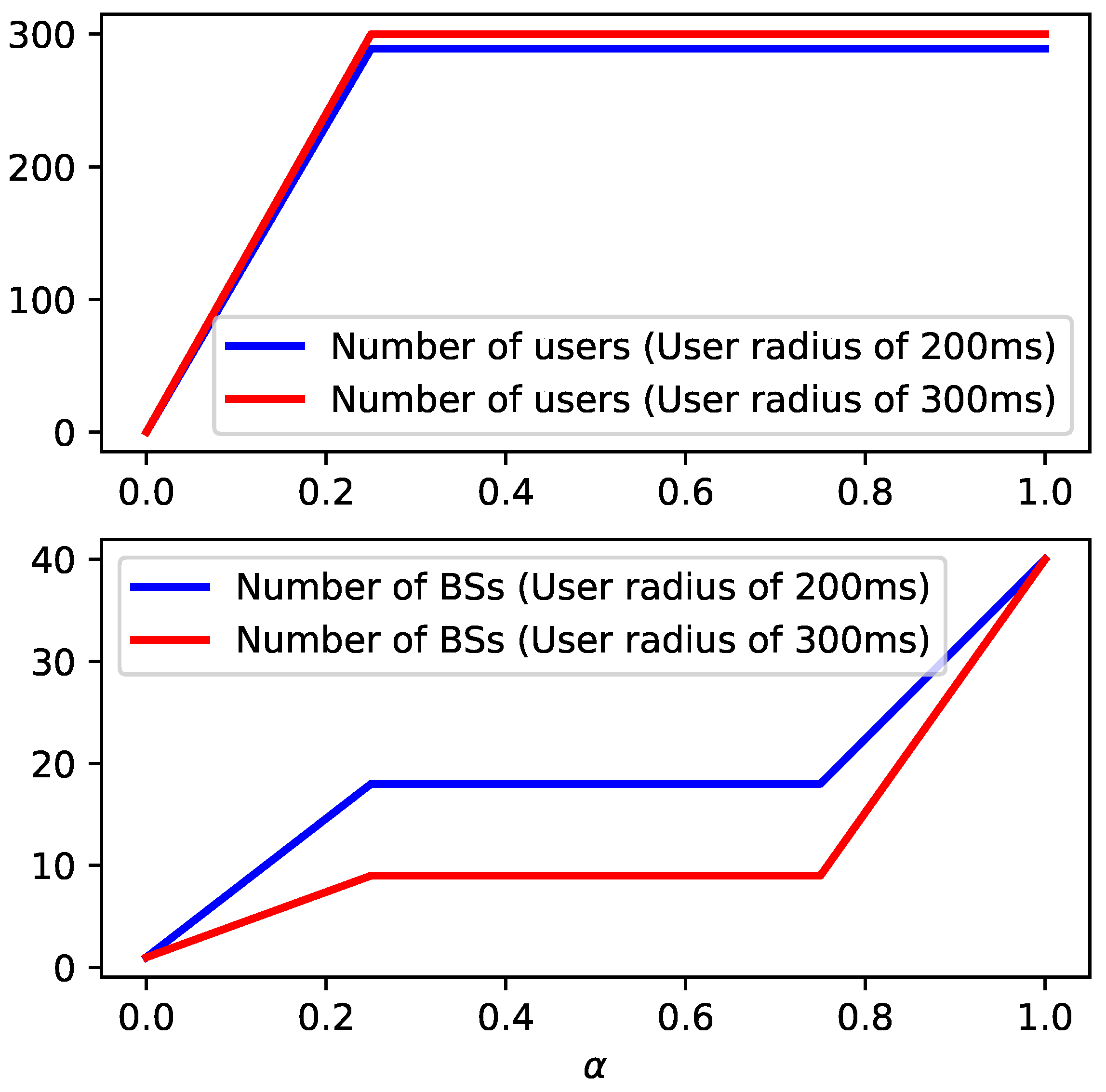
To give more insights concerning the behavior of model
, in
Figure 3 and
Figure 4 the impact of varying parameter
for a sparse and a complete input graph, respectively, is plotted. For both figures, the number of covered users and active BSs is plotted while also varying the transmission radius between BSs and users from 200 ms to 300 ms. Each instance is composed of
BSs and
users. We mention that each point in these curves corresponds to an optimal solution to the problem.
From
Figure 3 and
Figure 4, one can see that the higher the transmission radius between BSs and users is, the higher the number of covered users. Additionally, the lower the number of BSs required to connect the backbone network. In particular, in
Figure 4, the number of active BSs is less than in
Figure 3 since the backbone is fully connected. Finally, it is observed that the objective values increase with parameter
. In
Table 5 and
Table 6, the numerical results obtained with Algorithm 2 for the sparse and complete graph instances, respectively, solved in the previous tables are reported. In particular, in
Table 5 and
Table 6, the same column information is reported. More precisely, in columns 1–3, the instance number, the density of the graph, and the value of parameter
are reported. Next, in columns 4–10, the best objective value obtained in the previous tables, the best objective found with Algorithm 1, the CPU time in seconds required by the algorithm, its number of iterations, the number of attended or covered users in the network instance, and the number of BSs required to connect the backbone in the output solution of the problem are reported. Finally, the gaps in percentage that we compute by
are reported. From these tables, one can observe that the solutions obtained by the proposed local search heuristic are near-optimal, with a worst gap obtained of 0.88% in the case of the sparse graphs and a worst gap of 3.03% for the complete graphs. It is further noted that the worst CPU time is lower than one minute for all the tested instances. One can also see that the larger the value of parameter
, the larger the number of BSs required to construct the backbone. Finally, it is observed that most of the users are covered for all tested instances. To further investigate the behavior of Algorithm 2, in
Table 7 and
Table 8 numerical results obtained with
versus Algorithm 2 for a large sparse connected and a fully connected graph instance, respectively, are compared. In these tables, the legend is the same. In columns 1–3, the instance number, the density of the graph, and the value of the parameter
are reported. Next, in columns 4–6, the best objective function value of model
, the number of branch and bound nodes, and its CPU time in seconds are presented. Subsequently, the best objective value obtained with Algorithm 2, its CPU time in seconds, the number of iterations of the algorithm, the number of covered users, the number of active BSs, and the gaps in percentage that we compute by
are shown. From
Table 7 and
Table 8, it is observed that
requires more than one hour to obtain the optimal solution except for the instances using
. In this case, the problem becomes much more simple to solve optimally. Next, one can observe that the Algorithm 2 has an even better performance with a worst gap percentage of 0.21%. Finally, one can also see that most of the users are covered without using a large number of active BSs forming the backbone.
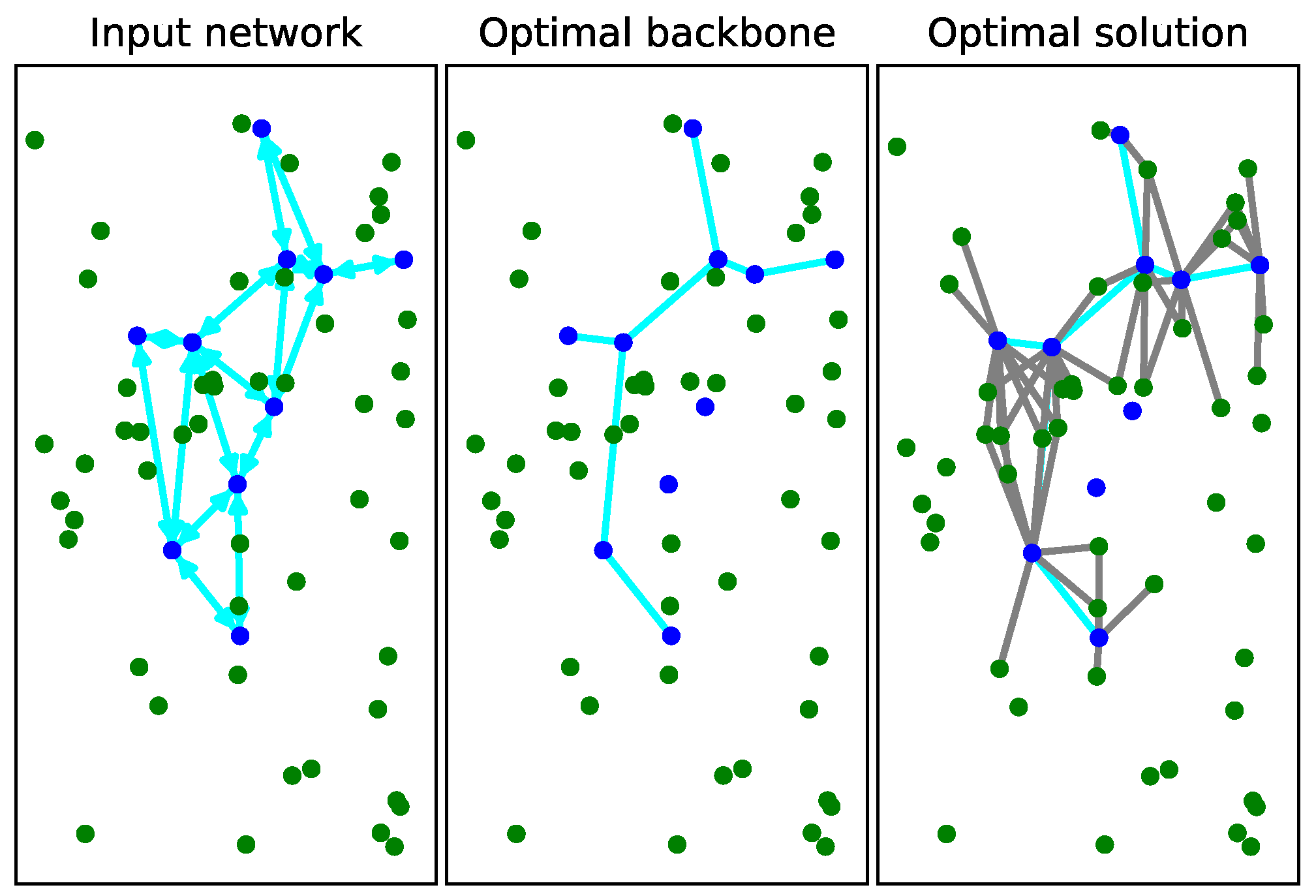
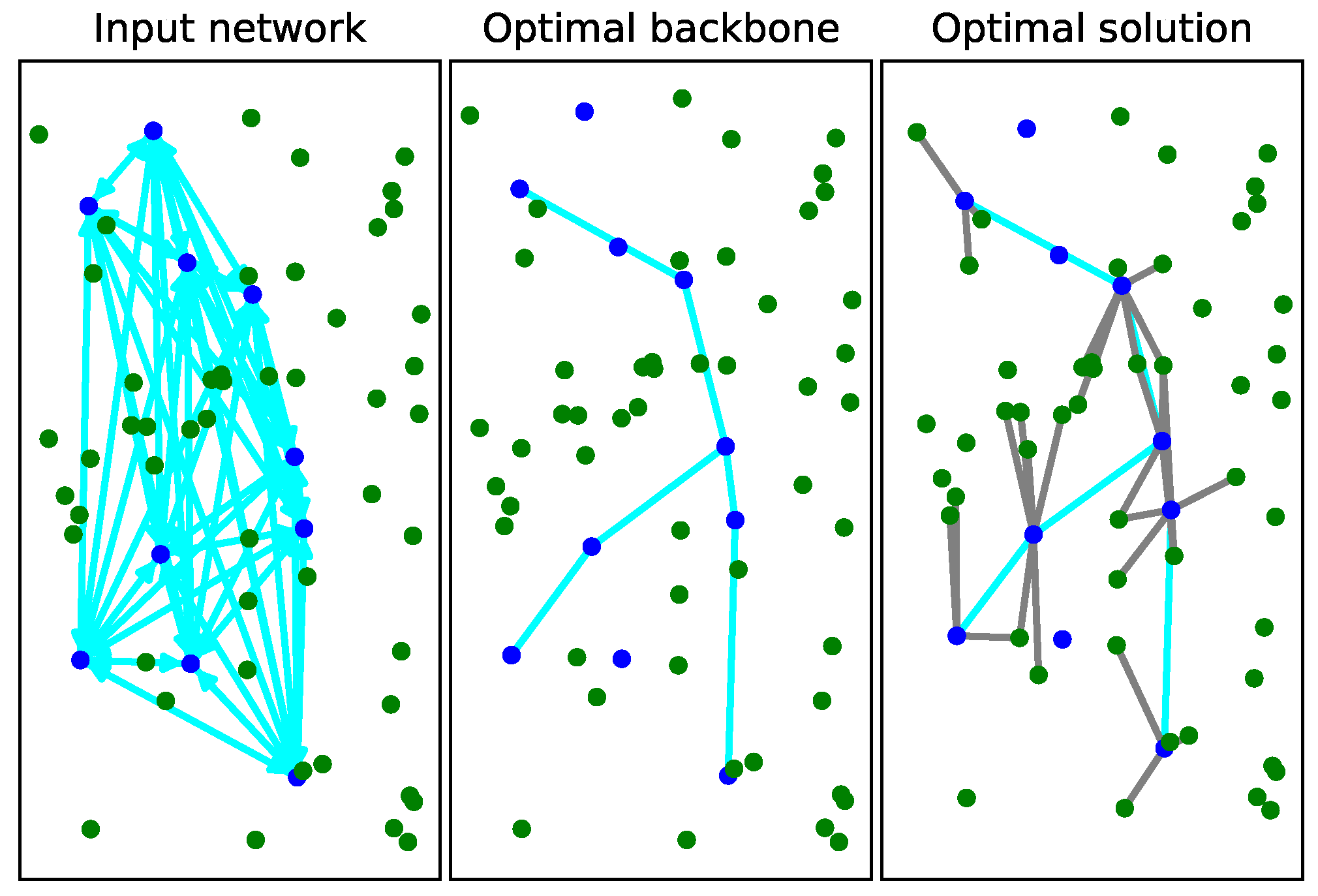
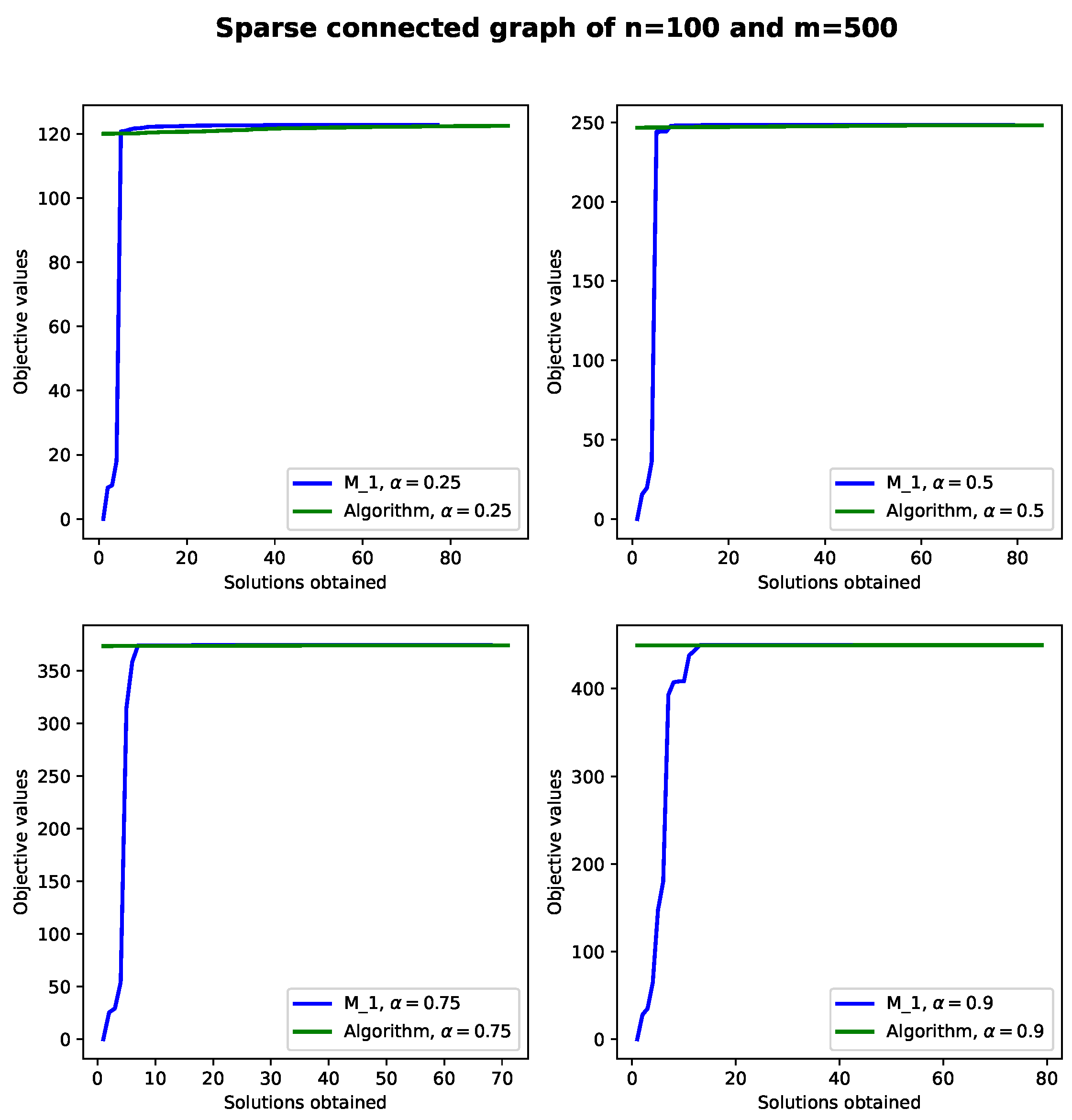
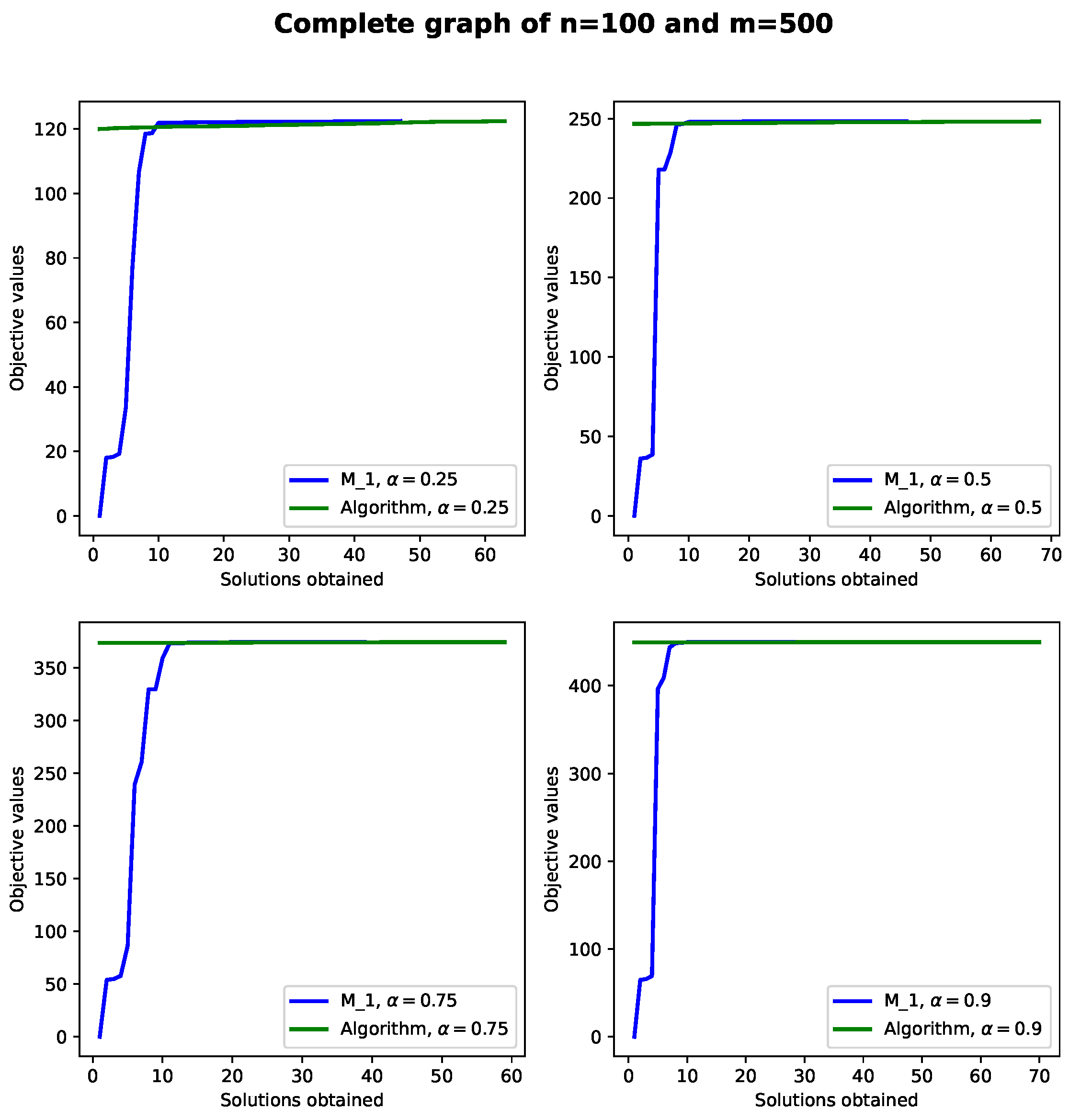
To provide further insights concerning the behavior of Algorithm 2, in
Figure 5 and
Figure 6 feasible solutions in terms of objective values for a sparsely and fully connected input network obtained with
while varying
in the interval [0.25;0.9] are presented. In both figures, each network is composed of
nodes for the backbone and
users. In particular, in
Figure 5 a radial transmission distance of 300 ms for the BSs is used and 200 ms for the distances between BSs and users. In
Figure 6, the distances between BSs and users are set to 200 ms as well. Finally, we mention that both figures report objective values and velocities obtained with
and Algorithm 2 when finding feasible solutions. The numerical results obtained in
Figure 5 and
Figure 6 show that CPLEX finds very poor solutions at the beginning. More precisely, CPLEX takes at least 10 s to reach good quality solutions, whereas Algorithm 2 can find very good objective values in fractions of a second. After this time, it is observed that CPLEX and Algorithm 2 are both competitive in the sense that they reach similar solutions. Another observation is that one can ensure that the objective values are near-optimal ones. This can be ensured because the Mipgaps obtained with CPLEX are lower than 1% [
7]. Finally, it is observed that varying the parameter
does not seem to have a significant effect on the performance of either
or the Algorithm 2. However, note that the higher the value of the parameter
, the larger the number of users that can be covered.