Investigation of the Optical Spectra of Barium-Zinc (Aluminum) Fluoroborates and Barium-Zinc Fluorocarbonate from First Principles

Abstract

The Raman scattering, infrared absorption, and reflection spectra of hexagonal non-centrosymmetric BaZnBO₃F and BaAlBO₃F₂ and centrosymmetric BaZn₃BO₃F₂ and BaZnCO₃F₂ are calculated using the standard procedures of the CRYSTAL package with the basis of localized orbitals and the B3LYP hybrid functional within the framework of the Hartree-Fock conjugate perturbation method. It is shown that the layered structure of crystals manifests itself in the spectra of vibrational modes polarized along and perpendicular to the c axis with wavenumbers for the lattice region formed by displacements of atoms in [BaF]∞ and [MAO₃]∞ (M: Zn, Al; A: B, C) layers, for molecular deformation outside and in the plane of anions BO₃ and CO₃. The quantitative and qualitative composition of the spectra is determined by the symmetry of the crystal lattice.

1. Introduction

The coherent light generated by solid-state lasers is used in various fields: photochemical synthesis, medical and scientific instrumentation, and optoelectronic devices. Lasers operating in the ultraviolet (UV) and deep ultraviolet (DUV) ranges are widely used for these purposes. The search for new nonlinear optical (NLO) materials with high second harmonic generation (SGH) in the required wavelength range is an important and challenging task [1,2,3,4,5,6]. The NLO materials used, or planned for use, must meet certain requirements; in particular, they must have non-centrosymmetric (NCS) space groups of symmetry, contain anions in π-delocalized systems, have a short absorption edge or a large band gap, large SGH (d_ij), which should be greater than that of a standard sample, such as KH₂PO₄ (KDP, $d_{36}~0.39 \mathrm{p}\mathrm{m}/V$), and a moderate birefringence (Δn = 0.07–0.1) [1,7,8].

Over the past decades, great progress has been made in experimental research and the theoretical design of UV, DUV NLO crystals. Volumetric data have been accumulated both on general issues of new NLO materials [9,10,11,12] and on individual representatives of borates [7,13] and carbonates [8,14]. It is the planar and isoelectronic anions $\mathrm{B}{\mathrm{O}}_3^{3-}$ and $\mathrm{C}{\mathrm{O}}_3^{2-}$ that have moderate birefringence and large second-order microscopic hyperpolarizabilities, which make their compounds promising for study.

Powerful tools for studying NLO materials are infrared absorption spectroscopy (IRS) and Raman scattering (RS), which provide complete information about vibrational modes. Since the vibration wavenumbers depend on chemical bonds and symmetry, it is possible to identify the structural elements of complex crystalline systems. On the other hand, polarization Raman spectroscopy can provide detailed information on the symmetry labels of vibrational modes. Polarizing IRS and RS can also be used to identify polymorphic forms.

Among crystals with NLO properties, there is a group with the participation of barium. Among them, BaZnBO₃F has an SHG coefficient 2.8 ± 3 [15,16,17] times higher than that in KDP. In BaAlBO₃F₂, this index is twice as high [18]. BaZnCO₃F₂ [19] and BaZn₃(BO₃)₂F₂ [20] crystals have a similar structure. They are centrosymmetric (CS) and do not have the characteristic NLO properties, but they have birefringence and are of great importance for the creation of new materials. Some properties of these crystals were previously studied. The second and third-order nonlinear optical properties of the BaAlBO₃F₂ crystal were studied in [21,22,23]. In [24,25], the band structure, density of states, charge density, and elasticity-related properties of BaAlBO₃F₂ were obtained by ab initio density functional calculations. In [26], the electronic and optical properties of d¹⁰ borate-carbonate systems, including BaZnBO₃F and BaZnCO₃F₂, were studied, and it was found that, in d¹⁰ systems, there is a strong p-d interaction between O-p and Zn-d orbitals, and it increases the bandwidth of the valence band and reduces the band gap zones.

Raman optical spectra were studied experimentally for BaZnBO₃F in [16]. It is shown that the peaks located at 1231, 936, and 651 cm⁻¹ can be attributed to the asymmetric B–O (ν4) bond stretching, symmetric stretching (ν1), and out-of-plane bending (ν3) of BO₃ units. The strongest peak at 387 cm⁻¹ and the weak peak at 311 cm⁻¹ were assigned in [16] to the symmetric valence modes of the ZnO₃F₂ block, while 181 and 121 cm⁻¹ were attributed to vibrations of the BaO₆F₃ group. The IR spectrum of BaZn₃(BO₃)₂F₂ was measured in [17].

An important role in the study of vibrational properties is played by the symmetry of the crystals. It determines the qualitative spectra of infrared absorption and Raman scattering of light, and the study of polarization dependences sheds light on the structural features. Therefore, in this work, the structural, electronic, and vibrational properties of hexagonal barium-zinc (aluminum) fluoroborates and barium-zinc fluorocarbonate were calculated from the first principles by the methods of Hartree-Fock/Kohn-Sham (CPHF/KS) coupled perturbations, and then, the correlation dependences of the crystal structure symmetry and optical polarized spectra were established [27,28].

2. Calculation Method

The structure and vibrational properties of crystals were studied by density functional theory (DFT) methods in combination with Hartree-Fock (HF) in the CRYSTAL17 software package [29]. Crystalline orbitals are given by linear combinations of localized atomic orbitals of the Gaussian type, whose exponents and coefficients are determined from the full electron set B_1s²2s²2p¹3sp⁰3p⁰3d⁰, C_1s²2s²2p²3s⁰3p⁰3d⁰, O_1s²2s²2p⁴3s⁰3p⁰3d⁰, F_1s²2sp²25⁵3sp⁰3p⁰3d⁰, Al_1s²2s²2sp²3s⁰3p⁶4p¹5p⁰d⁰, Zn_1s²2s²3s²2sp²4s⁰2p⁶3p⁶4p⁰3d¹⁰4d⁰4f⁰ [30], and pseudopotential Ba_s²sp²sp⁰sp⁰p⁶3p¹4p⁰3d⁰ ones [31,32]. The hybrid B3LYP functional, which combines the 20% Hartree-Fock exchange with the B3 exchange functional [33] and the LYP correlation functional [34], was used. Previously, this functional was successfully used to study the optical spectra of simple and binary carbonates [35,36]. We have shown that for related compounds ABCO₃F (A: K, Rb, Cs; B: Mg, Ca, Sr, Zn, Cd) [37], taking into account the dispersion interaction in the form of the D3 correction with the PBE gradient functional (PBE-D3) ensures good agreement between the experimental and theoretical crystallographic parameters, while the combination of B3LYP-D3 leads to overestimated lattice constants. The thresholds controlling the accuracy of the Coulomb and exchange series are sets equal to 8, 8, 8, 8, 16 [38]. The reciprocal space is discretized by the Monkhorst-Pack [39] 12 × 12 grid, with 133 independent k-points in the irreducible part of the Brillouin zone. The accuracy of the self-consistency procedure was no less than 10⁻¹⁰ a.u. (1 a.u. = 27.21 eV).

To calculate the vibrational spectra of Raman scattering, infrared absorption, and reflection within the framework of the conjugate perturbation method CPHF/KS [40,41], the standard CRYSTAL package procedures [42] were used. Frequencies ν_n are obtained by diagonalizing the mass-weighted Hessian matrix, which is determined by the numerical differentiation of analytical gradients with respect to the Cartesian coordinates of atoms:$W_{\alpha i,\beta j}\left(\Gamma \right)=\frac{H_{\alpha i,\beta j}}{\sqrt{M_{\alpha }{M}_{\beta }}}$. Here, H_αi,βj is the second energy derivative, which is calculated numerically from analytical gradients, M_α and M_β are atomic masses; the Greek and Latin indices, respectively, refer to the atoms and Cartesian coordinates of the matrix W. Oscillator strengths $f_{n,ij}=\frac{1}{4\pi {\epsilon }_0}\frac{4\pi }{V}\frac{Z_{n,i}{Z}_{n,j}}{{\nu }_n^2}$ were calculated for each n-mode using the Born vector $Z_{n,i}=\sum _{\alpha ,i}{t_{n,\alpha j}Z}_{\alpha ,ij}^{*}\frac{1}{\sqrt{M_{\alpha }}}$ [43], and the atomic effective Born tensors $Z_{\alpha ,ij}^{*}$ are calculated using the Berry phase approach [44]. The intensity of Raman scattering for an oriented single crystal (for example, for the direction ij) associated with the mode with frequency ${\nu }_n$ is proportional to the element ϱ of the Raman scattering tensor and is given by ${\varrho }_{ij}^n=\frac{{\partial }^3{E}_{tot}}{\partial Q_n\partial {\mathsf{{\rm E}}}_i\partial {\mathsf{{\rm E}}}_{\mathrm{j}}}$, where E_tot is the total energy of the crystal, Ε—the strength of the external electric field, and Q—the normal coordinate of the n mode [45].

In ionic compounds, the long-range Coulomb effects due to the coherent displacement of the crystal nuclei are neglected. Therefore, the Hessian matrix must be corrected to obtain longitudinal optical (LO) modes. This additional contribution, the so-called non-analytic member, depends on the dynamic permittivity tensor and the Born effective charge tensor. Knowing the parameters, one can calculate the LO-TO splitting.

The procedure for computer simulation of the infrared spectrum is described in [46]. The key quantity in calculating infrared spectra is the complex permittivity tensor ε(ν), which is calculated for each nonequivalent polarization direction on the base of the classical Drude-Lorentz model:$\epsilon \left(\nu \right)={\epsilon }_{\propto ,ij}+\sum _n\frac{f_{n,ii}{\nu }_n^2}{{\nu }_n^2-{\nu }^2-i\nu {\gamma }_n}$, where ε(∞) is the static permittivity tensor at λ→∞, ν_n, f_n and γ_n are the TO frequency, oscillator strength, and damping coefficient for the n oscillation mode, respectively. In the CRYSTAL program code, the real and imaginary parts of ε(ν) are calculated; the maxima of the first function correspond to TO frequencies, and the maxima of the imaginary part 1/ε(ν) correspond to LO frequencies. The reflectance curve R(ν) is computed for each nonequivalent polarization direction with $R_{ii}\left(\nu \right)={\left|\frac{\sqrt{{\epsilon }_{ii}\left(\nu \right)-{\sin }^2\theta }-\cos \theta }{\sqrt{{\epsilon }_{ii}\left(\nu \right)-{\sin }^2\theta }+\cos \theta }\right|}^2$, where θ is the angle between the incident ray and the normal to the crystal surface.

3. Crystal Structure and Chemical Bond

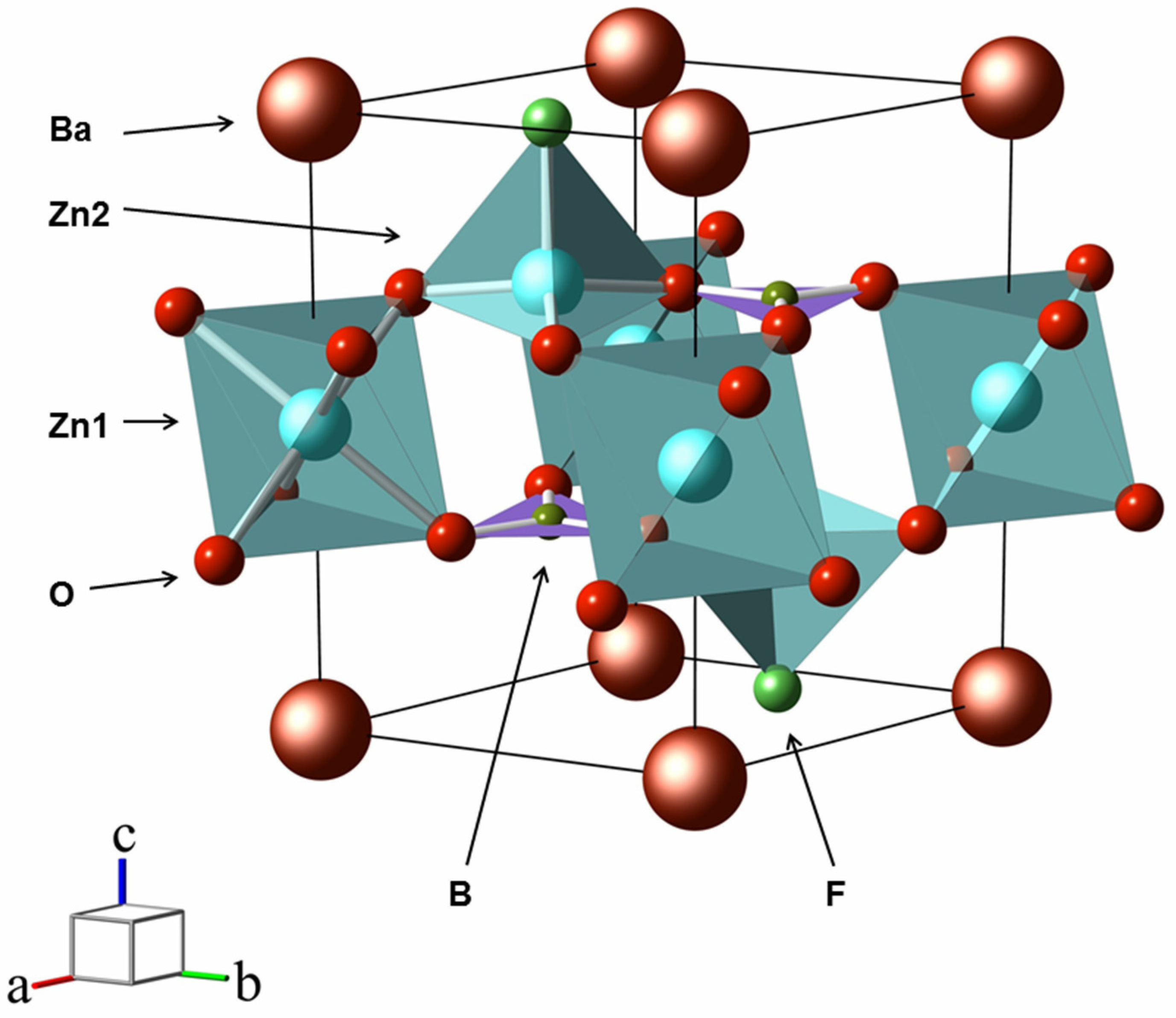
Crystal structure parameters of the studied compounds, obtained in experiments and from the first principles, are shown in

Table 1. Crystal structure parameters of fluoroborates, fluorocarbonates BaMAO₃F (M: Zn, Al; A: C, B): a, c—lattice constants, M-O, M-F—average distances between metal and oxygen atoms, fluorine, A-O—average distances inside the AO₃ anion. All values are in Å.

Crystal	Method	a, Å	c, Å	Ba-O	Ba-F	M-O	M-F	A-O
BaZnBO3F	B3LYP	5.0963	4.2907	2.8018	2.9423	1.9626	2.1454	1.3794
	Exp [15]	5.0658	4.2800	2.796	2.925	1.940	2.140	1.372
BaAlBO3F2	B3LYP	4.9239	9.5477	2.9704	2.8848	1.8079	1.8968	1.3777
	Exp [44]	4.8770	9.3824	2.9232	2.8621	1.7932	1.8324	1.3681
BaZn3(BO3)2F2	B3LYP	4.9285	7.6606	3.0393	2.8551	2.1154 1.9446	1.9886	1.3804
	Exp [20]	4.8900	7.7146	3.0316	2.8341	2.1135 1.9338	1.970	1.3745
BaZnCO3F2	B3LYP	4.8963	9.8897	2.9777	2.8641	2.0350	2.0122	1.2929
	Exp [19]	4.8523	9.854	2.9541	2.8398	2.0306	1.9984	1.2868

.

BaZnBO₃F (BZBF) belongs to the space group $P\overline{6}$ Its crystal structure is layered: the Ba and Zn atoms are located in the layer with z = 0, while the Zn atoms and BO₃ units are in the z = c/2 plane. Here and further in the text, the coordinate system is chosen so that z is directed along the c axis and x, y is in the a, b plane. Alkaline earth metal Ba atoms form BaO₆F₃ polyhedra with Ba-O and Ba-F distances given in Table 1, while zinc atoms form ZnO₃F₂ units. Neighboring [ZnBO₃]_∞ and [BaF]_∞ layers are linked by infinite F-Zn-F chains, resulting in a three-dimensional framework. Within the same [ZnBO₃]_∞ layer, neighboring BO₃ groups have an ideal coplanar alignment and, in different layers, they are also parallel to each other, which, according to [17], produces a cooperative effect and makes the maximal contribution to the NLO response. The chemical bond inside the layers is much stronger than between the layers, as evidenced by the population of the electron shells overlapping with the Zn-O atoms in 0.124 e (e is the electron charge) and Zn-F in 0.044 e. The chemical bond inside the anion is covalent since the population of the bond overlap B-O is 0.405 e.

In BaAlBO₃F₂ (BABF), the c axis is approximately twice as large as the a axis and the atoms in the unit cell are arranged in four layers: [AlBO₃]_∞ at z = 0, c/2, and [BaF]_∞ at z = c/4, 3/4. The symmetry group is $P\overline{6}2$ [46], not $P\overline{6}$ as was previously determined in [47]. It has a higher order and, in addition to the C₃ and S₆ axes, it contains the C₂ axes and vertical reflection planes σ_2v. As a result, in the immediate environment of the barium atom, there are six oxygen atoms, in addition to six fluorine atoms, while the order of their sequence in comparison with BZBF is reversed: first fluorine, then oxygen. The connecting links between the layers are F-Al-F- chains, where the Al-F bond overlap population (0.225 e) is greater than the Al-O overlap population (0.199 e). The bond within the BO₃ anionic group becomes weaker with the occupancy of 0.375 e.

In BaZn₃(BO₃)F₂ (BZ3BF), the symmetry group $P\overline{3}$ contains an inversion rather than the reflection plane ${\sigma }_h$ in $P\overline{6}$. Due to this symmetry, the first hyperpolarizability tensor χ⁽²⁾ vanishes and there are no NLO properties. The unit cell contains one formula unit with two equivalent BO₃ groups and three zinc atoms, of which Zn1 and two Zn2 occupy nonequivalent crystallographic positions. This resulted in a different environment: Zn1O₆ and Zn₂O₃F, where the Zn1-O and Zn2-O bond lengths are 2.1154 and 1.9446 Å, respectively. For barium atoms, the BaF₆O₆ environment is the same as in BABF. The layered structure is preserved, but now the alternation of layers is as follows: [BaF]_∞ at z = 0, c; [Zn₂BO₃]_∞ z = 0.328c, 0.672c and Zn1 atoms at z = c/2 (Figure 1). In this case, the [BaF]_∞ and [Zn₂BO₃]_∞ layers are not planar; their thicknesses are 0.235 and 0.025 Å. The interaction between the layers is carried out as follows: for [BaF]_∞, [Zn₂BO₃]_∞ through the Zn2-F bond with an overlap population of 0.125 e, and between them through the Zn1-O bond with a population of 0.074 e. The chemical bond B-O is still covalent and the population of 0.369 e is less here than in other borate anions.

BaZnCO₃F₂ (BZCF), just like in BABF, has two formula units, but in its symmetry group, instead of the C₂ axis, the vertical reflection axes σ_2v have the C₆ and S₆ axes and, as a consequence, the inversion and the P6₃/m symmetry group. The structure remains layered: [BaF]_∞ at z = 0, c/2 alternate with [ZnCO₃]_∞ layers at z = c/4, 3c/4. The fluorine atoms in the [BaF]_∞ layer are located above and below the barium atoms, so that the layer thickness is 0.117 Å, which is more than two times less than in BABF. The environment of the barium atom does not change BaF₆O₆, just as for the second metal ZnF₂O₃ against AlO₃F₂. The electronic charge of the aluminum atom is greater +1.38 |e| than that of zinc +1.28 |e|, while the formal valence charges differ by one unit. The overlap population on the Zn-O and Zn-F bond lines will be less than 0.77 and 0.90 e, respectively. In this case, the bond in the carbonate-ion will be stronger, since here the overlap population is 0.492 e.

Thus, the crystal structures of BZBF, BZ3BF, BABF, and BZCF are layered: it necessarily contains a [BaF]_∞ layer in which fluorine is located in the plane (BZBF), under and above the plane (BZ3BF, BABF, BZCF). There is one [ZnBO₃]_∞ layer in BZBF and two in the others; moreover, in BZ3BF, the [Zn₂BO₃]_∞ layers do not alternate with [BaF]_∞, but they are interconnected via Zn1 cations. The symmetry groups BZBF and BZ3BF have the same order, in the others, they are twice as high. The number of formula units is also correlated. The crystal structures of BABF and BZCF are identical, but, for the latter, the symmetry group contains an inversion instead of a mirror reflection.

4. Vibrational Spectra

The material optical properties are determined by tensor components of the electric dipole moment μ (vector), polarizability α (the second rank tensor), the first hyperpolarizability β (the 3-rd rank tensor), the second hyperpolarizability γ (the 4-th rank tensor), which, in addition to μ, can be analytically assessed using the CPHF/KS procedure. Knowing these tensors, one can obtain nonlinear susceptibilities of the second χ ⁽²⁾ and third ⁽³⁾ orders. The second-order susceptibility leads to the second-harmonic generation, frequency mixing, and parametric generation, while the third-order susceptibility is responsible for a third-harmonic generation in stimulated Raman scattering [7]. The first-order hyperpolarizability β and the second-order electrical susceptibility χ⁽²⁾ are related by the relation ${\chi }_{ijk}^{\left(2\right)}={\beta }_{ijk}\frac{2\pi }{V}$. In turn, the electrical susceptibility corresponds to the second harmonic generation coefficient $d_{ijk}^{2\omega }={\chi }_{ijk}^{\left(2\right)}/2 (a.u.).$ The calculated coefficients for NCS BZBF are $d_{111}=d_{122}=-0.567, d_{112}=d_{222}=1.930$; for BABF $d_{112}=-d_{222}=0.921$. Birefringence Δn, determined by the difference of the square roots of the components of the permittivity tensor in these crystals, is 0.061 and 0.051, respectively. In CS crystals BZ3BF and BZCF, the coefficients are equal to zero, and Δn are equal to 0.107 and 0.108, respectively.

In the Raman and infrared absorption spectra of carbonates and borates, two regions stand out. The low-frequency region with wavenumbers in the range of 0–500 cm⁻¹ is due to lattice vibrations involving cations and above 600 cm⁻¹ intramolecular vibrations of the corresponding anions are observed. The lattice region is unique for each compound, while the intramolecular region has a similar appearance for each class.

General ideas about the optical vibrations active in the IRS and RS can be obtained from symmetry. In a BZBF crystal of $P\overline{6}$ symmetry, the total vibrational representation at the point Γ ($\overrightarrow{k}=0)$ is decomposed into irreducible representations as follows:${\Gamma }_{vib}=2A\prime \left(RS\right)+{4A}^{″}\left(IRS\right)+5E^{\prime }\left(IRS, RS\right)+E^{″}\left(RS\right)$. The number before the symbol A of the single and E of the doubly degenerate irreducible representation indicates the number of oscillations and in brackets the type of activity. In IRS for one-dimensional representation, the electric field vector is polarized along the z-axis, for two-dimensional xy. It will be the same in other crystals. In RS for the one-dimensional representation of $A^{\prime }$ hereinafter the xx-, yy-, zz- intensity components are non-zero. Vibrations of $E^{\prime }$ symmetry have the xx-, yy-, xy- polarization, and $E^{″}$—the xz-, yz- polarization. There are 7 atoms in the unit cell and there will be 18 optical vibrations in total, the polarization vectors of which for the irreducible representation $A^{\prime }$ are built from xy—$\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$,$E^{″} \mathrm{h}\mathrm{a}\mathrm{s}$ only z-displacements of oxygen atoms, and for $E^{\prime }$ and $A^{″}$ respectively xy- and z-$\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}$ of all cell atoms.

There are 14 atoms in the BZ3BF unit cell, and the distribution over irreducible representations of the symmetry group $P\overline{3}$ has the form: Γ_vib = 6A_g(RS) + 7A_u (IRS) + 6E_g (RS) + 7E_u(IRS). In RS for Eg, the xx-, yy-, xy-, xz-, yz- components will be different from zero. The A_u and E_u polarization vectors of active vibrations will be built, respectively, from the z-, xy- displacements of all atoms (oxygen O_xyz), while for A_g, E_g there will be no Zn1_z and Zn1_xy displacements of the nonequivalent zinc and barium atoms.

For BABF and BZCF crystals of the same structural type with two formula units of 8 atoms each, there should be 45 optical vibrations. However, the selection rules state that only 22 will be active in the IRS, RS in the first case: ${\Gamma }_{vib}=3A_1^{\prime }\left(RS\right)+4A_2^{\prime }+4A_1^{″}+4A_2^{″}\left(IRS\right)+10E^{\prime }\left(IRS, RS\right)+5E^{″}\left(RS\right)$, and even less in the second: Γ_vib = 3A_g(RS) + 4B_g + 4A_u (IRS) + 4B_u + 2E_1g (RS) + 5E_2g(RS) + 5E_1u(IRS) +3E_2u. Symmetry vibrations E″, E_1g correspond to xz- and yz-polarizations in the Raman spectrum. The presence of inversion in the symmetry group of BZCF instead of mirror reflection in BABF leads to a different arrangement of polarization vectors. To represent E′, they include xy- displacements of atoms Al, F, B, O and x(y)- atoms of Ba. For E1_u representation, fluorine atoms can only displace in the direction of the x(y) axis. Polarization vectors of A_g and E_1g symmetries are formed, respectively, from Oxy, F_z and O_z, F_xy displacements. For E″ symmetry vibrations, rotations of anions in the direction of the z axis are accompanied by x(y) vibrations of barium and xy- fluorine atoms. Barium atoms do not participate in vibrations of the E_2g symmetry, which causes a different arrangement of the BABF and BZCF spectra. These results are summarized in

Table 2. Irreducible representations (IRP), wavenumbers (cm⁻¹) of active infrared (IRS), and Raman (RS) spectra of lattice and intramolecular vibrational modes of noncentrosymmetric (NCS) and centrosymmetric (CS) crystals with one and two formula units (Z).

Spectra	IRS		RS
IRP	${\mathit{A}}^{″},{\mathit{A}}_{\mathit{u}},{\mathit{A}}_2^{″},{\mathit{A}}_{\mathit{u}}$	${\mathit{E}}^{\prime },{\mathit{E}}_{\mathit{u}},{\mathit{E}}^{\prime },{\mathit{E}}_{1\mathit{u}}$	${\mathit{A}}^{\prime },{\mathit{A}}_{\mathit{g}},{\mathit{A}}_1^{\prime },{\mathit{A}}_{\mathit{g}}$	${\mathit{E}}^{\prime },{\mathit{E}}_{\mathit{g}},{\mathit{E}}^{\prime },{\mathit{E}}_{2\mathit{g}}$	${\mathit{E}}^{″},{\mathit{E}}_{1\mathit{g}}$
BaZnBO3F NCS, Z = 1	166.6, 283.7, 380.3, 761.8	125.7, 192.6, 324.2, 668.1, 1273.4	403.4, 961.9	125.7, 192.6, 324.2, 668.1, 1273.4	226.5
BaZn3(BO3)2F2 CS, Z = 1	112.6, 169.3, 252.0, 397.0, 473.5, 720.9, 963.0	92.0, 149.5, 186.4, 242.5, 359.4, 696.0, 1262.1	129.3, 313.4, 391.3, 489.7, 751.1, 961.4	106.7, 221.2, 283.8, 358.5, 693.6, 1259.4
BaAlBO3F2 NCS, Z = 2	137.1, 370.0, 489.4, 720.1	120.5, 123.8, 238.4, 270.4, 510.3, 512.8, 744.9, 745.8, 1288.6, 1289.8	361.8, 461.4, 988.5	120.5, 123.8, 238.4, 270.4, 510.3, 512.8, 744.9, 745.8, 1288.6, 1289.8	80.0, 134.5, 164.3, 333.7, 356.7
BaZnCO3F2 CS, Z = 2	141.2, 201.9, 392.5, 838.9	103.6, 169.9, 286.1, 747.6, 1516.8	279.9, 404.2, 1123.3	89.0, 244.7, 286.6, 748.4, 1520.9	181.6, 286.9

, where the wavenumbers of the corresponding vibrational modes are also given.

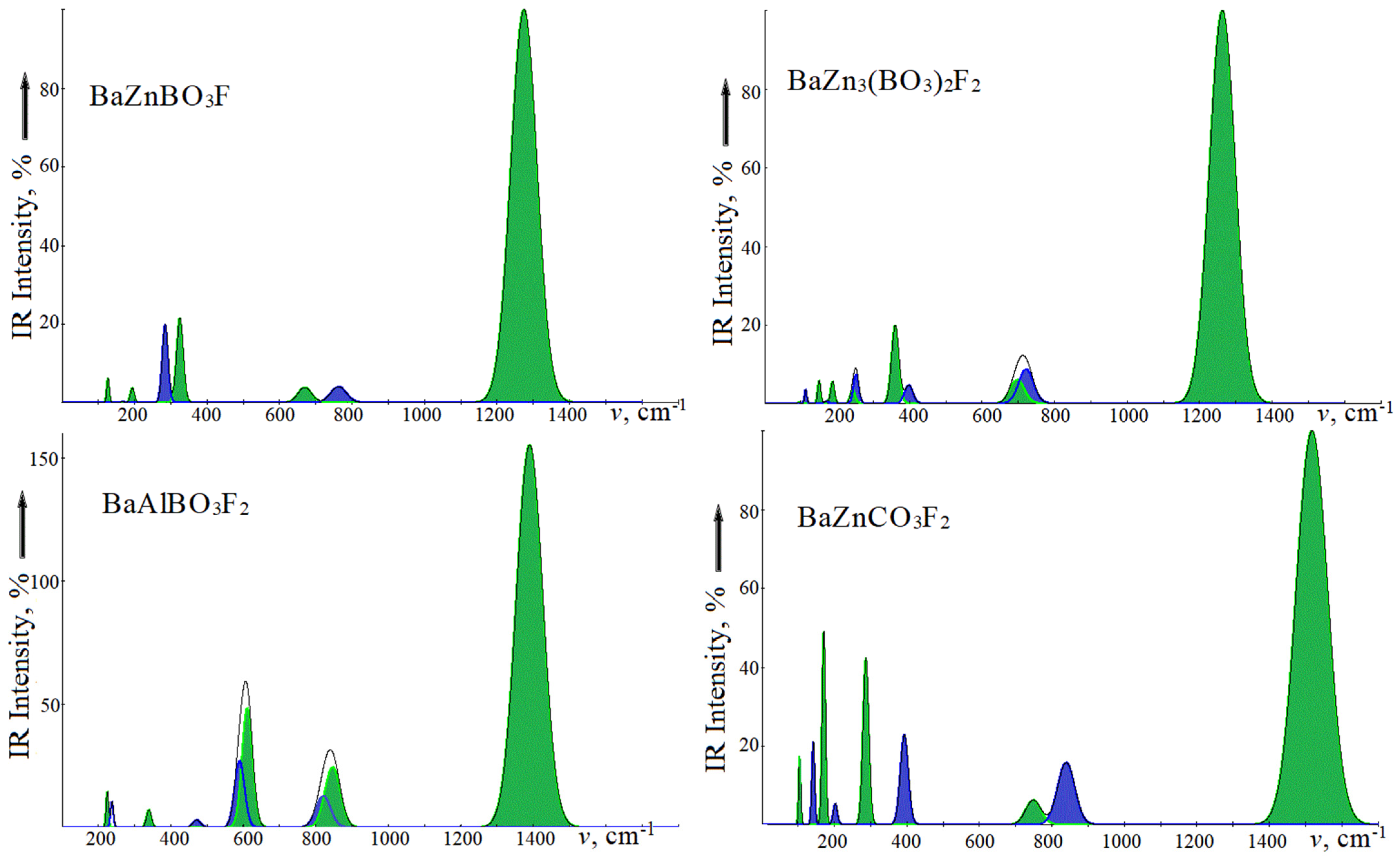
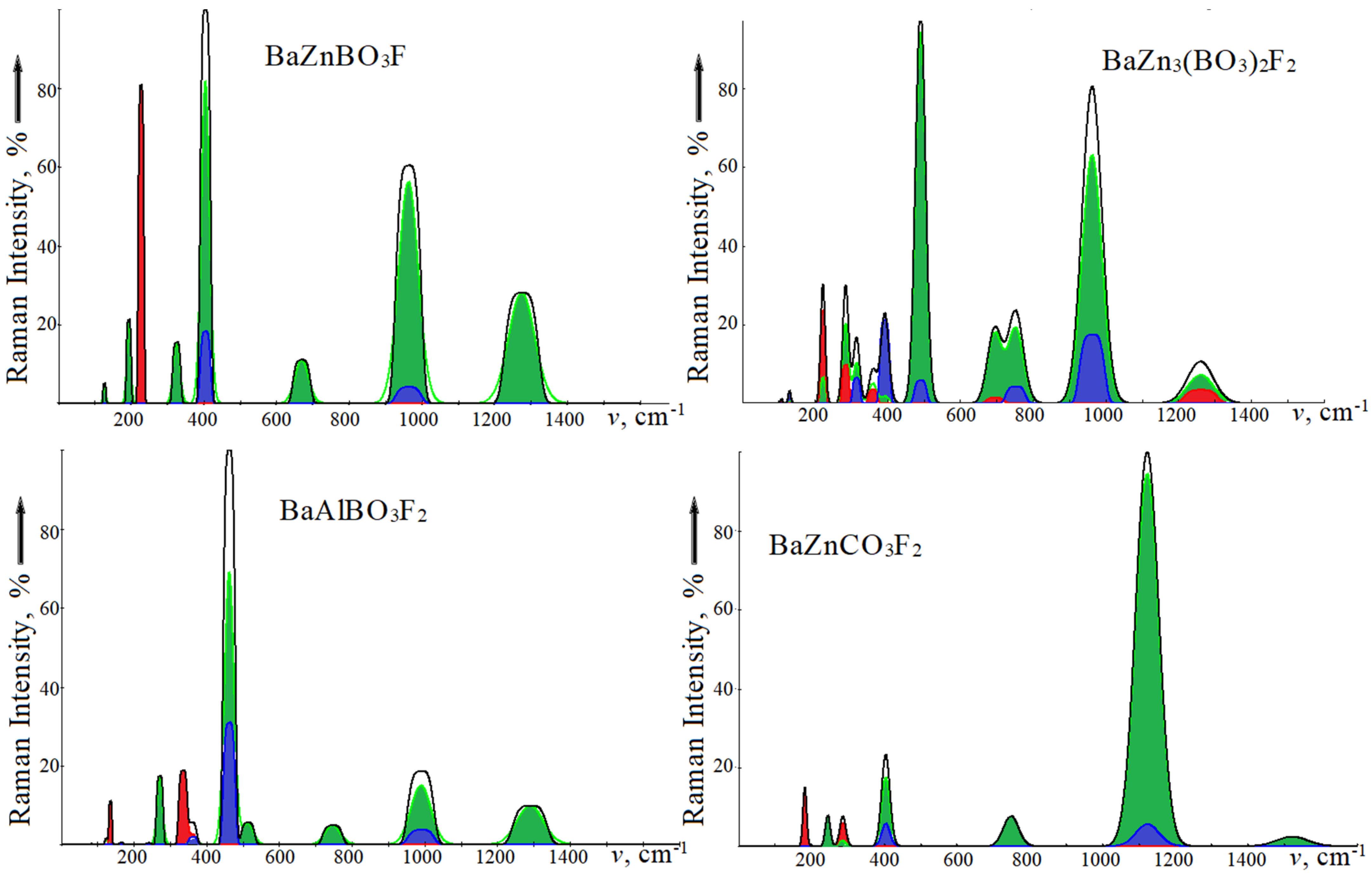
Figure 2 shows the infrared absorption spectra, and Raman light scattering of the studied crystals is presented in Figure 3. For ease of comparison, the oscillation intensities are given as a percentage. In IRS, intramolecular modes of the ν3 type with wave numbers in the series BZBF, BZ3BF, BABF, BZCF 1273.4, 1262.1, 1288.6, 1516.8 cm^–1 are taken as 100%. In RS of borates, the lattice modes of symmetry $A^{\prime },A_g,A_1^{\prime }$ with wave numbers 403.4, 489.7, and 461.4 cm^–1 are taken as 100%, and the intramolecular mode ν1 with a wave number of 1123.3 cm^–1 in carbonate is taken as 100%. A high intensity of the ν3 mode is observed in the IRS of carbonates [35] and fluorocarbonates [37]. The Raman spectra of fluoroborates and fluorocarbonates are different in the intensities just in the lattice and intramolecular regions. The most intense vibrations in borates will be the modes whose polarization vectors are formed by rotational motions of oxygen atoms in the xy plane.

For BZBF in the IRS lattice region, a weak vibration of the E′ symmetry with a wavenumber of 125.7 cm⁻¹ corresponds to the displacement of the layers in opposite directions when the atoms in [BaF]_∞ vibrate in antiphase, and in the [ZnBO₃]_∞ layer, in one direction. For the 192.6 cm⁻¹ vibration, these two layers are shifted in the opposite direction. For a high-intensity vibration at 324.2 cm⁻¹ in the [ZnBO₃]_∞ layer, the Zn cation and the BO₃ anion are displaced in opposite directions. The contribution of Ba and F atoms is extremely insignificant. For the A” symmetry mode with wavenumbers 166.6 and 283.8 cm⁻¹, the cations and anions in each layer are displaced in opposite directions of the z axis. In the first case, the Ba and BO₃ motion directions are coincident, and in the second, they are opposite.

In RS, in addition to the most intense vibration at 403.4 cm⁻¹, there will be a vibration of E″ symmetry with a wavenumber of 226.5 cm⁻¹, which corresponds to displacements of oxygen atoms of the “swing” type relative to the z axis, with the definite xz-, yz- polarization. Symmetry modes E′ will have xy-polarization and lower intensity.

BZ3BF has a chemical composition similar to BZBF, but with three times more atoms per cell, zinc atoms occupy nonequivalent positions of Zn1 and Zn2, and, therefore, its spectra contain more bands, including the number in the lattice region 200–400 cm⁻¹. Thus, in IRS, the lowest frequency (92.0 cm⁻¹) will be the vibration corresponding to displacements of the [BaF]_∞ and [ZnBO₃] layers in opposite xy-directions. Such an oscillation is not accompanied by the change in the dipole moment inside the layer; therefore, its intensity is low. In the next vibration at 149.5 cm⁻¹, the atoms of the [BaF]_∞ layer vibrate in opposite directions, while BO₃ vibrates in the z- direction. The vibration with a wavenumber of 186.4 cm⁻¹ will be the same type, with the difference that zinc atoms participate. For the 242.5 cm⁻¹ mode, the Zn1 and Zn2 atoms are displaced in opposite directions. Vibrations in this region can be formed due to the weak Zn(1,2)-O interaction, as indicated by the atomic displacement vectors. The low-frequency A_u symmetry modes have the same character, but only for vibrations along the z axis. For a vibration with a wavenumber of 397.0 cm⁻¹, atoms from the [BaF]_∞ layer are displaced to one side, and Zn1, BO₃—to the other. For a wavenumber of 473.5 cm⁻¹, Zn2 and BO₃ are shifted in opposite directions.

In contrast to the NCS BZBF, in RS and IRS of BZ3BF, the wavenumbers of doubly degenerate modes differ since there are no Ba_xy, Zn1_xy shifts in the polarization vectors of the E_g symmetry. Thus, a vibration with a wavenumber of 106.7 cm⁻¹ is formed by displacements of the Zn2 atoms and BO₃ units for two molecules in opposite xy directions; 221.2 cm⁻¹—by rocking BO₃ along the z axis, by the displacement of fluorine atoms in the xy plane; 283.8 cm⁻¹—scissor-type rockings for BO₃ along z-axis, by counter motions of fluorine. The highest frequency and lowest intensity vibration at 358.5 cm⁻¹ are formed by the counter motions of atoms in the [Zn₂BO₃]_∞ layers and molecules relative to each other. Similarly, the wavenumbers of vibrations of the A_g symmetry differ from those of the A_u symmetry.

In NCS BABF, the wavenumbers of the E′ modes in IRS and RS coincide, while in CS BZCF the E_1u and E_2g modes differ. The nature of oscillations in them is similar to the already considered BZBF and BZ3BF. A distinctive feature is the appearance of two close vibrations with wavenumbers 510.3 and 512.8 cm⁻¹, which are formed by deformation vibrations in BO₃ with the simultaneous rocking of Al and F. In BABF with two formula units, the number of doubly degenerate E′ symmetry modes is twice as large as similar ones in BZBF, but there are no single ones. Instead of one E″ mode, five of them appear in BABF, but only two of them at 134.5, 333.7 cm⁻¹ have a noticeable intensity, which is manifested by characteristic polarization in the spectrum of Figure 2.

BZCF differs from BZBF by replacing the divalent anion CO3 with the trivalent BO3 by adding a second fluorine atom and the associated increase in formula units in the cell. But the BZCF symmetry group contains twice as many elements and it has an inversion. As a result, the number of oscillations active in the IRS and RS did not increase. With the same structure as BABF in BZCF, the number of E symmetry vibrations is two times less. However, due to different intensities, this is not visible in Figure 2 and Figure 3.

The region of intramolecular vibrations IRS has a qualitatively similar shape and is characterized by a high-intensity deformation mode ν3 with a wavenumber of ~1280 cm⁻¹ in fluoroborates, 1516 cm⁻¹—in fluorocarbonate, and modes ν4 ~700 cm⁻¹ and ν2 ~760 cm⁻¹. In BABF, two modes, ν4 and ν3, are observed, and in BZCF, each one is due to the presence of an inversion in the symmetry group. In the Raman spectra, the ν1 modes in fluoroborates have wavenumbers of ~960–990 cm⁻¹ and lower intensity. In centrosymmetric crystals, the wavenumbers of the ν3 mode differ from the values in IRS by 1–5 cm⁻¹.

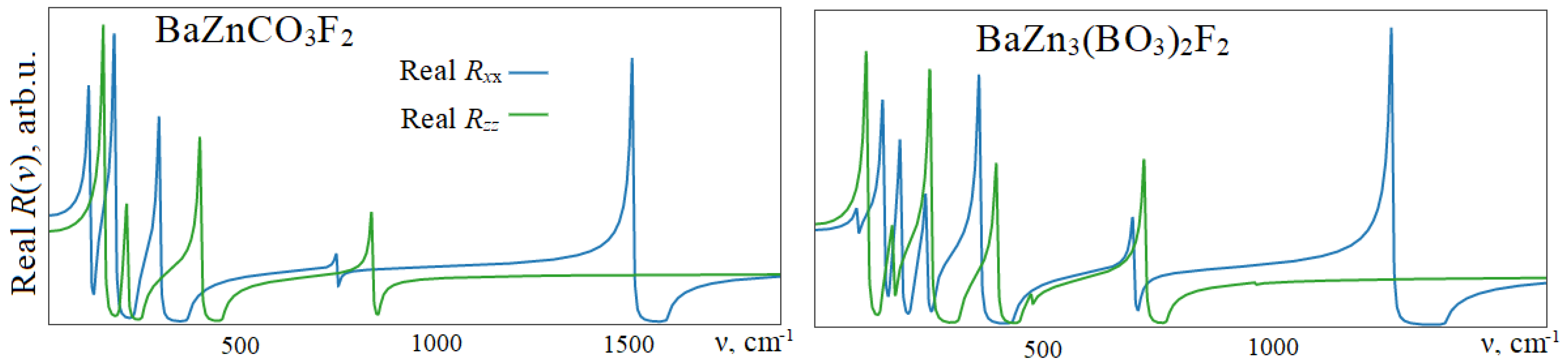
In Figure 4, the real parts of the reflectance are shown for centrosymmetric barium-zinc fluorocarbonate BaZnCO₃F₂ and fluoroborate BaZn₃(BO₃)₂F₂. For other fluoroborates, the spectra are qualitatively similar. The values of ε(∞) that were used for their calculation are equal for BZCF and BZ3BF, for polarizations xx—2.45, 2.65, and for zz—2.12, 2.32, respectively. The maxima in the spectra correspond to the TO- modes from Table 2, and the minima—to the LO- modes. In BZCF, for E_1u symmetry modes, in ascending order of wavenumber ν, these are 118.0, 222.6, 361.2, 750.8, and 1607.6 cm⁻¹, and for A_u symmetry modes: 183.4, 242.9, 452.0, and 857.8 cm⁻¹. The largest TO-LO splitting Δν will be for the xx- polarized intramolecular deformation mode ν3, and the smallest, for the ν4 mode, where it is only 3 cm⁻¹. The ν2 mode with zz polarization also has a small splitting of 19 cm⁻¹. In BZ3BF, the maximum splitting also falls on the ν3 mode, where it is equal to 119.4 cm⁻¹, and the minimum—on ν2 with the value of 0.3 cm⁻¹. The intensity of the latter is so small that it practically does not show up in the spectrum. Instead, the LO pair characteristic of TO- modes is observed with values of 708.5 (E_u) and 770.7 (A_u) cm⁻¹.

In NCS BZBF, the largest splitting of 146.9 cm⁻¹ is exhibited by the TO- mode of symmetry A” with a wavenumber of 283.8 cm⁻¹. For the ν3 mode, it is smaller and amounts to 107.0 cm⁻¹; for ν4, 7.7 cm⁻¹; and for ν2, 20.0 cm⁻¹. A distinctive feature of NCS crystals is the presence of negative biases, when the longitudinal optical modes LO become smaller than TO. Thus, for A” symmetry modes with wavenumbers 166.6 and 380.4cm⁻¹ TO-LO, the splittings are 1.4 and $-$0.3 cm⁻¹. Negative biases are also observed in BABF, but now these are E′ symmetry modes. In the BABF reflection spectrum, the ν3 and ν4 modes are split, and Δν takes on large values for the former and close to zero for the latter. Thus, the LO modes at 1289.4, 744.9, and 512.5 cm^–1 have almost zero oscillator strength f_n and zero biases, whereas at 1390.8, 773.3, and 568.7 cm^–1 they differ significantly from the TO modes. The analysis of the polarization vectors shows that the differences in the wavenumbers of the TO and LO modes for ν3 and ν4 are caused by an increase in the contribution of the amplitudes of aluminum atoms with a reduction in the contributions from the BO₃ group, while for the lattice, on the contrary, the contribution from aluminum decreases from 40 to 27%, and the contribution of fluorine, boron, and oxygen increases. The contributions of the amplitudes of barium atoms in these vibrations are less than 0.1%.

The electronic components of the permittivity tensor in BZBF and BABF for the xx- and zz-components are 2.46, 2.42 and 2.28, 2.27, respectively. The contribution of the nuclear ion component is almost twice as large as 5.10, 5.37 and 3.34, 5.45. For the NCS crystals of BZCF and BZ3BF, the values for the xx component of the ε(ν) tensor are approximately the same, 5.10 and 5.80, while for the zz components, the difference is significant (3.34 vs. 7.20).

5. Conclusions

Barium forms a series of hexagonal, layered crystals, where the simplest BaZnBO₃F has good nonlinear optical properties. Its infrared absorption and Raman scattering spectra are characterized by a set of bands with clear polarization dependence. So, for IRS and RS in the region of intramolecular vibrations, there will be three peaks each, formed by ν4, ν2, ν3 and ν4, ν1, ν3 vibrations of the anion, respectively. The increase in the number of zinc cations, while maintaining the chemical composition of BaZn₃(BO₃)₂F₂, is accompanied by the appearance of an inversion center and an increase in the number of lattice and intramolecular ν2 and ν1 vibrations. Replacing the zinc cation with the aluminum cation leads to an increase in the number of formula units while maintaining the mirror reflection symmetry operation. The number of lattice modes increases, and the ν4 and ν3 modes are split, but the values of the wavenumbers in both spectra still remain the same. When the BO₃ anion is replaced by CO₃, a fluorine atom is added, and the number of formula units increases. Due to the appearance of an inversion center, the number of intramolecular modes in the spectra does not change, while the wavenumbers, of course, become different. Thus, we established the correlation between structural transformations and the structure of vibrational spectra, which, based on computer simulation, can be used to predict new materials with desired properties.