Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci
Abstract
1. Introduction
2. The Tariffs and Characteristics of the Triangular Fibonacci Symmetrical Functions
3. Materials and Methods
4. The Fibonacci Riccati Method
- When , (13) has its own solution ,
- When , (13) possesses the given solution ,
- When , (13) has its own solutions
- When , (13) possesses its own solutions
- When and , (13) has its own solution
- When and , (13) has the solution .
- When and , (13) has the solutions .
- When , (13) possesses its own solution .
- When and , (13) possesses a solution
- When and , (13) has its own solution .
5. Separation Variable Solutions of the Burgers Model in (3+1)-Dimension
6. Novel Localized Excitements of the Burgers System in (3+1)-Dimension
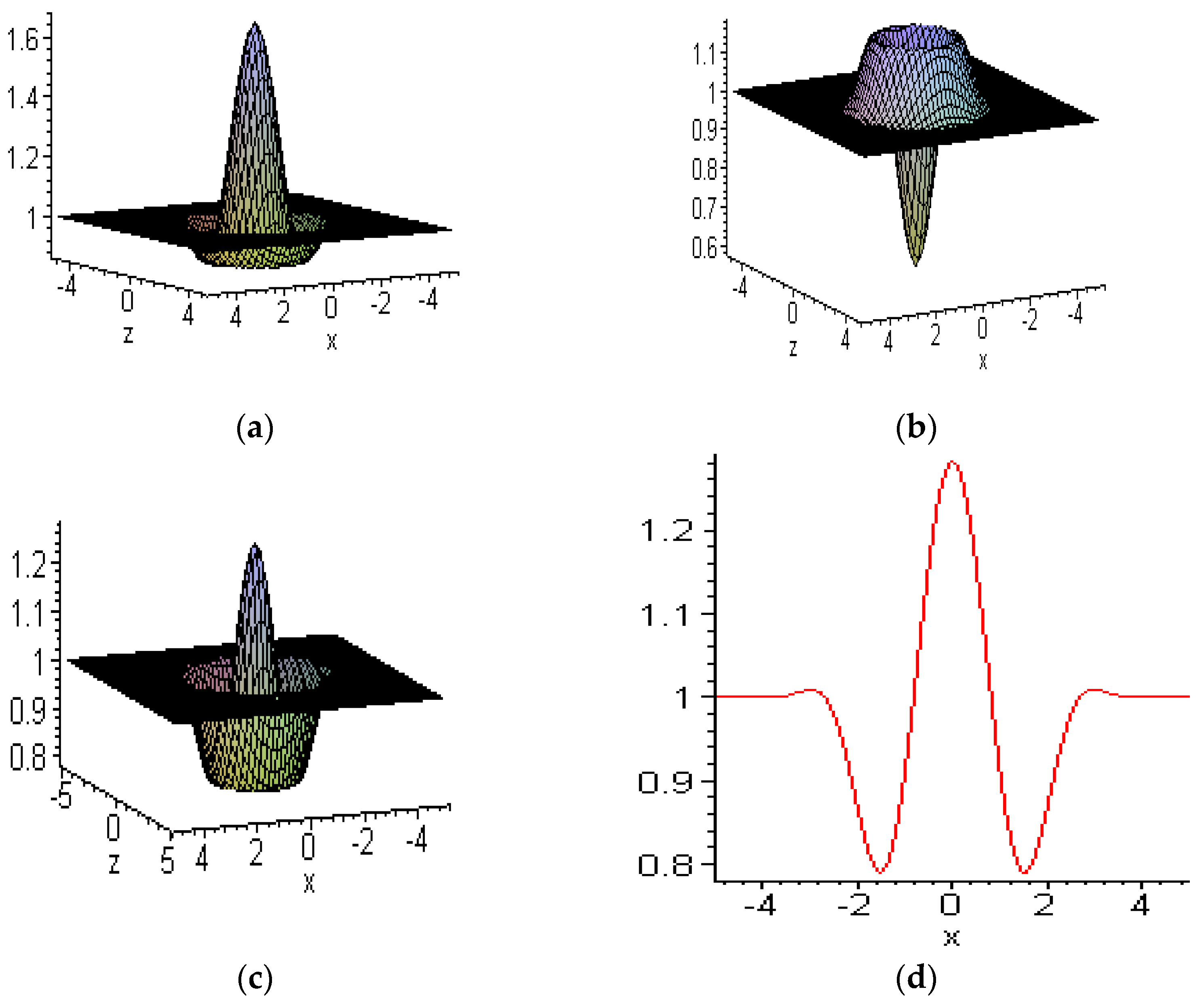
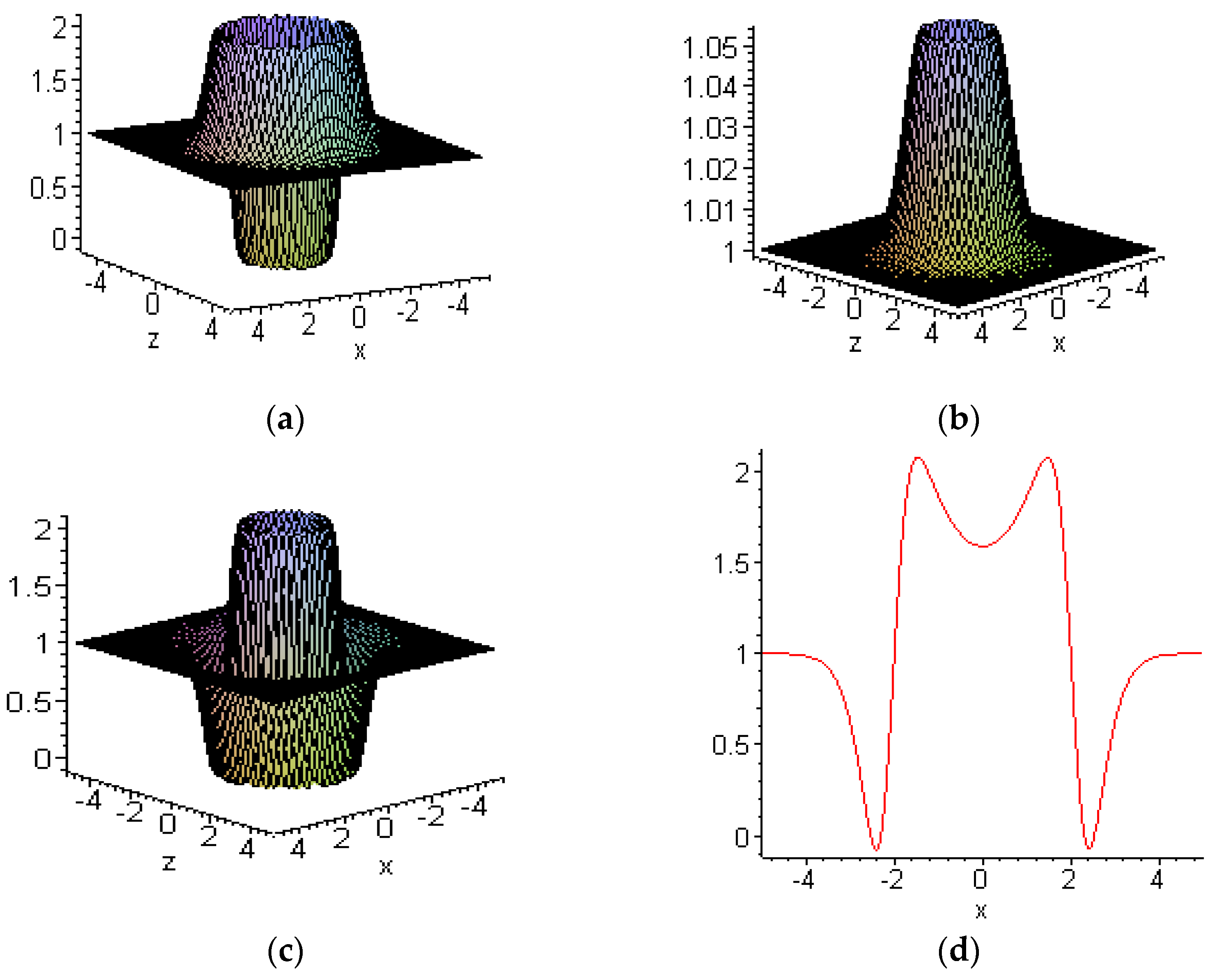
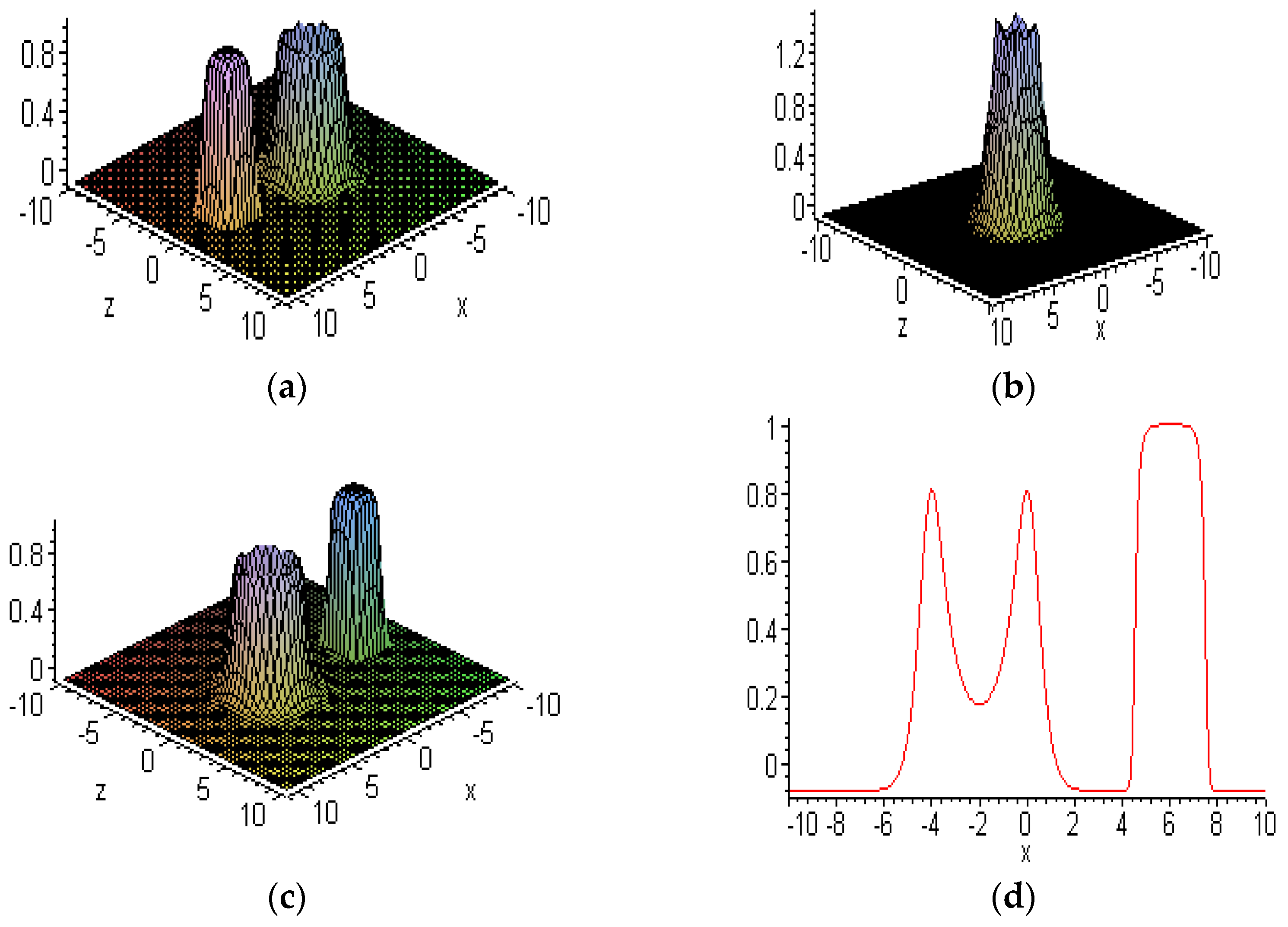
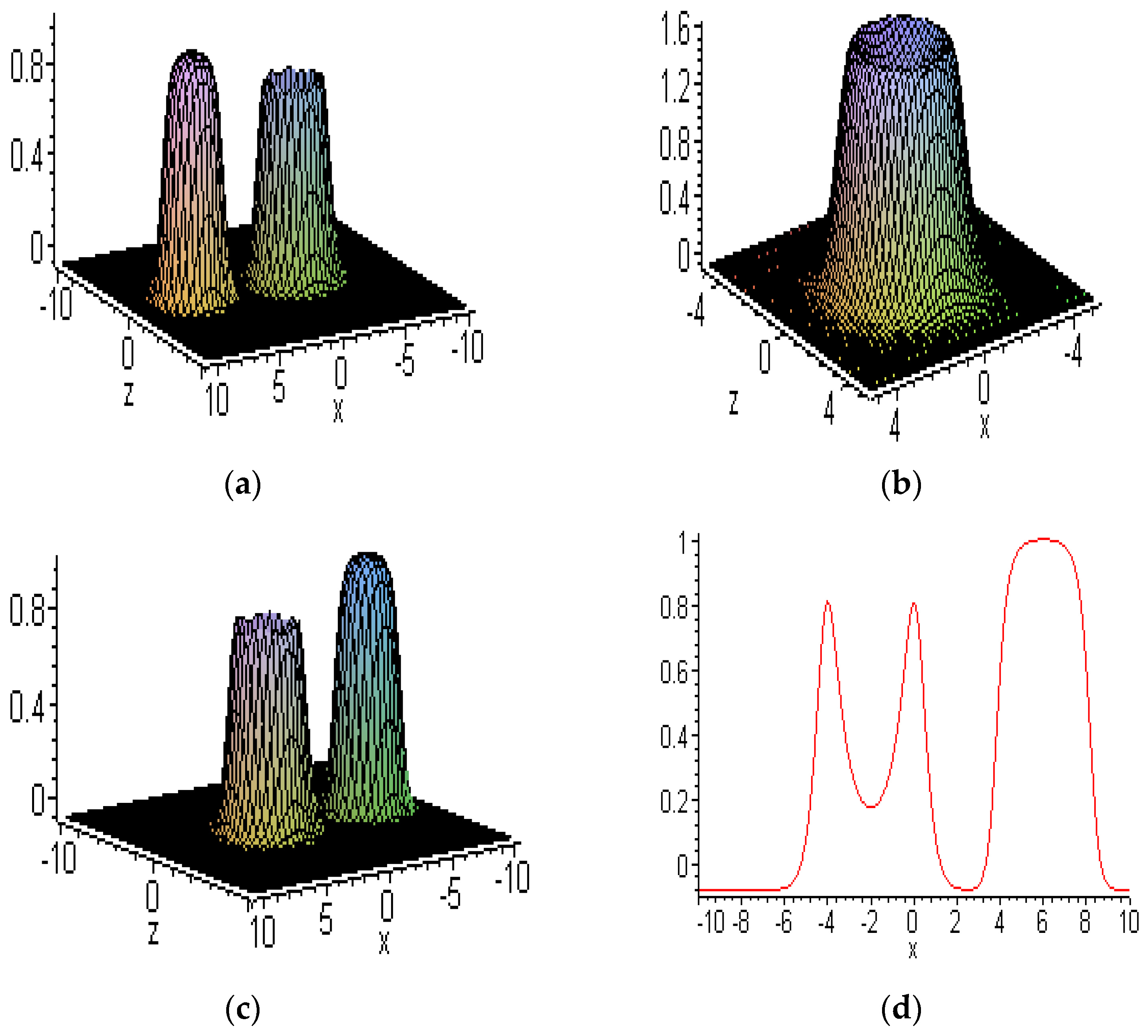
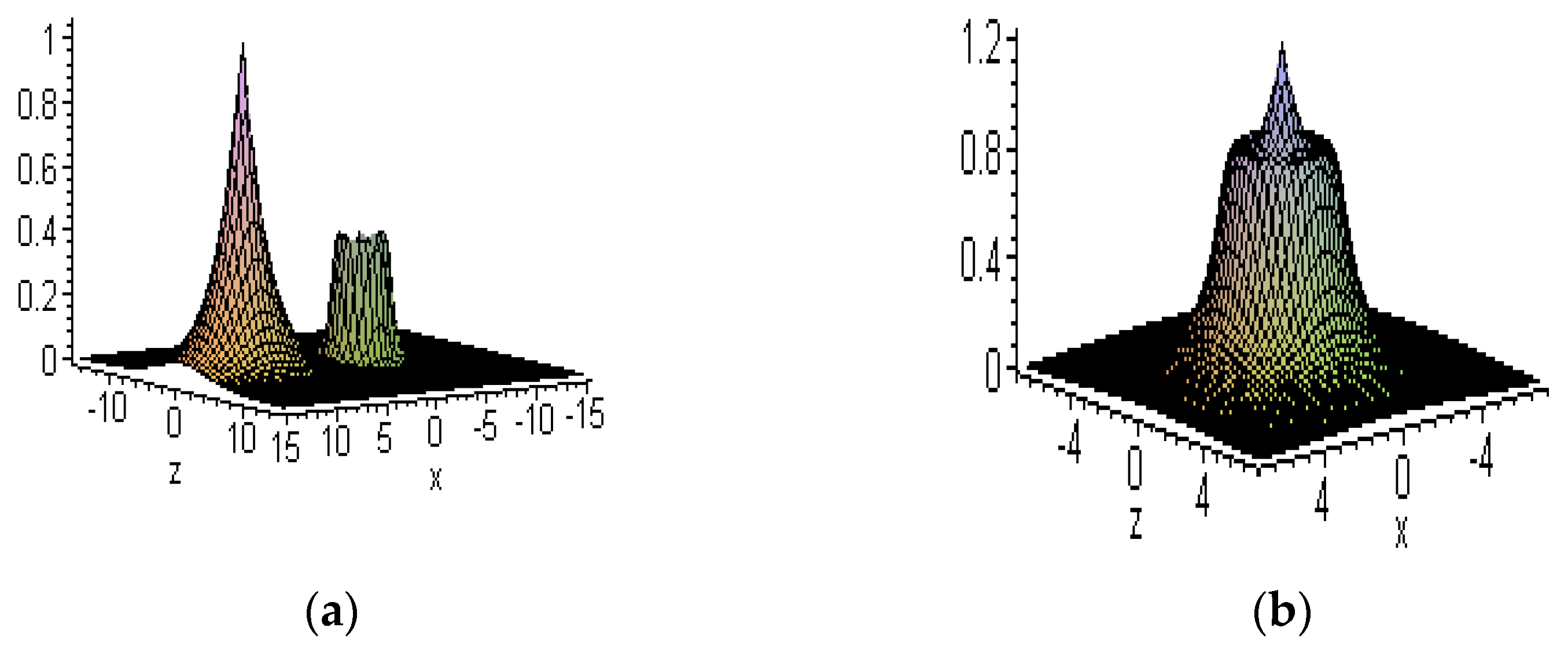
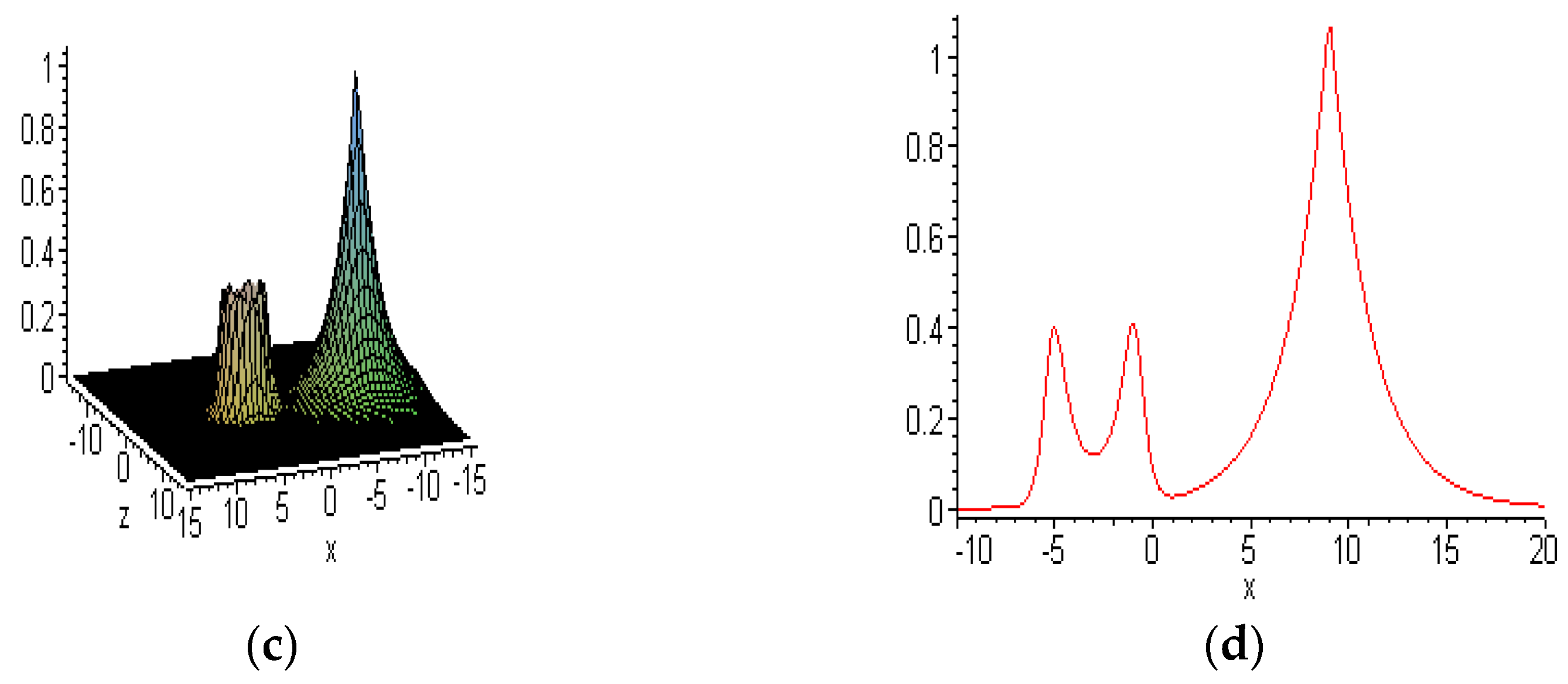
6.1. Embed-Solitons
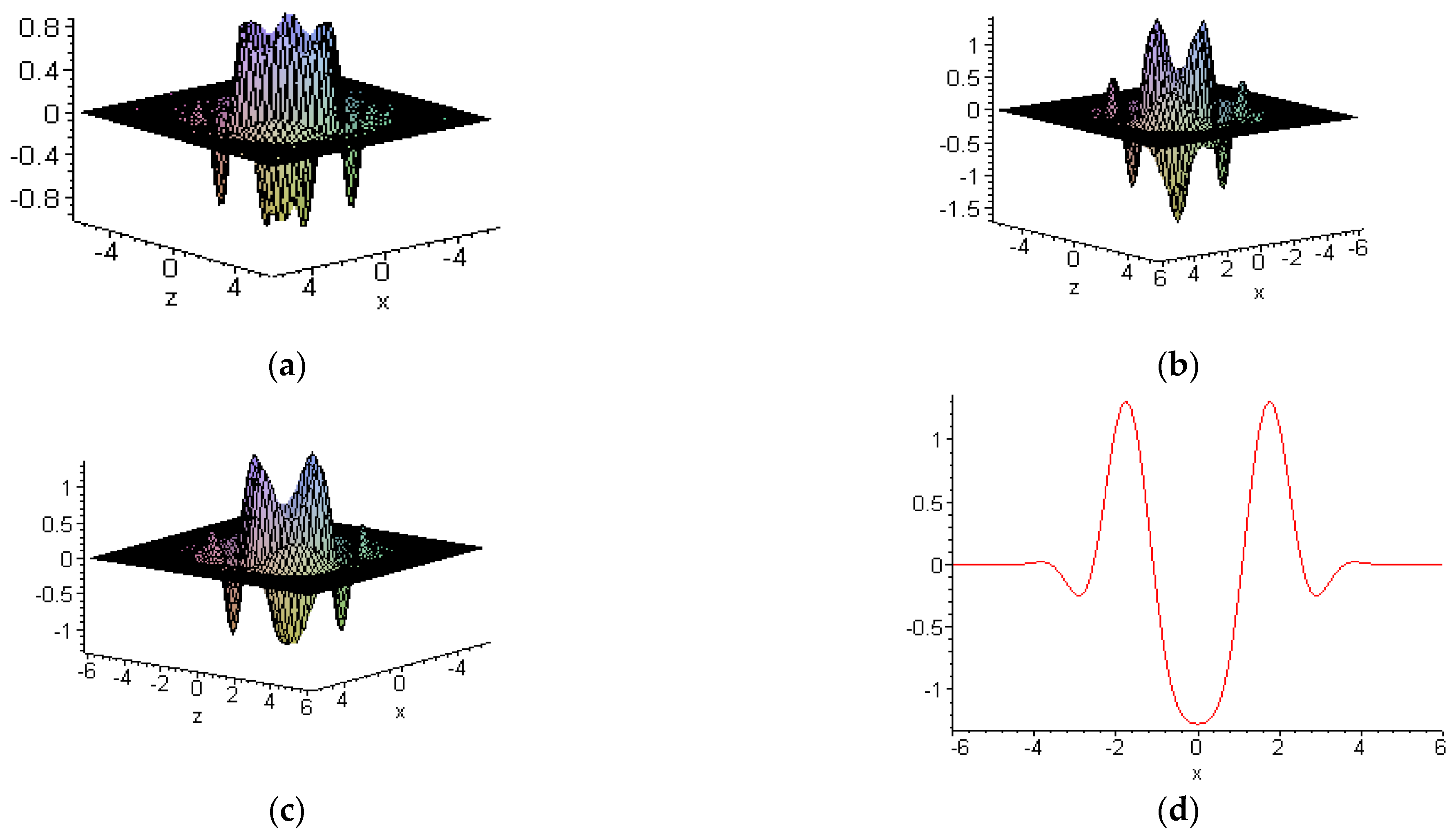
6.2. Other New Solitons
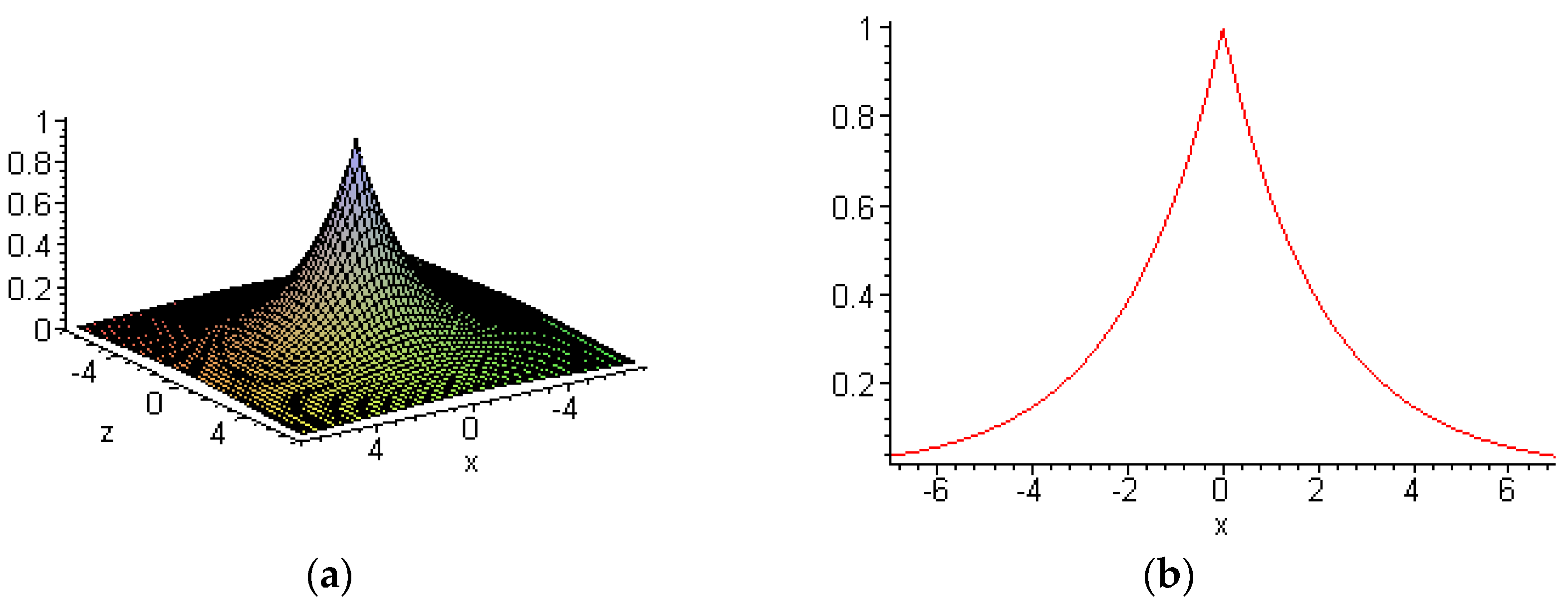
6.3. Interactions between Embedded and other Solitons
7. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, Z.; Kong, L.; Cao, Y.; Liu, A.; Li, Z.; Wu, Q.; Huang, J.; Gao, L.; Zhu, T. Real-time dynamics of optical controlling for bound states of mode-locked fiber laser with short-range interaction. Opt. Laser Technol. 2022, 149, 107859. [Google Scholar] [CrossRef]
- Wang, X.; Xing, Y.; Chen, G.; Lin, X.; Zhang, Z.; Zhu, Q.; Peng, J.; Li, H.; Dai, N.; Li, J. Temporal optical rogue waves in high power short-cavity Yb-doped random fiber laser. Opt. Laser Technol. 2022, 149, 107797. [Google Scholar] [CrossRef]
- Pakzad, H.R.; Nobahar, D. Dust-ion acoustic solitons in superthermal dusty plasmas. New Astron. 2022, 93, 101752. [Google Scholar] [CrossRef]
- Shen, M.; Li, X.; Zhang, Y.; Yang, X.; Chen, S. Effects of the interfacial Dzyaloshinskii-Moriya interaction on magnetic dynamics. J. Phys. D Appl. Phys. 2022, 55, 213002. [Google Scholar] [CrossRef]
- Younas, U.; Bilal, M.; Ren, J. Diversity of exact solutions and solitary waves with the influence of damping effect in ferrites materials. J. Magn. Magn. Mater. 2022, 549, 168995. [Google Scholar] [CrossRef]
- Islam, M.N.; Ilhan, O.A.; Akbar, M.A.; Benli, F.B.; Soybaş, D. Wave propagation behavior in nonlinear media and resonant nonlinear interactions. Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106242. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W. Modulational instability and sister chirped femtosecond modulated waves in a nonlinear Schrodinger equation with self-steepening and self-frequency shift. Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106240. [Google Scholar] [CrossRef]
- Dong, J.; Ling, L.; Zhang, X. Kadomtsev-Petviashvili equation: One-constraint method and lump pattern. Phys. D Nonlinear Phenom. 2022, 432, 133152. [Google Scholar] [CrossRef]
- Weng, W.; Zhang, G.; Zhang, M.; Zhou, Z.; Yan, Z. Semi-rational vector rogon-soliton solutions and asymptotic analysis for any n-component nonlinear Schrodinger equation with mixed boundary conditions. Phys. D Nonlinear Phenom. 2022, 432, 133150. [Google Scholar] [CrossRef]
- Sheng, H.H.; Yu, G.F. Solitons, breathers and rational solutions for a (2+1)-dimensional dispersive longwave system. Phys. D Nonlinear Phenom. 2022, 432, 133140. [Google Scholar] [CrossRef]
- Didenkulova, E. Mixed turbulence of breathers and narrowband irregular waves: mKdV framework. Phys. D Nonlinear Phenom. 2022, 432, 133130. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Liu, C.; Guo, B.; Wei, J. Rogue waves, semirational rogue waves and W-shaped solitons in the three-level coupled Maxwell-Bloch equations. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106172. [Google Scholar] [CrossRef]
- Sun, Y.L.; Chen, J.; Ma, W.X.; Yu, J.P.; Khalique, C.M. Further study of the localized solutions of the (2+1)-dimensional B-Kadomtsev-Petviashvili equation. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106131. [Google Scholar] [CrossRef]
- Tian, H.Y.; Tian, B.; Sun, Y.; Zhang, C.R. Three-component coupled nonlinear Schrodinger system in a multimode optical fiber: Darboux transformation induced via a rank-two projection matrix. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106097. [Google Scholar] [CrossRef]
- Dikande, A.M. On a Model for Nerve Impulse Generation Mediated by Electromechanical Processes. Braz. J. Phys. 2022, 52, 41. [Google Scholar] [CrossRef]
- Lavanya, C. Propagation and Soliton Collision of Positron Acoustic Waves in Four-component 208 Space Plasmas. Braz. J. Phys. 2022, 52, 38. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K. Lie symmetry analysis, optimal system, exact solutions and dynamics of solitons of a (3+1)-dimensional generalised BKP–Boussinesq equation. Pramana 2022, 96, 31. [Google Scholar] [CrossRef]
- Nisar, K.S.; Inc, M.; Jhangeer, A.; Muddassar, M.; Infal, B. New soliton solutions of Heisenberg ferromagnetic spin chain model. Pramana 2022, 96, 28. [Google Scholar] [CrossRef]
- Houwe, A.; Rezazadeh, H.; Bekir, A.; Doka, S.Y. Traveling-wave solutions of the Klein–Gordon equations with M-fractional derivative. Pramana 2022, 96, 26. [Google Scholar] [CrossRef]
- Alam, M.S.; Talukder, M.R. Characteristic behaviour of N-order ion acoustic rogue waves solution in electron-positron-ion plasmas. Plasma Res. Express 2022, 4, 015001. [Google Scholar] [CrossRef]
- Cisneros-Ake, L.A. Stability of multi-hump localized solutions in the Holstein model for linear acoustic and soft nonlinear optical interactions. Phys. D Nonlinear Phenom. 2022, 431, 133138. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Bright and dark solitons in a nonlinear saturable medium. Phys. Lett. A 2022, 427, 127913. [Google Scholar] [CrossRef]
- Chandramouli, S.; Farhat, A.; H Musslimani, Z. Time-dependent Duhamel renormalization method with multiple conservation and dissipation laws. Nonlinearity 2022, 35, 1286–1310. [Google Scholar] [CrossRef]
- Sudhakar, S.; Vignesh Raja, S.; Govindarajan, A.; Batri, K.; Lakshmanan, M. Low-power optical bistability in PT-symmetric chirped Bragg gratings with four-wave mixing. J. Opt. Soc. Am. B Opt. Phys. 2022, 39, 643. [Google Scholar] [CrossRef]
- Perna, S.; Bruckner, F.; Serpico, C.; Suess, D.; d’Aquino, M. Computational micromagnetics based on normal modes: Bridging the gap between macrospin and full spatial discretization. J. Magn. Magn. Mater. 2022, 546, 168683. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Mustafa, B.; Ali, K.; Althubiti, S. Chirped periodic waves for an cubic-quintic nonlinear Schrodinger equation with self steepening and higher order nonlinearities. Chaos Solitons Fractals 2022, 156, 111804. [Google Scholar] [CrossRef]
- Velasco-Juan, M.; Fujioka, J. Lagrangian nonlocal nonlinear Schrodinger equations. Chaos Solitons Fractals 2022, 156, 111798. [Google Scholar] [CrossRef]
- Sugati, T.G.; Seadawy, A.R.; Alharbey, R.A.; Albarakati, W. Nonlinear physical complex hirota dynamical system: Construction of chirp free optical dromions and numerical wave solutions. Chaos Solitons Fractals 2022, 156, 111788. [Google Scholar] [CrossRef]
- Li, Q.; Shan, W.; Wang, P.; Cui, H. Breather, lump and N-soliton wave solutions of the (2+1)-dimensional coupled nonlinear partial differential equation with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2022, 106, 106098. [Google Scholar] [CrossRef]
- Evslin, J.; Halcrow, C.; Romanczukiewicz, T.; Wereszczynski, A. Spectral Walls at One Loop. arXiv 2022, arXiv:2202.08249. [Google Scholar] [CrossRef]
- Sreedharan, A.; Kuriyattil, S.; Wuster, S. Hyper-entangling mesoscopic bound states. arXiv 2022, arXiv:2202.06120. [Google Scholar]
- Evslin, J. Moving Kinks and Their Wave Packets. arXiv 2022, arXiv:2202.04905. [Google Scholar] [CrossRef]
- He, Y.; Slunyaev, A.; Mori, N.; Chabchoub, A. Experimental evidence of nonlinear focusing in standing water waves. arXiv 2022, arXiv:2202.04775. [Google Scholar] [CrossRef] [PubMed]
- Muller-Hoissen, F. Binary Darboux transformation of the first member of the nega- tive part of the AKNS hierarchy and solitons. arXiv 2022, arXiv:2202.04512. [Google Scholar]
- Zabolotnykh, A.A. Plasma solitons in gated two-dimensional electron systems: Exactly solvable analytical model for the regime beyond weak non-linearity. arXiv 2022, arXiv:2202.04503. [Google Scholar] [CrossRef]
- Lei, Z.; Ren, X.; Yang, Z. Radiation of the energy-critical wave equation with compact support. arXiv 2022, arXiv:2202.02045. [Google Scholar]
- Jin, H.-Y.; Wang, Z.-A.; Wu, L. Global dynamics of a three-species spatial food chain model. J. Differ. Equ. 2022, 333, 144–183. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Ruan, S. Global dynamics and bifurcations in a four-dimensional replicator system. Discret. Contin. Dyn. Syst.-B 2013, 18, 259–271. [Google Scholar] [CrossRef]
- Jin, H.-Y.; Wang, Z.-A. Global stabilization of the full attraction-repulsion Keller-Segel system. Discret. Contin. Dyn. Syst. 2020, 40, 3509–3527. [Google Scholar] [CrossRef]
- Li, Q.-K.; Lin, H.; Tan, X.; Du, S. H∞ Consensus for Multiagent-Based Supply Chain Systems under Switching Topology and Uncertain Demands. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4905–4918. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y. Stock intelligent investment strategy based on support vector machine parameter optimization algorithm. Neural Comput. Appl. 2020, 32, 1765–1775. [Google Scholar] [CrossRef]
- Shao, Z.; Zhai, Q.; Han, Z.; Guan, X. A linear AC unit commitment formulation: An application of data-driven linear power flow model. Int. J. Electr. Power Energy Syst. 2023, 145, 108673. [Google Scholar] [CrossRef]
- Cai, Y.-J.; Wu, J.-W.; Lin, J. Nondegenerate N-soliton solutions for Manakov system. Chaos Solitons Fractals 2022, 164, 112657. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, B.; Wang, D.-S. Localised Nonlinear Wave Interaction in the Generalised Kadomtsev-Petviashvili Equation. East Asian J. Appl. Math. 2021, 11, 301–325. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, L. Some novel physical structures of a (2+1)-dimensional variable-coefficient Korteweg–de Vries system. Chaos Solitons Fractals 2023, 171, 113430. [Google Scholar] [CrossRef]
- Saleh, M.H.; Altwaty, A.A. Optical solitons of the extended Gerdjikov-Ivanov Equation in DWDM system by extended simplest equation method. Appl. Math. Inf. Sci. 2020, 14, 901–907. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Bhrawy, A.H.; Ahmed, B. Biswas, Anjan, Solitons and other solutions to Complex-Valued Klein-Gordon equation in ϕ-4 field theory. Appl. Math. Inf. Sci. 2015, 9, 2793–2801. [Google Scholar]
- Zhu, H.-P.; Zheng, C.-L. Embed-Solitons and their evolutional behaviors of (3+1)-dimensional Burgers System. Commun. Theor. Phys. 2007, 48, 57–62. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.-B. Quasi-periodic structures based on symmetrical lucas Function of (2+1)-dimensional modified dispersive water-wave system. Commun. Theor. Phys. 2009, 52, 1004. [Google Scholar] [CrossRef]
- Friedman, I.; Riano, O.; Roudenko, S.; Son, D.; Yang, K. Well-posedness and dynamics of solutions to the generalized KdV with low power nonlinearity. arXiv 2022, arXiv:2202.01130. [Google Scholar] [CrossRef]
- Ali, U.; Ahmad, H.; Baili, J.; Botmart, T.; Aldahlan, M.A. Exact analytical wave solutions for space-time variable-order fractional modified equal width equation. Results Phys. 2022, 33, 105216. [Google Scholar] [CrossRef]
- Bilal, M.; Ahmad, J. A variety of exact optical soliton solutions to the generalized (2+1)-dimensional dynamical conformable fractional Schrodinger model. Results Phys. 2022, 33, 105198. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ali, K.K.; Inc, M.; Mehanna, M.S.; Rezazadeh, H.; Akinyemi, L. New solutions for the generalized resonant nonlinear Schrodinger equation. Results Phys. 2022, 33, 105153. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Kantz, H. Modified method of simplest equation and its application to nonlinear PDEs. Appl. Math. Comput. 2010, 216, 2587–2595. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssif, M.Y.; Helal, K.A.A.; Juma, M.Y.A.; Elhag, A.E.; Elamin, A.E.A.M.A.; Aiyashi, M.A.; Abo-Dahab, S.M. Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci. Symmetry 2023, 15, 1473. https://doi.org/10.3390/sym15081473
Youssif MY, Helal KAA, Juma MYA, Elhag AE, Elamin AEAMA, Aiyashi MA, Abo-Dahab SM. Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci. Symmetry. 2023; 15(8):1473. https://doi.org/10.3390/sym15081473
Chicago/Turabian StyleYoussif, Mokhtar. Y., Khadeeja A. A. Helal, Manal Yagoub Ahmed Juma, Amna E. Elhag, Abd Elmotaleb A. M. A. Elamin, Mohammed A. Aiyashi, and Sayed M. Abo-Dahab. 2023. "Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci" Symmetry 15, no. 8: 1473. https://doi.org/10.3390/sym15081473
APA StyleYoussif, M. Y., Helal, K. A. A., Juma, M. Y. A., Elhag, A. E., Elamin, A. E. A. M. A., Aiyashi, M. A., & Abo-Dahab, S. M. (2023). Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci. Symmetry, 15(8), 1473. https://doi.org/10.3390/sym15081473







