Abstract
The article presents a novel algorithm for merging Bayesian networks generated by different methods, such as expert knowledge and data-driven approaches, while leveraging a symmetry-based approach. The algorithm combines the strengths of each input network to create a more comprehensive and accurate network. Evaluations on traffic accident data from Prague in the Czech Republic and accidents on railway crossings demonstrate superior predictive performance, as measured by prediction error metric. The algorithm identifies and incorporates symmetric nodes into the final network, ensuring consistent representations across different methods. The merged network, incorporating nodes selected from both the expert and algorithm networks, provides a more comprehensive and accurate representation of the relationships among variables in the dataset. Future research could focus on extending the algorithm to deal with cycles and improving the handling of conditional probability tables. Overall, the proposed algorithm demonstrates the effectiveness of combining different sources of knowledge in Bayesian network modeling.
1. Introduction
Bayesian networks are probabilistic graphical models used to represent uncertain knowledge about causal relationships between variables. They have been widely used in various domains such as medical diagnosis, decision making, and natural language processing. In these domains, Bayesian networks are primarily utilized for observational studies, where they are employed to model relationships and dependencies between variables based on observed data. Additionally, Bayesian networks can be applied in a causality view, allowing for the exploration of causal relationships between variables [1]. One of the main challenges in constructing Bayesian networks is to determine the network structure, which specifies the dependencies between variables [2].
Currently, there are several methods available for constructing Bayesian networks, such as score-based methods and constraint-based methods. However, these methods may not incorporate expert knowledge and may produce networks that do not meet the user’s expectations [3].
In this paper, we propose a novel algorithm for merging two Bayesian networks to create a final network that incorporates both expert knowledge and data information. Our approach is based on selecting nodes and edges from each network and merging them to form a final network. The selection process is independent of the node evaluation method used in the input networks, providing flexibility in the choice of evaluation method.
While the typical usage of our algorithm is to merge one network created by an algorithm and the other by an expert, our approach is not limited to this specific use case. Our algorithm allows for the incorporation of expert knowledge into the network construction process, providing a way to easily modify the structure of a network without having to start from scratch.
The motivation for our approach is to provide a more flexible and customizable approach to network construction that can incorporate both data and expert knowledge. By incorporating expert knowledge, we hope to address the limitations of current methods and enable users to create networks that better reflect their expectations and requirements. We evaluated our proposed algorithm on two datasets, demonstrating its effectiveness in constructing accurate Bayesian networks.
1.1. Probability Theory
Probability theory is an important mathematical tool used in Bayesian networks [2,4]. We define a random variable X as a variable whose values are uncertain and subject to probability distributions. A probability distribution is a function that maps every value x of the random variable to a probability of that value occurring.
The joint probability distribution is a probability distribution that represents the probability of every possible combination of values of the random variables [5]. On the other hand, the marginal probability distribution is the probability distribution that represents the probability of a single random variable , ignoring the values of the other variables. Additionally, the conditional probability distribution represents the probability of a random variable taking a certain value, given that another random variable has taken a certain value [2].
Two random variables X and Y are marginally independent if [5]. They are conditionally independent given a third random variable Z if [2].
Understanding these concepts is essential for building and analyzing Bayesian networks [2,5,6].
1.2. Bayesian Network
A Bayesian network is a directed acyclic graph (DAG) where V is a set of nodes or variables and is a set of directed edges. Each node corresponds to a random variable , and each edge represents a direct influence of on . We say that is a parent of . Each node has a corresponding probability distribution , where denotes the set of parents of in G [7].
The joint probability distribution over all variables in the network can be written as
This is known as the chain rule of probability. It states that the joint probability of all variables in the network can be factorized into the local conditional probabilities of each variable given its parents [2].
Review of Algorithms for Bayesian Networks
Learning Bayesian networks involves inferring the structure and parameters of the network from data. There are three main types of algorithms for learning Bayesian networks: algorithms for learning structure, algorithms for learning parameters, and inference algorithms.
- Algorithms for learning structure include score-based methods and structure-based methods. Score-based methods aim to learn the network structure by searching for the structure that maximizes a scoring function, such as the Bayesian Information Criterion (BIC) [8] or the Akaike Information Criterion (AIC) [9]. These methods do not impose any constraints on the search space and are often used when no prior knowledge about the network structure is available. Structure-based methods, on the other hand, use prior knowledge about the structure of the network to constrain the search space. These methods impose a set of constraints on the possible network structures, such as the absence of certain edges or the presence of specific edge patterns. Examples of structure-based algorithms include constraint-based algorithms such as the PC (Peter and Clark) algorithm [10] and the Grow–Shrink algorithm [11].
- Algorithms for learning parameters aim to estimate the parameters of a given network structure. These algorithms can be used in conjunction with either score-based or structure-based methods. Examples of learning parameter algorithms include maximum likelihood estimation [6] and Bayesian parameter estimation [2].
- Inference algorithms are used to compute the probabilities of events of interest in a Bayesian network. Exact inference methods, such as variable elimination [2], provide the exact probability distribution of the events of interest, while approximate inference methods, such as Monte Carlo methods [2], provide an approximation of the probability distribution.
1.3. State of the Art
Bayesian networks are a powerful tool for modeling complex systems and decision-making problems [12,13]. The use of Bayesian networks has become increasingly popular due to their ability to handle uncertain information and the ability to represent complex relationships between variables [1]. As the number of applications of Bayesian networks grows, the need for combining or merging them has become an important research topic. Merging Bayesian networks is challenging and requires addressing various issues, such as preserving the characteristics of the individual networks, avoiding cycles, and maintaining the conditional independence relations among variables [2]. There are several approaches for combining or merging Bayesian networks, including methods based on learning the structure from data and methods for combining networks with a fixed structure.
To provide a comprehensive overview of the state-of-the-art, the first part of the discussion will focus on papers that have a primary focus on combining Bayesian networks. The subsequent part of the state-of-the-art analysis will concentrate on similar approaches, such as ensemble learning and learning Bayesian network structures. These approaches, although not solely focused on merging networks, are relevant in the context of integrating probabilistic models.
Del Sagrado and Moral [14] propose a qualitative method for combining Bayesian networks. Their approach considers the intersection and union of nodes and conditional probability tables (CPTs) from the original networks. By preserving the structural and parametric characteristics while avoiding cycles in the merged network, their method ensures the integrity of the individual networks’ properties.
Jiang, Leong, and Kim-Leng [15] present a framework for combining Bayesian networks, specifically focused on finding the ideal structure. They begin with three Bayesian networks representing different medical fields and develop a method to merge them while preserving conditional independence relations among variables and avoiding cycles in the merged network. Their work contributes to the integration of domain-specific knowledge and the creation of a comprehensive network structure.
Feng, Zhang, and Liao [16] propose an algorithm for merging Bayesian networks that utilizes a scoring function to evaluate the quality of each node. Based on their scores, nodes are selected for merging. Their theoretical analysis demonstrates that their algorithm is effective in preserving the structural and parametric characteristics of the original networks. By providing a quantitative approach to merging networks, their work enhances the accuracy and reliability of the resulting merged network.
Gross et al. [17] propose an analytical threshold for combining Bayesian networks. Their method involves the generation of multiple approximate structures, and then selecting a representative structure based on the occurrence frequency of dominant directed edges between nodes. They analytically deduce an appropriate decision threshold using an adapted one-dimensional random walk. Experimental results validate the effectiveness of their approach in capturing associations among nodes and achieving better prediction performance. Their work contributes to the field by providing an analytical framework for merging networks, improving the efficiency and accuracy of the process.
The proposed algorithm for merging Bayesian networks presented in this research differs from the previously discussed approaches in several key aspects. While Del Sagrado and Moral’s qualitative method, Feng, Zhang, and Liao’s scoring-based algorithm, and Jiang, Leong, and Kim-Leng’s framework-based approach focus on preserving the structural and parametric characteristics of the original networks, the proposed algorithm prioritizes improving the accuracy of the merged network while considering the quality of the data. It can handle both singly and multiply connected networks, without assuming the existence of cliques or trees in the original networks. By incorporating expert knowledge and data information, the algorithm aims to create a merged network that accurately represents the relationships between variables.
In addition to merging Bayesian networks, there are also other techniques for combining probabilistic models. One such approach is ensemble learning, which combines multiple models to improve the accuracy of predictions [18]. Ensemble learning is a technique for combining multiple models to improve the accuracy and robustness of predictions [19,20]. It involves training multiple models independently or sequentially and then aggregating their predictions to obtain a final prediction. In contrast, the proposed algorithm for merging Bayesian networks combines two existing networks into a merged network that preserves the conditional independence relations among variables while taking into account the quality of the data. It is specifically designed for merging Bayesian networks and is focused on improving the accuracy of the merged network rather than simplifying the network structure. In summary, while both ensemble learning and the proposed algorithm for merging Bayesian networks are techniques for combining probabilistic models to improve accuracy, they differ in their approach and focus. Ensemble learning combines multiple models, which can be of different types or trained on different datasets, to improve prediction accuracy, whereas the proposed algorithm combines two existing Bayesian networks with a fixed structure to create a more accurate and effective merged network.
The proposed algorithm, which focuses on merging Bayesian networks, exhibits certain resemblances with Greedy Equivalence Search (GES), a widely used algorithm for learning the structure of a Bayesian network [21,22]. The algorithm iteratively builds a network by adding and removing edges while maintaining a partially directed acyclic graph that represents the Markov equivalence class of the true graph. GES starts with an empty network and uses a score-based approach to identify the next edge to add or remove. Specifically, it considers all possible edge additions and removals and chooses the one that leads to the greatest increase in the network score. The algorithm continues until no further improvements can be made. GES is known for its efficiency and ability to handle large datasets, although it may not always identify the true network structure [21].
The proposed algorithm shares some similarities with GES, such as its iterative process and use of a score-based approach. However, there are several key differences. First, our algorithm prioritizes the selection of nodes based on their potential to improve the network score, whereas GES considers all possible edge additions and removals at each iteration. Second, our algorithm includes a cycle detection step that allows it to avoid adding edges that would create cycles in the network, which is not explicitly addressed in GES. Third, the proposed algorithm focuses primarily on merging Bayesian networks, while GES is focused on structure creation.
Finally, our algorithm includes a step for manually computing conditional probability functions when the input networks do not provide a suitable function, whereas GES relies solely on the input network structures and functions. This is particularly useful when dealing with incomplete or noisy data, where it may be necessary to manually compute probabilities or combine information from multiple sources. Despite these differences, both algorithms aim to learn the structure of a Bayesian network by iteratively adjusting the network based on a score-based approach. While GES is a well-established and widely used algorithm for learning the structure of Bayesian networks, our proposed algorithm focuses primarily on merging Bayesian networks and may provide an alternative approach for integrating and modifying existing Bayesian network structures in certain contexts.
2. Materials and Methods
In this section, we will explore the Merging Algorithm for combining two Bayesian networks into a single, more accurate network. The section covers the following topics:
- Mathematical description of the algorithm;
- Solutions to issues related to cycles and CPT computation;
- Description of the node evaluation method used for algorithm evaluation.
2.1. Evaluation Method
In order to evaluate the quality of the Bayesian networks and determine the scores of the nodes, we employ an evaluation method based on the prediction error. Let y be the output variable, and let denote the set of parent variables of y.
For a given data record n, let be the observed value of y, and let be the predicted value of Y based on the input network and the observed values of its parents. The prediction error for the n-th data record is then defined as the absolute difference between the observed and predicted values:
The prediction error for the entire dataset is then defined as the sum of the prediction errors for all data records:
where N is the number of data records.
The node scores are derived from the prediction error, where a smaller prediction error indicates higher prediction accuracy and a better fit to the observed data. This scoring criterion ensures that the algorithm prioritizes nodes that contribute to more accurate predictions by considering smaller prediction errors as better evaluations.
It is important to note that the scores in and (see Section 2.2.1), corresponding to the two input networks, are calculated using the same evaluation method based on the prediction error. This consistency allows for a fair and consistent comparison between the nodes from both networks.
The choice of the scoring method can have an impact on the algorithm proceedings and the resulting solution. The algorithm itself is not directly affected by the choice of the scoring method. Instead, it operates based on the numerical scores derived from the scoring method, in this case prediction error. Different scoring criteria or evaluation methods may lead to different outcomes in terms of node selection and merging decisions. However, it is important to note that the algorithm itself is not inherently dependent on the specific evaluation method used for the nodes. Nonetheless, when applying the algorithm to different datasets or scenarios, it is crucial to carefully consider the scoring method and its implications.
2.2. Algorithm
The Merging Algorithm requires the following inputs [23]:
- Two Bayesian networks, each containing a structure and conditional probability tables assigned to each node.
- Score values for all nodes in the networks, obtained using a chosen score method.
- A dataset that corresponds to the nodes in the Bayesian network structure.
Before describing the Merging Algorithm, there are a few remarks related to the algorithm that we would like to mention:
- The issue of conditional probability tables (CPTs) will not be covered in the algorithm description to avoid unnecessary complexity. They will be addressed in a separate section.
- The dataset is not needed for the algorithm, as it is only necessary for node score, CPT counting, and Bayesian network evaluation.
- The algorithm does not depend on the chosen node score method, as long as the lower the value of the node score, the better the dataset fits on that node.
- Throughout the algorithm, the input networks will be referred to as “first” and “second”, while the resulting network will be referred to as “final”.
- The final network is initially empty, and nodes and edges are added during the algorithm’s execution.
In terms of computational efficiency, the proposed algorithm for constructing the Bayesian network demonstrates favorable performance. The algorithm itself is designed to be efficient and generally completes within seconds, regardless of the size of the dataset. However, it is important to note that the evaluation of node scores, which involves comparing and calculating the evaluation values for each node, could be a time-consuming operation. The time required for evaluating the nodes may vary depending on the complexity of the network structure and the number of nodes involved. Nevertheless, the overall computational time remains relatively quick. To facilitate the application of the algorithm, an R package was developed, providing users with a tool for Bayesian network construction and analysis.
2.2.1. Algorithm Inputs
The input dataset for the Merging Algorithm generally contains n variables or nodes . It is important to note that in the previous sections, the variables or nodes were denoted with capital letters. However, to avoid confusion and maintain consistency within the Merging Algorithm, we will now use smaller letters to represent the variables or nodes.
The input for the Merging Algorithm consists of two Bayesian networks represented by directed acyclic graphs (DAGs) and , where V is the set of nodes that corresponds to dataset X. Each node in V has a corresponding probability distribution in and in , where and denote the sets of parents of in and , respectively.
The set of edges for is denoted as , where , and denotes the edge from node to node in . Similarly, the set of edges for is denoted as , where , and denotes the edge from node to node in . The values of a and b correspond to the number of edges in and , respectively.
It is important to note that both input Bayesian networks must have the same set of nodes, but their sets of edges may differ. This means that the node set V is identical in both networks, but the probability distributions assigned to each node may differ. The goal of the Merging Algorithm is to combine the two input networks to obtain a new, merged network , where is a set of edges denoted as where c denotes the number of edges in .
For each node in both networks and , a local probability distribution is assigned such that , where denotes the set of parents of in input Bayesian network . The set of local probability distributions for is denoted as , and the set of local probability distributions for is denoted as . These local probability distributions describe the conditional probability distributions for each node in their respective networks.
In addition to defining the Bayesian network for each input network, we assign a score to each node in both networks. The score is a value that represents the importance of each node in the network. We denote the vector of scores for the first Bayesian network as , and it is defined as . Similarly, we denote the vector of scores for the second Bayesian network as , and it is defined as .
Finally, we define a vector that includes the absolute values of score differences computed from vectors and for each node in . This vector is defined as .
Additionally, we introduce an empty set to store symmetric nodes.
The Merging Algorithm outputs the Final Bayesian Network, which contains both the structure and the conditional probability functions. Before the algorithm begins, the Final Bayesian Network is initialized as an empty set of nodes, edges, and conditional probability functions denoted as , , and , respectively. During the algorithm, the sets in the Final Bayesian Network will be populated with nodes, edges, and conditional probability functions.
2.3. Mathematical Description
The algorithm description presented in this section is based on the dissertation thesis of the author [23]. It will be presented as a series of sequential steps, where the algorithm moves from one step to the next in the sequence, unless explicitly stated.
- For each node x in the input dataset :
- (a)
- Retrieve the set of parent nodes of node x in the first input network, denoted as .
- (b)
- Retrieve the set of parent nodes of node x in the second input network, denoted as .
- (c)
- If the sets of parents are equal:
- Retrieve the conditional probability table of node x in the first input network, denoted as .
- Retrieve the conditional probability table of node x in the second input network, denoted as .
- If the conditional probability tables are equal , add node x to the set of symmetric nodes .
- (d)
- If the sets of parents are not equal, move on to the next node.
- Add Symmetric Nodes to Final Sets.
- (a)
- For each node x in the set of symmetric nodes :
- Add the selected node x and its parents to the final node set : .
- Add the edges between the parents and node x to the final edge set : , where represents the edge from node to node in . This way, we are selecting edges from where the target node is the node x. The index k is not necessary in this context.
- Add the conditional probability table of node x to the final set of conditional probability tables : .
- Choose a node that was not already chosen from X.In the first step of the Merging Algorithm, a node is chosen from the input dataset X based on the difference between node scores. The node with the highest score difference is selected, and this node will not be selected again. Mathematically, the index with the highest value from the vector of absolute score differences, S, is found using the argmax function, and this index is stored in the variable i. The selected node is denoted as , and its score is set to zero to avoid being selected again in the future. The first step can be summarized by the following equations:where represents the selected node from the input dataset.
- Choose input Bayesian Network. The second step is to choose an input Bayesian network. This is determined by comparing the score values in the corresponding score vectors, and . Specifically, we check whether the score of the selected node in is greater than the score in (i.e., whether ). If this is the case, we choose as the input network for the current step. Otherwise, we choose as the input network. We denote the index of the chosen input network as j, which is defined as follows:Once the input network has been selected, we can proceed to the next step of the algorithm.
- Add the selected node into Final Network.In the third step of the algorithm, we check if the selected node is already present in the final node set . This is done by introducing the variable , which is set to 0 if is already present in and 1 otherwise. Mathematically,This variable will be useful in later steps of the algorithm.If the variable is equal to 1, we add the selected node to the final node set , i.e., . Otherwise, nothing happens, i.e., remains the same.
- Search the input edges of the selected node .To summarize, in step 4, we are searching for edges in the input Bayesian network that are directed towards the selected node . We accomplish this by iterating over all the edges in the set for the selected input network (indexed by j), and checking if the target node of each edge is equal to the selected node . The edges that meet this condition are saved into the set :The mathematical notation for this step, as given in Equation (8), specifies the set of edges in such that the target node index t is equal to the index i of the selected node . The variable k iterates over all edges in , while s iterates over all possible source nodes in the node set . Finally, the condition ensures that the edges we consider are only from the input network we have chosen.
- Find parents of the selected node .We have already identified the edges leading to the selected node in the set H. The goal of this step is to find the parents of the selected node .Mathematically, we create a new set of nodes that will include all the parents of the selected node , regardless of whether they are already in the final node set . The set is defined as follows:This notation goes through all nodes in the set X and selects those that satisfy the condition that there exists an edge in the set H where the index of the source node s is equal to the index p of the node in the set X. The relevant nodes are then saved to the set .
- Algorithm branching based on the value of the variable.The variable was introduced in point 5 in order to determine whether the selected node is already present in the final node set . Depending on its value, the algorithm will branch into two paths:
- If , it means that the selected node is already present in the final node set from previous iterations. In this case, we can proceed to point 9, keeping in mind that adding this node may create a cycle.
- If , it means that the selected node has already been added to the final node set in this iteration. Therefore, we can proceed to point 12. It is important to note that no cycle can occur in this case.
The branching of the algorithm is based on this simple principle: If the selected node is already in the final node set , then no cycle can occur, so we can proceed to the next step. Otherwise, we need to be careful not to introduce a cycle by adding the node to the final set, and so we proceed to a different path in the algorithm. - Find parents of the selected node present in the set .In this step, we are in the branch where the selected node is already present in the final node set . Therefore, we need to determine whether there are any parents of already in the set . To achieve this, we take the intersection of sets and P, where is the set of parents of the selected node . We denote the resulting set by T:If T is empty, it means that no parents of are in the final node set , and therefore a cycle cannot be created. In this case, the algorithm continues with point 12. Otherwise, it continues with point 10. We can express this mathematically as
- Find cycle.Unfortunately, we now risk that by adding the selected node with its parent links, we will cause a cycle in the final network. We will therefore prepare a set U of all relevant edges in which we will search for the cycle. It will consist of the set of edges of the final network and the set of edges between the selected node and its parents H. Mathematically written, we haveWe then apply a cycle search algorithm to this set.Detecting cycles in directed graphs is a well-known problem in graph theory, and there are various algorithms to accomplish this task. However, discussing these algorithms is outside the scope of this particular algorithm. For completeness, we reference a well-known algorithm for cycle detection in directed graphs by Tarjan [24].All we need here is information on whether the set U contains a cycle. We introduce the auxiliary variable cycle. Its value will depend on this information as follows:
- New setup while the same selected node is .We have reached a point where we cannot add the edges between the selected node and its parents due to the cycle in the final network.If this is the first time the selected node is being processed in the current iteration, we can try selecting the other input Bayesian network even though the selected node has a worse score in it. In this case, we change the value of the variable j as follows:We also need to clear all the temporary sets, set the variable to false (since the selected node is already present in the set ), and continue with point 6:If, however, this is the second time the selected node is being processed in the current iteration, and there is still a cycle in the final network, the algorithm will leave the node as it is. This means that it remains in the final set of nodes , and the algorithm continues at point 14.Note that searching for cycles in oriented graphs is a separate topic in graph theory, and we will not delve into it here. For more information, refer to [24].Regrettably, this approach could result in the final network being no better than the input networks. Additional information on this matter can be found in a separate section (Section 2.5).
- Add missing parents into the final node set .At this point, we will add the missing parents to the final node set . We have the parents of the selected node available in the set P and we just need to unite with the final node set .This approach also avoids problems with the presence of a parent in both sets P and .
- Add edges into the final edge set .We will now do the same with the relevant edges (i.e. edges leading to the selected node ) of the selected node stored in the set H. Again, we will use the union of this set and the final edge set .
- Assignment of the local probability function.So far, all points of the algorithm have solved the structure of the network. Now, it is time to assign a local probability function to the selected node .This is based on the previous point of the algorithm:
- The previous point is point 13.In this case, the selected node and its input edges correspond to the node and the input edges from the selected Bayesian network. Thus, the conditional probability function from the selected Bayesian network is simply added into the final set of conditional probability functions :
- The previous point is point 11.In this situation, we do not have a chance to assign a conditional probability function directly from the input Bayesian networks. Section 2.6 deals with the issue of calculating conditional probability functions of a selected node when it is not possible to take any of the input networks.For this description, it is enough to somehow obtain the conditional probability function and then assign it to the selected node . This function is then added into the final set of conditional probability functions :
After the selected node and its parents, as well as the edges between them, have been added to the final network, if possible, we perform the setup for the next iteration. This involves setting all variables and auxiliary sets to their default values:If the vector of score value differences S includes only zero values,then the algorithm ends. Otherwise, the algorithm proceeds to point 3 to select the next node.
2.4. Flowchart of Algorithm
The proposed algorithm for merging two Bayesian networks in this study follows a systematic and structured approach. A flowchart representing the key steps of the algorithm is presented in Figure 1. This flowchart provides a visual representation of the sequential process employed to merge the networks.
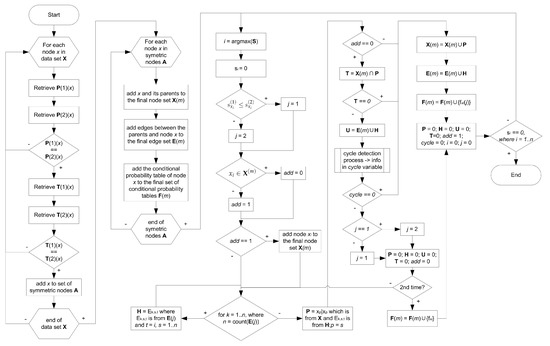
Figure 1.
Flowchart of the proposed merging algorithm.
2.5. Dealing with Cycles
The proposed algorithm includes a cycle detection step that allows it to avoid adding edges that would create cycles in the network. Specifically, the algorithm checks if adding an edge between the parents of the selected node and the selected node would create a cycle in the final network (point 11). If so, the algorithm does not add the edge and continues without updating the final network.
While this approach is effective in preventing cycles, it may result in the final network being suboptimal. To address this, one possible solution is to consider alternative edge configurations that would not create cycles. This can be done by computing the node score for different combinations of edges and selecting the configuration that results in the highest score.
Another option is to explore methods for breaking cycles after they have been created. One such method is to convert the cyclic graph into a DAG by removing one or more edges. This can be done using a variety of techniques, such as the Meek rules [25] or the Fast Causal Inference (FCI) algorithm [10]. However, it is important to note that these methods may not always lead to a unique DAG and may require additional heuristics or expert knowledge to resolve ambiguities.
Additionally, the article in [26] suggests another approach for handling cycles in Bayesian networks. It discusses embedding cyclic structures within acyclic Bayesian networks, allowing for the utilization of the factorization property and informative priors on network structure. In the context of linear Gaussian models, the cyclic structures are treated as multivariate nodes. To perform inference, a Markov Chain Monte Carlo algorithm is employed, enabling exploration of the posterior distribution on the space of graphs. By adopting this approach, the article presents a framework that overcomes the limitations of acyclic Bayesian networks in representing cyclic structures, thus facilitating the modeling and analysis of networks with enhanced flexibility and accuracy.
Another approach to handling cycles in Bayesian networks involves the introduction of latent (hidden) variables [27]. These latent variables act as mediators or moderators within the network, assisting in breaking the cycles. By representing unobserved factors that influence the observed variables, latent variables provide a means to model complex dependencies without violating the acyclic property of Bayesian networks. This approach allows for capturing intricate relationships and accounting for underlying factors that may not be directly observable.
In summary, while the proposed algorithm includes a cycle detection step to prevent cycles from being created in the final network, there are still opportunities to explore alternative edge configurations and methods for breaking cycles in order to improve the overall performance of the algorithm.
2.6. Filling in Missing Conditional Probability Tables
When merging Bayesian networks, it is possible that some CPTs may not be available in the input networks. This can occur if a node has a different set of parents in different input networks. In this case, the proposed algorithm assigns a new CPT to the node based on a default method or a user-defined function. However, there are situations where these methods cannot be used, such as when there are not enough data to estimate the parameters of the CPT.
One possible solution to this problem is to use the Expectation Maximization (EM) algorithm [28]. The EM algorithm is an iterative approach that can be used to estimate the parameters of a model when some data are missing or incomplete. In the context of Bayesian networks, the EM algorithm can be used to estimate the missing parameters of a CPT based on the available data.
Another possible solution is to use a maximum likelihood estimator (MLE) to estimate the missing parameters [29]. The MLE is a statistical method that can be used to estimate the parameters of a model based on the available data. In the context of Bayesian networks, the MLE can be used to estimate the missing parameters of a CPT based on the available data.
Both the EM algorithm and the MLE require a sufficient amount of data to estimate the missing parameters. In cases where there are not enough data, it may be necessary to use prior knowledge or expert opinion to assign values to the missing parameters.
The choice of method for filling in missing CPTs will depend on the specific context and available data. In general, the EM algorithm and the MLE are effective methods for estimating missing parameters in Bayesian networks and may be useful tools for addressing this problem in the context of merging networks.
3. Results
In this section, we present the results of applying the proposed algorithm to merge two Bayesian networks created by an algorithm and an expert. We conducted our experiments on two datasets: traffic accident data in Prague and railway crossing accident data in the Czech Republic.
For each dataset, we begin by describing the data used in our experiments and provide a detailed description of the two input Bayesian networks. To assess the quality of the input nodes in the network, we used a prediction error metric previously discussed in detail in Section 2.1. We applied this metric to evaluate the two input networks, one created by an expert and the other by a Hill-Climbing algorithm.
To ensure a comprehensive analysis, we partitioned the dataset into a training set and a validation set. The training set accounted for two-thirds of the data and was utilized to assess the performance of the merged network and select the nodes to be incorporated. The results obtained from evaluating the training set will be presented, shedding light on the merged network’s performance based on a significant portion of the data.
Furthermore, we will present the results of the validation set evaluation for each experiment. The validation set encompasses the remaining one-third of the data and enables us to evaluate the generalization and performance of the merged network on unseen data. This evaluation provides valuable insights into the effectiveness of the merged network in real-world scenarios and its ability to perform well beyond the training data.
Moreover, it is important to address the potential concern regarding the term “training dataset” used in this context. While the conventional definition of “training data” in statistical learning refers to labeled data used for training machine learning models, we have adapted the terminology in our work. In our context, “training dataset” specifically refers to the portion of the original dataset utilized for calculating node evaluations and subsequent evaluation processes.
Finally, we evaluate the overall performance of the merged network using the same evaluation method: prediction error. We demonstrate that the final network achieves the best evaluation value in comparison with the input networks, highlighting the effectiveness of the proposed algorithm in combining Bayesian networks created by different methods and experts. The results also showcase the algorithm’s ability to improve the accuracy of the resulting network for both the traffic accident data and the railway crossing accident data.
3.1. Example S1—Traffic Accident Data
This example is based on the dataset which is in the Supplementary Material-Example S1.
3.1.1. Data Description
For this example, we have traffic accident data from 2012 provided by City Hall in Prague. The data contain 14 variables related to the weather at the time of an accident, the place where the accident happened, the accident itself, and damage-related variables. Based on the numerical value of the accident severity variable, which is calculated using a formula based on the number of minor and major injuries, deaths, and material damage connected with the accident, we divide it into three intervals representing a light accident, a medium accident, and a serious accident [30]. The dataset contains 3894 records.
The variables in the dataset include the type of accident, specific places and objects in the traffic accident area, road division, alcohol presence, location of the accident, type of collision of moving vehicles, state of the surface, type of solid barrier, wind conditions, location of the accident (other division), layout, main causes of an accident, visibility, number of involved vehicles, and accident severity. Each of these variables has several realizations (between two and five).
3.1.2. Description of Input Networks
The Bayesian network created by the expert consists of 18 variables grouped into five categories: main variables, driver- and weather-related variables, location-related variables, other variables, and the output variable of accident severity. The main variables are the main causes of the accident, the type of accident, and the type of collision. The driver- and weather-related variables include alcohol present, state of surface, visibility, and wind conditions. The location-related variables include road division, location of accident, location of crossing, specific places nearby, and layout. The other variables are the number of participants and type of barrier.
The main causes of the accident impact the type of accident, which in turn impacts the type of collision. All of these main variables directly impact the output variable of accident severity. The driver- and weather-related variables are connected to the main causes of the accident. The location-related variables begin with road division, which impacts the location of the accident and the location of the crossing. The location of the accident and specific places nearby impact the type of collision. The number of participants and type of barrier are not directly related to the output variable but are influenced by the type of collision.
The second Bayesian network was learnt using the Hill-Climbing algorithm, a popular and widely used method for learning the structure of Bayesian networks. The input to the algorithm was only the traffic accident data described in Section 3.1.1. One condition was set for this algorithm, which was that the accident severity node must be an output node and have no children.
Therefore, we now have two Bayesian networks created specifically for this task, one by an expert and the other by an algorithm. We will now proceed with the evaluation of input network followed by the use the proposed merge algorithm to combine these two networks and evaluate its performance.
3.1.3. Node Evaluation Results
We applied the prediction error metric described in the previous subsection to evaluate the node scores of both input networks. Table 1 shows the prediction error values for the nodes in the expert and algorithm network in the second and third columns, respectively.

Table 1.
Evaluation scores of the expert, algorithm, and the merged network. The “Selected network” column indicates the input network (Exp for expert, Alg for algorithm, and Sym for symmetrical nodes that are same in both networks) that the node was selected from in the final merged network.
The evaluation scores in Table 1 show that the algorithm network had better predictions for most of the variables, with a total evaluation score of 7132.95 compared to the expert network’s score of 8542.93. Notably, the algorithm network had substantially better predictions for the variables of wind conditions and road division, with scores of 144.85 and 608.61, respectively, compared to the expert network’s scores of 248.05 and 1028.11. These results suggest that the algorithm was able to identify relationships in the data that were not accounted for in the expert network. However, it is important to note that the expert network did have better predictions for some variables, such as location of the accident and accident severity.
3.1.4. Final (Merged) Network
Based on the evaluation results, the merged network shows an improvement in performance compared to the input networks. The merged network includes nodes selected from both the expert and algorithm networks, with the output variable Accident Severity chosen from the expert network. This means that substantial information from the expert network is included in the merged network. However, it is important to note that the node Location Accident or Location intersection, which had better evaluation in the expert network than in the algorithm network, could not be selected due to the risk of creating a cycle in the merged network. Overall, the merged network provides a more comprehensive and accurate representation of the relationships among variables in the dataset.
3.1.5. Overall Network Evaluation
In this subsection, we will present an evaluation of the final network created by merging the expert and algorithm networks according to the proposed algorithm. To assess the performance of the final network, we have calculated the evaluation scores of each node in the expert and algorithm networks as well as in the merged network. These results are based on the evaluation of the training dataset. We will discuss the differences between the selected nodes and the ranking of the nodes based on their evaluation scores. Additionally, we will analyze the overall performance of the merged network and compare it to the individual input networks.
Based on the table and the proposed algorithm, the merged network was constructed by selecting nodes from the input networks with the highest evaluation scores and the greatest difference in evaluation values between the expert and algorithm networks. The nodes were then ranked and selected for the final network based on this order.
The “Alcohol present” node was added to the network at the beginning using symmetry, which means it was included in the merged network without undergoing the node selection process based on evaluation scores and differences between the expert and algorithm networks.
The second node selected was Layout, as it had the highest difference in evaluation value between the expert and algorithm networks. It was selected from the algorithm network due to its lower evaluation value.
The next node selected was Type of collision, as it had the second-highest difference in evaluation value and could not be selected from the input networks due to cycles. It was selected from the expert network.
The remaining nodes were selected from the algorithm network, with the exception of Location accident, which was selected from the expert network due to its higher evaluation value.
Two nodes, Type of accident and Specific places nearby, could not be selected from the input networks due to cycles and were left as they were in the final network.
Overall, the merged network showed better results than the individual input networks, indicating that combining the knowledge from multiple sources can lead to more accurate predictions in accident analysis.
3.1.6. Validation Results
Table 2 presents the validation scores of the expert network, algorithm network, and the final merged network. Each row corresponds to a specific node in the networks, while the columns represent the evaluation scores for each network.

Table 2.
Validation scores of the expert, algorithm, and final network for Example S1.
The merged network has a lower evaluation score (2272.93) compared to both the expert network (2731.96) and the algorithm network (2340.42). This indicates that the merged network performs better in terms of prediction accuracy and has a smaller prediction error.
It is worth noting that the node “Location accident” has a higher evaluation score in the merged network (91.20) compared to the algorithm network (91.14), but a lower score than the expert network (79.98). This is due to the consideration of potential cyclic dependencies in the merged network, which led to the exclusion of the node with a better evaluation in the expert network. Despite this limitation, the merged network still provides an improved overall performance.
3.2. Example S2—Railway Crossing Accident Data
This example is based on the dataset which is in the Supplementary Material—Example S2.
3.2.1. Data Description
The dataset used for railway crossing accidents consists of records of all train accidents reported by the police in the Czech Republic from January 2013 to December 2021. Each accident record within the dataset contains 12 parameters. These parameters encompass details about the accident itself, such as the number of individuals killed and injured, material damage incurred, and the cause of the accident. Additionally, information pertaining to the railway line, including electrification, gauge, and the number of tracks, as well as details about the road, are also included.
Furthermore, the dataset incorporates an output parameter that signifies the severity of the accident. This severity is categorized into four levels: no injury, moderate, serious, and fatal accidents. The assignment of severity levels is based on the number of individuals injured or killed in a particular accident.
Overall, the dataset consists of a total of 1378 records, each capturing crucial information about railway crossing accidents in the Czech Republic during the specified time period.
3.2.2. Description of Input Networks
Another node in this network, Cause, has no parents and influences the Railway electrification node. The Railway electrification node, in turn, impacts three other nodes: Railway tracks, Region, and Material damage over 400,000 CZK. The Region node impacts the Road class node, while the Material damage over 400,000 CZK node influences the Severe injury node. The Severe injury node further impacts the Accident severity output parameter. Additionally, the Accident severity node influences two nodes: Killed and Light injury.
On the other hand, the network created by the expert begins with the Season node, which has no parents. It influences the Cause node, which subsequently impacts three other nodes: Railway electrification, Road class, and Accident severity. The Railway electrification node impacts four nodes: Railway gauge, Railway tracks, Material damage over 400,000 CZK, and Accident severity. The Road class node affects the Accident severity and Region nodes. The Region node, in turn, is influenced by two other nodes: Railway gauge and Railway tracks. Lastly, the Accident severity node impacts a total of four nodes: Material damage over 400,000 CZK, Killed, Severe injury, and Light injury.
3.2.3. Node Evaluation Results
We utilized the previously mentioned prediction error metric to assess the node scores of both input networks. The second and third columns of Table 3 present the prediction error values for the nodes in the expert and algorithm networks, respectively.

Table 3.
Evaluation scores of the expert, algorithm, and the merged network. The “Selected network” column indicates the input network (Exp for expert, Alg for algorithm, Sym for symmetrical nodes that are same in both networks) that the node was selected from in the final merged network.
The assessment scores in Table 3 indicate that the expert network outperformed the algorithm network in terms of predictions for the majority of variables. The expert network achieved a total evaluation score of 2974.08, whereas the algorithm network scored 3097.11. Notably, the expert network demonstrated significantly superior predictions for the variables related to Severe injury, with a score of 103.92, compared to the algorithm network’s score of 252.20. These findings suggest that the expert was capable of identifying relationships in the data that were overlooked by the algorithm network. Nevertheless, it is important to acknowledge that the algorithm network did yield better predictions for certain variables, such as Road class or Accident Severity.
3.2.4. Final (Merged) Network
Upon evaluating the prediction error of both networks, the algorithmic network exhibited a slightly inferior overall evaluation score of 3097.11, whereas the expert network achieved a score of 2974.08. It is worth mentioning that five nodes had identical scores in both networks, indicating that these nodes had the same parents in both networks. Among the remaining seven nodes, the expert network outperformed the algorithmic network for five nodes, while the algorithmic network performed better for two nodes. Notably, the connected network, which combines the strengths of both networks, achieved the best score of 2954.60, affirming the effectiveness of the algorithm.
3.2.5. Overall Network Evaluation
The evaluation scores provided in Table 3 offer detailed insights into the performance of the expert and algorithmic networks for each node. The expert network showcased superior performance for several nodes, including Cause, Material damage over 400,000 CZK, Railway gauge, and Severe injury. These results suggest that the expert network, leveraging its domain-specific knowledge and expertise, was able to capture the underlying relationships and make more accurate predictions for these variables.
On the other hand, the algorithmic network demonstrated a notable strength in predicting the Road class node. However, it is important to note that the algorithmic network’s higher score for the Region node does not indicate better evaluation. Instead, this selection might be attributed to the need to consider cycles in the network structure, despite the algorithmic network’s slightly higher evaluation score for the Region node.
It is worth mentioning that certain nodes, such as Killed, Light injury, Railway electrification, Railway tracks, and Season, obtained identical scores in both networks. This indicates that these nodes were symmetrical, sharing the same parents in both the expert and algorithmic networks.
The merged network, incorporating the strengths of both networks, attained the best overall evaluation score of 2954.60, showcasing the effectiveness of combining the expertise and algorithmic approaches. This suggests that the merging algorithm successfully leveraged the complementary strengths of the expert and algorithmic networks to enhance the predictive performance.
3.3. Validation Results
Based on the information provided in Table 4, it is evident that both the expert and algorithmic networks demonstrated strengths in predicting specific nodes. The expert network achieved a notable total validation score of 990.56, showcasing its strong predictive capabilities for nodes such as Cause, Killed, Light injury, Material damage over 400,000 CZK, Railway gauge, and Severe injury. These nodes exhibited lower evaluation scores, indicating superior performance by the expert network in predicting their values. On the other hand, the algorithmic network obtained a total validation score of 1031.21, highlighting its proficiency in predicting nodes such as Accident severity or Road class.

Table 4.
Validation scores of the expert, algorithm, and final network for Example S2.
The merging process effectively leveraged the strengths of both networks to create a merged network with an improved overall validation score. The merged network achieved a total validation score of 979.86, indicating its enhanced predictive performance compared to the individual networks. By combining the expertise of the expert network with the strengths of the algorithmic network, the merged network demonstrated the potential for enhanced accuracy in predicting various variables. This underscores the value of integrating expert knowledge and algorithmic approaches to optimize predictive modeling in the given domain.
4. Discussion
The proposed algorithm for merging Bayesian networks has demonstrated its ability to effectively combine knowledge from multiple sources, including networks created by both human experts and automated algorithms. By applying the algorithm to two datasets, we were able to create a final merged network that exhibited superior prediction accuracy compared to the individual input networks.
The evaluation results demonstrated that the merged networks achieved better predictions for most variables, highlighting the algorithm’s ability to identify relationships that are better evaluated from the input networks. By combining the deep domain knowledge and expertise of experts with the processing power and objectivity of algorithms, a more comprehensive and accurate analysis can be achieved. Experts contribute their valuable experience, intuition, and contextual understanding to identify relevant variables, interpret complex relationships, and provide qualitative insights that may not be readily available in the data. Algorithms, on the other hand, efficiently process large datasets, uncover hidden patterns, and minimize biases, enabling objective analysis. Leveraging the strengths of both experts and algorithms, a merged network is created using the proposed merging algorithm. This merged network integrates the best of both approaches, incorporating expert insights and algorithmic predictions, resulting in a powerful framework.
In the context of discussing the limitations of the proposed algorithm, two key challenges are identified: dealing with cycles and filling in missing CPTs. Regarding the handling of cycles, the algorithm incorporates a cycle detection step to prevent their creation in the final network. However, this cautious approach may lead to suboptimal results, as alternative edge configurations that could avoid cycles are not considered. To overcome this limitation, exploring different edge combinations and computing node scores to select the highest-scoring configuration could improve the algorithm’s performance. Additionally, methods such as the Meek rules or the Fast Causal Inference algorithm can be utilized to break cycles post-creation, although achieving a unique DAG may require additional heuristics or expert knowledge.
The second limitation pertains to missing CPTs when merging Bayesian networks. In situations where nodes have different sets of parents in the input networks, some CPTs may not be available. The proposed algorithm handles this by assigning new CPTs based on default methods or user-defined functions. Two potential solutions are discussed for this issue. First, the EM algorithm can be employed to estimate parameters iteratively based on the available data. Second, a maximum likelihood estimator can be utilized to estimate parameters using statistical methods. However, both approaches rely on having a sufficient amount of data, and when data are limited, incorporating prior knowledge or expert opinions becomes necessary for assigning values to the missing parameters.
The next limitation to consider in the proposed algorithm is the potential impact of the starting distance between the two input networks, G1 and G2. The starting distance, which refers to the initial dissimilarity or divergence between the networks, can influence the final merged network structure. In such cases, it becomes crucial to carefully select and preprocess the input networks to minimize the initial distance. Preprocessing steps, such as data normalization, can help reduce the initial dissimilarity and improve the algorithm’s convergence. Nevertheless, it is important to acknowledge that the starting distance between G1 and G2 can introduce a degree of uncertainty and potential bias in the merged network, which may impact the accuracy of the final results.
The other limitation of our study is that we have not explicitly analyzed the maximal difference in evaluation values between the expert networks and algorithmic networks. This information could provide valuable insights into the varying evaluations and weightings of influencing factors by the different sources. By understanding these differences, we could effectively address potential disparities and improve the reliability and accuracy of the merged network. The absence of this analysis is a limitation of our study, and future research should consider examining and incorporating these differences to gain a deeper understanding of potential sources of prediction errors and areas for algorithmic improvement.
Despite the aforementioned limitations, the evaluation results strongly support the effectiveness of the proposed algorithm in merging Bayesian networks. It showcases the algorithm’s ability to harness knowledge from multiple sources, resulting in an improved and more accurate final network.
5. Conclusions
In this study, we have presented an algorithm for merging Bayesian networks created by different sources, such as experts and algorithms, and demonstrated its effectiveness in improving the accuracy of accident analysis. By combining the knowledge from multiple sources, our algorithm has shown promising results in identifying relationships in the data that were not accounted for in the merged network.
One important finding of our research is the significant improvement in the accuracy of the merged network compared to the individual input networks. Through the integration of diverse knowledge sources, the merged network captures a broader range of factors and their relationships, leading to more comprehensive and accurate predictions in accident analysis. This highlights the potential of our algorithm to enhance prediction capabilities.
To provide a different example rather than the one presented in this article, let us consider the healthcare domain. In medical diagnosis, the merging of expert knowledge with algorithmic models can lead to more reliable and accurate predictions. The algorithm can capture subtle patterns and relationships that may not be apparent to individual experts, while the experts can provide contextual knowledge and interpretability to the resulting model. This combined approach can enhance diagnostic accuracy, support treatment decisions, and improve patient outcomes.
Regarding future research, there are two key areas to explore. First, the handling of cycles in the merged network and the creation of conditional probability tables (CPTs) could be investigated. This would involve exploring alternative methods for handling cycles, such as incorporating causal inference techniques or exploring different edge configurations. Additionally, exploring alternative approaches for creating CPTs, such as the EM algorithm or maximum likelihood estimation, could help improve the accuracy and reliability of the merged network.
Furthermore, conducting network comparisons with other methods, such as likelihood-based approaches and ROC analysis, would provide a comprehensive assessment of the performance of the merged network. This would allow for a more thorough understanding of the strengths and limitations of our algorithm compared to alternative techniques. Additionally, comparing our merging algorithm with ensemble learning methods, such as stacking, would provide further insights into the benefits and trade-offs of different ensemble approaches.
In addition, an important consideration for future research is the faithfulness of the merged network. Faithfulness refers to the property of the merged network accurately reflecting the conditional independence relationships present in the underlying data-generating process. While our algorithm aims to capture the dependencies between variables, ensuring the faithfulness of the merged network requires careful validation. Future studies could explore techniques for evaluating the faithfulness of the merged network, such as validating against domain knowledge and conducting statistical tests for conditional independence. Sensitivity analyses could also be conducted to assess the robustness of the merged network to different modeling assumptions.
In conclusion, our research highlights the potential of merging Bayesian networks as a powerful approach for combining expertise and algorithmic models. Through the integration of multiple knowledge sources, we can enhance the accuracy and comprehensiveness of predictions in various domains. By further exploring the handling of cycles and CPTs, conducting network comparisons, and evaluating the algorithm against ensemble methods, we can continue to improve the performance and applicability of our algorithm. We believe that our work opens new avenues for research and has practical implications in decision-making processes across different fields.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym15071461/s1, Example S1—Dataset: Traffic Accident Dataset provided by City Hall in Prague from the year 2012; File Name: supplementary_1example.csv; Example S2—Dataset: Traffic Accident on Railway Crossing, Exported from the portal of the Czech police, URL: http://nehody.policie.cz/, file name: supplementary_2example.csv.
Author Contributions
Conceptualization, M.V.; Methodology, Z.L. and M.Š.; Validation, M.V.; formal analysis, M.Š.; algorithm programming, M.V.; Writing—review and editing M.V and M.Š.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
The article was funded by internal resources of the Faculty of Transportation Sciences, Czech Technical University in Prague—Future Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data used in this article consist of traffic accident data from 2012 obtained from Prague, the Czech Republic. Due to the nature of the data and privacy regulations, the traffic accident dataset used in this research cannot be publicly published. However, the authors are committed to facilitating access to the data upon official request. Interested researchers can request access to the dataset by contacting the authors directly and following the required procedures. The data, including both the raw data and any prepared or processed versions, will be made available in a zip file accompanying the article during the submission process.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| CPT | Conditional Probability Table |
| DAG | Directed Acyclic Graph |
| EM | Expectation Maximization |
| FCI | Fast Causal Inference |
| GES | Greedy Equivalence Search |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MLE | Maximum Likelihood Estimator |
| PC (algorithm) | Peter and Clark (algorithm) |
References
- Glymour, M.; Pearl, J.; Jewell, N.P. Causal Inference in Statistics: A Primer; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Scanagatta, M.; Salmerón, A.; Stella, F. A survey on Bayesian network structure learning from data. Prog. Artif. Intell. 2019, 8, 425–439. [Google Scholar] [CrossRef]
- Kjærulff, U.B.; Madsen, A.L. Probabilistic Networks—An Introduction to Bayesian Networks and Influence Diagrams; Aalborg University: Aalborg, Denmark, 2005; pp. 10–31. [Google Scholar]
- Wasserman, L. All of Statistics: A Concise Course in Statistical Inference; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Darwiche, A. Modeling and Reasoning with Bayesian Networks; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, prediction, and search. In Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000; pp. 7–94. [Google Scholar]
- Chickering, D.M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 2003, 3, 507–554. [Google Scholar]
- Govender, I.H.; Sahlin, U.; O’Brien, G.C. Bayesian network applications for sustainable holistic water resources management: Modeling opportunities for South Africa. Risk Anal. 2022, 42, 1346–1364. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yazdi, M.; Huang, H.Z.; Huang, C.G.; Peng, W.; Nedjati, A.; Adesina, K.A. A fuzzy rough copula Bayesian network model for solving complex hospital service quality assessment. Complex Intell. Syst. 2023. [Google Scholar] [CrossRef] [PubMed]
- Del Sagrado, J.; Moral, S. Qualitative combination of Bayesian networks. Int. J. Intell. Syst. 2003, 18, 237–249. [Google Scholar] [CrossRef]
- Jiang, C.a.; Leong, T.Y.; Kim-Leng, P. PGMC: A framework for probabilistic graphical model combination. In Proceedings of the American Medical Informatics Association Annual Symposium, Washington, DC, USA, 22–26 October 2005; Volume 2005, p. 370. [Google Scholar]
- Feng, G.; Zhang, J.D.; Liao, S.S. A novel method for combining Bayesian networks, theoretical analysis, and its applications. Pattern Recognit. 2014, 47, 2057–2069. [Google Scholar] [CrossRef]
- Gross, T.J.; Bessani, M.; Junior, W.D.; Araújo, R.B.; Vale, F.A.C.; Maciel, C.D. An analytical threshold for combining bayesian networks. Knowl. Based Syst. 2019, 175, 36–49. [Google Scholar] [CrossRef]
- Hansen, L.; Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef]
- Opitz, D.W.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning: Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; pp. 1–34. [Google Scholar]
- Scutari, M.; Vitolo, C.; Tucker, A. Learning Bayesian networks from big data with greedy search: Computational complexity and efficient implementation. Stat. Comput. 2019, 29, 1095–1108. [Google Scholar] [CrossRef]
- Kareem, S.; Okur, M.C. Bayesian Network Structure Learning Using Hybrid Bee Optimization and Greedy Search; Çukurova University: Adana, Turkey, 2018. [Google Scholar]
- Vaniš, M. Optimization of Bayesian Networks and Their Prediction Properties. Ph.D. Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2021. [Google Scholar]
- Tarjan, R. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Meek, C. Causal inference and causal explanation with background knowledge. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; pp. 403–410. [Google Scholar]
- Wiecek, W.; Bois, F.Y.; Gayraud, G. Structure learning of Bayesian networks involving cyclic structures. arXiv 2019, arXiv:1906.04992. [Google Scholar]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Cengage Learning: Boston, MA, USA, 2021. [Google Scholar]
- Vaniš, M.; Urbaniec, K. Employing Bayesian Networks and conditional probability functions for determining dependences in road traffic accidents data. In Proceedings of the 2017 Smart City Symposium Prague (SCSP), Prague, Czech Republic, 26–27 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).