Security Analysis of Imperfect Gaussian Modulation Caused by Amplitude Modulator in Continuous–Variable Quantum Key Distribution
Abstract
1. Introduction
2. Non–Ideal Gaussian Modulation in CV–QKD System
2.1. The Realization Process of Gaussian Modulation
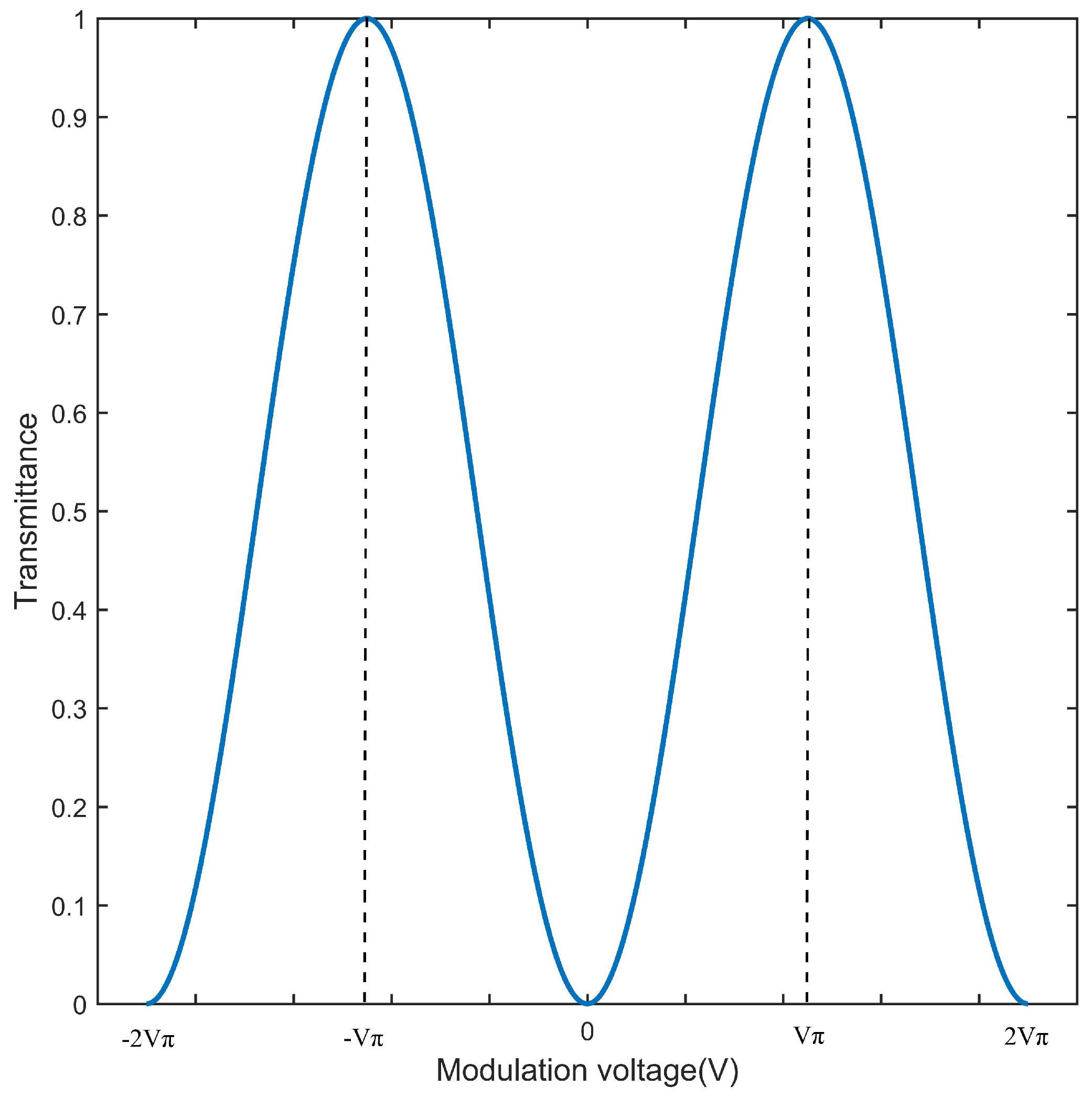
2.2. Non–Ideal Gaussian Modulation Caused by Amplitude Modulator Curve
3. Practical Security Analysis of Non–ideal Gaussian Modulation
3.1. Parameter Estimation under Non–ideal Gaussian Modulation
3.2. Calculation of Secret Key Rate
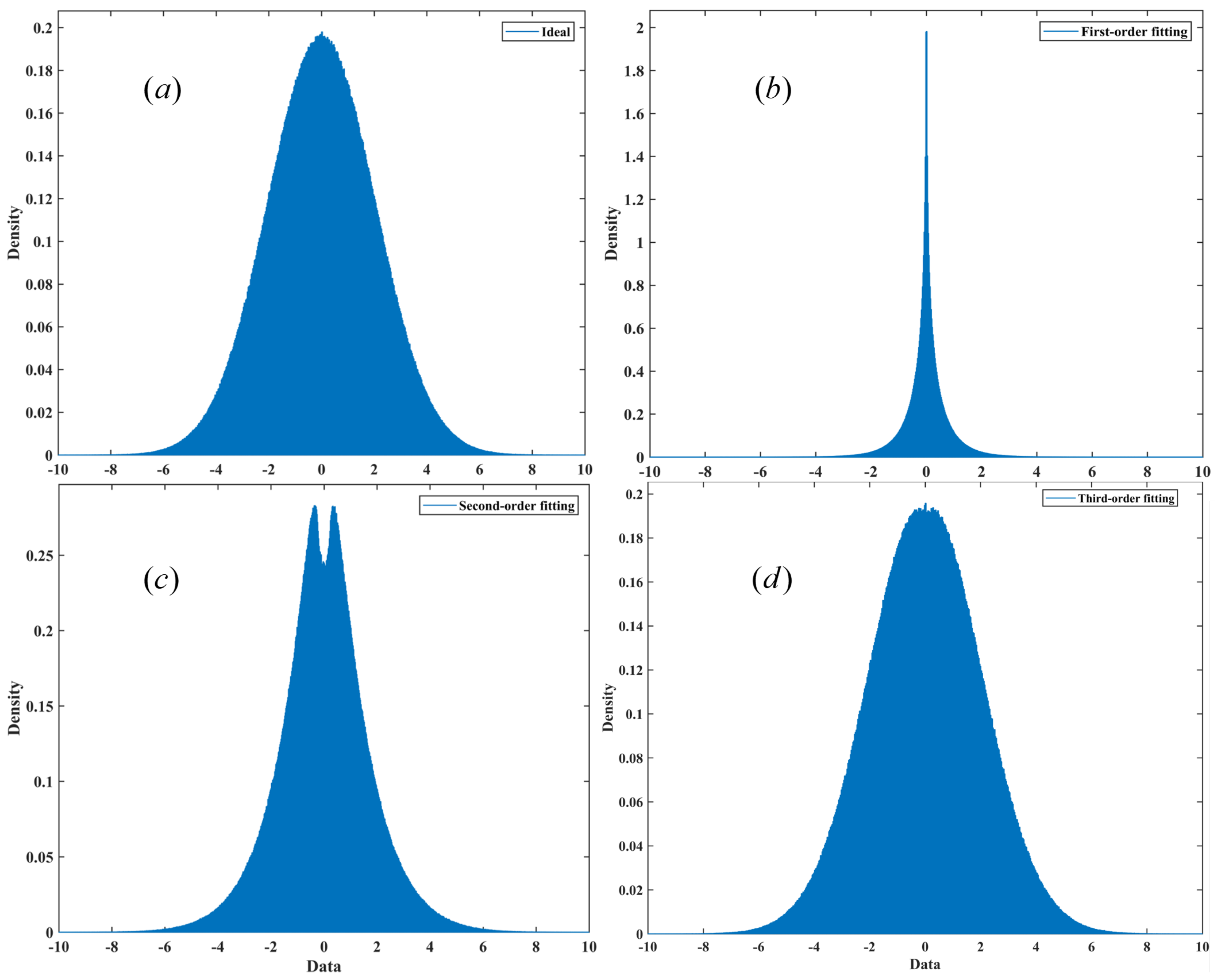
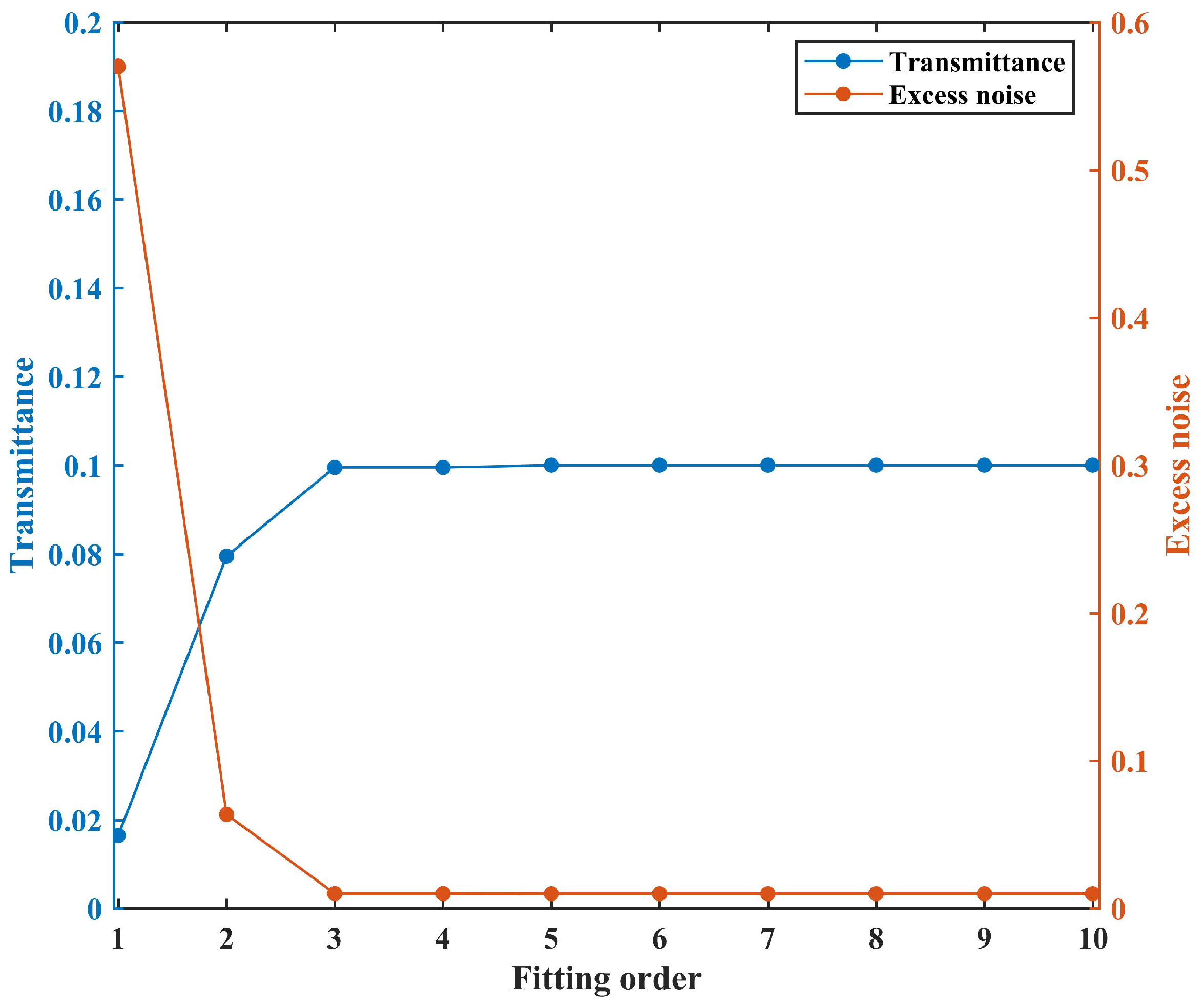
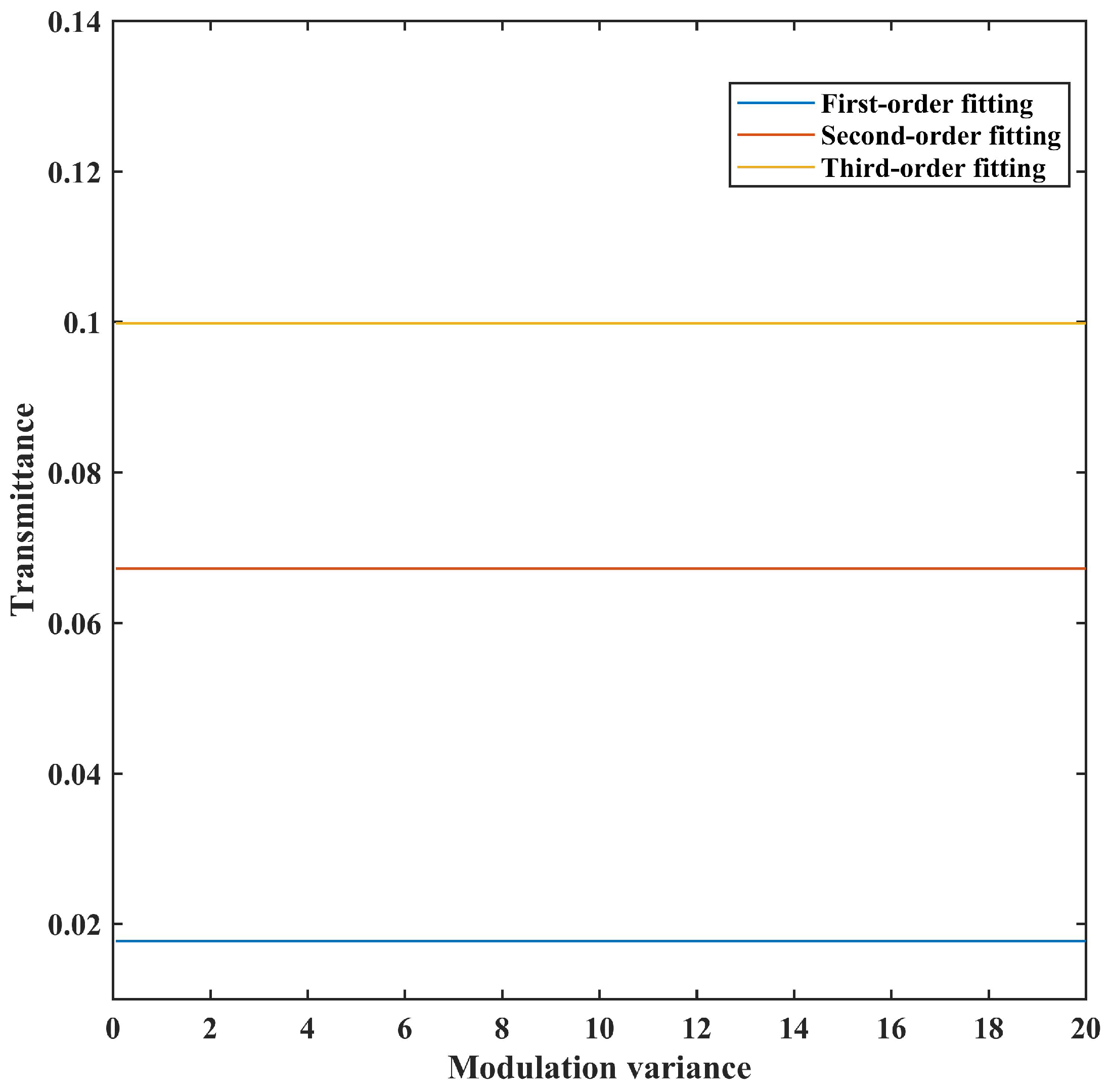
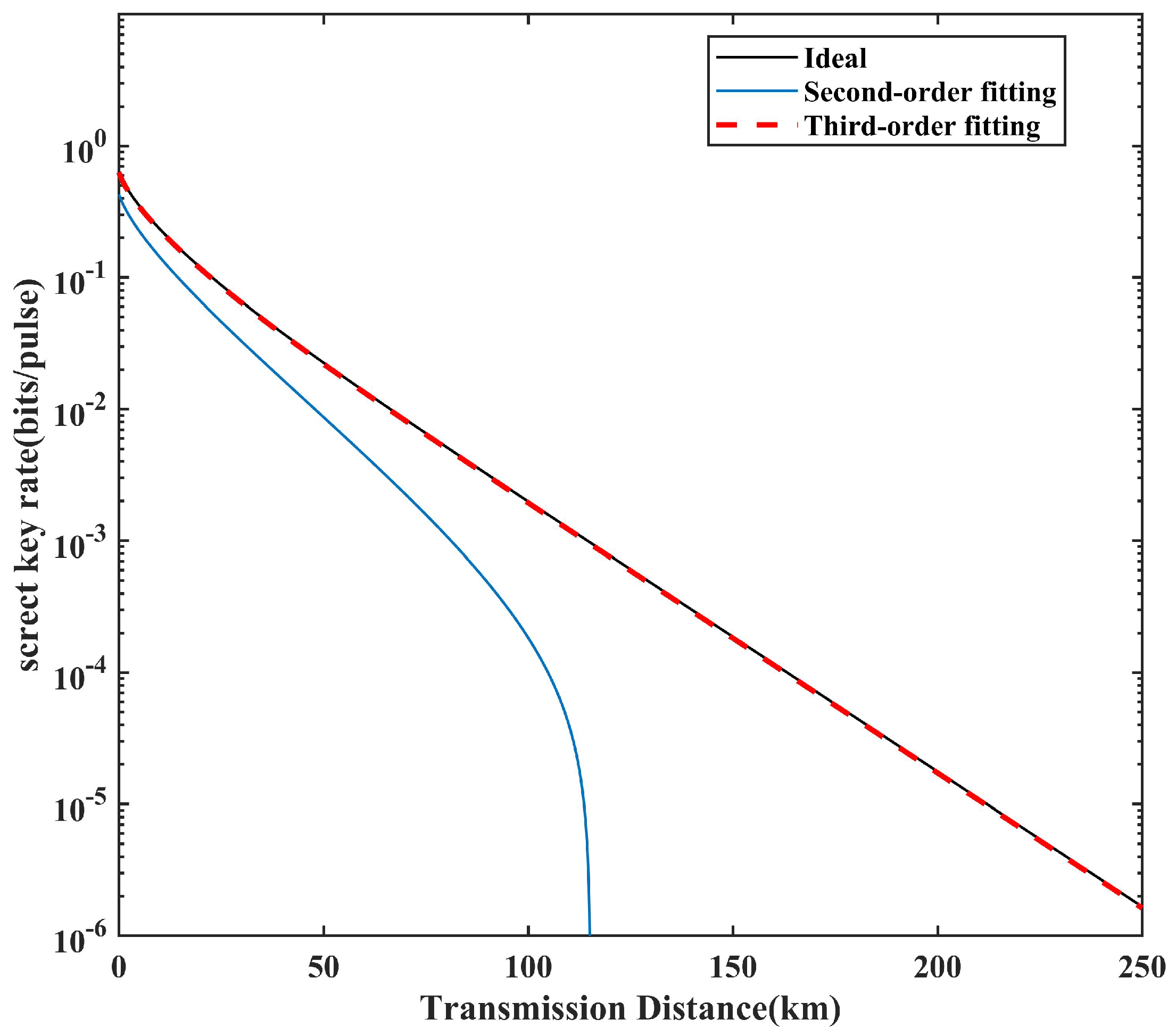
4. Simulation and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laudenbach, F.; Pacher, C.; Fung, C.H.F.; Poppe, A.; Peev, M.; Schrenk, B.; Hentschel, M.; Walther, P.; Hübel, H. Continuous-variable quantum key distribution with Gaussian modulation—the theory of practical implementations. Adv. Quantum Technol. 2018, 1, 1800011. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar]
- Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum Cryptography—A Simplified Undergraduate Experiment and Simulation. Physics 2022, 4, 104–123. [Google Scholar] [CrossRef]
- Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Security of continuous-variable quantum key distribution via a Gaussian de Finetti reduction. Phys. Rev. Lett. 2017, 118, 200501. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Upadhyaya, T.; Lütkenhaus, N. Asymptotic security analysis of discrete-modulated continuous-variable quantum key distribution. Phys. Rev. X 2019, 9, 041064. [Google Scholar] [CrossRef]
- Ghorai, S.; Grangier, P.; Diamanti, E.; Leverrier, A. Asymptotic security of continuous-variable quantum key distribution with a discrete modulation. Phys. Rev. X 2019, 9, 021059. [Google Scholar] [CrossRef]
- Wang, X.; Xu, M.; Zhao, Y.; Chen, Z.; Yu, S.; Guo, H. Non-Gaussian reconciliation for continuous-variable quantum key distribution. Phys. Rev. Appl. 2023, 19, 054084. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Yu, S.; Li, Z.; Guo, H. Continuous-mode quantum key distribution with digital signal processing. NPJ Quantum Inf. 2023, 9, 28. [Google Scholar] [CrossRef]
- Laudenbach, F.; Schrenk, B.; Pacher, C.; Hentschel, M.; Fung, C.H.F.; Karinou, F.; Poppe, A.; Peev, M.; Hübel, H. Pilot-assisted intradyne reception for high-speed continuous-variable quantum key distribution with true local oscillator. Quantum 2019, 3, 193. [Google Scholar]
- Roumestan, F.; Ghazisaeidi, A.; Renaudier, J.; Vidarte, L.T.; Diamanti, E.; Grangier, P. High-rate continuous variable quantum key distribution based on probabilistically shaped 64 and 256-QAM. In Proceedings of the 2021 European Conference on Optical Communication (ECOC), IEEE, Bordeaux, France, 13–16 September 2021; pp. 1–4. [Google Scholar]
- Pan, Y.; Wang, H.; Shao, Y.; Pi, Y.; Li, Y.; Liu, B.; Huang, W.; Xu, B. Experimental demonstration of high-rate discrete-modulated continuous-variable quantum key distribution system. Opt. Lett. 2022, 47, 3307–3310. [Google Scholar] [PubMed]
- Wang, X.; Wang, H.; Zhou, C.; Chen, Z.; Yu, S.; Guo, H. Continuous-variable quantum key distribution with low-complexity information reconciliation. Opt. Express 2022, 30, 30455–30465. [Google Scholar]
- Tian, Y.; Wang, P.; Liu, J.; Du, S.; Liu, W.; Lu, Z.; Wang, X.; Li, Y. Experimental demonstration of continuous-variable measurement-device-independent quantum key distribution over optical fiber. Optica 2022, 9, 492–500. [Google Scholar]
- Sarmiento, S.; Etcheverry, S.; Aldama, J.; López, I.; Vidarte, L.; Xavier, G.B.; Nolan, D.; Stone, J.; Li, M.; Loeber, D.; et al. Continuous-variable quantum key distribution over a 15 km multi-core fiber. New J. Phys. 2022, 24, 063011. [Google Scholar]
- Wang, T.; Xu, Y.; Zhao, H.; Li, L.; Huang, P.; Zeng, G. Multi-rate and multi-protocol continuous-variable quantum key distribution. Opt. Lett. 2023, 48, 719–722. [Google Scholar]
- Aldama, J.; Sarmiento, S.; Etcheverry, S.; Valivarthi, R.; Grande, I.L.; Vidarte, L.T.; Pruneri, V. Small-form-factor Gaussian-modulated coherent-state transmitter for CV–QKD using a gain-switched DFB laser. Opt. Express 2023, 31, 5414–5425. [Google Scholar]
- Huang, D.; Huang, P.; Li, H.; Wang, T.; Zhou, Y.; Zeng, G. Field demonstration of a continuous-variable quantum key distribution network. Opt. Lett. 2016, 41, 3511–3514. [Google Scholar] [PubMed]
- Huang, Y.; Shen, T.; Wang, X.; Chen, Z.; Xu, B.; Yu, S.; Guo, H. Realizing a downstream-access network using continuous-variable quantum key distribution. Phys. Rev. Appl. 2021, 16, 064051. [Google Scholar]
- Milovančev, D.; Vokić, N.; Laudenbach, F.; Pacher, C.; Hübel, H.; Schrenk, B. High rate CV–QKD secured mobile WDM fronthaul for dense 5G radio networks. J. Light. Technol. 2021, 39, 3445–3457. [Google Scholar]
- Wang, X.; Chen, Z.; Li, Z.; Qi, D.; Yu, S.; Guo, H. Experimental upstream transmission of continuous variable quantum key distribution access network. Opt. Lett. 2023, 48, 3327–3330. [Google Scholar] [PubMed]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The Evolution of Quantum Key Distribution Networks: On the Road to the Qinternet. IEEE Commun. Surv. Tutorials 2022, 24, 839–894. [Google Scholar]
- Ridene, S. Novel T-shaped GaSb/InAsN quantum wire for mid-infrared laser applications. Phys. Lett. A 2017, 381, 3324–3331. [Google Scholar]
- Ridene, R.; Mastour, N.; Gamra, D.; Bouchriha, H. Energetic behavior of excitons in hybrid organic–inorganic parabolic quantum dots and its electric field dependence. Int. J. Mod. Phys. B 2015, 30, 1550211. [Google Scholar]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 2013, 87, 052309. [Google Scholar] [CrossRef]
- Huang, J.Z.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Li, H.W.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar]
- Gehring, T.; Händchen, V.; Duhme, J.; Furrer, F.; Franz, T.; Pacher, C.; Werner, R.F.; Schnabel, R. Implementation of continuous-variable quantum key distribution with composable and one-sided-device-independent security against coherent attacks. Nat. Commun. 2015, 6, 8795. [Google Scholar]
- Walk, N.; Hosseini, S.; Geng, J.; Thearle, O.; Haw, J.Y.; Armstrong, S.; Assad, S.M.; Janousek, J.; Ralph, T.C.; Symul, T.; et al. Experimental demonstration of Gaussian protocols for one-sided device-independent quantum key distribution. Optica 2016, 3, 634–642. [Google Scholar]
- Liu, W.; Wang, X.; Wang, N.; Du, S.; Li, Y. Imperfect state preparation in continuous-variable quantum key distribution. Phys. Rev. A 2017, 96, 042312. [Google Scholar]
- Li, Z.; Wang, X.; Chen, Z.; Shen, T.; Yu, S.; Guo, H. Impact of non-orthogonal measurement in Bell detection on continuous-variable measurement-device-independent quantum key distribution. Quantum Inf. Process. 2023, 22, 236. [Google Scholar]
- Wang, T.; Huang, P.; Wang, S.; Zeng, G. Polarization-state tracking based on Kalman filter in continuous-variable quantum key distribution. Opt. Express 2019, 27, 26689–26700. [Google Scholar] [PubMed]
- Jain, N.; Derkach, I.; Chin, H.M.; Filip, R.; Andersen, U.L.; Usenko, V.C.; Gehring, T. Modulation leakage vulnerability in continuous-variable quantum key distribution. Quantum Sci. Technol. 2021, 6, 045001. [Google Scholar]
- Shen, T.; Huang, Y.; Wang, X.; Tian, H.; Chen, Z.; Yu, S. Strengthening practical continuous-variable quantum key distribution against measurement angular error. Opt. Express 2021, 29, 30978–30990. [Google Scholar]
- Muralekrishnan, R.; Venkatasubramani, L.N.; Mir, S.A.; Venkitesh, D. Influence of sub-system non–idealities on the performance of Gaussian modulated CV–QKD. In Proceedings of the 2022 Workshop on Recent Advances in Photonics (WRAP), IEEE, Mumbai, India, 4–6 March 2022; pp. 1–2. [Google Scholar]
- Hajomer, A.A.; Jain, N.; Mani, H.; Chin, H.M.; Andersen, U.L.; Gehring, T. Modulation leakage-free continuous-variable quantum key distribution. NPJ Quantum Inf. 2022, 8, 136. [Google Scholar]
- Scott, D.W. Box–muller transformation. Wiley Interdiscip. Rev. Comput. Stat. 2011, 3, 177–179. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, X.; Chen, Z.; Xu, B.; Yu, S. Security Analysis of Imperfect Gaussian Modulation Caused by Amplitude Modulator in Continuous–Variable Quantum Key Distribution. Symmetry 2023, 15, 1452. https://doi.org/10.3390/sym15071452
Li Z, Wang X, Chen Z, Xu B, Yu S. Security Analysis of Imperfect Gaussian Modulation Caused by Amplitude Modulator in Continuous–Variable Quantum Key Distribution. Symmetry. 2023; 15(7):1452. https://doi.org/10.3390/sym15071452
Chicago/Turabian StyleLi, Zhenghua, Xiangyu Wang, Ziyang Chen, Bingjie Xu, and Song Yu. 2023. "Security Analysis of Imperfect Gaussian Modulation Caused by Amplitude Modulator in Continuous–Variable Quantum Key Distribution" Symmetry 15, no. 7: 1452. https://doi.org/10.3390/sym15071452
APA StyleLi, Z., Wang, X., Chen, Z., Xu, B., & Yu, S. (2023). Security Analysis of Imperfect Gaussian Modulation Caused by Amplitude Modulator in Continuous–Variable Quantum Key Distribution. Symmetry, 15(7), 1452. https://doi.org/10.3390/sym15071452





