Newton-like Polynomial-Coded Distributed Computing for Numerical Stability
Abstract
1. Introduction
2. Preliminaries
2.1. Matrix–Vector Multiplication within the CDC Framework
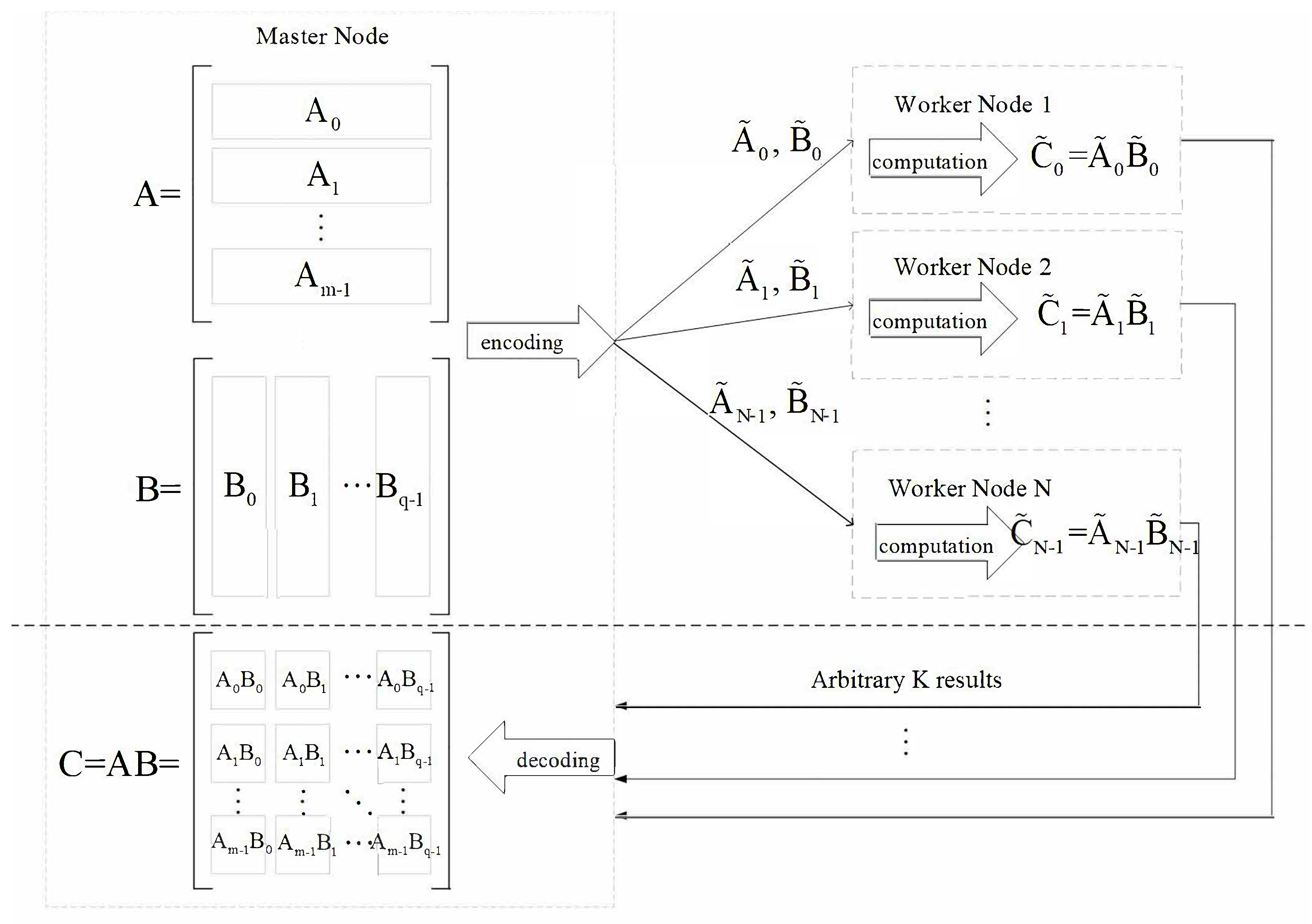
2.2. Matrix–Matrix Multiplication within the CDC Framework
2.3. Newton Interpolation Polynomial (NIP) Encoding
3. Proposed NLPC-Based CDC (NLPC-CDC)
3.1. NLPC-CDC for Matrix–Vector Multiplication
3.2. NLPC-CDC for Matrix–Matrix Multiplication
4. Numerical Study
4.1. Matrix–Vector Multiplication
4.2. Matrix–Matrix Multiplication
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (1)
- We first consider the case where . In this case, determinant . Therefore, is non-zero, and hence we prove the determinant is non-zero.
- (2)
- We assume that the determinant is non-zero for an arbitrary Newton-interpolation matrix, namelywhere takes actual values at random from . We let Q denote the above matrix within the determinant.
- (3)
- We prove that the determinant of an arbitrary Newton-interpolation matrix is non-zero.
References
- Fan, M.; Hong, C.; Yingke, L. Blind Recognition of Forward Error Correction Codes Based on a Depth Distribution Algorithm. Symmetry 2021, 13, 1094. [Google Scholar] [CrossRef]
- Abbas, N.; Zhang, Y.; Taherkordi, A. Mobile edge computing: A survey. IEEE Internet Things J. 2017, 5, 450–465. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q. Edge Computing: Vision and Challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Zhu, H.; Luan, T.H.; Dong, M. Guest editorial: Fog computing on wheels. Peer-Peer Netw. Appl. 2018, 11, 735–737. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, J.; Liu, A. Fog-Based Computing and Storage Offloading for Data Synchronization in IoT. IEEE Internet Things J. 2018, 6, 4272–4282. [Google Scholar] [CrossRef]
- Sisinni, E.; Saifullah, A.; Han, S. Industrial internet of things: Challenges, opportunities, and directions. IEEE Internet Things J. 2018, 14, 4724–4734. [Google Scholar] [CrossRef]
- Pokamestov, D. Adaptation of Signal with NOMA and Polar Codes to the Rayleigh Channel. Symmetry 2022, 14, 2103. [Google Scholar] [CrossRef]
- Shen, X.; Gao, J.; Wu, W.; Li, M.; Zhou, C.; Zhuang, W. Holistic network intelligence for 6G. IEEE Commun. Surv. Tutotrials 2022, 24, 1–30. [Google Scholar] [CrossRef]
- Li, J.; Dang, S.; Huang, Y.; Chen, P.; Qi, X.; Wen, M. Composite multiple-mode orthogonal frequency division multiplexing with index modulation. IEEE Trans. Wirel. Commun. 2022, 22, 3748–3761. [Google Scholar] [CrossRef]
- Li, J.; Dang, S.; Wen, M.; Li, Q.; Chen, Y.; Huang, Y. Index Modulation Multiple Access for 6G Communications: Principles, Applications, and Challenges. IEEE Netw. 2023, 37, 52–60. [Google Scholar] [CrossRef]
- Liu, N.; Li, K.; Tao, M. Code design and latency analysis of distributed matrix multiplication with straggling servers in fading channels. China Commun. 2021, 18, 15–29. [Google Scholar] [CrossRef]
- Shin, D.-J.; Kim, J.-J. Cache-Based Matrix Technology for Efficient Write and Recovery in Erasure Coding Distributed File Systems. Symmetry 2023, 15, 872. [Google Scholar] [CrossRef]
- Dean, J.; Barroso, L.A. The tail at scale. Commun. ACM 2013, 56, 74–80. [Google Scholar] [CrossRef]
- Herault, T.; Hoarau, W. FAIL-MPI: How fault-tolerant is fault-tolerant MPI? In Proceedings of the IEEE International Conference on Cluster Computing, Barcelona, Spain, 25–28 September 2006. [Google Scholar]
- Dai, M. SAZD: A low computational load coded distributed computing framework for IoT systems. IEEE Internet Things J. 2020, 7, 3640–3649. [Google Scholar] [CrossRef]
- Yu, Q.; Maddah-Ali, M.A.; Avestimehr, A.S. Polynomial Codes: An Optimal Design for High-Dimensional Coded Matrix Multiplication. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Hasırcıoğlu, B.; Gómez-Vilardebó, J.; Gündüz, D. Bivariate Hermitian Polynomial Coding for Efficient Distributed Matrix Multiplication. In Proceedings of the IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Hasırcıoğlu, B.; Gómez-Vilardebó, J.; Gündüz, D. Bivariate Polynomial Coding for Efficient Distributed Matrix Multiplication. IEEE J. Sel. Areas Inf. Theory 2021, 2, 814–829. [Google Scholar] [CrossRef]
- Gautschi, W.; Inglese, G. Lower bounds for the condition number of vandermonde matrices. Numer. Math. 1987, 52, 241–250. [Google Scholar] [CrossRef]
- Gautschi, W. How (un) stable are vandermonde systems. Asymptot. Comput. Anal. 1990, 124, 193–210. [Google Scholar]
- Reichel, L.; Opfer, G. Chebyshev-vandermonde systems. Math. Comput. 1991, 57, 703–721. [Google Scholar] [CrossRef]
- Shen, X.; Gao, J.; Wu, W. AI-assisted network-slicing based next-generation wireless networks. IEEE Open J. Veh. Technol. 2020, 1, 45–66. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 37. [Google Scholar]
- Trefethen, L.N. Approximation Theory and Approximation Practice; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2013; Volume 128. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, M.; Lai, X.; Tong, Y.; Li, B. Newton-like Polynomial-Coded Distributed Computing for Numerical Stability. Symmetry 2023, 15, 1372. https://doi.org/10.3390/sym15071372
Dai M, Lai X, Tong Y, Li B. Newton-like Polynomial-Coded Distributed Computing for Numerical Stability. Symmetry. 2023; 15(7):1372. https://doi.org/10.3390/sym15071372
Chicago/Turabian StyleDai, Mingjun, Xiong Lai, Yanli Tong, and Bingchun Li. 2023. "Newton-like Polynomial-Coded Distributed Computing for Numerical Stability" Symmetry 15, no. 7: 1372. https://doi.org/10.3390/sym15071372
APA StyleDai, M., Lai, X., Tong, Y., & Li, B. (2023). Newton-like Polynomial-Coded Distributed Computing for Numerical Stability. Symmetry, 15(7), 1372. https://doi.org/10.3390/sym15071372





