Ternary Hybrid Nanofluid Flow Emerging on a Symmetrically Stretching Sheet Optimization with Machine Learning Prediction Scheme

Abstract

Nanofluids holding three distinct sorts of nanosized particles suspended in base fluid possess excellent thermal performance. In light of this novel use in coolant applications, the current work dealt with the optimal design and performance estimation of a ternary hybrid nanofluid, based on a modern machine learning prediction technique. The synthesis of $\left(Cu\right)$, $\left(Ti{O}_2\right)$, and $\left(Si{O}_2\right)$ ternary hybrid nanoparticles suspended in water over a symmetrically stretching sheet was scrutinized. The flow over a stretching sheet is the most noteworthy symmetry analysis for momentum and thermal boundary layers, due to the implications of heat transfer, and is applied in various industries and technological fields. The governing equations were transformed to a dimension-free series of ODEs, by handling similarity transformable with symmetry variables, after which, the series of ODEs were treated scientifically, with the help of the Wolfram Language tool. The precision of the current estimates was assessed by comparison to existing research. Moreover, the natures of the physical phenomena were forecast by designing a support vector machine algorithm with an emphasis on machine learning, which delivers a robust and efficient structure for every fluid application that infers physical influences. To validate the proposed research, some of the statistical metrics were taken for error assessment between true and anticipated values. It was revealed that the presented approach is the best strategy for predicting physical quantities. This investigation established that ternary hybrid nanofluid possesses excellent thermal performance, greater than that of hybrid nanofluid. The current optimization process delivers a new beneficial viewpoint on the production of polymer sheets, glass fiber, petroleum, plastic films, heat exchangers, and electronic devices. Hence, the obtained results are recommended for the development of industrial devices setups.

1. Introduction

The study of fluid flow over various symmetries, and of the related properties, has attracted much interest among researchers, due to the enhancing capacity of heat transfer, and widespread usage in the engineering and scientific domains. This symmetry analysis is significant, from both a theoretical and practical point of view [1,2]. In particular, academicians and investigators have developed a fluid flow over a stretching sheet symmetry concept, to simulate heat transfer, and to identify precise solutions [3]. The result provides a response to the high demand for a cooling mechanism with improved heat transfer performance, in industries such as metallurigical process, heat exchangers, etc. The current paper studied the physical phenomena of ternary hybrid nanofluid flow immersing a symmetrically stretching sheet.

Fluids are utilized as base fluids depending upon thermal flow, such as water, ethylene glycol, oils, etc. Due to their low thermal conductivity, these fluids perform inadequately in a variety of industrial applications. Modern technology has delivered new concepts for improving thermal transport performance in a variety of techniques for the description of petroleum procedures, chemical industries, and food processing, among others. According to Choi et al. [4], an efficient technique is the dispersion of nanoparticles in the liquid phase: this mixture of two phases is known as a nanofluid. Makinde et al. [5] derived the boundary layer flow of a nanofluid through a stretching sheet. The material characteristics of nanofluids are extremely sensitive to slight changes in thermophysical properties: these special features have enabled researchers to analyze the material properties of nanofluids, as reported in [6,7,8].

A few years after these findings, researchers discovered that the thermal properties of a base fluid are improved when more than one nanosized particle is dispersed in a clear fluid: these blends are termed ’hybrid nanofluids’. Hybrid nanofluids are effective at cooling down thermal systems with high temperature levels, and have a variety of thermal applications, mainly in solar energy, heat exchangers, cooling for generators, transformers, heat pipes, and nuclear systems. Jana et al. [9] revised the hybrid nanofluid model through experiments. In a hybrid nanofluid, heat conduction mechanisms strengthen practically with an increase in the volume fraction of the nanoparticles: this finding had already been established by Suresh et al. [10]. Other noteworthy initiatives [11,12,13,14,15,16,17,18,19] emphasize hybrid nanofluids.

In recent years, three dissimilar kinds of nanoparticles were suspended in a pure fluid, by scientists and experimenters, in order to construct an unexplored category of nanofluids: ’ternary hybrid nanofluid’ was the name given to this novel category of nanofluids. Specialists were driven to change the existing nanofluids as a result of the increased demand for cooling substances combined with great thermal potential at the industrial level: this need led to the introduction of a trihybrid nanofluid with the specified thermal properties. The behaviors of the trihybrid nanofluid $(Ti{O}_2+CuO+MgO/H_{2}O)$ were addressed by Mousavi et al. [20]. To increase the viscosity of the trihybrid nanofluid, Sahoo et al. [21] attempted to promote a novel correlation. Recently, a few notable studies on ternary hybrid nanofluid have attracted further investigation [22,23,24,25,26,27].

A review of the literature indicates that ours is the first attempt to handle the impact of $(Cu+Ti{O}_2+Si{O}_2/H_{2}O)$ over a stretching sheet in the involvement of a heat source/sink, the motivations for which were that:

• Copper $Cu$ contains significantly higher thermal and electrical conductivity than $Ti{O}_2$ and $Si{O}_2$; it is exploited as a structural material, a conductor of heat and electricity, and a component of many metal alloys;
• Titanium dioxide $Ti{O}_2$ is a divalent metal and non-toxic; it is widely used in photoelectric solar panels, thermal energy storage, and thermal management of electronic devices, due to its unique thermal characteristics;
• Due to the greater electron negativity of $Si$, sulfatase is not produced by $Si{O}_2$ comparably to $Ti{O}_2$.

In light of this reasoning, our research focused on the flow of an incompressible, laminar, ternary hybrid nanofluid over a stretching sheet. Finally, a support vector machine was programmed to forecast the physical phenomenon as a novelty.

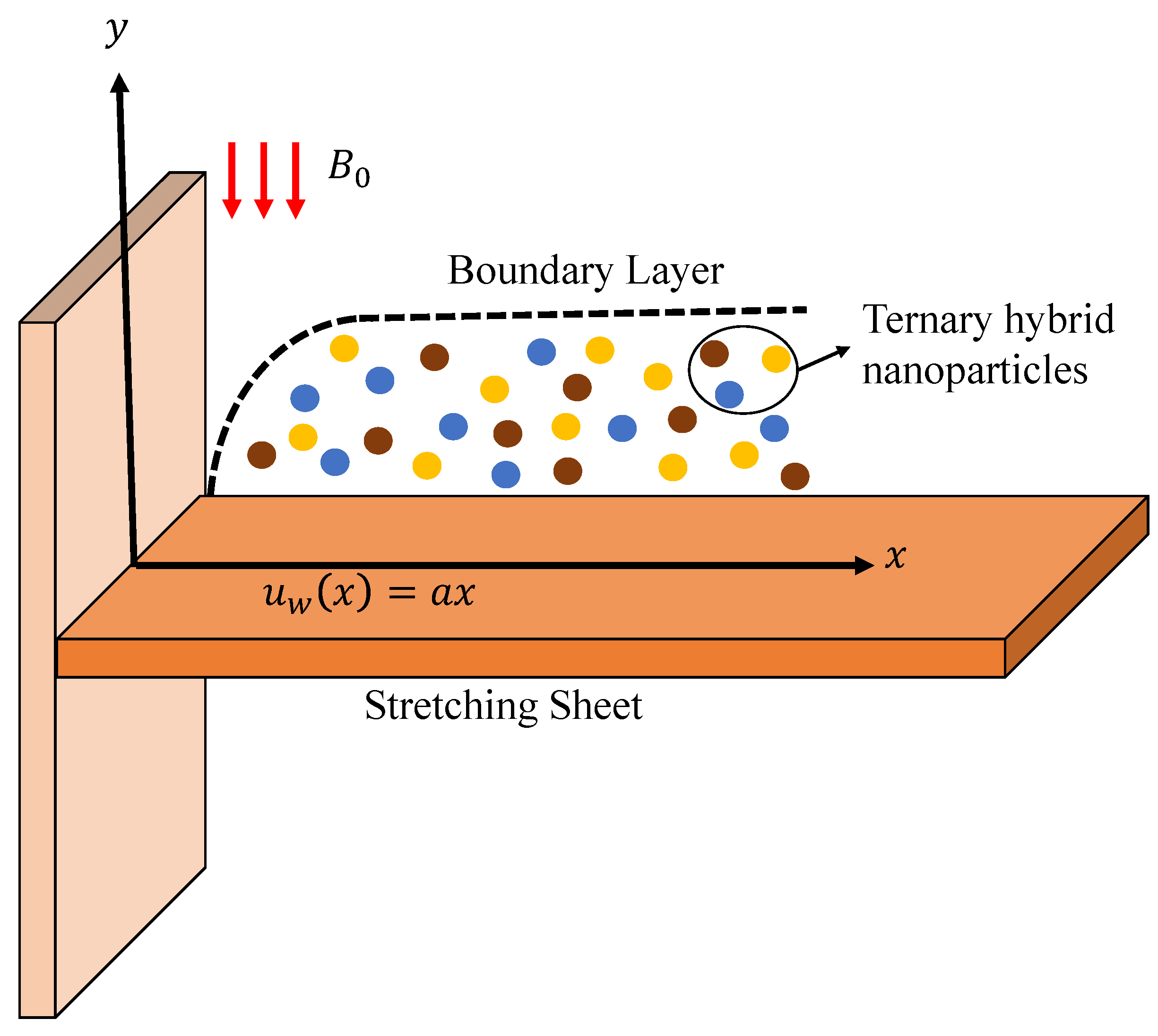
2. Modeling and Mathematical Formulation

A stretching surface containing copper $Cu$, titanium dioxide $Ti{O}_2$, and silicon dioxide $Si{O}_2$ nanoparticles based with water $H_{2}O$ was taken into attention for an incompressible, laminar flow of ternary hybrid nanofluid. We assumed that the thermal was being transported over a surface that was moving at a speed of $u_w=ax$, and that the ambient temperature was symbolized by $T_{\infty }$. The intensity of the magnetic field $B_0$ was distributed perpendicular to the surface. The fluid temperature was denoted by T. Figure 1 highlights a physical depiction of the current model. Employing the conventional boundary layer approximation and the aforementioned assumptions, the considered ternary hybrid nanofluid flow was governed by conservation principles, as follows [28]:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0;$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{thnf}}{{\rho }_{thnf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{thnf}}{{\rho }_{thnf}}{B}_0^{2}u;$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{thnf}}{{\left(\rho c_p\right)}_{thnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{1}{{\left(\rho c_p\right)}_{thnf}}{Q}_c(T-T_{\infty }),$$

(3)

along with the boundary conditions

$$\begin{array}{cc}\hfill & u=U_w,v=0,k_{thnf}\frac{\partial T}{\partial y}=-h_t(T_w-T)\mathrm{at}y=0,\hfill \\ & u\to 0,T\to T_{\infty },\mathrm{as}y\to \infty .\hfill \end{array}$$

(4)

Figure 1. Geometrical coordinates and sketch of the flow configuration.

Above, $(u,v)$ depict velocity components in the $(x,y)$ direction. The correlation [22] and thermophysical features [28,29] of ternary hybrid nanofluid are displayed in Table 1 and Table 2. The Brinkman model [30] was taken into account for effective dynamic viscosity, in terms of volume fraction as a core component in the flow region. Sahoo [31] has proved that the Brinkman model is almost zero for the lower volume fraction up to $0.05\%$ of the $A{L}_2{O}_3-SiC-Ti{O}_2/$water ternary hybrid nanofluid.

Table 1. Correlations of ternary hybrid nanofluids.

Properties	Ternary Hybrid Nanofluid
Viscosity	${\mu }_{thnf}=\frac{{\mu }_f}{{(1-{\varphi }_1)}^{2.5}{(1-{\varphi }_2)}^{2.5}{(1-{\varphi }_3)}^{2.5}}$
Density	${\rho }_{thnf}=(1-{\varphi }_1)[(1-{\varphi }_2)[(1-{\varphi }_3)+{\varphi }_3\frac{{\rho }_3}{{\rho }_f}]+{\varphi }_2\frac{{\rho }_2}{{\rho }_f}]+{\varphi }_1\frac{{\rho }_1}{{\rho }_f}$
Heat capacity	${\left(\rho c_p\right)}_{thnf}=(1-{\varphi }_1)[(1-{\varphi }_2)[(1-{\varphi }_3)+{\varphi }_3\frac{{\left(\rho c_p\right)}_3}{{\left(\rho c_p\right)}_f}]+{\varphi }_2\frac{{\left(\rho c_p\right)}_2}{{\left(\rho c_p\right)}_f}]+{\varphi }_1\frac{{\left(\rho c_p\right)}_1}{{\left(\rho c_p\right)}_f}$
Electrical conductivity	$\frac{{\sigma }_{thnf}}{{\sigma }_{hnf}}=\frac{(1+2{\varphi }_1){\sigma }_1+(1-2{\varphi }_1){\sigma }_{hnf}}{(1-{\varphi }_1){\sigma }_1+(1+{\varphi }_1){\sigma }_{hnf}};$
	$\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=\frac{(1+2{\varphi }_2){\sigma }_2+(1-2{\varphi }_2){\sigma }_{nf}}{(1-{\varphi }_2){\sigma }_2+(1+{\varphi }_2){\sigma }_{nf}};\frac{{\sigma }_{nf}}{{\sigma }_f}=\frac{(1+2{\varphi }_3){\sigma }_3+(1-2{\varphi }_3){\sigma }_f}{(1-{\varphi }_3){\sigma }_3+(1+{\varphi }_3){\sigma }_f}$
Thermal conductivity	$\frac{K_{thnf}}{K_{hnf}}=\frac{k_1+2k_{hnf}-2{\varphi }_1(k_{hnf}-k_1)}{k_1+2k_{hnf}+{\varphi }_1(k_{hnf}-k_1)};$
	$\frac{K_{hnf}}{K_{nf}}=\frac{k_2+2k_{nf}-2{\varphi }_2(k_{nf}-k_2)}{k_2+2k_{nf}+{\varphi }_2(k_{nf}-k_2)};\frac{K_{nf}}{K_f}=\frac{k_3+2k_f-2{\varphi }_3(k_f-k_3)}{k_3+2k_f+{\varphi }_3(k_f-k_3)}$

Table 2. Thermophysical properties of $Cu$, $Ti{O}_2$, $Si{O}_2$, and $H_{2}O$.

Properties	$\mathit{Cu}$	${\mathit{TiO}}_2$	${\mathit{SiO}}_2$	${\mathit{H}}_2\mathit{O}$
$\rho$ (kg/m${}^3$)	8933	4250	2270	997
$C_p$ (J/kg K)	385	686.2	765	4179
$\sigma$ (S/m)	1.67	$2.4\times {10}^6$	$3.5\times {10}^6$	$5.5\times {10}^{-6}$
k (W/m K)	400	8.953	1.4013	0.6071

The set of dimension-free variables were

$$u=ax{F}^{\prime }\left(\eta \right),v=-\sqrt{av}F\left(\eta \right),\theta =\frac{T-T_{\infty }}{T_w-T_{\infty }},\eta =\sqrt{\frac{a}{v}}y.$$

(5)

Equation (5) was incorporated into Equations (2) and (3), which resulted in non-linear ordinary differential equations in the following form:

$$\frac{{\mu }_{thnf}}{{\mu }_f}{F}^{‴}+\frac{{\rho }_{thnf}}{{\rho }_f}(F{F}^{″}-F^{\prime 2})-\frac{{\sigma }_{thnf}}{{\sigma }_f}M{F}^{\prime }=0$$

(6)

$$\frac{k_{thnf}}{k_f}\frac{{\left(\rho c_p\right)}_f}{{\left(\rho c_p\right)}_{thnf}}{\theta }^{″}+PrF{\theta }^{\prime }+\frac{{\left(\rho c_p\right)}_f}{{\left(\rho c_p\right)}_{thnf}}QPr\theta =0,$$

(7)

with the related boundary conditions:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & F\left(0\right)=1,F^{\prime }\left(0\right)=0,F^{\prime }(\infty )=0\hfill \\ & {\theta }^{\prime }\left(0\right)=-\gamma \frac{k_{thnf}}{k_f}(1-\theta \left(0\right)),\theta (\infty )=0,\hfill \end{array}\right.\end{array}$$

(8)

where the dimensionless parameters $M,Pr,$ and Q characterized the magnetic parameter, Prandtl number, and heat source/sink parameter, respectively. The mathematical formation of these parameters was

$$M=\frac{{\sigma }_f{B}_0^2}{a{\rho }_f},Pr=\frac{v_f}{{\alpha }_f},Q=\frac{Q_c}{{\left(\rho c_p\right)}_{f}a}.$$

The physical quantities were described as

$$C{f}_x=\frac{{\mu }_{thnf}}{{\mu }_{f}a{x}^2}{\left[\frac{\partial u}{\partial y}\right]}_{y=0}\mathrm{and}N{u}_x=-x\frac{k_{thnf}}{k_f(T_w-T_{\infty })}{\left[\frac{\partial T}{\partial y}\right]}_{y=0}.$$

(9)

After substituting Equation (5) into (9), the revised structure of the aforesaid expressions was given by

$$\sqrt{R{e}_x}C{f}_x=\frac{{\mu }_{thnf}}{{\mu }_f}{F}^{″}\left(0\right),\frac{N{u}_x}{\sqrt{R{e}_x}}=\frac{k_{thnf}}{k_f}{\theta }^{\prime }\left(0\right).$$

(10)

3. Materials and Methods

3.1. Numerical Scheme

For the simulation of nonlinear differential equations, various solution schemes have been operated by investigators. In the current analysis, the method of lines (MOL) scheme was treated, to handle the momentum equation (6) and energy equation (7), along with the boundary conditions in (8), numerically. The method of lines is a technique for solving a system of ordinary differential equations (ODEs). The main advantage is that it allows the solution to take advantage of sophisticated general-purpose methods. When compared to other traditional investigative methods [32], the numerical method of lines yields superior results. The applicability of the MOL delivers the prospect of improving the precision of the response.

Verification of Simulation Results

A comparison of the numerical results to previously offered results in the relevant literature was conducted, in order to evaluate the competency of the numerical code in the present problem. An impressive agreement was found while testing the tabular data (Table 3) and confirming the reliability and precision of the current solution approach. Hence, the method of lines technique provides a promising opportunity to improve the exactness of the result.

Table 3. Comparison result of $(-{\theta }^{\prime }\left(0\right))$ for several values of $Pr$.

$\mathit{Pr}$	Khan and Pop [33]	Gorla and Sidawi [34]	Manjunatha et al. [28]	Present Result
2	0.9113	0.9114	0.9113	0.9114
7	1.8954	1.8905	1.8954	1.8954
20	3.3539	3.3539	3.3539	3.3539

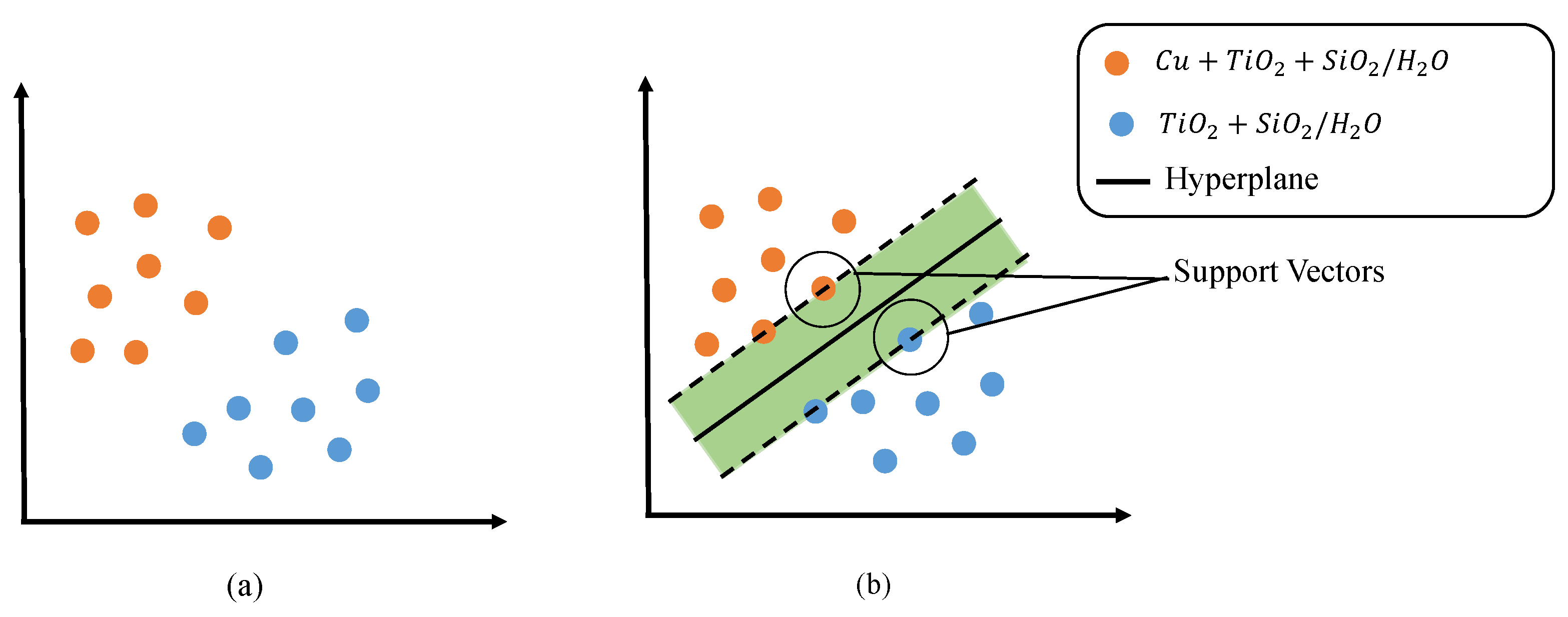
3.2. Machine Learning Scheme

3.2.1. Description of Dataset

The recommended parameters for nanofluids in a certain region were simulated by utilizing numerical analysis; an extension was to analyze the influence of the parameters, using an iterative approach. As the utilized nanoparticles were extremely magnetically sensitive, a few of the parameters could be the magnetic field that was delivered to the fluid, such as the magnetic parameter (M), heat source/sink parameter (Q), and volume fraction parameters (${\varphi }_1,{\varphi }_2,{\varphi }_3$) with the range of $0.5\le M\le 1.5$, $0.01\le Q\le 0.05$, $0.01\le {\varphi }_1,{\varphi }_2,{\varphi }_3\le 0.05$. The considered datasets were split into training and testing datasets: these were all taken into account, premised on their intended purpose, e.g., heat exchangers in the industrial and medical sectors.

3.2.2. Prediction Algorithm

A prominent machine learning approach, named regression, exploits the independent variable, to anticipate the value of the target variable. This approach is based on supervised learning, which is designed for labeled data. The main goal of regression is to establish connections between the input variables and the prediction [35,36,37]. The regression patterns differ in how they handle the correlation between the independent and dependent variables, as well as the total count of independent variables. In this paper, a support vector machine (SVM) was taken into account, to work as a prediction algorithm. An SVM is a type of regression algorithm, because it tries to evaluate the finest and most ideal hyperplane with the maximum margin from each support vector.

A support vector machine employs structural risk minimization to reduce model error. As seen in Figure 2, the fundamental concept of an SVM setup is to discover the support vector: it classifies the data into one of two classes, after taking a summary of the data information. SVMs have been implemented in a wide range of diverse research fields, including social sciences [38], engineering science [39,40,41], and biomedicine [42].

Figure 2. A schematic diagram of the SVM.

Consider a given set of data with the notation $\zeta ={\zeta }_1,{\zeta }_2,\dots {\zeta }_N$ and $\xi ={\xi }_1,{\xi }_2,\dots {\xi }_N$, where ${\zeta }_N$ and ${\xi }_N$ stand, respectively, for the input, such as $M,Q,{\varphi }_1,{\varphi }_2,{\varphi }_3$, and for target variables, such as skin friction coefficient and Nusselt number. Primarily, the SVM develops a regression function $f\left(\xi \right)$, to predict the target variables ${\xi }_1,{\xi }_2,\dots {\xi }_N$, based on a variety of input variables ${\zeta }_1,{\zeta }_2,\dots {\zeta }_N$; then, it classifies the friction rate and heat transfer rate of the hybrid nanofluid and the ternary hybrid nanofluid as two classes. The following is a construction of an optimization regression:

$$f\left(\xi \right)=\mathcal{W}\varphi \left(\zeta \right)+\mathcal{B}.$$

(11)

3.2.3. Evaluation Criteria

An essential phase of ML computing is model verification in terms of error estimation. In this study, the prediction accuracy served to validate the proposed model. To scrutinize the forecasting models completely, this paper employed five performance metrics, which were mean square error $\left(MSE\right)$, root mean square error $\left(RMSE\right)$, mean absolute error $\left(MAE\right)$, mean absolute percentage error $\left(MAPE\right)$, and coefficient of determination $\left(R^2\right)$:

• Mean square error

  $$MSE=\frac{1}{N}\sum _{i=1}^N{({\xi }_i-\widehat{{\xi }_i})}^2;$$

  (12)
• Root mean square error

  $$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{({\xi }_i-\widehat{{\xi }_i})}^2};$$

  (13)
• Mean absolute error

  $$MAE=\frac{1}{N}\sum _{i=1}^N|{\xi }_i-\widehat{{\xi }_i}|;$$

  (14)
• Mean absolute percentage error

  $$MAPE=\frac{1}{N}\sum _{i=1}^N|\frac{{\xi }_i-\widehat{{\xi }_i}}{{\xi }_i}|\ast 100;$$

  (15)
• Coefficient of determination

  $$R^2=1-\frac{{\sum }_{i=1}^N{({\xi }_i-\widehat{{\xi }_i})}^2}{{\sum }_{i=1}^N{({\xi }_i-\overline{{\xi }_i})}^2}.$$

  (16)

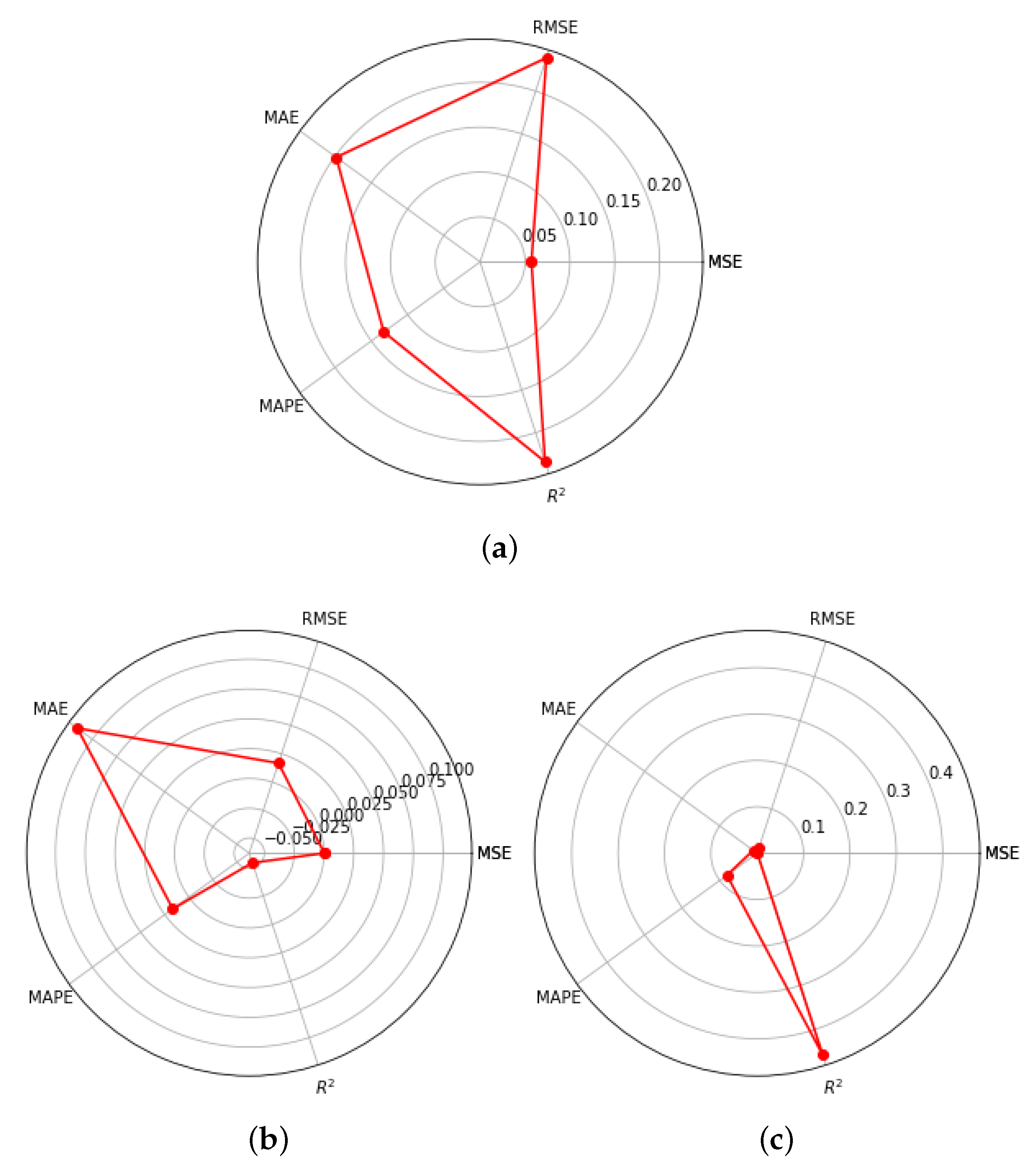
4. Result and Discussion

The function of a magnetic parameter on the velocity regime at $Q=0.01,Pr=6.2$, ${\varphi }_1,{\varphi }_2,{\varphi }_3=0.1$ is signified in Figure 3 by the display of tri-nanocomposite particles. The velocity is facilitated as a descent in boundary layer thickness based on an ascending magnetic parameter. Due to the Lorentz force’s appearance in the momentum equations, a tendency toward the velocity field is observed. The infliction of a magnetic field on an electrically conducting fluid creates Lorentz force, and it is perceived as a negative force that opposes the direction of nanoparticle flow, and causes the flow to go slowly downward. The variation in magnetic parameters on the temperature profile indicates the opposite trend when compared to the momentum field. This outcome is frequently utilized in the production and transmission of electrical energy.

Figure 3. Influence of magnetic parameter M on (a) $F^{\prime }\left(\eta \right)$ and (b) $\theta \left(\eta \right)$.

The influence of volume fraction on the velocity and temperature fields, at $M=0.5$, $Pr=6.2$, and $Q=0.01$, is depicted in Figure 4. The proposed combination of nanoparticles became less dense and flowed more effortlessly in the nanofluid, because it conducted better heat. As these less dense nanosized particles dragged the fluid with them in their direction of motion, the velocity and temperature ascended, as indicated in geometry analysis. Hence, the rising volume fraction of nanoparticles boosted the velocity and temperature of the fluid. This output potentially lowers air pollution, when nanoparticles are treated to perform as a coolant in motorcars.

Figure 4. Influence of heat source or sink parameter Q on (a) $F^{\prime }\left(\eta \right)$ and (b) $\theta \left(\eta \right)$.

Figure 5 describes how the heat source/sink parameter affected the velocity and temperature profiles at $M=0.5$, $Pr=6.2$, and ${\varphi }_1,{\varphi }_2,{\varphi }_3=0.1$; it shows that the velocity profiles were diminished versus the ascending heat source/sink parameter. In addition, the temperature distribution experienced the same nature as the momentum boundary layer thickness. This reveals that the tri-nanocomposite fluid generated more heat than the dual nanocomposite fluid; therefore, the physical significance of the heat source/sink parameter enriched the nature of the energy.

Figure 5. Influence of volume fraction parameter ${\varphi }_1,{\varphi }_2,{\varphi }_3$ on (a) $F^{\prime }\left(\eta \right)$ and (b) $\theta \left(\eta \right)$.

4.1. Result of ML-Based Model

Figure 6 elucidates the SVM classification performance, by the construction of a hyperplane for the given 60 datasets. The skin friction coefficient, with respect to the variation of the magnetic parameter in the range $(0.5,5)$, is captured in Figure 6a. The friction rate for the hybrid nanofluid was $-1.14326$ and $-1.53957$, and for the ternary hybrid nanofluid, it was $-1.5836$ and $-1.97992$. In addition, the support vectors of both fluids are highlighted in Figure. This indicates that the rising magnetic parameter had the strength to reduce the friction rate. The Nusselt number for the variation of the heat source/sink parameter and volume fraction in the range $(0.01,0.1)$ is depicted in Figure 6b,c. The heat transfer rates of the hybrid and ternary hybrid nanofluids for the behavior of the heat source/sink parameter were $-0.14587$, $-0.14507$, and $-0.14499$, $-0.14420$. For an increasing volume fraction, the heat transfer rates of the hybrid nanofluid and the trihybrid nanofluid were $-0.09905$, $-0.11432$, and $-0.11602$, $-0.13130$, respectively. It is evident from both these results in Nusselt number that the heat source/sink exhibited a better heat transfer rate.

Figure 6. Classification behavior based on given datasets with support vector machine.

4.2. Model Accuracy

The radar plot was exhibited in the research, to compare the actual and predicted values, in terms of the metrics ($MSE,RMSE,MAE,MAPE,R^2$) evaluation criteria. Figure 7 highlights the calculated accuracy results of the friction rate and the heat transfer rates. For the friction rate, the higher error $R^2$ value indicates the efficiency of the proposed SVM model. The higher $MAE$ and $R^2$ error values for the Nusselt number, with the variation of the heat source/sink parameter and volume fraction, reveal the precision. Furthermore, the training and testing error values are listed in Table 4, which shows how much difference was attained between true and predicted value, in terms of error; in addition, the results proved that the anticipated and numerically simulated findings of the checking dataset were in strong agreement with minimal error.

Figure 7. Classification behavior based on given datasets with support vector machine.

Table 4. Training vs testing error values.

Dataset	Parameter	Physical Quantities	$\mathbf{MSE}$	$\mathbf{RMSE}$	$\mathbf{MAE}$	$\mathbf{MAPE}$	${\mathit{R}}^2$
Training	M	$F^{″}\left(0\right)$	0.07142	0.07142	0.07142	0.2672	0.7083
Testing			0	0	0	0	1
Training	Q	${\theta }^{\prime }\left(0\right)$	0	0	0	0	1
Testing			0	0	0	0	1
Training	${\varphi }_1,{\varphi }_2,{\varphi }_3$	${\theta }^{\prime }\left(0\right)$	0	0	0	0	1
Testing			0	0	0	0	1

5. Enumerated Key Points

The considered problems were numerically solved, and the support vector machine simulations were employed as a result of generalized principles (for momentum and heat). Two-phase ($Ti{O}_2+Si{O}_2$) and three-phase ($Cu+Ti{O}_2+Si{O}_2$) nanoparticles suspended in water ($H_{2}O$) were examined for comparative study:

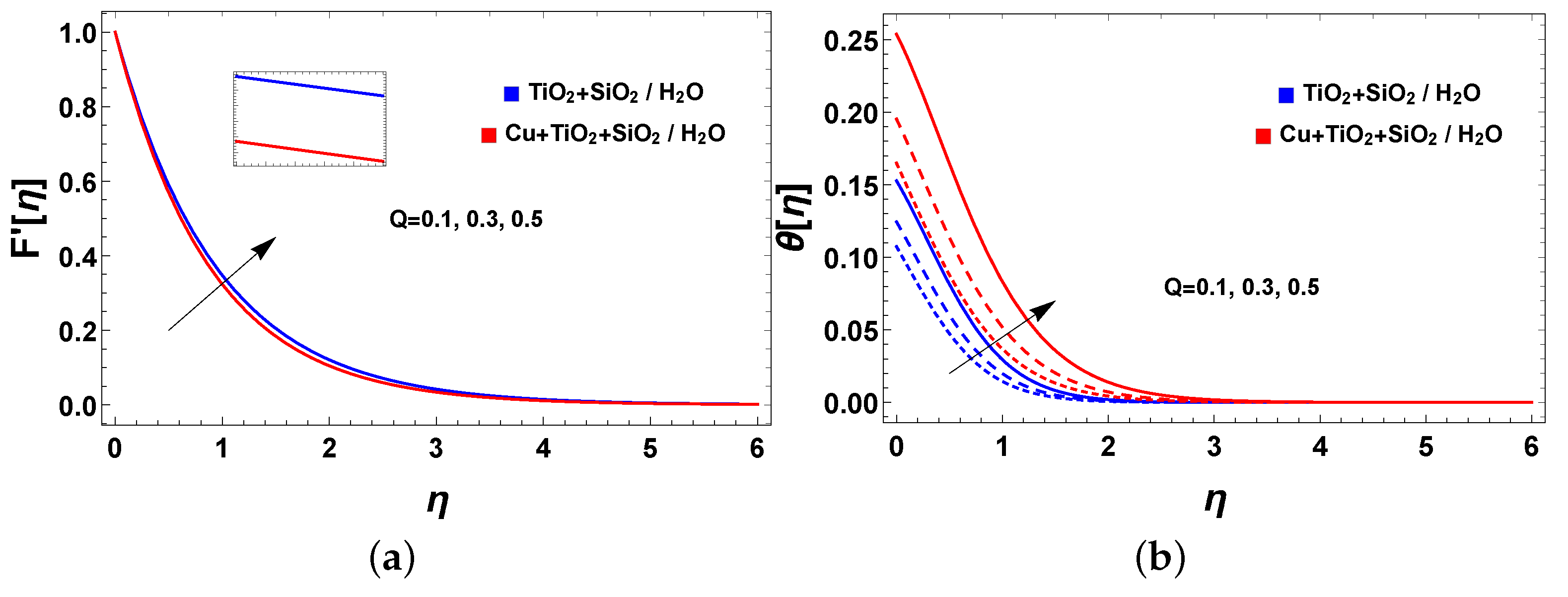
• The boundary layer thickness of the momentum and thermal profile was diminished and improved for an increasing magnetic parameter; this observation will play a vital role in both industrial and scientific progress;
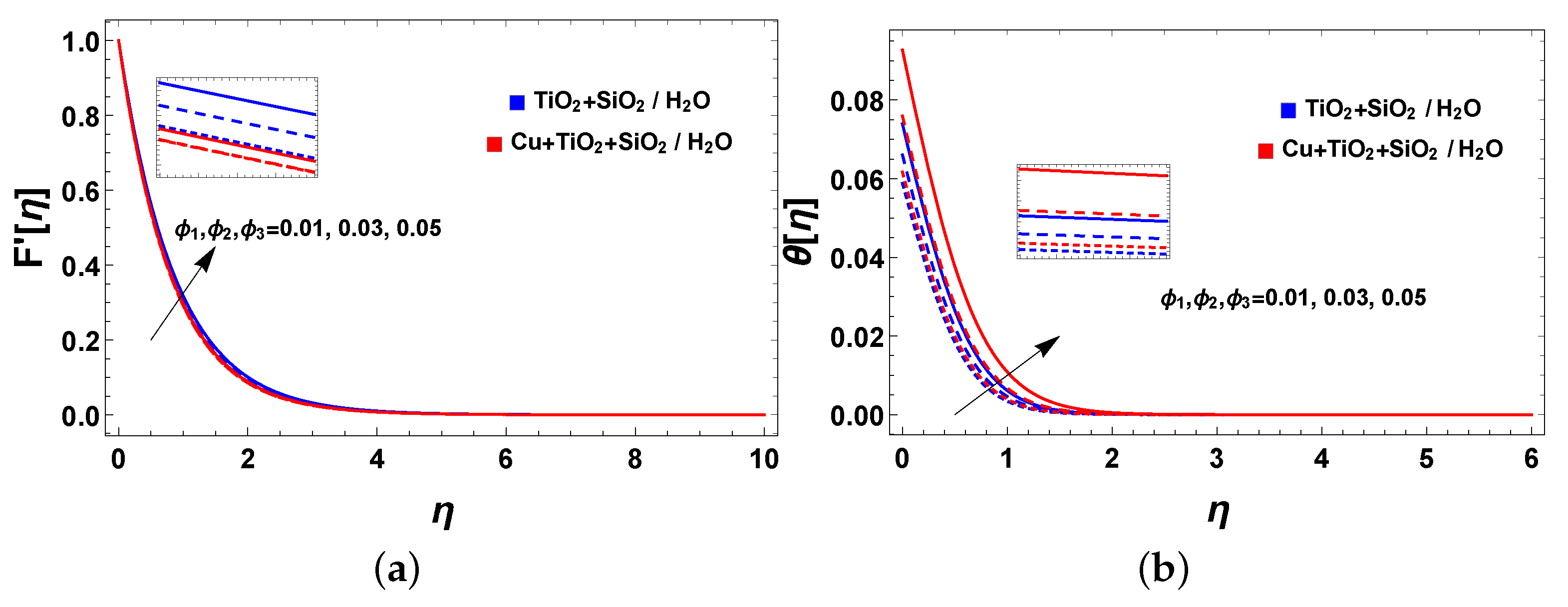
• The proposed mixture of nanoparticles became slightly dense, and moved more rapidly in the nanofluid as it achieved more heat effectively. It is interesting to note that the volume fraction improved the velocity and temperature fields. The same behavior was observed in the heat source/sink parameter;
• Based on the numerical simulation of skin friction coefficient and Nusselt number, the support vector machine delivers the possibility of specifying the physical phenomena of hybrid and ternary hybrid nanofluids with minimal error;
• The observations revealed that ternary hybrid nanofluids exhibit a higher thermal performance through the stretched sheet than fluids containing dual-phase nanoparticles. It is noteworthy that the tri-nanosized particle dispersion in the base fluid was suggested for cooling applications;
• Ternary hybrid nanoparticles are considered in solar cells, optical chemical sensors, biosensors, and electrical insulators; they are mainly utilized to putrefy dangerous compounds and cooling procedures.
• In the future, the K-means clustering machine learning scheme is expected to reduce the error of $R^2$ for three-phase nanoparticles suspended in water. In addition, exploring different physical factors can reveal remarkable occurrences.