The Conchoidal Twisted Surfaces Constructed by Anti-Symmetric Rotation Matrix in Euclidean 3-Space
Abstract
1. Introduction
2. Materials and Methods
3. Conchoidal Twisted Surfaces in Euclidean 3-Space
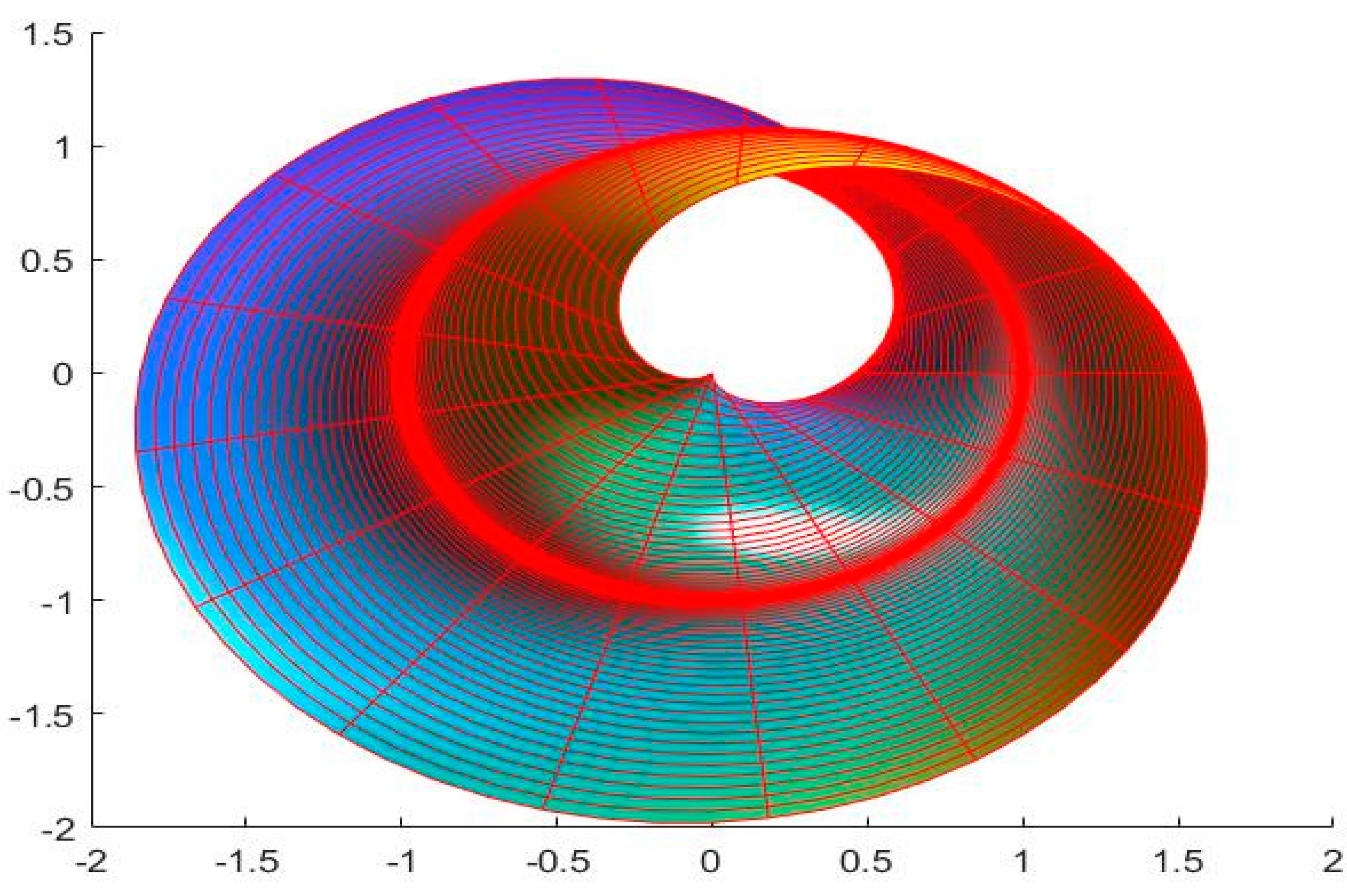
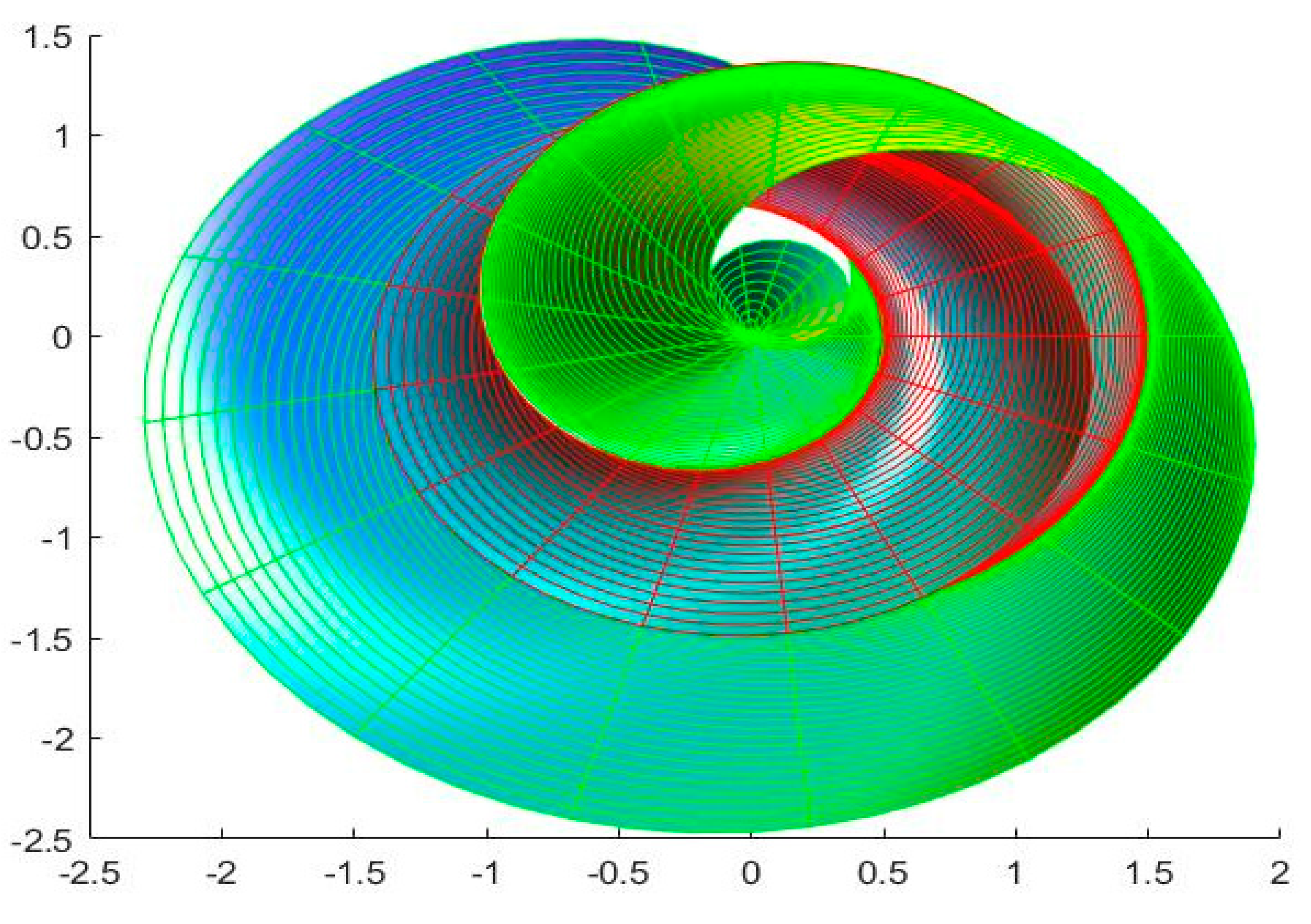
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eisenhart, L.P. An Introduction to Differential Geometry; Princeton University Press: Princeton, NJ, USA, 1940. [Google Scholar]
- Fuchs, D. Evolutes and Involutes of Spatial Curves. Am. Math. Mon. 2013, 120, 217–231. [Google Scholar] [CrossRef]
- Hacısalihoğlu, H.H. Differential Geometry; Academic Press Inc.: Ankara, Turkey, 1994. [Google Scholar]
- Sabuncuoğlu, A. Differential Geometry; Nobel Yayın Dağıtım: Ankara, Turkey, 2010. [Google Scholar]
- Sun, J.; Zhao, Y. The Geometrical Characterizations of the Bertrand Curves of the Null Curves in Semi-Euclidean 4-Space. Mathematics 2021, 9, 3294. [Google Scholar] [CrossRef]
- Alluhaibi, N.; Abdel-Baky, R.A.; Naghi, M. On the Bertrand Offsets of Timelike Ruled Surfaces in Minkowski 3-Space. Symmetry 2022, 14, 673. [Google Scholar] [CrossRef]
- Lockwood, E.H. A Book of Curves; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Sendra, J.R.; Sendra, J. An algebraic analysis of conchoids to algebraic curves. AAECC Appl. Algebra Eng. Commun. Comput. 2008, 19, 413–428. [Google Scholar] [CrossRef]
- Peternell, M.; Gruber, D.; Sendra, J. Conchoid surfaces of rational ruled surfaces. Comput. Aided Geom. Des. 2011, 28, 427–435. [Google Scholar] [CrossRef]
- Bulca, B.; Oruç, S.N.; Arslan, K. Conchoid curves and surfaces in Euclidean 3-Space. Balıkesir Univ. J. Grad. Sch. Nat. Appl. Sci. 2018, 20, 467–481. [Google Scholar] [CrossRef]
- Oruç, S.N.; Oruç, A. Characterization of Conchoid Curves and Surfaces in Euclidean Spaces. Master’s Thesis, Uludağ University, Graduate School of Natural and Applied Sciences, Bursa, Turkey, 2019. [Google Scholar]
- Dede, M. Spacelike Conchoid curves in the Minkowski plane. Balk. J. Math. 2013, 1, 28–34. [Google Scholar]
- Aslan, M.Ç.; Şekerci, G.A. An Examination of The Condition Under Which A Conchoidal Surfaces is A Bonnet Surface in the Euclidean 3-Space. Facta Univ. Ser. Math. Inform. 2021, 36, 627–641. [Google Scholar] [CrossRef]
- Ikawa, T. Bour’s theorem and Gauss map. Yokohama Math. J. 2000, 48, 173–180. [Google Scholar]
- Goemans, W.; Ignace, V.W. Twisted Surfaces in Euclidean and Minkowski 3-Space. In Proceedings of the PADGE 2012, Leuven, Belgium, 27–30 August 2012; Shaker Verlag: Aachen, Germany, 2013. [Google Scholar]
- Goemans, W.; Ignace, V.W. Constant curvature twisted surfaces in 3-dimensional Euclidean and Minkowski 3-space. In Proceedings of the Conference RIGA; Publishing House of the University of Bucharest: Bucharest, Romania, 2014; pp. 117–130. [Google Scholar]
- Gray, A.; Abbena, E.; Salamon, S. Modern Differential Geometry of Curves and Surfaces with Mathematica; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Dolaşır, S. The Properties of the Twisted Surface. Master’s Thesis, Uşak University, Uşak, Turkey, 2018. [Google Scholar]
- Kazan, A.; Karadağ, H.B. Twisted surfaces in the Pseudo-Galilean space. New Trends Math. Sci. 2017, 5, 72–79. [Google Scholar] [CrossRef]
- Dede, M.; Ekici, C.; Goemans, W.; Ünlütürk, Y. Twisted surfaces with vanishing curvature in Galilean 3-space. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850001. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelik, S.; Karadağ, H.B.; Kuşak Samancı, H. The Conchoidal Twisted Surfaces Constructed by Anti-Symmetric Rotation Matrix in Euclidean 3-Space. Symmetry 2023, 15, 1191. https://doi.org/10.3390/sym15061191
Çelik S, Karadağ HB, Kuşak Samancı H. The Conchoidal Twisted Surfaces Constructed by Anti-Symmetric Rotation Matrix in Euclidean 3-Space. Symmetry. 2023; 15(6):1191. https://doi.org/10.3390/sym15061191
Chicago/Turabian StyleÇelik, Serkan, Hacı Bayram Karadağ, and Hatice Kuşak Samancı. 2023. "The Conchoidal Twisted Surfaces Constructed by Anti-Symmetric Rotation Matrix in Euclidean 3-Space" Symmetry 15, no. 6: 1191. https://doi.org/10.3390/sym15061191
APA StyleÇelik, S., Karadağ, H. B., & Kuşak Samancı, H. (2023). The Conchoidal Twisted Surfaces Constructed by Anti-Symmetric Rotation Matrix in Euclidean 3-Space. Symmetry, 15(6), 1191. https://doi.org/10.3390/sym15061191







