The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise
Abstract
1. Introduction
2. Wave Equation for SJM Equation
3. Exact Solutions of SJM Equation
3.1. Application of the REM-Method
3.2. Application of the HSI-Method
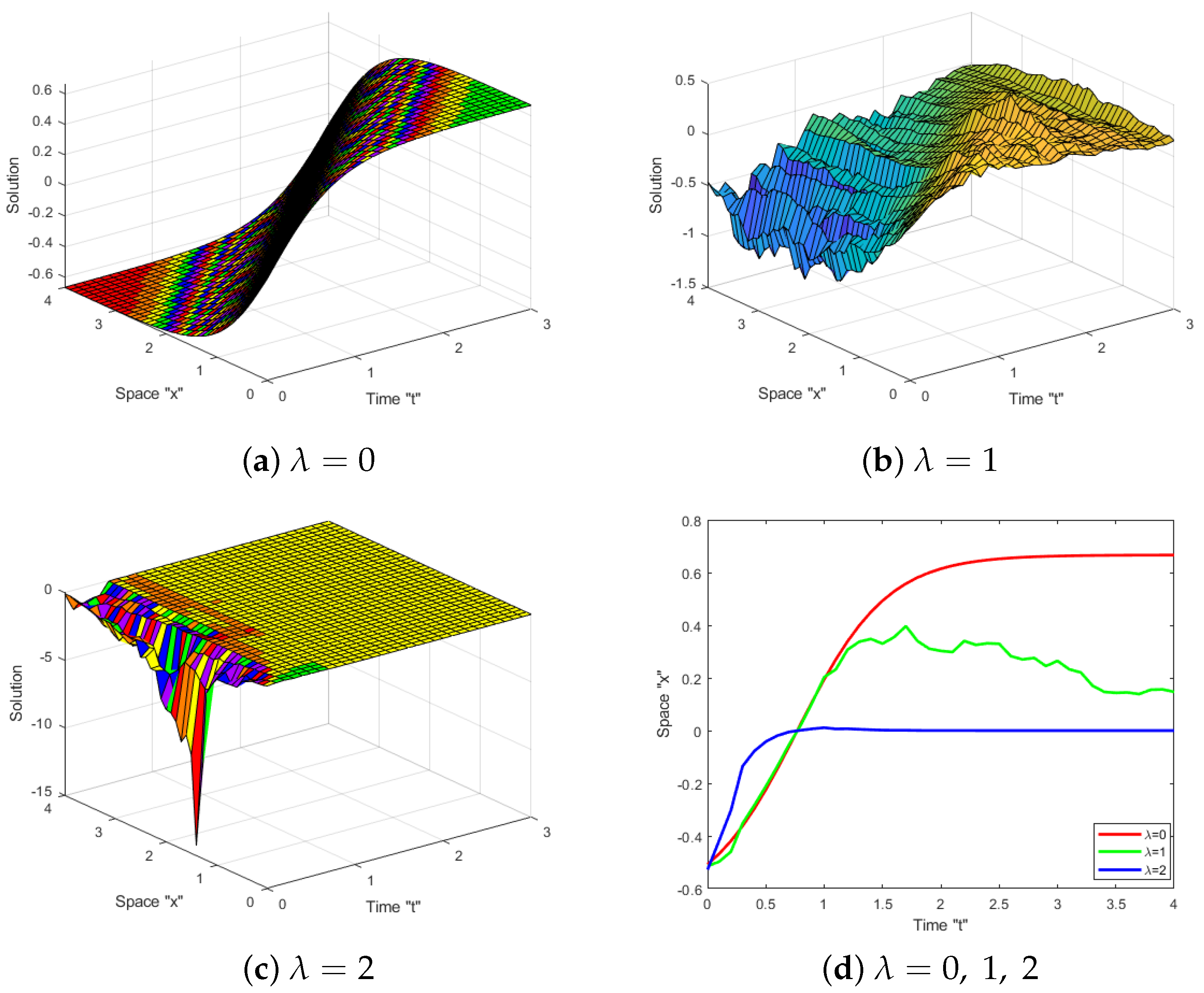
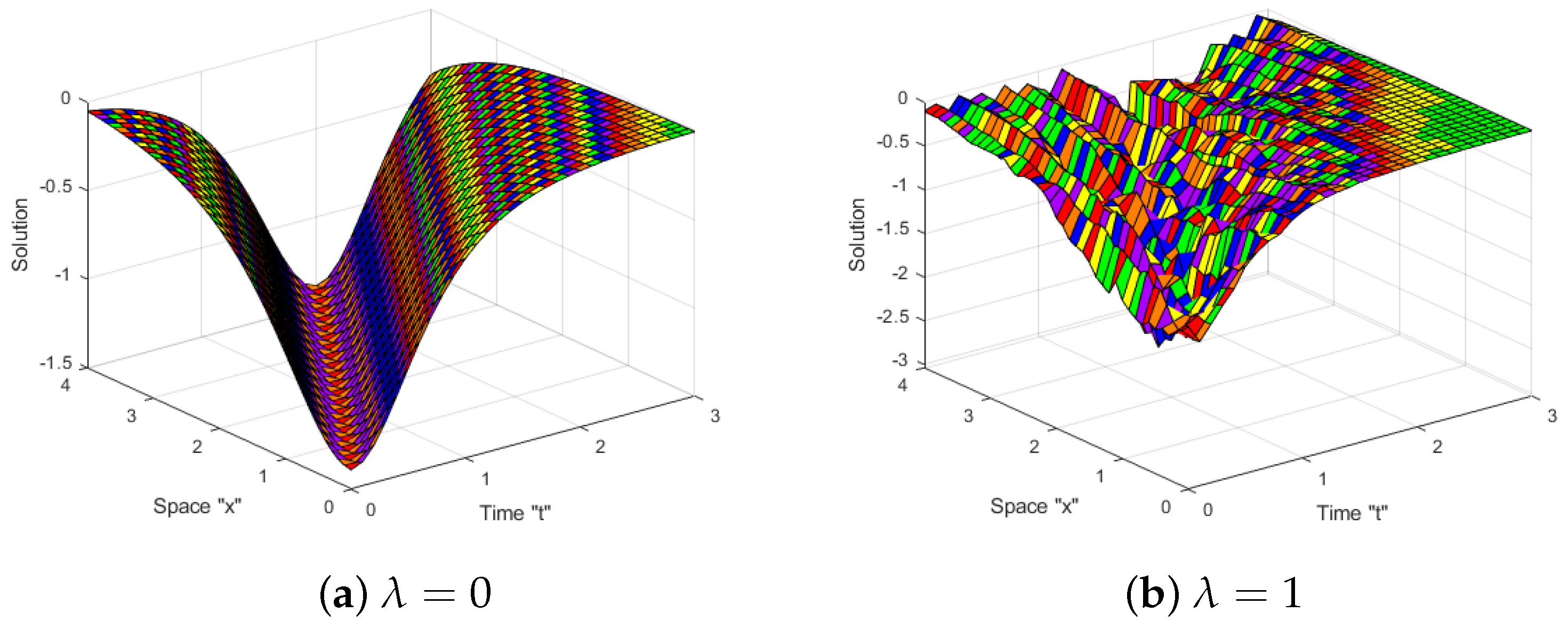
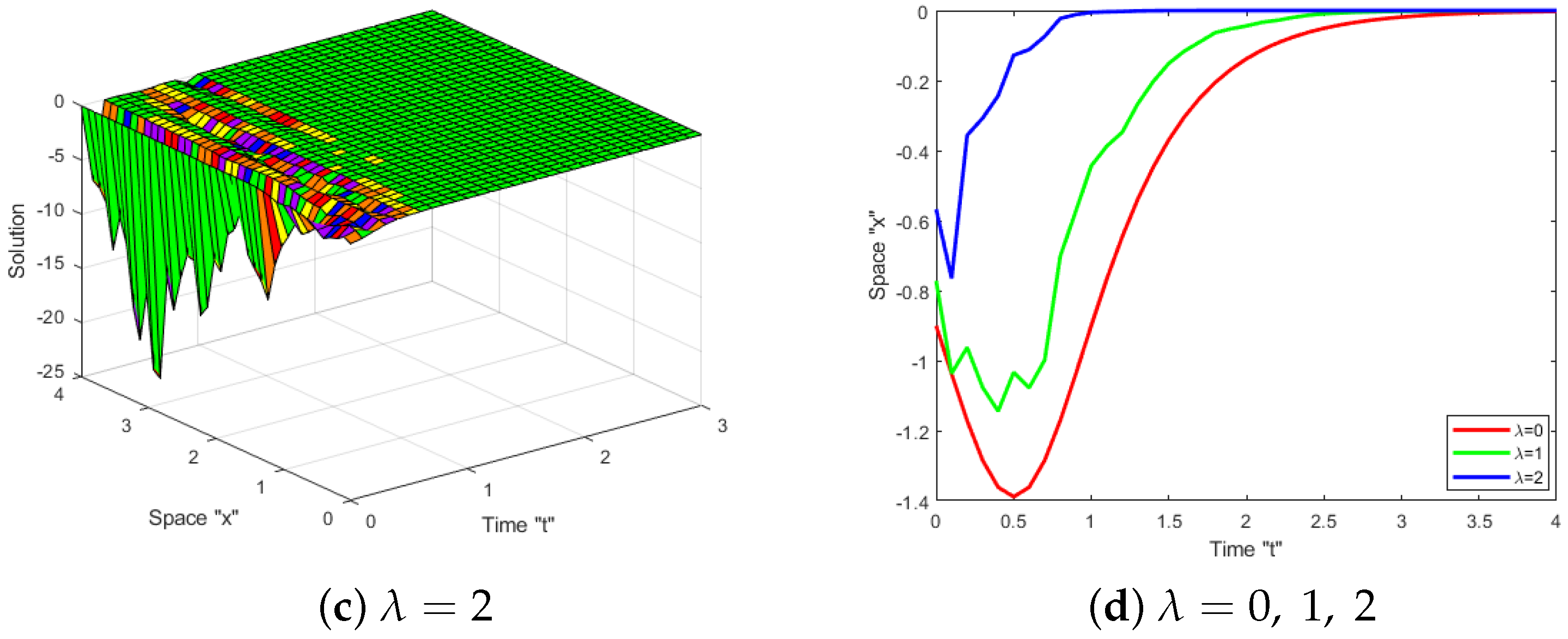
4. Impacts of Noise
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malfliet, W.; Hereman, W. The tanh method. I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Riaz, M.B.; Jhangeer, A.; Atangana, A.; Awrejcewicz, J.; Munawar, M. Supernonlinear wave, associated analytical solitons, and sensitivity analysis in a two-component Maxwellian plasma. J. King Saud Univ.—Sci. 2022, 34, 102108. [Google Scholar] [CrossRef]
- Samina, S.; Jhangeer, A.; Chen, Z. A study of phase portraits, multistability and velocity profile of magneto-hydrodynamic Jeffery–Hamel flow nanofluid. Chin. J. Phys. 2022, 80, 397–413. [Google Scholar] [CrossRef]
- Jhangeer, A.; Rezazadeh, H.; Seadawy, A. A study of travelling, periodic, quasiperiodic and chaotic structures of perturbed Fokas–Lenells model. Pramana 2021, 95, 41. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Alshammari, M. Impact of Brownian Motion on the Analytical Solutions of the Space-Fractional Stochastic Approximate Long Water Wave Equation. Symmetry 2022, 14, 740. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D. Variational theory and new abundant solutions to the (1+2)-dimensional chiral nonlinear Schrödinger equation in optics. Phys. Lett. A 2021, 412, 127588. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding optical solitons of generalized nonlinear Schrödinger equations. Optik 2022, 261, 169163. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; Aly, E.S. The Soliton Solutions of the Stochastic Shallow Water Wave Equations in the Sense of Beta-Derivative. Mathematics 2023, 11, 1338. [Google Scholar] [CrossRef]
- Huo, C.; Li, L. Lie Symmetry Analysis, Particular Solutions and Conservation Laws of a New Extended (3+1)-Dimensional Shallow Water Wave Equation. Symmetry 2022, 14, 1855. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-ϕ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Mohammed, W.W. Stochastic amplitude equation for the stochastic generalized Swift–Hohenberg equation. J. Egypt. Math. Soc. 2015, 23, 482–489. [Google Scholar] [CrossRef]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dyn. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Aly, E.S.; EL-Morshedy, M. Exact solutions of the stochastic Maccari system forced by multiplicative noise. ZAMM J. Appl. Math. Mech. 2022, 103, e202100199. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C. The analytical solutions of the stochastic mKdV equation via the mapping method. Mathematics 2022, 10, 4212. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey–Stewartson Equations. Symmetry 2022, 14, 2176. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C. The soliton solutions for the (4 + 1)-dimensional stochastic Fokas equation. Math. Methods Appl. Sci. 2023, 46, 7589–7597. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Influence of White Noise and the Beta Derivative on the Solutions of the BBM Equation. Axioms 2023, 12, 447. [Google Scholar] [CrossRef]
- Jimbo, M.; Miwa, T. Solitons and infinite dimensional Lie-Algebras. Publ. Res. Inst. Math. Sci. 1983, 19, 943–1001. [Google Scholar] [CrossRef]
- Wang, D.; Sun, W.; Kong, C.; Zhang, H. New extended rational expansion method and exact solutions of Boussinesq equation and Jimbo–Miwa equations. Appl. Math. Comput. 2007, 189, 878–886. [Google Scholar] [CrossRef]
- Eslami, M. Solitary Wave solutions to the (3 + 1)-dimensional Jimbo–Miwa equation. Comput. Methods Differ. Equ. 2014, 2, 115–122. [Google Scholar]
- Liu, X.Q.; Jiang, S. New solutions of the (3 + 1)-dimensional Jimbo–Miwa equation. Appl. Math. Comput. 2004, 158, 177–184. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, Y.N.; Ba, J.M.; Dong, L. Explicit and Exact Solutions with Multiple Arbitrary Analytic Functions of Jimbo–Miwa Equation. Appl. Appl. Math. Int. J. 2009, 4, 279–289. [Google Scholar]
- Tang, X.Y.; Liang, Z.F. Variable separation solutions for the (3 + 1)-dimensional Jimbo–Miwa equation. Phys. Lett. A 2006, 351, 398–402. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for the Calogero–Bogoyavlenskii–Schiff, Jimbo–Miwa and YTSF equations. Appl. Math. Comput. 2008, 203, 592–597. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New solutions of distinct physical structures to high-dimensional nonlinear evolution equations. Appl. Math. Comput. 2008, 196, 363–370. [Google Scholar] [CrossRef]
- Li, Z.; Dai, Z. Abundant new exact solutions for the (3 + 1)-dimensional Jimbo–Miwa equation. J. Math. Anal. Appl. 2010, 361, 587–590. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C. Mohammed, W.W. Abundant Solitary Wave Solutions for the Boiti–Leon–Manna–Pempinelli Equation with M-Truncated Derivative. Axioms 2023, 12, 466. [Google Scholar] [CrossRef]
- He, J.H. Variational principles for some nonlinear partial dikerential equations with variable coencients. Chaos Solitons Fractals 2004, 19, 847–851. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise. Symmetry 2023, 15, 1153. https://doi.org/10.3390/sym15061153
Al-Askar FM, Cesarano C, Mohammed WW. The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise. Symmetry. 2023; 15(6):1153. https://doi.org/10.3390/sym15061153
Chicago/Turabian StyleAl-Askar, Farah M., Clemente Cesarano, and Wael W. Mohammed. 2023. "The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise" Symmetry 15, no. 6: 1153. https://doi.org/10.3390/sym15061153
APA StyleAl-Askar, F. M., Cesarano, C., & Mohammed, W. W. (2023). The Solitary Solutions for the Stochastic Jimbo–Miwa Equation Perturbed by White Noise. Symmetry, 15(6), 1153. https://doi.org/10.3390/sym15061153








