Abstract
This paper investigates a novel adaptive fixed-time disturbance observer (AFXDO)-based approximate optimal tracking control architecture for nonlinear systems with partially unknown dynamic drift and perturbation under an adaptive dynamic programming (ADP) scheme. To attenuate the impact of disturbance, a novel AFXDO was designed based on the principle of a fixed-time stable system without prior information of disturbance, making disturbance observer errors converge to zero in a fixed time independent of initial estimation error. Additionally, approximate optimal control is conducted by incorporating the real-time estimation of AFXDO into a critic-only ADP framework to stabilize the dynamics of tracking errors and strike a balance between consumption and performance. In particular, to address the heavy calculation burden and oscillation phenomenon in the traditional actor–critic structure, an improved adaptive update law with a variable learning rate was developed to update the weight for adjusting the optimal cost function and optimal control policy simultaneously, avoiding the initial chattering phenomenon and achieving a prescribed convergence without resorting to dual networks. With the efforts of AFXDO and a weight law with a variable learning rate, the track errors were achieved with fast transient performance and low control consumptions in a fixed time. By revisiting Lyapunov stability, the tracking error and weight estimation error were proven to be uniformly ultimately bounded, and the designed control tended to optimal control. The simulations were carried out on quadrotor tracking to demonstrate the effectiveness of the developed control scheme, which achieves rapid convergence by lower control consumption in 4 s, where the cost function is reduced by 19.13%.
1. Introduction
In engineering applications, tracking control for nonlinear systems has been treated as an ever-increasing hot research topic over the last few years by virtue of its extensive application scenarios including the robot [1], permanent magnet synchronous motor [2], unmanned surface vehicle [3], and quadrotor [4]. Due to the inevitable presence of unknown system dynamics or uncertain parameters with the property of symmetry or asymmetry, as well as the external disturbances induced by working scenarios, the investigated model with uncertain system dynamic drift and extraneous disturbances widely exists. Conventional proportional integral control can hardly suppress the disturbance and dynamic drift to guarantee a robust tracking performance. To date, existing control methods to enhance the tracking performance for nonlinear systems can be roughly classified as sliding mode control [5], adaptive control [6,7], etc. The neural network and fuzzy logic system are two tools to make decisions for partially unknown systems, and their effectiveness can be verified in many areas, such as [6,8,9,10]. There have been many studies devoted to improving the estimation performance of neural networks and fuzzy logic systems [11,12,13,14,15,16,17,18,19]. However, the heavy computation burden caused by FLS and NN with adjusting parameters is impractical in real-world applications.
Aside from the classical robust control to handle partially unknown nonlinear systems, many scholars have shed light on disturbance observer (DO) for nonlinear uncertain systems on account of its concise form and validity. Its principal advantage is that DO-based controllers not only significantly improve the anti-interference ability but also retain the desired control performance among theories and practical engineering applications [20,21,22,23]. For example, approximate tracking control is put forward with neural network (NN) and nonlinear DO to approximate the system uncertainties [20]. In [22], a sliding mode control was designed for spacecraft to regulate attitude, where a novel integral DO with an extra integral term was inserted to estimate the lumped disturbances with high precision. In [23], an improvement of the reduced-order proportional integral observer was considered for feedforward compensation to avoid the effect caused by disturbance. Although there emerge various DOs focusing on disturbance attenuation, the convergence results of observation errors can only be assured when the time tends to infinity, which is uneconomic for real-world plants in engineering applications.
Therefore, a novel disturbance observer is developed, while an optimal tracking controller is proposed with a variable learning rate weight law. The investigated framework can achieve high precision and the rapid convergence of tracking performance with lower control consumption by designing the following goals:
- An adaptive fixed-time disturbance observer (AFXDO) is put forward for the estimation of lumped disturbance;
- The controller is set up based on the proposed AFXDO;
- The weight law with a variable learning rate is proposed to avoid the oscillation phenomenon during the learning process.
2. Related Works
Thus, aiming to achieve zero-disturbance within an effective short time and obtain fast tracking performance, finite-time stability with adjustment settling time has received considerable attention [24,25,26,27,28], which means the time from the initial state to the stable state is adjustable. In [24], a new super-twisting algorithm is provided for high-order systems with matched and mismatched disturbances, where a finite-time DO was designed to enable disturbance estimation errors to converge to zero in a finite time. For a second-order multiagent system, a centralized controller was developed in [26] based on the estimation of disturbance, where a finite-time observer was proposed for each agent to estimate disturbance. In [28], adaptive control was developed for rigid spacecraft to achieve attitude-tracking performance, where actuator faults are estimated by designing finite-time DO in the spirit of an improved finite-time stable system. Note that finite-time DOs are preferable to ensure higher accuracy and stronger robustness than conventional DO with asymptotic convergence. However, the settling time of finite-time DO is closely related to initial estimation error, which cannot be estimated without the known initial circumstance. Moreover, the settling time will tend to infinity when the initial estimation is far from the actual perturbation, which promotes further extension of finite-time stability, named the fixed-time technique, explored by Polykov [29]. In terms of disturbance attenuation, fixed-time DO is featured with fixed-time stability, i.e., the settling time of estimation error is dominated chiefly by control parameters rather than the initial estimation error [30,31,32]. By importing a fixed-time disturbance observer, a novel composite control consisting of a fixed-time controller and an anti-saturation controller was developed in [30] for an uncertainties model with actuator saturation to guarantee trajectory tracking and attitude regulation. To enhance the robustness of disturbance, tracking control for velocity and attitude was conducted by non-smooth backstepping control and fixed-time DO to compensate for the lumped disturbances [31]. In [32], a fixed-time DO was developed to approximate lumped perturbations by utilizing the proposed new fast fixed-time stable system. Note that the published outcomes related to fixed-time stability are subject to the following defects: One is that the observer gains are always selected and associated with the upper bound of disturbance and its derivative to assure stability. Another is that it is inferior in handling performance optimization. Thus, in the absence of an upper bound of disturbance and its derivative, how to develop a novel control policy capable of performance optimization and fixed-time disturbance attenuation deserves deep investigation.
Reinforcement learning (RL) provides an efficient way to derive performance optimization by pursuing the maximum cost function, which offers a numerical method for solving optimal control. In the control field, it is equivalent to approximate dynamic programming (ADP). Its core is to solve the Hamilton–Jacobi–Bellman (HJB) equation for approximating optimal policy and corresponding optimal cost function via NN approximators, avoiding the curse of dimensionality existing in solving the optimal control of nonlinear systems. In particular, the optimal cost function and optimal control policy are estimated with an actor–critic dual networks framework. For example, the nonlinear control is designed for a nonlinear perturbation system, where the worst-case disturbance is attenuated by incorporating zero-sum differential game theory into the ADP scheme [33]. Note that the worst case is considered in control with over-conservative properties. To achieve disturbance attenuation, there emerges a wide range of results related to the ADP technique. For instance, the identifier–critic–actor architecture is developed in [34] with a fuzzy logic system to derive optimal control for a nonlinear system. The fuzzy logic model is well-identified, accompanied by trial and error to tune parameters heuristically. In [35], the optimal control is designed within an actor–critic framework, where the extra neural network is employed to identify the unmodeled dynamic, incurring a heavy computation burden. Thus, some scholars have focused on critic-only ADP with less computation complexity. The critic NN is adopted to update optimal cost function and optimal policy for nonlinear known systems simultaneously [36]. Subsequently, a series of ADP results are reported for partially known nonlinear systems, where the robustness of a closed-loop system can be ensured by game theory [37,38], adding robust terms [39], sliding mode control [40], or DO [41]. Specifically, DO-based ADP is a mainstream solution to achieve robustness and optimal performance [42,43,44,45]. On the condition that the derivative of disturbance is close to zero, the optimal tracking control is considered in [42] by integrating improved DO with dual network ADP. In [43], by introducing finite-time DO with known upper bound information, an optimal sliding mode controller is designed based on actor–critic ADP. In [44], by combining with DO, the actor–critic ADP is employed to derive the optimal control of sliding-mode dynamics. The steady control input is put forward based on novel DO, and optimal control is derived for optimal regulation problems in a single-network ADP in [45].
It would be worth mentioning that the above-involved DOs were developed under the assumption that the upper bound of disturbance is available or its derivative tends to zero, which are troublesome and unsuitable for dealing with various kinds of disturbances in practical implementations. In addition, only the asymptotic or finite-time convergence of disturbance estimation errors can be achieved in the existing whole ADP control scheme, and hysteretic disturbance estimation may induce poor tracking performance. Note that fixed-time DO can enable disturbance estimation errors to converge to zero in a preassigned time in spite of initial estimation errors, but previously reported fixed-time DOs are established on the condition that the upper bound of disturbance is available. It is a challenge to estimate lumped disturbances for identifying a system without the assumption of bounded information on lumped disturbance. Moreover, the critic NN is conducted to approximate the optimal cost function and optimal policy to derive optimal control without actor NN.
Motivated by the previous discussion, a novel adaptive fixed-time disturbance observer (AFXDO)-based approximate optimal tracking control architecture for nonlinear partially unknown systems is considered, where AFXDO is designed such that the estimation of perturbation can be accomplished within a fixed time. Then, approximate optimal control is conducted by incorporating the real-time estimation of AFXDO into a critic-only ADP framework, where weight law with variable learning rate is embedded in a single network. The outstanding features of the devised scheme are:
(1) Compared with the presenting DO, the stability of perturbation estimation error can be guaranteed with finite-time convergence [24,25,26,27,28] or asymptotic convergence [21,22,23], and the investigated AFXDO can achieve the fixed-time stability of the estimation dynamic with the core of fixed-time stability system, ensuring that estimation error with fixed-time convergence with one power term. In addition, in view of the mentioned disturbance observer with a strong assumption about perturbation, the adaptive rule is employed to adjust observer gain, removing the rigid hypothesis on the known boundedness of perturbation [21,22,23,24].
(2) In contrast to the existing ADP framework with the actor–critic framework [42,43,44], the proposed ADP is a much simpler structure without using actor NN to estimate optimal policy. Different from the critic-only ADP framework with known upper-bounded information where the Bellman error is minimized by gradient descent [39,40], herein, by adaptive adjusting observer gain to estimate the perturbance, a controller is set up to eliminate the impact of perturbance, while the optimal controller is proposed with critic-only ADP with the weight law driven by extracted weight error conducted via filter operation, where the variable learning rate is utilized to fulfill faster weight convergence without initial chattering phenomenon. A brief comparison between current controllers and the proposed scheme is summarized in Table 1.

Table 1.
Comparison between the existing controllers and proposed scheme.
The remainder of this research is organized as follows: The problem formulation and its preliminaries are described in Section 3. In Section 4, the novel fixed-time observer is designed, while the optimal control policy is put forward with improved adaptive law and the stability analysis of improved adaptive law and error system are discussed. The simulation cases are carried out in Section 5. In Section 6, we present some conclusions.
3. Problem Formulation and Preliminaries
3.1. Problem Formulation
The nonlinear multi-input multi-output (MIMO) system is described with uncertain dynamics and perturbance as follows:
where denotes the state vector and is the control input. and indicate the dynamic drift and control gain matrix. is assumed to be an uncertain smooth and nonlinear function, which can be decomposed as with known and bounded uncertainty . The time-varying disturbance represents bounded perturbation. The desired tracking trajectory and its first derivate are supposed to be bounded, which can conduce the system being controllable on a compact set [46].
To fulfill optimal tracking control for system (1) with reference command, the tracking error is defined as . Thus, the tracking error of the system can be obtained by
For the purpose of deriving the tracking error accurately, the controller is decomposed into two parts: the feedforward controller and the optimal tracking controller . The feedforward controller with a positive-definite diagonal matrix is developed by compensating the reference command and known dynamic drift to reduce the region of tracking error. Thus, by substituting into (2), the dynamic of the tracking error can be converted into
The control objective of this paper is to develop the optimal control policy for a nonlinear system in despite of perturbation and uncertain mode uniformly, such that the following goals are achieved:
- (1)
- The disturbance estimation error can converge to zero in a fixed time.
- (2)
- The trajectory tracking error and weight estimation error are uniformly ultimately bounded (UUB).
- (3)
- The designed control input approximates the optimal control policy.
Remark 1.
In essence, there exist numerous nonlinear systems with disturbance and uncertainty, which can be expressed in the form of nonlinear MIMO systems (1) or high-order versions, such as robots [1], quadrotors [4], and MEMS [47], whereassumptions of the boundedness of the uncertainty and disturbance are acceptable. For the sake of analysis, we mainly focus on (1) as a first-order system, although the high-order system can be investigated via the proposed controller scheme incorporated with the backstepping technique. Different from the vast controllers explored in former works [22,23,24,25,26,27,28,29,30,31,32], where controllers lean on Lyapunov stability in the traditional framework, the investigated controller is based on the ADP scheme. Noting the uncertain term and disturbance in the system (3), the optimal tracking control will be clarified with AFXDO.
3.2. Related Lemmas
Lemma 1
([32]). Suppose that there exists a positive function satisfying
where with and and positive constants and , then can converge to the origin before the settling time:
Lemma 2
([48]). For positive number and positive integer , there holds
Lemma 3
([49]). For positive constants and with satisfying , there holds
with positive .
4. Main Results
In this section, the optimal tracking control based on AFXDO is developed to fulfill the specified goals in the above section. For the controller , the novel fixed-time observer is ingeniously investigated to estimate the synthesized unknown term with adaptive observer gains. By virtue of the designed observer, the optimal control is derived with a critic-only ADP scheme, where an improved adaptive law with a variable learning rate is established for weight update. The flowchart of the proposed controller can be described in Figure 1.
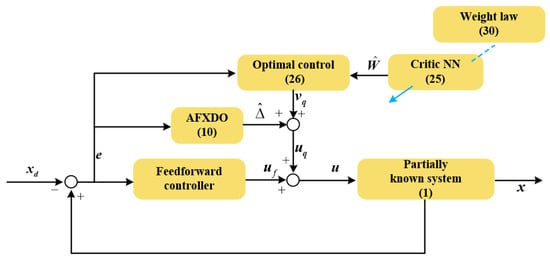
Figure 1.
The flowchart of the proposed controller.
4.1. Adaptive Fixed-Time Disturbance Observer
Inspired by [20], a novel AFXDO is developed without prior information of disturbance, ensuring that the estimation error converges to zero in a fixed time by virtue of adaptive observer gains. Noting that the uncertain dynamic drift and external disturbance are unknown, the AFXDO is conducted to estimate the synthesized unknown term as lumped disturbances:
Thus, the system (3) is transformed into , and the AFXDO is devised for each component of tracking error and lumped disturbances as
where and represent the estimation of tracking error and synthesized uncertainties , , for with positive constant . The parameters and are positive parameters, with and . The observer gains and are adapted from following rules:
with positive parameters , , , and to be chosen and . Theorem 1 is given for disturbance estimation error, which is proved in Appendix A.
Theorem 1.
Considering the system (1) and novel AFXDO (10) with adaptive gain update (11), the disturbance estimation error can converge to zero in a fixed time.
In view of the tracking error system (3), the feedback controller is set as follows:
where is employed to attenuate the impression of uncertainty and the extra term is the optimal control policy of the following system:
Remark 2.
The settling time is only related to the control parameters and does not vary along with the initial condition, which dominates superiority among other DOs with finite-time convergence [24,25,26,27,28] and asymptotic convergence [20,21,22,23]. In addition, there is one power term in the observer (10) rather than existing fixed-time DOs with two power terms [18,19,20] to achieve fixed-time convergence. Note that the fixed-time stable system in [32] can be shown in the following equation as
with positive constants and . Based on Lemma 1, we can derive settling time as
The improved version of (14) consisting of only the power term can be represented with positive constant as
which is the core of the designed observer. Moreover, the adaptive rule (11), which is simple and easily operated, can enable sufficiently large increases in and , removing the strict assumptions on perturbations, such as the known bounded information of the perturbation or its derivative and invariant perturbation [42,43]. Noting that there exist many parameters involved in the AFXDO, we summarize the fundamental guidelines for adjusting the observer performance as follows: The parameters ,
, , , and exponential related to , are key factors to guarantee the settling time and accuracy. Noting that the is the identical gain for and , we should make a compromise on the convergence rate and accuracy. In addition, the adaptive rules (11) are adopted for increasing gains and with adequate parameters for observer stability.
Remark 3.
Existing optimal controls based on the ADP scheme mainly concentrate on the optimal regulation problem, which is challenging for designing optimal tracking control, especially for uncertainty systems as well as nonvanishing tracking trajectories. The feedforward controller is conducted to compensate for the nonvanishing tracking trajectory and known drift dynamic. Thus, the optimal trajectory controller for system (1) is converted to an optimal regulation problem (3). For addressing the uncertainty, a novel AFXDO is ingeniously conducted for the estimation of lumped disturbances, where the disturbance estimation errors can converge to zero in a fixed time and observer gains are tuned adaptively without an assumption of the known upper bound of .
4.2. Optimal Tracking Control Scheme
The optimal control is considered to stabilize the system (13). Unlike the traditional controller in [29,30,31,32], there is only taking tracking performance into consideration without further exploring optimal control. A cost function is denoted related to tracking error and control input as
where with positive-definite diagonal matrices and . One can denote the optimal cost function:
Taking the time derivative of (18) along with (13), one can obtain the HJB equation as
where . According to (19), optimal control can be conducted by as
Noting that the optimal control (20) depends on the gradient of the cost function, i.e., , by substituting (20) into (19), the HJB Equation (19) can be represented as
However, it is difficult and even impossible to achieve the analytical solution due to the nonlinearity of the HJB equation. For addressing this issue, an NN approximator named critic-only NN is introduced to approximate the optimal cost function , and the optimal control policy can be achieved immediately rather than depending on another NN.
Specifically, the optimal cost function can be approximated by a single-layer NN, which can be expressed as
where represents the ideal weight of the NN, with indicating the number of neurons, being the corresponding activation function, and being the approximate error induced by the critic NN. From (22), the first derivative of with respect to tracking error can be obtained as
where and are the gradient of the activation function and approximation error with upper boundness and satisfying and . Thus, the optimal control can be given as:
Since the ideal weights that can accurately estimate the cost function are unavailable, its approximation can be estimated by estimation weight and corresponding regressors:
with representing an estimation of the ideal weight. The actual approximated optimal policy is induced by
Then approximation HJB Equation (19) with (26) can be expressed as
with being the HJB error associated with NN approximation error and disturbance error and denoting . With sufficiently large and the fixed-time convergence of AFXDO, it can be guaranteed that and converge to zero.
Then, (27) can be simplified as a linearization form:
with and . There have been many update laws for online updating weight, such as gradient descent and least squares methods [39,40] with fixed learning rates. Different from the Bellman error driving weight update in the inherent ADP schemes, the weight errors can be extracted by auxiliary operation, leading to the fact that weight errors can converge to the neighborhood of ideal weight and further enhance weight estimation performance—specifically, by introducing auxiliary matrix and vector , which are defined as:
with designed constant . Denoting , the estimation rule of weight in [50] can be employed for weight update as
with positive-definite diagonal matrices and and constant . The weight convergence can be guaranteed by following the theorem with ingenious derivation, in which there contains the weight error in (30).
Theorem 2.
For the approximation of the cost function with critic NN (22), if the estimation cost function can be evolved by the estimation of weight with update rule (30), the weight errors can be driven into the neighborhood of zero.
Proof of Theorem 2.
By integrating both sides of (29), the solution can be formulated as
Combined with (45), one can derive that there exists an auxiliary variable being associated to HJB error, i.e., , which satisfies . Following (30), this can be a further representation of the update rule:
where there exists a positive constant , such that holds. Obviously, the weight errors can be extracted via the update rule, leading to weight convergence. Under the condition that satisfies the persistent excitation (PE) condition, the positive-definite matrix can be derived from Lemma 1 in [50]. Consider the following Lyapunov function:
According to (30), one can derive the time derivative of , such that:
with denoting the minimized eigenvalue of the matrix, i.e., . By revisiting the Lyapunov theory, the weight errors can converge to the neighborhood of origin. □
Remark 4.
Contrary to most ADP schemes, where the Hamiltonian function is structured for the nominal system, the HJB equation is conducted related to (13), consisting of the estimation error, which leads to challenges for adjusting the optimal control policy and weight update. As opposed to the existing control within the ADP framework, where the weight update is carried out by minimizing the Bellman error with gradient descent [39,40], by imposing an auxiliary operation on intermediate parameters and employing the Gaussian function to tune the learning rate, the adaptive rule (30), which contains the weight errors, can compel the approximation of weight converge to an ideal weight. In particular, when the tracking error is far from the origin, is decreased to avoid the initial oscillation of weight, which further affects the control input. If the tracking error is close to zero, larger can enable online learning ability with an acceleration convergence of weight, and the PE condition can be easily verified by transferring it into the positive-definite property of matrix , avoiding introducing the concurrent learning or the experience replay employed in most ADP frameworks.
4.3. Stability Analysis
Theorem 3.
For the partially known nonlinear system (3) with uncertain parameters and unknown disturbance, by designing control (26) with weight updating laws (30), the following goals can be achieved.
- (1)
- The tracking error and weight error are UUB.
- (2)
- The approximate actual control input approximates the optimal control policy.
Proof of Theorem 3.
According to (13) and (26), there exist dynamics of tracking errors such as:
Thus, the following Lyapunov function is constructed for proving the stability of tracking errors:
with optimal function denoted by (18) and positive constants . In the following proof, each individual part of (36) is concretely analyzed based on Lemma 3.
First, we restate the convergence of as follows:
Thus, by substituting (35) into (36), it can be further reformulated in a simple form:
It can be derived from (31) that , so that
Therefore,
As long as , (40) can be rewritten as
with positive coefficients
Obviously, the upper bound of can be easily guaranteed from the NN approximation errors and HJB errors, while the observer error will converge to zero in a fixed time. If suitable parameters are selected to ensure the positiveness of , , and , it must satisfy the following conditions
Noting that critic NN errors can be bounded with finite constants, i.e., , it is obviously derived that as long as one of the following inequalities holds:
Furthermore, tracking error and NN weights error are UUB. From (24) and (26), one can infer that
Especially, if the critic NN error is zero, i.e., , we can obtain , resulting in
We can obtain from the Lyapunov Theorem, leading to and converging to zero. Thus, the actual control input approach to the optimal control policy is as follows:
□
5. Simulation and Discussion
We have simulated a typical disturbance nonlinear system and confirmed the availability and superiority of the optimal tracking control based on disturbance compensation. Whether it is a quadrotor or a UAV operating with a specific task, there is a complex nonlinear partially known system, which induces challenges for control design to realize tracking control. Many scholars have paid attention to this problem and achieved productive research [4,6]. The motion of the quadrotor can be described by the rigid body model, where the Euclidean position in an inertia frame and Euler angle in a body-fixed frame are expressed by and . Noting the rotation matrix
with representing roll, pitch, and yaw angles, and leaving out vane fluttering and air-operated friction, the dynamics of a quadrotor can be modeled as in the following formulae,
with and being mass and gravitational acceleration, . and are unknown bounded uncertainties. To employ the designed controller, (47) is transferred into the following compact form as
where
Denoting the synthesized unknown term as stated in (9), i.e., , the system parameters and reference command of position and velocity are listed in Table 2. The initial position and velocity are , .

Table 2.
Model parameters and reference commands.
On account of the mentioned controller design, the devised controller is based on AFXDO and optimal control policy, where the unknown term is estimated by AFXDO. The optimal control policy is designed based on the ADP framework with the novel adaptive law (30). The optimal cost function is approximated by critic NN, in which Gaussian basis functions are considered regressors
with , the width of the Gaussian function is set as , and the centers are evenly distributed over the state space . Correspondingly, we choose the initial weight for updating critic NN weights . The computer programming is clearly clarified in Table 3 with specific steps. We will verify the validity of the proposed scheme from the observer and weight law.

Table 3.
The computer programming of the proposed scheme.
- Case 1: Effect of disturbance observer on closed-loop performance
To verify the superiority of the proposed AFXDO, the following controllers are carried out, where different observers are inserted into the proposed ADP controller. For making a fair comparison, the controller parameters are set as: , , ,, and .
- (1)
- The designed ADP controller with extended state observer (ESO-ADP): The observer in [4] is utilized for the estimation of disturbance with the ADP framework. The bandwidth is set as .
- (2)
- The designed ADP controller with finite-time DO (FIDO-ADP): The finite-time DO in [28] is employed with adaptive gains to eliminate the effect of disturbance in a finite time. The parameters of the observer are set as , , , and .
- (3)
- The designed ADP controller with the proposed fixed-time DO (FXDO-ADP): During the operation of this method, we select the following parameters in AFXDO to ensure stability: , , , , and .
It is worth noting that the different observers are employed in the critic-only ADP scheme in the above algorithm. Based on the structure of the observer and the ADP framework, the time and space complexity are consistent. The simulation results are illustrated in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. The disturbance estimation via three observers and real disturbance is shown in Figure 1, where the disturbance estimation of different observers can accurately estimate the real disturbance within 2 s. In addition, the designed AFXDO with faster transient performance can achieve accurate disturbance estimation in 0.5 s. In order to verify that AFXDO can make the disturbance estimation error converge within a fixed time, the disturbance estimation errors via different observers are shown in Figure 3. Noting that the convergence time of the disturbance estimation error with FIDO is affected by the initial disturbance estimation error, when the initial estimation is poor, the convergence time will be larger. Compared with the optimal control based on ESO and FIDO, the optimal control based on AFXDO achieves accurate disturbance estimation in 0.5 s. The settling time of disturbance estimation error is irrelevant to the initial perturbation estimation error, which is less than the theoretical settling time of 17/3 s from Theorem 1. In Figure 4, the observer gains of AFXDO are depicted. Due to the design of the observer without the upper bound of the disturbance, the observer gain is updated adaptively online by (10), avoiding the assumption of a known upper bound of the disturbance.
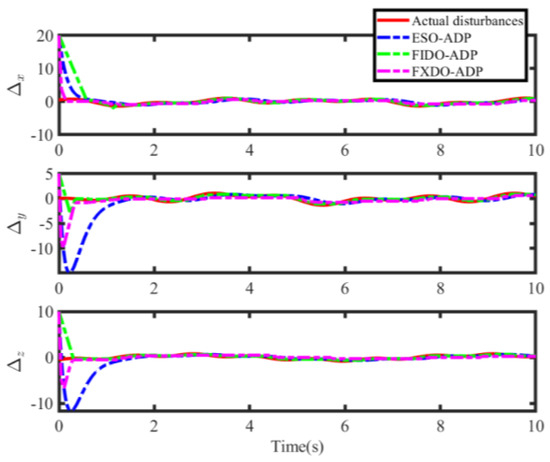
Figure 2.
The disturbance estimation via different observers.
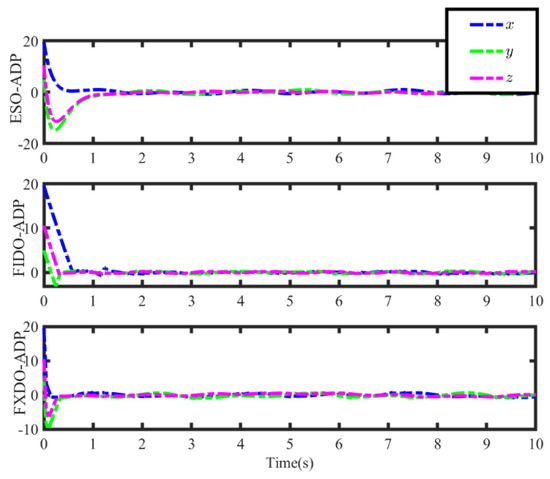
Figure 3.
The disturbance estimation error via different observers.
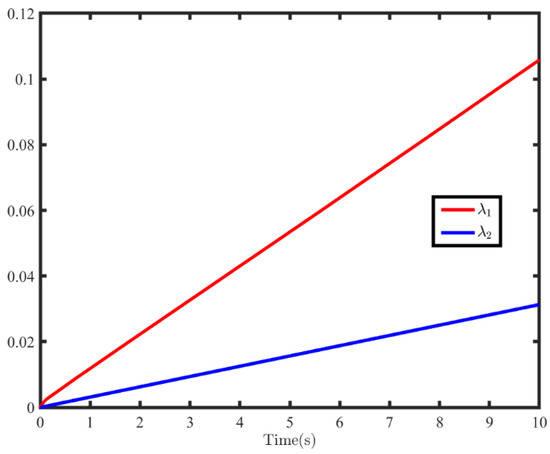
Figure 4.
The adaptive observer gains of AFXDO.
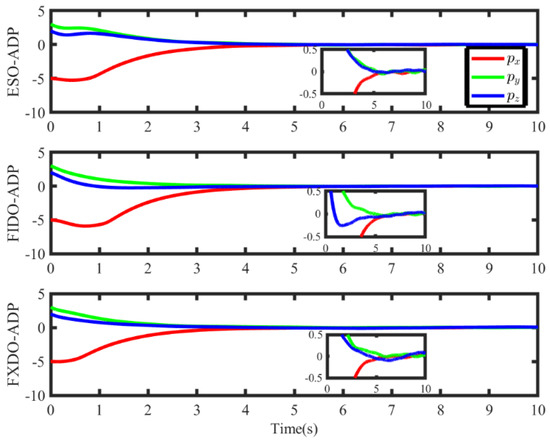
Figure 5.
The position tracking errors under three controllers.
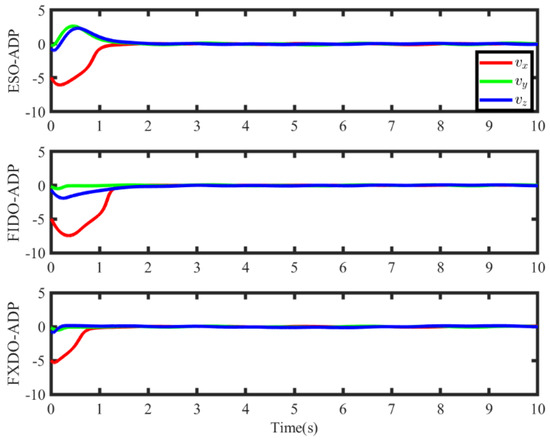
Figure 6.
The velocity tracking errors under three controllers.
As shown in Figure 3 and Figure 4, AFXDO achieves the rapid convergence of disturbance estimation. Due to the rapid convergence of disturbance, which will further affect the tracking performance, the position tracking error and velocity tracking error are shown under three controllers in Figure 5 and Figure 6. The accuracy of the position tracking error under the three controllers reaches 10−1 within 6 s. In addition, the trajectory tracking error of FXDO-ADP can enter steady-state performance within 5 s, which is smaller than that of the other two controllers, indicating that the rapid estimation of disturbance accelerates the convergence of the trajectory tracking error. As shown in Figure 5 and Figure 6, the velocity tracking errors with three controllers can enter the steady-state performance within 2 s. For ESO-ADP and FIDO-ADP, the tracking errors of FIDO-ADP can achieve steady-state performance within 1.3 s, which is faster than that of ESO-ADP. Further, the tracking errors of FXDO-ADP can enter the steady state within 1 s. Therefore, the transient performance of AFXDO-ADP is better than that of the ESO-ADP and FIDO-ADP controllers in terms of tracking errors of position and velocity. Due to the fact that AFXDO can make disturbance estimation follow real disturbance in a fixed time, the position and velocity tracking errors can enter a steady state within a short time.
Taking channel as an example, Figure 7 compares the control inputs of the three controllers, where the control inputs of FXDO-ADP and ESO-ADP are less. Combined with tracking errors in Figure 5 and Figure 6, the FXDO-ADP can achieve the rapid convergence of tracking errors with equivalent control consumption. Therefore, the controller makes the predefined cost function smaller among the three controllers.
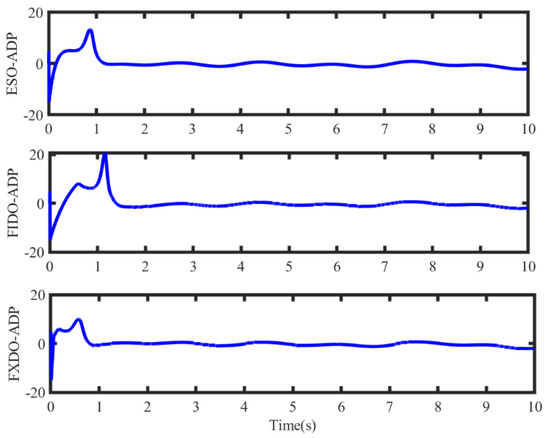
Figure 7.
The control inputs under three controllers.
- Case 2: Effect of weight update on learning performance
To explore the effectiveness of weight update for deriving the optimal policy, we compare the tracking performance and cost consumptions among the following schemes:
- (1)
- The designed ADP controller with a fixed learning rate (ADPFLR) [50]: The fixed learning rate is set as to accelerate the convergence of tracking errors.
- (2)
- The designed ADP controller with a proposed variable learning rate (ADPVLR): The weight is updated by (30) rather than the fixed learning rate in ADPFLR. The parameters are selected as , .
- (3)
- The actor–critic ADP controller with the gradient method [35] (ADP2): The learning rate in actor and critic NNs are set as , .
Different from critic-only ADP, there exist the actor NN and critic NN to conduct the actor–critic ADP, which leads to the space and time complexity increasing due to the extra actor NN. In addition, on account of the variable learning rate designed with tracking errors, the space and time complexity are nonincreasing, where the tracking error is essential for other weight laws. The simulation results are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. In Figure 8 and Figure 9, the position tracking error and velocity tracking error under three controllers are shown, where different weight laws are employed under the ADP framework. The position tracking error enters the steady-state performance within 5 s, and the velocity tracking error converges to the neighborhood of origin within 2 s. In specific, the ADP based on critic NN has better transient performance than the ADP2 control based on the actor–critic NN in terms of velocity tracking errors and can achieve accurate tracking within 1 s, which is due to the hysteresis caused by weight convergence of the actor–critic NN.
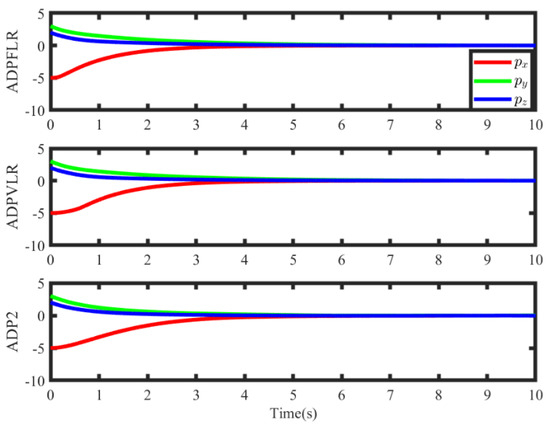
Figure 8.
The position tracking errors under different controllers.
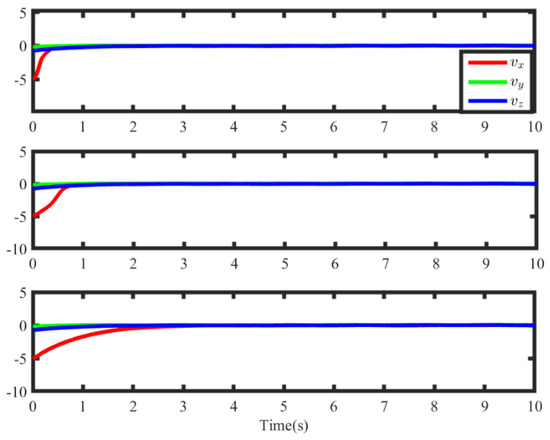
Figure 9.
The velocity tracking errors under different controllers.
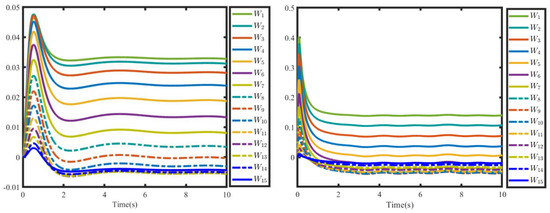
Figure 10.
The weights in actor and critic NNs of ADP2.
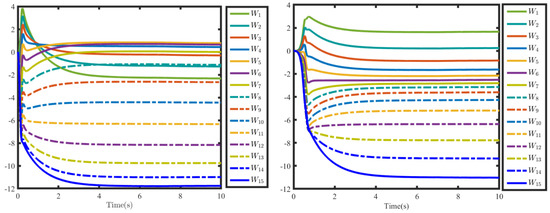
Figure 11.
The weights of ADPFLR and ADPVLR.
Figure 12.
The control inputs under different controllers.
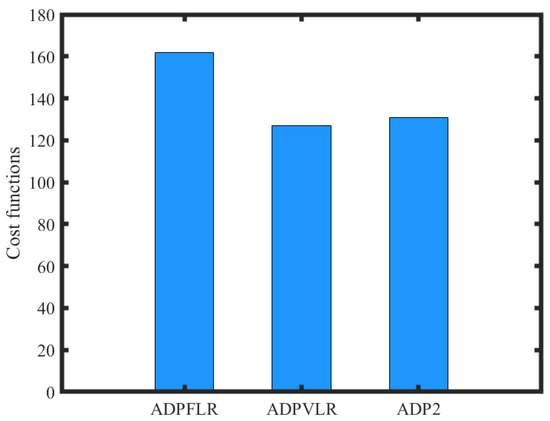
Figure 13.
The comparison of cost functions.
Figure 10 and Figure 11 show the weight of the NN under the three controllers. The weights of the actor NN and critic NN in ADP2 are described in Figure 10, where the weight estimation of the critic NN and actor NN have obvious chattering at the initial stage. Conversely, the weight of the critic NN converges to an ideal weight based on critic-only ADP, as shown in Figure 11. Under the critic-only ADP framework, the weight update law of critic NN extracts the weight error through the auxiliary filtering operation, such that the weight update is driven by the weight error implied in the updated law, resulting in the fast convergence of weight. Furthermore, Figure 11 compares the weight of ADPFLR and ADPVLR. As shown in Figure 11, the ADPVLR significantly reduces the chattering occurring at the initial stage of ADPFLR with a fixed learning rate, which indicates that the proposed variable learning rate is superior to the weight update with a fixed learning rate. Specifically, its key features can be described thus: when the tracking error is large, the learning rate is reduced to avoid chattering; when the tracking error is small, the learning rate is increased to accelerate the convergence rate.
Since the convergence of weight affects the optimal control, the control inputs of three controllers in the channel are shown in Figure 12. Compared with ADPFLR and ADPVLR, the control input of ADPVLR is smaller, which can be due to the weight of the variable learning rate when avoiding the initial large control input. In addition, the control input of ADP2 is small, which leads to the slow convergence of tracking errors. Considering both tracking errors and control consumption, the cost functions of the three controllers are shown in Figure 13, where ADPFLR with a fixed learning rate requires high control consumption to achieve fast tracking performance. By the weight update law (30), the cost function of ADPVLR is decreased by 19.13% from that of ADPFLR. By introducing the weight updating law of variable learning rate, ADPVLR has a tradeoff ability in control consumption and tracking performance, which not only achieves better tracking performance but also ensures lower control consumption.
By analyzing the effectiveness of disturbance observer and new weight law, although AFXDO is carried with large control consumption to achieve faster convergence, by combining AFXDO and weight law with a variable learning rate, the optimal control consumption is reduced, so the total control consumption is decreased, which induces lower cost functions.
Different from the uncertainty of the above system, , we set the only to unknown for a sensitive analysis of the system. The tracking performance of position and velocity are shown in Figure 14 and Figure 15. The position and velocity can follow the reference position and velocity in 4 s. The weight of the critic NN is described in Figure 16, avoiding the initial chattering phenomenon. We will validate the effectiveness of the completely unknown system in actual application.
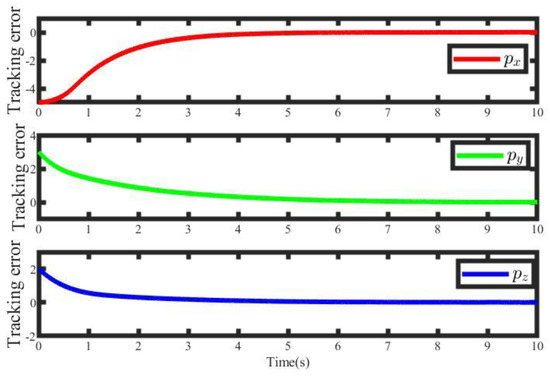
Figure 14.
The position tracking errors.
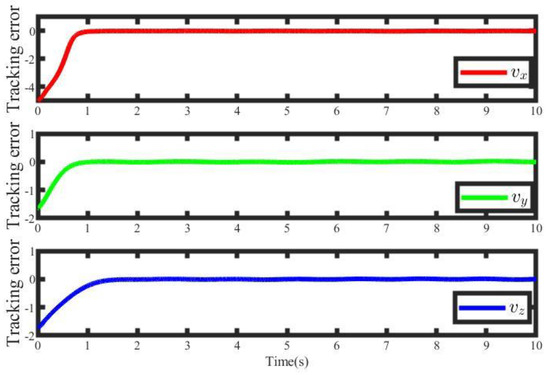
Figure 15.
The velocity tracking errors.
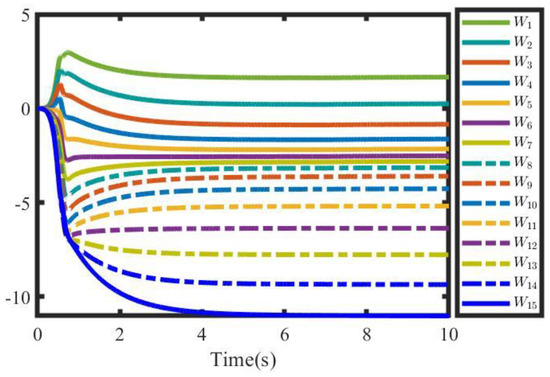
Figure 16.
The weight of critic NN.
6. Conclusions
The approximate tracking control with adaptive fixed-time estimation is developed to address the tracking problem of partially unknown nonlinear systems. After the procession of feedforward control for the error system, the novel adaptive fixed-time disturbance observer is designed such that the estimation error for disturbance can converge to zero within a fixed time. Then, an optimal control policy is derived by the critic-only ADP framework, where a novel weight adaptive law with a variable learning rate is proposed for updating weight without initial oscillation phenomena. The tracking errors and weight estimation errors can be proven to be UUB. The designed approximate optimal policy approaches the optimal control. The superiority of the proposed controller can be verified in the simulation, which well balances tracking performance and control consumption. Noting that control input and tracking error may exceed the capacity of the actuator and predefined region, which is not considered in controller design, future work will concentrate on the extension of the proposed controller with a new cost function for a partially unknown nonlinear system with input saturation and output constraints to reduce control consumption and improve tracking performance.
Author Contributions
Conceptualization, Y.G. and Z.L.; methodology, Y.G. and Z.L.; software, Y.G.; validation, Y.G.; formal analysis, Y.G.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G. and Z.L.; supervision, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the first author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The following derivation process is given for the settling time of disturbance estimation errors.
Proof.
Based on the observer (10), the observer error dynamics can be derived as
For simplicity and clarity, the following analyses are based on each component of estimation errors. Denote and the following candidate Lyapunov function is chosen:
with and . When , differentiating along (11) and (12) gives
As , and , it follows along (7) in Lemma 2 that
where
Furthermore, it follows for that
As , it follows from (6) in Lemma 2 that
where
Thus, the settling time of state error can be obtained as
After enters the sliding mode surface , holds according to the sliding-mode equivalent control theory, which yields the restatement of the disturbance dynamic as
with
Another Lyapunov function is considered as
where . Considering the above-mentioned two cases and following a similar technique, one can derive from that
with
Otherwise, it follows from that
with
After the settling time , the settling time of the perturbation estimation error can be computed as
Therefore, one can achieve after the settling time , which indicates perturbation estimation errors equal to zero. Among the observers, the adaptive observer gains and are increasing sufficiently to compensate for the impression of perturbation and remain unchanged after entering sliding mode surfaces for the estimation of state and perturbation. □
References
- Castellini, A.; Marchesini, E.; Farinelli, A. Partially observable monte carlo planning with state variable constraints for mobile robot navigation. Eng. Appl. Artif. Intell. 2021, 104, 104382. [Google Scholar] [CrossRef]
- Dai, Y.; Ni, S.; Xu, D.; Zhang, L.; Yan, X.G. Disturbance-observer based prescribed-performance fuzzy sliding mode control for PMSM in electric vehicles. Eng. Appl. Artif. Intell. 2021, 104, 104361. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. Quantized-communication-based neural network control for formation tracking of networked multiple unmanned surface vehicles without velocity information. Eng. Appl. Artif. Intell. 2022, 114, 105160. [Google Scholar] [CrossRef]
- Shao, X.; Yue, X.; Li, J. Event-triggered robust control for quadrotors with preassigned time performance constraints. Appl. Math. Comput. 2021, 392, 125667. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, G.; Wang, D. Observer-based fixed-time adaptive fuzzy control for SbW systems with prescribed performance. Eng. Appl. Artif. Intell. 2022, 114, 105026. [Google Scholar] [CrossRef]
- Wu, L.; Li, Z.; Liu, S.; Li, Z.; Sun, D. A novel multi-agent model-free adaptive control algorithm for a class of multivehicle systems with constraints. Symmetry 2023, 15, 168. [Google Scholar] [CrossRef]
- Wu, J.; Sun, W.; Su, S.F.; Wu, Y. Adaptive asymptotic tracking control for input-quantized nonlinear systems with multiple unknown control directions. IEEE Trans. Cybern. 2022, in press. [Google Scholar] [CrossRef]
- Qiyas, M.; Abdullah, S.; Khan, F.; Naeem, M. Banzhaf-Choquet-Copula-based aggregation operators for managing fractional orthotriple fuzzy information. Alex. Eng. J. 2022, 61, 4659–4677. [Google Scholar] [CrossRef]
- Khan, A.; Ashraf, S.; Abdullah, S.; Muhammad, A.; Thongchai, B. A novel decision aid approach based on spherical hesitant fuzzy Aczel-Alsina geometric aggregation information. AIMS Math. 2023, 8, 5148–5174. [Google Scholar] [CrossRef]
- Qiyas, M.; Naeem, M.; Abdullah, S.; Khan, F.; Khan, N.; Garg, H. Fractional orthotriple fuzzy rough Hamacher aggregation operators and-their application on service quality of wireless network selection. Alex. Eng. J. 2022, 61, 10433–10452. [Google Scholar] [CrossRef]
- Yahya, M.; Abdullah, S.; Almagrabi, A.O.; Botmart, T. Analysis of S-box based on image encryption application using complex fuzzy credibility Frank aggregation operators. IEEE Access 2022, 10, 88858–88871. [Google Scholar] [CrossRef]
- Mohammad, M.M.S.; Abdullah, S.; Al-Shomrani, M.M. Some linear Diophantine fuzzy similarity measures and their application in decision making problem. IEEE Access 2022, 10, 29859–29877. [Google Scholar] [CrossRef]
- Qiyas, M.; Madrar, T.; Khan, S.; Abdullah, S.; Botmart, T.; Jirawattanapaint, A. Decision support system based on fuzzy credibility Dombi aggregation operators and modified TOPSIS method. AIMS Math. 2022, 7, 19057–19082. [Google Scholar] [CrossRef]
- Ahmad, S.; Basharat, P.; Abdullah, S.; Botmart, T.; Jirawattanapanit, A. MABAC under non-linear diophantine fuzzy numbers: A new approach for emergency decision support systems. AIMS Math. 2022, 7, 17699–17736. [Google Scholar] [CrossRef]
- Midrar, T.; Khan, S.; Abdullah, S.; Botmart, T. Entropy based extended TOPOSIS method for MCDM problem with fuzzy credibility numbers. AIMS Math. 2022, 7, 17286–17312. [Google Scholar] [CrossRef]
- Ashraf, S.; Rehman, N.; Abdullah, S.; Batool, B.; Lin, M.; Aslam, M. Decision support model for the patient admission scheduling problem based on picture fuzzy aggregation information and TOPSIS methodology. Math. Biosci. Eng. 2022, 19, 3147–3176. [Google Scholar] [CrossRef]
- Batool, B.; Abdullah, S.; Ashraf, S.; Ahmad, M. Pythagorean probabilistic hesitant fuzzy aggregation operators and their application in decision-making. Kybernetes 2022, 51, 1626–1652. [Google Scholar] [CrossRef]
- Abdullah, S.; Al-Shomrani, M.M.; Liu, P.; Ahmad, S. A new approach to three-way decisions making based on fractional fuzzy decision-theoretical rough set. Int. J. Intell. Syst. 2022, 37, 2428–2457. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Chinram, R. Emergency decision support modeling under generalized spherical fuzzy Einstein aggregation information. J. Ambient Intell. Humaniz. Comput. 2022, 13, 2091–2117. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Zheng, S.; Lu, S.; Zhao, Q. Event-triggered fractional-order tracking control for an uncertain nonlinear system with output saturation and disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2022, in press. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Tie, M. Hybrid adaptive learning neural network control for steer-by-wire systems via sigmoid tracking differentiator and disturbance observer. Eng. Appl. Artif. Intell. 2021, 104, 104393. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Shen, G.; Xia, Y. Disturbance observer-based adaptive finite-time attitude tracking control for rigid spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6606–6613. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Nguyen, V.Q.; Le, K.M.; Tran, H.N.; Jeon, J.W. An adaptive sliding-mode controller with a modified reduced-order proportional integral observer for speed regulation of a permanent magnet synchronous motor. IEEE Trans. Ind. Electron. 2021, 69, 7181–7191. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Oh, H.; Kim, Y.; Moon, J.; Yang, J.; Chen, W.H. Finite-time disturbance observer-based modified super-twisting algorithm for systems with mismatched disturbances: Application to fixed-wing UAVs under wind disturbances. Int. J. Robust Nonlin. Control 2021, 31, 7317–7343. [Google Scholar] [CrossRef]
- Mirzaei, M.J.; Mirzaei, M.; Aslmostafa, E.; Asadollahi, M. Robust observer-based stabilizer for perturbed nonlinear complex financial systems with market confidence and ethics risks by finite-time integral sliding mode control. Nonlinear Dyn. 2021, 105, 2283–2297. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, W.X.; Wang, G. Distributed finite-time optimization of second-order multiagent systems with unknown velocities and disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2022, in press. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Zhao, Z.; Tang, X.; Yang, J.; Chen, I. Finite-time disturbance observer-based trajectory tracking control for flexible-joint robots. Nonlinear Dyn. 2021, 106, 459–471. [Google Scholar] [CrossRef]
- Huang, D.; Huang, T.; Qin, N.; Li, Y.; Yang, Y. Finite-time control for a UAV system based on finite-time disturbance observer. Aerosp. Sci. Technol. 2022, 129, 107825. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control. 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Sun, L.; Sun, G.; Jiang, J. Disturbance observer-based saturated fixed-time pose tracking for feature points of two rigid bodies. Automatica 2022, 144, 110475. [Google Scholar] [CrossRef]
- Sun, J.; Yi, J.; Pu, Z.; Tan, X. Fixed-time sliding mode disturbance observer-based nonsmooth backstepping control for hypersonic vehicles. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 4377–4386. [Google Scholar] [CrossRef]
- Gao, J.; Fu, Z.; Zhang, S. Adaptive fixed-time attitude tracking control for rigid spacecraft with actuator faults. IEEE Trans. Ind. Electron. 2018, 66, 7141–7149. [Google Scholar] [CrossRef]
- Hu, G.; Guo, J.; Guo, Z.; Cieslak, J.; Henry, D. ADP-based intelligent tracking algorithm for reentry vehicles subjected to model and state uncertainties. IEEE Trans. Ind. Informat. 2022, in press. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Modares, H.; Xu, C.Z. Robust actor-critic learning for continuous-time nonlinear systems with unmodeled dynamics. IEEE Trans. Fuzzy Syst. 2021, 30, 2101–2112. [Google Scholar] [CrossRef]
- El-Sousy, F.F.; Amin, M.M.; Al-Durra, A. Adaptive optimal tracking control via actor-critic-identifier based adaptive dynamic programming for permanent-magnet synchronous motor drive system. IEEE Trans. Ind. Appl. 2021, 57, 6577–6591. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Optimal Control of Affine Nonlinear Continuous-Time Systems. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 1568–1573. [Google Scholar]
- Xue, S.; Luo, B.; Liu, D. Event-triggered adaptive dynamic programming for zero-sum game of partially unknown continuous-time nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3189–3199. [Google Scholar] [CrossRef]
- Wang, D.; Mu, C.; Liu, D.; Ma, H. On mixed data and event driven design for adaptive-critic-based nonlinear H∞ control. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 993–1005. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Q.; Dong, H.; Zhao, X. ADP-based spacecraft attitude control under actuator misalignment and pointing constraints. IEEE Trans. Ind. Electron. 2017, 69, 9342–9352. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.T.; Tian, B.L.; Zong, Q. Event-based robust optimal consensus control for nonlinear multiagent system with local adaptive dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 2022, in press. [Google Scholar] [CrossRef]
- Song, R.; Lewis, F.L. Robust optimal control for a class of nonlinear systems with unknown disturbances based on disturbance observer and policy iteration. Neurocomputing 2020, 390, 185–195. [Google Scholar] [CrossRef]
- Pham, T.L.; Dao, P.N. Disturbance observer-based adaptive reinforcement learning for perturbed uncertain surface vessels. ISA Trans. 2022, 130, 277–292. [Google Scholar]
- Dong, H.; Yang, X. Learning-based online optimal sliding-mode control for space circumnavigation missions with input constraints and mismatched uncertainties. Neurocomputing 2022, 484, 13–25. [Google Scholar] [CrossRef]
- Zhang, H.; Park, J.H.; Yue, D.; Zhao, W. Nearly optimal integral sliding-mode consensus control for multiagent systems with disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4741–4750. [Google Scholar] [CrossRef]
- Xia, R.; Wu, Q.; Shao, S. Disturbance observer-based optimal flight control of near space vehicle with external disturbance. Trans. Inst. Meas. Control. 2020, 42, 272–284. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Shao, X.; Shi, Y.; Zhang, W. Input-and-measurement event-triggered output-feedback chattering reduction control for MEMS gyroscopes. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 5579–5590. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control. Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L.M. Uniform robust exact differentiator. IEEE Trans. Autom. Control. 2011, 56, 2727–2733. [Google Scholar] [CrossRef]
- Na, J.; Lv, Y.; Zhang, K.; Zhao, J. Adaptive identifier-critic-based optimal tracking control for nonlinear systems with experimental validation. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 459–472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).