Ollivier–Ricci Curvature Based Spatio-Temporal Graph Neural Networks for Traffic Flow Forecasting
Abstract
1. Introduction
- We introduce an edge bottleneck coefficient based on the Ollivier–Ricci curvature to measure the bottleneck coefficient of edges in the road network and take the neighborhood-to-neighborhood connectivity into consideration.
- We design a curvature graph convolution module to utilize this coefficient to guide the message-passing process of STGNNs and enhance their ability to capture the spatial dependence of road network nodes.
- Experiments conducted on two real-world traffic prediction benchmark datasets show that the proposed enhancement strategy for STGNNs based on Ollivier–Ricci curvature is effective.
2. Related Work
2.1. Deep Learning-Based Traffic Forecasting Methods
2.2. Spatial Dependence Graph Construction
2.3. Connection between Discrete Ricci Curvature and Network Properties
3. Methodology
3.1. Problem Definition
3.2. Ollivier–Ricci Curvature of Graphs
3.3. Curvature Enhanced Graph Neural Networks
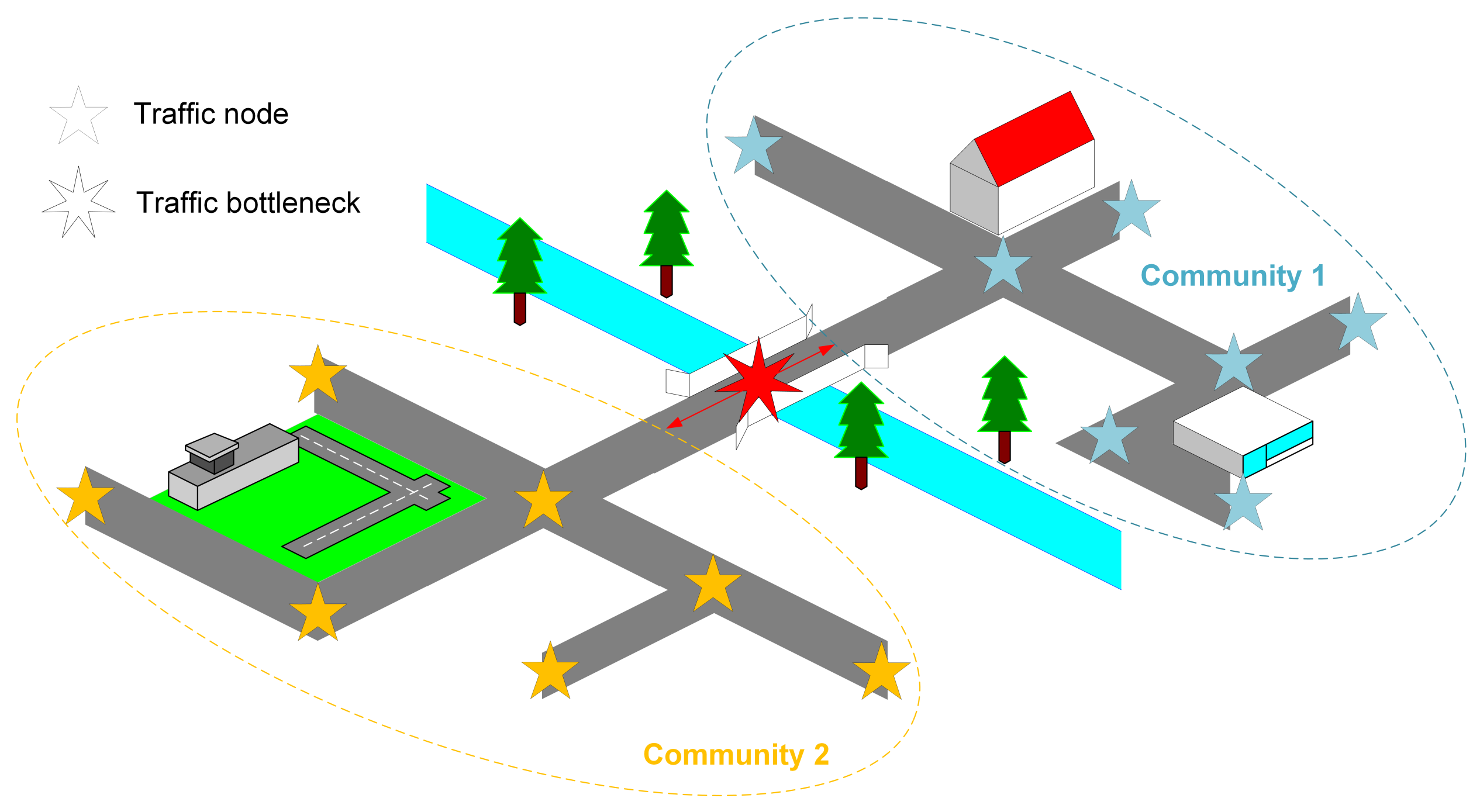
3.3.1. Edge Bottleneck Coefficients
3.3.2. Curvature Graph Convolution Module
3.3.3. Loss Function
4. Experiments
4.1. Data Description
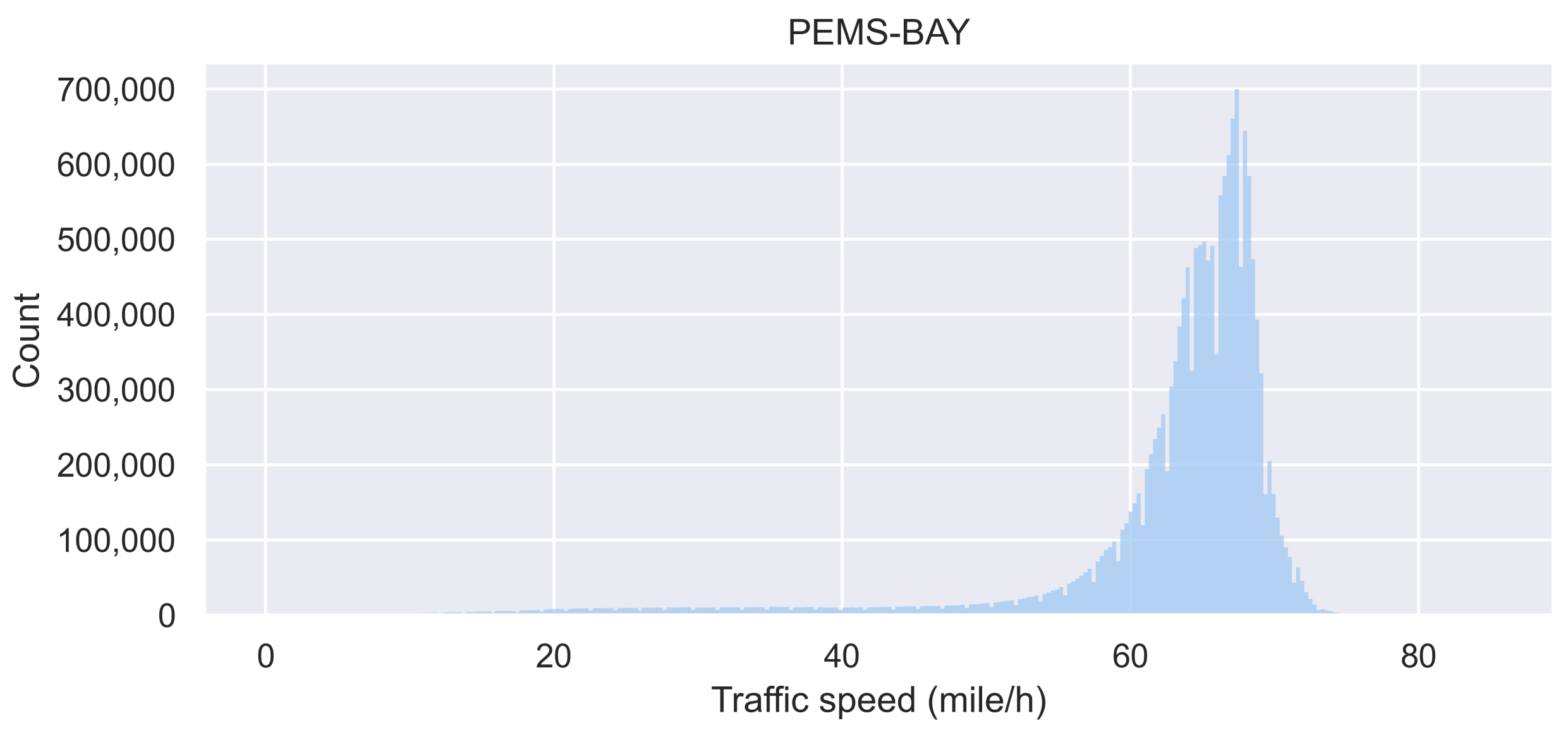
- PEMS–BAY. PEMS–BAY dataset is a traffic speed dataset collected by California Transportation Agencies (CalTrans), containing the traffic speed data from 1 January 2017 to 30 June 2017, collected from 325 sensors. The data distribution is shown in Figure 5.
- PEMSD7. PEMSD7 dataset contains traffic flow data collected by 883 sensors in District 7 of California from 1 July 2016 to 31 August 2016. The data distribution is shown in Figure 6.
4.2. Backbone Models and Evaluation Metrics
4.2.1. Backbone Models
- STGCN [21]In STGCN, the spatial dependence of traffic data is modeled by GCN, where the graph for message propagation is constructed based on the spatial distance between nodes. The temporal dependence is modeled by a 1D convolutional neural network.
- T-GCN [18]T-GCN adopts GCN and GRU to model spatial dependence and temporal dependence, respectively. The graph for message propagation is constructed based on spatial distances.
4.2.2. Comparison Setup
4.2.3. Evaluation Metrics
- Mean absolute error (MAE):
- Mean absolute percentage error (MAPE):
- Root mean squared error (RMSE):
4.3. Experimental Setup
4.3.1. Data Splitting
4.3.2. Data Preprocessing
- Distance-based message passing (node-to-node graph structure)For models using spatial distance information to guide message passing, to ensure the numerical stability of the training process, the distances between nodes are mapped to distance correlation indices by a Gaussian kernel as shown in Equation (13).
- Curvature-based message passing (neighborhood-to-neighborhood graph structure)To ensure the computational efficiency of message passing and lower the sparsity of the edge curvature matrix R, we mask R according to the sparse distance-based graph, i.e., only the curvature information of the connected edges of the closer nodes is considered. The mask matrix M is defined as Equation (14).The mask operation to the edge curvature matrix R is shown as Equation (16).where , and ⨀ denotes Hadamard product.
4.3.3. Hyperparameter Settings
4.4. Experimental Results
4.4.1. Quantitative Comparison Analysis
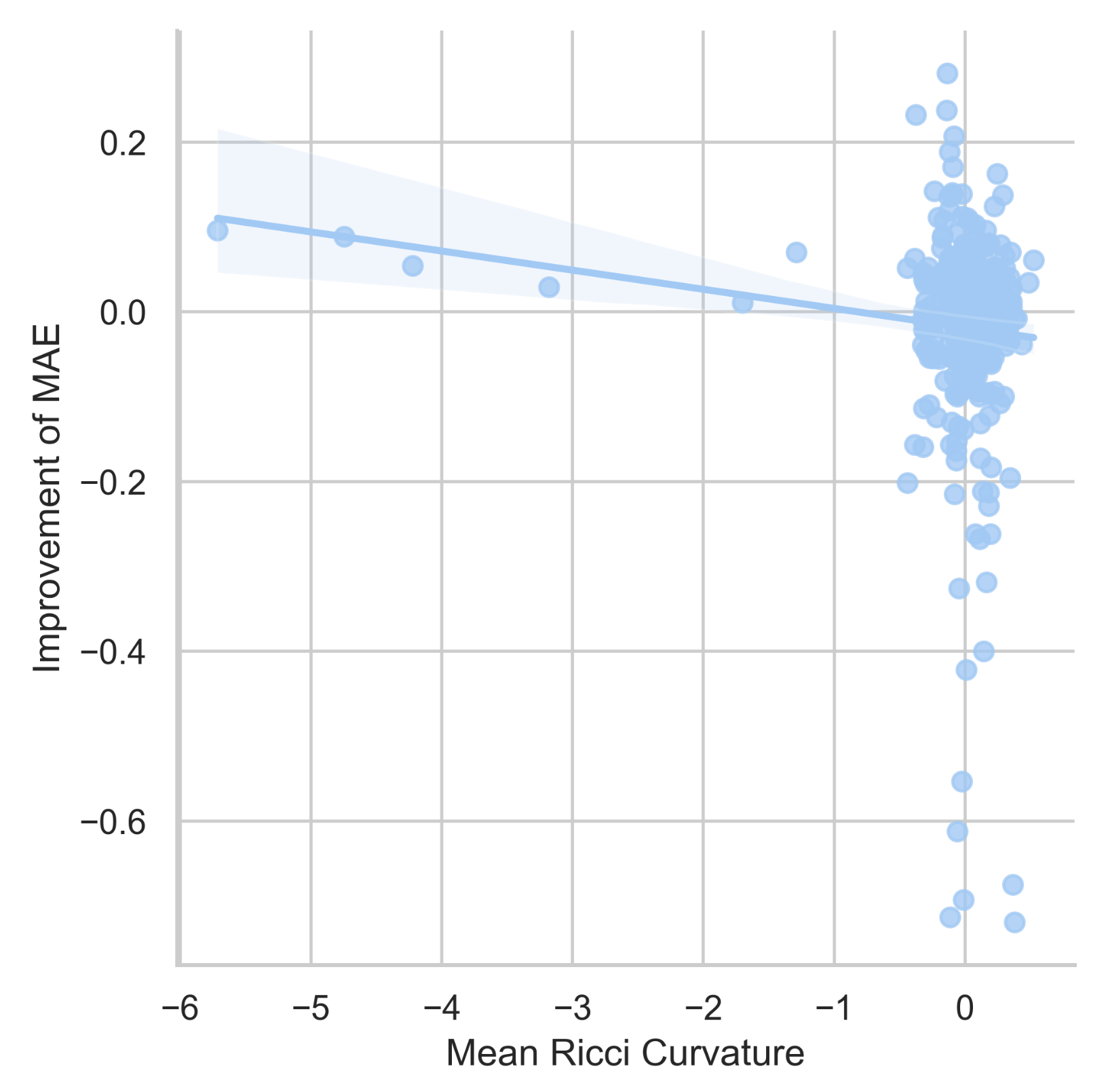
4.4.2. Relations between Ollivier–Ricci Curvature and Performance Improvement
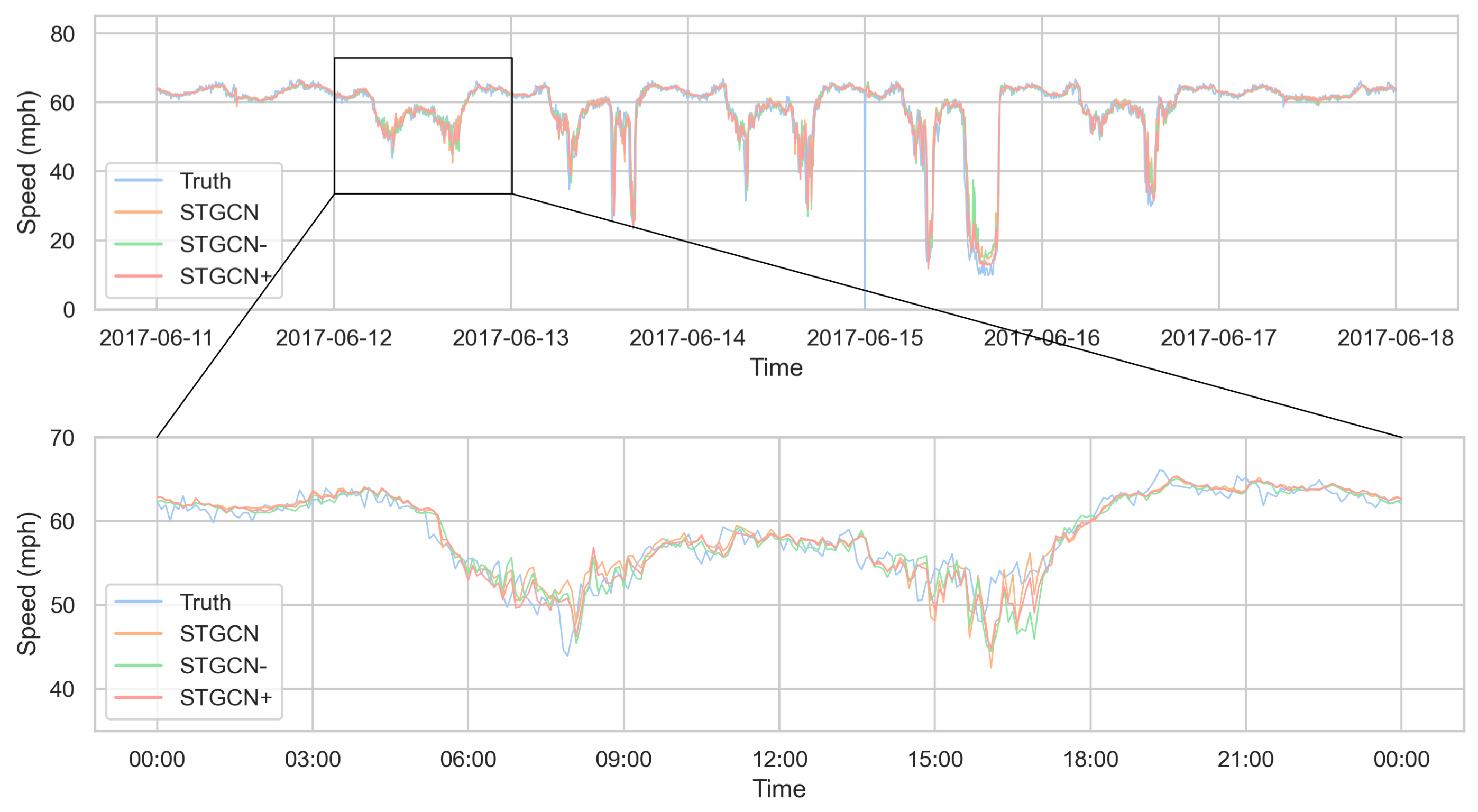
4.4.3. Qualitative Visualization Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STGNN | Spatio-temporal Graph Neural Network |
| GNN | Graph Neural Networks |
| MPNN | Message Passing Neural Networks |
| CNN | Convolutional Neural Networks |
| RNN | Recurrent Neural Networks |
| GRU | Gated Recurrent Unit |
| ARIMA | Autoregressive Integrated Moving Average |
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- Bui, K.H.N.; Cho, J.; Yi, H. Spatial-temporal graph neural network for traffic forecasting: An overview and open research issues. Appl. Intell. 2021, 52, 2763–2774. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MA, USA, 20–23 February 2023; pp. 1263–1272. [Google Scholar]
- Guo, K.; Hu, Y.; Qian, Z.; Liu, H.; Zhang, K.; Sun, Y.; Gao, J.; Yin, B. Optimized graph convolution recurrent neural network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1138–1149. [Google Scholar] [CrossRef]
- Xu, D.; Dai, H.; Wang, Y.; Peng, P.; Xuan, Q.; Guo, H. Road traffic state prediction based on a graph embedding recurrent neural network under the SCATS. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 103125. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Chen, F.; Wan, Y. Graph attention LSTM network: A new model for traffic flow forecasting. In Proceedings of the 2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; pp. 241–245. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Kang, Z.; Xu, H.; Hu, J.; Pei, X. Learning dynamic graph embedding for traffic flow forecasting: A graph self-attentive method. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2570–2576. [Google Scholar]
- Lee, K.; Rhee, W. DDP-GCN: Multi-graph convolutional network for spatiotemporal traffic forecasting. Transp. Res. Part C Emerg. Technol. 2022, 134, 103466. [Google Scholar] [CrossRef]
- Ollivier, Y. Ricci curvature of Markov chains on metric spaces. J. Funct. Anal. 2009, 256, 810–864. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Oord, A.v.d.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AR, USA, 12–17 February 2016; Volume 31. [Google Scholar]
- Ali, A.; Zhu, Y.; Zakarya, M. A data aggregation based approach to exploit dynamic spatio-temporal correlations for citywide crowd flows prediction in fog computing. Multimed. Tools Appl. 2021, 80, 31401–31433. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. Adv. Neural Inf. Process. Syst. 2018, 31, 5171–5181. [Google Scholar]
- Li, H.; Cao, J.; Jun, J.; Luo, Q.; He, S.; Wang, X. Augmentation-Free Graph Contrastive Learning of Invariant-Discriminative Representations. IEEE Trans. Neural Networks Learn. Syst. 2023. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Zhu, J.; Han, X.; Deng, H.; Tao, C.; Zhao, L.; Wang, P.; Lin, T.; Li, H. KST-GCN: A knowledge-driven spatial-temporal graph convolutional network for traffic forecasting. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15055–15065. [Google Scholar] [CrossRef]
- Ali, A.; Zhu, Y.; Zakarya, M. Exploiting dynamic spatio-temporal graph convolutional neural networks for citywide traffic flows prediction. Neural Netw. 2022, 145, 233–247. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph wavenet for deep spatial-temporal graph modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Z. Spatial-temporal fusion graph neural networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 4189–4196. [Google Scholar]
- He, S.; Shin, K.G. Towards fine-grained flow forecasting: A graph attention approach for bike sharing systems. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 88–98. [Google Scholar]
- Samal, A.; Sreejith, R.; Gu, J.; Liu, S.; Saucan, E.; Jost, J. Comparative analysis of two discretizations of Ricci curvature for complex networks. Sci. Rep. 2018, 8, 8650. [Google Scholar] [CrossRef]
- Ni, C.C.; Lin, Y.Y.; Luo, F.; Gao, J. Community detection on networks with Ricci flow. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Gao, L.; Liu, X.; Liu, Y.; Wang, P.; Deng, M.; Zhu, Q.; Li, H. Measuring road network topology vulnerability by Ricci curvature. Phys. A Stat. Mech. Its Appl. 2019, 527, 121071. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Yin, G.; Li, H.; Yang, L.; Su, Y.; Liu, Y.; Shan, X. Applying Ollivier-Ricci curvature to indicate the mismatch of travel demand and supply in urban transit network. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102666. [Google Scholar] [CrossRef]
- Wang, C.; Jonckheere, E.; Banirazi, R. Wireless network capacity versus Ollivier-Ricci curvature under Heat-Diffusion (HD) protocol. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3536–3541. [Google Scholar]
- Forman, R. Bochner’s method for cell complexes and combinatorial Ricci curvature. Discret. Comput. Geom. 2003, 29, 323–374. [Google Scholar] [CrossRef]
- Weber, M.; Saucan, E.; Jost, J. Characterizing complex networks with Forman-Ricci curvature and associated geometric flows. J. Complex Netw. 2017, 5, 527–550. [Google Scholar] [CrossRef]
- Saucan, E.; Wolansky, G.; Appleboim, E.; Zeevi, Y.Y. Combinatorial ricci curvature and laplacians for image processing. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; pp. 1–6. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational Optimal Transport. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Singapore, 20–23 February 2023; pp. 214–223. [Google Scholar]
- Kusner, M.; Sun, Y.; Kolkin, N.; Weinberger, K. From word embeddings to document distances. In Proceedings of the International Conference on Machine Learning, PMLR, Singapore, 20–23 February 2023; pp. 957–966. [Google Scholar]
- Li, H.; Cao, J.; Zhu, J.; Liu, Y.; Zhu, Q.; Wu, G. Curvature graph neural network. Inf. Sci. 2022, 592, 50–66. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, J. Introduction to graph neural networks. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–127. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. PyTorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Wang, J.; Jiang, J.; Jiang, W.; Li, C.; Zhao, W.X. Libcity: An open library for traffic prediction. In Proceedings of the 29th International Conference on Advances in Geographic Information Systems, Beijing, China, 2–5 November 2021; pp. 145–148. [Google Scholar]
- Ni, C.C.; Lin, Y.Y.; Gao, J.; Gu, X.D.; Saucan, E. Ricci curvature of the internet topology. In Proceedings of the 2015 IEEE conference on computer communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 2758–2766. [Google Scholar]






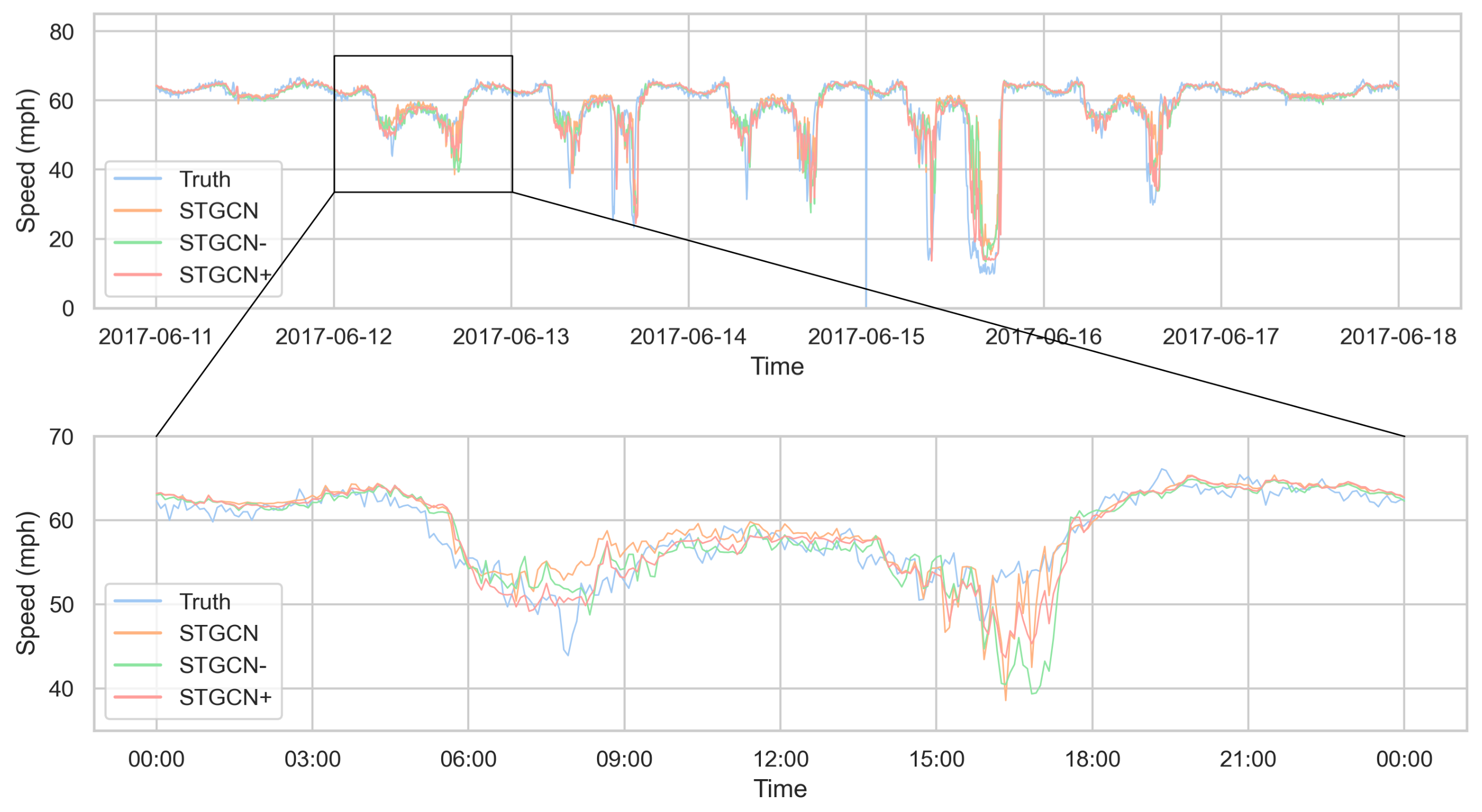
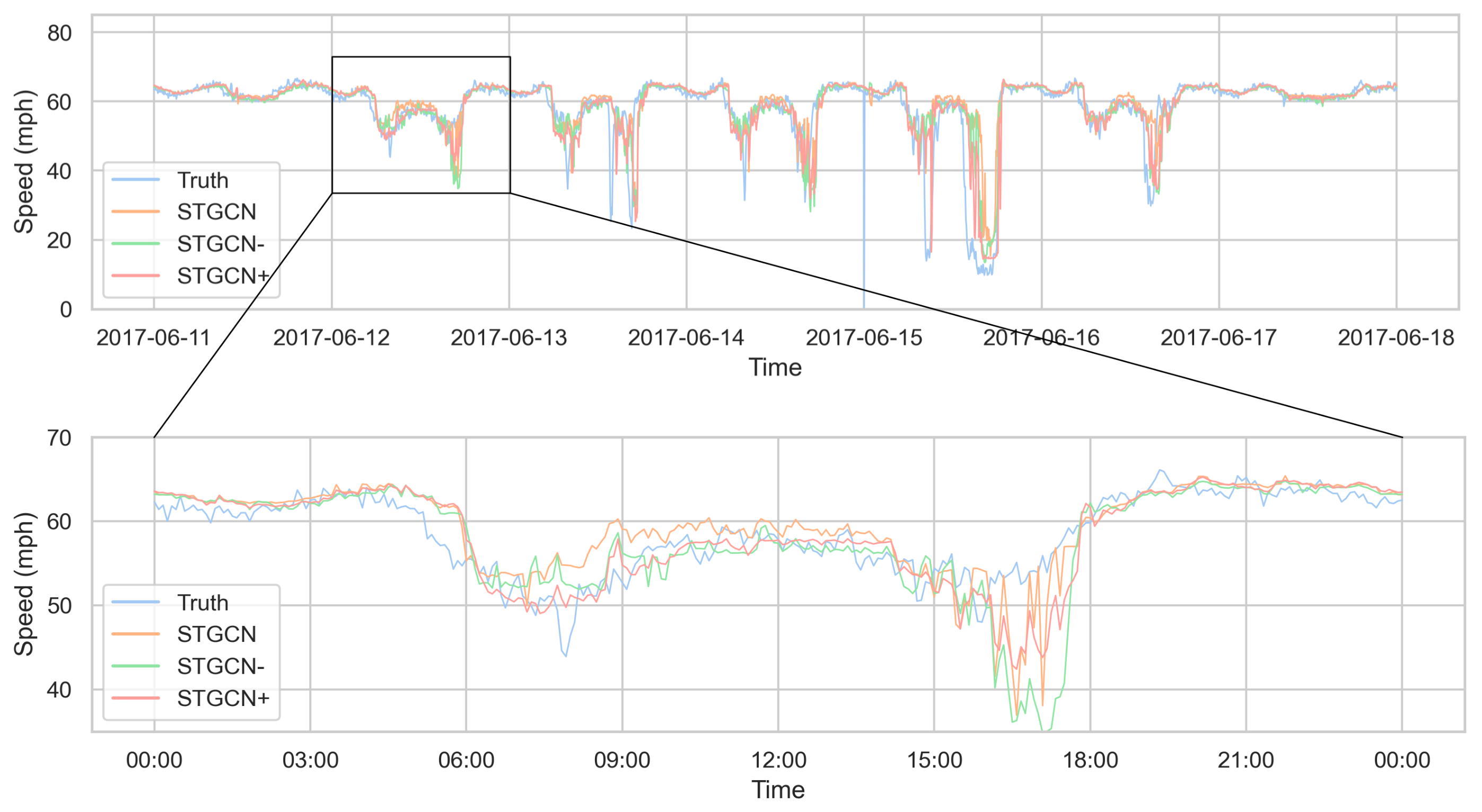
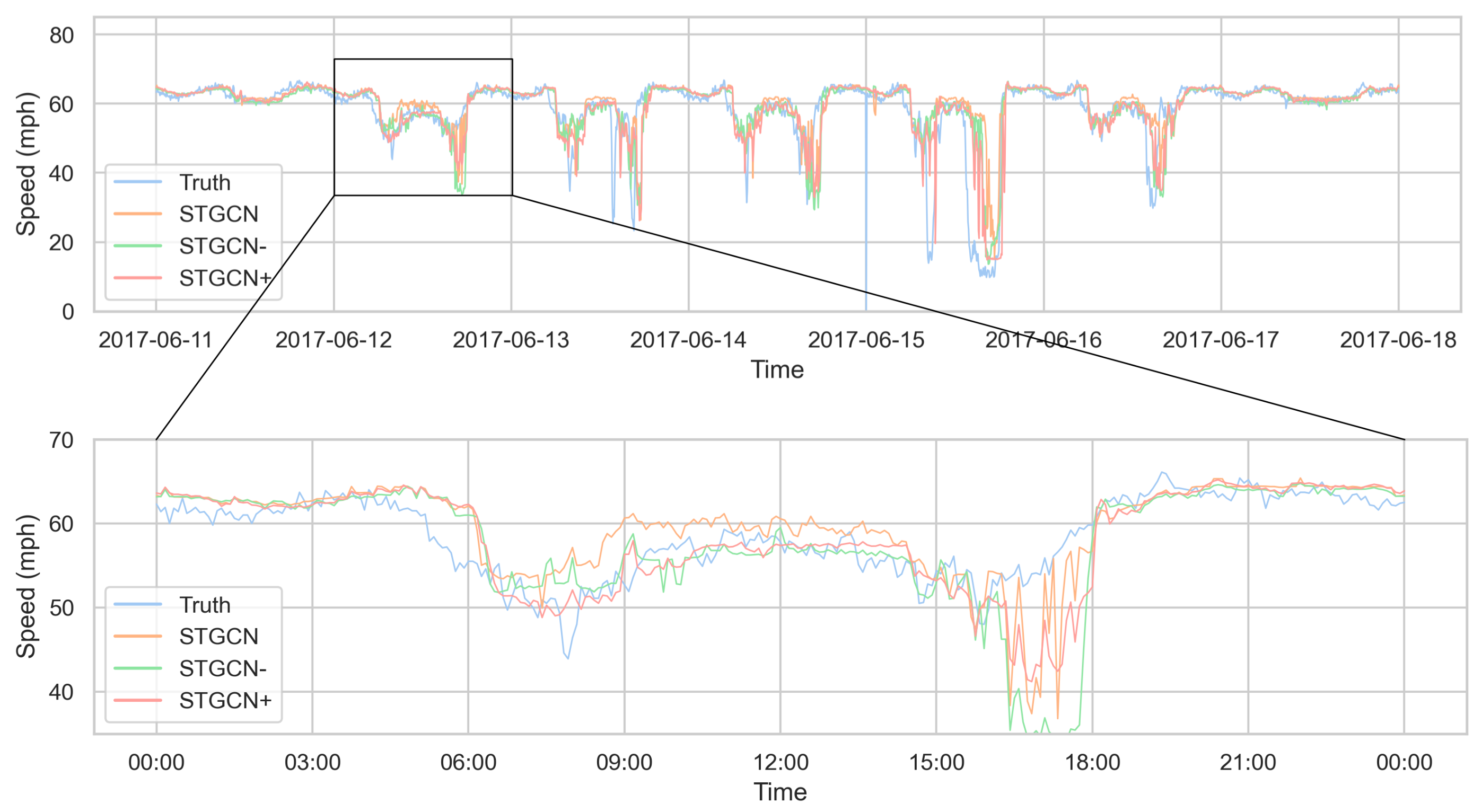
| Dataset | Number of Nodes | Sampling Interval | Time Span | Feature to be Predicted |
|---|---|---|---|---|
| PEMS-BAY | 325 | 5 min | 1 January 2017–30 June 2017 | Speed |
| PEMSD7 | 883 | 5 min | 1 July 2016–31 August 2016 | Flow |
| Model | Guidelines for Message Propagation | Spatial Dependence | Perspective on Measuring Relations |
|---|---|---|---|
| Backbone | Spatial distance graph | Spatial distance | node-to-node |
| Backbone+ | Edge bottleneck factor | Local topological structure | Neighborhood-to-neighborhood |
| Backbone- | Adjacency graph | Adjacency | node-to-node |
| Model | PEMS_BAY(15/30/45/60 min) | ||
|---|---|---|---|
| MAE | MAPE(%) | RMSE | |
| STGCN- | 1.426/1.904/2.233/2.491 | 3.15/4.63/5.58/6.24 | 3.002/4.325/5.122/5.669 |
| STGCN | 1.423/1.908/2.241/2.501 | 3.13/4.49/5.37/6.00 | 2.991/4.284/5.051/5.607 |
| STGCN+ | 1.400/1.878/2.223/2.516 | 2.98/4.34/5.27/6.01 | 2.907/4.176/4.983/5.608 |
| TGCN- | 1.714/2.112/2.381/2.616 | 3.62/4.71/5.41/6.00 | 3.228/4.110/4.596/4.990 |
| TGCN | 2.302/2.659/2.953/3.206 | 4.99/6.03/6.85/7.58 | 4.222/5.048/5.614/6.083 |
| TGCN+ | 1.613/2.109/2.464/2.774 | 3.37/4.69/5.68/6.54 | 3.147/4.254/4.955/5.494 |
| Model | PEMSD7(15/30/45/60 min) | ||
|---|---|---|---|
| MAE | MAPE(%) | RMSE | |
| STGCN- | 21.782/26.689/30.704/36.661 | 9.59/11.96/14.61/17.10 | 33.474/39.730/46.166/52.936 |
| STGCN | 21.409/25.053/28.437/31.608 | 9.28/10.87/12.41/13.80 | 33.423/38.328/42.671/46.803 |
| STGCN+ | 20.657/24.205/27.600/30.676 | 8.91/10.58/12.32/13.83 | 32.354/37.052/41.413/45.529 |
| TGCN- | 43.877/46.337/50.332/55.393 | 25.54/26.52/28.67/32.07 | 60.802/64.241/69.519/76.424 |
| TGCN | 37.439/40.000/43.732/49.147 | 22.89/24,45/27.02/31.26 | 52.751/56.269/61.202/68.157 |
| TGCN+ | 25.883/29.743/34.012/38.838 | 13.01/14.79/17.10/19.86 | 38.186/43.477/48.979/55.259 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Zhu, G.; Zhao, L.; Du, R.; Wang, Y.; Chen, Z.; Liu, Y.; He, S. Ollivier–Ricci Curvature Based Spatio-Temporal Graph Neural Networks for Traffic Flow Forecasting. Symmetry 2023, 15, 995. https://doi.org/10.3390/sym15050995
Han X, Zhu G, Zhao L, Du R, Wang Y, Chen Z, Liu Y, He S. Ollivier–Ricci Curvature Based Spatio-Temporal Graph Neural Networks for Traffic Flow Forecasting. Symmetry. 2023; 15(5):995. https://doi.org/10.3390/sym15050995
Chicago/Turabian StyleHan, Xing, Guowei Zhu, Ling Zhao, Ronghua Du, Yuhan Wang, Zhe Chen, Yang Liu, and Silu He. 2023. "Ollivier–Ricci Curvature Based Spatio-Temporal Graph Neural Networks for Traffic Flow Forecasting" Symmetry 15, no. 5: 995. https://doi.org/10.3390/sym15050995
APA StyleHan, X., Zhu, G., Zhao, L., Du, R., Wang, Y., Chen, Z., Liu, Y., & He, S. (2023). Ollivier–Ricci Curvature Based Spatio-Temporal Graph Neural Networks for Traffic Flow Forecasting. Symmetry, 15(5), 995. https://doi.org/10.3390/sym15050995







