Propagation of Ultrashort Optical Pulses in Fractal Objects
Abstract
1. Introduction
2. Power Laws of Dispersion
3. Model and Methods
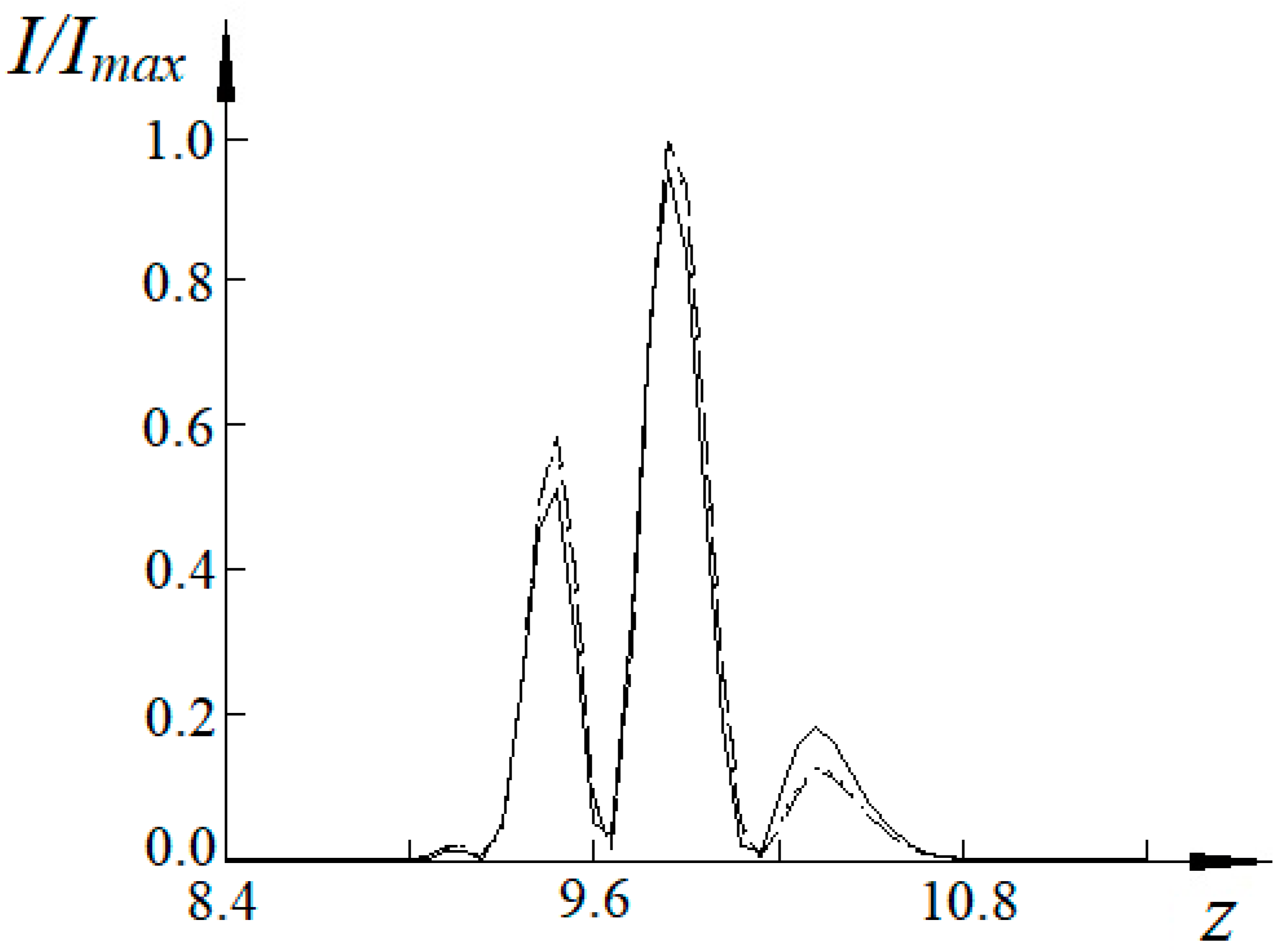
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hausdorff, F. Dimension und äußeres Maß. Math. Ann. 1918, 79, 157–179. [Google Scholar] [CrossRef]
- Saberi, A.A. Fractal structure of a three-dimensional Brownian motion on an attractive plane. Phys. Rev. E 2011, 84, 021113. [Google Scholar] [CrossRef] [PubMed]
- Husain, A.; Reddy, J.; Bisht, D.; Sajid, M. Fractal dimension of coastline of Australia. Sci. Rep. 2021, 11, 6304. [Google Scholar] [CrossRef] [PubMed]
- Marusina, M.Y.; Mochalina, A.P.; Frolova, E.P.; Satikov, V.I.; Barchuk, A.A.; Kuznetcov, V.I.; Gaidukov, V.S.; Tarakanov, S.A. MRI image processing based on fractal analysis. Asian Pac. J. Cancer Prev. 2017, 18, 51–55. [Google Scholar] [CrossRef]
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 2019, 6587138. [Google Scholar] [CrossRef]
- Eskandari, Z.; Keshtkar, A.; Ahmadi-Shokouh, J.; Ghanbari, L. Fractal Analysis—Applications in Physics, Engineering and Technology; Brambila, F., Ed.; IntechOpen: London, UK, 2017; Chapter 4. [Google Scholar] [CrossRef]
- Wallace, G.Q.; Lagugne-Labarthet, F. Advancements in fractal plasmonics: Structures, optical properties, and applications. Analyst 2019, 144, 13–30. [Google Scholar] [CrossRef]
- Sroor, H.; Naidoo, D.; Miller, S.W.; Nelson, J.; Courtial, J.; Forbes, A. Fractal light from lasers. Phys. Rev. A 2019, 99, 013848. [Google Scholar] [CrossRef]
- De Nicola, F.; Purayil, N.S.P.; Spirito, D.; Miscuglio, M.; Tantussi, F.; Tomadin, A.; De Angelis, F.; Polini, M.; Krahne, R.; Pellegrini, V. Multiband plasmonic Sierpinski carpet fractal antennas. ACS Photonics 2018, 5, 2418–2425. [Google Scholar] [CrossRef]
- Jia, S.; Fleischer, J.W. Nonlinear light propagation in fractal waveguide arrays. Opt. Express 2010, 18, 14409–14415. [Google Scholar] [CrossRef]
- Alexander, S.; Laerman, C.; Orbach, R.; Rosenberg, H.M. Fracton interpretation of vibrational properties of cross-linked polymers, glasses and irradiated quartz. Phys. Rev. B 1983, 28, 4615–4619. [Google Scholar] [CrossRef]
- Pretko, M.; Chen, X.; You, Y. Fracton phases of matter. Int. J. Mod. Phys. A 2020, 35, 2030003. [Google Scholar] [CrossRef]
- Vijay, S.; Haah, J.; Fu, L. Fracton topological order, generalized lattice gauge theory, and duality. Phys. Rev. B 2016, 94, 235157. [Google Scholar] [CrossRef]
- Nandkishore, R.M.; Hermele, M. Fractons. Annu. Rev. Condens. Matter Phys. 2019, 10, 295–313. [Google Scholar] [CrossRef]
- Konobeeva, N.N.; Belonenko, M.B. Tunneling current of fractal object with metal and superlattice. Nanosyst. Phys. Chem. Math. 2023, 14, 54–58. [Google Scholar] [CrossRef]
- Weiner, A.M. Ultrafast Optics; Wiley: New York, NY, USA, 2009; p. 598. [Google Scholar]
- Sazonov, S.V. On the nonlinear optics of the ultimately short pulses. Opt. Spectrosc. 2022, 130, 549–558. [Google Scholar] [CrossRef]
- Leblond, H.; Mihalache, D. Models of few optical cycle solitons beyond the slowly varying envelope approximation. Phys. Rep. 2013, 523, 61–126. [Google Scholar] [CrossRef]
- Dvuzhilova, Y.V.; Dvuzhilov, I.S.; Zaporotskova, I.V.; Galkina, E.N.; Belonenko, M.B. Three-dimensional few cycle optical pulses in optically anisotropic photonic carbon nanotube based crystals including nonlinear absorption. Rom. Rep. Phys. 2022, 74, 401. [Google Scholar]
- Dvuzhilova, Y.V.; Dvuzhilov, I.S.; Konobeeva, N.N.; Belonenko, M.B. Ultrashort optical pulses in photonic crystal with superlattice and defects. Rom. Rep. Phys. 2021, 73, 404. [Google Scholar]
- Mihalache, D. Localized structures in optical and matter-wave media: A selection of recent studies. Rom. Rep. Phys. 2021, 73, 403. [Google Scholar]
- Chowdhury, D.; Raju, S.; Sachdev, S.; Singh, A.; Strack, P. Multipoint correlators of conformal field theories: Implications for quantum critical transport. Phys. Rev. B 2013, 87, 085138. [Google Scholar] [CrossRef]
- Charmousis, C.; Gouteraux, B.; Kim, B.S.; Kiritsis, E.; Meyer, R. Effective holographic theories for low-temperature condensed matter systems. J. High Energy Phys. 2010, 2010, 151. [Google Scholar] [CrossRef]
- Maldacena, J. The Large-N Limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Di Francesco, P.; Mathieu, P.; Sénéchal, D. Conformal Field Theory; Springer: New York, NY, USA, 1997; p. 890. [Google Scholar]
- Nakayama, Y. Scale invariance vs conformal invariance. arXiv 2013, arXiv:1302.0884. [Google Scholar] [CrossRef]
- Policastro, G.; Son, D.T.; Starinets, A.O. From AdS/CFT correspondence to hydrodynamics. II. Sound waves. J. High Energy Phys. 2002, 12, 54. [Google Scholar] [CrossRef]
- Pal, S.S. Model building in AdS/CMT: DC conductivity and Hall angle. arXiv 2011, arXiv:1011.3117v4. [Google Scholar] [CrossRef]
- Konobeeva, N.N.; Belonenko, M.B. Propagation of few cycle optical pulses in marginal Fermi liquid and ADS/CFT correspondence. Phys. B Condens. Matter 2015, 478, 43–46. [Google Scholar] [CrossRef]
- Belonenko, M.B.; Konobeeva, N.N.; Galkina, E.N. Dynamics of few cycle optical pulses in a non-Fermi liquid and AdS/CFT correspondence. Mod. Phys. Lett. B 2015, 29, 1550096. [Google Scholar] [CrossRef]
- Vlasov, S.N.; Petrishchev, V.A.; Talanov, V.I. Averaged description of wave beams in linear and nonlinear media (the method of moments). Radiophys. Quantum Electron. 1971, 14, 1062–1070. [Google Scholar] [CrossRef]
- Silberberg, Y. Collapse of optical pulses. Opt. Lett. 1990, 15, 1282–1284. [Google Scholar] [CrossRef]
- Faulkner, T.; Polchinski, J. Semi-holographic Fermi liquids. J. High Energy Phys. 2011, 2011, 12. [Google Scholar] [CrossRef]
- Rashba, E.I. Properties of semiconductors with an extremum loop. I. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 1960, 2, 1109–1122. [Google Scholar]
- Ohkawa, F.J.; Uemura, Y. Quantized surface states of a narrow-gap semiconductor. J. Phys. Soc. Jpn. 1974, 37, 1325–1333. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Rashba, E.I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C Solid State Phys. 1984, 17, 6039–6045. [Google Scholar] [CrossRef]
- Datta, S.; Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 1990, 56, 665–667. [Google Scholar] [CrossRef]
- Konobeeva, N.N.; Belonenko, M.B. Multidimensional light bullets in Fermi liquid in the presence of magnetic field and AdS/CFT correspondence. Nanosyst. Phys. Chem. Math. 2017, 8, 365–370. [Google Scholar] [CrossRef][Green Version]
- Aufray, B.; Kara, A.; Vizzini, S.; Oughaddou, H.; Léandri, C.; Ealet, B.; Lay, G.L. Graphene-like silicon nanoribbons on Ag(110): A possible formation of silicene. Appl. Phys. Lett. 2010, 96, 183102. [Google Scholar] [CrossRef]
- De Padova, P.; Quaresima, C.; Ottaviani, C.; Sheverdyaeva, P.M.; Moras, P.; Carbone, C.; Topwal, D.; Olivieri, B.; Kara, A.; Oughaddou, H.; et al. Evidence of graphene-like electronic signature in silicene nanoribbons. Appl. Phys. Lett. 2010, 96, 261905. [Google Scholar] [CrossRef]
- Konobeeva, N.N.; Belonenko, M.B. Multidimensional ultimately short optical pulses in silicene. Tech. Phys. Lett. 2017, 43, 386–389. [Google Scholar] [CrossRef]
- Konobeeva, N.N.; Belonenko, M.B. Two-dimensional extremely short optical pulses in silicene with random electric fields. arXiv 2016, arXiv:1611.01106v1. [Google Scholar] [CrossRef]
- Zhukov, A.; Bouffanais, R.; Konobeeva, N.N.; Belonenko, M.B. Peculiarities of the propagation of multidimensional extremely short optical pulses in germanene. Phys. Lett. A 2016, 380, 3117–3120. [Google Scholar] [CrossRef]
- Zhukov, A.; Bouffanais, R.; Belonenko, M.B.; Konobeeva, N.N.; George, T.F. Few-cycle optical pulses in a thin film of a topological insulator. Opt. Commun. 2014, 329, 151–153. [Google Scholar] [CrossRef]
- Xue, J.; Sanchez-Yamagishi, J.; Bulmash, D.; Jacquod, P.; Deshpande, A.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P.; LeRoy, B.J. Scanning tunnelling microscopy and spectroscopy of ultra-flat graphene on hexagonal boron nitride. Nat. Mater. 2011, 10, 282–285. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, E.; Ruter, C.E.; Stepic, M.; Shandarov, V.; Kip, D. Dark and bright blocker soliton interaction in defocusing waveguide arrays. Opt. Expr. 2006, 14, 11248–11255. [Google Scholar] [CrossRef] [PubMed]
- Belonenko, M.B.; Konobeeva, N.N.; Tuzalina, O.Y. Stabilization of electromagnetic solitons in thin films of topological insulators by constant electric field. Eur. Phys. J. B 2014, 87, 192. [Google Scholar] [CrossRef]
- Zosimov, V.V.; Lyamshev, L.M. Fractals and scaling in acoustics. Akust. Zhurnal 1994, 40, 709–737. [Google Scholar]
- Zhukov, A.V.; Bouffanais, R.; Fedorov, E.G.; Belonenko, M.B. Three-dimensional electromagnetic breathers in carbon nanotubes with the field inhomogeneity along their axes. J. Appl. Phys. 2013, 114, 143106. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; p. 356. [Google Scholar]
- Kim, M.H.; Yoon, D.H.; Kim, I. Lower and upper bounds for the anomalous diffusion exponent on Sierpinski carpets. J. Phys. A Math. Gen. 1993, 26, 5655–5660. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belonenko, M.B.; Zaporotskova, I.V.; Konobeeva, N.N. Propagation of Ultrashort Optical Pulses in Fractal Objects. Symmetry 2023, 15, 1035. https://doi.org/10.3390/sym15051035
Belonenko MB, Zaporotskova IV, Konobeeva NN. Propagation of Ultrashort Optical Pulses in Fractal Objects. Symmetry. 2023; 15(5):1035. https://doi.org/10.3390/sym15051035
Chicago/Turabian StyleBelonenko, Mikhail B., Irina V. Zaporotskova, and Natalia N. Konobeeva. 2023. "Propagation of Ultrashort Optical Pulses in Fractal Objects" Symmetry 15, no. 5: 1035. https://doi.org/10.3390/sym15051035
APA StyleBelonenko, M. B., Zaporotskova, I. V., & Konobeeva, N. N. (2023). Propagation of Ultrashort Optical Pulses in Fractal Objects. Symmetry, 15(5), 1035. https://doi.org/10.3390/sym15051035




