Symmetry in Regression Analysis: Perpendicular Offsets—The Case of a Photovoltaic Cell †
Abstract
1. Introduction
1.1. History
1.2. Today
1.3. Aim
2. Materials and Methods
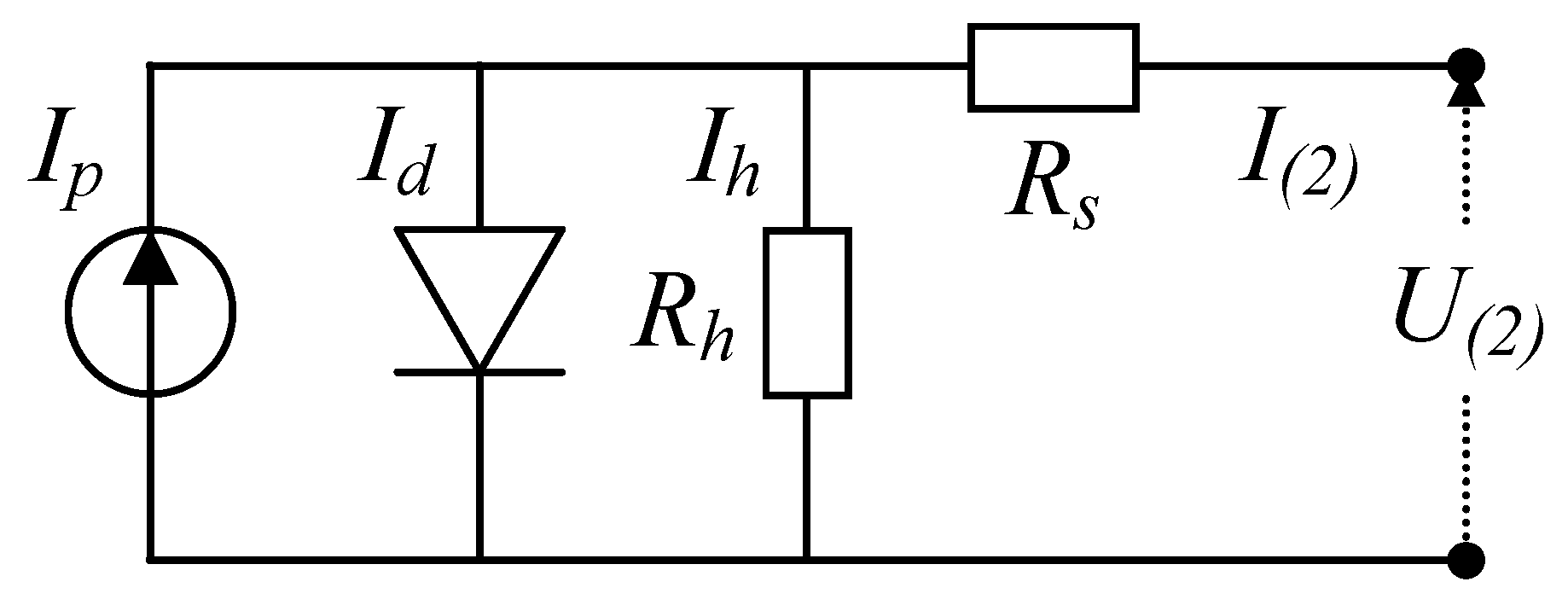
2.1. Single-Diode, Double-Diode, and PV Generator Models
2.2. Lambert Function
2.3. Explicit Equations
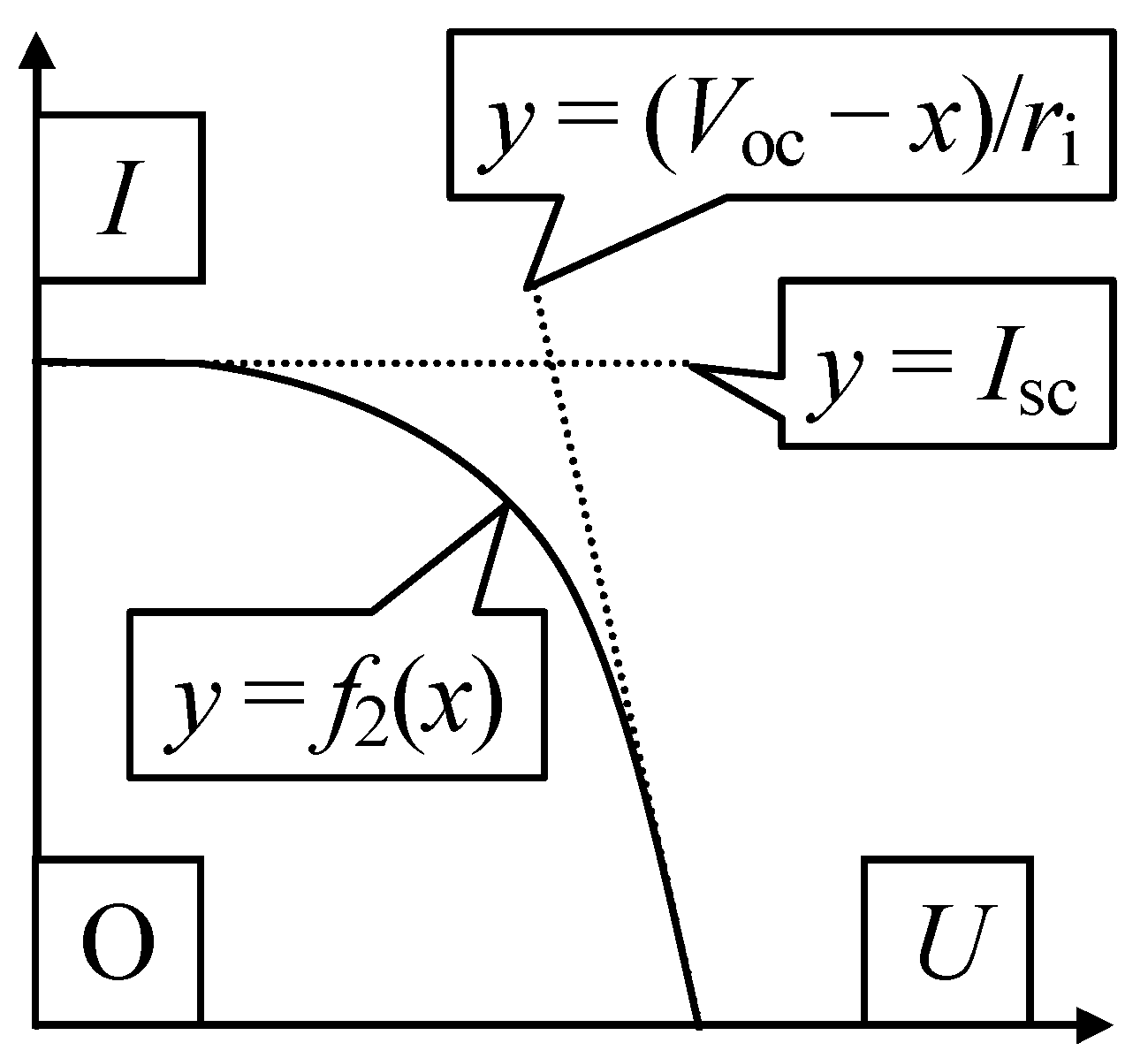
2.4. Limit Cases
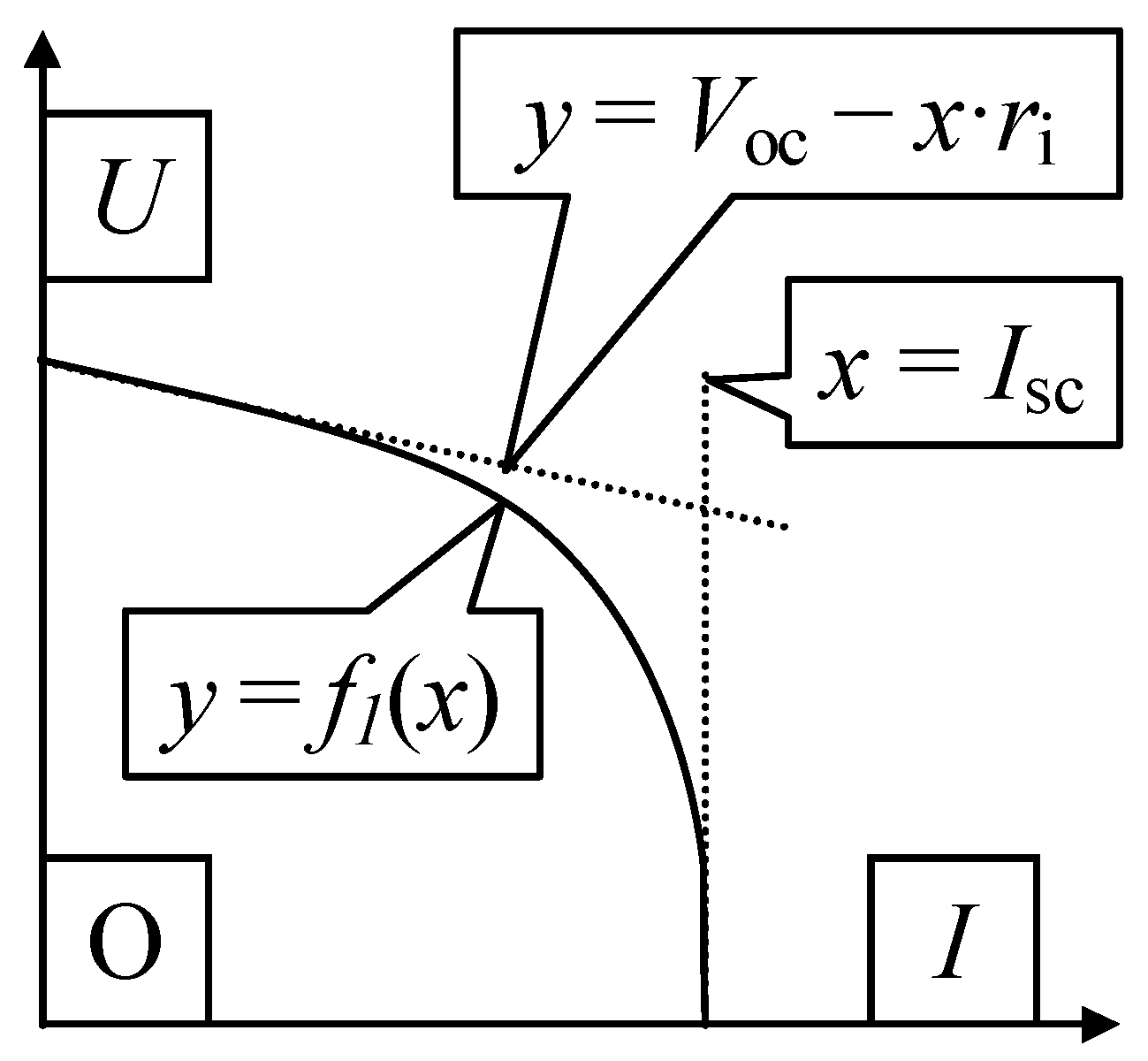
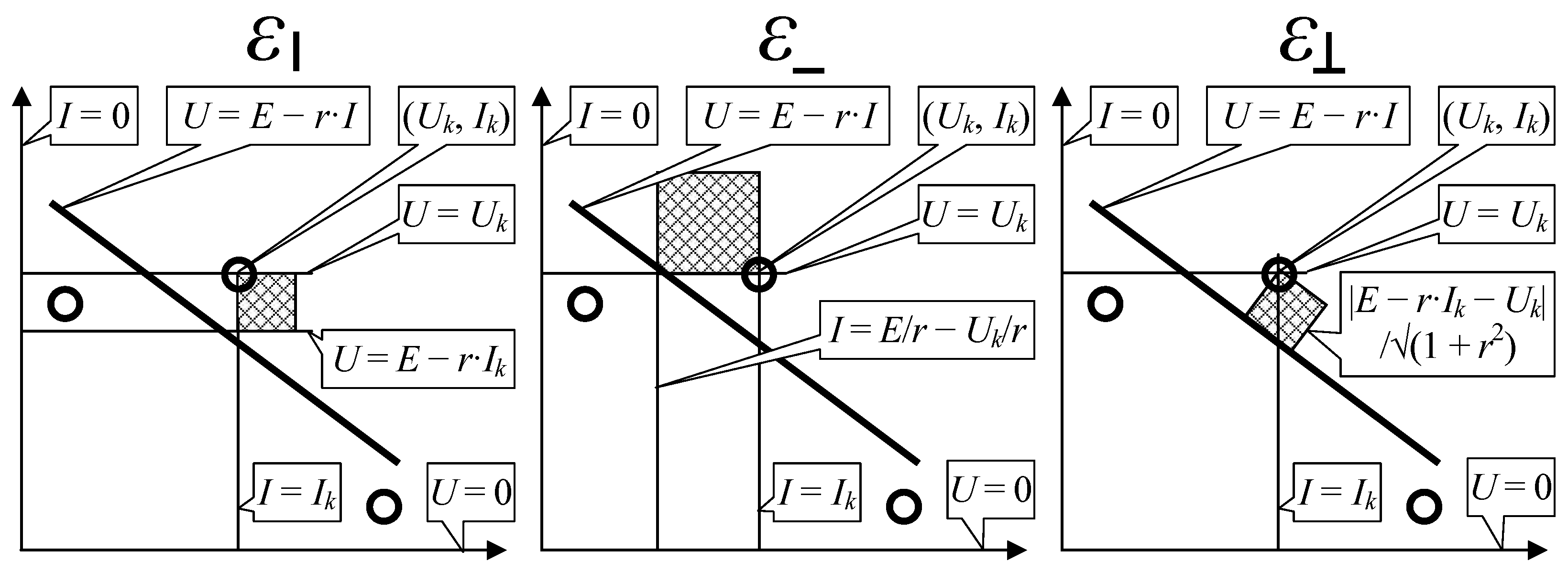
2.5. Minimizing Unexplained Variance (Errors)
2.6. Occam’s Razor: Two Simple Models
2.7. The Experiment and Data Treatment
3. Results and Discussion
3.1. Implementation of the Proposed Solution
| Algorithm 1: Providing perpendicular offsets. |
//Uses Minimize function solving an optimization problem (Equation (21)) //Implement pf function below Input: m //sample size //sample data () n //number of coefficients C //initial guess for coefficients () f //function evaluating the model with given coefficients () k //data pair index from which to construct the perpendicular offsets Function ; Return EndFunction Output: r //the squared perpendicular offset from k to f |
| Algorithm 2: Sum of perpendicular offsets. |
//Uses function pf defined in Algorithm 1 & implement function sp below Input: m //sample size //sample data () n //number of coefficients C //initial guess for coefficients () f //function evaluating the model with given coefficients () Function ; For () EndFor Return r EndFunction Output: s //sum of the squared perpendicular offsets |
| Algorithm 3: Nonlinear regression with perpendicular offsets. |
//Uses Minimize function solving an optimization problem (Equation (21)) //Uses InitialEstimate function providing an initial guess //Uses function sp defined in Algorithm 2 Input: m //sample size //sample data () n //number of coefficients C //initial guess for coefficients () f //function evaluating the model with given coefficients () //or any other good guess initialization Output: D //coefficients minimizing the sum of the perpendicular offsets |
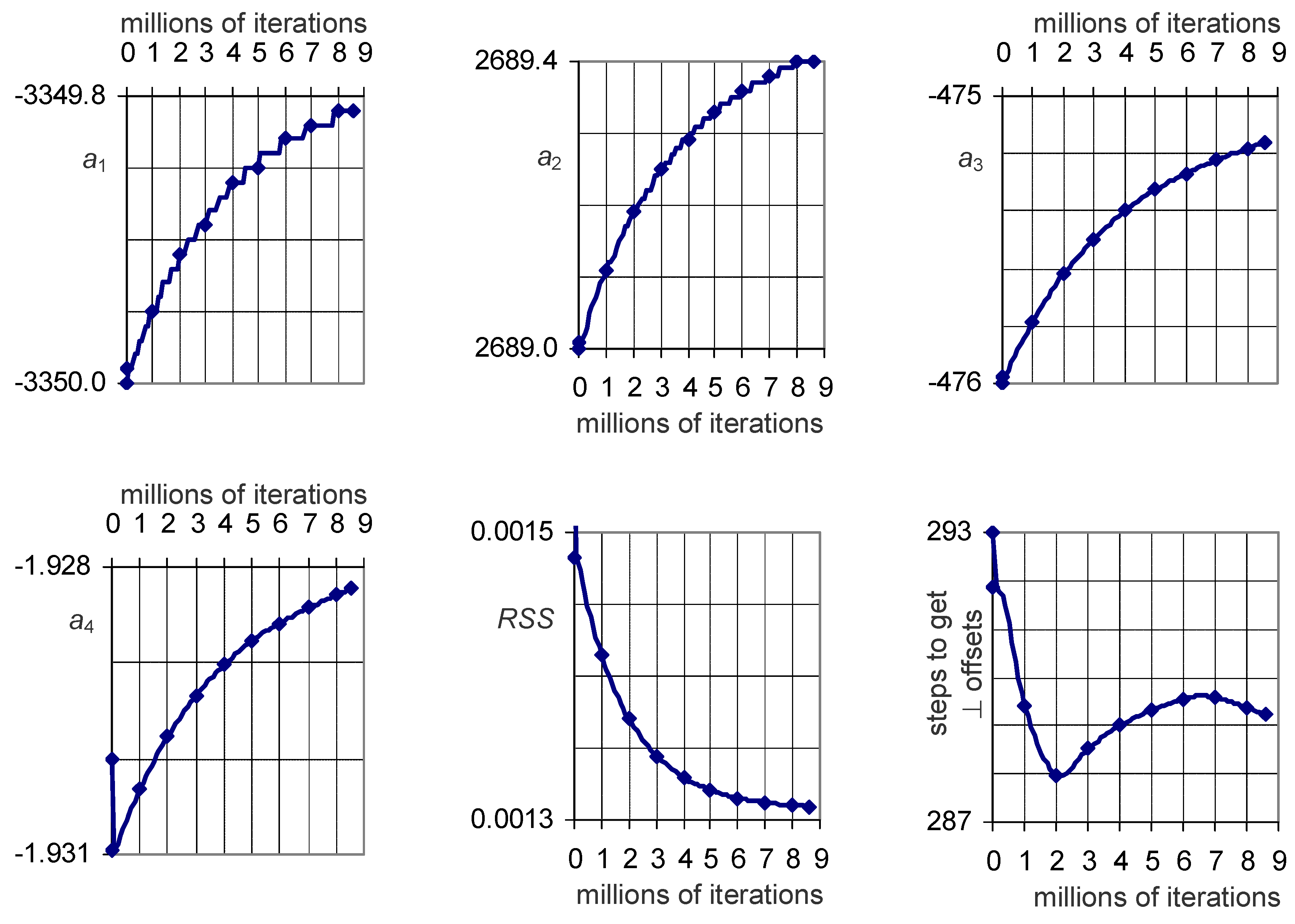
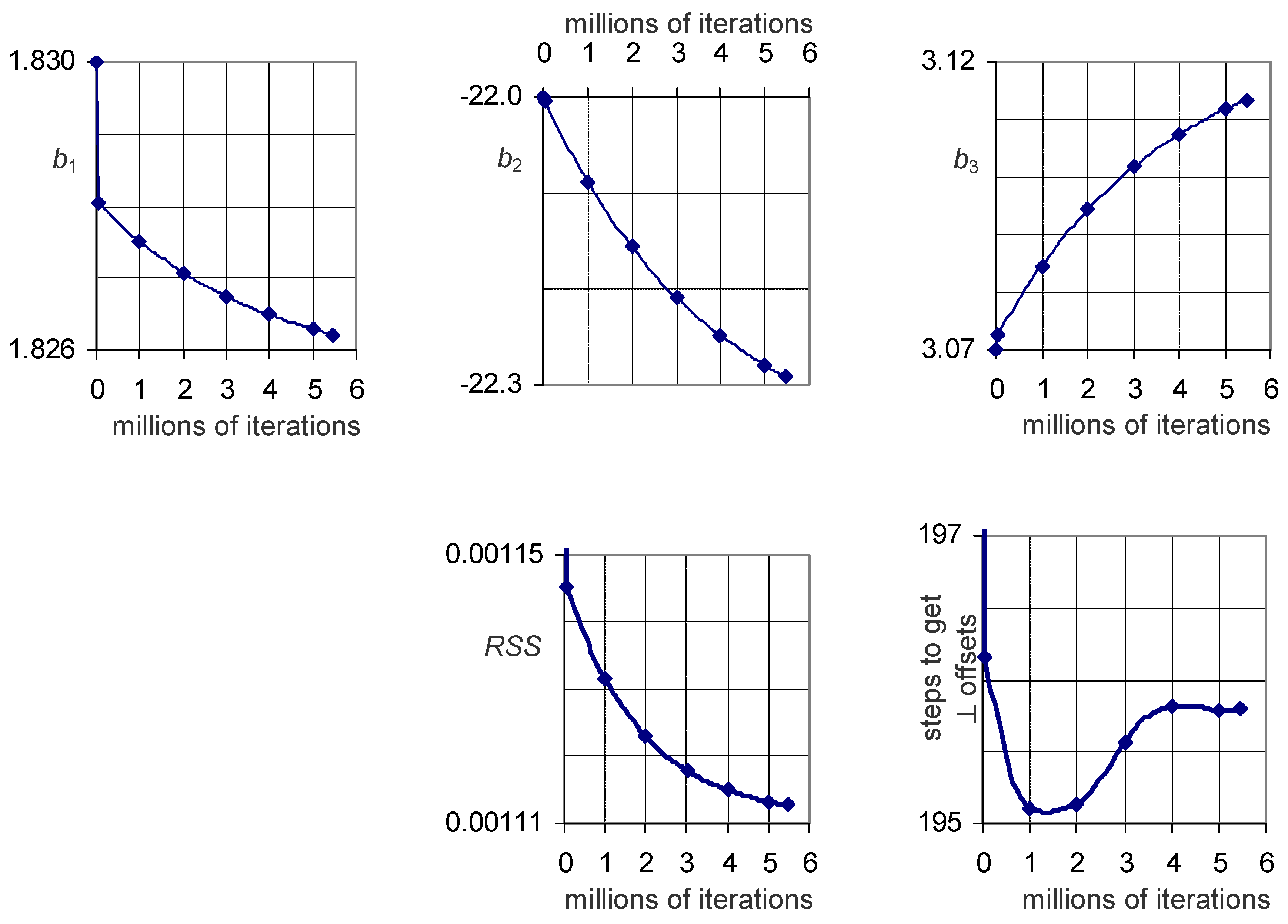
3.2. The Numerical Results
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV (cell) | Photovoltaic |
| PN (junction) | Positive (P)/negative (N) semiconductor interface |
| , , | Diffusion and recombination diode ideality factor(s) |
| Thermal voltage (, with T the temperature, in Kelvin (K)) | |
| kB | Boltzmann’s constant (kB = ) |
| e− | Electron (elementary) electric charge constant (e− = ) |
| e | Euler’s number, e = 2.71828182845904523... (e = ) |
| R | Regnault’s constant (R = ) |
| , | Shunt () and series () resistances (see §2.1) |
| F | Faraday’s constant (F = ) |
| Short-circuit intensity | |
| Open-circuit voltage | |
| Current intensity at maximum power point | |
| Voltage at maximum power point | |
| Power at maximum power point ( = ) | |
| Residual sum of squares (statistics) | |
| Adjusted determination coefficient (statistics) | |
| F | F (Fisher’s) value (statistics) |
References
- Ingen-Housz, J. Experiments upon Vegetables: Discovering Their Great Power of Purifying the Common Air in the Sunshine, and of Injuring It in the Shade and at Night: To Which Is Joined, a New Method of Examining the Accurate Degree of Salubrity of the Atmosphere; Elmsly and Payne: London, UK, 1779. [Google Scholar]
- Woodward, R.B. The total synthesis of chlorophyll. Pure Appl. Chem. 1961, 2, 383–401. [Google Scholar] [CrossRef]
- Galvani, L. De Viribus Electricitatis in Motu Musculari Commentarius; Apud Societatem Typographicam: Rome, Italy, 1791; pp. 363–418. [Google Scholar]
- Volta, A. On the electricity excited by the mere contact of conducting substances of different kinds. Philos. Trans. R. Soc. Lond. 1800, 90, 408–431. [Google Scholar] [CrossRef]
- Becquerel, E. Mémoire sur les effets électriques produits sous l’influence des rayons solaires. Comptes Rendus Acad. Sci. 1839, 9, 561–567. [Google Scholar]
- Cove, G.H. Thermo Electric Battery and Apparatus. U.S. Patent 824684A, 15 February 1905. [Google Scholar]
- Blankenship, R.E.; Tiede, D.M.; Barber, J.; Brudvig, G.W.; Fleming, G.; Ghirardi, M.; Gunner, M.R.; Junge, W.; Kramer, D.M.; Melis, A.; et al. Comparing photosynthetic and photovoltaic efficiencies and recognizing the potential for improvement. Science 2011, 332, 805–809. [Google Scholar] [CrossRef]
- Zhu, X.-G.; Long, S.P.; Ort, D.R. Improving photosynthetic efficiency for greater yield. Annu. Rev. Plant Biol. 2010, 61, 235. [Google Scholar] [CrossRef] [PubMed]
- Wijffels, R.H.; Barbosa, M.J. Application of Symmetry Operation Measures in Structural Inorganic Chemistry. Science 2010, 329, 796–799. [Google Scholar] [CrossRef]
- Geisz, J.F.; France, R.M.; Schulte, K.L.; Steiner, M.A.; Norman, A.G.; Guthrey, H.L.; Young, M.R.; Song, T.; Moriarty, T. Six-junction III–V solar cells with 47.1% conversion efficiency under 143 Suns concentration. Nat. Energy 2020, 5, 326–335. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Y.; Huang, J. Towards high performance organic photovoltaic cells: A review of recent development in organic photovoltaics. Polymers 2014, 6, 2473–2509. [Google Scholar] [CrossRef]
- Gao, K.; Zhu, Z.; Xu, B.; Jo, S.B.; Kan, Y.; Peng, X.; Jen, A.K.-Y. Highly efficient porphyrin-based OPV/perovskite hybrid solar cells with extended photoresponse and high fill factor. Adv. Mater. 2017, 29, 1703980. [Google Scholar] [CrossRef]
- Bălan, M.C.; Damian, M.; Jäntschi, L. Preliminary results on design and implementation of a solar radiation monitoring system. Sensors 2008, 8, 963–978. [Google Scholar] [CrossRef]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Pintér, G. An economic analysis of the shading effects of transmission lines on photovoltaic power plant investment decisions: A case study. Sensors 2021, 21, 4973. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Yan, X.; Tsai, C.-L. Linear regression. WIREs Comp. Stat. 2012, 4, 275–294. [Google Scholar] [CrossRef]
- Jäntschi, L.; Pruteanu, L.L.; Cozma, A.C.; Bolboacă, S.D. Inside of the linear relation between dependent and independent variables. Comput. Math. Meth. Med. 2015, 2015, 360752. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B (Methodol.) 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Kubáček, L. On a linearization of regression models. Appl. Math. 1995, 40, 61–78. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.-D. Results from the Use of Molecular Descriptors Family on Structure Property/Activity Relationships. Int. J. Mol. Sci. 2007, 8, 189–203. [Google Scholar] [CrossRef]
- Anta, J.A.; Idígoras, J.; Guillén, E.; Villanueva-Cab, J.; Mandujano-Ramírez, H.J.; Oskam, G.; Pellejà, L.; Palomares, E. A continuity equation for the simulation of the current–voltage curve and the time-dependent properties of dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2012, 14, 10285–10299. [Google Scholar] [CrossRef]
- Trabelsi, M.; Massaoudi, M.; Chihi, I.; Sidhom, L.; Refaat, S.S.; Huang, T.; Oueslati, F.S. An effective hybrid symbolic regression–deep multilayer perceptron technique for PV power forecasting. Energies 2022, 15, 9008. [Google Scholar] [CrossRef]
- Etxegarai, G.; Zapirain, I.; Camblong, H.; Ugartemendia, J.; Hernandez, J.; Curea, O. Photovoltaic energy production forecasting in a short term horizon: Comparison between analytical and machine learning models. Appl. Sci. 2022, 12, 12171. [Google Scholar] [CrossRef]
- Alanazi, M.; Alanazi, A.; Almadhor, A.; Rauf, H.T. Photovoltaic models’ parameter extraction using new artificial parameterless optimization algorithm. Mathematics 2022, 10, 4617. [Google Scholar] [CrossRef]
- Charfeddine, S.; Alharbi, H.; Jerbi, H.; Kchaou, M.; Abbassi, R.; Leiva, V. A stochastic optimization algorithm to enhance controllers of photovoltaic systems. Mathematics 2022, 10, 2128. [Google Scholar] [CrossRef]
- Agwa, A.M.; Elsayed, S.K.; Elattar, E.E. Extracting the parameters of three-diode model of photovoltaics using barnacles mating optimizer. Symmetry 2022, 14, 1569. [Google Scholar] [CrossRef]
- Cleary, T.; Nozarijouybari, Z.; Wang, D.; Wang, D.; Rahn, C.; Fathy, H.K. An experimentally parameterized equivalent circuit model of a solid-state lithium-sulfur battery. Batteries 2022, 8, 269. [Google Scholar] [CrossRef]
- Elshahed, M.; El-Rifaie, A.M.; Tolba, M.A.; Ginidi, A.; Shaheen, A.; Mohamed, S.A. An innovative hunter-prey-based optimization for electrically based single-, double-, and triple-diode models of solar photovoltaic systems. Mathematics 2022, 10, 4625. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Feng, H.; Li, H.-Y.; Li, L.-L. An improved whale algorithm for support vector machine prediction of photovoltaic power generation. Symmetry 2021, 13, 212. [Google Scholar] [CrossRef]
- Turysheva, A.; Voytyuk, I.; Guerra, D. Estimation of electricity generation by an electro-technical complex with photoelectric panels using statistical methods. Symmetry 2021, 13, 1278. [Google Scholar] [CrossRef]
- Shockley, W. The theory of p-n junctions in semiconductors and p-n junction transistors. Bell Syst. Tech. J. 1949, 28, 435–489. [Google Scholar] [CrossRef]
- Cowley, A.M. Titanium-silicon Schottky barrier diodes. Solid-State Electron. 1970, 13, 403–414. [Google Scholar] [CrossRef]
- Caprioglio, P.; Wolff, C.M.; Sandberg, O.J.; Armin, A.; Rech, B.; Albrecht, S.; Neher, D.; Stolterfoht, M. On the origin of the ideality factor in perovskite solar cells. Adv. Energy Mater. 2020, 10, 2000502. [Google Scholar] [CrossRef]
- Nanda, K.K. Current dependence of ideality factor of silicon diodes. Curr. Sci. 1998, 74, 234–237. [Google Scholar]
- Lambert, J.H. Observationes variae in mathesin puram. Acta Helvet. Phys. Math. Anat. Bot. Med. 1758, 3, 128–168. [Google Scholar]
- Álvarez, J.M.; Alfonso-Corcuera, D.; Roibás-Millán, E.; Cubas, J.; Cubero-Estalrrich, J.; Gonzalez-Estrada, A.; Jado-Puente, R.; Sanabria-Pinzón, M.; Pindado, S. Analytical modeling of current-voltage photovoltaic performance: An easy approach to solar panel behavior. Appl. Sci. 2021, 11, 4250. [Google Scholar] [CrossRef]
- Karmalkar, S.; Haneefa, S. A physically based explicit model of a solar cell for simple design calculations. IEEE Electron. Device Lett. 2008, 29, 449–451. [Google Scholar] [CrossRef]
- Saleem, H.; Karmalkar, S. An analytical method to extract the physical parameters of a solar cell from four points on the illuminated J − V curve. IEEE Electron. Device Lett. 2009, 30, 349–352. [Google Scholar] [CrossRef]
- Das, A.K. An explicit J − V model of a solar cell using equivalent rational function form for simple estimation of maximum power point voltage. Sol. Energy 2013, 98, 400–403. [Google Scholar] [CrossRef]
- Das, A.K. Analytical derivation of equivalent functional form of explicit J − V model of an illuminated solar cell from physics based implicit model. Sol. Energy 2014, 103, 411–416. [Google Scholar] [CrossRef]
- Pindado, S.; Cubas, J. Simple mathematical approach to solar cell/panel behavior based on datasheet information. Renew. Energy 2017, 103, 729–738. [Google Scholar] [CrossRef]
- Pindado, S.; Cubas, J.; Roibas-Millan, E.; Bugallo-Siegel, F.; Sorribes-Palmer, F. Assessment of explicit models for different photovoltaic technologies. Energies 2018, 11, 1353. [Google Scholar] [CrossRef]
- Marion, B.; Rummel, S.; Anderberg, A. Current–voltage curve translation by bilinear interpolation. Prog. Photovolt. Res. Appl. 2004, 12, 593–607. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Mekhamer, S.F.; Qais, M.H.; Alghuwainem, S.; Ullah, Z.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F.; Elkadeem, M.R. Probabilistic optimal power flow solution using a novel hybrid metaheuristic and machine learning algorithm. Mathematics 2022, 10, 3036. [Google Scholar] [CrossRef]
- Aurairat, A.; Plangklang, B. An alternative perturbation and observation modifier maximum power point tracking of PV systems. Symmetry 2022, 14, 44. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Wiliamowski, B.; Yu, H. Improved computation for Levenberg–Marquardt training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef]
- Bochkanov, S. ALGLIB Project. Copyright 1994–2017. Available online: http://alglib.net (accessed on 18 April 2023).
- Codère, C.E.; Bérczi, G.; Muller, P.; Vreman, P. FreePascal: Open Source Compiler for Pascal and Object Pascal—FreePascal IDE for win32 for i386, Version 3.2.2. 2021. Available online: http://freepascal.org (accessed on 18 April 2023).
- Monti, C.A.U.; Oliveira, R.M.; Roise, J.P.; Scolforo, H.F.; Gomide, L.R. Hybrid method for fitting nonlinear height–diameter functions. Forests 2022, 13, 1783. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, P.; Zhang, T.; Li, K.; Peng, F.; Zhu, C. Principle and performance analysis of the Levenberg–Marquardt algorithm in WMS spectral line fitting. Photonics 2022, 9, 999. [Google Scholar] [CrossRef]
- Jäntschi, L. A test detecting the outliers for continuous distributions based on the cumulative distribution function of the data being tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef]
- Jäntschi, L. Detecting extreme values with order statistics in samples from continuous distributions. Mathematics 2020, 8, 216. [Google Scholar] [CrossRef]
- Joiţa, D.-M.; Tomescu, M.A.; Bàlint, D.; Jäntschi, L. An application of the eigenproblem for biochemical similarity. Symmetry 2021, 13, 1849. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bàlint, D.; Bolboacă, S.D. Multiple linear regressions by maximizing the likelihood under assumption of generalized Gauss-Laplace distribution of the error. Comput. Math. Methods Med. 2016, 2016, 8578156. [Google Scholar] [CrossRef]
- Jäntschi, L.; Katona, G.; Diudea, M.V. Modeling molecular properties by Cluj indices. MATCH Commun. Math. Comput. Chem. 2000, 41, 151–188. [Google Scholar]
- Jäntschi, L. Structure-property relationships for solubility of monosaccharides. Appl. Water Sci. 2019, 9, 38. [Google Scholar] [CrossRef]

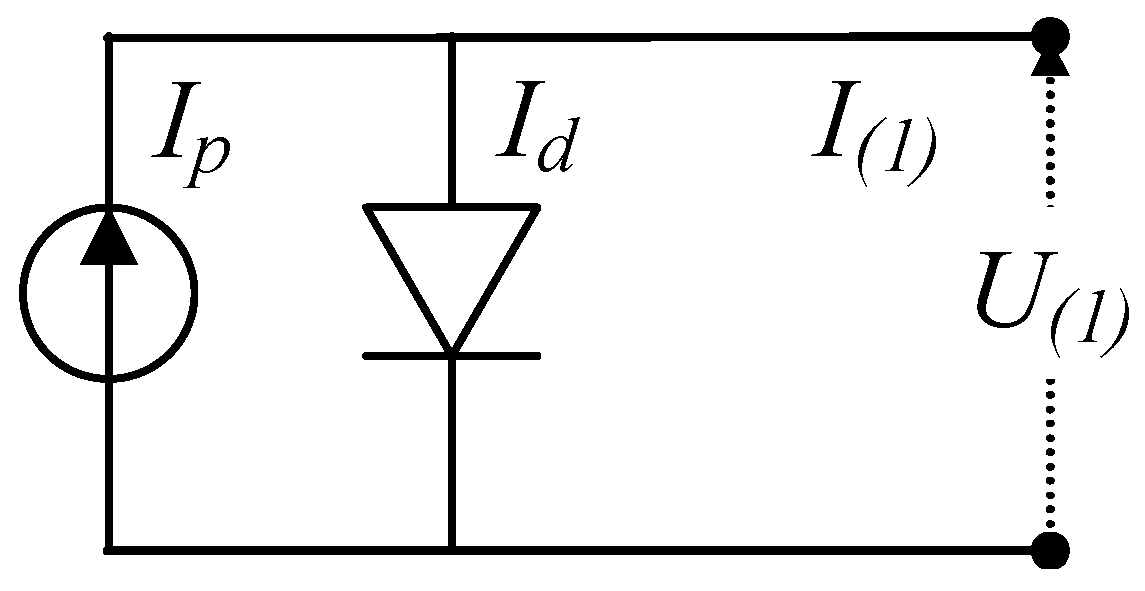
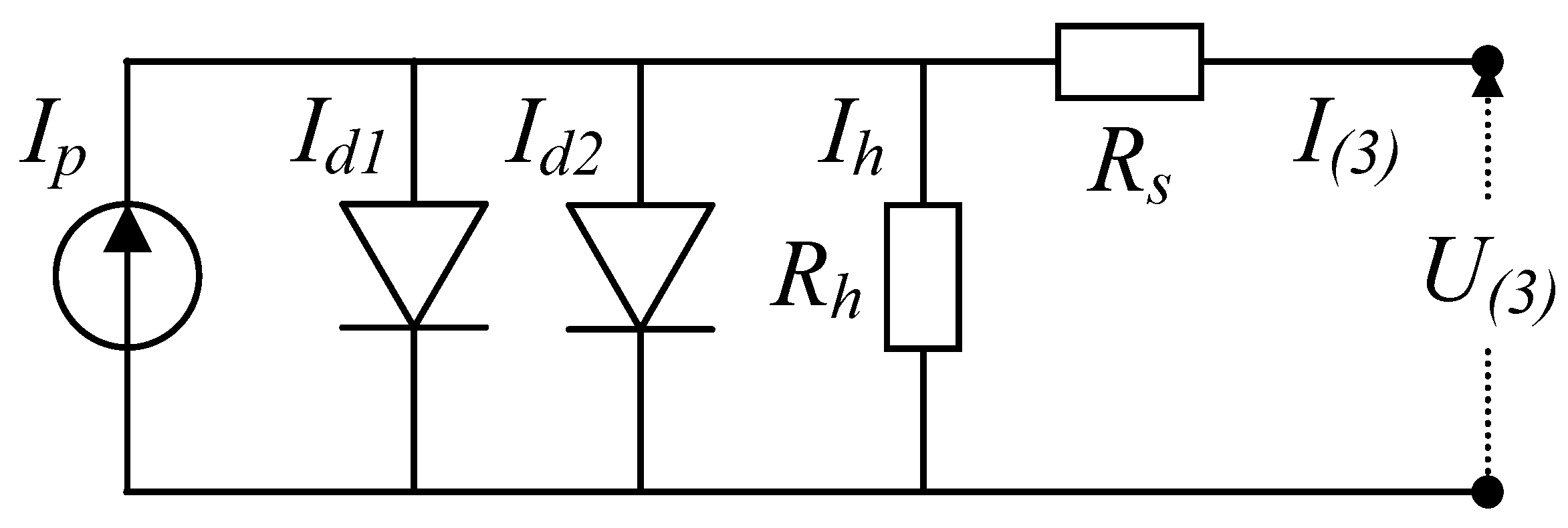
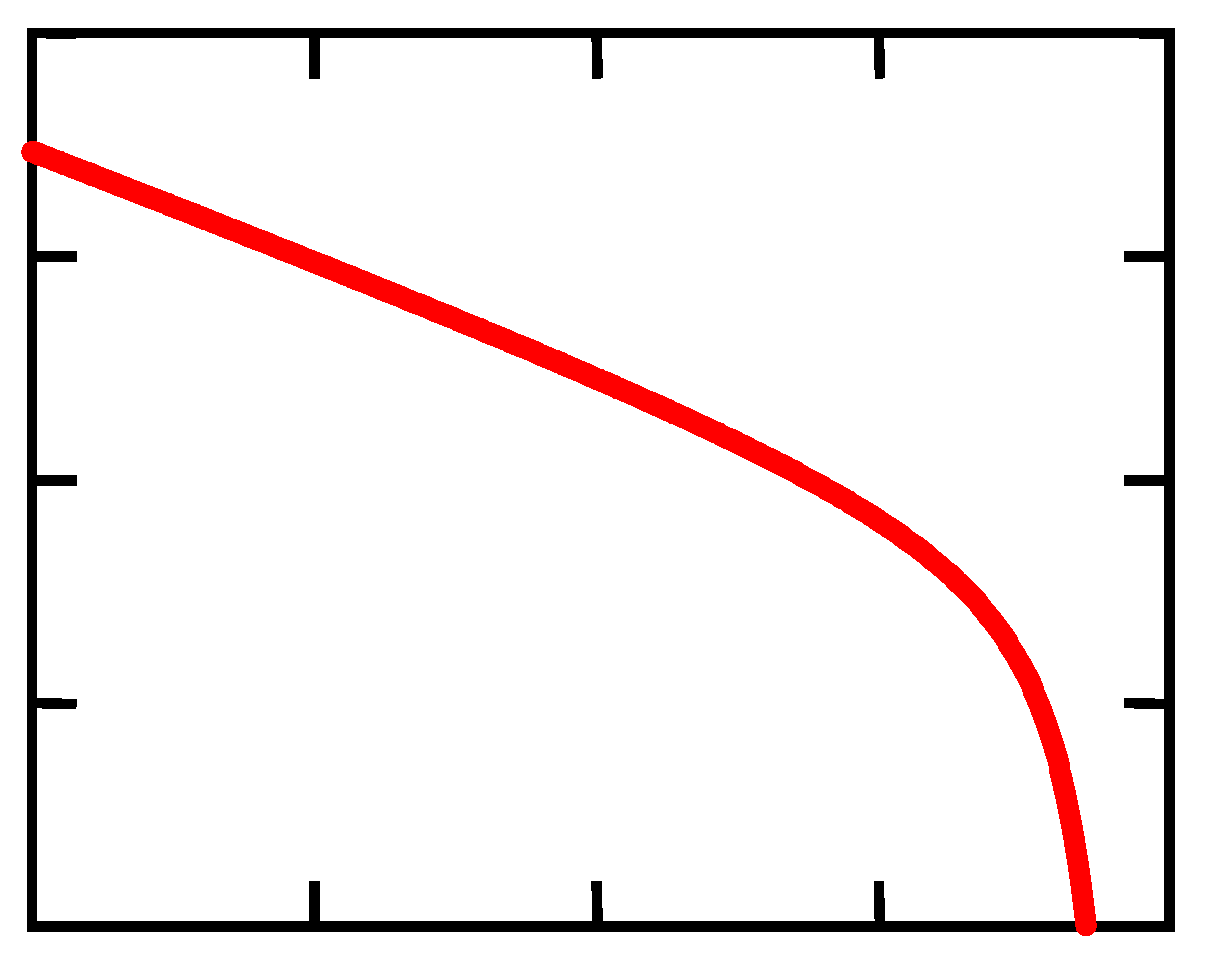
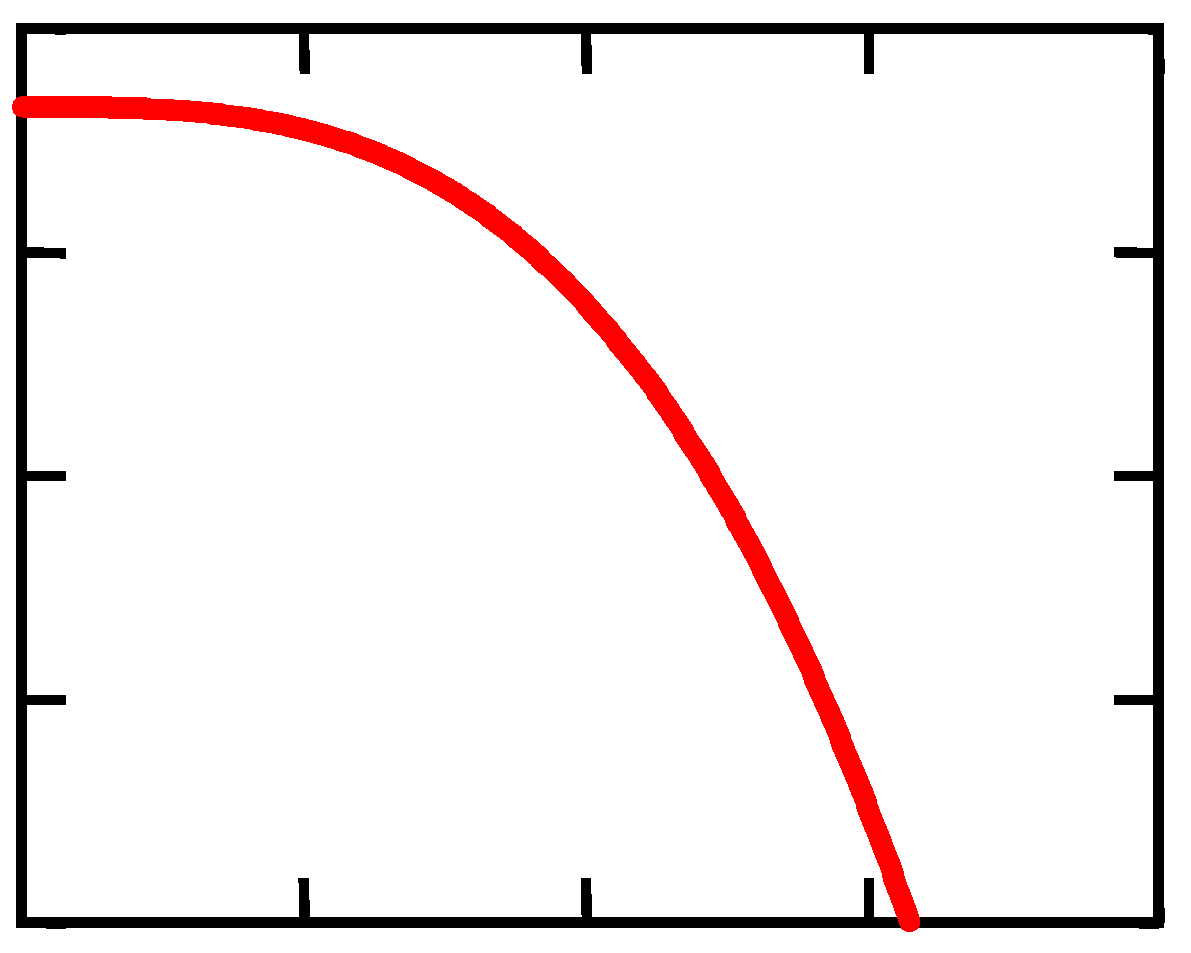
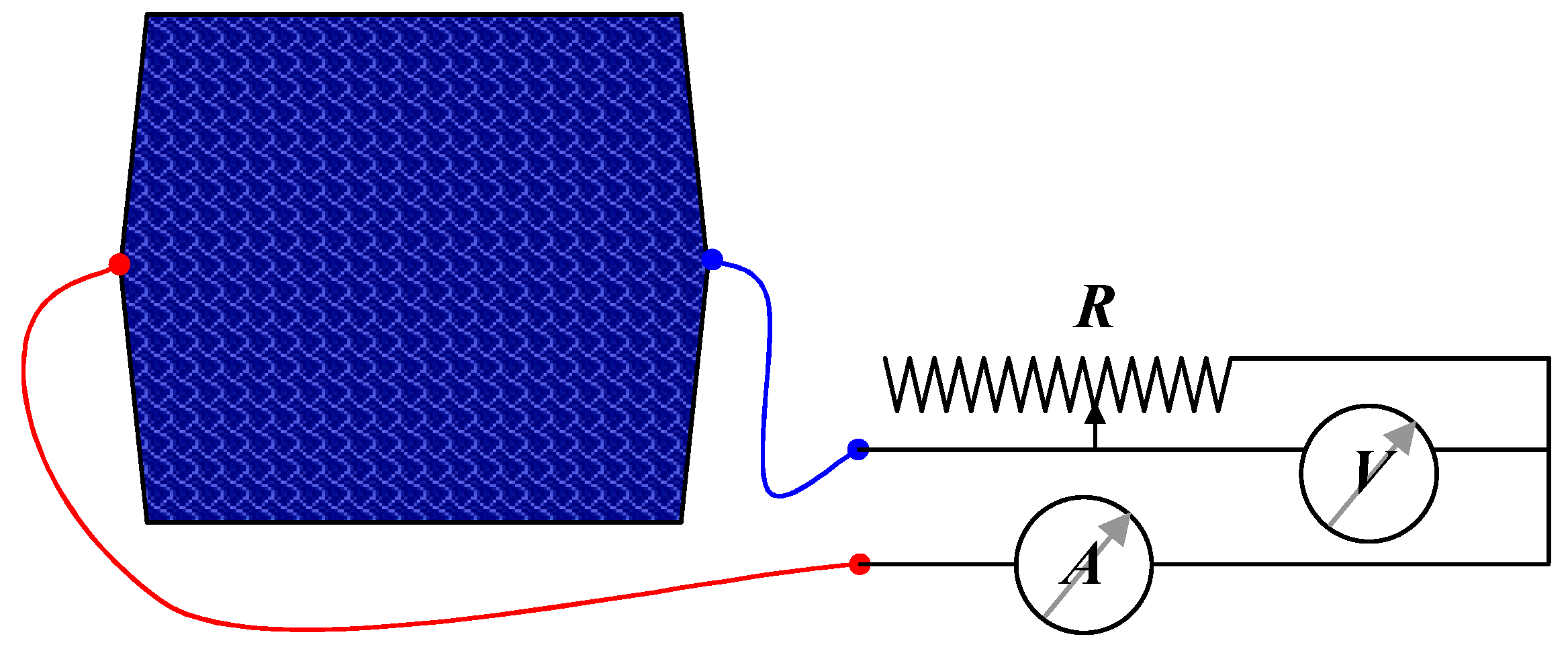
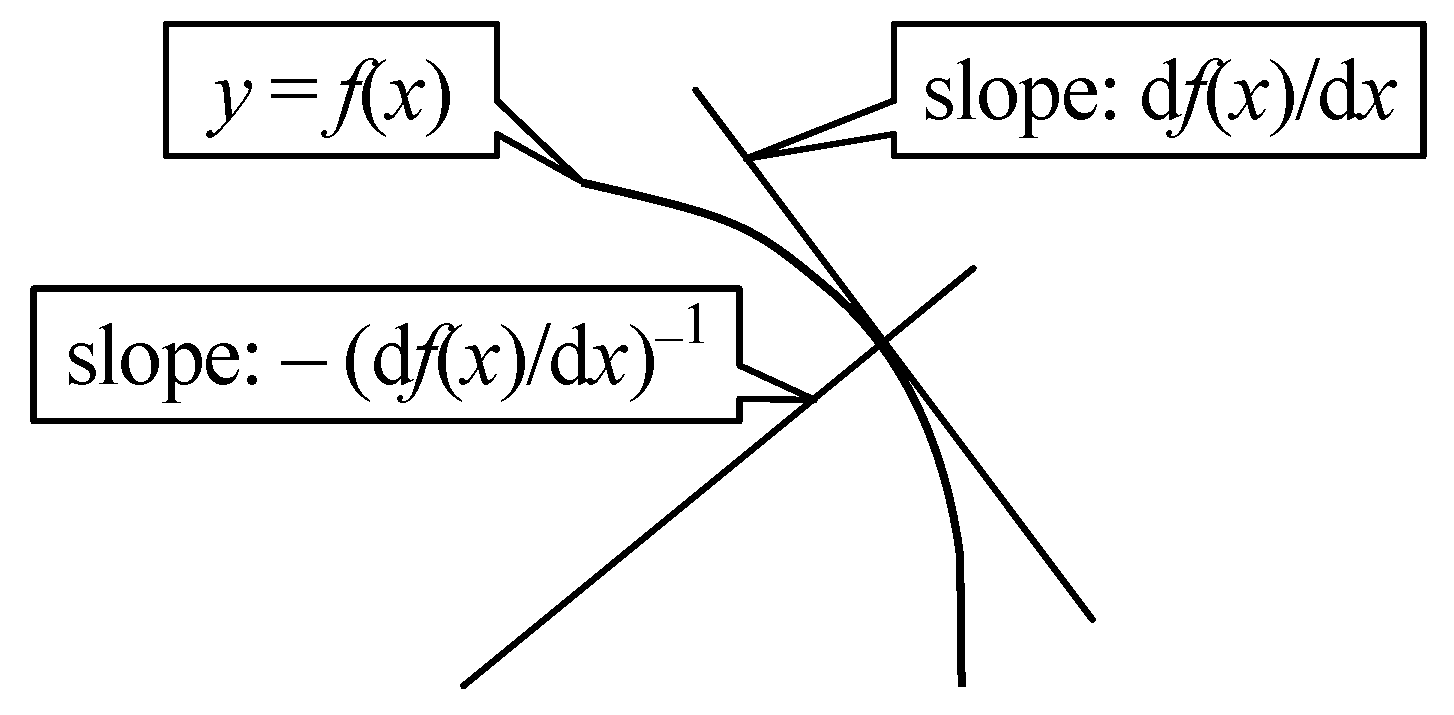
| I (mA) | 1.147 | 1.187 | 1.257 | 1.312 | 1.362 | 1.406 | 1.48 | 1.493 | 1.556 | 1.609 | 1.672 | 1.742 | 1.776 | 1.785 | 1.812 | 1.821 | 1.834 |
| U (mV) | 1132 | 1110 | 1080 | 1038 | 1010 | 973 | 930 | 900 | 845 | 772 | 703 | 593 | 493 | 405 | 332 | 254 | 163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jäntschi, L. Symmetry in Regression Analysis: Perpendicular Offsets—The Case of a Photovoltaic Cell. Symmetry 2023, 15, 948. https://doi.org/10.3390/sym15040948
Jäntschi L. Symmetry in Regression Analysis: Perpendicular Offsets—The Case of a Photovoltaic Cell. Symmetry. 2023; 15(4):948. https://doi.org/10.3390/sym15040948
Chicago/Turabian StyleJäntschi, Lorentz. 2023. "Symmetry in Regression Analysis: Perpendicular Offsets—The Case of a Photovoltaic Cell" Symmetry 15, no. 4: 948. https://doi.org/10.3390/sym15040948
APA StyleJäntschi, L. (2023). Symmetry in Regression Analysis: Perpendicular Offsets—The Case of a Photovoltaic Cell. Symmetry, 15(4), 948. https://doi.org/10.3390/sym15040948






