Study on the Anisotropy of Strength Properties of Columnar Jointed Rock Masses Using a Geometric Model Reconstruction Method Based on a Single-Random Movement Voronoi Diagram of Uniform Seed Points
Abstract
1. Introduction
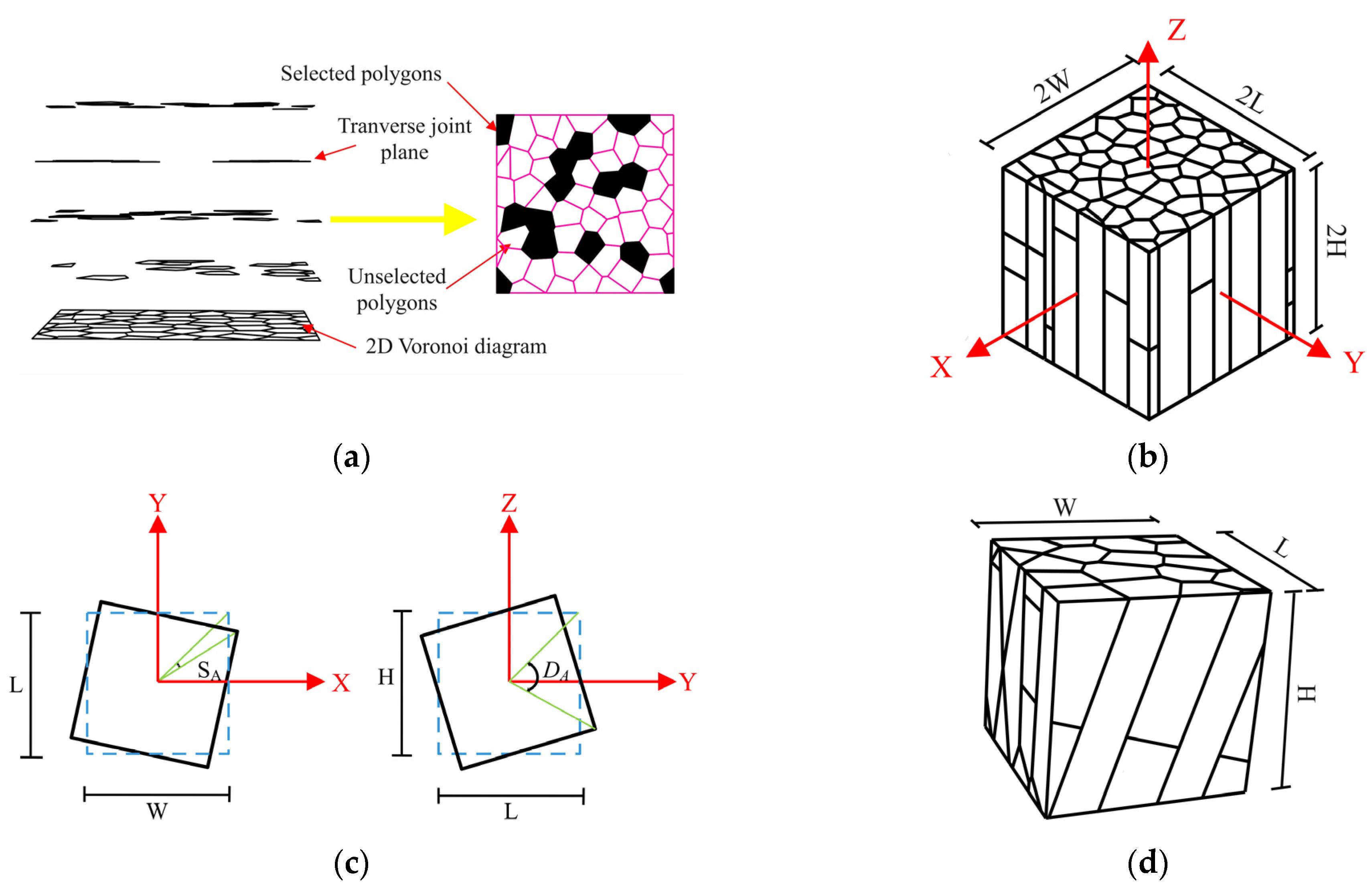
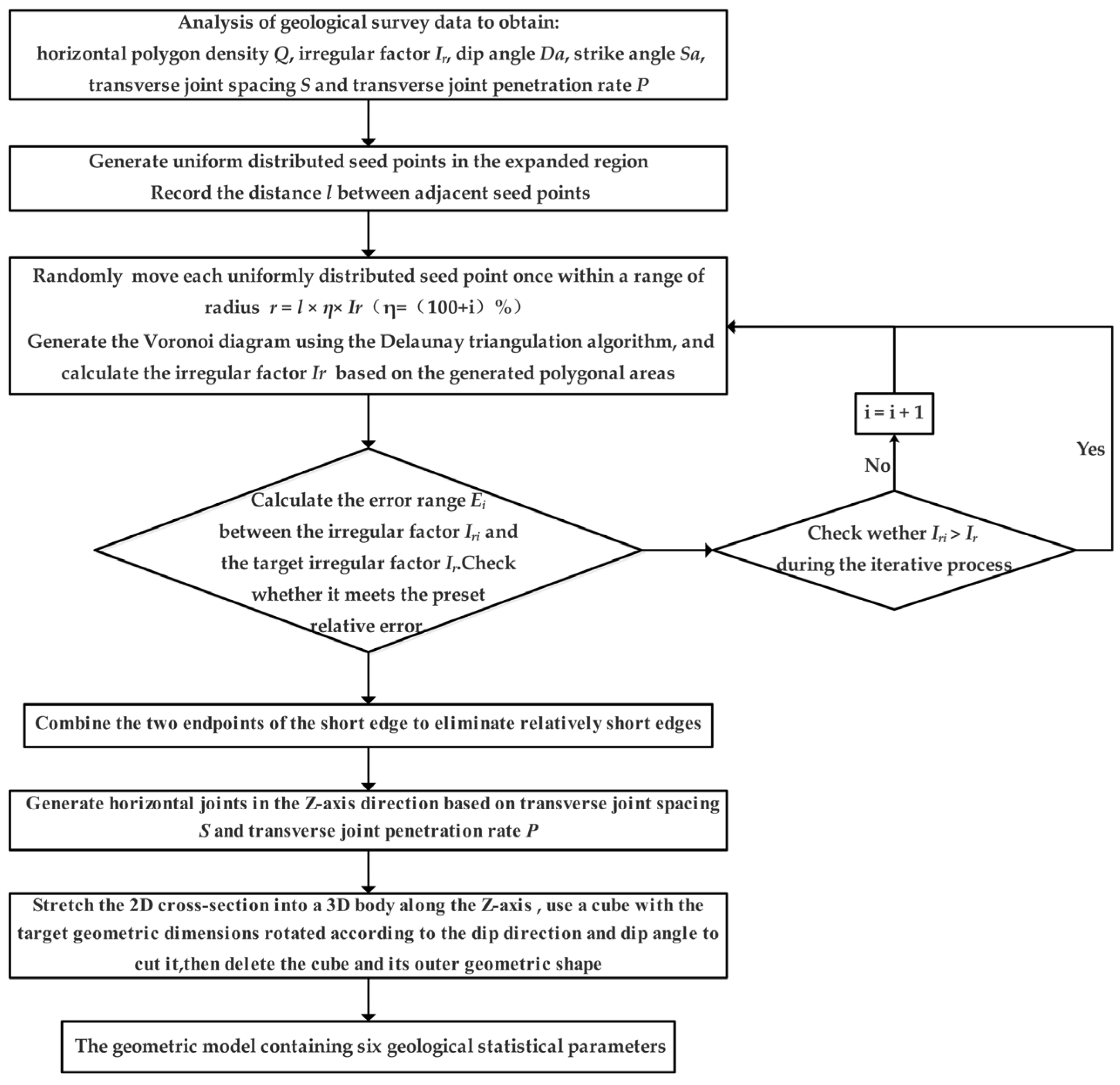
2. Geometric Model Reconstruction Method for CJRM
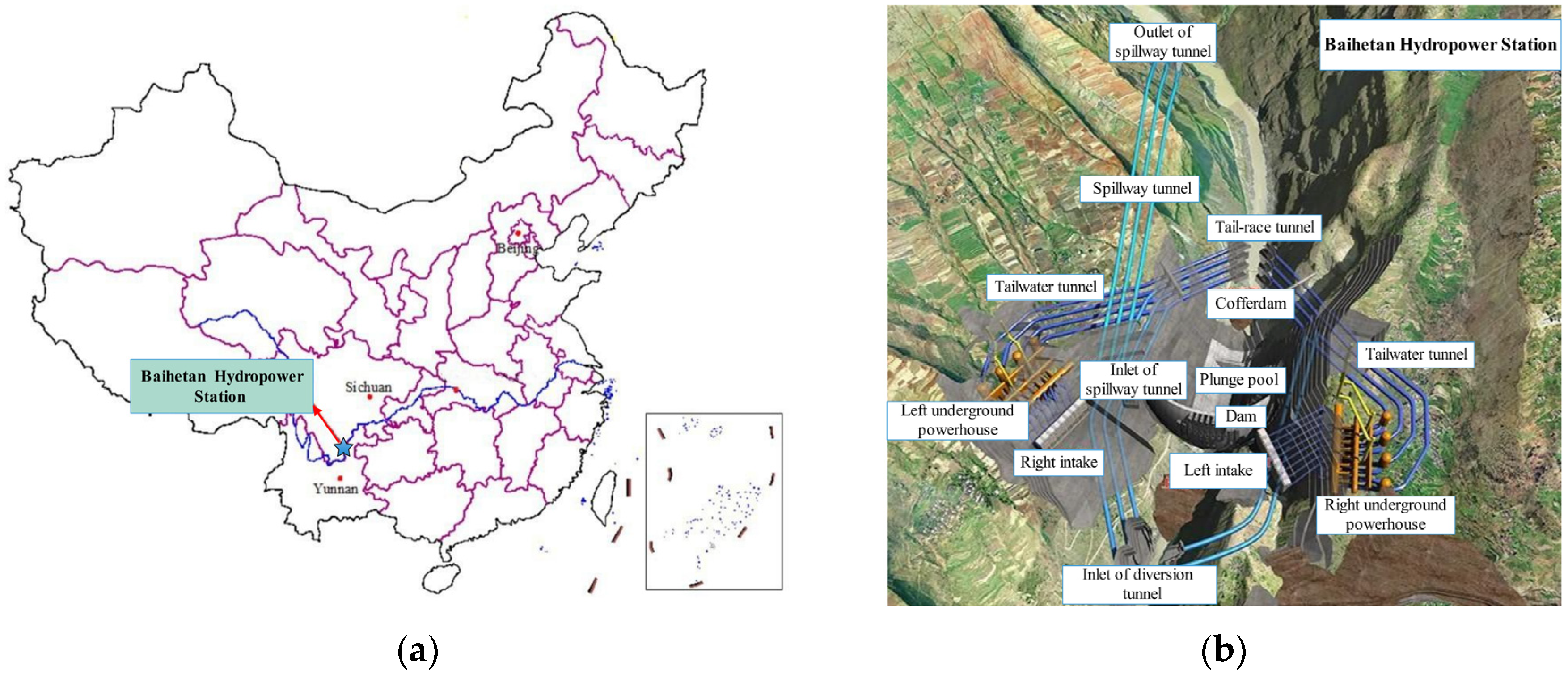
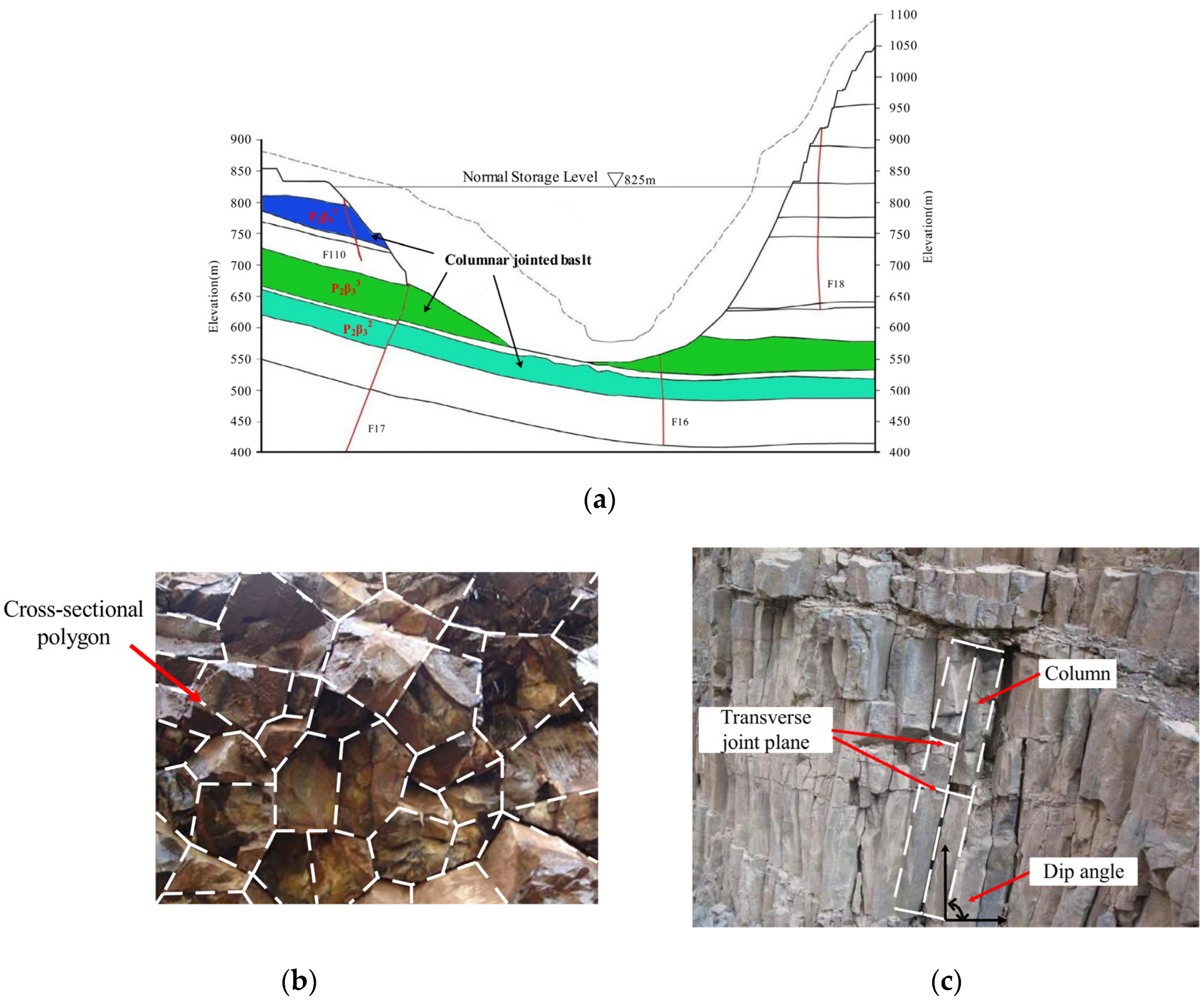
2.1. Engineering Background of the Baihetan Hydropower Station and Feasible Geological Statistical Parameters
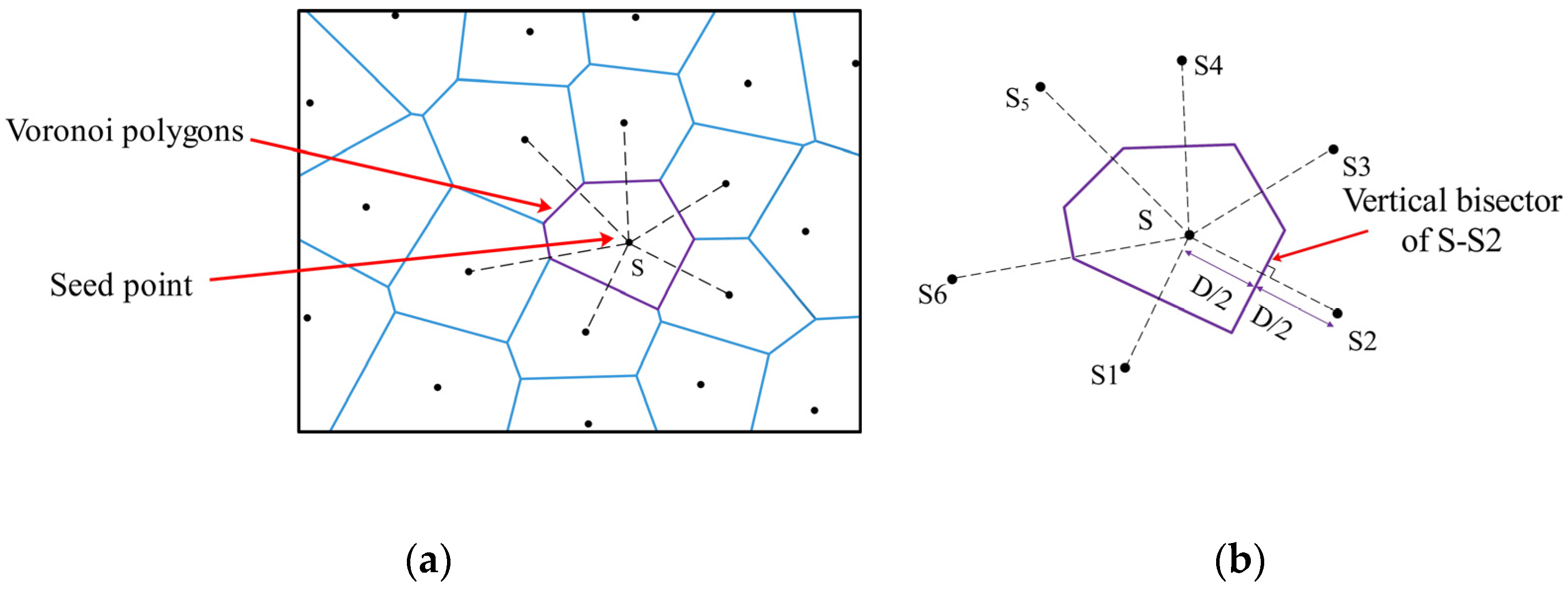
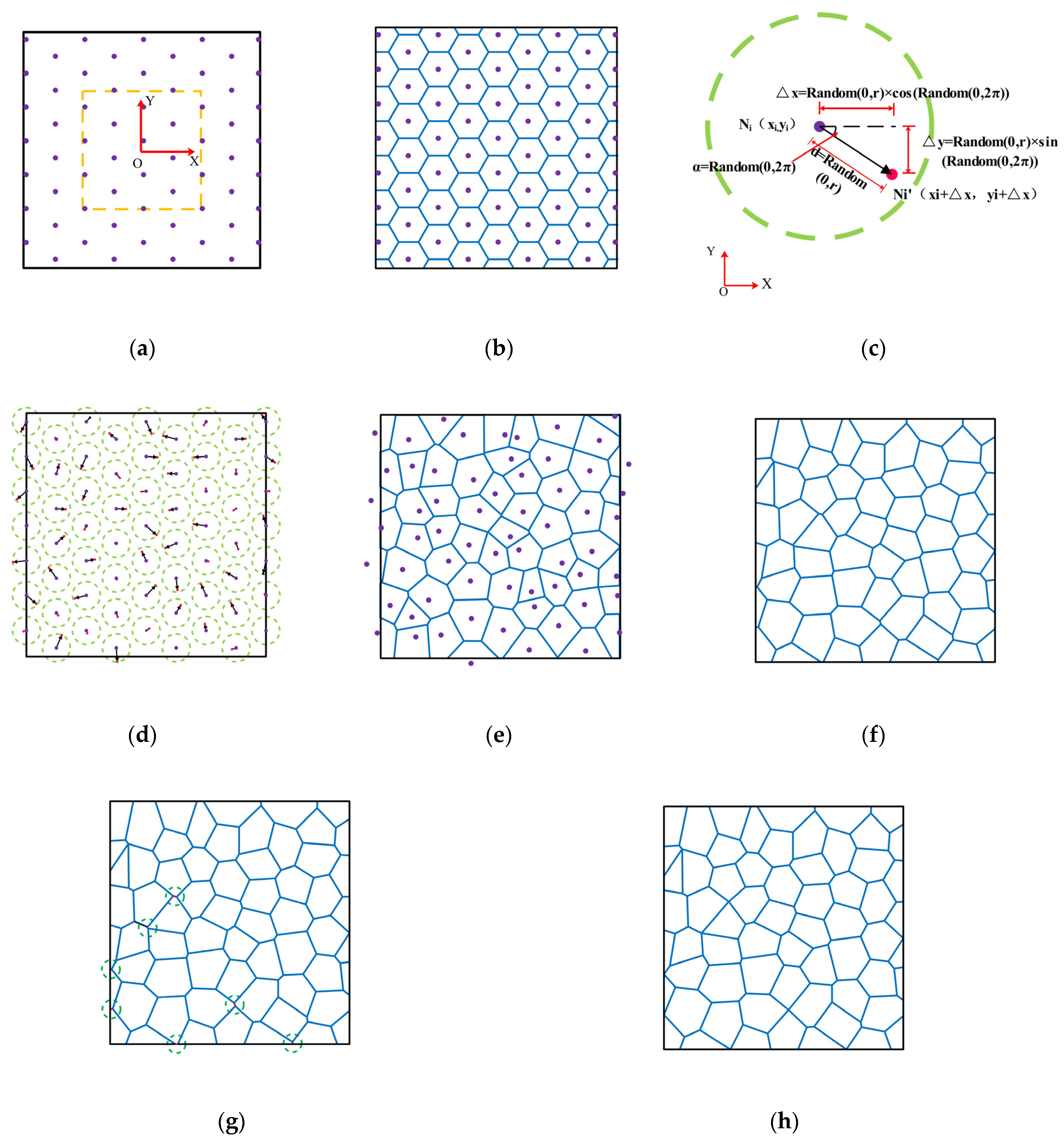
2.2. Single-Random Movement with a Range Constraint Voronoi Diagram of Uniform Seed Points
2.3. CJRM Geometric Model Reconstruction Method
2.4. Application of the CJRM Geometric Model Reconstruction Method
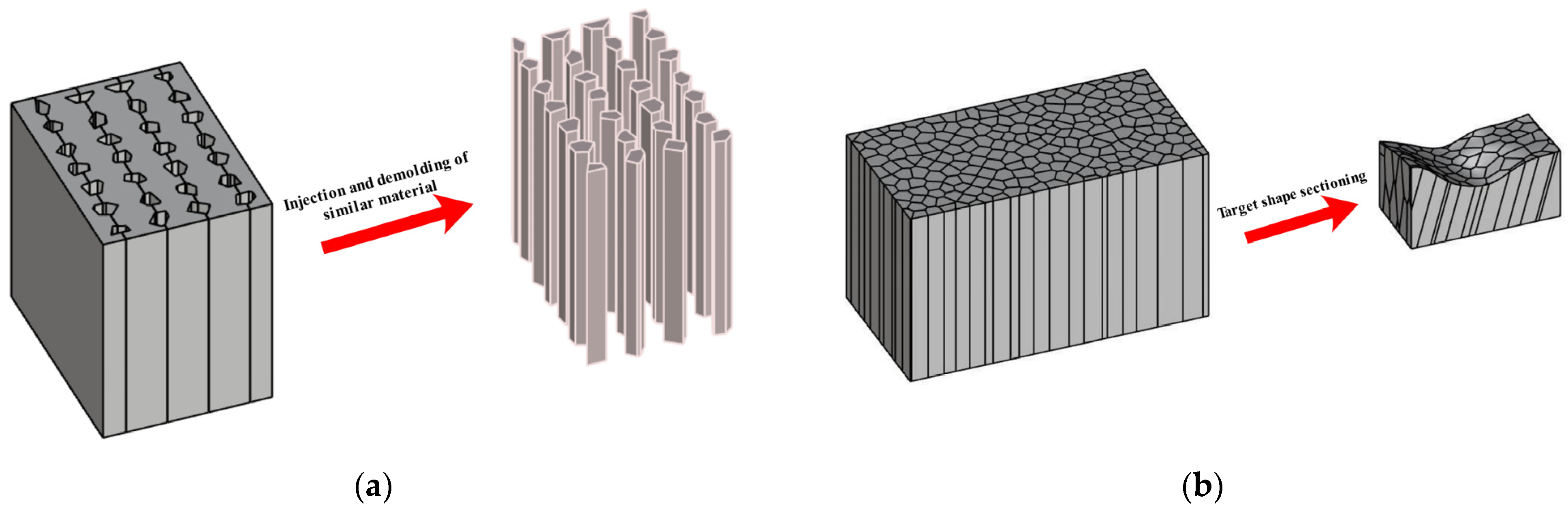
3. CJRM Numerical Simulation
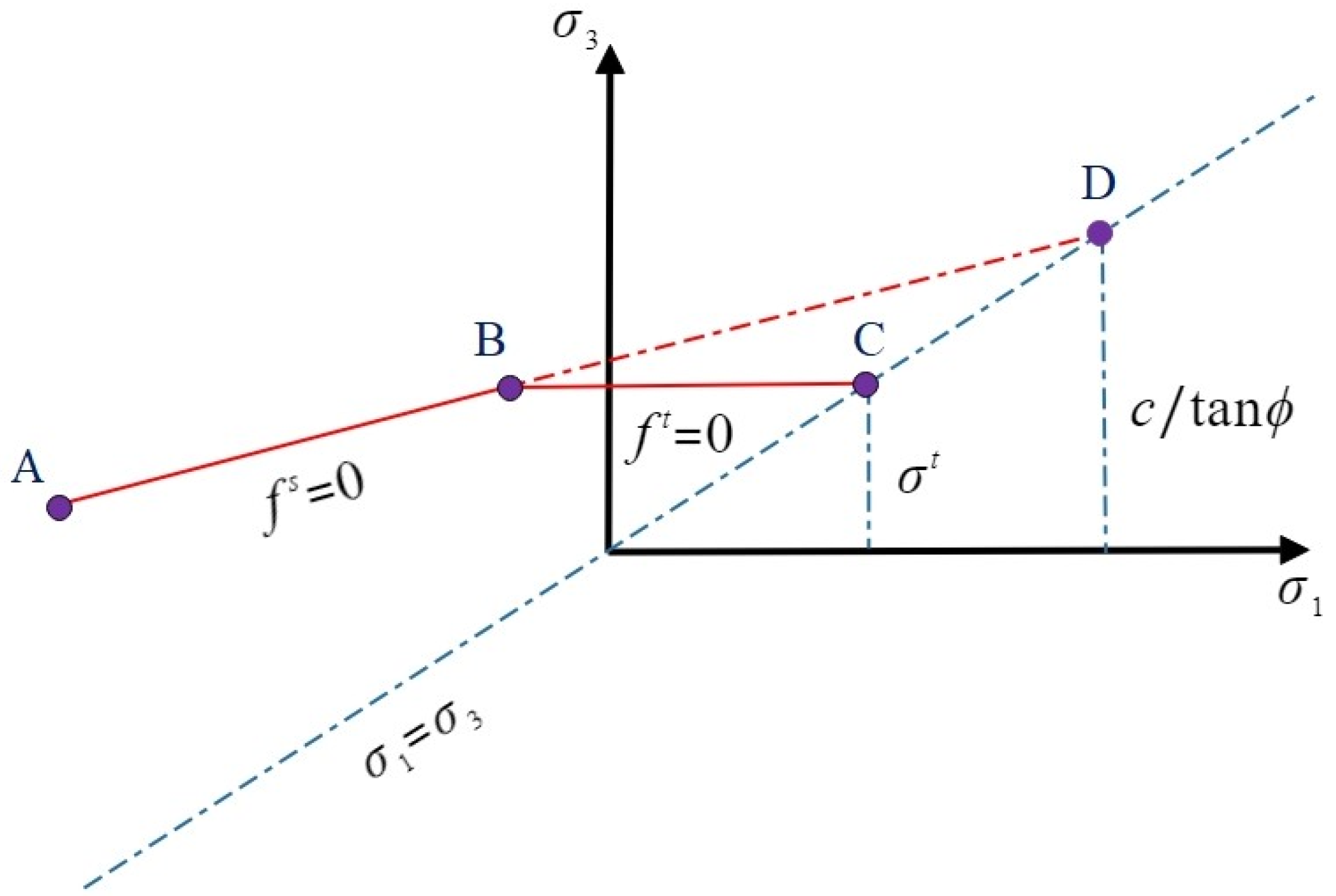
3.1. Numerical Modeling of CJRM
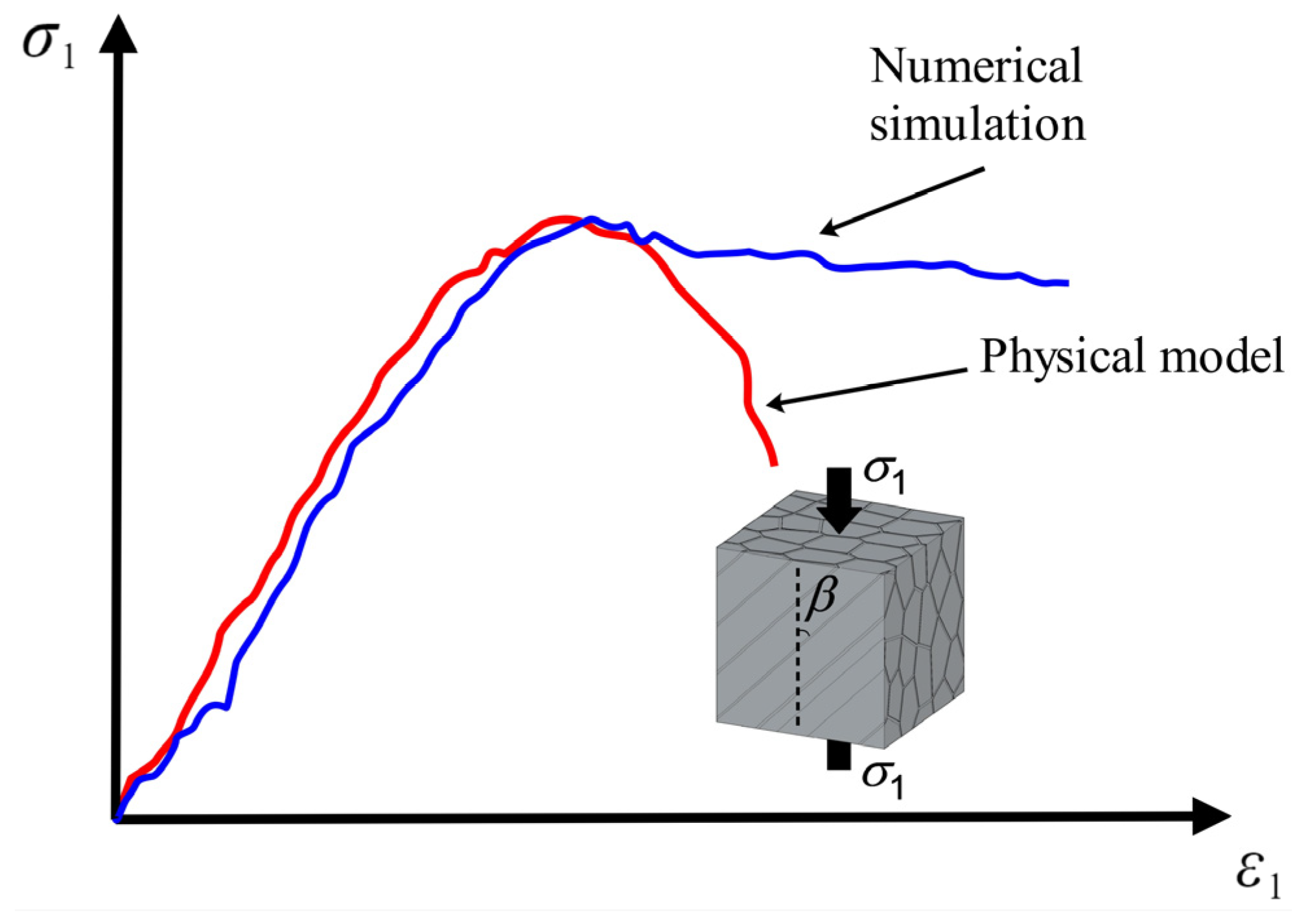
3.2. Validation of the Numerical Modeling
4. Calculation Results and Discussion
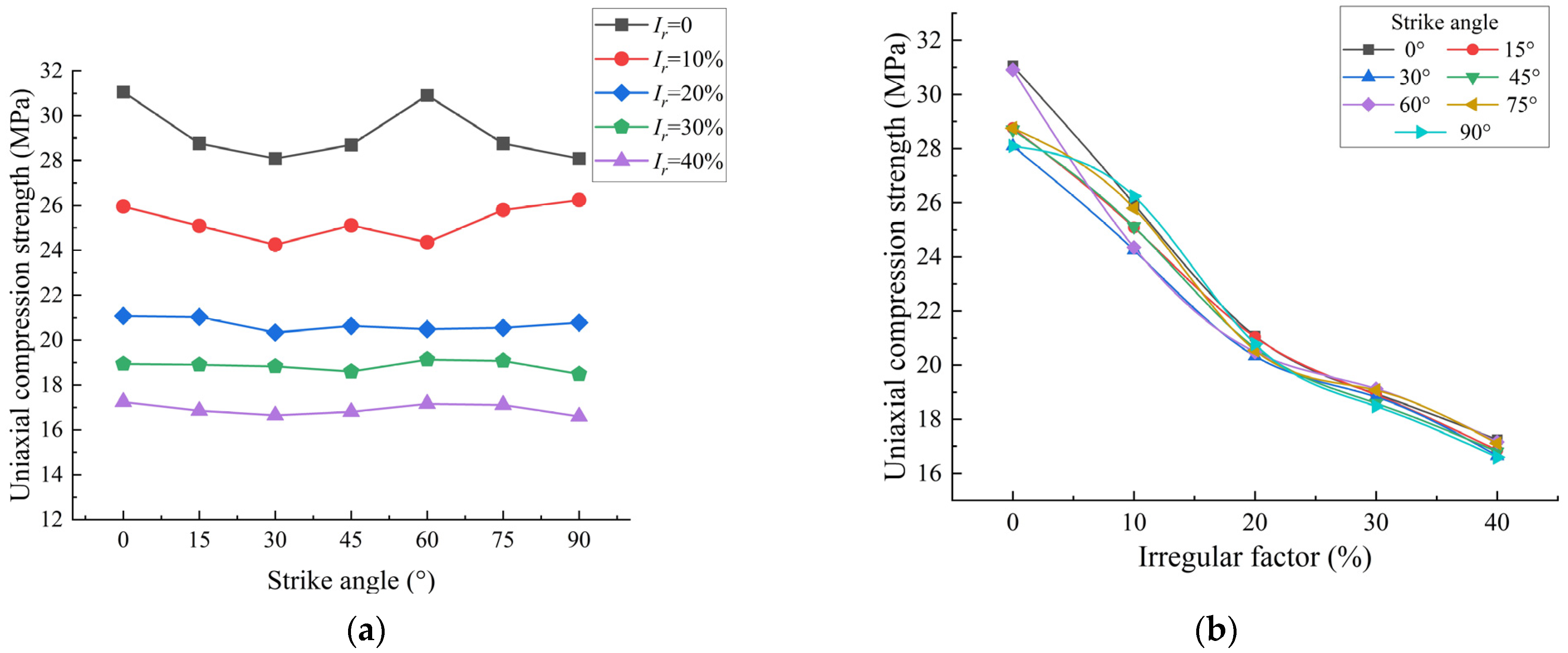
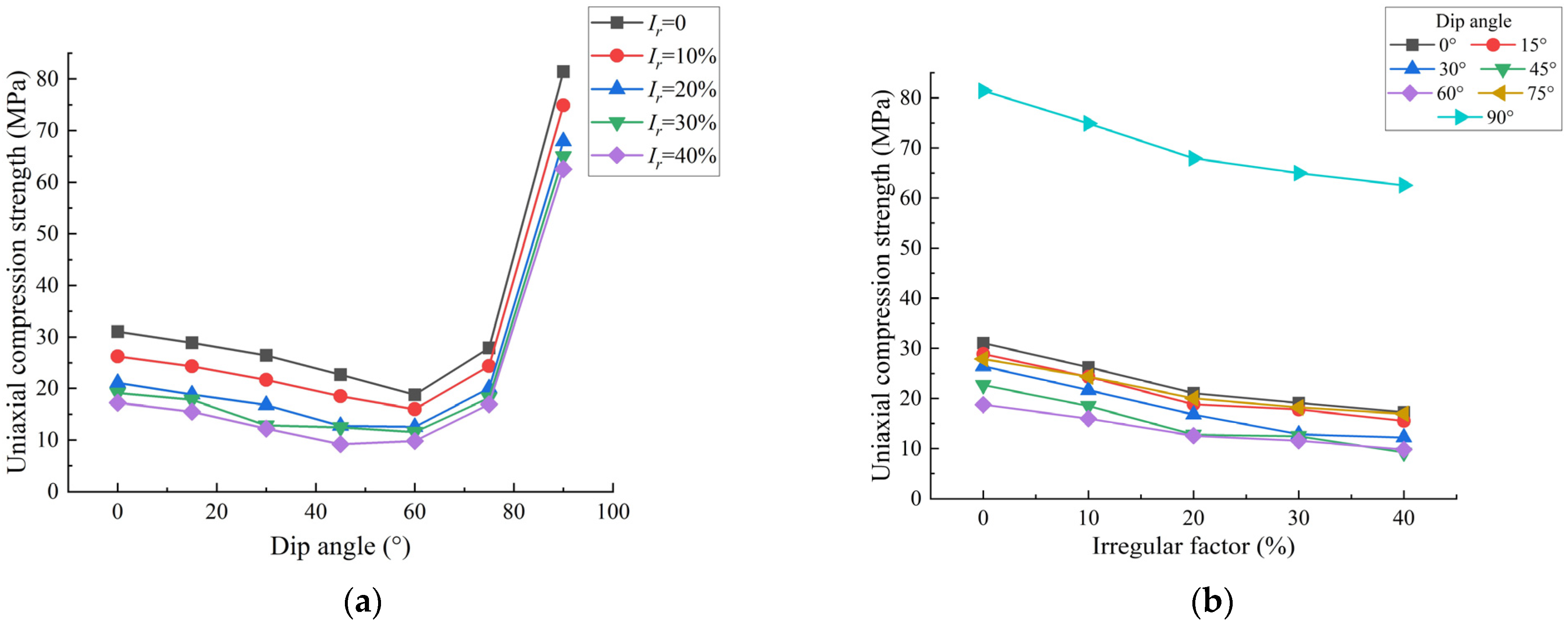
4.1. The Effect of Strike Angle on CJRM Strength Behavior with Different Irregular Factors
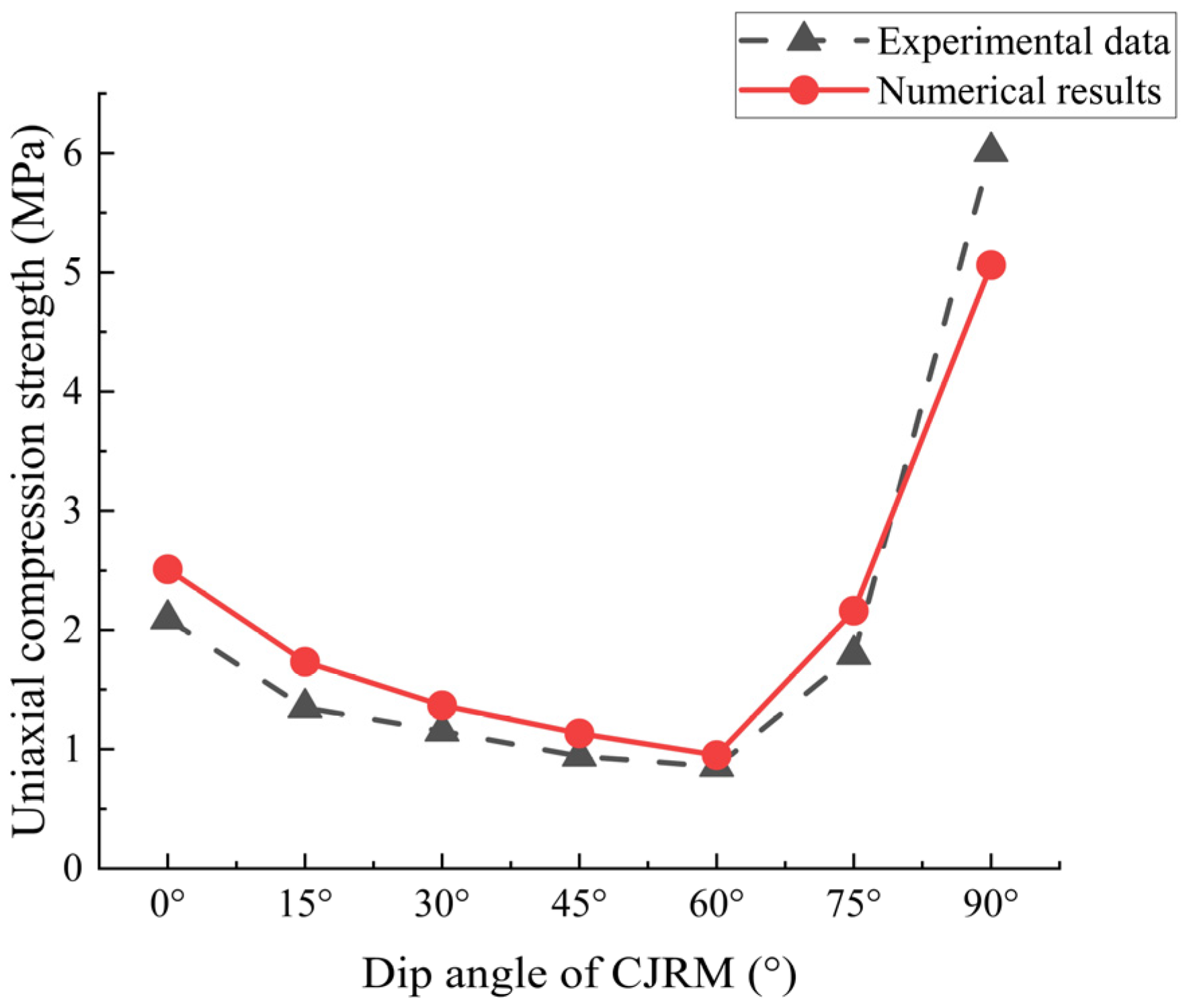
4.2. The Effect of Dip Angle on CJRM Strength Behavior with Different Irregular Factors
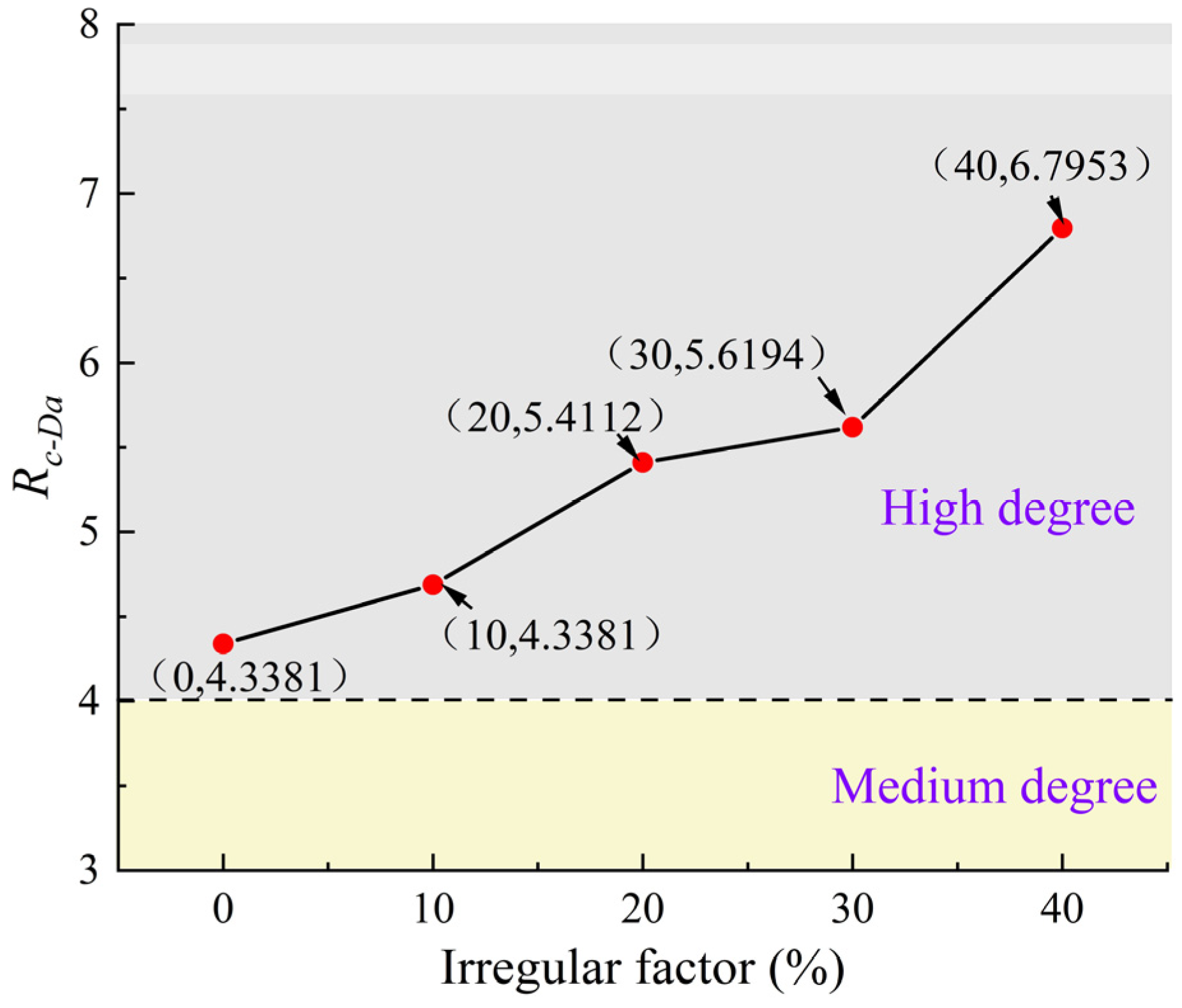
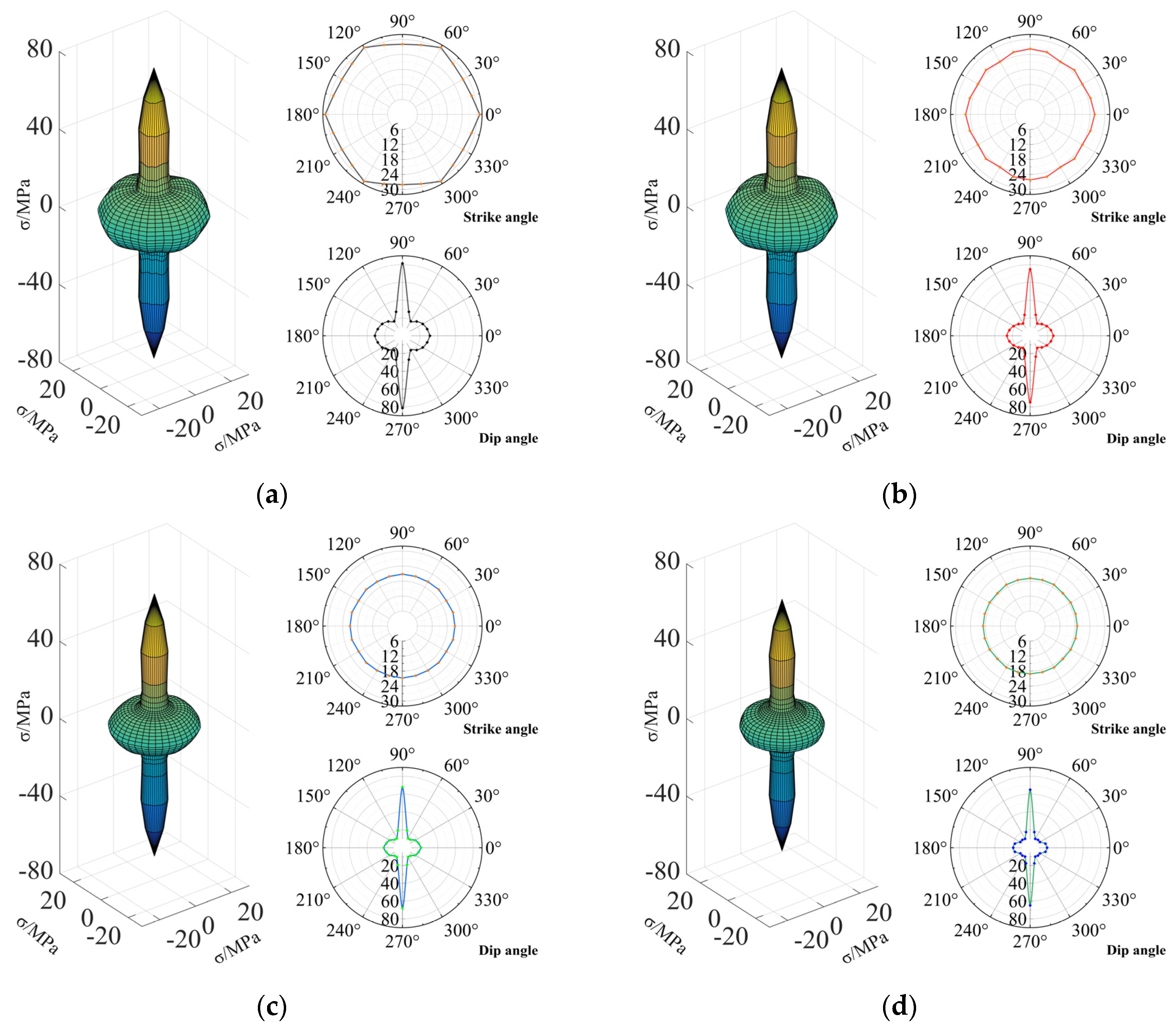
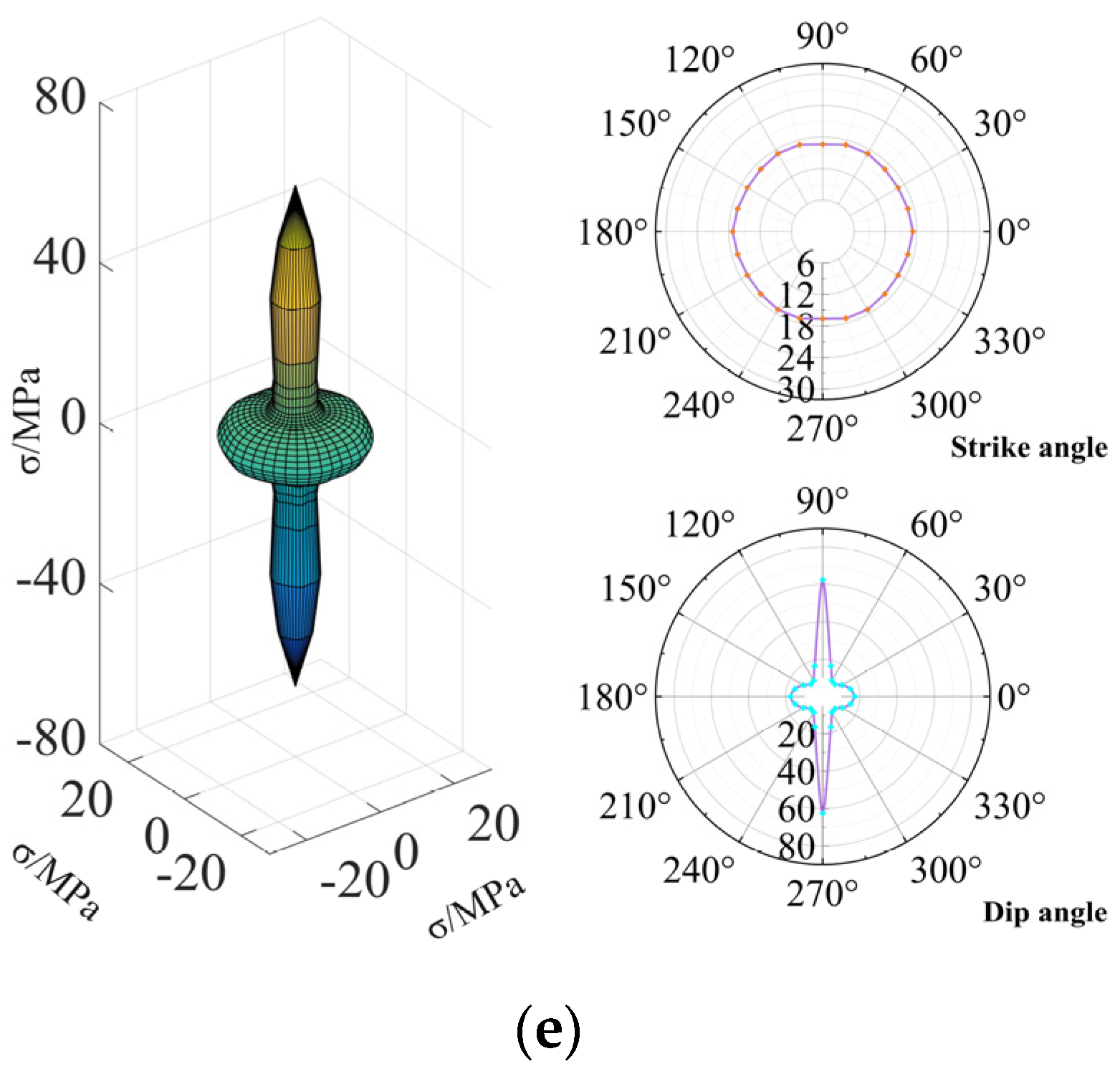
4.3. Three-Dimensional Strength Anisotropy of CJRM
5. Conclusions
- (1)
- A single-random movement with a range constraint Voronoi diagram of uniform seed points is proposed for simulating the irregular horizontal section of the CJRM. Based on this, a geometric model reconstruction method is developed using feasible geological statistical parameters, including horizontal polygon density, Q, irregular factor, Ir, dip angle, Da, strike angle, Sa, transverse joint spacing, S, and transverse joint penetration rate, P. With this method, a geometric modeling approach that is more practical and relatively simple, with better integration and actual engineering provided for the production of similar material models and numerical simulation modeling. In addition, the method also has exploitable value for other types of sedimentary rocks, such as conglomerates, sandstones, metamorphic rocks, such as shales, and intrusive rocks, such as granites.
- (2)
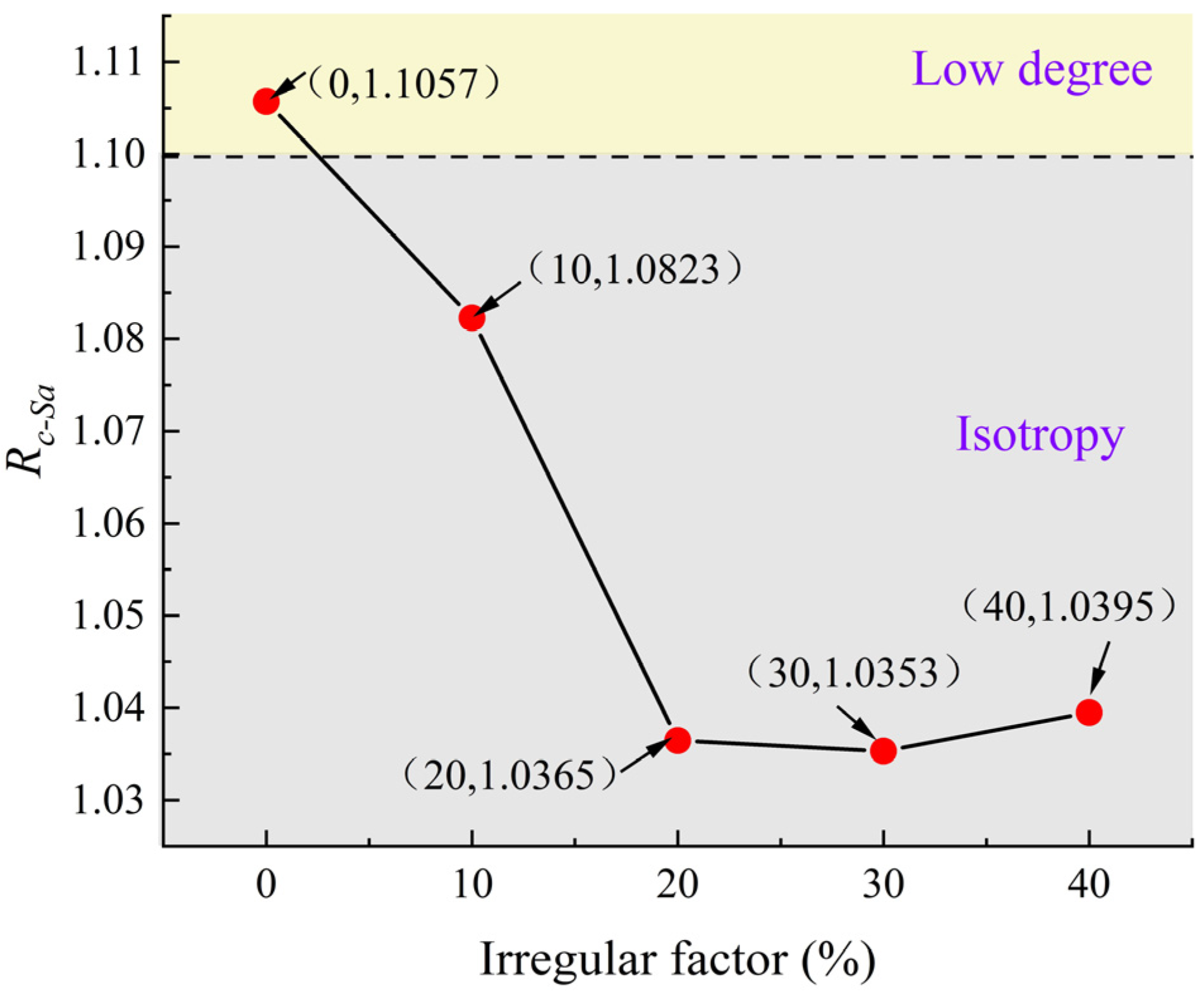
- In the numerical simulation of numerical CJRM models with different strike angles and irregular factors under uniaxial compression, when Ir = 0, the curve of the uniaxial compressive strengths versus the strike angle was W-shaped, the maximum strength and minimum strength with a small gap are at the strike angles of 0°and 30°, respectively. As the irregular factor increases, the uniaxial compressive strength with different strike angles decreases uniformly, and the strength anisotropy of the strike angle decreases from 1.1057 to 1.0395, indicating that the numerical CJRM models change from low degree anisotropy to isotropy. Therefore, the effect of the strike angle on the strength anisotropy of basalt CJRM can be considered negligible.
- (3)
- In the numerical simulation of numerical CJRM models with different dip angles and irregular factors under uniaxial compression, when Ir = 0, the curve of the uniaxial compressive strengths versus the dip angle shows a U-shape, with the maximum strength and minimum strength at the dip angles of 90°and 60°, respectively. As the irregular factor increases, the uniaxial compressive strength with different dip angles decreases, and the decreases are all from sharp to steady. The effect of the irregular factor on strength behavior has the strongest and weakest impact on the dip angles at 60° and 90°, respectively. The strength anisotropy of the dip angle increases from 4.3381 to 6.7953, showing an increasing strong anisotropy at a high degree, indicating that the effect of the dip angle on the strength behavior is enhanced. Therefore, in the engineering design and construction of the CJRM, great attention should be paid to the effect of the dip angle on strength anisotropy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilman, J.J. Basalt columns: Large scale constitutional supercooling? J. Volcanol. Geoth Res. 2009, 184, 347–350. [Google Scholar] [CrossRef]
- Mondal, T.K.; Chowdhury, A.; Sain, A.; Chatterjee, S. Understanding the maturity of columnar joints and its spatial relationship with eruptive centre: A critical appraisal from the Rajmahal basalt, India. Phys. Earth Planet. Inter. 2022, 326, 106867. [Google Scholar] [CrossRef]
- Philpotts, A.R.; Burkett, D.H. Structures, Textures, and Cooling Histories of Columbia River Basalt Flows: Discussion and Reply: Discussion. Geol. Soc. Am. Bull. 1987, 99, 886–887. [Google Scholar] [CrossRef]
- Zhu, S.; Zheng, J.; Zhu, Z.; Zhu, Q.; Zhou, L. Experiments on Three-Dimensional Flaw Dynamic Evolution of Transparent Rock-Like Material under Osmotic Pressure. Tunn. Undergr. Space Technol. 2022, 128, 13. [Google Scholar] [CrossRef]
- Hao, X.-J.; Feng, X.-T.; Yang, C.-X.; Jiang, Q.; Li, S.-J. Analysis of Edz Development of Columnar Jointed Rock Mass in the Baihetan Diversion Tunnel. Rock Mech. Rock Eng. 2016, 49, 1289–1312. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, Z.; Xu, J.; Zhou, M.; Jiang, Q.; Li, G. Study on Deformation and Control Measures of Columnar Jointed Basalt for Baihetan Super-High Arch Dam Foundation. Rock Mech. Rock Eng. 2017, 51, 2569–2595. [Google Scholar] [CrossRef]
- Shi, A.C.; Wei, Y.F.; Zhang, Y.H.; Tang, M.F. Study on the Strength Characteristics of Columnar Jointed Basalt with a True Triaxial Apparatus at the Baihetan Hydropower Station. Rock Mech. Rock Eng. 2020, 53, 4947–4965. [Google Scholar] [CrossRef]
- Sun, Q.C.; Li, S.J.; Guo, H.S.; Zheng, M.Z.; Yang, Z.Y. In Situ Test of Excavation Damaged Zone of Columnar Jointed Rock Masses under Different Borehole Conditions. Bull. Eng. Geol. Environ. 2021, 80, 2991–3007. [Google Scholar] [CrossRef]
- Lin, P.; Shi, J.; Wei, P.; Fan, Q.; Wang, Z. Shallow Unloading Deformation Analysis on Baihetan Super-High Arch Dam Foundation. Bull. Eng. Geol. Environ. 2019, 78, 5551–5568. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Q.; Huang, H.; Xue, X. Study on Creep Models and Parameter Inversion of Columnar Jointed Basalt Rock Masses. Eng. Geol. 2021, 290, 106206. [Google Scholar] [CrossRef]
- Zhao, Y.S.; Cheng, Z.Q.; Gao, Y.T.; Wu, S.C.; Chen, C.C. Review of Geomechanical Similar-Material Test Systems. Arab. J. Geosci. 2020, 13, 19. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, J.C.; Xu, W.Y.; Wang, R.B.; Wang, H.L.; Yan, L.; Lin, Z.N. Experimental Investigation of the Anisotropic Mechanical Properties of a Columnar Jointed Rock Mass: Observations from Laboratory-Based Physical Modelling. Rock Mech. Rock Eng. 2017, 50, 1919–1931. [Google Scholar] [CrossRef]
- Xiao, W.M.; Deng, R.G.; Zhong, Z.B.; Fu, X.M.; Wang, C.Y. Experimental Study on the Mechanical Properties of Simulated Columnar Jointed Rock Masses. J. Geophys. Eng. 2015, 12, 80–89. [Google Scholar] [CrossRef]
- Lu, W.B.; Zhu, Z.D.; He, Y.X.; Que, X.C. Strength Characteristics and Failure Mechanism of a Columnar Jointed Rock Mass under Uniaxial, Triaxial, and True Triaxial Confinement. Rock Mech. Rock Eng. 2021, 54, 2425–2439. [Google Scholar] [CrossRef]
- Que, X.C.; Zhu, Z.D.; Niu, Z.H.; Lu, W.N. Estimating the Strength and Deformation of Columnar Jointed Rock Mass Based on Physical Model Test. Bull. Eng. Geol. Environ. 2021, 80, 1557–1570. [Google Scholar] [CrossRef]
- Xia, Y.J.; Liu, B.C.; Zhang, C.Q.; Liu, N.; Zhou, H.; Chen, J.; Tang, C.N.; Gao, Y.; Zhao, D.C.; Meng, Q.K. Investigations of Mechanical and Failure Properties of 3D Printed Columnar Jointed Rock Mass under True Triaxial Compression with One Free Face. Geomech. Geophys. Geo Energy Geo Resour. 2022, 8, 1–24. [Google Scholar] [CrossRef]
- Xia, Y.-J.; Zhang, C.Q.; Zhou, H.; Hou, J.; Su, G.S.; Gao, Y.; Liu, N.; Singh, H.K. Mechanical Behavior of Structurally Reconstructed Irregular Columnar Jointed Rock Mass Using 3D Printing. Eng. Geol. 2020, 268, 105509. [Google Scholar] [CrossRef]
- Di, S.J.; Xu, W.Y.; Ning, Y.; Wang, W.; Wu, G.Y. Macro-Mechanical Properties of Columnar Jointed Basaltic Rock Masses. J. Cent. South Univ. Technol. 2011, 18, 2143–2149. [Google Scholar] [CrossRef]
- Zhu, X.D.; Hu, L.X.; Jiang, Q.; Li, S.J.; Li, J. Failure Characteristics and Support Optimal Design of Columnar Jointed Rock Mass at a Diversion Tunnel. Appl. Mech. Mater. 2013, 353, 1680–1684. [Google Scholar] [CrossRef]
- Meng, Q.X.; Wang, H.L.; Xu, W.Y.; Chen, Y.L. Numerical Homogenization Study on the Effects of Columnar Jointed Structure on the Mechanical Properties of Rock Mass. Int. J. Rock Mech. Min. Sci. 2019, 124, 104127. [Google Scholar] [CrossRef]
- Meng, Q.X.; Yan, L.; Chen, Y.L.; Zhang, Q. Generation of Numerical Models of Anisotropic Columnar Jointed Rock Mass Using Modified Centroidal Voronoi Diagrams. Symmetry 2018, 10, 618. [Google Scholar] [CrossRef]
- Zhang, J.C.; Jiang, Q.; Feng, G.L.; Li, S.J.; Pei, S.F.; He, B.G. Geometrical Characteristic Investigation of the Baihetan Irregular Columnar Jointed Basalt and Corresponding Numerical Reconstruction Method. J. Cent. South Univ. 2022, 29, 455–469. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, W.Y.; Wang, H.L.; Wang, R.B.; Yan, L.; Hu, M.T. Anisotropic Mechanical Behaviour of Columnar Jointed Rock Masses Subjected to Cyclic Loading: An Experimental Investigation. Int. J. Rock Mech. Min. Sci. 2021, 148, 104954. [Google Scholar] [CrossRef]
- Dershowitz, W.S.; Einstein, H.H. Characterizing Rock Joint Geometry with Joint System Models. Rock Mech. Rock Eng. 1998, 21, 21–51. [Google Scholar] [CrossRef]
- Minciacchi, D.; Granato, A. How Relevant Are Subcortical Maps for the Cortical Machinery? An Hypothesis Based on Parametric Study of Extrarelay Afferents to Primary Sensory Areas. Adv. Psychol. 1997, 119, 149–168. [Google Scholar]
- Duyckaerts, C.; Gilles, G. Voronoi Tessellation to Study the Numerical Density and the Spatial Distribution of Neurones. J. Chem. Neuroanat. 2000, 20, 83–92. [Google Scholar] [CrossRef]
- Bae, S.W. An Almost Optimal Algorithm for Voronoi Diagrams of Non-Disjoint Line Segments. Comput. Geom. Theory Appl. 2016, 52, 34–43. [Google Scholar] [CrossRef]
- Boots, B.; Sugihara, K.; Chiu, S.N.; Okabe, A. Spatial Tessellations:Concepts and Applications of Voronoi Diagrams; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ning, Y.U.; Weiya, X.U.; Wentang, Z.; Guotao, M.; Anchi, S.H.I.; Guanye, W.U. Study of Random Simulation of Columnar Jointed Rock Mass and Its Representative Elementary Volume Scale. Chin. J. Rock Mech. Eng. 2008, 27, 1202–1208. [Google Scholar]
- Di, S.J.; Zheng, W.T.; Zhang, J.K. Back Analysis on Mechanical Deformation Parameters of Columnar Jointed Rock Mass. Appl. Mech. Mater. 2011, 55–57, 1947–1950. [Google Scholar] [CrossRef]
- Ramamurthy, T. Strength and Modulus Responses of Anisotropic Rocks. Compr. Rock Eng. 1993, 19, 147–166. [Google Scholar]
- Ramamurthy, T.; Rao, G.V.; Singh, J. Engineering Behaviour of Phyllites. Eng. Geol. 1993, 33, 209–225. [Google Scholar] [CrossRef]
| Bulk Density (kg/m3) | Elastic Modulus (GPa) | Friction Angle (°) | Poisson’s Ratio | Tensile Strength (MPa) | Cohesion (MPa) |
|---|---|---|---|---|---|
| 2800 | 60 | 56.13 | 0.2 | 5 | 12.4 |
| Cohesion (MPa) | Normal Stiffness (GPa/m) | Shear Stiffness (GPa/m) | Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|
| 0.6 | 100 | 50 | 36 | 0 |
| Bulk Density (kg/m3) | Elastic Modulus (GPa) | Friction Angle (°) | Poisson’s Ratio | Tensile Strength (MPa) | Cohesion (MPa) |
|---|---|---|---|---|---|
| 1170 | 1.24 | 51.3 | 0.19 | 0.84 | 1.37 |
| Cohesion (MPa) | Normal Stiffness (GPa/m) | Shear Stiffness (GPa/m) | Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|
| 0.04 | 9.21 | 4.72 | 32 | 0.04 |
| Size (m) | Polygon Density (m−2) | Irregular Factor | Dip Angle (°) | Strike Angle (°) | Transverse Joint Spacing (m) | Transverse Joint Penetration |
|---|---|---|---|---|---|---|
| 3 × 3 × 3 | 20.15 | 0 10% 20% 30% 40% | 0 | 0 | 0 | 0 |
| 15 | ||||||
| 30 | ||||||
| 45 | ||||||
| 60 | ||||||
| 75 | ||||||
| 90 |
| Size (m) | Polygon Density (m−2) | Irregular Factor | Dip Angle (°) | Strike Angle (°) | Transverse Joint Spacing (m) | Transverse Joint Penetration |
|---|---|---|---|---|---|---|
| 3 × 3 × 3 | 20.15 | 0 10% 20% 30% 40% | 0 | 0 | 0 | 0 |
| 15 | ||||||
| 30 | ||||||
| 45 | ||||||
| 60 | ||||||
| 75 | ||||||
| 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Wang, L.; Zhu, S.; Wu, J. Study on the Anisotropy of Strength Properties of Columnar Jointed Rock Masses Using a Geometric Model Reconstruction Method Based on a Single-Random Movement Voronoi Diagram of Uniform Seed Points. Symmetry 2023, 15, 944. https://doi.org/10.3390/sym15040944
Zhu Z, Wang L, Zhu S, Wu J. Study on the Anisotropy of Strength Properties of Columnar Jointed Rock Masses Using a Geometric Model Reconstruction Method Based on a Single-Random Movement Voronoi Diagram of Uniform Seed Points. Symmetry. 2023; 15(4):944. https://doi.org/10.3390/sym15040944
Chicago/Turabian StyleZhu, Zhende, Luxiang Wang, Shu Zhu, and Junyu Wu. 2023. "Study on the Anisotropy of Strength Properties of Columnar Jointed Rock Masses Using a Geometric Model Reconstruction Method Based on a Single-Random Movement Voronoi Diagram of Uniform Seed Points" Symmetry 15, no. 4: 944. https://doi.org/10.3390/sym15040944
APA StyleZhu, Z., Wang, L., Zhu, S., & Wu, J. (2023). Study on the Anisotropy of Strength Properties of Columnar Jointed Rock Masses Using a Geometric Model Reconstruction Method Based on a Single-Random Movement Voronoi Diagram of Uniform Seed Points. Symmetry, 15(4), 944. https://doi.org/10.3390/sym15040944







