MHD Stagnation Point of Blasius Flow for Micropolar Hybrid Nanofluid toward a Vertical Surface with Stability Analysis
Abstract
1. Introduction
2. Formulation of the Mathematical Model
3. Temporal Stability Analysis
4. Result and Discussion
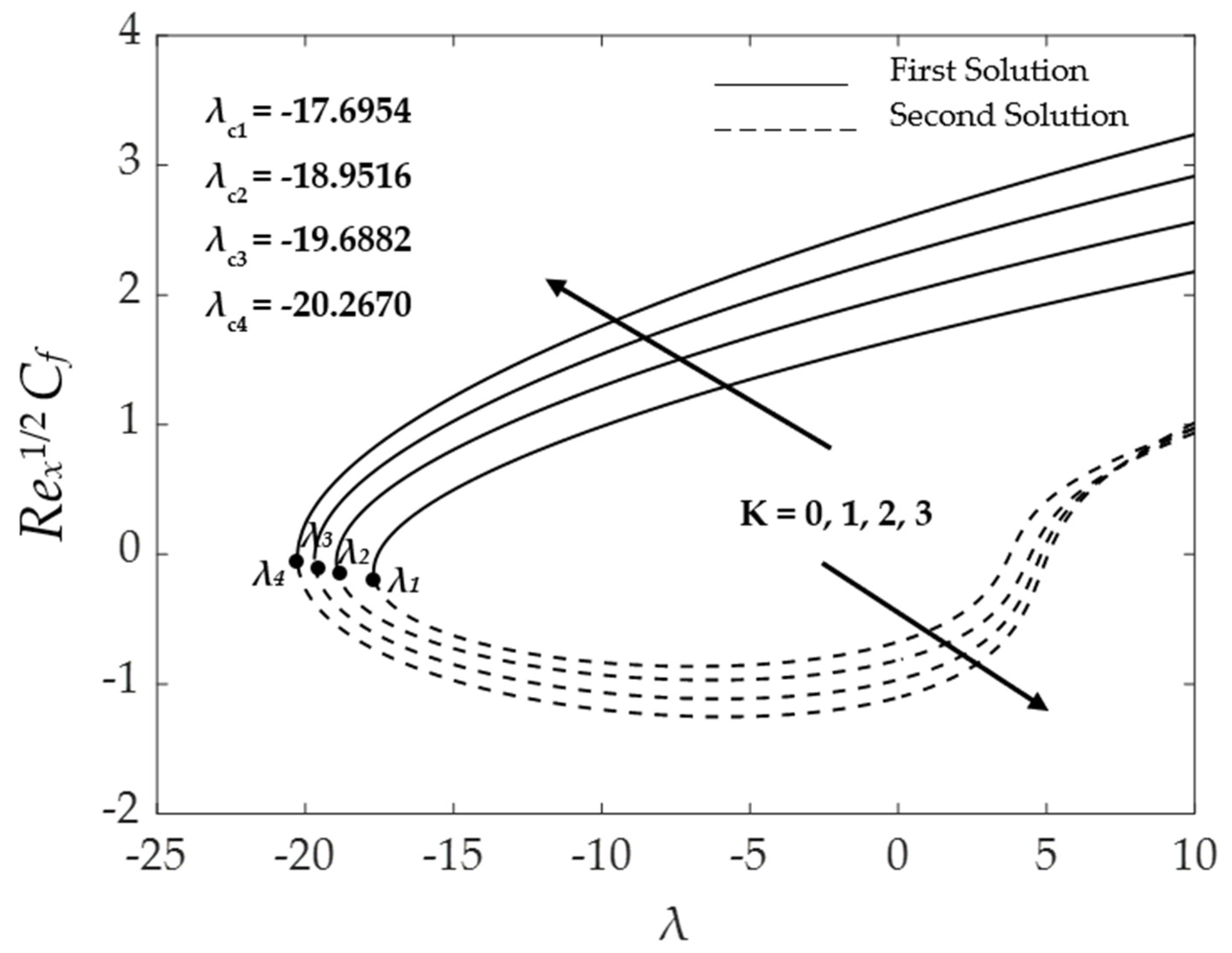
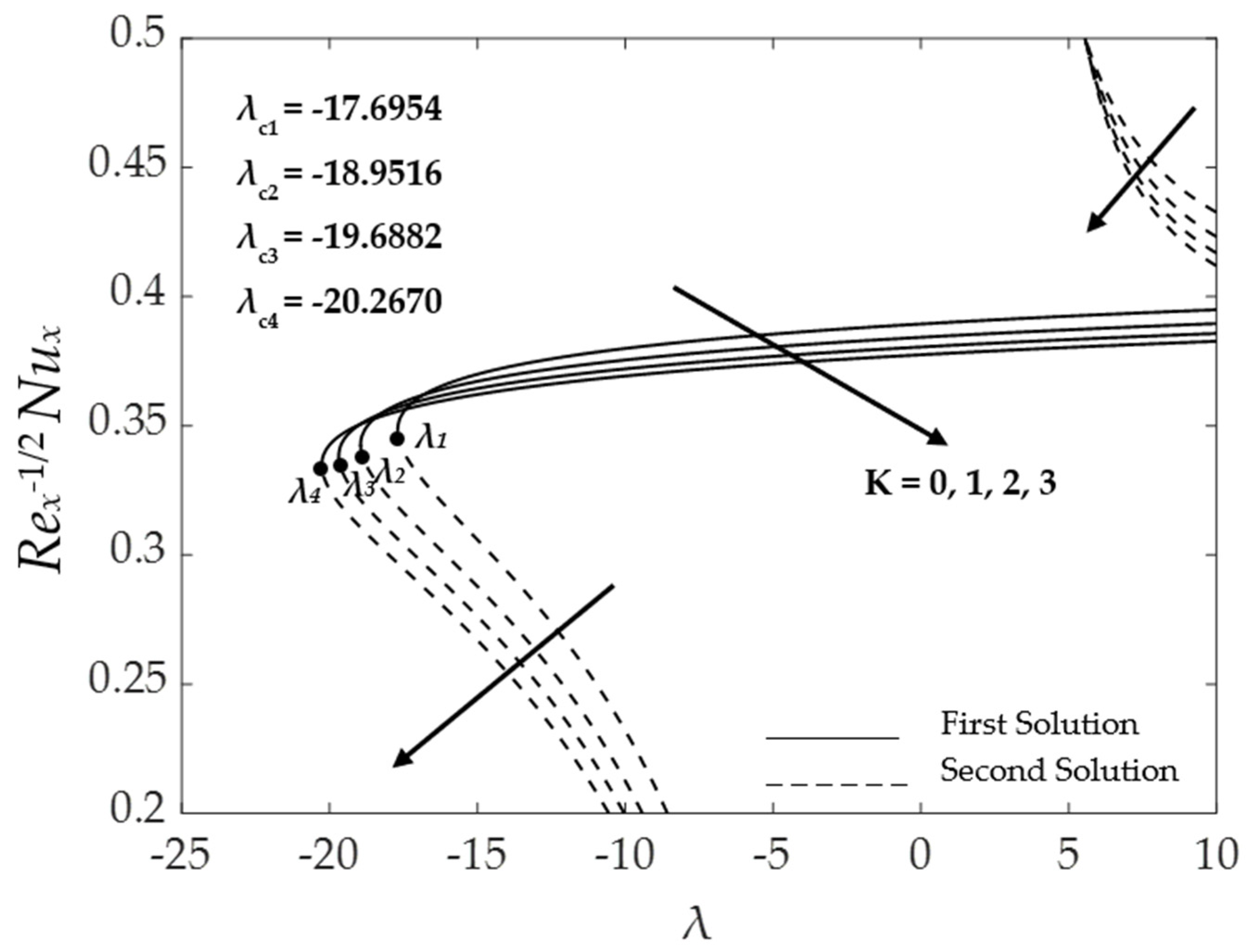
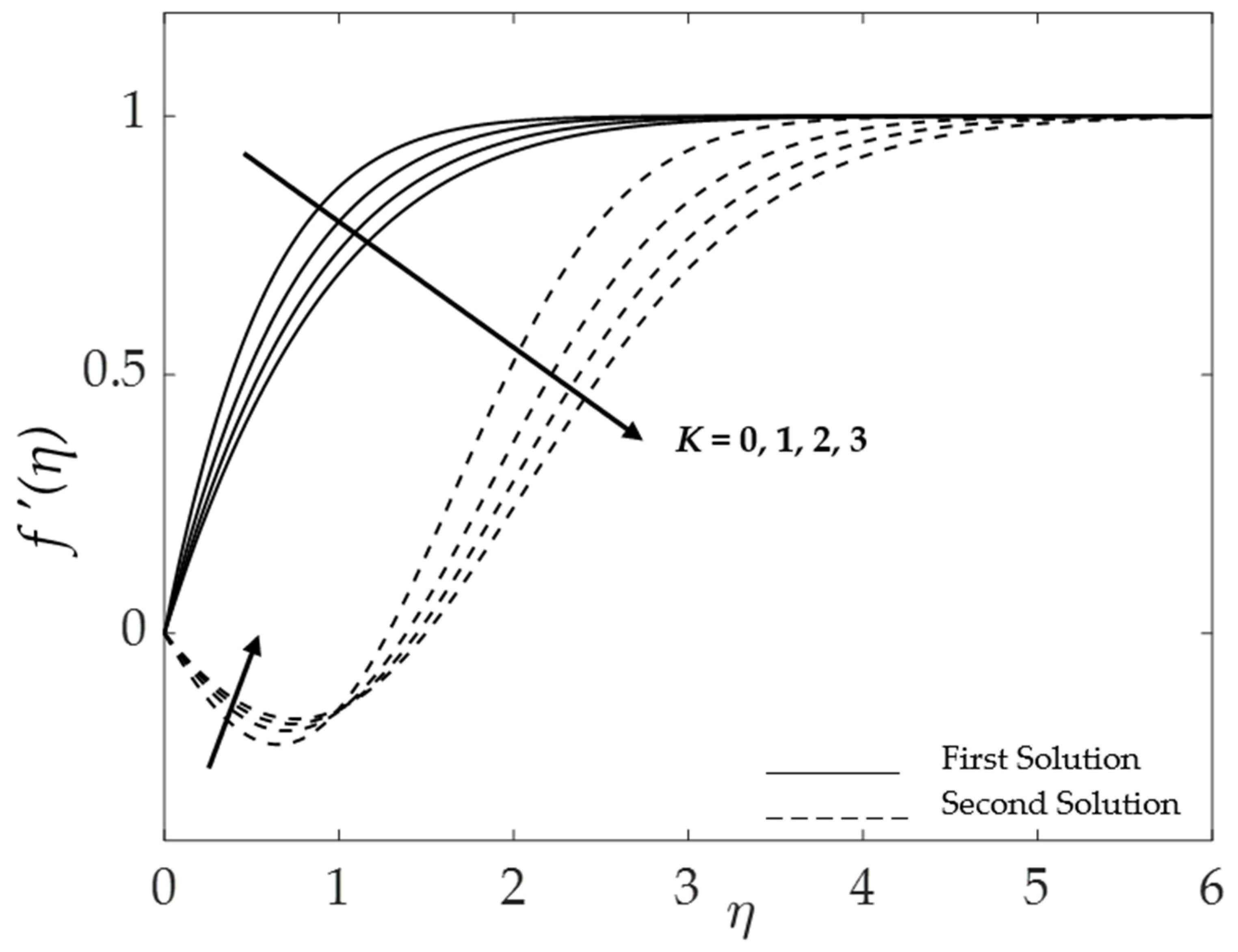
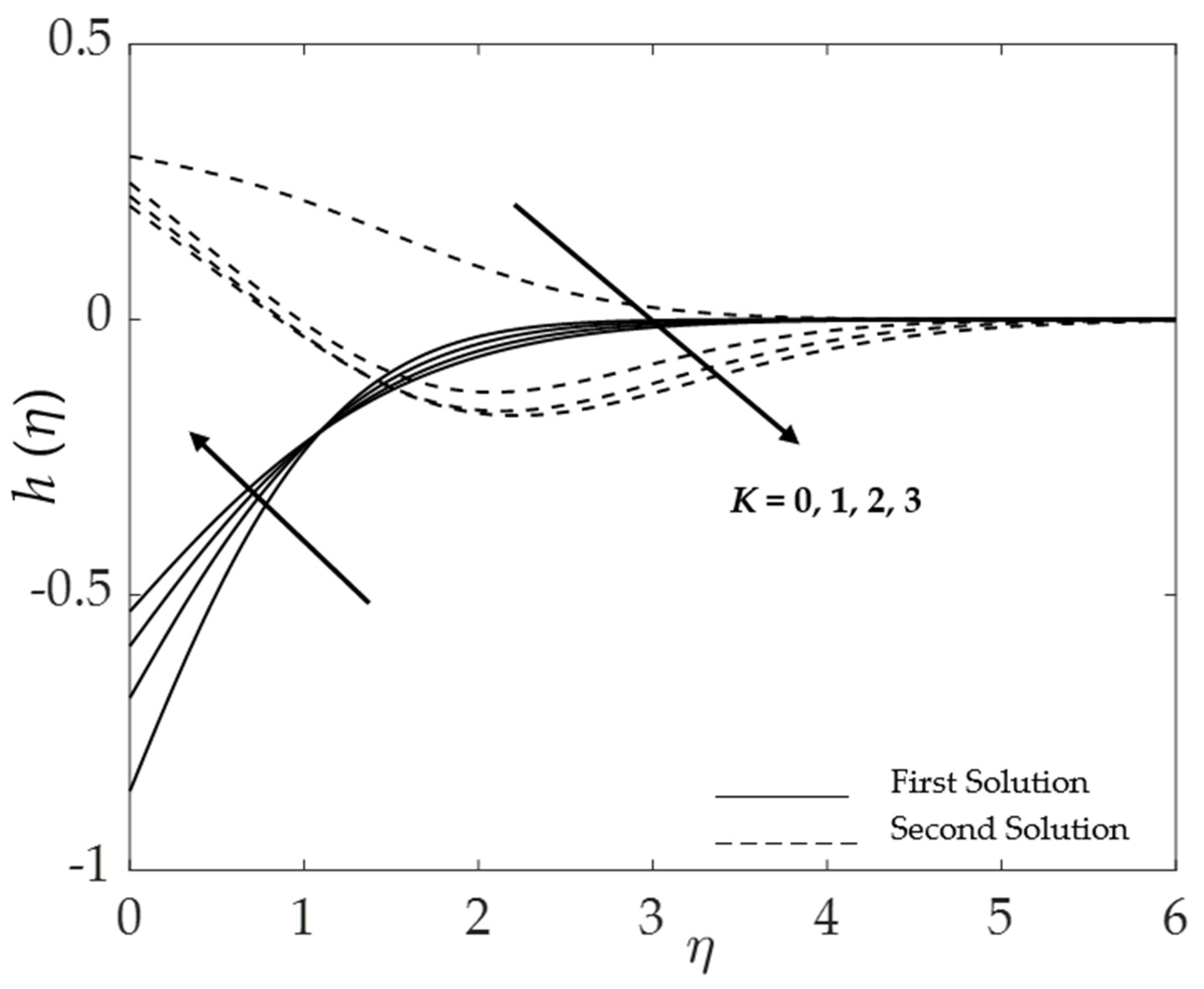
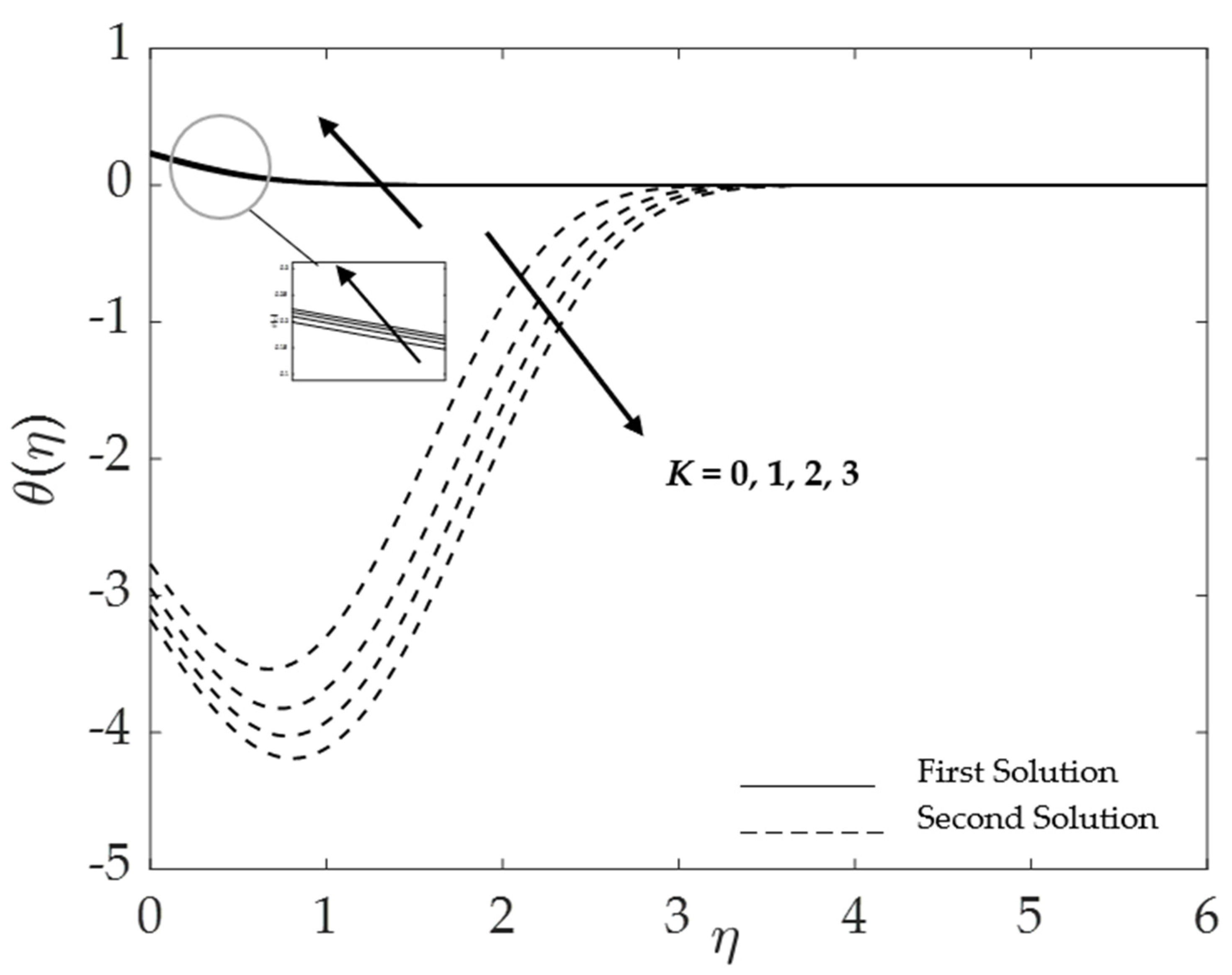
4.1. Effect of the Material Parameter
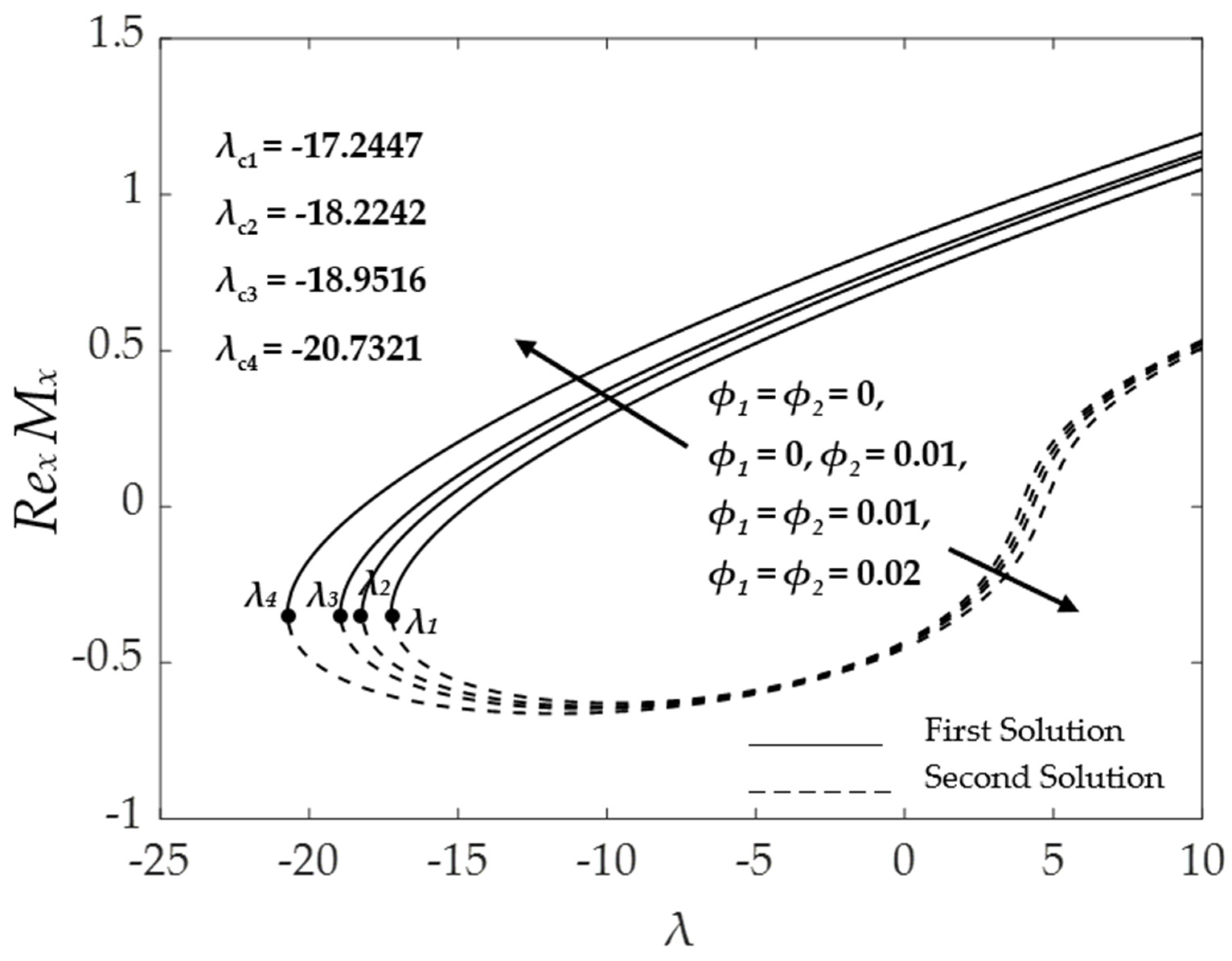
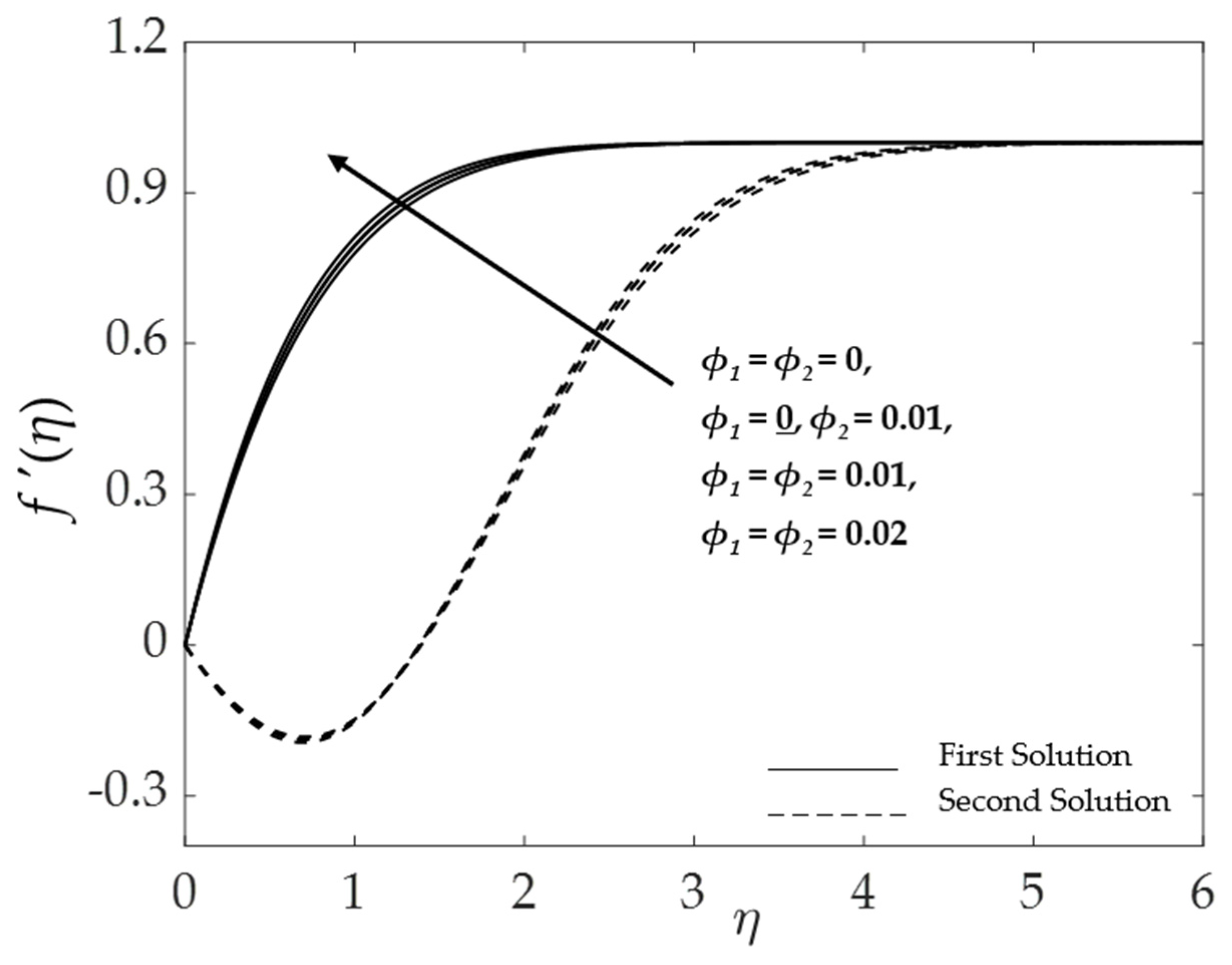
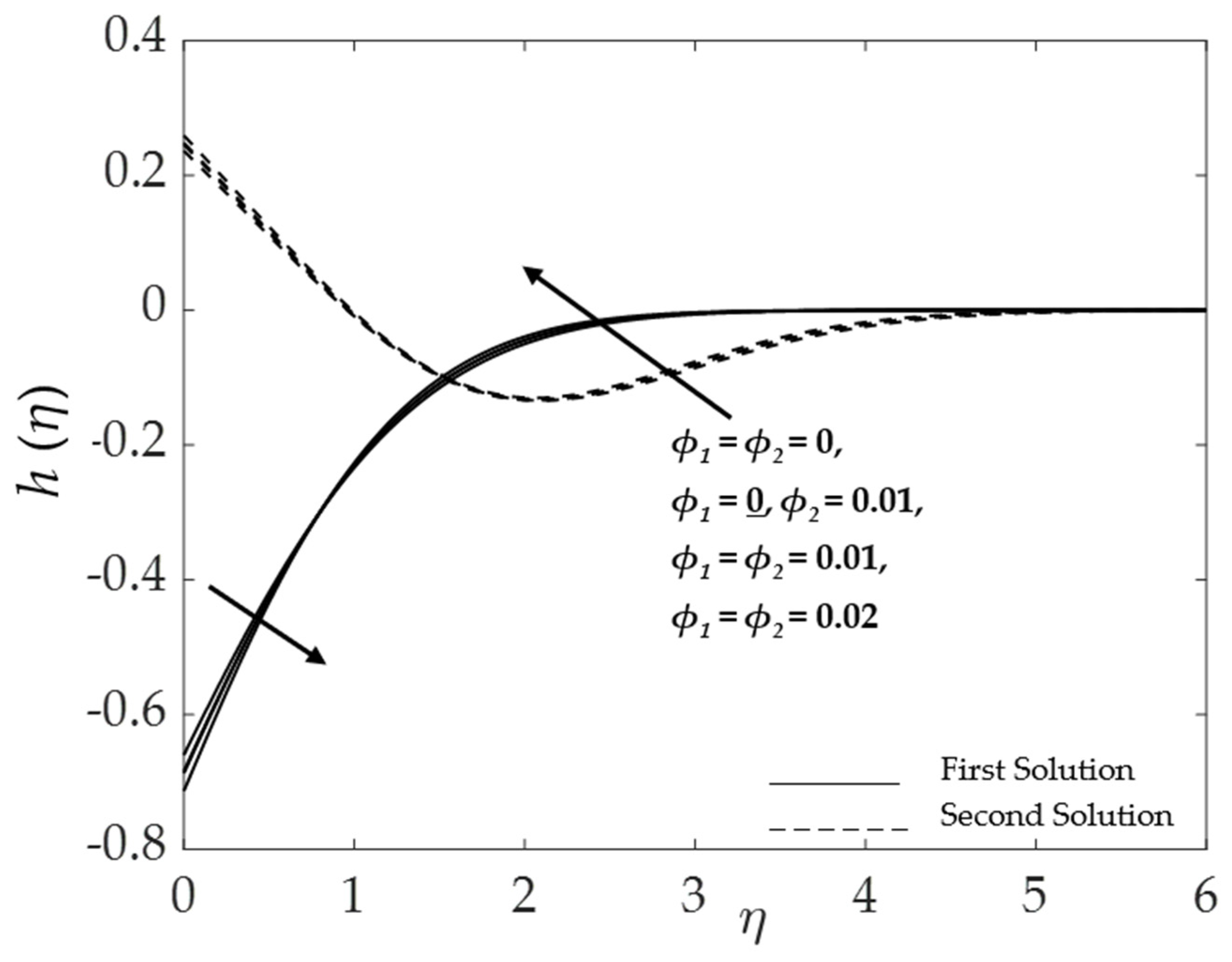
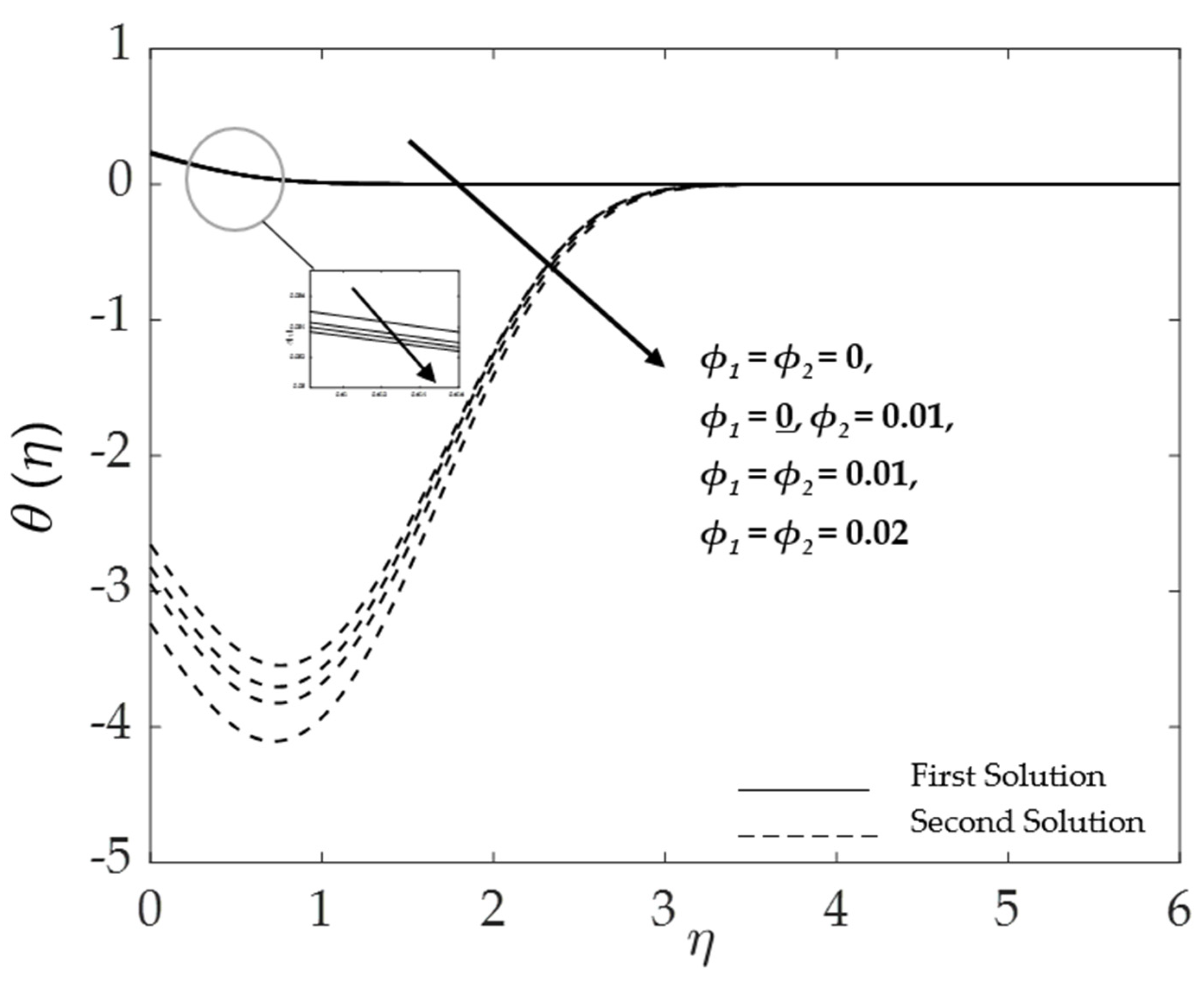
4.2. Effect of the Hybrid Nanoparticles Volume Fraction
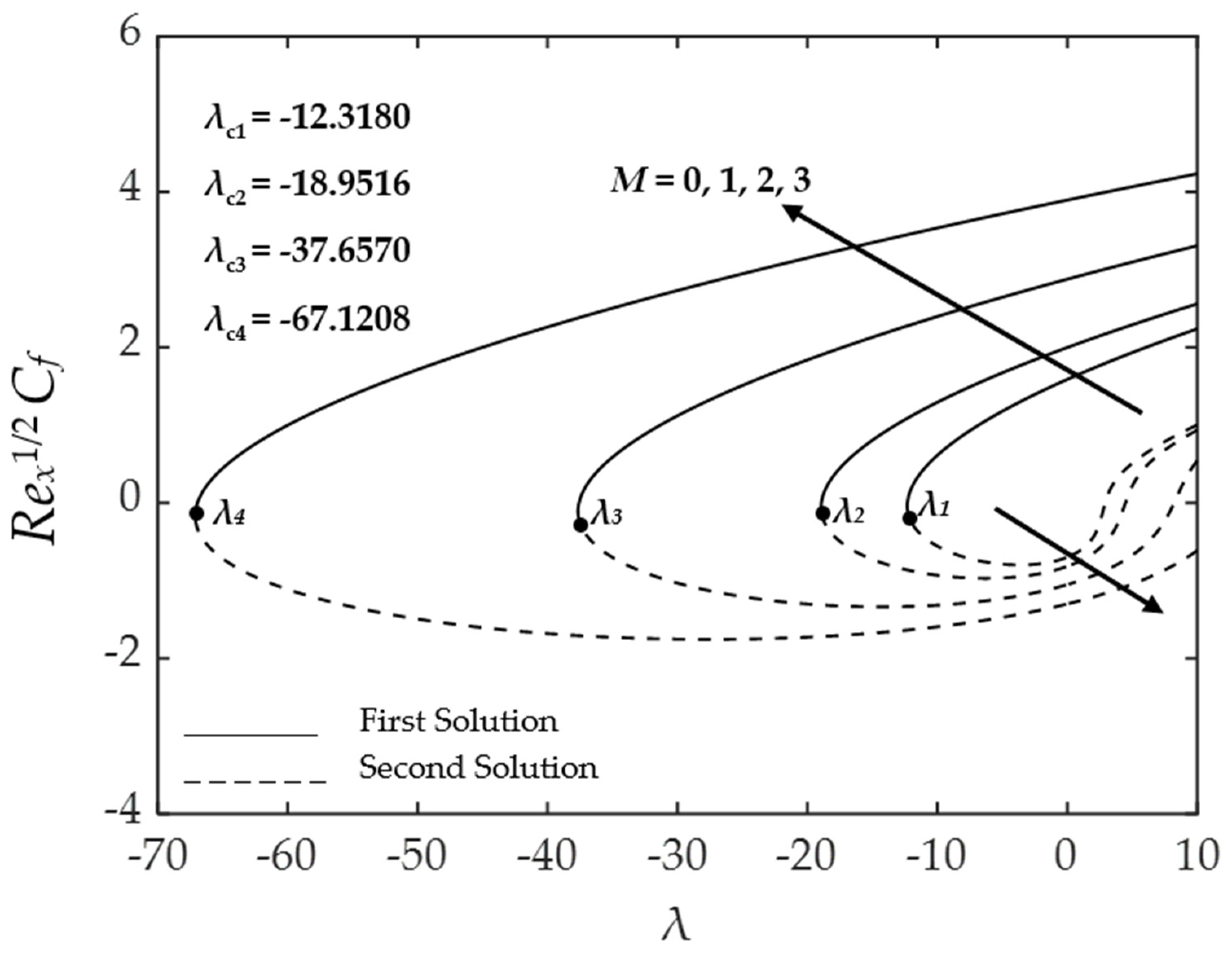
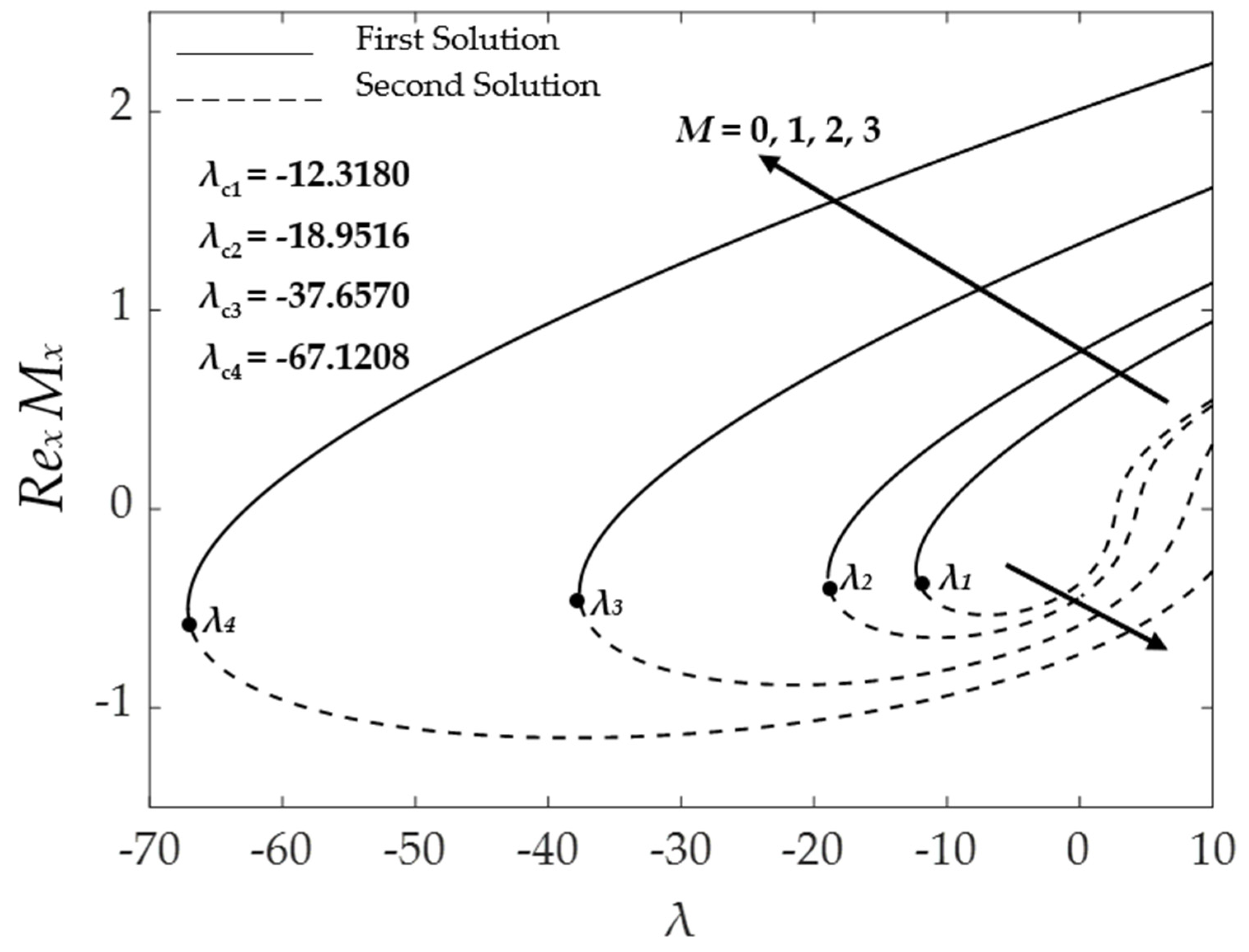
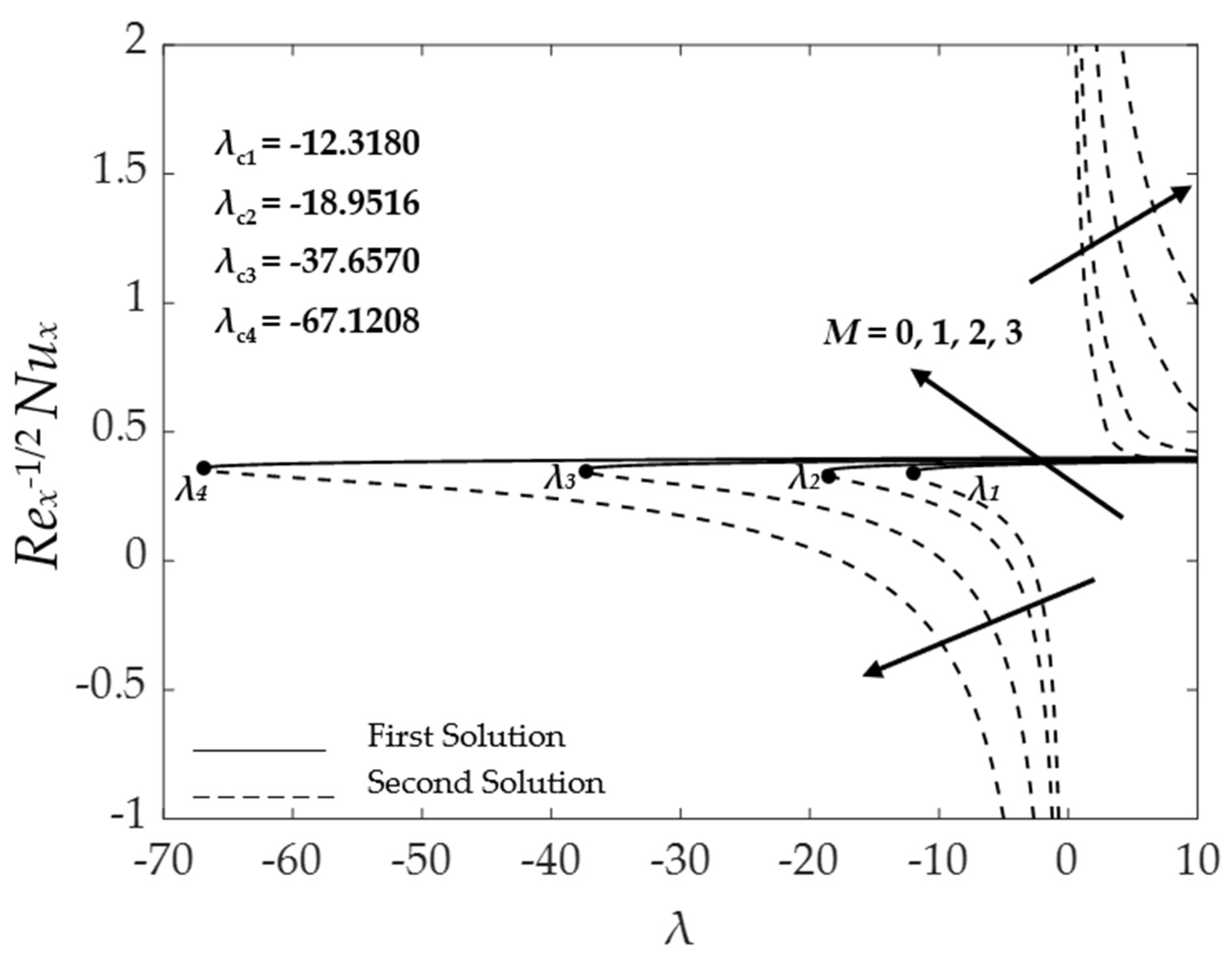
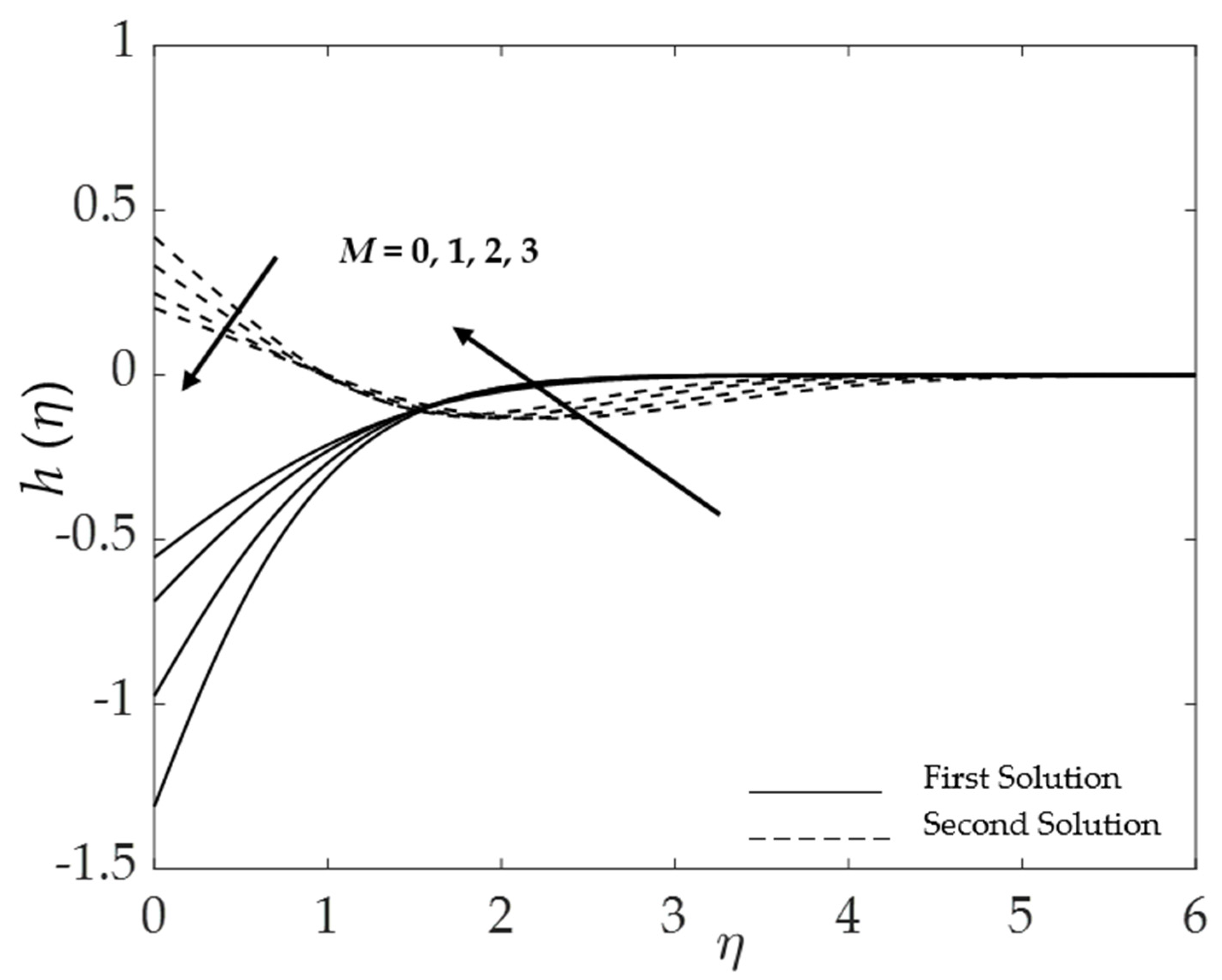
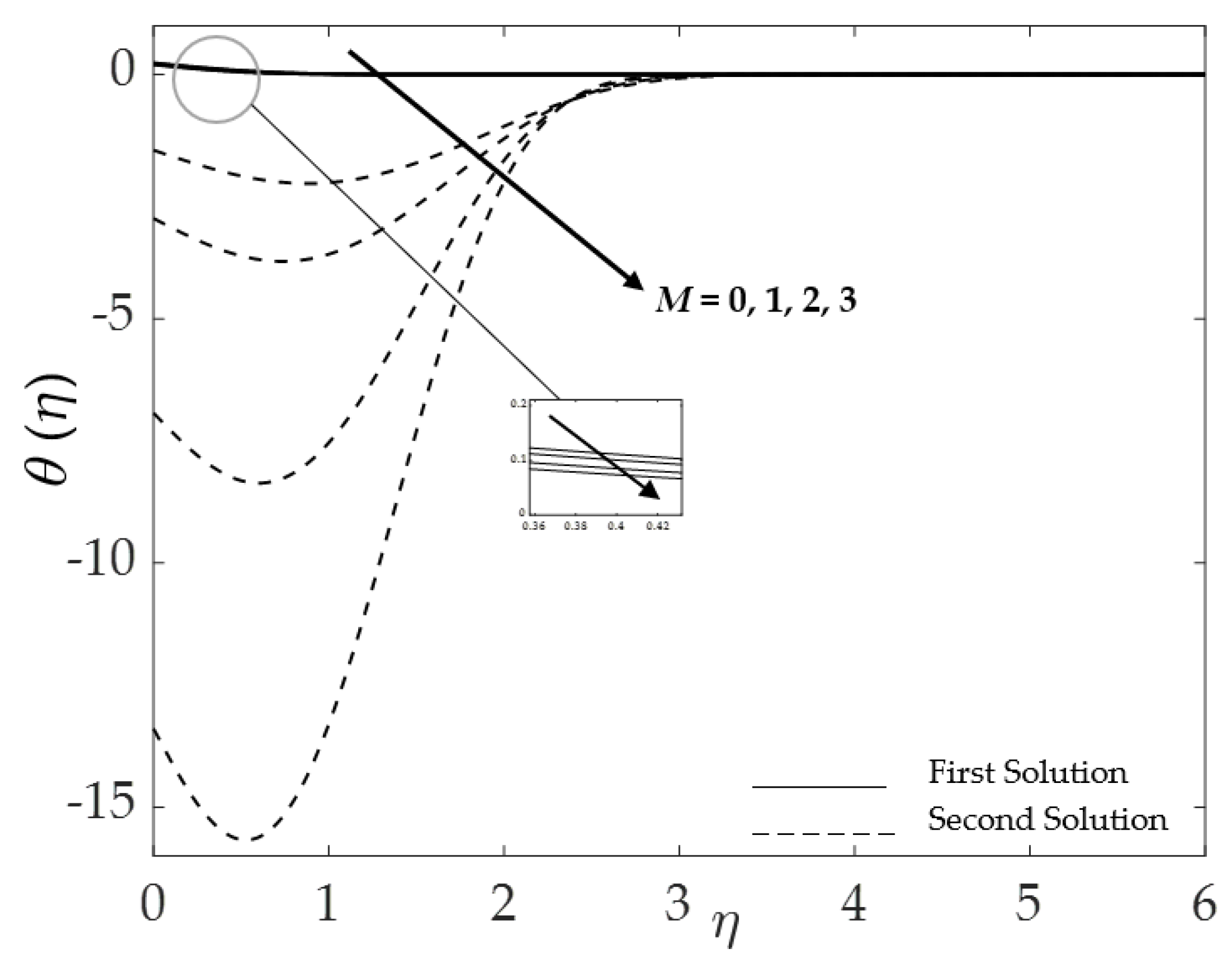
4.3. Effect of the Magnetic Parameter
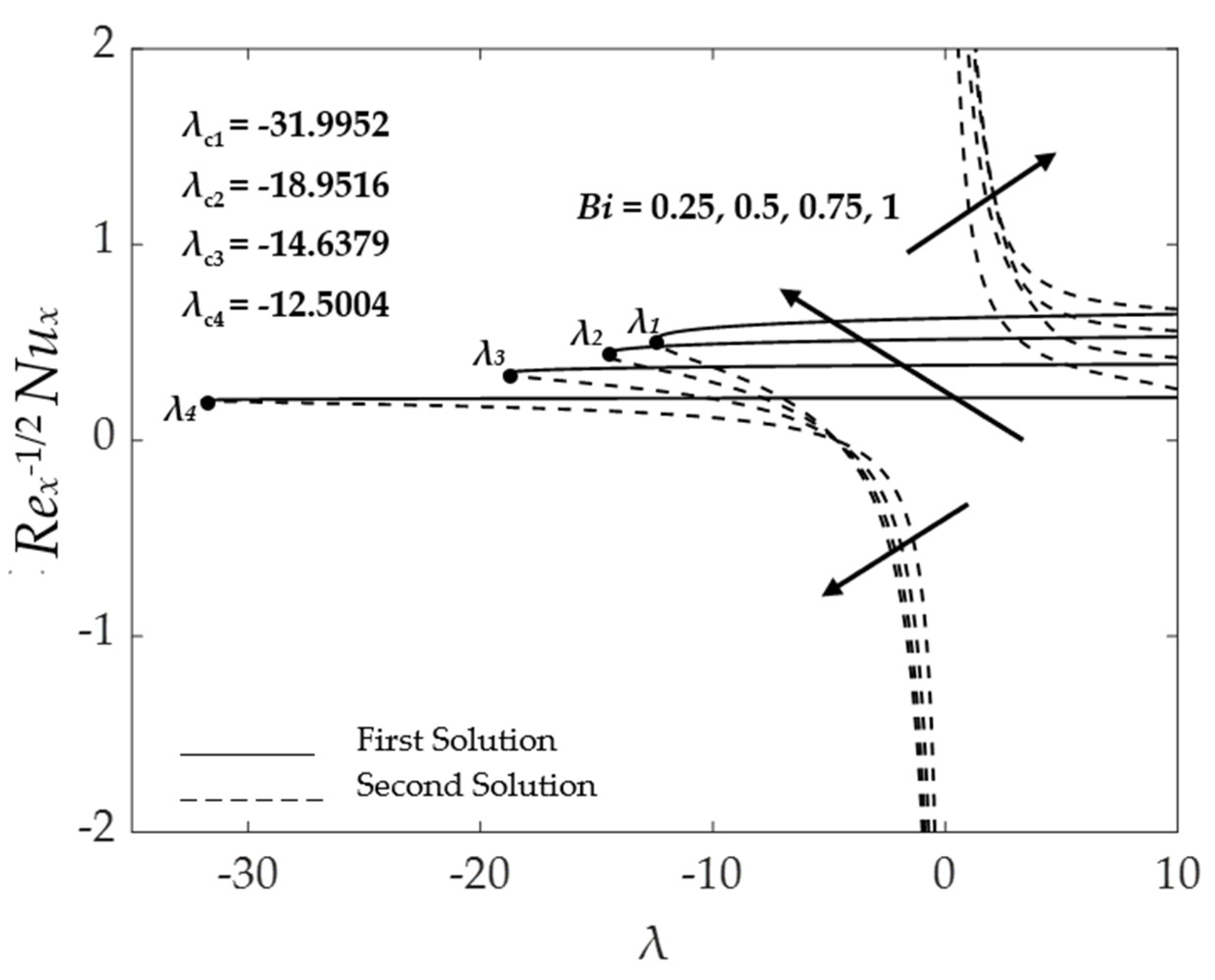
4.4. Effect of the Biot Number
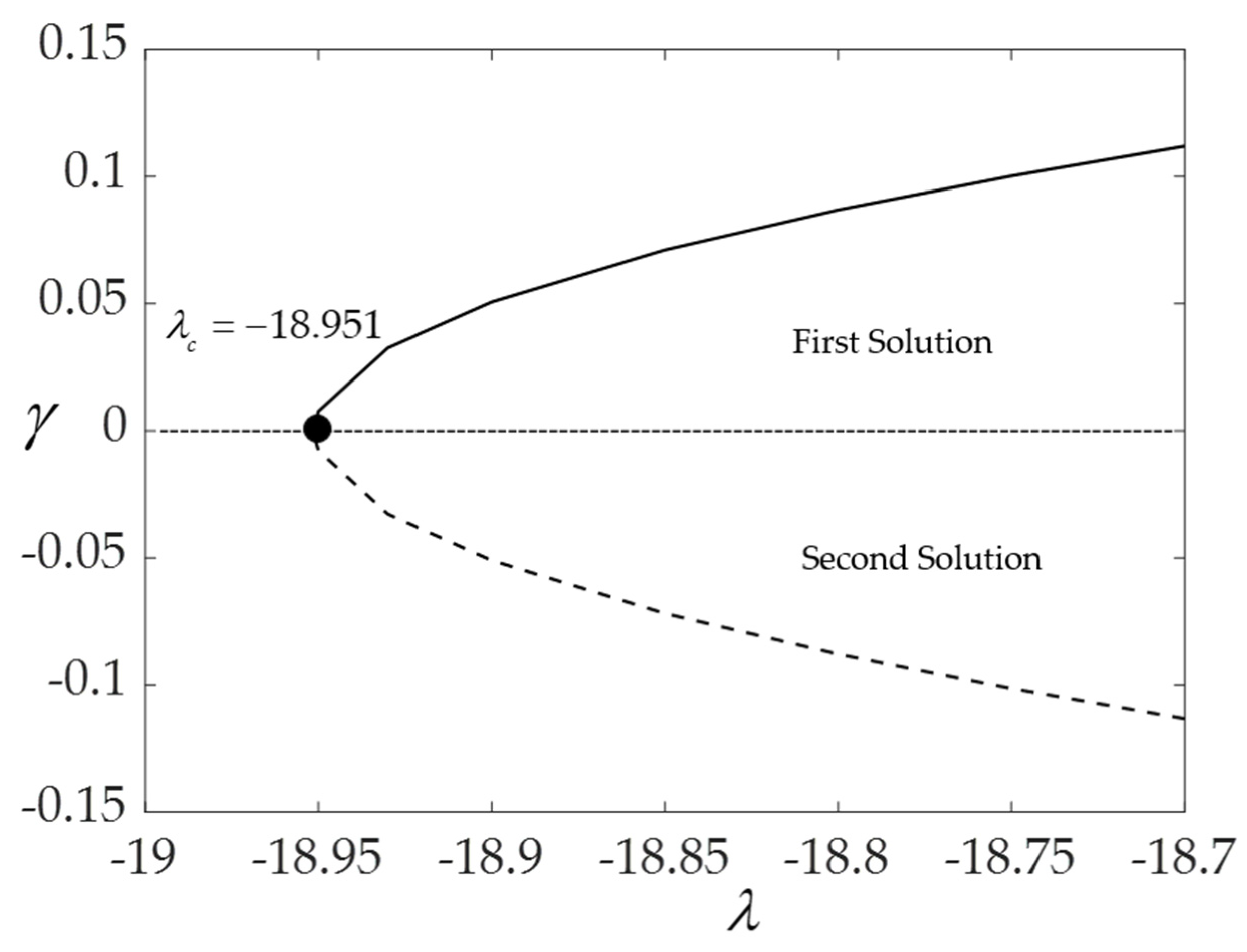
4.5. Stability Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| positive constant | |
| uniform applied magnetic field | |
| Biot number | |
| friction factor coefficient | |
| specific heat at constant pressure | |
| heat capacitance of the fluid | |
| dimensionless stream function | |
| acceleration due to gravity | |
| Grashof number | |
| the surface heat transfer coefficient | |
| thermal conductivity of the fluid | |
| material parameter | |
| characteristic length | |
| magnetic parameter | |
| micro-gyration constant | |
| the microinertia density | |
| local Nusselt number | |
| Prandtl number | |
| radius of the cylinder | |
| local Reynolds number | |
| time (s) | |
| fluid temperature | |
| surface constant temperature | |
| temperature characteristic | |
| ambient temperature | |
| surface temperature | |
| velocity component along the x and r direction, respectively | |
| velocity of inviscid flow | |
| Cartesian coordinates | |
| Greek symbols | |
| thermal diffusivity of fluid | |
| thermal expansion coefficient | |
| vortex viscosity | |
| similarity variable | |
| dimensionless temperature | |
| constant mixed convection parameter | |
| dynamic viscosity | |
| kinematic viscosity of the fluid | |
| density of the fluid | |
| electric conductivity | |
| nanoparticle volume fraction | |
| spin gradient viscosity | |
| unknown eigenvalue | |
| dimensionless time variable | |
| stream function | |
| Subscripts | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| 1 | solid component for Al2O3 (Alumina) |
| 2 | solid component for Cu (Copper) |
| Superscript | |
| differentiation with respect to | |
References
- Soid, S.K.; Ishak, A.; Pop, I. MHD stagnation-point flow over a stretching/shrinking sheet in a micropolar fluid with a slip boundary. Sains Malays. 2018, 47, 2907–2916. [Google Scholar] [CrossRef]
- Eringen, A. Theory of Micropolar Fluids. Indiana Univ. Math. J. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Ishak, A. Thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. Meccanica 2010, 45, 367–373. [Google Scholar] [CrossRef]
- Uddin, M.S.; Bhattacharyya, K.; Shafie, S. Micropolar fluid flow and heat transfer over an exponentially permeable shrinking sheet. Propuls. Power Res. 2016, 5, 310–317. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, M.; Naz, M. MHD stagnation flow of a micropolar fluid through a porous medium. Meccanica 2010, 45, 869–880. [Google Scholar] [CrossRef]
- Ishak, A.; Lok, Y.Y.; Pop, I. Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Commun. 2010, 197, 1417–1427. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Nadeem, S.; Hashim, I. Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects. Meccanica 2015, 50, 2007–2022. [Google Scholar] [CrossRef]
- Ul Haq, R.; Nadeem, S.; Akbar, N.S.; Khan, Z.H. Buoyancy and radiation effect on stagnation point flow of micropolar nanofluid along a vertically convective stretching surface. IEEE Trans. Nanotechnol. 2015, 14, 42–50. [Google Scholar] [CrossRef]
- Ramachandran, P.S.; Mathur, M.N. Heat transfer in the stagnation point flow of a micropolar fluid. Acta Mech. 1980, 36, 247–261. [Google Scholar] [CrossRef]
- Guram, G.S.; Smith, A.C. Stagnation flows of micropolar fluids with strong and weak interactions. Comput. Math. Appl. 1980, 6, 213–233. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Filip, D.; Pop, I. Stagnation point flow of a micropolar fluid towards a stretching sheet. Int. J. Non-Linear Mech. 2004, 39, 1227–1235. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Mixed convective flow and heat transfer of a dual stratified micropolar fluid induced by a permeable stretching/shrinking sheet. Entropy 2019, 21, 1162. [Google Scholar] [CrossRef]
- Subhani, M.; Nadeem, S. Numerical analysis of micropolar hybrid nanofluid. Appl. Nanosci. 2019, 9, 447–459. [Google Scholar] [CrossRef]
- Olayemi, O.A.; Al-Farhany, K.; Obalalu, A.M.; Ajide, T.F.; Adebayo, K.R. Magnetoconvection around an elliptic cylinder placed in a lid-driven square enclosure subjected to internal heat generation or absorption. Heat Transf. 2022, 51, 4950–4976. [Google Scholar] [CrossRef]
- Mishra, N.K.; Sharma, M.; Sharma, B.K.; Khanduri, U. Soret and Dufour effects on MHD nanofluid flow of blood through a stenosed artery with variable viscosity. Int. J. Mod. Phys. B 2023, 2350266. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Mahdy, A. Transient flow of micropolar dusty hybrid nanofluid loaded with Fe3O4-Ag nanoparticles through a porous stretching sheet. Results Phys. 2021, 21, 103777. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.-S.M. Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef]
- Goldanlou, A.S.; Badri, M.; Heidarshenas, B.; Hussein, A.K.; Rostami, S.; Shadloo, M.S. Numerical investigation on forced hybrid nanofluid flow and heat transfer inside a three-dimensional annulus equipped with hot and cold rods: Using symmetry simulation. Symmetry 2020, 12, 1873. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar] [CrossRef]
- Obalalu, A.M.; Ahmad, H.; Salawu, S.O.; Olayemi, O.A.; Odetunde, C.B.; Ajala, A.O.; Abdulraheem, A. Improvement of mechanical energy using thermal efficiency of hybrid nanofluid on solar aircraft wings: An application of renewable, sustainable energy. In Waves in Random and Complex Media; Taylor & Francis Group: London, UK, 2023; pp. 1–30. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. On both MHD and slip effect in micropolar hybrid nanofluid past a circular cylinder under stagnation point region. Can. J. Phys. 2019, 97, 392–399. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Pop, I.; Abu Bakar, S.; Ishak, A. Stagnation point flow of a micropolar fluid filled with hybrid nanoparticles by considering various base fluids and nanoparticle shape factors. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 2320–2344. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Radiative and magnetohydrodynamic micropolar hybrid nanofluid flow over a shrinking sheet with Joule heating and viscous dissipation effects. Neural Comput. Appl. 2022, 34, 3783–3794. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N. Double solutions and stability analysis of micropolar hybrid nanofluid with thermal radiation impact on unsteady stagnation point flow. Mathematics 2021, 9, 276. [Google Scholar] [CrossRef]
- Haider, M.I.; Asjad, M.I.; Ali, R.; Ghaemi, F.; Ahmadian, A. Heat transfer analysis of micropolar hybrid nanofluid over an oscillating vertical plate and Newtonian heating. J. Therm. Anal. Calorim. 2021, 144, 2079–2090. [Google Scholar] [CrossRef]
- Al-Hanaya, A.M.; Sajid, F.; Abbas, N.; Nadeem, S. Effect of SWCNT and MWCNT on the flow of micropolar hybrid nanofluid over a curved stretching surface with induced magnetic field. Sci. Rep. 2020, 10, 8488. [Google Scholar] [CrossRef]
- Sharma, B.K.; Khanduri, U.; Mishra, N.K.; Chamkha, A.J. Analysis of Arrhenius activation energy on magnetohydrodynamic gyrotactic microorganism flow through porous medium over an inclined stretching sheet with thermophoresis and Brownian motion. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089221128768. [Google Scholar] [CrossRef]
- Sharma, B.K.; Gandhi, R. Combined effects of Joule heating and non-uniform heat source/sink on unsteady MHD mixed convective flow over a vertical stretching surface embedded in a Darcy-Forchheimer porous medium. Propuls. Power Res. 2022, 11, 276–292. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.K.; Mishra, N.K.; Al-Mdallal, Q.M. Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials 2023, 13, 652. [Google Scholar] [CrossRef]
- Obalalu, A.M.; Wahaab, F.A.; Adebayo, L.L. Heat transfer in an unsteady vertical porous channel with injection/suction in the presence of heat generation. J. Taibah Univ. Sci. 2020, 14, 541–548. [Google Scholar] [CrossRef]
- Obalalu, A.M. Heat and mass transfer in an unsteady squeezed Casson fluid flow with novel thermophysical properties: Analytical and numerical solution. Heat Transf. 2021, 50, 7988–8011. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Heat transfer enhancement of Cu−Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 2014, 147059. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Numerical investigation of three-dimensional hybrid Cu-Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Roşca, A.V.; Roşca, N.C.; Pop, I. Mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with a second order velocity model. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 75–91. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1881–1891. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Weidman, P. Axisymmetric rotational stagnation point flow impinging on a radially stretching sheet. Int. J. Non-Linear Mech. 2016, 82, 1–5. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATHLAB; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521824040. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]




| Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| Density | ||
| Dynamic viscosity | ||
| Thermal conductivity | where | |
| Electrical conductivity | where | |
| Heat capacity | ||
| Thermal expansion |
| Physical Properties | Al2O3 | Cu | Water |
|---|---|---|---|
| Prandtl number, Pr | 6.2 | ||
| 0.85 | 1.67 | 21 | |
| 40 | 400 | 0.613 | |
| 765 | 385 | 4179 | |
| 0.05 | |||
| 3970 | 8933 | 997.1 |
| Pr | ||||||||
|---|---|---|---|---|---|---|---|---|
| Khashi’ie et al. [44] | Result | Khashi’ie et al. [44] | Result | |||||
| First Solution | Second Solution | First Solution | Second Solution | First Solution | Second Solution | First Solution | Second Solution | |
| 0.7 | 1.7063 | 1.2387 | 1.70632265 | 1.23872774 | 0.7641 | 1.0226 | 0.76406346 | 1.02263139 |
| 1.0 | 1.6754 | 1.1332 | 1.67543657 | 1.13319247 | 0.8708 | 1.1691 | 0.87077860 | 1.16912606 |
| 7.0 | 1.5179 | 0.5824 | 1.51791262 | 0.58240096 | 1.7224 | 2.2191 | 1.72238160 | 2.21919411 |
| 10.0 | 1.4928 | 0.4958 | 1.49283867 | 0.49577941 | 1.9446 | 2.4940 | 1.94461739 | 2.49402854 |
| 20.0 | 1.4485 | 0.3436 | 1.44848293 | 0.34364027 | 2.4576 | 3.1646 | 2.45759005 | 3.16460845 |
| 25.0 | - | - | 1.43546650 | 0.29898184 | - | - | 2.64901124 | 3.43169660 |
| 30.0 | - | - | 1.42528871 | 0.26393460 | - | - | 2.81614709 | 3.67382853 |
| 35.0 | - | - | 1.41700206 | 0.23526178 | - | - | 2.96547712 | 3.89784204 |
| K | M | Buoyancy Assisting Flow (λ = 1) | Buoyancy Opposing Flow (λ = −1) | |||||
|---|---|---|---|---|---|---|---|---|
| Rex1/2 Cf | Rex Mx | Rex−1/2 Nux | Rex1/2 Cf | Rex Mx | Rex−1/2 Nux | |||
| 0 | 1 | 1 | 1.97922464 | 0.76391084 | 0.38057597 | 1.84976934 | 0.68708906 | 0.37910938 |
| 1 | 2.0172647 | 0.80745604 | 0.38320124 | 1.89246669 | 0.73150002 | 0.38183689 | ||
| 2 | 0 | 1.71224371 | 0.77248271 | 0.39006488 | 1.59709875 | 0.71213373 | 0.38870291 | |
| 1 | 2.06065407 | 0.82753810 | 0.38487081 | 1.93793993 | 0.75293929 | 0.38357284 | ||
| 2 | 2.37147874 | 0.85861598 | 0.38110822 | 2.23798198 | 0.77586364 | 0.37983740 | ||
| 3 | 2.64941168 | 0.88067491 | 0.37811387 | 2.50565957 | 0.79194192 | 0.37686108 | ||
| 1 | 0 | 1.66276884 | 0.59712546 | 0.37962477 | 1.51439939 | 0.51082685 | 0.37762116 | |
| 1 | 2.06065407 | 0.82753810 | 0.38487081 | 1.93793993 | 0.75293929 | 0.38357284 | ||
| 2 | 2.92254421 | 1.36368321 | 0.39289368 | 2.83216499 | 1.30502064 | 0.3922474 | ||
| 3 | 3.93032828 | 2.03436344 | 0.39910432 | 3.86075439 | 1.98690311 | 0.39874551 | ||
| 4 | 1 | 1 | 2.13961467 | 0.89160541 | 0.38893447 | 2.02308939 | 0.81910872 | 0.38778014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohut, F.H.; Ishak, A.; Soid, S.K. MHD Stagnation Point of Blasius Flow for Micropolar Hybrid Nanofluid toward a Vertical Surface with Stability Analysis. Symmetry 2023, 15, 920. https://doi.org/10.3390/sym15040920
Sohut FH, Ishak A, Soid SK. MHD Stagnation Point of Blasius Flow for Micropolar Hybrid Nanofluid toward a Vertical Surface with Stability Analysis. Symmetry. 2023; 15(4):920. https://doi.org/10.3390/sym15040920
Chicago/Turabian StyleSohut, Farizza Haniem, Anuar Ishak, and Siti Khuzaimah Soid. 2023. "MHD Stagnation Point of Blasius Flow for Micropolar Hybrid Nanofluid toward a Vertical Surface with Stability Analysis" Symmetry 15, no. 4: 920. https://doi.org/10.3390/sym15040920
APA StyleSohut, F. H., Ishak, A., & Soid, S. K. (2023). MHD Stagnation Point of Blasius Flow for Micropolar Hybrid Nanofluid toward a Vertical Surface with Stability Analysis. Symmetry, 15(4), 920. https://doi.org/10.3390/sym15040920









