Constant Time Calculation of the Metric Dimension of the Join of Path Graphs

Abstract

The distance between two vertices of a simple connected graph G, denoted as $d(u,v)$, is the length of the shortest path from u to v and is always symmetrical. An ordered subset $W=\left\{w_1,w_2,w_3,\cdots ,w_k\right\}$ of $V\left(G\right)$ is a resolving set for G, if for ∀$u,v\in V\left(G\right)$, there exists $w_i\in W$ ∋ $d(u,w_i)\ne d(v,w_i)$. A resolving set with minimal cardinality is called the metric basis. The metric dimension of G is the cardinality of metric basis of G and is denoted as $dim\left(G\right)$. For the graph $G_1=(V_1,E_{1,})$ and $G_2=(V_2,E_2)$, their join is denoted by $G_1+G_2$. The vertex set of $G_1+G_2$ is $V_1\cup V_2$ and the edge set is $E=E_1\cup E_2\cup \left\{uv,u\in V_1,v\in V_2\right\}$. In this article, we show that the metric dimension of the join of two path graphs is unbounded because of its dependence on the size of the paths. We also provide a general formula to determine this metric dimension. We also develop algorithms to obtain metric dimensions and a metric basis for the join of path graphs, with respect to its symmetries.

1. Introduction

The study of metric dimension, $dim\left(G\right)$, was first initiated by Slater and Peter [1,2]. They were studying the problem of determining the exact location of an intruder in a network. They used the terms “locating set” and “location number” to define their concepts. Independently, Hararay and Melter [3] studied the same concepts and used the term “metric dimension”. They calculated the metric dimensions of trees and grid graphs and gave a characterization of graphs with small metric dimensions.

In this article, we use the terminology developed by Hararay and Melter. The metric dimension is defined to be the cardinality of the smallest “resolving set” [3]. Chartrand et al. [4] used the term “metric basis” for the smallest resolving set. An ordered subset $W=\{w_1,w_2,\cdots ,w_k\}\subset V\left(G\right)$ is a metric basis for a simple graph G, and then the k-vector, $\left(d(v,w_1),d(v,w_2),\cdots ,d(v,w_k)\right)$, is termed as the representation of the vertex v with respect to the ordered subset W and is denoted as $r\left(v\right|W)$.

The concept of metric dimension in graphs has drawn a lot of interest from researchers. Chartrand et al. [4] calculated the metric dimensions of trees and unicyclic graphs. They also gave the characterization of graphs with metric dimensions 1, $n-2$ and $n-1$. Klien and Yi [5] studied the metric dimensions of para-line graphs. They also compared the metric dimensions of graphs, line graphs and para-line graphs. Ahmed et al. [6] calculated the exact values for the metric dimensions of the kayak paddles graph. They also calculated the metric dimensions of cycles with a chord. Sedlar and Skrekovski [7] showed that the vertex and edge metric dimensions of unicyclic graphs obtain values from two particular consecutive integers, which can be determined from the structure of the graph. Abrishami et al. [8] calculated the local metric dimensions for graphs having small clique numbers. Hayat et al. [9] determined the exact values of metric dimensions of multi-partite graphs, effectively generalizing the already established results of bipartite graphs. For further studies on metric dimensions, we refer the reader to [10,11,12,13,14,15,16,17,18] and the references therein.

The metric basis and metric dimensions have also been studied under numerous graph operations. Cáceres et al. [19] studied the metric dimensions of the Cartesian product of graphs. They established that there is a family of graphs G with bounded metric dimensions such that the metric dimension of $G\times G$ is unbounded. Jiang and Polyanskii [20] showed that the metric dimensions of the Cartesian product of n copies of G of order q, is $(2+o\left(1\right))n/lo{g}_{q}n$. Fehr et al. [21] studied the metric dimensions of Cayley digraphs. Nazeer et al. [22] calculated the metric dimensions of path-related graphs for applications in network optimization. Eroh et al. [23] studied the effect on metric dimensions of a graph G when a vertex and/or edge is deleted from G. Sebő et al. [24] used the concept of metric dimensions, strong metric generators and isometric embedding to show that the existence of connected joins of graphs can be solved in polynomial time.

Metric dimensions of graphs have applications in robot navigation and drug discovery [4], combinatorial optimization [24] and strategies for the mastermind game [25]. It was observed by Khuller et al. in [26] that the metric dimension of an arbitrary n-vertex graph may be approximated in polynomial time. An obvious question is, can we reduce this calculation time for some special types of graphs? In this article, we try to answer this for the join of two path graphs.

1.1. Motivation

Metric dimension of the join of two graphs was studied by Shahida and Sunitha [27]. They considered two paths of lengths m and n and showed that

$$dim(P_m+P_n)=\left\{\begin{array}{cc}1\hfill & m=n=1\hfill \\ 2\hfill & 2\le m\le 3\hfill \\ ⌊\frac{m}{2}⌋+n-1\hfill & 1\le n,4\le m\hfill \end{array}\right.$$

(1)

If we consider $m=6$ and $n=4$, then by Equation (1), $dim(P_6+P_4)=6$. Let us assume that the vertices are labelled as $\{v_1,v_2,\cdots ,v_{m+n}\}$; then it is an easy exercise to show that the set $\{v_2,v_4,v_7,v_8\}$ is a resolving set for $P_6+P_4$, implying that $dim(P_6+P_4)\ne 6$.

Rawat and Pradhan [28] improved the results of Shahida and Sunitha and calculated that

$$dim(P_m+P_n)=\left\{\begin{array}{cc}3;\hfill & 2\le m\le 5\mathrm{and}2\le n\le 3,\hfill \\ 4;\hfill & 2\le m\le 5\mathrm{and}n=6\mathrm{or}4\le m\le 6\mathrm{and}n=4,5\hfill \\ 5;\hfill & m=n=6\hfill \\ ⌈\frac{n}{2}⌉;\hfill & 2\le m\le 3\mathrm{and}7\le n\hfill \\ ⌈\frac{n}{2}⌉+1;\hfill & 4\le m\le 6\mathrm{and}7\le n\hfill \\ ⌈\frac{m}{2}⌉+⌈\frac{n}{2}⌉-2\hfill & 7\le n\mathrm{and}7\le m\hfill \end{array}\right.$$

(2)

Let us now consider $m=11$ and $n=11$. Then, by Equation (2), $dim(P_{11}+P_{11})=10$. Again, assuming that the vertices are labeled as $\{v_1,v_2,\cdots ,v_{m+n}\}$, one can easily see that the set $\{v_2,v_4,v_7,v_9,v_{13},v_{15},v_{18},v_{20}\}$ is a resolving set for $P_{11}+P_{11}$. One can also verify that the above result does not hold whenever $m\ge 11$ or $n\ge 11$.

The above discussion shows that there is an obvious vacuum in the literature for the calculation of metric dimension of join of two path graphs. Haryanto et al. [29] tried to fill this gap and calculated the metric dimensions of $P_2+P_t$. The question of $dim(P_s+P_t)$ is still open when $s>2$.

The present study was aimed at calculating the metric dimensions of $P_m+P_n$ for all values of m and n. This enabled the calculation of $dim(P_m+P_n)$ in constant time. We also provide an algorithm of complexity $O\left(n\right)$ to calculate the metric bases for $P_m+P_n$. Since the joining of graphs is a symmetric operation, we can see that $P_m+P_n$ is siomorphic to $P_n+P_m$.

1.2. Preliminaries

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple, connected and undirected graph. The number of vertices in a graph is said to be the order of the graph. The distance between two vertices $u,v$ of a graph G, denoted by $d(u,v)$, is the length of the shortest path between them. It is clear that $d(u,v)=d(v,u)$, since the distance is always symmetrical. The representation of a vertex $u\in V\left(G\right)$ with respect to an ordered set $W=\left\{w_1,w_2,w_3,\cdots ,w_k\right\}\subseteq V\left(G\right)$, denoted by $r\left(u\right|W)$, is the k-tuple $(d(u,w_1),d(u,w_2),\cdots ,d(u,w_k))$. We say that $W\subseteq V\left(G\right)$ resolves the graph G, if for any two vertices $u,v\in G$, there exists at least one $w_i\in W$ such that $d(u,w_i)\ne d(v,w_i)$; equivalently, W resolves G if for any two vertices $u,v\in G$, we have, $r\left(u\right|W)\ne r(v\left|W\right)$. A resolving set W of minimum cardinality is called the metric basis for the graph G, and $\left|W\right|$ is the metric dimension of G.

Let $G=(V_1,E_1)$ and $H=(V_2,E_2)$ be simple, connected and non-trivial graphs. The join of these graphs, $G+H$, is a graph with $V(G+H)=\{V_1\cup V_2\}$ and $E(G+H)=\{E_1\cup E_2\cup \{e=uv,u\in V_1,v\in V_2\}\}.$ From the definition of a join of graphs, we see that the join operation is a symmetric operation. We can also easily conclude that $d(u,v)=1$ whenever $u\in V_1,v\in V_2$.

Two graphs G and H are said to be isomorphic, denoted as $G\cong H$, if there exists a bijection, $\theta :V\left(G\right)\to V\left(H\right)$, such that $u\sim v$ in G if and only if $\theta \left(u\right)\sim \theta \left(v\right)$ in H.

In what follows, for simplicity we will write $W\cup w$ to represent the union of a set and a single vertex.

2. Metric Dimension of the Join of Two Path Graphs

In this section we study the resolving set of the join of two path graphs. Let $P_s$ and $P_t$ be paths of order s and t respectively; then, the join of these two paths $P_s+P_t$ is as given in the following.

$$V(P_s+P_t)=V\left(P_s\right)\cup V\left(P_t\right)=\{v_i:1\le i\le s\}\cup \{v_j:s+1\le j\le s+t\}$$

(3)

$$E(P_s+P_t)=E\left(P_s\right)\cup E\left(P_t\right)\cup \{v_i{v}_j,1\le i\le s,s+1\le j\le s+t\}$$

(4)

Note that for $v_i,v_j\in P_s$, $d(v_i,v_j)=1$ if $i=j+1$ or $i=j-1$ (equivalently $v_i\sim v_j$), and $d(v_i,v_j)=2$ otherwise. On the other hand, $\forall v_i\in P_s,\forall v_j\in P_t$, we have $d(v_i,v_j)=1$. We also consider $s+t=n$, whenever n is considered as an order of this graph. These concepts can be clarified from Figure 1. The join operation for graphs is a symmetric operation since $V\left(P_s\right)\cup V\left(P_t\right)=V\left(P_t\right)\cup V\left(P_s\right)$, and

$$E(P_t+P_s)=E\left(P_t\right)\cup E\left(P_s\right)\cup \{v_j{v}_i,1\le i\le s,s+1\le j\le s+t\}.$$

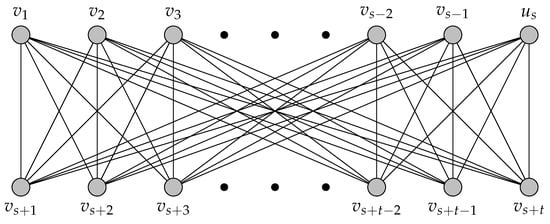
Figure 1. Join of $P_s$ and $P_t$.

We provide a concrete short example of the symmetry at work in this operation.

Example 1.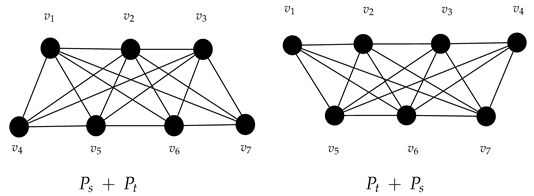 

Let us consider the joins $P_s+P_t$ and $P_t+P_s$ when $P_s\simeq P_3$ and $P_t\simeq P_4$. Their figure is provided below.

Let us define a mapping $\Phi :P_s+P_t\to P_t+P_s$, where $\Phi \left(v_1\right)=v_5$, $\Phi \left(v_2\right)=v_6$, $\Phi \left(v_3\right)=v_7$, $\Phi \left(v_4\right)=v_1$, $\Phi \left(v_5\right)=v_2$, $\Phi \left(v_6\right)=v_3$, and $\Phi \left(v_7\right)=v_4$.

It can be easily verified that $P_s+P_t\simeq P_t+P_s$ under the mapping Φ. This ensures that $P_s+P_t$ and $P_t+P_s$ are the same graph with respect to their symmetry. It can also be concluded that if a set W is a resolving set for $P_s+P_t$, then $\Phi \left(W\right)$ is a resolving set for $P_t+P_s$, owing to the symmetry between them.

We now move on to state and prove our results for this section.

Theorem 1. 

For $s=1,2,3,6$ and $t\le 6$

$$dim(P_s+P_t)=\left\{\begin{array}{cc}1+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋\hfill & t=1\hfill \\ 2+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋\hfill & 2\le t\le 5\hfill \\ 3+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋\hfill & t=6\hfill \end{array}\right.$$

(5)

Proof. 

For this proof, we will discuss all the cases of s and t separately. Note that the vertices are labeled as $v_1,v_2,\cdots ,v_s,v_{s+1},v_{s+2},\cdots ,v_{s+t}$.

Case 1. 

When $s=1$. For $t=1$ and 2, the results are obvious, since $P_1+P_1=P_2$ and $P_1+P_2=K_3$. We discuss the remaining cases of t in the following.

[a.]

$\mathbf{t}=\mathbf{3}$: From Equation (1), $dim(P_1+P_3)=2$. Let $W=\left\{v_1,v_2\right\}$; then, $r\left(v_3\right|W)=(1,1)$ and $r\left(v_4\right|W)=(1,2)$, ‘indicating that $W=\left\{v_1,v_2\right\}$ is a resolving set for $P_1+P_3$. Let us consider the set $W-\left\{v_1\right\}$. In that case, $r\left(v_1\right|W)=r\left(v_3\right|W)=\left(1\right)$, and if we consider the set $W-\left\{v_2\right\}$, we can see that $r\left(v_2\right|W)=r\left(v_3\right|W)=r\left(v_4\right|W)=\left(1\right)$, implying that these two sets do not resolve $P_1+P_3$, and hence $dim(P_1+P_3)=2$.

In the remaining cases, we only show that a resolving set of stated cardinality exists. These resolving sets are very small and well structured, and it can be easily shown that a smaller resolving set does not exist. We will omit this part of the proof from all other cases.

[b.]

$\mathbf{t}=\mathbf{4}$: Equation (1)$\Rightarrow dim(P_1+P_4)=2.$ Let us take $W=\left\{v_2,v_3\right\}$ as a resolving set; then, $r\left(v_1\right|W)=(1,1)$, $r\left(v_4\right|W)=(2,1)$ and $r\left(v_5\right|W)=(2,2)$, giving us $dim(P_1+P_4)=2.$

[c.]

$\mathbf{t}=\mathbf{5}$: By Equation (1), $dim(P_1+P_5)=2$. Let $W=\left\{v_2,v_6\right\}$; then, $r\left(v_1\right|W)=(1,1)$, $r\left(v_3\right|W)=(1,2)$, $r\left(v_4\right|W)=(2,2)$ and $r\left(v_5\right|W)=(2,1)$, implying that $W=\left\{v_2,v_6\right\}$ is a resolving set.

[d.]

$\mathbf{t}=\mathbf{6}$: Again, with the help of Equation (1), $dim(P_1+P_6)=3$. Let $W=\left\{v_1,v_3,v_5\right\}$; then, $r\left(v_2\right|W)=(1,1,2)$, $r\left(v_4\right|W)=(1,1,1)$, $r\left(v_6\right|W)=(1,2,1)$ and $r\left(v_7\right|W)=(1,2,2)$, giving us, $dim(P_1+P_6)=3$.

Case 2. 

When $s=2$. For $t=1$ and 2, the results are again obvious, since $P_2+P_1=K_3$ and $P_2+P_2=K_4$. Following the same pattern as above, we discuss the remaining cases of t as follows.

[a.]

$\mathbf{t}=\mathbf{3}$: $dim(P_2+P_3)=3$ by Equation (1). Let $W=\left\{v_1,v_2,v_3\right\}$; then, $r\left(v_4\right|W)=(1,1,1)$ and $r\left(v_5\right|W)=(1,1,2)$$⟹dim(P_2+P_3)=3.$

[b.]

$\mathbf{t}=\mathbf{4}$: From Equation (1), $dim(P_2+P_4)=3.$ Let $W=\left\{v_1,v_3,v_4\right\}$; then, $r\left(v_2\right|W)=(1,1,1)$, $r\left(v_5\right|W)=(1,2,1)$, $r\left(v_6\right|W)=(1,2,2)$; hence, $dim(P_2+P_4)=3.$

[c.]

$\mathbf{t}=\mathbf{5}$: $dim(P_2+P_5)=3$ by using Equation (1). Let $W=\left\{v_1,v_3,v_7\right\}$; then, $r\left(v_2\right|W)=(1,1,1)$, $r\left(v_4\right|W)=(1,1,2)$, $r\left(v_5\right|W)=(1,2,2)$, $r\left(v_6\right|W)=(1,2,1)$; hence, $dim(P_2+P_5)=3.$

[d.]

$\mathbf{t}=\mathbf{6}$: Equation (1) $⟹dim(P_2+P_6)=4$. Let $W=\left\{v_1,v_2,v_4,v_6\right\}$; then, $r\left(v_3\right|W)=(1,1,1,2)$, $r\left(v_5\right|W)=(1,1,1,1)$, $r\left(v_7\right|W)=(1,1,2,1)$ and $r\left(v_8\right|W)=(1,1,2,2)$, giving us the result.

Case 3. 

When $s=3$. When $t=1$, we obtain $P_3+P_1$, which is isomophic to $P_1+P_3$, and the result follows from Case 1.a. Similarly, when $t=2$, we have $P_3+P_2\cong P_2+P_3$, and the result follows from Case 2.a. The remaining cases for different values of t are given in the following.

[a.]

$\mathbf{t}=\mathbf{3}$: $dim(P_3+P_3)=3$ by Equation (1). Let $W=\left\{v_1,v_2,v_4\right\}$; then, $r\left(v_3\right|W)=(2,1,1)$, $r\left(v_5\right|W)=(1,1,1)$ and $r\left(v_6\right|W)=(1,1,2)$. Hence, $dim(P_3+P_3)=3.$

[b.]

$\mathbf{t}=\mathbf{4}$: Using Equation (1), we obtain $dim(P_3+P_4)=3$. Let $W=\left\{v_1,v_4,v_5\right\}$; then, $r\left(v_2\right|W)=(1,1,1)$, $r\left(v_3\right|W)=(2,1,1)$, $r\left(v_6\right|W)=(1,2,1)$, $r\left(v_7\right|W)=(1,2,2)$⟹$dim(P_3+P_4)=3.$

[c.]

$\mathbf{t}=\mathbf{5}$: From Equation (1), $dim(P_3+P_5)=3$. Let $W=\left\{v_1,v_4,v_8\right\}$; then, $r\left(v_2\right|W)=(1,1,1)$, $r\left(v_3\right|W)=(2,1,1)$, $r\left(v_5\right|W)=(1,1,2)$, $r\left(v_6\right|W)=(1,2,2)$, $r\left(v_7\right|W)=(1,2,1)$, and hence $dim(P_3+P_5)=3.$

[d.]

$\mathbf{t}=\mathbf{6}$: By Equation (1), $dim(P_3+P_6)=4$. Let $W=\left\{v_1,v_2,v_5,v_7\right\}$; then, $r\left(v_3\right|W)=(2,1,1,1)$, $r\left(v_4\right|W)=(1,1,1,2)$, $r\left(v_6\right|W)=(1,1,1,1)$, $r\left(v_8\right|W)=(1,1,2,1)$ and $r\left(v_9\right|W)=(1,1,2,2)$, implying $dim(P_3+P_6)=4.$

Case 4. 

When $s=6$. When $t=1$, we obtain $P_6+P_1$, which is isomophic to $P_1+P_6$, and the result follows from Case 1.d. Similarly when $t=2$, we have $P_6+P_2\cong P_2+P_6$ (Case 2.d), and when $t=3$, we have $P_6+P_3\cong P_3+P_6$, and $dim(P_6+P_3)$ is the same as in Case 3.d.

[a.]

$\mathbf{t}=\mathbf{4}$: Equation (1)$\Rightarrow dim(P_6+P_4)=4.$ Let $W=\left\{v_2,v_4,v_7,v_8\right\}$; then, $r\left(v_1\right|W)=(1,2,1,1)$, $r\left(v_3\right|W)=(1,1,1,1)$, $r\left(v_5\right|W)=(2,1,1,1)$, $r\left(v_6\right|W)=(2,2,1,1)$, $r\left(v_9\right|W)=(1,1,2,1)$, $r\left(v_{10}\right|W)=(1,1,2,2)$, and hence $dim(P_s+P_t)=4.$

[b.]

$\mathbf{t}=\mathbf{5}$: By Equation (1), $dim(P_6+P_5)=4.$ Let $W=\left\{v_2,v_4,v_7,v_{11}\right\}$; then, $r\left(v_1\right|W)=(1,2,1,1)$, $r\left(v_3\right|W)=(1,1,1,1)$, $r\left(v_5\right|W)=(2,1,1,1)$, $r\left(v_6\right|W)=(2,2,1,1)$, $r\left(v_8\right|W)=(1,1,1,2)$, $r\left(v_9\right|W)=(1,1,2,2)$, $r\left(v_{10}\right|W)=(1,1,2,1)$; hence, $dim(P_6+P_4)=4.$

[c.]

$\mathbf{t}=\mathbf{6}$: From Equation (1), $dim(P_6+P_6)=5.$ Let $W=\left\{v_1,v_2,v_4,v_8,v_{10}\right\}$; then, $r\left(v_3\right|W)=(2,1,1,1,1)$, $r\left(v_5\right|W)=(2,2,1,1,1)$, $r\left(v_6\right|W)=(2,2,2,1,1)$, $r\left(v_7\right|W)=(1,1,1,1,2)$, $r\left(v_9\right|W)=(1,1,1,1,1)$, $r\left(v_{11}\right|W)=(1,1,1,2,1)$ aand $r\left(v_{12}\right|W)=(1,1,1,2,2)$, and hence, $dim(P_6+P_6)=5.$ □

Theorem 2. 

When $s=4,5$ and $t\le 6$; then,

$$dim(P_s+P_t)=\left\{\begin{array}{cc}2\hfill & t=1\hfill \\ 3\hfill & 2\le t\le 3\hfill \\ 4\hfill & 4\le t\le 6\hfill \end{array}\right.$$

(6)

Proof. 

We again discuss this for all cases of s and t seperately.

Case 1. 

When $s=4$. When $t=1$, we obtain $P_4+P_1$, which is isomophic to $P_1+P_4$, and the result follows from Theorem 3.1 Case 1.b. Similarly, when $t=2$, we have $P_4+P_2\cong P_2+P_4$ (Theorem 1, Case 2.b), and $t=3$ gives $P_4+P_3\cong P_3+P_4$ (Theorem 1, Case 3.b).

[a.]

$\mathbf{t}=\mathbf{4}$. From Equation (6), $dim(P_4+P_4)=4$. Let $W=\left\{v_1,v_2,v_5,v_6\right\}$; then, $r\left(v_3\right|W)=(2,1,1,1)$, $r\left(v_4\right|W)=(2,2,1,1)$, $r\left(v_7\right|W)=(1,1,2,1)$ and $r\left(v_8\right|W)=(1,1,2,2)$, giving us $dim(P_4+P_4)=4.$

[b.]

$\mathbf{t}=\mathbf{5}$. By Equation (6), $dim(P_4+P_5)=4$. Let $W=\left\{v_1,v_2,v_5,v_7\right\}$; then, $r\left(v_3\right|W)=(2,1,1,1)$, $r\left(v_4\right|W)=(2,2,1,1)$, $r\left(v_6\right|W)=(1,1,1,1)$, $r\left(v_8\right|W)=(1,1,2,1)$ and $r\left(v_9\right|W)=(1,1,2,2)$. Hence $dim(P_4+P_5)=4.$

[c.]

$\mathbf{t}=\mathbf{6}$, Equation (6) $⟹dim(P_4+P_6)=4$. Let $W=\left\{v_1,v_2,v_6,v_8\right\}$; then, $r\left(v_3\right|W)=(2,1,1,1)$, $r\left(v_4\right|W)=(2,2,1,1)$, $r\left(v_5\right|W)=(1,1,1,2)$, $r\left(v_7\right|W)=(1,1,1,1)$, $r\left(v_9\right|W)=(1,1,2,1)$ and $r\left(v_{10}\right|W)=(1,1,2,2)$, and hence $dim(P_4+P_6)=4.$

Case 2. 

When $s=5$. When $t=1$, we obtain $P_5+P_1$, which is isomophic to $P_1+P_5$, and the result follows from Theorem 1, Case 1.c. Similarly, when $t=2$, we have $P_5+P_2\cong P_2+P_5$ (Theorem 1, Case 2.c); when $t=3$, we have $P_5+P_3\cong P_3+P_5$ (Theorem 1, Case 3.c); when $t=4$, we obtain $P_5+P_4\cong P_4+P_5$ (Same Theorem, Case 1.b); and when $t=6$, we have $P_5+P_6\cong P_6+P_5$ (Theorem 1, Case 4.b).

[a.]

$\mathbf{t}=\mathbf{5}$, by Equation (6), $dim(P_5+P_5)=4$. Let $W=\left\{v_1,v_3,v_6,v_{10}\right\}$; then, $r\left(v_2\right|W)=(1,1,1,1)$, $r\left(v_4\right|W)=(2,1,1,1)$, $r\left(v_5\right|W)=(2,2,1,1)$, $r\left(v_7\right|W)=(1,1,1,2)$, $r\left(v_8\right|W)=(1,1,2,2)$ and $r\left(v_9\right|W)=(1,1,2,1)$, implying $dim(P_5+P_5)=4.$ □

We now move on to $P_s+P_t$ when $s\ge 1$ and $t\ge 7$. Before proceeding further, we define some new notation and concepts which will be used later on.

Let ${\beta }_x=(x-1)$ and ${\alpha }_x={\beta }_{x}mod5$, where $x\in Z^{+}\cup \left\{0\right\}$. The term ${\beta }_{x}mod5$ is used for the remainder, when ${\beta }_x$ is divided by 5. Using these concepts, we partition the vertex set of $P_s$ from Figure 1 as follows:

$$S_1=\left\{v_{2i-1}:i\in \left\{1,\cdots ,⌈\frac{{\alpha }_s}{2}⌉\right\}\right\}{S}_2=\left\{v_{2i}:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_s}{2}⌋\right\}\right\}$$

$$S_3=\left\{v_{5i+{\alpha }_s}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}{S}_4=\left\{v_{5i+{\alpha }_s-1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$$

$$S_5=\left\{v_{5i+{\alpha }_s-2}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}{S}_6=\left\{v_{5i+{\alpha }_s-3}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$$

$$S_7=\left\{v_{5i+{\alpha }_s-4}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋+1\right\}\right\}$$

We also partition the vertex set of $P_t$ from Figure 1 along the same lines. This partition is given in the following:

$$T_1=\left\{v_{2i+{\beta }_s}:i\in \left\{1,\cdots ,⌈\frac{{\alpha }_t}{2}⌉\right\}\right\}{T}_2=\left\{v_{2i+s}:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_t}{2}⌋\right\}\right\}$$

$$T_3=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

$$T_4=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

$$T_5=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-2}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

$$T_6=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-3}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋+1\right\}\right\}$$

$$T_7=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋+1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

From the definition of $S_i$, we can easily deduce certain properties which will be helpful later on. We provide them in the following.

(I)

When $1\le s\le 5$, we obtain $0\le {\beta }_s\le 4$. This gives $⌊\frac{{\beta }_s}{5}⌋=0$, implying, $S_i=\varphi$ for $i\in \{3,4,5,6\}$.

(II)

For $s>5$, $S_i\ne \varphi$ for $i\in \{3,4,5,6,7\}$.

(III)

When $smod5=1$, we obtain ${\alpha }_s={\beta }_{s}mod5=0$⇒$S_1=S_2=\varphi$.

(IV)

When $smod5=2$, $S_1\ne \varphi$ and $S_2=\varphi$.

(V)

When $smod5=0,3,4$, $S_1\ne \varphi$ and $S_2\ne \varphi$.

Similarly, for the partitions $T_i$, we list the following properties.

(VI)

Since $t\ge 7$, $T_i\ne \varphi$ for $i\in \{3,4,5,6,7\}$.

(VII)

When $tmod5=1$, $T_1=T_2=\varphi$.

(VIII)

When $tmod5=2$, $T_1\ne \varphi$ and $T_2=\varphi$.

(IX)

When $tmod5=0,3,4$, $T_1\ne \varphi$ and $T_2\ne \varphi$.

We also claim that $v_s\in S_7$. To realize this, we proceed as follows.

Since $s\in Z^{+}$, ${\beta }_s\in Z^{+}\cup \left\{0\right\}$. Now

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\beta }_{s}mod5=r\mathrm{where}0\le r\le 4\hfill \\ \Rightarrow \hfill & (s-1)mod5=r:0\le r\le 4\hfill \\ \Rightarrow \hfill & s-1=5q+r:0\le r\le 4\mathrm{and}q\in Z^{+}\cup \left\{0\right\}\hfill \\ \Rightarrow \hfill & ⌊\frac{s-1}{5}⌋=⌊q+\frac{r}{5}⌋:0\le r\le 4\mathrm{and}q\in Z^{+}\cup \left\{0\right\}\hfill \\ \Rightarrow \hfill & ⌊\frac{s-1}{5}⌋=q:q\in Z^{+}\cup \left\{0\right\}\hfill \end{array}\right.\end{array}$$

(7)

Next, we investigate the last vertex of $S_7$, i.e., $v_{5i+{\alpha }_s-4}$, when $i=⌊\frac{{\beta }_s}{5}⌋+1$. Now,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}5i+{\alpha }_s-4\hfill & =5\left(\left(⌊\frac{s-1}{5}⌋\right)+1\right)+(s-1)mod5-4\hfill \\ & =5(q+1)+r-4\mathrm{since}⌊\frac{s-1}{5}⌋=q\mathrm{and}(s-1)mod5=r\hfill \\ & =5q+r+1\hfill \\ & =s\mathrm{since}5q+r=s-1.\hfill \end{array}\right.\end{array}$$

Hence, $v_s\in S_7=\left\{v_{5i+{\alpha }_s-4}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋+1\right\}\right\}$.

It is worthwhile to mention here that, at the end of this article, we provide an algorithm based on our results. The loops counters in the algorithm work in such a way that the above-stated properties of $S_i$ and $T_i$ are handled inherently, and the end user does not need to worry about these finer points of mathematics.

Armed with this knowledge, we now proceed to state and prove the main result of this article.

Theorem 3. 

For $s\ge 1$ and $t\ge 7$ (or vice versa), the metric dimension of $P_s+P_t$ is

$$dim(P_s+P_t)=2\left(⌊\frac{{\beta }_s}{5}⌋+⌊\frac{{\beta }_t}{5}⌋\right)+⌈\frac{{\alpha }_s}{2}⌉+⌈\frac{{\alpha }_t}{2}⌉$$

(8)

Proof. 

This proof is completed in two parts. In part 1, we establish that we can in fact generate a resolving set W of $P_s+P_t$ of the above cardinality. In part 2, we show that there does not exist any resolving set of $P_s+P_t$ having fewer vertices than W.

Part I

Let $W=W_s\cup W_t$. Here, $W_s\subseteq V\left(P_s\right)$ and $W_t\subseteq V\left(P_t\right)$ and $W_s=W_{s_1}\cup W_{s_2}\cup W_{s_3}$ and $W_t=W_{t_1}\cup W_{t_2}\cup W_{t_3}$, where $W_{s_i}$ and $W_{t_i}$ are defined as:

$$W_{s_1}=S_1=\left\{v_{2i-1}:i\in \left\{1,\cdots ,⌈\frac{{\alpha }_s}{2}⌉\right\}\right\}$$

$$W_{s_2}=S_6=\left\{v_{5i+{\alpha }_s-3}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$$

$$W_{s_3}=S_4=\left\{v_{5i+{\alpha }_s-1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$$

$$W_{t_1}=T_1=\left\{v_{2i+{\beta }_s}:i\in \left\{1,\cdots ,⌈\frac{{\alpha }_t}{2}⌉\right\}\right\}$$

$$W_{t_2}=T_5=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-2}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

$$W_{t_3}=T_3=\left\{v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}\right\}$$

It is easy to calculate that $\left|W\right|=2\left(⌊\frac{{\beta }_s}{5}⌋+⌊\frac{{\beta }_t}{5}⌋\right)+⌈\frac{{\alpha }_s}{2}⌉+⌈\frac{{\alpha }_t}{2}⌉$. We will prove that the set W, generated above, is indeed a resolving set for $P_s+P_t$. For this, we will show that, for any pair of distinct vertices $v_a,v_b\in V\left(G\right)$, there exists $v_w\in W$, such that $d(v_a,v_w)\ne d(v_b,v_w)$.

Let $v_a,v_b\in V(P_s+P_t)$, $v_a\ne v_b$; then, without loss of generality, $1\le a<b\le s+t$, since otherwise, we can just rename the indices to obtain the same. We only consider the case when $v_a,v_b\notin W$. From the fact that $v_a\notin W$, it is obvious that $v_a$ enjoys any one of the following forms:

(1)

$v_a\in S_2$; equivalently; $v_a\cong v_{2i}:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_s}{2}⌋\right\}$

(2)

$v_a\in S_7$; equivalently; $v_a\cong v_{5i+{\alpha }_s-4}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋+1\right\}$

(3)

$v_a\in S_5$; equivalently; $v_a\cong v_{5i+{\alpha }_s-2}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$

(4)

$v_a\in S_3$; equivalently; $v_a\cong v_{5i+{\alpha }_s}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$

(5)

$v_a\in T_2$; equivalently; $v_a\cong v_{s+2i}:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_t}{2}⌋\right\}$

(6)

$v_a\in T_6$; equivalently; $v_a\cong v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-3}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋+1\right\}$

(7)

$v_a\in T_4$; equivalently; $v_a\cong v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}$

(8)

$v_a\in T_7$; equivalently; $v_a\cong v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋+1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_t}{5}⌋\right\}$

It should be noted that $v_b\notin W$ ensures that $v_b$ also adheres to the above given forms, and since $b>a$, we will use the index $j>i$ to denote different forms of $v_b$.

The proof is divided into different cases. The proof for every case follows a set pattern, wherein for every $v_a,v_b\notin W$, we find $v_w\in W$, such that $d(v_a,v_w)\ne d(v_b,v_w)$. This ensures that the representations $r\left(v_a\right|W)\ne r\left(v_b\right|W)$.

Case 1. 

When $v_a,v_b\in P_s$, since $v_a\in P_s$, $v_a$ can assume any one of the forms (1) to (4). We discuss all these cases separately.

[a.]

Suppose that $v_a$ is of the form as given in (1); then, $v_a\cong v_{2i}⟹a=2i:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_s}{2}⌋\right\}$. Let us take $w=a-1=2i-1⟹v_w\cong v_{2i-1}$; then, $d(v_a,v_w)=d(v_{2i},v_{2i-1})=1$.

Given that $v_b\in P_s$, it can assume any of the forms (1) to (4). For all of them, it is given that $a<b$, and we will be using this information to solve all four cases of $v_b$ in one go. We will not be repeating this information in all the other cases, but it is inherently present in there.

Now $b>a>a-1⟹v_b\nsim v_{a-1}=v_w$, and since $v_b,v_w\in P_s$, we obtain $d(v_b,v_w)=2$.

[b.]

Let $v_a$ be of the form given in (2); then, $v_a\cong v_{5i+{\alpha }_s-4}\Rightarrow a=5i+{\alpha }_s-4:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋+1\right\}$.

Now, if $v_b\ncong v_{5i+{\alpha }_s-2}$, then by letting $w=a+1=5i+{\alpha }_s-3$, we obtain $v_w=v_{5i+{\alpha }_s-3}$. Since $b\ne 5i+{\alpha }_s-4$$(b\ne a)$ and $b\ne 5i+{\alpha }_s-2$, we obtain $v_b\nsim v_w$. Again, $v_b,v_w\in V\left(P_s\right)$⇒$d(v_b,v_w)=2$, while $d(v_a,v_w)=1$.

If $v_b\cong v_{5i+{\alpha }_s-2}$, then defining w as above gives us $v_b\sim v_w$. For this case, let $w=a+3=5i+{\alpha }_s-1\Rightarrow v_w=v_{5i+{\alpha }_s-1}$. From the structure of $v_a,v_b,v_w\in P_s$, it is clear that $v_a\nsim v_w$, while $v_b\sim v_w$. Hence, $d(v_b,v_w)=1$, while $d(v_a,v_w)=2$.

[c.]

If $v_a$ is of the form given in (3), then $v_a\cong v_{5i+{\alpha }_s-2}⟹a=5i+{\alpha }_s-2:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. Let $w=a-1=5i+{\alpha }_s-3⟹v_w\cong v_{5i+{\alpha }_s-3}$. Now $v_a\sim v_w\Rightarrow d(v_a,v_w)=1$. Again, since $w=a-1<a<b$ and $v_w,v_b\in P_s$, we obtain $v_b\nsim v_w$, giving us $d(v_b,v_w)=2$.

[d.]

If $v_a$ is of the form given in (4), then $v_a\cong v_{5i+{\alpha }_s}⟹a=5i+{\alpha }_s:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. Let $w=a-1=5i+{\alpha }_s-1⟹v_w\cong v_{5i+{\alpha }_s-1}$. We obtain $d(v_a,v_w)=1$. It is again an easy task to show that $d(v_b,v_w)=2$ for all $v_b\notin W$ and $v_b\in P_s$.

Case 2. 

When $v_a,v_b\in P_t$, following the same proof techniques as in Case 1, it can be easily shown that there always exists a $v_w\in W$, belonging to $P_t$, such that $d(v_a,v_w)\ne d(v_b,v_w)$.

Case 3. 

When $v_a\in P_s$ and $v_b\in P_t$:

[a.]

Let $v_a$ be of the form as given in (1); then, $v_a\cong v_{2i}⟹a=2i:i\in \left\{1,\cdots ,⌊\frac{{\alpha }_s}{2}⌋\right\}$. From here, we obtain that $a\le 2⌊\frac{{\alpha }_s}{2}⌋$.

When s is odd, $a\le 2⌊\frac{{\alpha }_s}{2}⌋\Rightarrow a\le ((s-1)mod5)={\alpha }_s$.

When s is even, $a\le 2⌊\frac{{\alpha }_s}{2}⌋\Rightarrow a\le ((s-1)mod5-1)={\alpha }_s-1$.

Let us consider the set $W_{s_2}=\left\{v_{5j+{\alpha }_s-3}:j\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$; then, $W_{s_2}\ni v_{{\alpha }_s+2}=v_{5+{\alpha }_s-3}\le v_{5j+{\alpha }_s-3}:j\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. The above argument ensures that the smallest element of the set $W_{s_2}$ is $v_{{\alpha }_s+2}$. Let $v_w=v_{{\alpha }_s+2}$; then, $d(v_a,v_w)=2$, since $a\le {\alpha }_s$ if s is odd, and $a\le {\alpha }_s-1$ if s is even.

On the other hand, since $v_b\in P_t$, $d(v_b,v_w)=1$, since $v_w\in P_s$.

[b.]

Let $v_a$ be of the form given in (2); then, $v_a\cong v_{5i+{\alpha }_s-4}\Rightarrow a=5i+{\alpha }_s-4:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋+1\right\}$. Let $w=a+3=5i+{\alpha }_s-1$; then, by construction of $v_w$, we obtain $d(v_a,v_w)=2$ and $d(v_b,v_w)=1$ for all $v_b\in P_t$.

[c.]

If $v_a$ is of the form given in (3); then, $v_a\cong v_{5i+{\alpha }_s-2}⟹a=5i+{\alpha }_s-2:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. Let $a=5j+{\alpha }_s-2$ for some specific $j\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. Let $k\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$ such that $k\ne j$. Consider the vertex $v_w=v_{5k+{\alpha }_s-3}\in W_{s_2}$. Since $k\ne j$, $v_{5k+{\alpha }_s-3}\nsim v_{5j+{\alpha }_s-2}$, giving us $d(v_a,v_w)=2$ and $d(v_b,v_w)=1$ for all $v_b\in P_t$.

[d.]

If $v_a$ is of the form given in (4), then $v_a\cong v_{5i+{\alpha }_s}⟹a=5i+{\alpha }_s:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}$. Let $w=a-3=5i+{\alpha }_s-3$; then, by construction of $v_w$, we obtain $d(v_a,v_w)=2$ and $d(v_b,v_w)=1$ for all $v_b\in P_t$.

We have completed our argument to establish that W, as defined above, is indeed a resolving set for $P_s+P_t$. In the next part, we will show that $W-\{v_w:v_w\in W\}$ is not a resolving set. This will ensure that there does not exist a resolving set smaller than W and $\left|W\right|$ is the metric dimension for $P_s+P_t$.

Part II

Since $v_s\in V_7$, we obtain $v_s\notin W_s$. We now calculate the distance $d(v_s,v_w)$ for all $v_w\in W_s$. Different cases arise for such a $v_w$.

Case I. 

When $v_w\in W_{s_1}$, depending on the value of s, $W_{s_1}$ changes. We discuss these different cases in the following.

[a.]

When $smod5=1$, we obtain $W_{s_1}=\varnothing$, and there is no distance to calculate.

[b.]

When $smod5=2$, then $W_{s_1}=\left\{v_1\right\}$, i.e., $v_w=v_1$. If $s=2$, then $d(v_w,v_s)=1$; otherwise, $d(v_w,v_s)=2$.

[c.]

When $smod5=3$, again $W_{s_1}=\left\{v_1\right\}$; i.e., $v_w=v_1$ and $d(v_w,v_s)=2$.

[d.]

When $smod5=4$, we obtain, $W_{s_1}=\{v_1,v_3\}$; i.e., $v_w=v_1$ or $v_w=v_3$. If $s=4$, we obtain $d(v_1,v_s)=2$ and $d(v_3,v_s)=1$, and $d(v_w,v_s)=2$ for all other such values of s.

[e.]

When $smod5=0$, we again see that $W_{s_1}=\{v_1,v_3\}$—i.e., $v_w=v_1$ or $v_w=v_3$ and $d(v_w,v_s)=2$—for all such values of s.

Case II. 

When $v_w\in W_{s_2}$. Then, $v_w\in \left\{v_{5i+{\alpha }_s-3}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$. We claim that $v_s\nsim v_w$ for all $v_w\in W_{s_2}$. Contrarily, let us suppose that $v_s\sim v_w$. Since $v_s$ is the last vertex of path $P_s$ and $v_w\in P_s$, we only have the possibility that the vertex with the largest index in $W_{s_2}$ is adjacent to $v_s$, implying

$$\begin{array}{cc}\hfill & 5⌊\frac{{\beta }_s}{5}⌋+{\alpha }_s-3+1=s\hfill \\ \hfill \Rightarrow & 5⌊\frac{s-1}{5}⌋+((s-1)mod5)-2=s\hfill \end{array}$$

Using the values from the equation set 7, we obtain $s-3=s$, which is a contradiction. Hence, $v_s\nsim v_{5⌊\frac{{\beta }_s}{5}⌋+{\alpha }_s-3}$, implying $v_s\nsim v_w$ for all $v_w\in W_{s_2}$, giving us $d(v_s,v_w)=2$ for all $v_w\in W_{s_2}$.

Case III. 

When $v_w\in W_{s_3}$. Then, $v_w\in \left\{v_{5i+{\alpha }_s-1}:i\in \left\{1,\cdots ,⌊\frac{{\beta }_s}{5}⌋\right\}\right\}$. We claim that $v_s\nsim v_w$ for all $v_w\in W_{s_3}$. On the contrary, let us suppose that $v_s\sim v_w$. Since $v_s$ is the last vertex of path $P_s$ and $v_w\in P_s$, we only have the possibility that the vertex with the largest index in $W_{s_3}$ is adjacent to $v_s$, implying

$$\begin{array}{cc}\hfill & 5⌊\frac{{\beta }_s}{5}⌋+{\alpha }_s-1+1=s\hfill \\ \hfill \Rightarrow & 5⌊\frac{s-1}{5}⌋+((s-1)mod5)=s\hfill \end{array}$$

Again, using the values from equation set 7, we obtain $s-1=s$, which is a contradiction. Hence, $v_s\nsim v_{5⌊\frac{{\beta }_s}{5}⌋+{\alpha }_s-1}$, implying $v_s\nsim v_w$ for all $v_w\in W_{s_3}$, giving us $d(v_s,v_w)=2$ for all $v_w\in W_{s_3}$.

It is our aim to show that whenever we formulate the set $W^{\prime }=W-\{v_w:v_w\in W\}$, there exists a vertex, say $v_a\notin W^{\prime }$, such that $r\left(v_s\right|W^{\prime })=r\left(v_a\right|W^{\prime })$. Again, different cases arise depending on $v_w$.

Case A. 

When $v_w\in W_{s_1}$, depending on the value of s, $W_{s_1}$ changes. We discuss these different cases in the following.

[a.]

When $smod5=1$, we obtain $W_{s_1}=\varnothing$, and there is nothing to discuss.

[b.]

When $smod5=2$, $W_{s_1}=\left\{v_1\right\}$; i.e., $v_w=v_1$.

If $s=2$, then $r(v_s=v_2|W^{\prime })=(1,1,\cdots ,1)$, since all elements of $W^{\prime }$ are in $W_t$. Since $v_w\notin W^{\prime }$, by letting $v_a=v_w=v_1$, we see that $r(v_a=v_w|W^{\prime })=(1,1,\cdots ,1)$, since again, all elements of $W^{\prime }$ are in $W_t$. Hence, $W^{\prime }$ is not a resolving set.

On the other hand, if $s\ne 2$ and $smod5=2$, we again see that $W_{s_1}=\left\{v_1\right\}$. Let $W^{\prime }=W-v_1$. Then, by the argument in Cases II and III and by the fact that $d(v_s,v_b)=1$ for all $v_b\in P_t$, we obtain

$$r\left(v_s\right|W^{\prime })=(\stackrel{W_s-v_w}{\overbrace{2,2,\cdots ,2}},\stackrel{W_t}{\overbrace{1,1,\cdots ,1}}).$$

Considering the vertex $v_a=v_w=v_1$, since $v_2\notin W$, all elements of W occur after $v_2$; i.e., all elements of $W-v_1$ occur after $v_2$; hence,

$$r\left(v_1\right|W^{\prime })=(\stackrel{W_s-v_w}{\overbrace{2,2,\cdots ,2}},\stackrel{W_t}{\overbrace{1,1,\cdots ,1}}).$$

Hence, $W^{\prime }$ is not a resolving set.

[c.]

When $smod5=3$, again $W_{s_1}=\left\{v_1\right\}$. Considering the vertex $v_a=v_1$ and proceeding in the same way as above, we see that, $r\left(v_s\right|W^{\prime })=r\left(v_1\right|W^{\prime })$.

[d.]

When $smod5=4$, $W_{s_1}=\{v_1,v_3\}$; i.e., $v_w=v_1$ or $v_w=v_3$.

If $s=4$, we can formulate $W^{\prime }$ in two ways; i.e., $W^{\prime }=W-v_1$ or $W^{\prime }=W-v_3$. If $W^{\prime }=W-v_1$, by comparing $r\left(v_2\right|W^{\prime })$ and $r\left(v_4\right|W^{\prime })$, we see that $W^{\prime }$ is not a resolving set. On the other hand, if $W^{\prime }=W-v_3$, comparing $r\left(v_3\right|W^{\prime })$ and $r\left(v_4\right|W^{\prime })$ gives us that $W^{\prime }$ is not a resolving set.

If $s\ne 4$ but $smod5=4$, letting $v_a=v_w$ and comparing $r\left(v_w\right|W^{\prime })$ and $r\left(v_s\right|W^{\prime })$ gives us that $W^{\prime }$ is not a resolving set.

[e.]

When $smod5=0$, again, $W_{s_1}=\{v_1,v_3\}$—i.e., $v_w=v_1$ or $v_w=v_3$. As in the case, $s\ne 4$ and $smod5=4$, by letting $v_a=v_w$ and comparing the representations of $v_w$ and $v_s$ with respect to $W^{\prime }=W-v_w$, we see that $W^{\prime }$ is not a resolving set.

Case B. 

When $v_w\in W_{s_2}$, it is again an easy task to show that

$$r\left(v_w\right|W^{\prime })=(\stackrel{W_s-v_w}{\overbrace{2,2,\cdots ,2}},\stackrel{W_t}{\overbrace{1,1,\cdots ,1}}),$$

where $W^{\prime }=W-v_w$. Similarly,

$$r\left(v_s\right|W^{\prime })=(\stackrel{W_s-v_w}{\overbrace{2,2,\cdots ,2}},\stackrel{W_t}{\overbrace{1,1,\cdots ,1}}).$$

This again shows that $W^{\prime }$ is not a resolving set.

Case C. 

When $v_w\in W_{s_3}$, considering the representations $r\left(v_w\right|W^{\prime })$ and $r\left(v_s\right|W^{\prime })$, where $W^{\prime }=W-v_w$, we see that $r\left(v_w\right|W^{\prime })=r\left(v_s\right|W^{\prime })$, and again, $W^{\prime }$ is not a resolving set.

For the part where $W-v_w$ is not a resolving set for all $v_w\in W_t$, the procedure is the same as for $W_s$.

This completes the second part of our theorem. Combining these two together, we see that W is indeed a resolving set with minimal cardinality. Hence, $dim(P_s+P_t)=\left|W\right|$. This completes our result. □

The above results conclude that the metric dimension of $P_s+P_t$ is not an exact number and increases with the size of both paths—i.e., the metric dimension of $P_s+P_t$ is unbounded.

3. Algorithms for Metric Bases and Metric Dimensions of ${\mathit{P}}_{\mathit{s}}+{\mathit{P}}_{\mathit{t}}$

Theorems 1–3 enable us to calculate the metric dimensions of $P_s+P_t$ in constant time. An algorithm is developed in the following.

Algorithm 1 Calculating the metric dimension of $P_s+P_t$ for $s\ge 1$ and $t\ge 1$.

Input s and t

1: ${\beta }_s\leftarrow s-1$ 2: ${\alpha }_s\leftarrow (s-1)mod5$ 3: ${\beta }_t\leftarrow t-1$ 4: ${\alpha }_t\leftarrow (t-1)mod5$ 5: $dim\leftarrow 0$ 6: if $t\le 6$ then 7:   if $s\in \{1,2,3,6\}$ then 8:     if $t=1$ then 9:       $dim\leftarrow 1+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋$ 10:     end if 11:     if $2\le t\le 5$ then 12:       $dim\leftarrow 2+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋$ 13:     end if 14:     if $t=6$ then 15:       $dim\leftarrow 3+⌊\frac{s}{2}⌋-⌊\frac{s}{5}⌋$ 16:     end if 17:   end if 18:   if $s\in \{4,5\}$ then 19:     if $t=1$ then 20:       $dim\leftarrow 2$ 21:     end if 22:     if $2\le t\le 3$ then 23:       $dim\leftarrow 3$ 24:     end if 25:     if $4\le t\le 6$ then 26:       $dim\leftarrow 4$ 27:     end if 28:   end if 29: else $dim\leftarrow 2\left(⌊\frac{{\beta }_s}{5}⌋+⌊\frac{{\beta }_t}{5}⌋\right)+⌈\frac{{\alpha }_s}{2}⌉+⌈\frac{{\alpha }_t}{2}⌉$ 30: end if

Output $dim$

It can be readily observed that the algorithm uses assignment and if–else statements only. Each of these steps has a complexity of $O\left(1\right)$. Combining their complexities together gives us a complexity of $O\left(1\right)$ for the whole algorithm.

These theorems also provide us a way to calculate the metric bases for $P_s+P_t$. Theorems 1 and 2 establish that the metric bases for $P_s+P_t$ can be calculated in constant time for $1\le s,t\le 6$. Based on Theorem 3, we developed the following algorithm to calculate the metric bases for $P_s+P_t$ when $s\ge 1$ and $t\ge 7$.

Algorithm 2 Calculating the metric basis of $P_s+P_t$ for $s\ge 1$ and $t\ge 7$.

Input s and t

1: ${\beta }_s\leftarrow s-1$ 2: ${\alpha }_s\leftarrow (s-1)mod5$ 3: ${\beta }_t\leftarrow t-1$ 4: ${\alpha }_t\leftarrow (t-1)mod5$ 5: $W\leftarrow \varnothing$ 6: for $1\le i\le ⌈\frac{{\alpha }_s}{2}⌉$ do 7:  $W\leftarrow W\cup v_{2i-1}$ 8: end for 9: for $1\le i\le ⌊\frac{{\beta }_s}{5}⌋$ do 10:  $W\leftarrow W\cup v_{5i+{\alpha }_s-3}\cup v_{5i+{\alpha }_s-1}$ 11: end for 12: for $1\le i\le ⌈\frac{{\alpha }_t}{2}⌉$ do 13:  $W\leftarrow W\cup v_{2i+{\beta }_s}$ 14: end for 15: for $1\le i\le ⌊\frac{{\beta }_s}{5}⌋$ do 16:  $W\leftarrow W\cup v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋-2}\cup v_{5i+{\alpha }_s+{\alpha }_t+5⌊\frac{{\beta }_s}{5}⌋}$ 17: end for

Output W

The first five statements of the above algorithm are assignments, each having a complexity of $O\left(1\right)$. Loops in steps 6, 9, 12 and 15 are not nested. The counter ensures that every loop runs less than $n=s+t$ times, with a maximum complexity of $O\left(n\right)$. By adding these complexities together, we again obtain $O\left(n\right)$; i.e., the algorithm runs in linear time.

The metric basis we calculated in the algorithm will work for both $P_s+P_t$ and $P_t+P_s$ because of isomorphism and symmetry. Let us use this algorithm to solve an example already mentioned in introduction.

Example 2. 

Let $s=11$ and $t=11$; then, ${\beta }_s={\beta }_t=10$ and $⌊\frac{{\beta }_s}{5}⌋=⌊\frac{{\beta }_t}{5}⌋=2$. Again, ${\alpha }_s={\alpha }_t=0$ and $⌈\frac{{\alpha }_s}{2}⌉=⌈\frac{{\alpha }_t}{2}⌉=0$. Loops in steps 6 and 12 do not satisfy the condition, and hence will not contribute anything to W. The loop in step 9 will run twice and will give us $W=\{v_2,v_4,v_7,v_9\}$. Similarly, the loop in step 15 will run twice, and we will then obtain $W=\{v_2,v_4,v_7,v_9,v_{13},v_{15},v_{18},v_{20}\}$.

4. Conclusions

We considered the join of two path graphs $P_s$ and $P_t$ and calculated their metric dimensions and metric basis.

We also provided algorithms to calculate the metric dimensions and metric basis of $P_s+P_t$. We concluded that the metric-dimension algorithm has a complexity of $O\left(1\right)$, and the metric-basis algorithm runs with $O\left(n\right)$ complexity.

Since the metric dimension of an arbitrary n-vertex graph can be approximated in polynomial time [26], we have effectively reduced a lot of computational complexity for the case of $P_s+P_t$, and by symmetry, that of $P_t+P_s$.