An Experimental Study of Cavitation Bubble Dynamics near a Complex Wall with a Continuous Triangular Arrangement
Abstract
1. Introduction
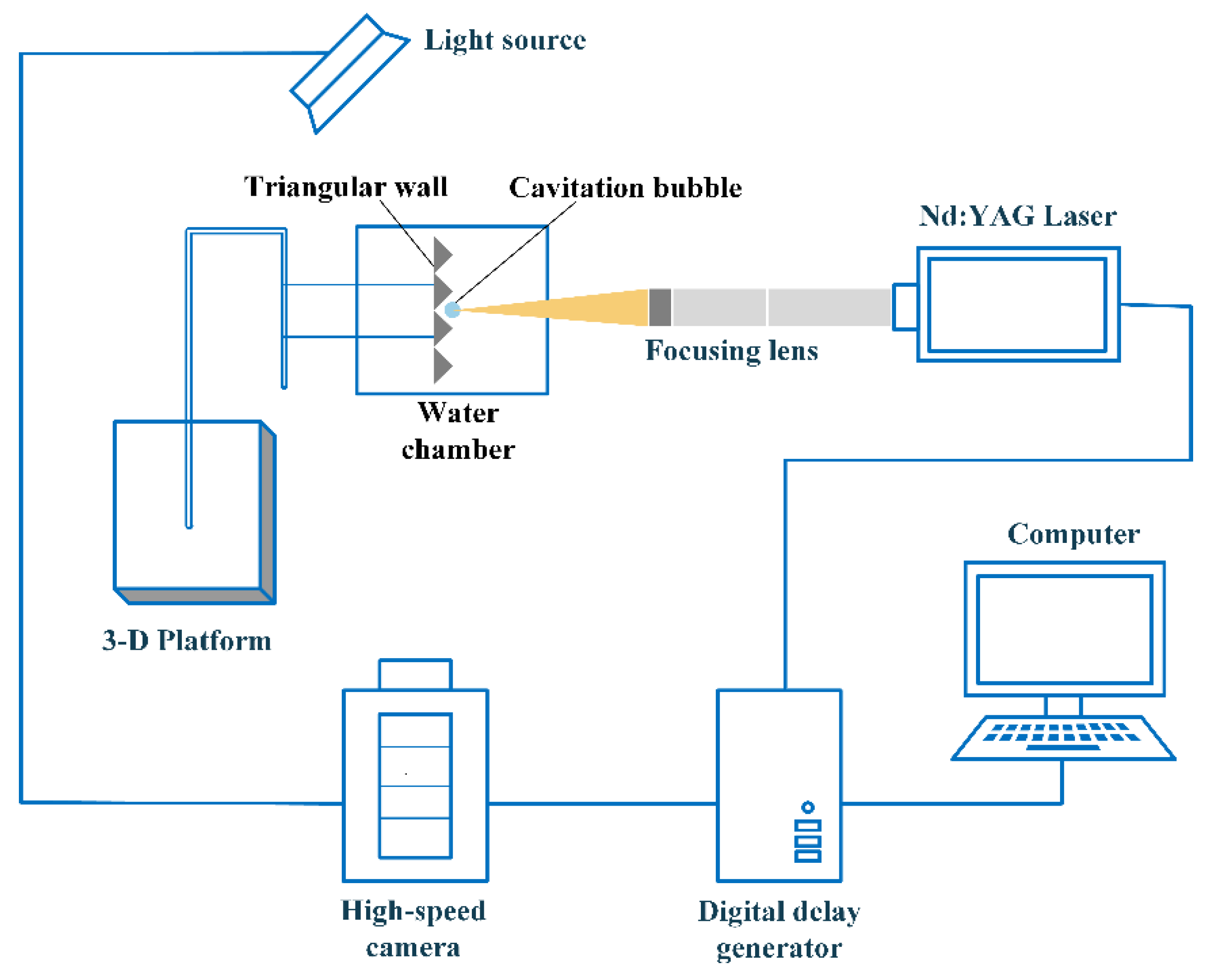
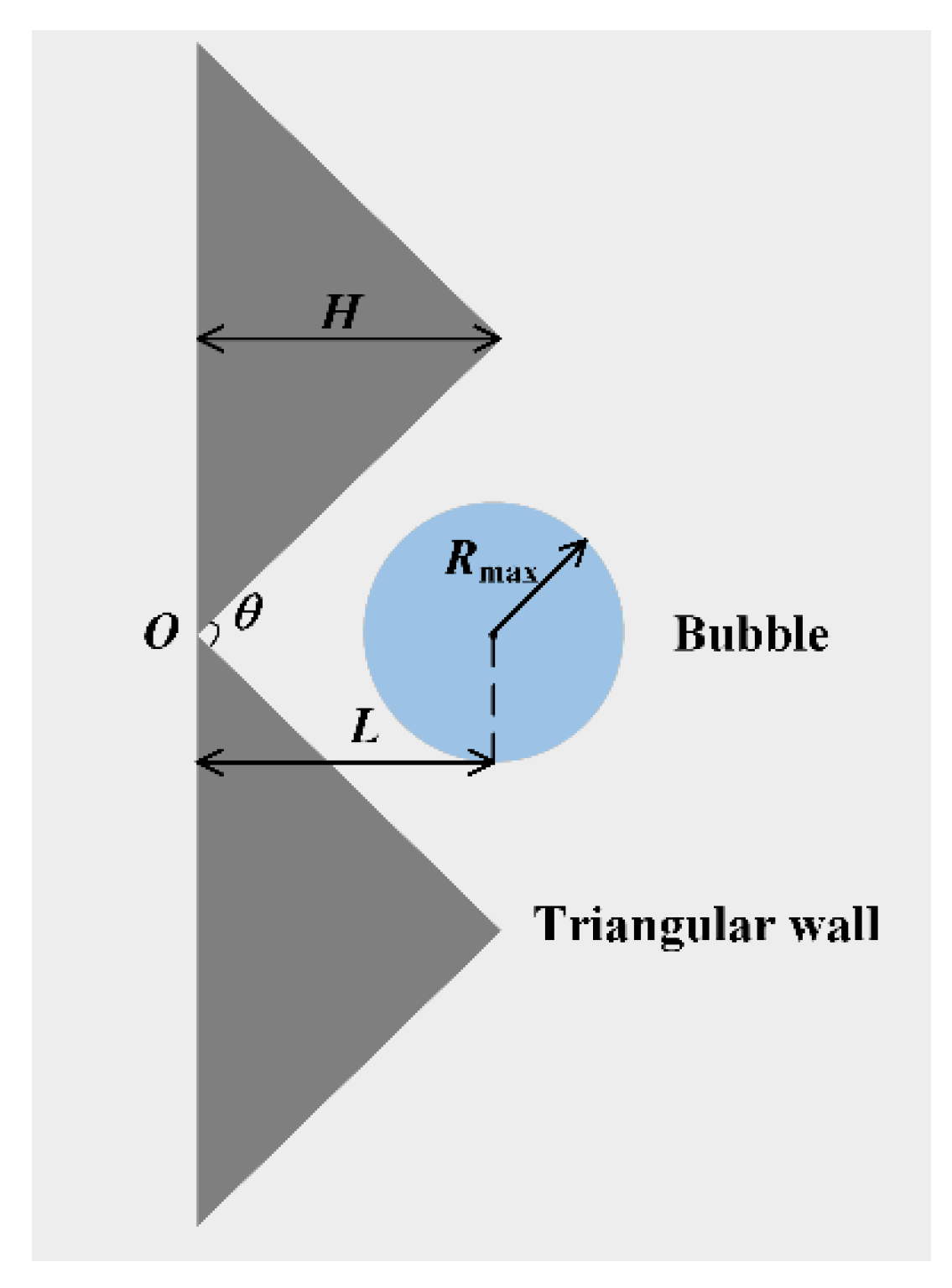
2. Experimental Setup and Parameter Definition
3. Main Characteristics of Cavitation Bubble Dynamics
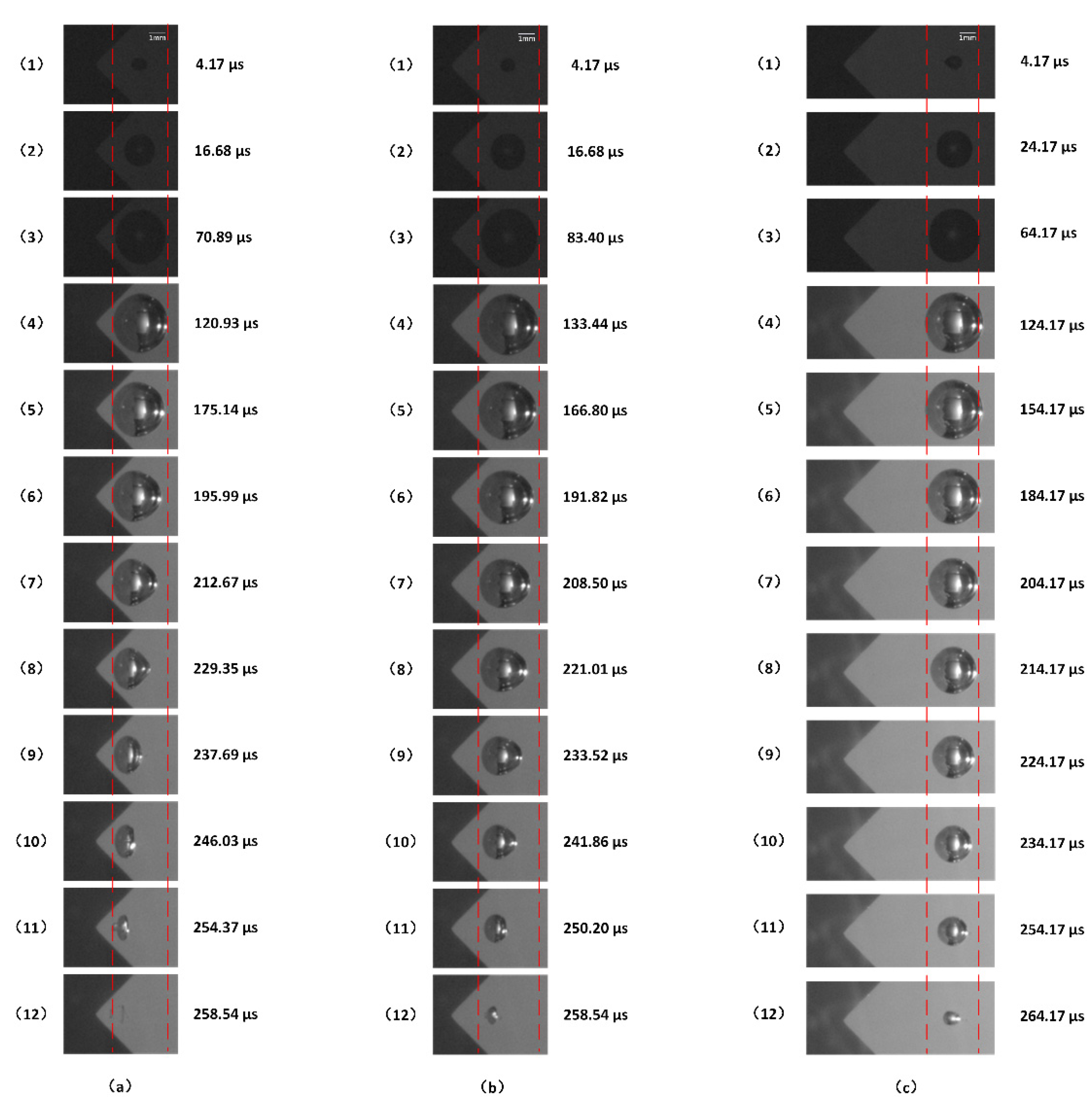
3.1. Typical Cases
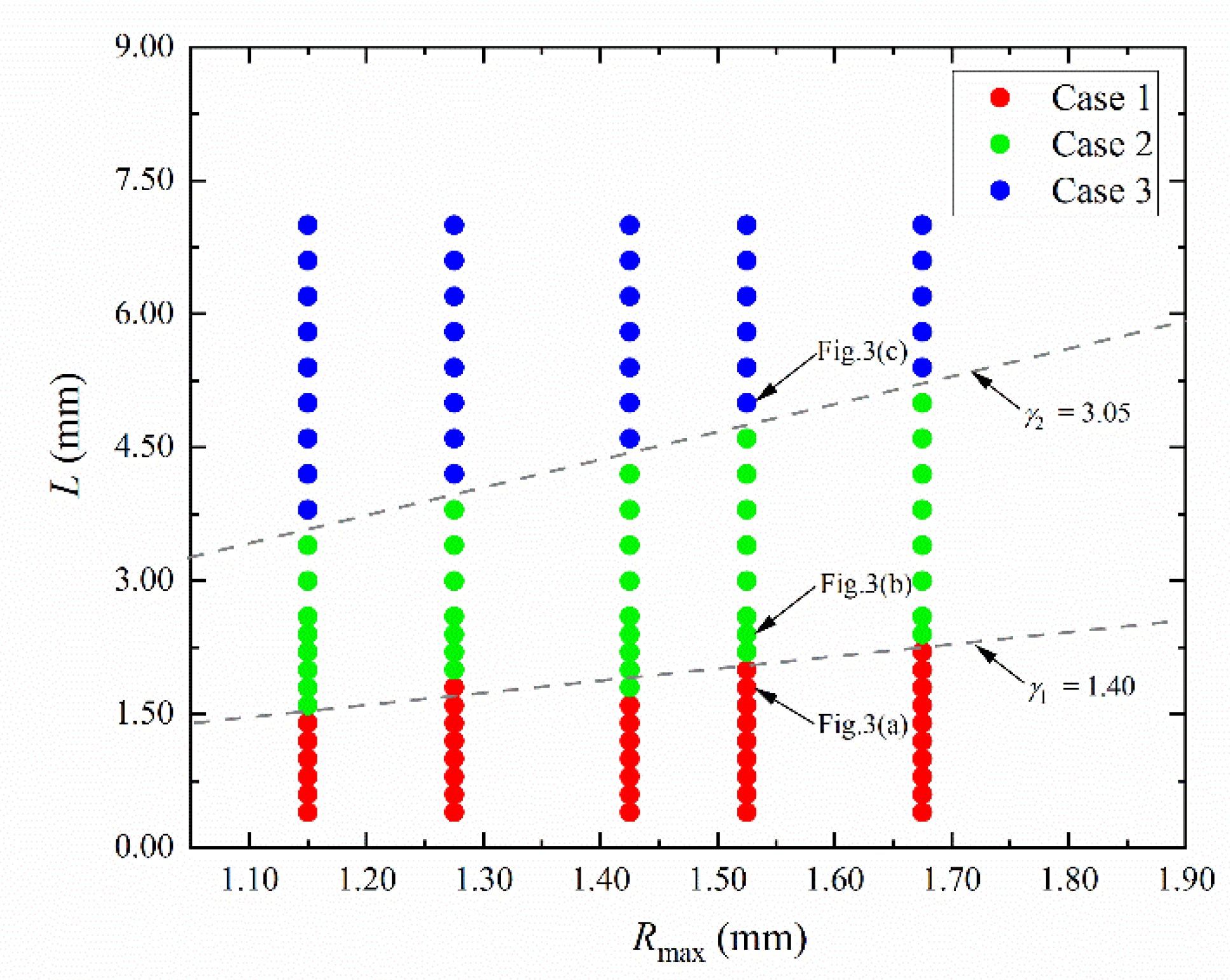
3.2. Parameter Range Corresponding to Different Cases
4. Non-Uniform Collapse at the Characteristic Location of a Bubble Wall
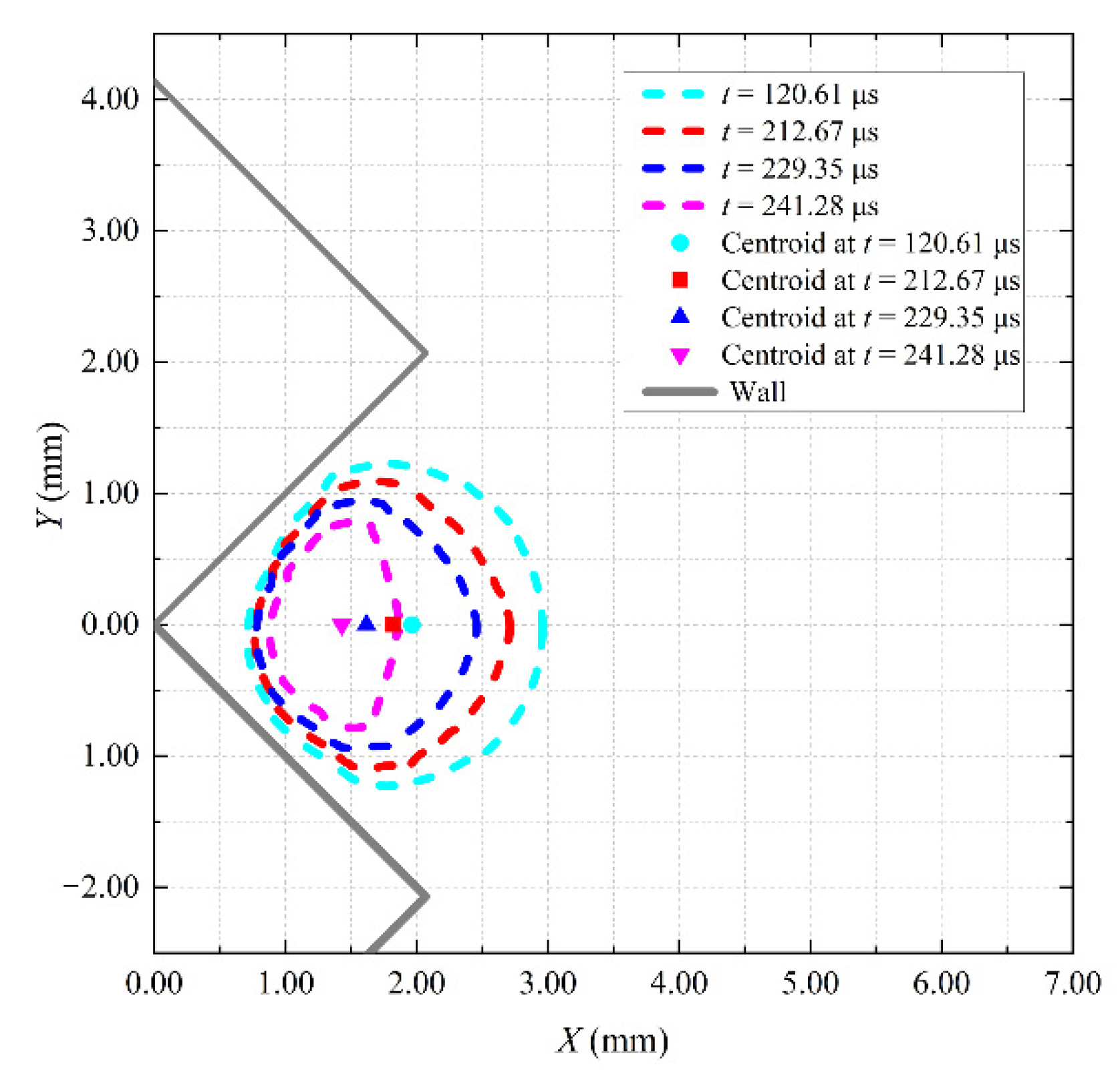
5. Movement Characteristics of a Cavitation Bubble
6. Conclusions
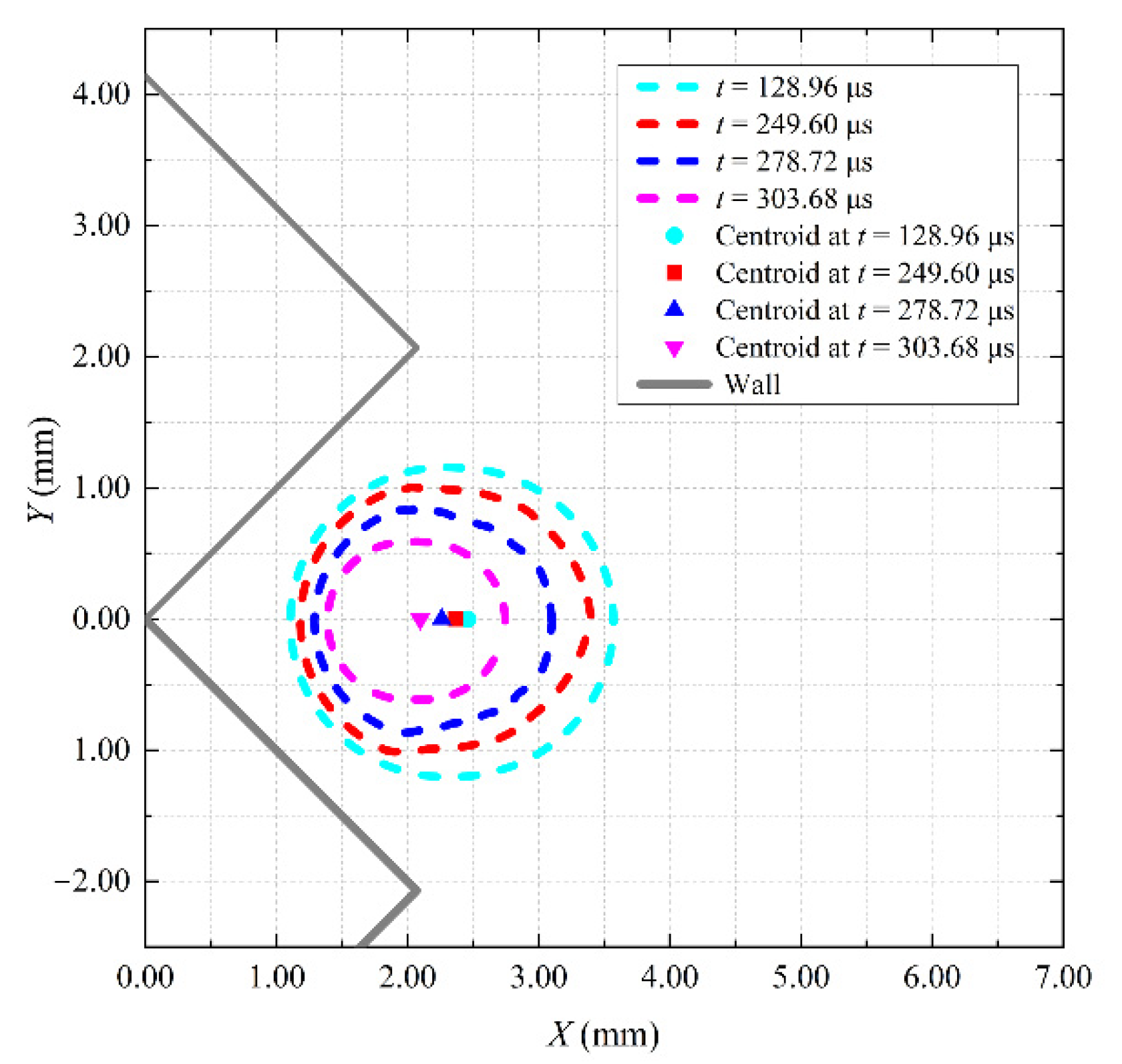
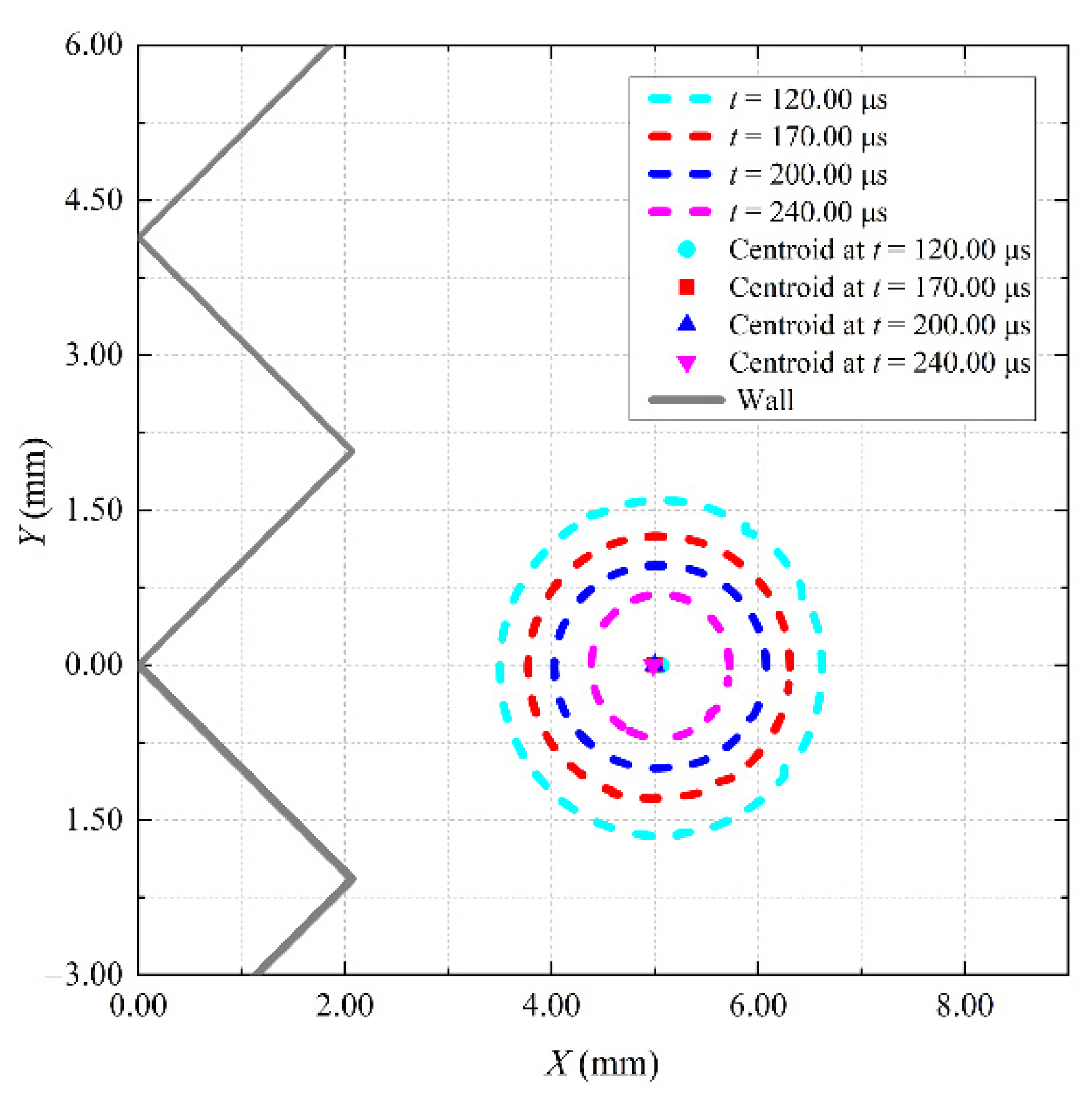
- According to the difference in the collapse speed of the left and right bubble walls and the difference in the centroid movement distance under different parameters, the collapse dynamics of the bubble near a complex wall with a continuous triangular arrangement can be divided into three typical cases. For case 1, the difference in the contraction velocity between the left and right bubble walls is the most obvious, and the distance of the centroid movement of the bubble is the largest. For case 3, the bubble centroid basically does not move and appears spherical collapse. Case 2 is between case 1 and case 3. According to a large number of experimental results under different parameters, the corresponding parameter range of each case is given. When γ < 1.40, the collapse dynamics of the bubble are similar to case 1. When 1.40 < γ < 3.05, the collapse dynamics of the bubble are similar to case 2. When γ > 3.05, the collapse dynamics of the bubble are similar to case 3.
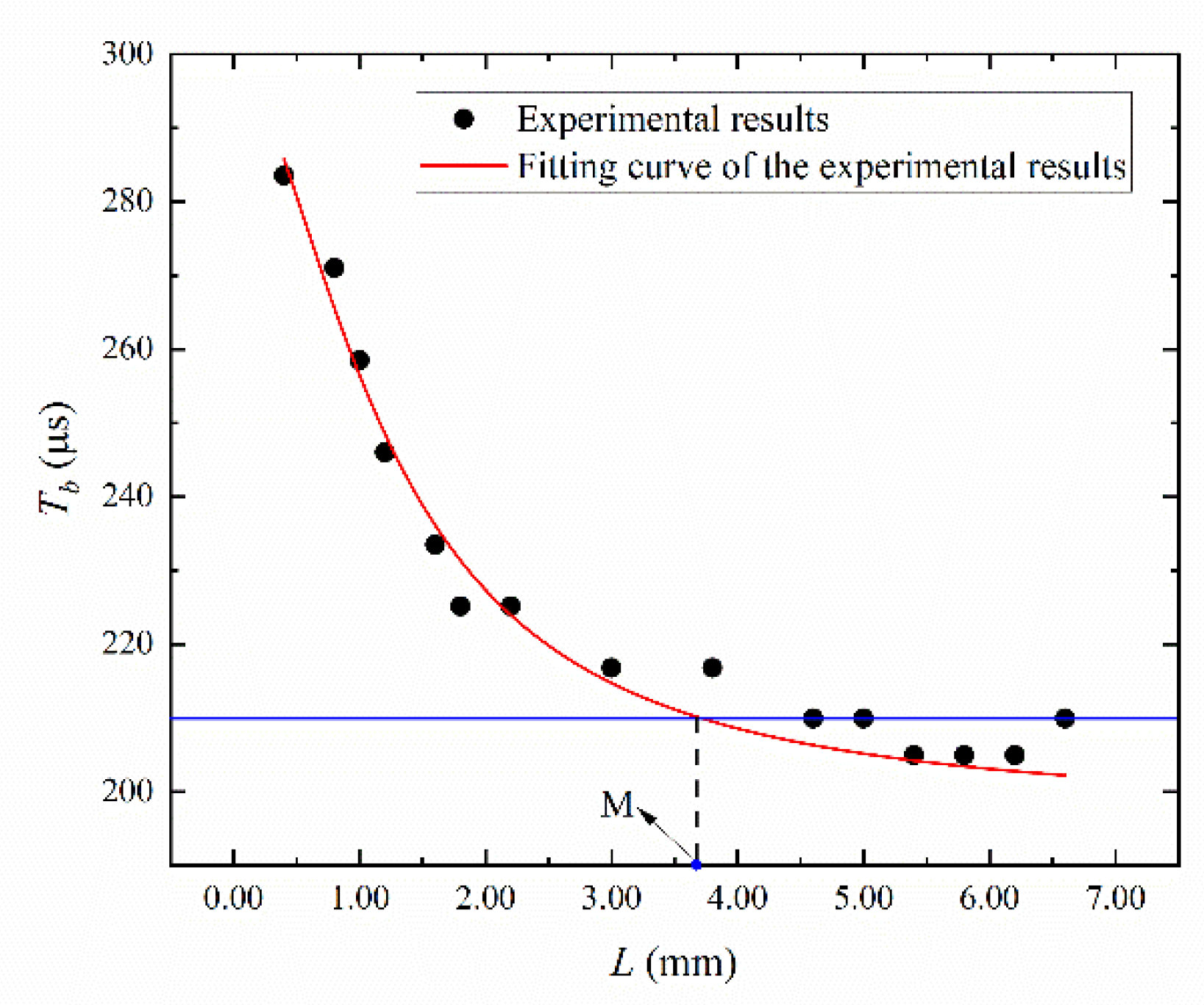
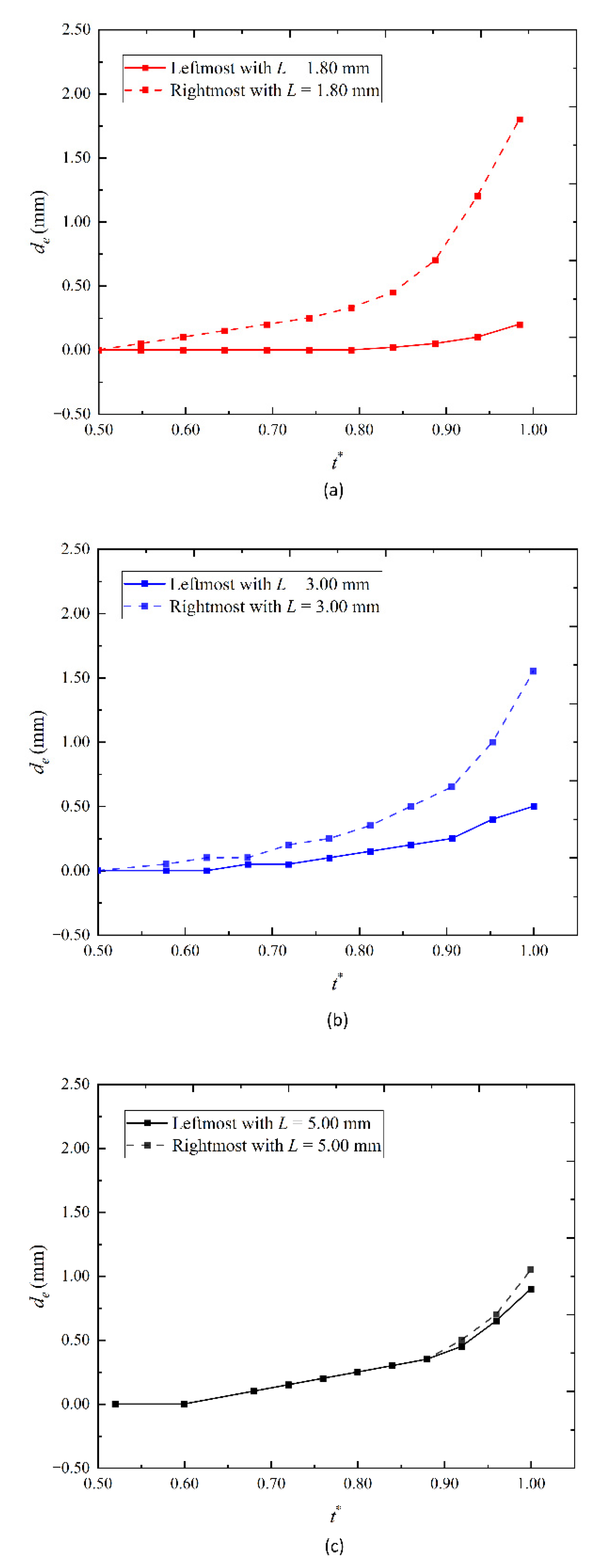
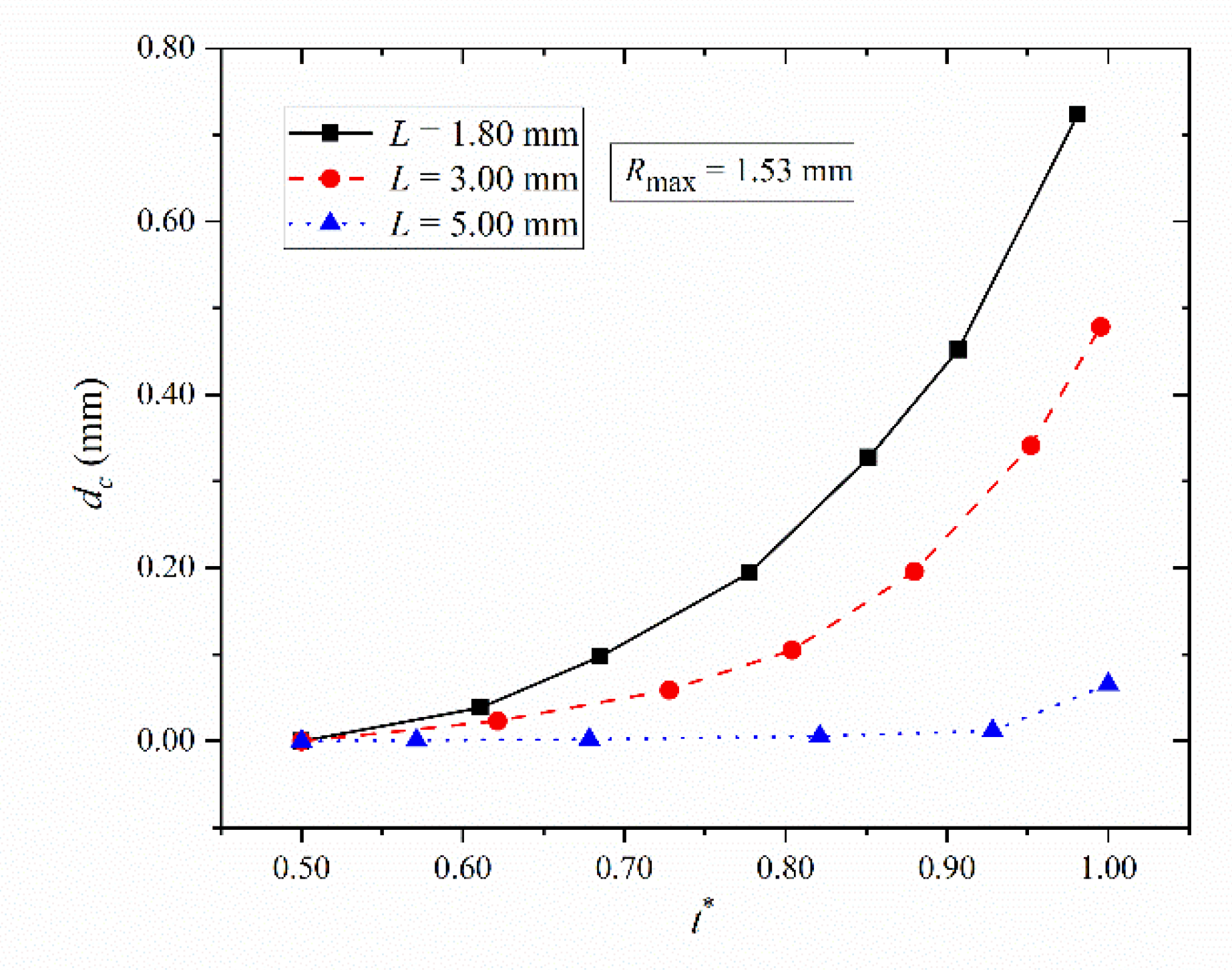
- Tb gradually decreases with the increase in L. When L is very large, Tb obtained by classical bubble wall motion equation is in good agreement with the experimental results, and Tb tends to a stable value. This shows that Tb can be effectively predicted by this equation when L is large.
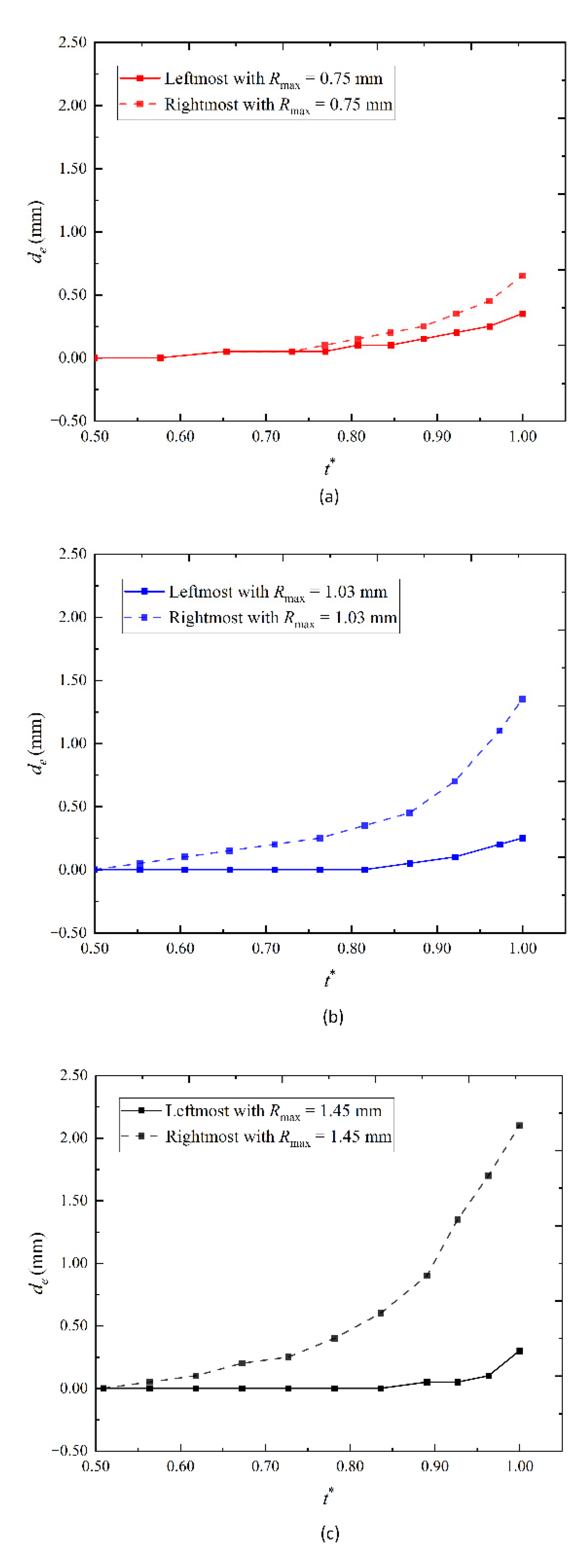
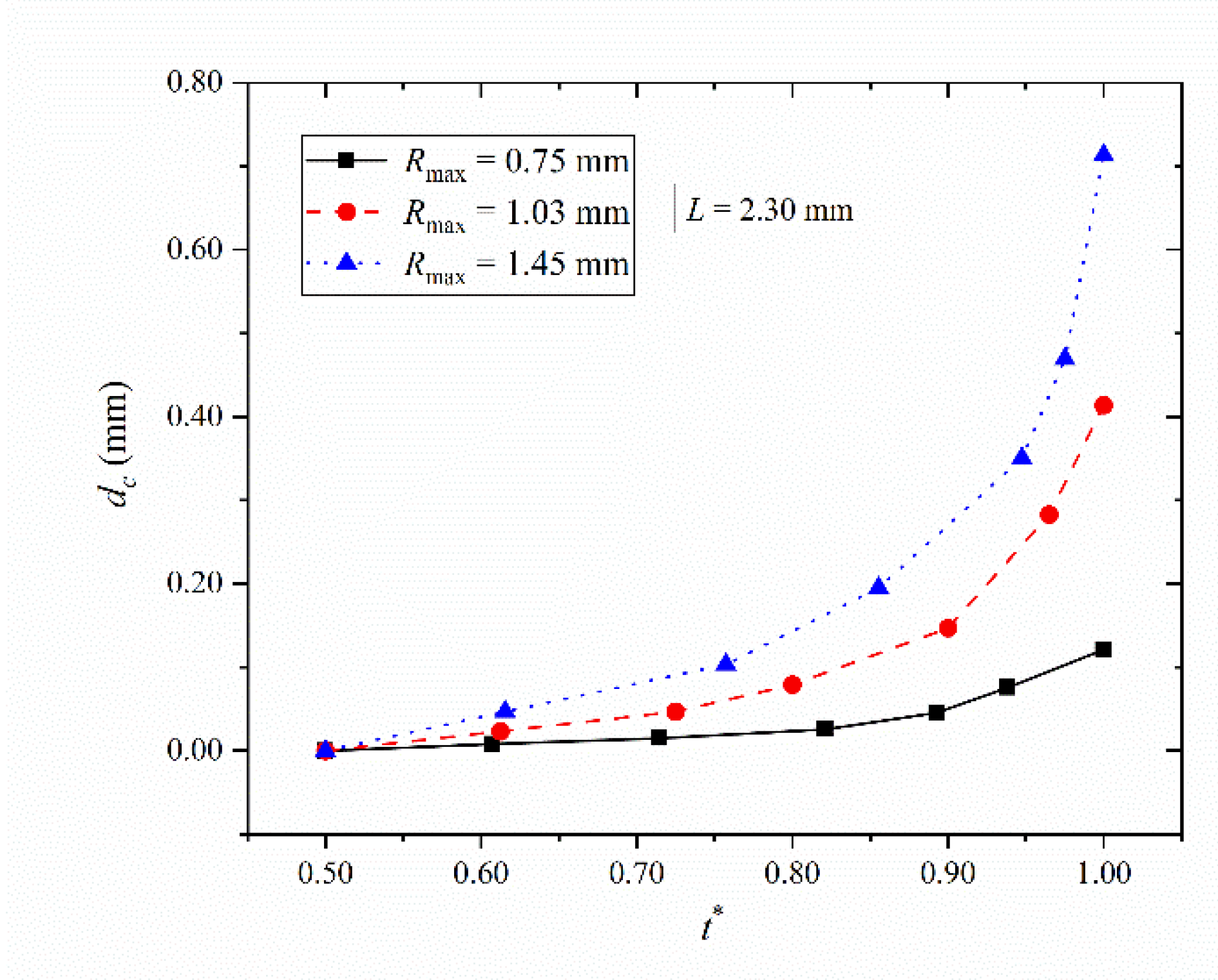
- The larger Rmax is or the smaller L is, the more significant the effect of the complex wall is, the more significant is the collapse speed of the left and right bubble walls, and, the greater the movement distance towards the complex wall during the collapse stage. To some extent, it can indicate that the bubble collapse near the complex wall is very violent, which is beneficial to the field of cavitation cleaning on the complex wall.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thanu, D.P.; Antoniswamy, A.; Swaminathan, V.V.; Srinadhu, E.S.; Dole, N.; Zhao, M.; Balachandran, R.; Agrawal, D.; Kumar, J.; Keswani, M. Use of Surfactants in Acoustic Cleaning. Surfactants Precis. Clean. 2022, 193–226. [Google Scholar] [CrossRef]
- Kim, H.; Lee, Y.; Lim, E. Design and fabrication of a horn-type megasonic waveguide for nanoparticle cleaning. IEEE Trans. Semicond. Manuf. 2013, 26, 221–225. [Google Scholar] [CrossRef]
- Chu, C.L.; Lu, T.Y.; Fuh, Y.K. The suitability of ultrasonic and megasonic cleaning of nanoscale patterns in ammonia hydroxide solutions for particle removal and feature damage. Semicond. Sci. Technol. 2020, 35, 045001. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; Huang, X.; Quinto-Su, P.A.; Wu, T.; Ohl, C.-D. Motion of micrometer sized spherical particles exposed to a transient radial flow: Attraction, repulsion, and rotation. Phys. Rev. Lett. 2011, 107, 074503. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Avila, S.R.; Prabowo, F.; Kumar, A.; Ohl, C.-D. Improved ultrasonic cleaning of membranes with tandem frequency excitation. J. Membr. Sci. 2012, 415, 776–783. [Google Scholar] [CrossRef]
- Olim, M. A theoretical evaluation of megasonic cleaning for submicron particles. J. Electrochem. Soc. 1997, 144, 3657. [Google Scholar] [CrossRef]
- Chahine, G.L.; Kapahi, A.; Choi, J.K.; Hsiao, C.T. Modeling of surface cleaning by cavitation bubble dynamics and collapse. Ultrason. Sonochem. 2016, 29, 528–549. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, Z.; Stone, H.A.; Liu, S. Motion of a free-settling spherical particle driven by a laser-induced bubble. Phys. Rev. Lett. 2017, 119, 084501. [Google Scholar] [CrossRef]
- Neppiras, E.A. Acoustic cavitation. Phys. Rep. 1980, 61, 159–251. [Google Scholar] [CrossRef]
- Chen, D.; Weavers, L.K.; Walker, H.W. Ultrasonic control of ceramic membrane fouling by particles: Effect of ultrasonic factors. Ultrason. Sonochem. 2006, 13, 379–387. [Google Scholar] [CrossRef]
- Dijkink, R.; Ohl, C.D. Measurement of cavitation induced wall shear stress. Appl. Phys. Lett. 2008, 93, 254107. [Google Scholar] [CrossRef]
- Ohl, C.D.; Arora, M.; Dijkink, R.; Janve, V.; Lohse, D. Surface cleaning from laser-induced cavitation bubbles. Appl. Phys. Lett. 2006, 89, 074102. [Google Scholar] [CrossRef]
- Vogel, A.; Lauterborn, W.; Timm, R. Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 1989, 206, 299–338. [Google Scholar] [CrossRef]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Li, X.; Duan, Y.; Zhang, Y.; Tang, N.; Zhang, Y. Retardant effects of collapsing dynamics of a laser-induced cavitation bubble near a solid wall. Symmetry 2019, 11, 1051. [Google Scholar] [CrossRef]
- Blake, J.R.; Cerone, P. A note on the impulse due to a vapour bubble near a boundary. ANZIAM J. 1982, 23, 383–393. [Google Scholar] [CrossRef]
- Blake, J.R.; Taib, B.B.; Doherty, G. Transient cavities near boundaries. Part 1. Rigid boundary. J. Fluid Mech. 1986, 170, 479–497. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z. Review on progress of the interactions between cavitation bubble and boundary. Nucl. Sci. Eng. 2022, 42, 598–615. [Google Scholar]
- Zhong, P.; Cocks, F.H.; Cioanta, I.; Preminger, G.M. Controlled, forced collapse of cavitation bubbles for improved stone fragmentation during shock wave lithotripsy. J. Urol. 1997, 158, 2323–2328. [Google Scholar] [CrossRef] [PubMed]
- Tomita, Y.; Robinson, P.B.; Tong, R.P.; Blake, J.R. Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 2002, 466, 259–283. [Google Scholar] [CrossRef]
- Shima, A.; Tomita, Y.; Gibson, D.C.; Blake, J.R. The growth and collapse of cavitation bubbles near composite surfaces. J. Fluid Mech. 1989, 203, 199–214. [Google Scholar] [CrossRef]
- Shervani-Tabar, M.T.; Rouhollahi, R. Numerical study on the effect of the concave rigid boundaries on the cavitation intensity. Sci. Iran. 2017, 24, 1958–1965. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Zhang, X.; Tang, N. Collapsing dynamics of a laser-induced cavitation bubble near the edge of a rigid wall. Ultrason. Sonochem. 2020, 67, 105157. [Google Scholar] [CrossRef]
- Brujan, E.A.; Noda, T.; Ishigami, A.; Ogasawara, T.; Takahira, H. Dynamics of laser-induced cavitation bubbles near two perpendicular rigid walls. J. Fluid Mech. 2018, 841, 28–49. [Google Scholar] [CrossRef]
- Tagawa, Y.; Peters, I.R. Bubble collapse and jet formation in corner geometries. Phys. Rev. Fluids 2018, 3, 081601. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Xie, X.Y.; Zhang, Y.N.; Zhang, Y.X. High-speed experimental photography of collapsing cavitation bubble between a spherical particle and a rigid wall. J. Hydrodyn. 2018, 30, 1012–1021. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Zhang, Y.; Du, X. Experimental study of influences of a particle on the collapsing dynamics of a laser-induced cavitation bubble near a solid wall. Exp. Therm. Fluid Sci. 2019, 105, 289–306. [Google Scholar] [CrossRef]
- Wang, X.; Wu, G.; Zheng, X.; Du, X.; Zhang, Y. Theoretical investigation and experimental support for the cavitation bubble dynamics near a spherical particle based on Weiss theorem and Kelvin impulse. Ultrason. Sonochem. 2022, 89, 106130. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, F.; Zhang, Y.; Du, X. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Exp. Therm. Fluid Sci. 2018, 98, 645–661. [Google Scholar] [CrossRef]
- Morad, A.M.; Selima, E.S.; Abu-Nab, A.K. Bubbles interactions in fluidized granular medium for the van der Waals hydrodynamic regime. Eur. Phys. J. Plus 2021, 136, 306. [Google Scholar] [CrossRef]
- Morad, A.M.; Selima, E.S.; Abu-Nab, A.K. Thermophysical bubble dynamics in N-dimensional Al2O3/H2O nanofluid between two-phase turbulent flow. Case Stud. Therm. Eng. 2021, 28, 101527. [Google Scholar] [CrossRef]
- Abu-Nab, A.K.; Morad, A.M.; Selima, E.S. Impact of magnetic-field on the dynamic of gas bubbles in N-dimensions of non-Newtonian hybrid nanofluid: Analytical study. Phys. Scr. 2022, 97, 105202. [Google Scholar] [CrossRef]
- Abu-Nab, A.K.; Selima, E.S.; Morad, A.M. Theoretical investigation of a single vapor bubble during Al2O3/H2O nanofluids in power-law fluid affected by a variable surface tension. Phys. Scr. 2021, 96, 035222. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, Y.; Zhang, Y. Experimental study of a laser induced cavitation bubble near a complex boundary. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 062039. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, X.; Ding, Z.; Li, A.; Lu, X.; Zhang, Y. Investigation on the cavitation bubble collapse and the movement characteristics near spherical particles based on Weiss theorem. Ultrason. Sonochem. 2023, 93, 106301. [Google Scholar] [CrossRef]
- Plesset, M.S. The dynamics of cavitation bubbles. Int. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wang, X.; Lu, X.; Zhang, Y.; Zhang, Y.; Yu, J. An Experimental Study of Cavitation Bubble Dynamics near a Complex Wall with a Continuous Triangular Arrangement. Symmetry 2023, 15, 693. https://doi.org/10.3390/sym15030693
Zheng X, Wang X, Lu X, Zhang Y, Zhang Y, Yu J. An Experimental Study of Cavitation Bubble Dynamics near a Complex Wall with a Continuous Triangular Arrangement. Symmetry. 2023; 15(3):693. https://doi.org/10.3390/sym15030693
Chicago/Turabian StyleZheng, Xiaoxiao, Xiaoyu Wang, Xuan Lu, Yuning Zhang, Yuning Zhang, and Jiaxin Yu. 2023. "An Experimental Study of Cavitation Bubble Dynamics near a Complex Wall with a Continuous Triangular Arrangement" Symmetry 15, no. 3: 693. https://doi.org/10.3390/sym15030693
APA StyleZheng, X., Wang, X., Lu, X., Zhang, Y., Zhang, Y., & Yu, J. (2023). An Experimental Study of Cavitation Bubble Dynamics near a Complex Wall with a Continuous Triangular Arrangement. Symmetry, 15(3), 693. https://doi.org/10.3390/sym15030693





