Gravitational Refraction of Compact Objects with Quadrupoles

Abstract

We use the material medium approach to derive the refractive index that can be associated with the gravitational field of a compact object with a quadrupole moment. We consider both a static deformation and a stationary rotation of the gravitational source as the source of the quadrupole. We show that up to the first order in the quadrupole, the refractive indices of both configurations are equivalent such that from the point of view of refraction, a mimicking effect can occur. This also holds at the level of the deflection angle. We argue that it is possible to use the refractive indices and the parameters of the trajectories of light rays that propagate in a gravitational field to determine the physical parameters of the source.

1. Introduction

Ideas and methods relating to optical engineering have been applied to many disciplines beyond optics [1]. One of the areas of application is gravitational lensing in Einstein’s general theory of relativity, which was the first experimental test of Einstein’s general theory of relativity, performed by measuring the gravitational deflection of light rays from the Sun during a total solar eclipse in 1919 [2]. The study of the effects of gravitational lensing makes it possible to estimate the total mass of a galaxy acting as a lens [3].

In connection with the significantly increased possibilities of modern astrophysical observations, it becomes relevant to calculate the effect of gravitational lensing of various astrophysical objects. For example, James Webb, the latest telescope, obtained an image of the galaxy SPT-S J041839-4751.8, which features the ideal “Einstein ring” surrounding it [4], which is a kind of optical illusion that is generated due to the gravitational lensing effect.

One of the famous and reliable approaches to the study of gravitational lensing is the material medium approach, which was first used by Tamm [5] and then by Balazs [6] to calculate the effect of a rotating body on the polarization of light. In this approach, the impact of gravity on the ray of light reduces to the problem of the propagation of waves in a material medium in a flat spacetime. This concept is the basis of the material medium approach. This method is attractive because it suggests that classical optics is as reasonable as Riemannian geometry for the study of electromagnetic effects in a weak gravitational field.

There are various methods for the approximate and exact determination of the light deflection angle, such as the null geodesics approach, which applies either perturbation procedures [7,8] or direct integration of the null geodesic equations [9,10,11]. On the other hand, it is known that there is a certain similarity between mechanical and optical phenomena, which historically manifested itself in the fact that a number of optical phenomena could be described equally well within the framework of both the wave and corpuscular theories. In particular, the motion of light in an inhomogeneous medium is, in many respects, analogous to the motion of a material particle in a potential field. According to general relativity, light is deflected in a gravitational field. This deviation can be interpreted as the motion of light in a medium with an inhomogeneous refractive index. Consequently, a certain refractive index can be assigned to the gravitational field. In this work, we follow this analogy and derive the refractive index of a gravitational field with a quadrupole by using the material medium approach.

The angle of deflection of a ray of light has been calculated accurately in the equatorial plane around the Schwarzschild and Kerr gravitating masses [12,13]. Nevertheless, the contribution to the light deflection due to the quadrupole moment seems to be significant and requires careful consideration. Indeed, compact objects are characterized by deviations from spherical symmetry that are described by the gravitational quadrupole moment. Therefore, studying the quadrupole is necessary to understand the physics of compact objects.

This work is organized as follows. In Section 2, we consider the effect of refraction in the gravitational field of a static, slightly deformed mass distribution. In Section 3, we study the linearized Kerr metric and calculate the corresponding refractive index and deflection angle. In Section 4, we compare the results of the previous sections and show that there exists a “mimicking” effect that allows us to consider any refraction effect due to either the gravitational field of a stationary rotating body or a static deformed body. We also show that it is possible to determine the physical parameters of the gravitational source by analyzing the refractive indices and the parameters of light rays that are deflected in the corresponding gravitational field. Finally, Section 5 contains a summary of our results.

2. Refraction in a Slightly Deformed Spacetime

In Einstein’s theory, in a vacuum, a spherically symmetric gravitational field is described by the Schwarzschild solution, which according to Birkhoff’s theorem is unique. Deformations from spherical symmetry are usually described by means of multipole moments, of which the most important one is the quadrupole. In the case of an axially symmetric mass distribution with a quadrupole, no uniqueness theorem exists, and therefore, the corresponding gravitational field can be described by different metrics [14].

A particular simple metric was presented in [15], where it was proposed to use the Zipoy–Voorhees transformation [16,17] to generate a quadrupolar vacuum solution. In the literature, this metric is known as the Zipoy–Voorhees metric, $\delta$ metric, $\gamma$ metric, and q metric [16,17,18,19,20,21,22,23]. Interior solutions with quadrupoles were found in [24], and a method to generate perfect fluid quadrupolar solutions was presented in [25]. Approximate interior solutions and properties for the exterior q metric were considered in [26,27,28]. In a recent work [29], six different generalizations of the Schwarzschild metric with quadrupoles were analyzed. A common feature of these metrics is that in all of them, the hypersurface $r=2m$ is singular. There probably exist other exact solutions to Einstein’s vacuum equations with the same properties.

Recently, in [26], a different approximate generalization of the Schwarzschild metric with a quadrupole was derived, which can be written as

$$\begin{array}{ccc}\hfill d{s}^2& =& \left(1-\frac{2m}{r}\right)\left(1-\frac{qm}{r-m}\right)d{t}^2\hfill \\ & & -\left[1+\frac{qm(r-2m)}{{(r-m)}^2}\right]\frac{d{r}^2}{1-\frac{2m}{r}}\hfill \\ & & -\left(1+\frac{qm}{r-m}\right)r^2(d{\theta }^2+{sin}^2\theta d{\phi }^2),\hfill \end{array}$$

(1)

where m is the mass and q is the quadrupole parameter. The most interesting feature of this approximate solution is that its Kretschmann scalar

$$K=\frac{48m^2}{r^6}\left(1+q\frac{r-4m}{r-m}+\mathcal{O}\left(q^2\right)\right)$$

(2)

shows that the hypersurface $r=2m$ is regular. Instead, there exists a curvature singularity at $r=m$ aside from the central singularity located at $r=0$, which is also present in the Schwarzschild spacetime.

2.1. Refractive Index

For the calculation of the corresponding refractive index, we now represent the above approximate metric in isotropic coordinates $(t,\rho ,\theta ,\phi )$. To this end, let us consider the coordinate transformation

$$r=\rho {\left(1+\frac{m}{2\rho }\right)}^2+qh\left(\rho \right),$$

(3)

where the additional auxiliary function $h\left(\rho \right)$ stays for the deformation from spherical symmetry. By introducing this transformation into the line element in Equation (1) and expanding up to the first order in q, the corresponding function $h\left(\rho \right)$ turns out to be

$$h\left(\rho \right)=\frac{m^2}{4\rho }\frac{(m^2-4{\rho }^2)}{(m^2+4{\rho }^2)}.$$

(4)

Finally, we can rewrite the line element in the form

$$d{s}^2=A\left(\rho \right)d{t}^2-B\left(\rho \right)d\overrightarrow{\rho }{}^2$$

(5)

where we have introduced the notation

$$d\overrightarrow{\rho }{}^2=d{\rho }^2+{\rho }^{2}d{\theta }^2+{\rho }^{2}sin{\theta }^{2}d{\phi }^2$$

(6)

and the functions $A\left(\rho \right)$ and $B\left(\rho \right)$ are

$$\begin{array}{c}\hfill A\left(\rho \right)=\frac{{\left(m-2\rho \right)}^2}{{\left(m+2\rho \right)}^2}\left[1+q\frac{4m\rho }{m^2-4{\rho }^2}\right],\end{array}$$

(7)

$$\begin{array}{c}\hfill B\left(\rho \right)=\frac{1}{16}\frac{{\left(m+2\rho \right)}^4}{{\rho }^4}\left[1+q\frac{2m}{m+\rho }\right].\end{array}$$

(8)

In the limiting case $q=0$, the above metric reduces to the Schwarzschild metric in the isotropic form [30,31].

To derive the expression for the refractive index, we follow the procedure proposed by Sen in [31] for static fields. We consider the trajectory of a light ray such that $d{s}^2=0$. Then, the velocity of the light ray $v\left(\rho \right)$ can be determined from the expression

$$v^2\left(\rho \right)=\frac{d\overrightarrow{\rho }{}^2}{d{t}^2}=\frac{A\left(\rho \right)}{B\left(\rho \right)}.$$

(9)

Furthermore, the velocity of the light ray in terms of the radial coordinate r can be obtained as follows:

$$v\left(r\right)=v\left(\rho \right)\left(\frac{dr}{d\rho }\right),$$

(10)

where the expression $dr/d\rho$ can be determined from Equations (3) and (4) as follows:

$$\frac{dr}{d\rho }=1-\frac{m^2}{4{\rho }^2}+\frac{q{m}^2}{4}\frac{(16m^2{\rho }^2-m^4)}{{\rho }^2{(m^2+4{\rho }^2)}^2}.$$

(11)

Using the inverse transformation, the new coordinate $\rho$ can be written as

$$\rho =\frac{1}{2}\left(2r-3m\right)+\frac{q{m}^2}{4\left(r-m\right)}.$$

(12)

Finally, the refractive index is related to the velocity by

$$n\left(r\right)=\frac{1}{v\left(r\right)}.$$

(13)

Then, from Equations (10), (11), and (13), we obtain

$$n\left(r\right)=\frac{r}{r-2m}\left[1+\frac{q}{2}\frac{m(2r-3m)}{{(r-m)}^2}\right].$$

(14)

This is the effective refractive index of the spacetime described by the approximate quadrupolar metric in Equation (1). As expected, in the limiting case $q=0$, it reduces to refractive index of the Schwarzschild spacetime [31], where $n_0=r/(r-2m)$. The second term is due to the slight deformation of the central gravitating body from the spherical symmetry. The behavior of the refractive index is illustrated in Figure 1. Notice that the divergences located at $r=m$ and $r=2m$ are due to the presence of the curvature singularity of the metric in Equation (1) and the Schwarzschild horizon, respectively.

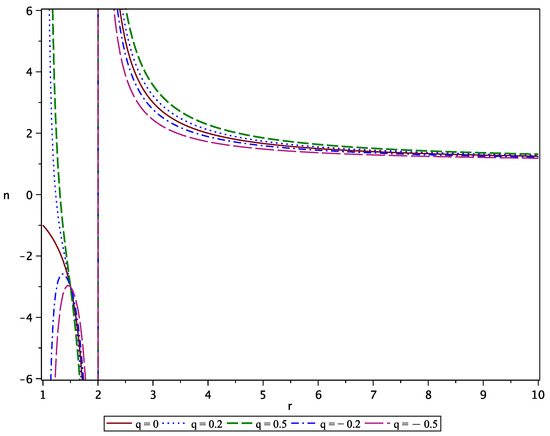
Figure 1. Refractive index as a function of r for different values of q and $m=1$. In the interval $r\in (1,2)$, the refractive index can become negative, depending on the value of q.

In particular, in the weak field approximation, the refractive index can be expressed by the infinite converging series

$$n{\left(r\right)}_{weak}\approx 1+\frac{2m}{r}+q\frac{m}{r}+\cdots$$

(15)

In the case of vanishing quadrupole parameter, the above expression yields the refractive index derived by different authors for the weak field limit of the Schwarzschild metric [13,31,32].

In Figure 2, we show the values of the quadrupole parameter q that are consistent with a positive value of the refractive index. We see that for $r>2m$, all the positive and negative values of q are allowed (green sector). For $r<m$, all the values of q are forbidden (gray sector) because it corresponds to the region of spacetime, which is located inside the curvature singularity. In the region $m<r<2m$, the condition $n>0$ implies that $q>0$, and for a given value of q, the allowed values of the radial coordinate are contained in the interval $r\in (1,1-q/2+\sqrt{q\left(2+q\right)}/2]$.

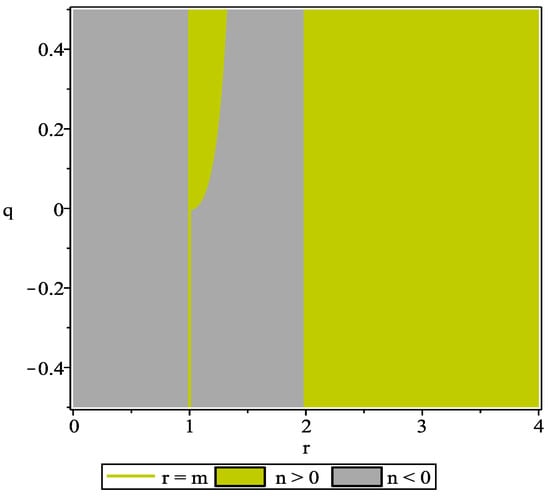
Figure 2. Regions with positive values for the refractive index. Here, $m=1.$

2.2. Deflection Angle

Now, we consider the light approaching from asymptotic infinity $(r=-\infty$) toward a static gravitational source with a quadrupole, which is placed at the origin and characterized by two parameters: m and q. The deflection angle in terms of refractive index is given as [33,34,35]

$$\Delta \psi =2\underset{R}{\overset{\infty }{\int }}\frac{dr}{r\sqrt{{\left(\frac{n\left(r\right)·r}{n\left(b\right)·b}\right)}^2-1}}-\pi$$

(16)

and has already been discussed in [31]. Here, b is the impact parameter, and R is the closest distance.

As mentioned in Section 2, we consider the contribution of the quadrupole parameter q only up to the first order. Therefore, the corresponding linearized expression for the deflection angle can be represented by

$$\Delta \psi =\Delta {\psi }_0+q\Delta {\psi }_1$$

(17)

where $\Delta {\psi }_0$ is the deflection angle in the static spherical symmetric case (i.e., the bending angle in the Schwarzschild geometry). The second term is the contribution of the quadrupole parameter. Although the results in Equations (15) and (17) have been derived only for the particular solution in Equation (1), they are also valid for all known static and axisymmetric vacuum solutions with quadrupoles. In fact, in [29], it was shown that all such solutions are equivalent up to the second order in the quadrupole parameter q. Since the results in Equations (15) and (17) are linear in q, they are valid for the entire class of known static and axisymmetric vacuum solutions. In [31], the deflection angle $\Delta {\psi }_0$ was calculated in a more rigorous manner. Nevertheless, it is useful to find the weak field limit since it allows us to perform the computations directly and verify our results with those of other solutions. The conditions of the weak field limit are $1/a=1m/R<<1$. The final expression for $\Delta \psi$ for a ray of light grazing the static gravitational mass with the closest distance of approach b can be expressed as follows:

$$\Delta \psi =\underset{b}{\overset{\infty }{\int }}\left[F\left(r\right)+q{F}_1\left(r\right)\right]dr,$$

(18)

where

$$F\left(r\right)=\frac{2\left[\left(b+2m\right)r+b^2\right]}{\sqrt{r^2-b^2}\left(r+b\right)r},$$

(19)

and

$$F_1\left(r\right)=\frac{2m}{\sqrt{r^2-b^2}\left(r+b\right)}.$$

(20)

The integration of the exact form of Equation (19) involves some complicated algebraic expressions containing elliptical functions and was evaluated earlier by Sen in [31]. However, in the weak field limit, the bending angle reduces to

$$\Delta \psi =\frac{4m}{R}\left(1+\frac{q}{2}\right),$$

(21)

where R is the radius of the object. A positive quadrupole leads to an increase in the deflection angle allowed, whereas a negative quadrupole generates the opposite effect.

3. Refraction in a Slowly Rotating Spacetime

In this section, we investigate a spacetime in which the quadrupole is generated by the rotation of the gravitational source. As a result of the rotation, the spacetime becomes stationary, and we assume axial symmetry. In this case, and for most practical purposes, the linearized Kerr metric satisfactorily describes the gravitational field around a slowly rotating mass distribution. In the equatorial plane $\theta =\pi /2$, the linearized Kerr metric can be obtained up to the first power in $\frac{a}{r}$ as follows [36]:

$$d{s}^2=\left(1-\frac{2m}{r}\right)d{t}^2-\frac{1}{1-\frac{2m}{r}}d{r}^2-r^{2}d{\theta }^2-r^{2}d{\phi }^2+\frac{4am}{r}d\phi dt,$$

(22)

where a is the rotation parameter, defined as the specific angular momentum. Notice that this metric is invariant with respect to the interchange of $a\to -a$ and $\phi \to -\phi$, which corresponds physically to a change in the direction of rotation. From the point of view of the oblate deformation of the body induced by the rotation, the direction is not important because the quadrupole is proportional to $a^2$. Nevertheless, gravitational effects exist that linearly depend on a. Indeed, the approximate solution in Equation (22) generates the frame-dragging effect as a result of the slow rotation of the source. Notice that the metric in Equation (22) is axially symmetric due to the presence of the non-diagonal term $g_{t\phi }$, which cannot be eliminated by means of a coordinate transformation. A more technical approach consists of calculating the Killing vectors of the metric in Equation (22). This would lead to the conclusion that the Killing vectors of Equation (22) do not coincide with those of the spherically symmetric Schwarzschild metric.

In the following sections, we will investigate the first-order contribution of the rotational parameter a to the deflection angle. Strictly speaking, we cannot say that this contribution is due to the presence of a rotational quadrupole because, as mentioned above, it is proportional to $a^2$. Nevertheless, since in realistic situations the parameter a is small, it is possible to study first-order contributions and denote them as “quadrupole contributions due to rotation”. We will use this convention because it also allows us to compare our results with the first-order contribution of the parameter q.

3.1. Refractive Index

To derive the expression for the refractive index, as before, we follow the procedure proposed by Sen in [37]. Thus, we first express the above line element in an isotropic form with the new spatial coordinate

$$\rho =\frac{1}{2}\left[(r-m)+r^{\frac{1}{2}}{(r-2m)}^{\frac{1}{2}}\right],$$

(23)

In other words, we have

$$r=\rho \left(1+\frac{m^2}{4{\rho }^2}\right),$$

(24)

such that

$$\frac{dr}{d\rho }=1-\frac{m^2}{4{\rho }^2}.$$

(25)

Hence, the isotropic form of the linearized Kerr metric is

$$\begin{array}{c}\hfill d{s}^2=\frac{{(1-\frac{m}{2\rho })}^2+\frac{4am}{\rho }\frac{d\phi }{dt}}{{(1+\frac{m}{2\rho })}^2}d{t}^2-{\left(1+\frac{m}{2\rho }\right)}^4[d{\rho }^2+{\rho }^2(d{\phi }^2+d{\theta }^2)].\end{array}$$

(26)

Therefore, from Equation (13), the velocity of light in the present case can be expressed as

$$\begin{array}{c}\hfill v(\rho ,\theta )=\frac{\sqrt{{(1-\frac{m}{2\rho })}^2+\frac{4am}{\rho }\frac{d\phi }{dt}}}{{(1+\frac{m}{2\rho })}^3}.\end{array}$$

(27)

According to Equations (10), (13), and (22), the refractive index in the linearized Kerr spacetime is

$$\begin{array}{c}\hfill n\left(r\right)=\frac{r}{r-2m}\left[1-\frac{2am}{r-2m}\frac{d\phi }{dt}\right].\end{array}$$

(28)

We see that the contribution to the Schwarzschild term depends on the rotation parameter a and the frame-dragging parameter $d\phi /dt$. On the other hand, following a standard procedure based on the analysis of null geodesics [30], the frame-dragging parameter for a slowly rotating mass can be expressed as [13]

$$\frac{d\phi }{dt}=b\frac{r-2m}{r^3-2abm},$$

(29)

where b is the impact parameter. Then, up to the first order in a, the refractive index in Equation (28) becomes

$$\begin{array}{c}\hfill n\left(r\right)=\frac{r}{r-2m}\left[1-\frac{2abm}{r^3}\right].\end{array}$$

(30)

As expected, in the static case $a=0$, this expression reduces to the refractive index for the Schwarzschild spacetime. In Figure 3, we illustrate how the refractive index behaves as a function of the angular momentum. We see that the net value of the index diminishes as the parameter a increases.

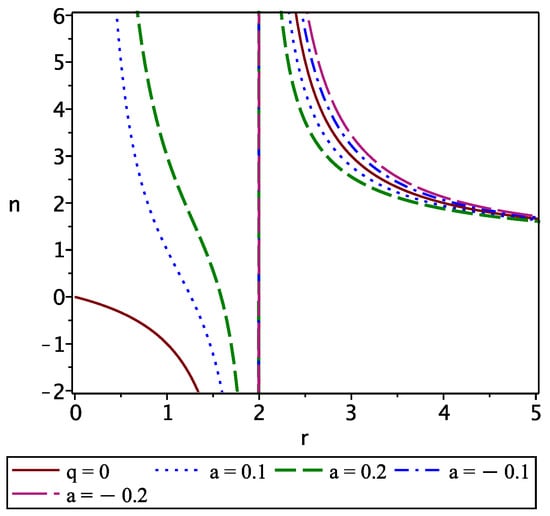
Figure 3. The refractive index as a function of the radial distance for different values of the specific angular momentum a. Here, we set $m=1$ and $b=10$.

Furthermore, in the weak field limiting case, the Kerr refractive index can be expressed as

$$\begin{array}{c}\hfill n{\left(r\right)}_{weak}\approx 1+\frac{2m}{r}-\frac{2abm}{r^3}.\end{array}$$

(31)

3.2. Deflection Angle

The value of the deflection angle can be calculated by means of Equation (16), and the corresponding linearized expression can be obtained by using a similar procedure as in Equation (17). Then, we have

$$\Delta \psi =\Delta {\psi }_0+a\Delta {\psi }_1,$$

(32)

with

$$\Delta \psi =\underset{b}{\overset{\infty }{\int }}\left[F\left(r\right)+a{F}_1\left(r\right)\right]dr,$$

(33)

where the function $F\left(r\right)$ is given in Equation (19) and $F_2\left(r\right)$ is

$$F_1\left(r\right)=-\frac{4m\left(b^2+br+r^2\right)}{b{r}^2\left(b+r\right)\sqrt{r^2-b^2}}.$$

(34)

In the limiting case $a=0$, we obtain the deflection angle of the Schwarzschild spacetime [31].

Consider the weak field limit (i.e., for a slowly rotating body, we can assume that $a^2/r^2\ll 1$ and $1/a=2m/R\ll 1$, where R is the radius of the body). Then, in evaluating the above integral (Equation (33)), we find the deflection angle up to the first order in the rotation parameter a. The integral of the second term is the contribution coming from the rotation of the spacetime. Thus, the term $\Delta {\psi }_1$ is due to the induced frame-dragging effect as a result of the rotating term in the metric in Equation (22). Then, the deflection angle becomes

$$\Delta \psi =\frac{4m}{R}\left(1+\frac{a}{R}\right).$$

(35)

Equivalent results were obtained by using other methods in [12,13,37,38,39].

4. Analysis of the Results

In the previous sections, we have shown that the refractive index depends explicitly on the value of the quadrupole. In the case of a deformed gravitational source, the quadrupole parameter q contributes to the refraction as expressed in Equation (14). Moreover, if the quadrupole is due to the rotation of the gravitational source, the refractive index can be expressed as in Equation (30) and depends explicitly on the rotation parameter a. A comparison of the refractive indices in Equations (14) and (30) leads to

$$q=-\frac{4ab{(r-m)}^2}{(2r-3m)r^3}.$$

(36)

We see that for each value of a, it is always possible to find the corresponding value of q. This behavior is illustrated in Figure 4.

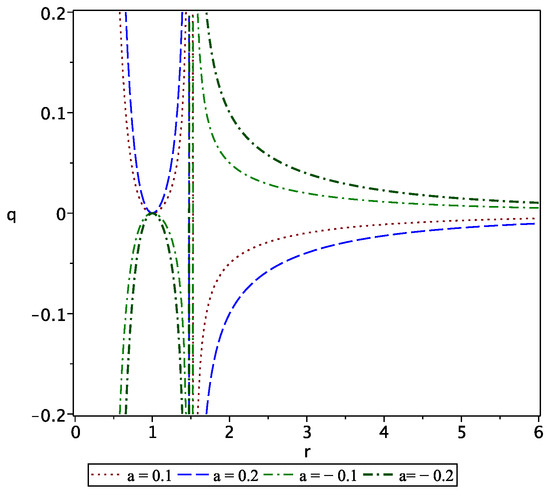
Figure 4. Equivalence between the static quadrupole q and the stationary quadrupole a in terms of the radial distance r.

This means that any measurement of the refractive index performed, for instance, at a distance $r_1$ from the center of a gravitational source can be explained in two different ways. First, the refraction is due to the rotation of the source with specific angular momentum a or, according to Equation (36), a deformation of the source with a quadrupole $q_1=q\left(r_1\right)$. This can be considered a “mimicking effect”, in which the effective refraction in the field of a rotating body can be explained equivalently by the presence of a static deformed body.

As a possible application of the above results, we will now show that the effective gravitational refraction can be used to determine the parameters of the gravitational source. Consider a light ray that propagates in a vacuum and is effectively refracted at a distance $r_1$ from the center of a rotating compact object. Let the incidence and refraction angles of the ray be ${\theta }_{i_1}$ and ${\theta }_{r_1}$, respectively (see Figure 5).

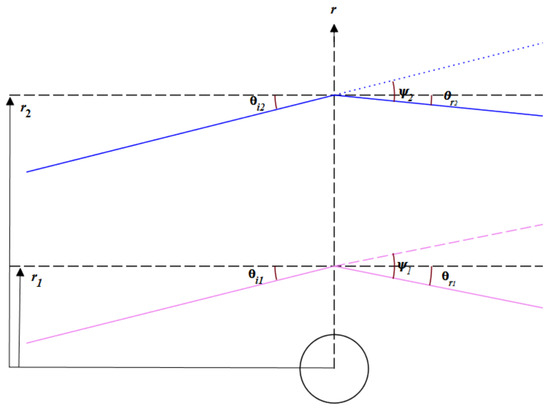
Figure 5. Parameters of two light rays that are deflected in a gravitational field.

Then, according to Snell’s law, from the values of the incidence and refraction angles, we can derive the value of the refractive index as follows:

$$n_1=\frac{sin{\theta }_{i_1}}{sin{\theta }_{r_1}}.$$

(37)

On the other hand, according to Equation (17), the effective refractive index $n_1$ for the rotating body can be expressed as

$$n_1=\frac{r_1}{r_1-2m}\left(1-\frac{2am}{r_1^2}\right),$$

(38)

where we used the relationship $b_1=r_1$.

Consider a second ray with incidence and refraction angles ${\theta }_{i_1}$ and ${\theta }_{r_2}$, respectively. Again, the effective refractive index can be calculated by using Snell’s law ($n_2=sin{\theta }_{i_2}/sin{\theta }_{r_2}$) and satisfies the relationship

$$n_2=\frac{r_2}{r_2-2m}\left(1-\frac{2am}{r_2^2}\right).$$

(39)

Finally, by solving Equations (38) and (39), we obtain

$$m=\frac{1}{2}\frac{r_1^2(n_1-1)-r_2^2(n_2-1)}{n_1{r}_1-n_2{r}_2},a=\frac{r_1{r}_2[n_2{r}_1(n_1-1)-n_1{r}_2(n_2-1)]}{r_1^2(n_1-1)-r_2^2(n_2-1)}.$$

(40)

Thus, we have shown that by measuring the refractive indices of two light rays and different distances from the center of a body, it is possible to determine its physical parameters, namely the mass and angular momentum. Of course, as a result of the mimicking effect mentioned above, it is also possible to find the respective value of the quadrupole parameter q, which would correspond to a static deformed body.

5. Conclusions

In this work, we used the material medium approach to study the bending of light in the gravitational field of a mass distribution with a quadrupole. We considered two different physical configurations that led to the appearance of a quadrupole, namely a static deformed body with a quadrupole parameter q and a stationary rotating body with specific angular momentum a. The bending of light was treated as a refraction effect, which could be analyzed with certain advantages within the framework of the material medium approach.

We calculated the refractive index and the deflection angle in two different spacetimes. The first one was described by an approximate static solution of Einstein’s equations with the quadrupole parameter and the second one by the linearized limiting case of the Kerr geometry. In both cases, we derived explicit expressions for the refractive index and deflection angle.

We showed that any measurement of the refractive index can be explained either as occurring in a stationary rotating field or in the static field of a deformed mass distribution. This “mimicking” effect allowed us to calculate explicitly the value of the quadrupole parameter in terms of the parameters of the rotating body and the distance at which the refractive index was measured.

In addition, we investigated the deflection of two light rays in the gravitational field of a rotating compact body. It was proven that by analyzing the properties of the light rays from the point of view of an effective refraction phenomenon, it is possible to determine the mass and angular momentum. This opens the possibility of performing an indirect measurement of the parameters of a relativistic compact object by analyzing the refractive indices and the trajectories of light rays that propagate in its gravitational field.