Regular and Intra-Regular Ternary Semirings in Terms of m-Polar Fuzzy Ideals
Abstract
1. Introduction
1.1. Innovative Contribution
1.2. Related Works
1.3. Organization of the Paper
2. Preliminaries
3. Characterization of Ternary Semirings by -Polar Fuzzy Sets
- (1)
- Then for all, the setthat isfor all, is called a t-cut or a level set.
- (2)
- The support ofis defined to be the set that isfor all.
3.1. m-Polar Fuzzy Ternary Subsemirings and Ideals in Ternary Semirings
- (1)
- that is;
- (2)
- that isfor all
- (1)
- (2)
- (resp.) for all.
- (1)
- (2)
- (3)
- .
- (1)
- is a ternary subsemiring ofif and only ifis an-PFTS of ;
- (2)
- is a LIresp. MI, RIofif and only iis an-PFLI resp.-PFMI, -PFRIof.
- (1)
- is an-PFTS of if and only ifand
- (2)
- is an-PFLI of if and only ifand
- (3)
- is an-PFRI of if and only ifand
- (4)
- is an-PFMI of if and only ifand
- (1)
- Let, andbe three-PF ternary subsemirings of. Thenis also an-PF ternary subsemiring of;
- (2)
- Let, andand be three-PFRI resp.-PFMI, -PFLIof. Thenis also an-PFLI resp.-PFMI, -PFRIof
3.2. m-Polar Fuzzy Generalized Bi-Ideals in Ternary Semirings
3.3. m-Polar Fuzzy Bi-Ideals in Ternary Semirings
- (1)
- (2)
- (3)
3.4. m-Polar Fuzzy Quasi-Ideals in Ternary Semirings
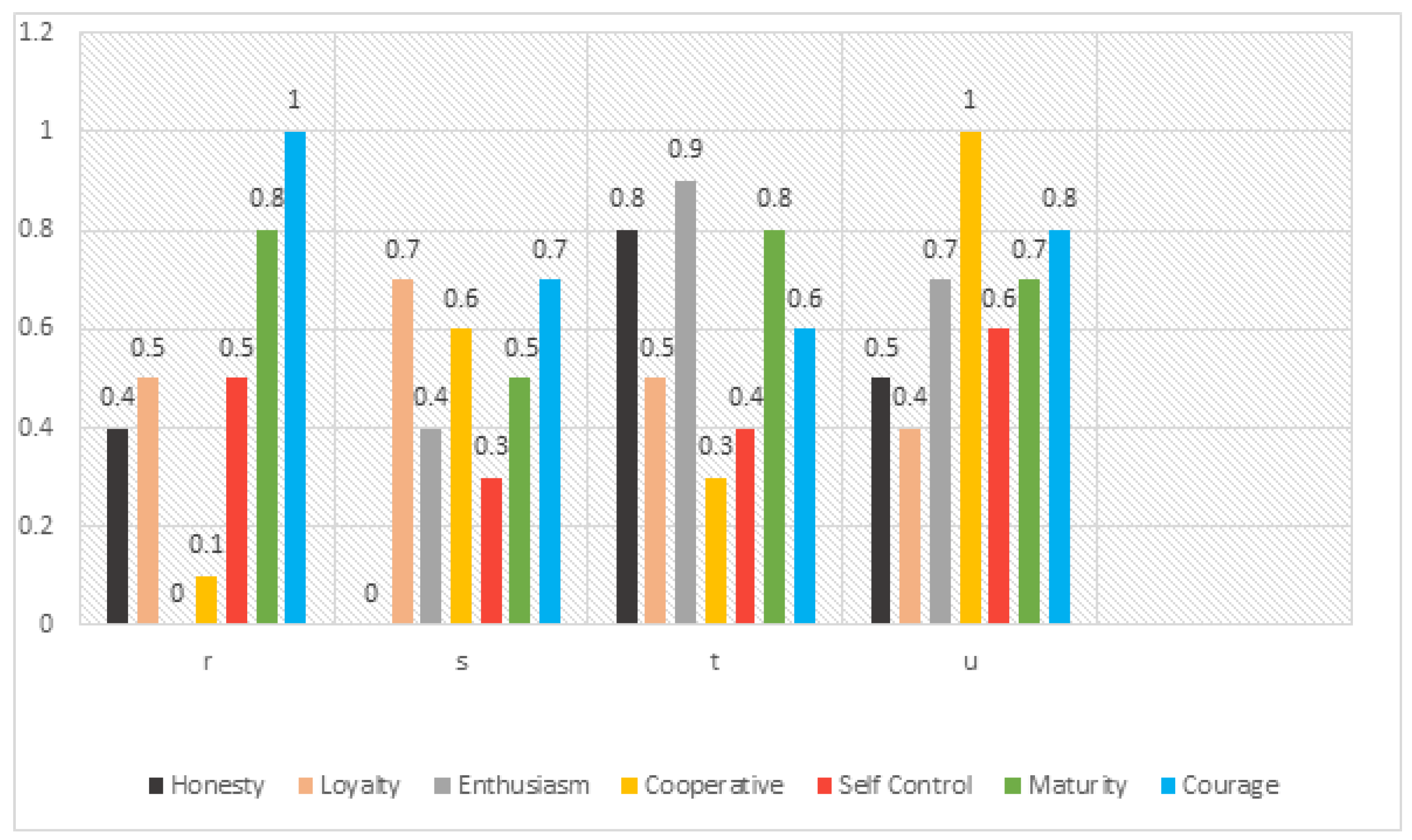
3.5. Applications of Proposed Work
4. Characterization of Regular, and Intra-Regular Ternary Semirings by -Polar Fuzzy Ideals
- (1)
- is regular;
- (2)
- for each-PFRI , -PFMI and-PFLI of
- (1)
- is regular;
- (2)
- for every-PFBI of;
- (3)
- for every-PFQI of.
5. Comparative Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy groups. J. Math. Appl. 1971, 35, 512–517. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. In Proceedings of the NAFIPS/IFIS/NASA’94, First International Joint Conference of the North American Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Bashir, S.; Fatima, M.; Shabir, M. Regular ordered ternary semigroups in terms of bipolar fuzzy ideals. Mathematics 2019, 7, 233. [Google Scholar] [CrossRef]
- Bashir, S.; Mazhar, R.; Abbas, H.; Shabir, M. Regular ternary semirings in terms of bipolar fuzzy ideals. Comput. Appl. Math. 2020, 39, 1–18. [Google Scholar] [CrossRef]
- Shabir, M.; Liaquat, S.; Bashir, S. Regular and intra-regular semirings in terms of bipolar fuzzy ideals. Comput. Appl. Math. 2019, 38, 1–19. [Google Scholar] [CrossRef]
- Saqib, M.; Akram, M.; Bashir, S. Certain efficient iterative methods for bipolar fuzzy system of linear equations. J. Intelligent Fuzzy Syst. 2020, 39, 3971–3985. [Google Scholar] [CrossRef]
- Saqib, M.; Akram, M.; Bashir, S.; Allahviranloo, T. Numerical solution of bipolar fuzzy initial value problem. J. Intell. Fuzzy Syst. 2021, 40, 1309–1341. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Ma, S.; Wang, X. m-polar fuzzy sets: An extension of bipolar fuzzy sets. Sci. World J. 2014, 2014, 416530. [Google Scholar] [CrossRef]
- Ho, D.T.; Garibaldi, J.M. Context modelling in fuzzy systems. In Proceedings of the IEEE International Conference on Fuzzy Systems IEEE, Brisbane, Australia, 10 June 2012; pp. 1–7. [Google Scholar]
- Lehmer, D.H. A ternary analogue of abelian groups. Am. J. Math. 1932, 54, 329–338. [Google Scholar] [CrossRef]
- Dutta, T.K.; Kar, S. On regular ternary semirings, Advances in algebra. In Proceedings of the ICM Satellite Conference in Algebra and Related Topics; World Scientific: Singapore, 2003; pp. 343–355. [Google Scholar]
- Dutta, T.K.; Kar, S. A note on regular ternary semirings. Kyungpook Math. J. 2006, 46, 357–365. [Google Scholar]
- Kavikumar, J.; Khamis, A.B. Fuzzy Ideals and Fuzzy Quasi-ideals in Ternary Semirings. IAENG Int. J. Appl. Math. 2007, 37, 2. [Google Scholar]
- Kavikumar, J.; Khamis, A.B.; Jun, Y.B. Fuzzy bi-ideals in ternary semirings. Int. J. Math. Stat. Sci. 2009, 1, 54–58. [Google Scholar]
- Akram, M.; Farooq, A.; Shum, K.P. On m-polar fuzzy lie subalgebras. Ital. J. Pure Appl. Math. 2016, 36, 445–454. [Google Scholar]
- Akram, M.; Farooq, A. m-polar fuzzy Lie ideals of Lie algebras. Quasigroups Relat. Syst. 2016, 24, 141–150. [Google Scholar]
- Mandal, S.; Sahoo, S.; Ghorai, G.; Pal, M. Genus value of m-polar fuzzy graphs. J. Intell. Fuzzy Syst. 2018, 34, 1947–1957. [Google Scholar]
- Akram, M.; Adeel, A. m-Polar fuzzy graphs and m-polar fuzzy line graphs. J. Discret. Math. Sci. Cryptogr. 2017, 20, 1597–1617. [Google Scholar] [CrossRef]
- Al-Masarwah, A. m-polar fuzzy ideals of BCK/BCI-algebras. J. King Saud-Univ.-Sci. 2019, 31, 1220–1226. [Google Scholar] [CrossRef]
- Al-Masarwah, A.; Ahmad, A.G. m-polar (α, β)-fuzzy ideals in BCK/BCI-algebras. Symmetry 2019, 11, 44. [Google Scholar] [CrossRef]
- Al-Masarwah, A.N.A.S.; Ahmad, A.G. A new form of generalized m-PF ideals in BCK/BCI-algebras. Ann. Commun. Math. 2019, 2, 11–16. [Google Scholar]
- Al-Masarwah, A. On (complete) normality of m-pF subalgebras in BCK/BCI-algebras. AIMS Math. 2019, 4, 740–750. [Google Scholar] [CrossRef]
- Shabir, M.; Aslam, A.; Pervaiz, F. m-polar fuzzy ideals in terms of LA-semigroups (Submitted).
- Bashir, S.; Shahzadi, S.; Al-Kenani, A.N.; Shabir, M. Regular and Intra-Regular Semigroups in Terms of m-Polar Fuzzy Environment. Mathematics 2021, 9, 2031. [Google Scholar] [CrossRef]
- Bashir, S.; Al-Kenani, A.N.; Arif, M.; Mazhar, R. A new method to evaluate regular ternary semigroups in multi-polar fuzzy environment. AIMS Math. 2022, 7, 12241–12263. [Google Scholar] [CrossRef]
- Rao, D.M.; Rao, G.S. Special elements of a ternary semiring. Int. J. Eng. Res. Appl. 2014, 4, 123–130. [Google Scholar]
- Rao, M.D.; Srinivasa Rao, G. A Study on Ternary Semirings. Int. J. Math. Arch. 2014, 12, 24–30. [Google Scholar]
| Acronyms | Representation |
|---|---|
| m-PF | m-Polar fuzzy |
| BFS | Bipolar fuzzy set |
| RI (resp, LI, MI) | Right ideal (resp. Left ideal, Lateral ideal) |
| GBI (resp. BI, QI) | Generalized bi-ideal (resp. Bi-ideal, Quasi ideal) |
| m-PFTS | m-Polar fuzzy ternary subsemiring |
| m-PFI | m-Polar fuzzy ideal |
| m-PFLI | m-Polar fuzzy left ideal |
| m-PFRI | m-Polar fuzzy right ideal |
| m-PFMI | m-Polar fuzzy lateral ideal |
| m-PFGBI | m-Polar fuzzy generalized bi-ideal |
| m-PFBI | m-Polar fuzzy bi-ideal |
| m-PFQI | m-Polar fuzzy quasi-ideal |
| Honesty | Loyalty | Enthusiasm | Cooperative | Self-Control | Maturity | Courage | |
| r | 0.4 | 0.5 | 0 | 0.1 | 0.5 | 0.8 | 1 |
| s | 0 | 0.7 | 0.4 | 0.6 | 0.3 | 0.5 | 0.7 |
| t | 0.8 | 0.5 | 0.9 | 0.3 | 0.4 | 0.8 | 0.6 |
| u | 0.5 | 0.4 | 0.7 | 1 | 0.6 | 0.7 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, S.; Ali Al-Shamiri, M.M.; Khalid, S.; Mazhar, R. Regular and Intra-Regular Ternary Semirings in Terms of m-Polar Fuzzy Ideals. Symmetry 2023, 15, 591. https://doi.org/10.3390/sym15030591
Bashir S, Ali Al-Shamiri MM, Khalid S, Mazhar R. Regular and Intra-Regular Ternary Semirings in Terms of m-Polar Fuzzy Ideals. Symmetry. 2023; 15(3):591. https://doi.org/10.3390/sym15030591
Chicago/Turabian StyleBashir, Shahida, Mohammed M. Ali Al-Shamiri, Shahzeen Khalid, and Rabia Mazhar. 2023. "Regular and Intra-Regular Ternary Semirings in Terms of m-Polar Fuzzy Ideals" Symmetry 15, no. 3: 591. https://doi.org/10.3390/sym15030591
APA StyleBashir, S., Ali Al-Shamiri, M. M., Khalid, S., & Mazhar, R. (2023). Regular and Intra-Regular Ternary Semirings in Terms of m-Polar Fuzzy Ideals. Symmetry, 15(3), 591. https://doi.org/10.3390/sym15030591







