Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations
Abstract
1. Introduction
2. Preliminaries
- 1.
- 2.
RKHS Method
- ; is given by (2).
- The set is dense in
- means the adjoint of
- 1.
- Let us estimate the following:where is a constant.
- 2.
- Doing the same thing to the derivative, we getdue to the uniform boundedness of we havewhere is a positive constant.
3. Convergence Analysis
- 1.
- converges to
- 2.
- 1.
- We havethe orthogonality of impliesand soSince is bounded, we deduce is convergent.where is a constant.ConsequentlyObserve that So forFurthermore,Consequently, we have asOn account of the completeness of we reach: as
- 2.
- Taking the limit in (18), we obtainUtilising the operator , we getit follows thatMultiplying (23) by and taking to findWe conclude,there exists such thatthat resulting from the density of .Now, we know that,Since is continuous and by letting we can easily deduce the result.
4. Numerical Experiments
- Step 1: Fix
- Step 2: Set
- Step 3: Calculate the coefficients using (11);
- Step 4: Set
- Step 5: Choose an initial guess
- Step 6: Set
- Step 7: Set
- Step 8:
- Step 9: If set Go to step 7. Else stop.
- where and n is the number of collocation points.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Diffrential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: San Diego, CA, USA, 2006. [Google Scholar]
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y.Q. A new collection of real-world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Akgül, A. A novel method for a fractional derivative with non-local and non-singular kernel. Chaos Solitons Fractals 2018, 114, 478–482. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 2004, 154, 621–640. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D.; Fokas, A.S. Solving PDEs of fractional order using the unified transform method. Appl. Math. Comput. 2018, 339, 738–749. [Google Scholar] [CrossRef]
- Cao, Q.-H.; Dai, C.-Q. Symmetric and anti-symmetric solitons of the fractional second- and third-order nonlinear Schrödinger equation. Chin. Phys. Lett. 2021, 38, 090501. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, Y.-L.; Wang, X.-T. Lie symmetry analysis of the time fractional generalized KdV equations with variable coefficients. Symmetry 2019, 11, 1281. [Google Scholar] [CrossRef]
- Cui, M.; Lin, Y. Nonlinear Numerical Analysis in the Reproducing Kernel Space; Nova Science Publishers Inc.: New York, NY, USA, 2009. [Google Scholar]
- Chen, S.-B.; Soradi-Zeid, S.; Dutta, H.; Mesrizadeh, M.; Jahanshahi, H.; Chu, Y.-M. Reproducing kernel Hilbert space method for nonlinear second order singularly perturbed boundary value problems with time-delay. Chaos Solitons Fractals 2021, 144, 110674. [Google Scholar] [CrossRef]
- Dou, H.-X.; Deng, L.-J. A proximal algorithm with convergence guarantee for a nonconvex minimization problem based on reproducing kernel Hilbert space. Symmetry 2021, 13, 2393. [Google Scholar] [CrossRef]
- Yildirim, E.N.; Akgül, A.; Inc, M. Reproducing kernel method for the solutions of non-linear partial differential equations. Arab J. Basic Appl. Sci. 2018, 28, 80–86. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Osman, M.S.; Park, C.; Lee, J.R.; Alsulam, H.; Alhodaly, M. Development of the reproducing kernel Hilbert space algorithm for numerical pointwise solution of the time-fractional nonlocal reaction-diffusion equation. Alex. Eng. J. 2022, 61, 10539–10550. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Sahihi, H. Reproducing kernel method to solve fractional delay differential equations. Appl. Math. Comput. 2021, 400, 126095. [Google Scholar] [CrossRef]
- Attia, N.; Akgül, A.; Seba, D.; Nour, A. An efficient numerical technique for a biological population model of fractional order. Chaos Solitons Fractals 2021, 141, 110349. [Google Scholar] [CrossRef]
- Li, X.; Wu, B. A new reproducing kernel collocation method for nonlocal fractional boundary value problems with non-smooth solutions. Appl. Math. Lett. 2018, 86, 194–199. [Google Scholar] [CrossRef]
- Du, H.; Chen, Z.; Yang, T. A stable least residue method in reproducing kernel space for solving a nonlinear fractional integro-differential equation with a weakly singular kernel. Appl. Numer. Math. 2020, 157, 210–222. [Google Scholar] [CrossRef]
- Du, H.; Chen, Z.; Yang, T. A meshless method in reproducing kernel space for solving variable-order time fractional advection–diffusion equations on arbitrary domain. Appl. Numer. Math. 2021, 116, 107014. [Google Scholar] [CrossRef]
- Hasan, S.; Maayah, B.; Bushnaq, S.; Momani, S. A modified reproducing kernel Hilbert space method for solving fuzzy fractional integro-differential equations. Bol. Soc. Paran. Mat. 2023, 41, 1–16. [Google Scholar] [CrossRef]
- Babolian, E.; Javadi, S.; Moradi, E. Error analysis of reproducing kernel Hilbert space method for solving functional integral equations. J. Comput. Appl. Math. 2016, 300, 300–311. [Google Scholar] [CrossRef]
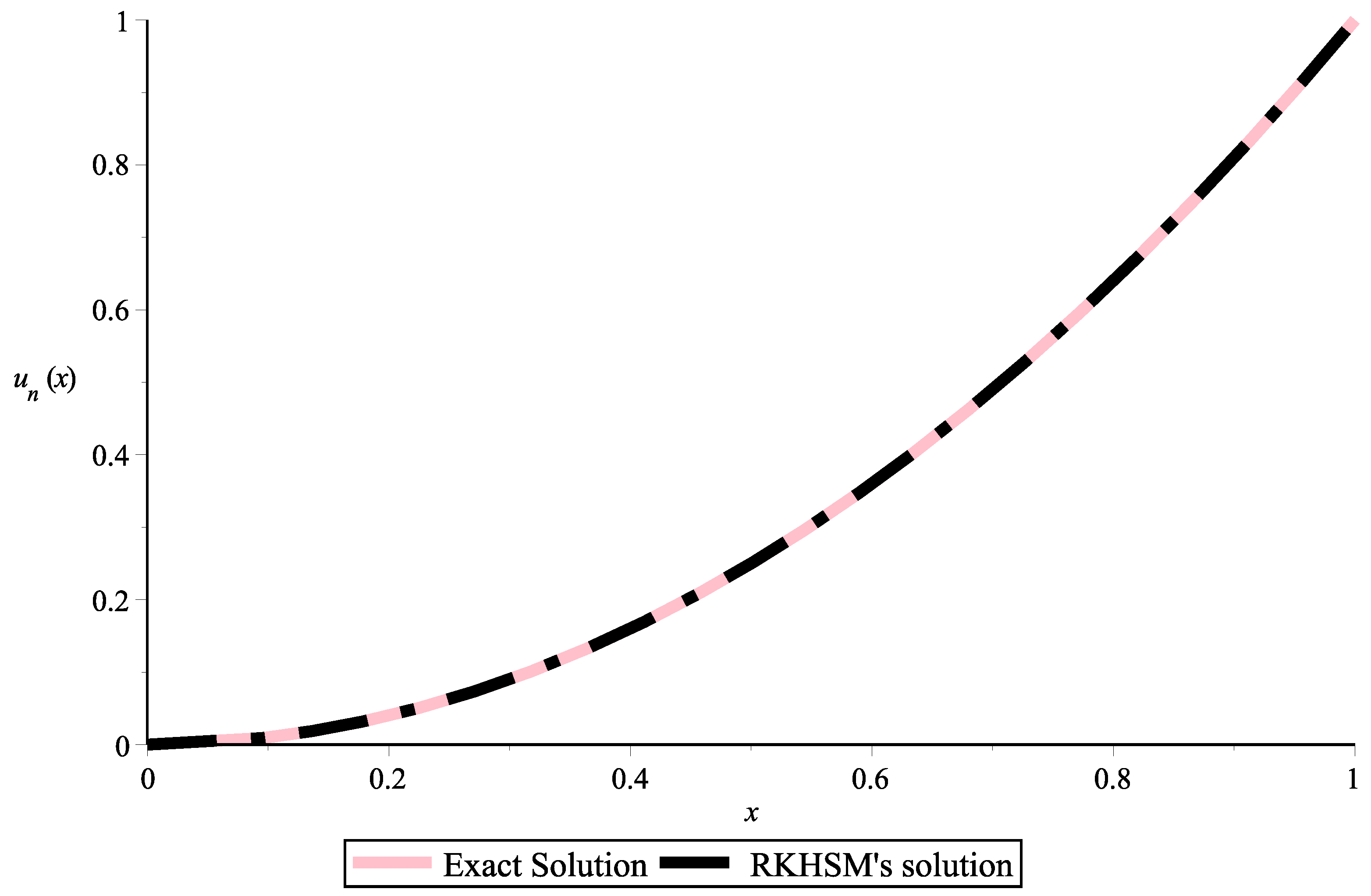


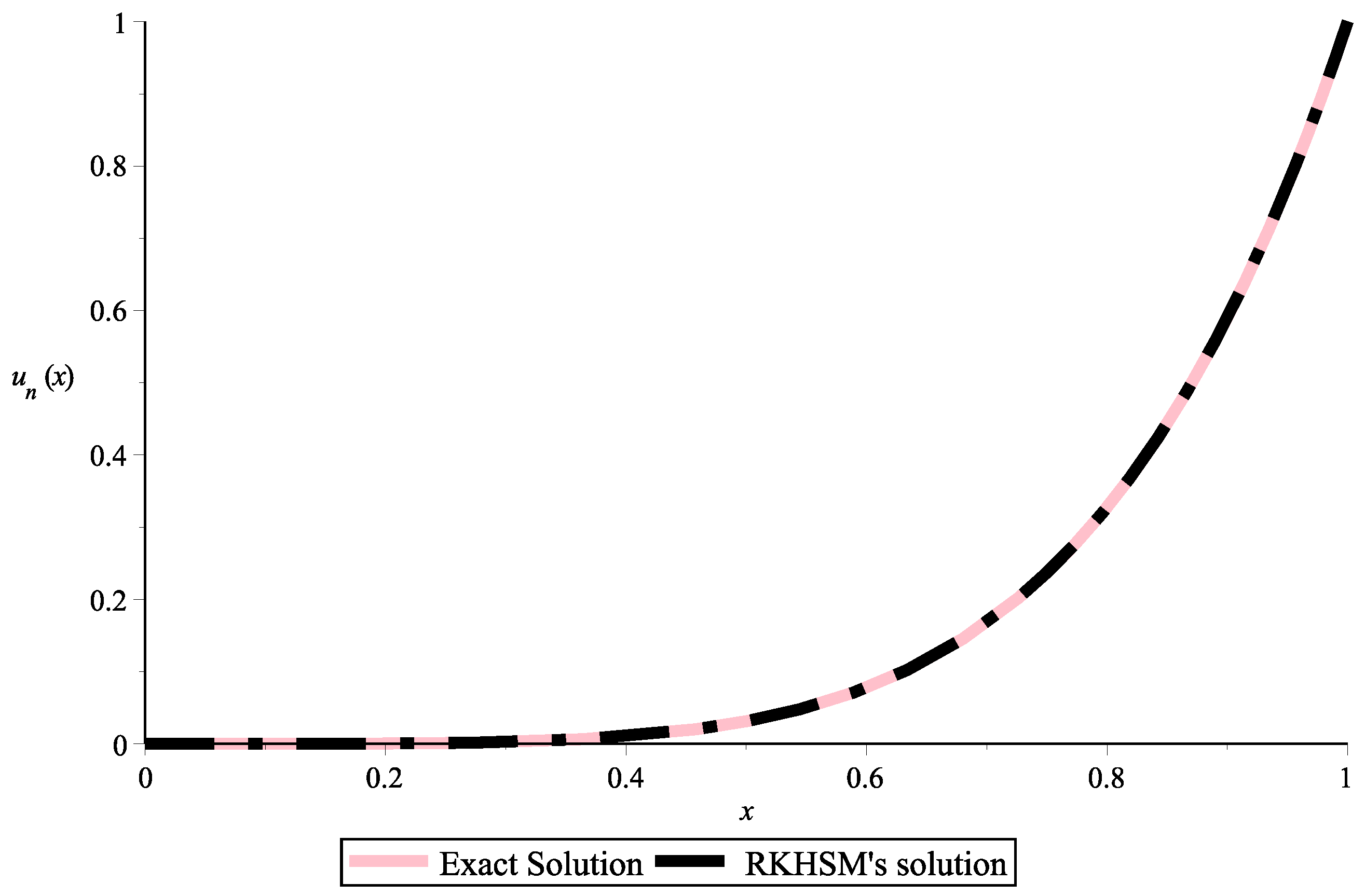
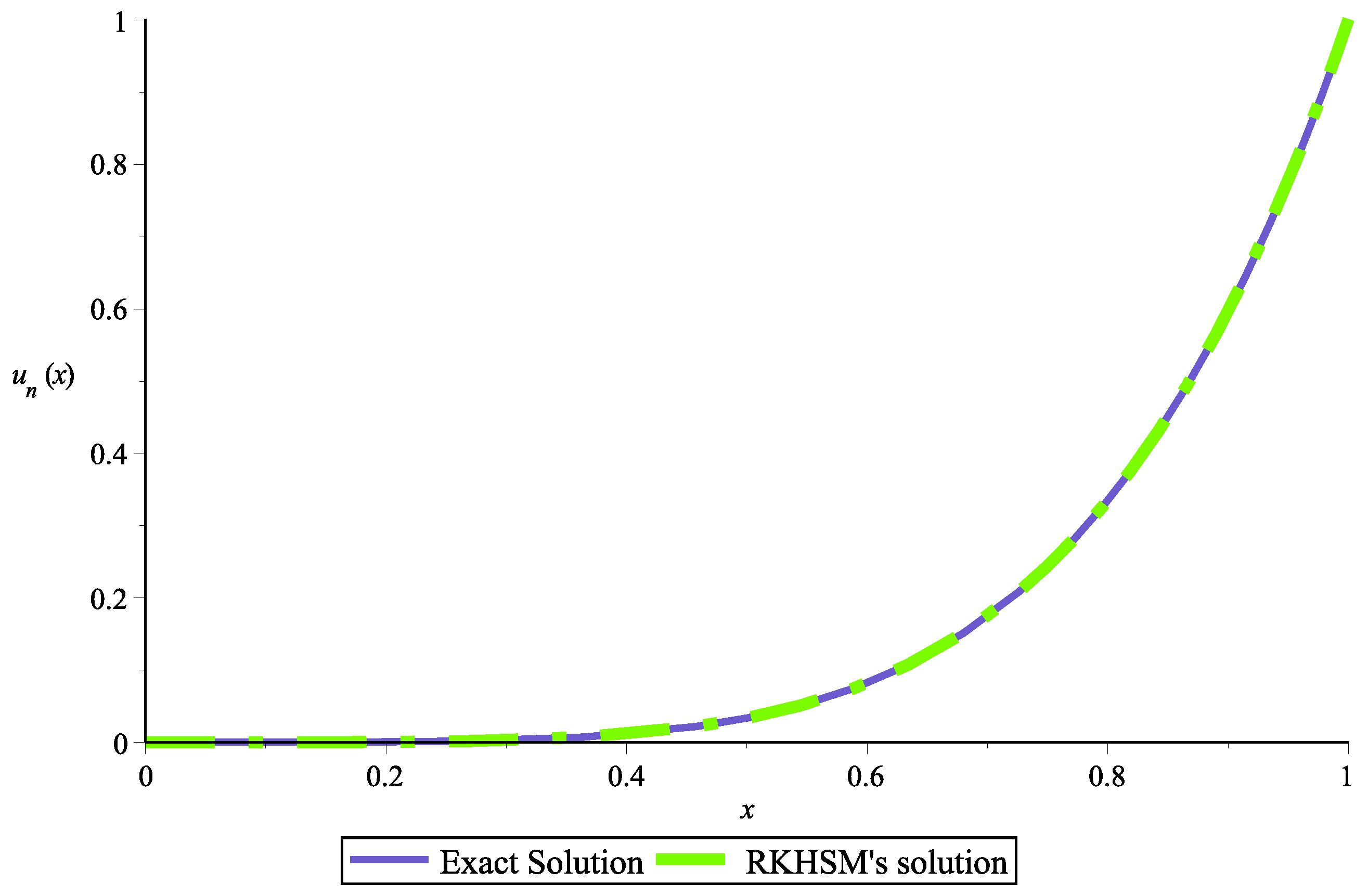
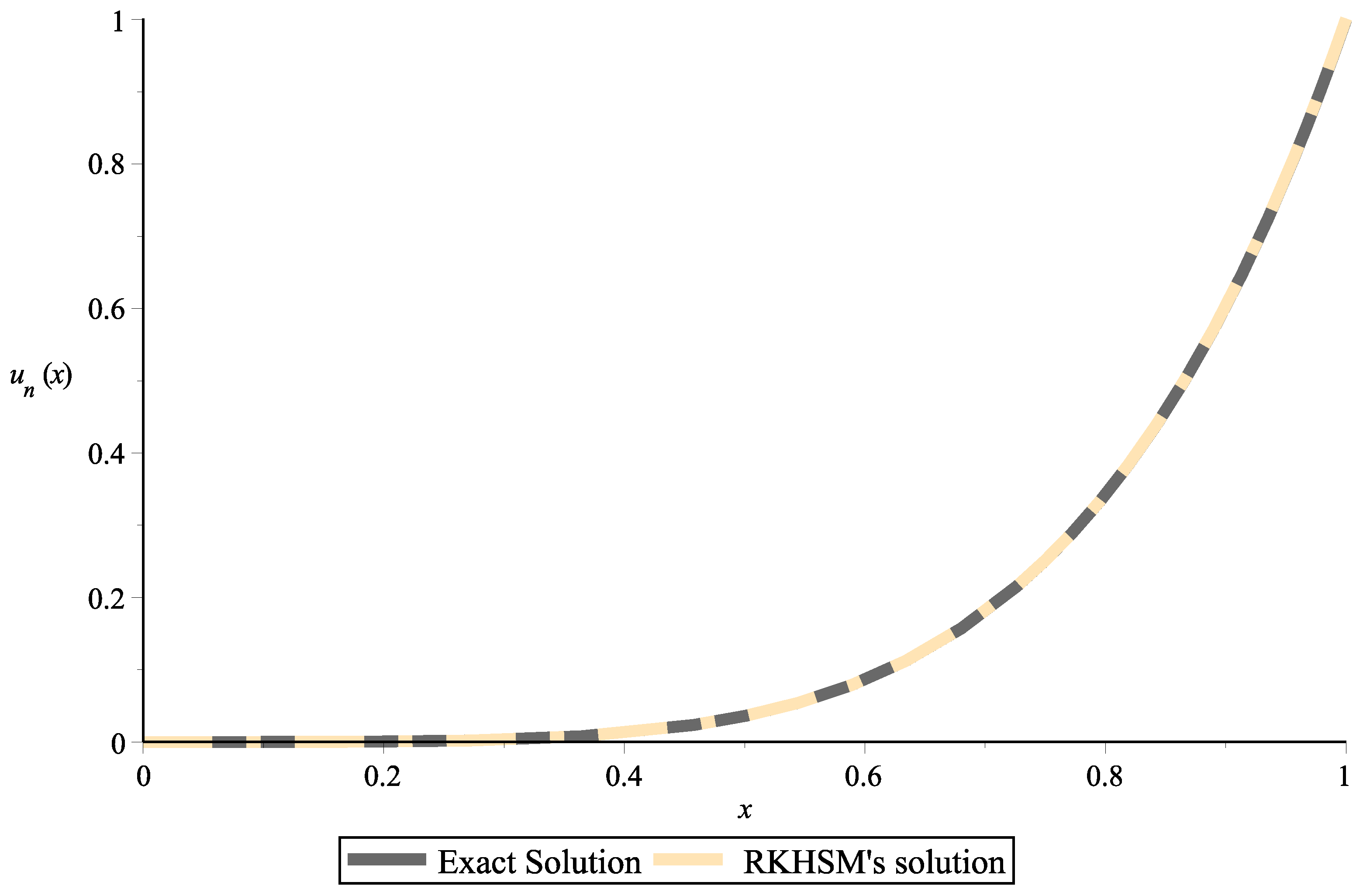
| t | Exact Solution | RKHSM | Absolute Error |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 |
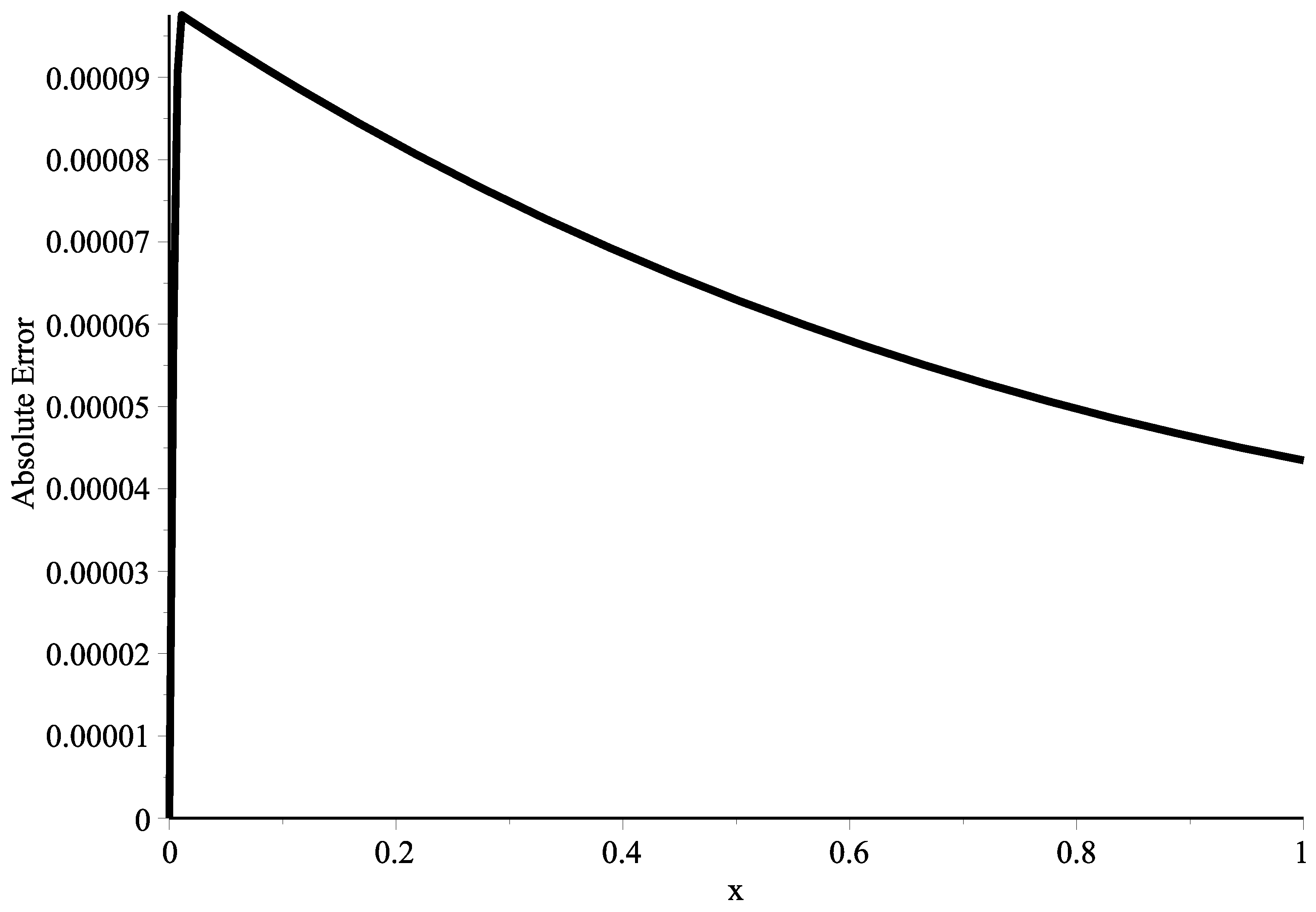
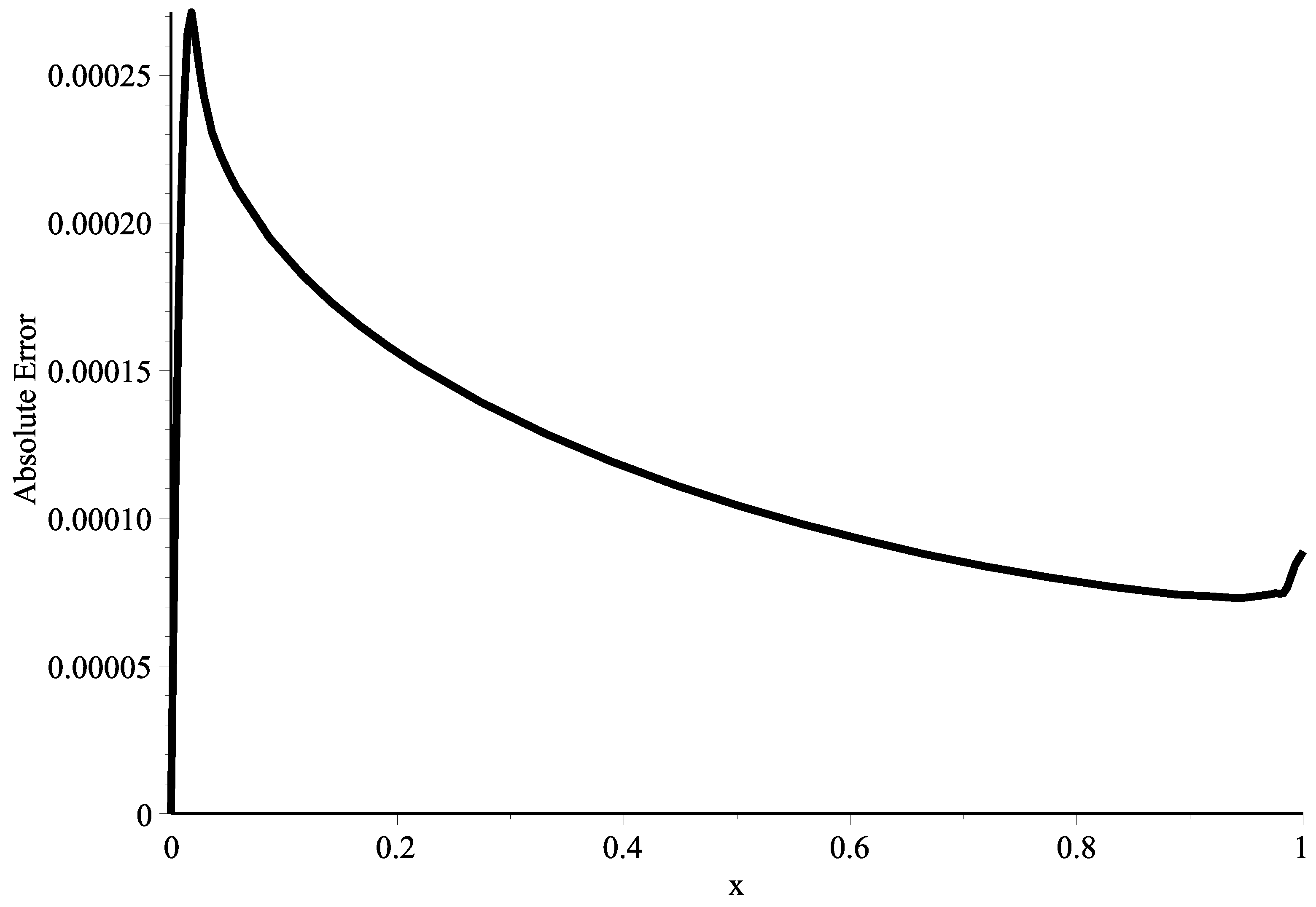
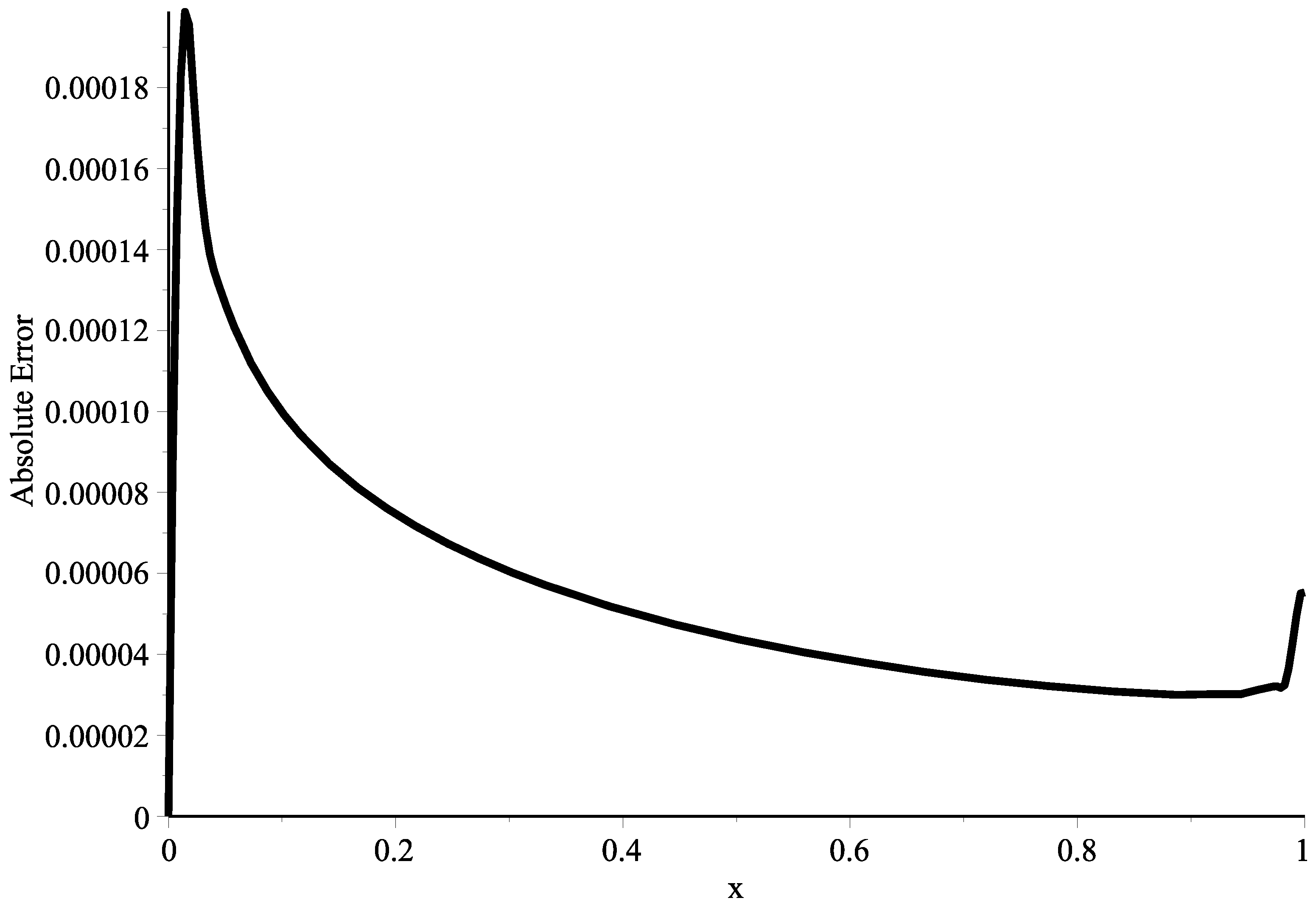
| Absolute Errors | |||
|---|---|---|---|
| t | |||
| 0 | 0 | ||
| 1 | |||
| t | Exact Solution | RKHSM | Absolute Error |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 |
| Absolute Errors | |||
|---|---|---|---|
| t | |||
| 0 | 0 | ||
| 1 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attia, N.; Akgül, A.; Alqahtani, R.T. Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations. Symmetry 2023, 15, 532. https://doi.org/10.3390/sym15020532
Attia N, Akgül A, Alqahtani RT. Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations. Symmetry. 2023; 15(2):532. https://doi.org/10.3390/sym15020532
Chicago/Turabian StyleAttia, Nourhane, Ali Akgül, and Rubayyi T. Alqahtani. 2023. "Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations" Symmetry 15, no. 2: 532. https://doi.org/10.3390/sym15020532
APA StyleAttia, N., Akgül, A., & Alqahtani, R. T. (2023). Extension of the Reproducing Kernel Hilbert Space Method’s Application Range to Include Some Important Fractional Differential Equations. Symmetry, 15(2), 532. https://doi.org/10.3390/sym15020532








