Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering
Abstract
1. Introduction
2. Mathematical Model and Methodology
3. Error Analysis
4. Numerical Examples
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd-Elhameed, W.M.; Badah, B.M.; Amin, A.K.; Alsuyuti, M.M. Spectral Solutions of Even-Order BVPs Based on New Operational Matrix of Derivatives of Generalized Jacobi Polynomials. Symmetry 2023, 15, 345. [Google Scholar] [CrossRef]
- Ryoo, C.-S.; Kang, J.-Y. Some Identities Involving Degenerate q-Hermite Polynomials Arising from Differential Equations and Distribution of Their Zeros. Symmetry 2022, 14, 706. [Google Scholar] [CrossRef]
- Karp, D.; Prilepkina, E. Beyond the Beta Integral Method: Transformation Formulas for Hypergeometric Functions via Meijer’s G Function. Symmetry 2022, 14, 1541. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Ansari, K.J. Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry 2021, 13, 2370. [Google Scholar] [CrossRef]
- Sitnik, S.M.; Yadrikhinskiy, K.V.; Fedorov, V.E. Symmetry Analysis of a Model of Option Pricing and Hedging. Symmetry 2022, 14, 1841. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. Asymptotic Behavior of Three Connected Stochastic Delay Neoclassical Growth Systems Using Spectral Technique. Mathematics 2022, 10, 3639. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. Threshold of Stochastic SIRS Epidemic Model from Infectious to Susceptible Class with Saturated Incidence Rate Using Spectral Method. Symmetry 2022, 14, 1838. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. Dynamics and simulations of stochastic COVID-19 epidemic model using Legendre spectral collocation method. AIMS Math. 2023, 8, 4220–4236. [Google Scholar] [CrossRef]
- Mujumdar, A.S. Book Review: Handbook of Industrial Drying, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Bruce, D.M.; Ginger, S.A. Mathematical modeling of grain drying in counter-flow beds: Investigation of crossover of air and grain temperatures. J. Agric. Eng. Res. 1993, 55, 143–161. [Google Scholar] [CrossRef]
- Lopez, I.I.R.; Espinosa, H.R.; Lozada, P.A.; Pozos, M.E.B.; Alvarado, M.A.G. Analytical model for variable moisture diffusivity estimation and drying simulation of shrinkable food products. J. Food Eng. 2012, 108, 427–435. [Google Scholar] [CrossRef]
- Barati, E.; Esfahani, J.A. A new solution approach for simultaneous heat and mass transfer during convective drying of mango. J. Food Eng. 2011, 102, 302–309. [Google Scholar] [CrossRef]
- Vahishosseini, S.M.; Barati, E.; Esfahani, J.A. Green’s function method (GFM) and mathematical solution for coupled equations of transport problem during convective drying. J. Food Eng. 2016, 187, 24–36. [Google Scholar] [CrossRef]
- Moore, T.J.; Jones, M.R. Solving nonlinear heat transfer problems using variation of parameters. Int. J. Therm. Sci. 2015, 93, 29–35. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T. Spectral and High-Order Methods with Applications; Mathematics Monograph Series; Science Press: Beijing, China, 2006. [Google Scholar]
- Hussain, M.; Dincer, I. Numerical simulation of two dimensional heat and moisture transfer during drying of a rectangular object. Numer. Heat Transf. Part A 2003, 43, 867–878. [Google Scholar] [CrossRef]
- Tzempelikos, D.A.; Mitrakos, D.; Vouros, A.P.; Bardakas, A.V.; Filios, A.E.; Margaris, D.P. Numerical modelling of heat and mass transfer during convective drying of cylindrical quince slices. J. Food. Eng. 2015, 156, 10–21. [Google Scholar] [CrossRef]
- Aversa, M.; Curcio, S.; Calabro, V.; Iorio, G. An analysis of the transport phenomena occurring during food drying process. J. Food Eng. 2007, 78, 922–934. [Google Scholar] [CrossRef]
- Bakalis, S.; Kyritsi, A.; Sarathanos, V.K.; Sanniotis, V.Y. Modeling of rice hydration using finite elements. J. Food Eng. 2009, 94, 321–325. [Google Scholar] [CrossRef]
- Nilnont, W.; Thepa, S.; Janjai, S.; Kasayapanand, N.; Thamrongmas, C.; Bala, B. Finite elements simulation for coffee (Coffea arabica) drying. Food Bioprod. Process. 2011, 90, 341–350. [Google Scholar] [CrossRef]
- Lamnatou, C.; Papanicolaou, E.; Belessiotis, V.; Kyriakis, N. Finite-volume modelling of heat and mass transfer during convective drying of porous bodies non-conjugate and conjugate formulations involving the aerodynamic effects. Renew. Energy 2010, 35, 1391–1402. [Google Scholar] [CrossRef]
- Mishkin, M.; Saguy, I.; Karel, M. Dynamic optimization of dehydration process: Minimizing browning in dehydration of potatoes. J. Food Sci. 1983, 48, 17–21. [Google Scholar] [CrossRef]
- Wang, N.; Brennan, J.G. A mathematical model of simultaneous heat and moisture transfer during drying of potato. J. Food Eng. 1995, 24, 47–60. [Google Scholar] [CrossRef]
- Alvarado, M.A.; Aguirre, F.M.P.; Lopez, I.I.R. Analytical solution of simultaneous heat and mass transfer equations during food drying. J. Food Eng. 2014, 142, 9–45. [Google Scholar]
- Hafez, R.M.; Zaky, M.A. High-order continuous Galerkin methods for multi-dimensional advection–reaction–diffusion problems. Eng. Comput. 2020, 36, 1813–1829. [Google Scholar] [CrossRef]
- Yang, Y.; Rządkowski, G.; Pasban, A.; Tohidi, E.; Shateyi, S. A high accurate scheme for numerical simulation of two-dimensional mass transfer processes in food engineering. Alex. Eng. J. 2021, 60, 2629–2639. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S. An efficient dissipation preserving Legendre Galerkin spectral method for the Higgs boson equation in the de Sitter spacetime universe. Appl. Num. Math. 2021, 160, 281–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Guan, F.; Tian, J.; Li, Z.; Zhang, S.; Zhao, M. Preparation and numerical simulation of food gum electrospun nanofibers. J. Food Eng. 2023, 341, 111352. [Google Scholar] [CrossRef]
- González-Pérez, J.E.; Romo-Hernández, A.; Ramírez-Corona, N.; López-Malo, A. Modeling mass transfer during osmodehydration of apple cubes with sucrose or apple juice concentrate solutions: Equilibrium estimation, diffusion model, and state observer based approach. J. Food Process. Eng. 2022, 45, e14125. [Google Scholar] [CrossRef]
- Pinheiro, R.M.M.; da Silva, W.P.; do Amaral Miranda, D.S.; eSilva, C.M.D.P.S.; Pessoa, T. Osmotic dehydration of cubic pieces of melon: Description through a three-dimensional diffusion model considering the resistance to mass flows on the surface. Heat Mass Transf. 2021, 57, 405–415. [Google Scholar] [CrossRef]
- Greiciunas, E.; Municchi, F.; Pasquale, N.D.; Icardi, M. Numerical simulation of crust freezing in processed meat: A fully coupled solid–fluid approach. Numer. Heat Transf. Part A Appl. 2020, 78, 378–391. [Google Scholar] [CrossRef]
- Chasiotis, V.K.; Tzempelikos, D.A.; Filios, A.E.; Moustris, K.P. Artificial neural network modelling of moisture content evolution for convective drying of cylindrical quince slices. Comput. Electron. Agric. 2020, 172, 105074. [Google Scholar] [CrossRef]
- Malekjani, N.; Jafari, S.M. Simulation of food drying processes by Computational Fluid Dynamics (CFD); recent advances and approaches. Trends Food Sci. Technol. 2018, 78, 206–223. [Google Scholar] [CrossRef]
- Clodoveo, M.L.; Muraglia, M.; Fino, V.; Curci, F.; Fracchiolla, G.; Corbo, F.F.R. Overview on Innovative Packaging Methods Aimed to Increase the Shelf-Life of Cook-Chill Foods. Foods 2021, 10, 2086. [Google Scholar] [CrossRef] [PubMed]
- Miranda-Zamora, W.; Tirado-Kulieva, A.; Ricse, D. Computational Applications for the Evaluation and Simulation of the Thermal Treatment of Canned Foods. In A Glance at Food Processing Applications; IntechOpen: London, UK, 2022. [Google Scholar]
- Khan, S.U.; Ali, I. Convergence and error analysis of a spectral collocation method for solving system of nonlinear Fredholm integral equations of second kind. Comput. Appl. Math. 2019, 38, 125. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, I. Applications of Legendre spectral collocation method for solving system of time delay differential equations. Adv. Mech. Eng. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Ali, I.; Khan, S.U. Analysis of stochastic delayed SIRS model with exponential birth and saturated incidence rate. Chaos Solitons Fract. 2020, 138, 110008. [Google Scholar] [CrossRef]
- Saleem, M.T.; Ali, I. Numerical Simulations of Turing Patterns in a Reaction- diffusion Model with the Chebyshev Spectral Method. Eur. Phys. J. Plus 2018, 133, 399. [Google Scholar] [CrossRef]
- Raza, N.; Zainab, U.; Araci, S.; Esi, A. Identities involving 3-variable Hermite polynomials arising from umbral method. Adv. Differ. Equ. 2020, 2020, 640. [Google Scholar] [CrossRef]
- Duran, U.; Acikgoz, M.; Esi, A.; Araci, S. A Note on the (p, q)-Hermite Polynomials. Appl. Math. Inf. Sci. 2018, 12, 227–231. [Google Scholar] [CrossRef]
- Khan, W.A.; Araci, S.; Acikgoz, M.; Esi, A. Laguerre-based Hermite-Bernoulli polynomials associated with bilateral series. Tbilisi Math. J. 2018, 11, 111–121. [Google Scholar]
- Pfeiffer, H.P.; Kidder, L.E.; Scheel, M.A.; Teukolsky, S.A. A multidomain spectral method for solving elliptic equations. Comput. Phys. Commun. 2003, 152, 253–273. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Costa, B. Spectral methods for partial differential equations. Cubo-Revista de Matemática 2004, 6, 1–32. [Google Scholar]
- Heideman, M.T.; Johnson, D.H.; Burrus, C.S. Gauss and the history of the fast Fourier transform. Arch. Hist. Exact Sci. 1985, 34, 265–277. [Google Scholar] [CrossRef]
- Van Loan, C. Computational Frameworks for the Fast Fourier Transform; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Frigo, M.; Johnson, S.G. A Modified Split-Radix FFT With Fewer Arithmetic Operations. IEEE Trans. Signal Process. 2007, 55, 111–119. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Trefethen, L.N. Spectral methods in MATLAB; SIAM: Philadelphia, USA, 2000. [Google Scholar]
- Canuto, H.; Quaterolli, Z. Spectral Methods; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zhang, X. Mapped barycentric Chebyshev differentiation matrix method for the solution of regular Sturm–Liouville problems. Appl. Math. Comput. 2010, 217, 2266–2276. [Google Scholar] [CrossRef]
- Taher, A.H.S.; Malek, A.; Momeni-Masuleh, S.H. Chebyshev differentiation matrices for efficient computation of the eigenvalues of fourth-order Sturm–Liouville problems. Appl. Math. Model. 2013, 37, 4634–4642. [Google Scholar] [CrossRef]

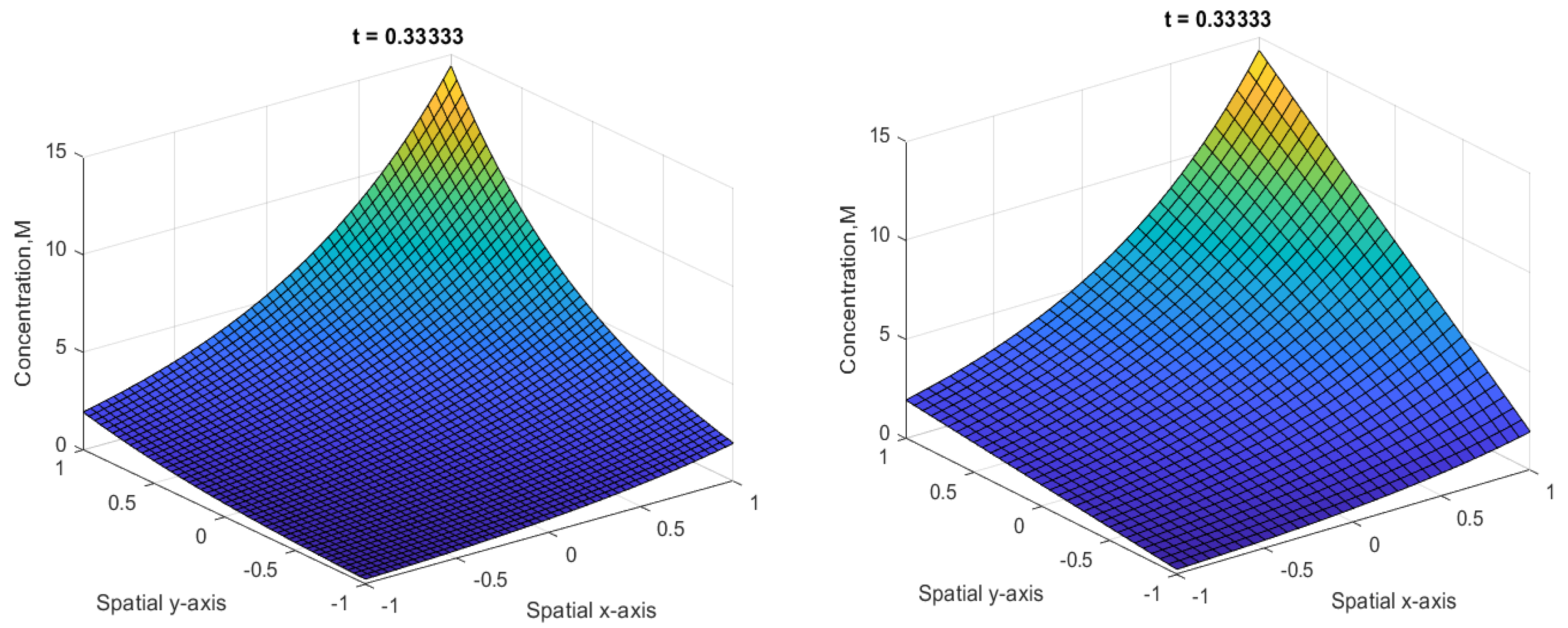
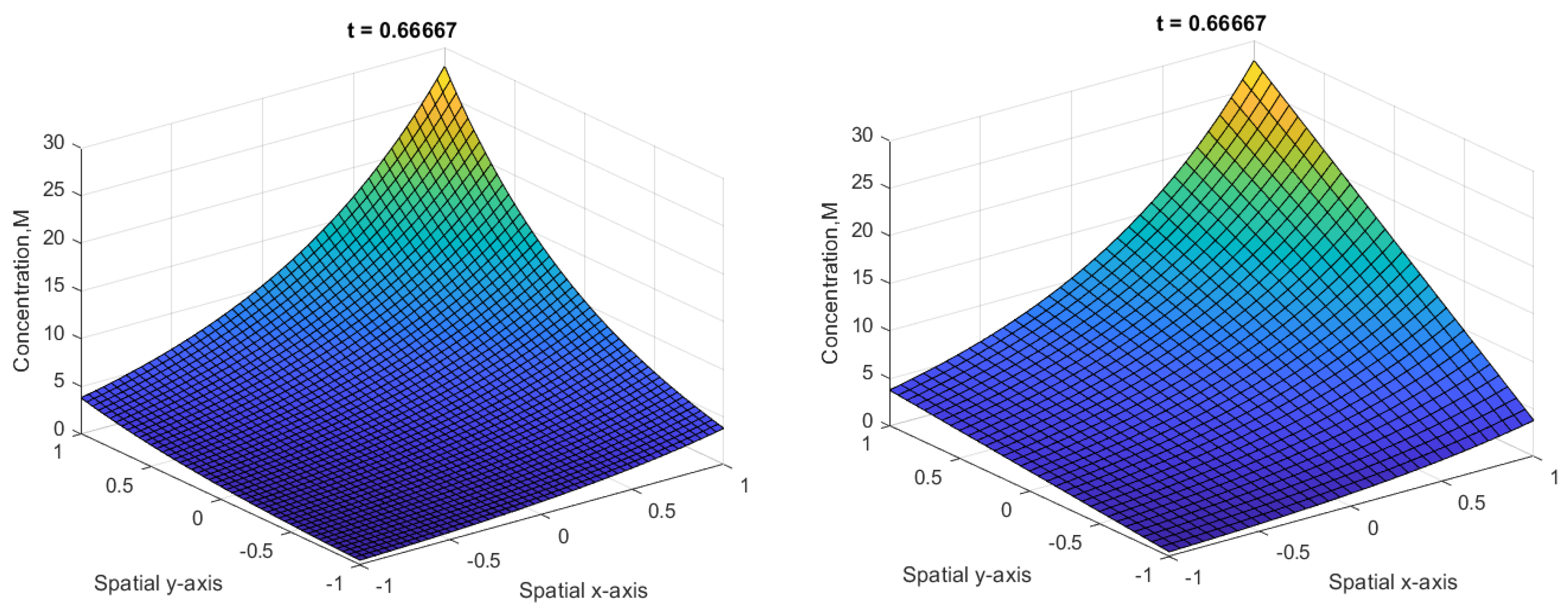

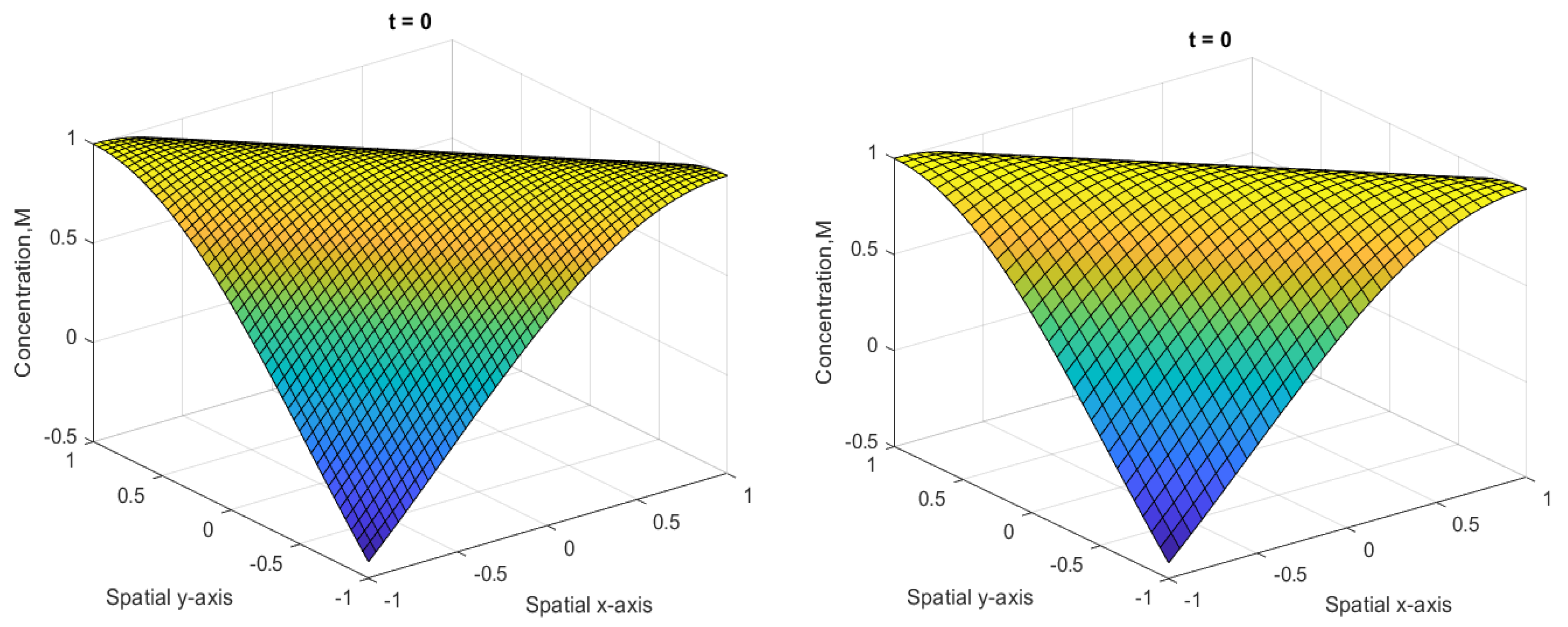
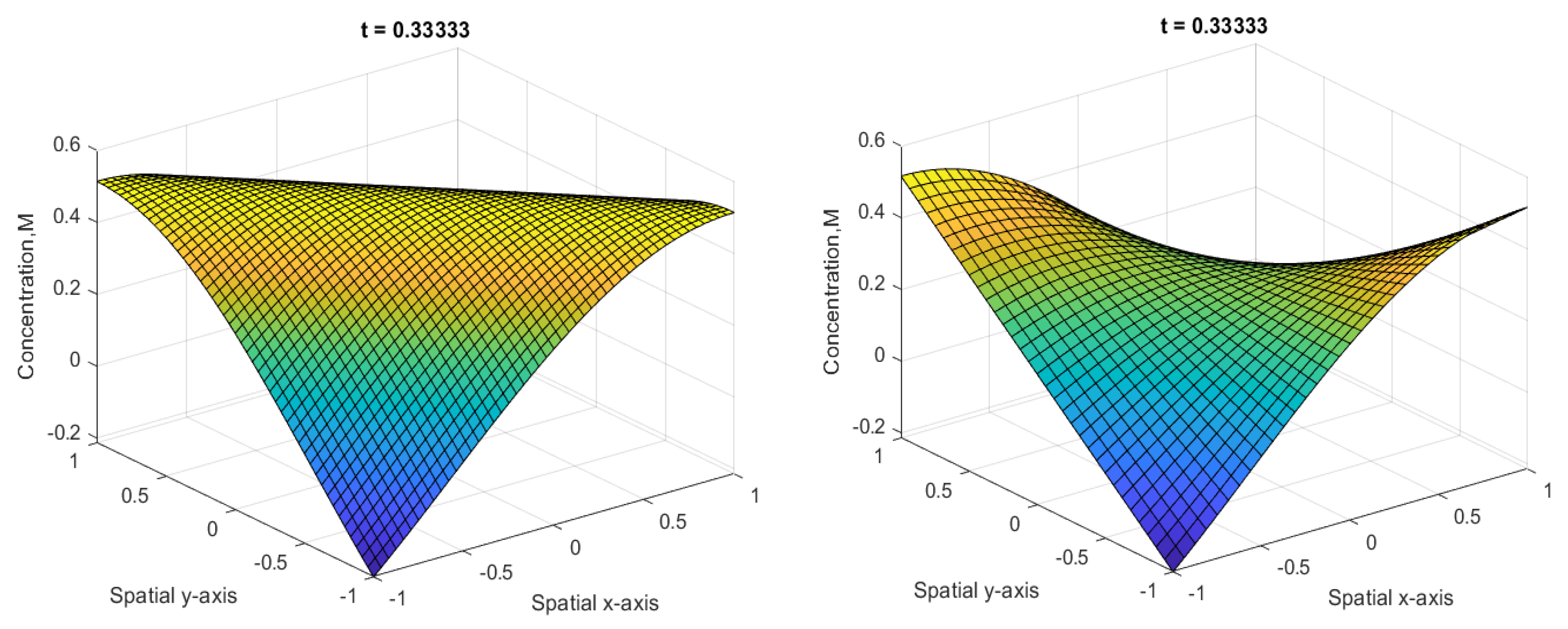

| Error | ||||
|---|---|---|---|---|
| 0 | ||||
| 0 | ||||
| 0 |
| Error | ||||
|---|---|---|---|---|
| 0 | ||||
| 0 | ||||
| 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Saleem, M.T. Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering. Symmetry 2023, 15, 527. https://doi.org/10.3390/sym15020527
Ali I, Saleem MT. Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering. Symmetry. 2023; 15(2):527. https://doi.org/10.3390/sym15020527
Chicago/Turabian StyleAli, Ishtiaq, and Maliha Tehseen Saleem. 2023. "Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering" Symmetry 15, no. 2: 527. https://doi.org/10.3390/sym15020527
APA StyleAli, I., & Saleem, M. T. (2023). Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering. Symmetry, 15(2), 527. https://doi.org/10.3390/sym15020527






