Comparative Study of the Geodesic Structure of Time-Conformal Quantum-Corrected AdS–Schwarzschild Black Hole

Abstract

This manuscript reports the dynamics of a time-conformal quantum-corrected AdS–Schwarzschild black hole. The quantum-corrected parameter and the time-conformal factors are inserted in the AdS–Schwarzschild black. These insertions in the said space- time are taken to study and understand the phenomena of the formation of gravitational waves and Hawking radiations. The Hawking temperature distributions and Bekenstein–Hawking entropy for the inner and outer horizon of the new developed black hole solution are calculated and discussed. The motion of neutral and charged particles in the orbits of the said black hole is discussed under the influence of effective potential and effective force in the new development of the black hole solution. The escape velocity for the time-conformal black hole is obtained and compared with the escape velocity of the exact black hole. The roles of the quantum-corrected parameter and the effect of the time-conformal factor are high- lighted, and their influences are discussed in different situations. Einstein’s field equations are also obtained for the time-conformal quantum-corrected AdS–Schwarzschild black hole. The Lyapunov exponent is used for the stability of the said black hole spacetime. The effects of different parameters on different dynamical aspects of the black hole are explored.

1. Introduction

The accelerated expansion of the universe is due to the existence of the hidden source of energy, which is deeply connected to the cosmological constant $\mathsf{\Lambda }$. This constant was introduced by Einstein in his field equations for the very first time in 1917. The discovery of this constant is one of the greatest contributions in the field of modern cosmology. The physical reason for cosmic accelerative expansion remains a deep mystery. The literature of the theory of general relativity claims that the expansion of the universe is an accelerated process that leads to two possibilities: the first one is that 75 percent of the energy density of the universe exists in a novel form with a huge quantity of negative pressure, also known as dark energy, while in the second case the general relativity break down on cosmological scales must be replaced with a more physical and complete theory of gravity. The highly non-linear Einstein field equations (a system of ten coupled ODEs) are not easy to solve with analytical methods. However, there are particular solutions to these equations, such as the Schwarzschild solution, the Reissner–Nordstrm solution, and the Kerr solution. The Schwarzschild and Reissner–Nordstrm solutions define the fields of non-rotating neutral spherical symmetric and non-rotating spherical symmetric charged black holes [1,2]. The study of black holes plays an essential role in rooting out the mysteries of dark energy and dark matter since we are not fully familiar with what is happening inside and near the horizon of a black hole but have hope that quantum gravity theory may answer these questions. The theory of general relativity reports the black-body radiations of black holes (BH), called Hawking radiations [3]. These radiations are due to the quantum effects in the surroundings of the event horizon of BH, which also play an active part in the reduction in the mass and rotational energy of BH. The BHs also radiate mass and energy in the formation of gravitational waves. These observations concluded that BHs will possibly disappear at a certain stage.

The study of particle motion near the event horizon of a BH provides a better understanding of BH spacetime geometry. There are several articles that investigate the dynamics of neutral and charged particles in the vicinity of Reissner–Nordström and regular BHs [4,5,6,7]. The innermost stable circular orbits (ISCO) of BHs captured the attention of various researchers because the inclusion of the magnetic field changes the dynamic of the charged particle moving in ISCO [8,9,10,11]. Kazakov and Solodukhin [12] discussed the deformation of the Schwarzschild solution caused by the quantum fluctuations of the spherically symmetric metric. They reduced the 4D theory of gravity with the Einstein action to the effective two-dimensional dilaton gravity. Malakolkalami and Ghadiri [13] briefly discussed the null geodesics and stability of the orbits of the Schwarzschild–anti de Sitter black hole surrounded by quintessence. Eslamzadeh and Kourosh Nozari [14] reported the radiation and dynamics of the quantum deformed Schwarzschild black hole, which is surrounded by the quintessence field, with the help of the tunneling process. They considered two horizons, i.e., a black hole horizon and a cosmological horizon, and discussed the temperature around both horizons. They reported that the temperature at the black hole horizon is higher than the cosmological horizon. There are several articles on the time-conformal black holes and time-conformal spacetime [15,16]. The gravitational waves background with terrestrial detectors is discussed in [17]. The dynamics of neutral and charged particles in the time-conformal Schwarzschild black hole spacetime are given [18]. Al Zehrani et al. [19] discussed the circumstances under which the test particle can escape to infinity from the orbits of the magnetized Schwarzschild black hole. The chaotic motion of a magnetized particle at the surrounding of the weakly magnetized Kerr black hole is investigated in [20,21,22,23]. Different perturbation methods are used for different purposes [24].

In this work, we are going to perturb the quantum-corrected AdS–Schwarzschild black hole by a time-conformal factor and explore the dynamics of neutral and charged particle moving at the circular orbits of this time-conformal BH. This study will help us to understand the phenomenon of the formation of gravitational waves and Hawking radiations. As the mass and energy of the BH decreases with time, this study will explore the correction to the mass and energy of the BH when the gravitational waves formed. The paper is organized as follows:

In Section 2, we obtained the Noether symmetries and the corresponding conservation laws of quantum-corrected AdS–Schwarzschild (QC-AdS-SBH) [25]. In Section 3, the metric of the said spacetime is perturbed by a time-conformal factor $e^{\frac{ϵt}{\alpha }}$ and the results are compared with Section 2. In Section 4, we discussed the thermodynamics of time-conformal QC-AdS-SBH by using inner and outer horizon of the BH. In Section 5, Einstein’s field equations are obtained for the time-conformal QC-AdS-SBH. Section 6 reports the dynamics of neutral test particles moving in the circular orbits of the BH. In Section 7, we introduce the magnetic field around the ISCO of the BH and discuss the motion of charged particles. The stability of the orbits of time-conformal QC-AdS-SBH is discussed with the help of the Lyapunov exponent in Section 8. Section 9 contains the observation and discussion of different aspects of the BH. The paper is concluded in Section 10.

2. Noether Symmetries of Quantum-Corrected AdS–Schwarzschild Solution and Conservation Laws

The line element of quantum-corrected AdS–Schwarzschild solution is

$${d{s}^2}_e=\mathsf{\Omega }\left(r\right)d{t}^2-\frac{1}{\mathsf{\Omega }\left(r\right)}d{r}^2-r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(1)

where the coefficient of the metric is defined as

$$\mathsf{\Omega }\left(r\right)=\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}.$$

M refers to the mass of the quantum-corrected AdS–Schwarzschild black hole, a is the the quantum-corrected term, and $\mathsf{\Lambda }$ denotes the cosmological constant. t is the time coordinate that is recorded by a standard clock at rest at spatial infinity, where the coordinate r is a radial coordinate of BH. $\theta$ is polar, and $\varphi$ is azimuthal angle. The Lagrangian corresponding to Equation (1) is

$${\pounds }_e=\mathsf{\Omega }\left(r\right){\dot{t}}^2-\frac{1}{\mathsf{\Omega }\left(r\right)}{\dot{r}}^2-r^2\left({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2\right),$$

(2)

here, “˙” denotes the derivative w.r.t to arc length parameter s. The operator

$${\mathsf{{\rm Y}}}_e^{\left[1\right]}={\mathsf{{\rm Y}}}_e+{\eta }_{es}^k\frac{\partial }{\partial {\dot{y}}^k},$$

(3)

is the first-order extension of the Noether symmetry generater:

$${\mathsf{{\rm Y}}}_e={\xi }_e\frac{\partial }{\partial s}+{\eta }_e^k\frac{\partial }{\partial y^k}.$$

(4)

The Noether symmetry equation takes the form

$${\mathsf{{\rm Y}}}_e^{\left[1\right]}{\pounds }_e+\left(D{\xi }_e\right){\pounds }_e=D{A}_e,$$

(5)

the operator $A_e$ is the gauge function, and D is the total differential operator of the form

$$D=\frac{d}{ds}=\frac{\partial }{\partial s}+\dot{y}\frac{\partial }{\partial y}+\ddot{y}\frac{\partial }{\partial \dot{y}}+\dots$$

(6)

The Noether symmetry Equation (5) provides the following system of 19 partial differential equations for the Lagrangian given in Equation (2)

$$\begin{array}{cc}& 2{\eta }_s^0\mathsf{\Omega }\left(r\right)-A_t^0=0,2{\eta }_s^1+\mathsf{\Omega }\left(r\right)A_r^0=0,2{\eta }_s^2{r}^2+A_{\theta }^0=0,2{\eta }_s^3{r}^{2}sin{\left(\theta \right)}^2+A_{\varphi }^0=0,\hfill \\ & {\eta }_{\varphi }^2+sin{\left(\theta \right)}^2{\eta }_{\theta }^3=0,{\eta }_t^2{r}^2-{\eta }_{\theta }^0\mathsf{\Omega }\left(r\right)=0,{\eta }_t^3{r}^{2}sin{\left(\theta \right)}^2-{\eta }_{\varphi }^0\mathsf{\Omega }\left(r\right)=0,\hfill \\ & \mathsf{\Omega }{\left(r\right)}^2{\eta }_r^0-{\eta }_t^1=0,{\eta }_{\varphi }^1+r^{2}sin{\left(\theta \right)}^2\mathsf{\Omega }\left(r\right){\eta }_r^3=0,{\eta }_{\theta }^1-r^2\mathsf{\Omega }\left(r\right){\eta }_r^2=0,\hfill \\ & 2{\eta }^1+2r{\eta }_{\theta }^2-r{\xi }_s^0=0,-{\mathsf{\Omega }}_r\left(r\right){\eta }^1+2\mathsf{\Omega }\left(r\right){\eta }_r^1-\mathsf{\Omega }\left(r\right){\xi }_s^0=0,\hfill \\ & {\mathsf{\Omega }}_r\left(r\right){\eta }^1+2\mathsf{\Omega }\left(r\right){\eta }_t^0-\mathsf{\Omega }\left(r\right){\xi }_s^0=0,A_s^0=0,{\xi }_t^0=0,{\xi }_r^0=0,\hfill \\ & 2sin\left(\theta \right){\eta }^1+2rcos\left(\theta \right){\eta }^2+rsin\left(\theta \right)(2{\eta }_{\varphi }^3-{\xi }_s^0)=0,{\xi }_{\theta }^0=0,{\xi }_{\varphi }^0=0.\hfill \end{array}$$

(7)

The solution of system (7) is

$$\begin{array}{cc}& A^0=C_1,{\xi }^0=C_2,{\eta }^0=C_3,{\eta }^1=0,{\eta }^2=-C_{5}cos\left(\varphi \right)+C_{6}sin\left(\varphi \right),\hfill \\ & {\eta }^3=C4+C_{5}cot\left(\theta \right)sin\left(\varphi \right)+C_{6}cot\left(\theta \right)cos\left(\varphi \right).\hfill \end{array}$$

(8)

Noether symmetry generators [18] corresponding to the solution given in Equation (8) take the form

$$\begin{array}{cc}& {\mathsf{{\rm Y}}}_{\mathbf{1}}={\partial }_t,{\mathsf{{\rm Y}}}_{\mathbf{2}}={\partial }_s,{\mathsf{{\rm Y}}}_{\mathbf{3}}={\partial }_{\varphi },\hfill \\ & {\mathsf{{\rm Y}}}_{\mathbf{4}}=(cos\varphi ){\partial }_{\theta }-(cot\theta sin\varphi ){\partial }_{\varphi },{\mathsf{{\rm Y}}}_{\mathbf{5}}=(sin\varphi ){\partial }_{\theta }+(cot\theta cos\varphi ){\partial }_{\varphi }.\hfill \end{array}$$

(9)

The conservation laws that correspond to the above set of the exact Noether symmetries are given

Table 1. First Integrals.

Gen	First Integrals
${\mathsf{{\rm Y}}}_{\mathbf{1}}$	${\varphi }_1=2\mathsf{\Omega }\left(r\right)\dot{t}$
${\mathsf{{\rm Y}}}_{\mathbf{2}}$	${\varphi }_2=-\mathsf{\Omega }\left(r\right){\dot{t}}^2+\frac{1}{\mathsf{\Omega }\left(r\right)}{\dot{r}}^2+r^2\left({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2\right)$
${\mathsf{{\rm Y}}}_{\mathbf{3}}$	${\varphi }_3=-2r^2{sin}^2\theta \dot{\varphi }$
${\mathsf{{\rm Y}}}_{\mathbf{4}}$	${\varphi }_4=-2r^2\left(cos\varphi \dot{\theta }-cot\theta sin\varphi \dot{\varphi }\right)$
${\mathsf{{\rm Y}}}_{\mathbf{5}}$	${\varphi }_5=-2r^2\left(sin\varphi \dot{\theta }+cot\theta cos\varphi \dot{\varphi }\right)$

.

3. Time-Conformal Quantum-Corrected AdS–Schwarzschild Solution and the Corresponding Conservation Laws

Perturbing Equation (1) by the general time-conformal factor $e^{ϵg\left(t\right)}$, we have

$$d{s}^2=e^{ϵg\left(t\right)}d{s}_e^2,$$

(10)

The series expansion of Equation (10) up to the first order takes the form

$$d{s}^2=\left(1+ϵg\left(t\right)\right)d{s}_e^2.$$

(11)

The perturbed Lagrangian corresponds to the perturbed metric given in Equation (10) is:

$$\pounds =e^{ϵg\left(t\right)}{\pounds }_e,$$

(12)

the first-order series enpension of Equation (12) gives

$$\pounds =\left(1+ϵg\left(t\right)\right){\pounds }_e.$$

(13)

The perturbed Lagrangian £ can be written as

$$\pounds ={\pounds }_e+ϵ{\pounds }_a,$$

(14)

with the perturbed portion ${\pounds }_a=g\left(t\right){\pounds }_e$. The first-order approximate Noether symmetry [5] is defined as

$$\mathsf{{\rm Y}}={\mathsf{{\rm Y}}}_e+ϵ{\mathsf{{\rm Y}}}_a,$$

(15)

and the approximate gauge function takes the form $A=A_e+ϵA_a.$, where

$${\mathsf{{\rm Y}}}_a={\xi }_a\frac{\partial }{\partial s}+{\eta }_a^k\frac{\partial }{\partial y^k},$$

(16)

$\mathsf{{\rm Y}}$ is the first-order approximate Noether symmetry generator satisfies

$${\mathsf{{\rm Y}}}^{\left[1\right]}\pounds +\left(D\xi \right)\pounds =DA,$$

(17)

where ${\mathsf{{\rm Y}}}^{\left[1\right]}$ is the first-order prolongation of Equation (15). Equation (17) is split into two parts as

$${\mathsf{{\rm Y}}}_e{\pounds }_e+\left(D{\xi }_e\right){\pounds }_e=D{A}_e,$$

(18)

$${\mathsf{{\rm Y}}}_a^{\left[1\right]}{\pounds }_e+{\mathsf{{\rm Y}}}_e^{\left[1\right]}{\pounds }_a+\left(D{\xi }_e\right){\pounds }_a+\left(D{\xi }_a\right){\pounds }_e=D{A}_a.$$

(19)

By putting the exact solution (8) in Equation (19), we have the following system of 19 partial differential equations:

$$\begin{array}{cc}& 2{\eta }_s^4\mathsf{\Omega }\left(r\right)-A_t^1=0,2{\eta }_s^5+\mathsf{\Omega }\left(r\right)A_r^1=0,2{\eta }_s^6{r}^2+A_{\theta }^1=0,2{\eta }_s^7{r}^{2}sin{\left(\theta \right)}^2+A_{\varphi }^1=0,\hfill \\ & {\eta }_{\varphi }^6+sin{\left(\theta \right)}^2{\eta }_{\theta }^7=0,{\eta }_t^6{r}^2-{\eta }_{\theta }^4\mathsf{\Omega }\left(r\right)=0,{\eta }_t^7{r}^{2}sin{\left(\theta \right)}^2-{\eta }_{\varphi }^4\mathsf{\Omega }\left(r\right)=0,\hfill \\ & \mathsf{\Omega }{\left(r\right)}^2{\eta }_r^4-{\eta }_t^5=0,{\eta }_{\varphi }^5+r^{2}sin{\left(\theta \right)}^2\mathsf{\Omega }\left(r\right){\eta }_r^7=0,{\eta }_{\theta }^5-r^2\mathsf{\Omega }\left(r\right){\eta }_r^6=0,\hfill \\ & C_3{g}_t\left(t\right)r+2{\eta }^5+2r{\eta }_{\theta }^6-r{\xi }_s^1=0,C_3{g}_t\left(t\right)\mathsf{\Omega }\left(r\right)-{\mathsf{\Omega }}_r\left(r\right){\eta }^5+2\mathsf{\Omega }\left(r\right){\eta }_r^5-\mathsf{\Omega }\left(r\right){\xi }_s^1=0,\hfill \\ & C_3{g}_t\left(t\right)\mathsf{\Omega }\left(r\right)+{\mathsf{\Omega }}_r\left(r\right){\eta }^5+2\mathsf{\Omega }\left(r\right){\eta }_t^4-\mathsf{\Omega }\left(r\right){\xi }_s^1=0,A_s^1=0,{\xi }_t^1=0,{\xi }_r^1=0,\hfill \\ & C_3{g}_t\left(t\right)rsin\left(\theta \right)+2sin\left(\theta \right){\eta }^5+2rcos\left(\theta \right){\eta }^6+rsin\left(\theta \right)(2{\eta }_{\varphi }^7-{\xi }_s^1)=0,{\xi }_{\theta }^1=0,{\xi }_{\varphi }^1=0.\hfill \end{array}$$

(20)

where ${\eta }^4,{\eta }^5,{\eta }^6,{\eta }^7,{\xi }^1,$ and $A^1$ are functions of $(s,t,r,\theta ,\varphi )$. The system (20) of 19 partial differential equations with 7 unknown functions has the following solution [6]:

$$\begin{array}{cc}& A^1=b_1,{\xi }^1=b_2+C_3\frac{s}{\alpha },{\eta }^4=b_3,{\eta }^5=0,{\eta }^6=-b_{5}cos\left(\varphi \right)+b_{6}sin\left(\varphi \right),\hfill \\ & {\eta }^7=b_4+b_{5}cot\left(\theta \right)sin\left(\varphi \right)+b_{6}cot\left(\theta \right)cos\left(\varphi \right).\hfill \end{array}$$

(21)

Combining the solution given in Equations (8) and (21), we obtain the solution of the first-order perturbed Noether symmetry Equation (17) as

$$\begin{array}{cc}& A^0+ϵA^1=C_1+ϵb_1,{\xi }^0+ϵ{\xi }^1=C_2+ϵ(b_2+C_3\frac{s}{\alpha }),\hfill \\ & {\eta }^0+ϵ{\eta }^4=C_3+ϵb_3,{\eta }^1+ϵ{\eta }^5=0+ϵ\left(0\right),\hfill \\ & {\eta }^2+ϵ{\eta }^6=-C_{5}cos\left(\varphi \right)+C_{6}sin\left(\varphi \right)+ϵ\left(-b_{5}cos\left(\varphi \right)+b_{6}sin\left(\varphi \right)\right),\hfill \\ & {\eta }^3+ϵ{\eta }^7=C_4+C_{5}cot\left(\theta \right)sin\left(\varphi \right)+C_{6}cot\left(\theta \right)cos\left(\varphi \right)+\hfill \\ & ϵ\left(b4+b_{5}cot\left(\theta \right)sin\left(\varphi \right)+b_{6}cot\left(\theta \right)cos\left(\varphi \right)\right).\hfill \end{array}$$

(22)

The first-order perturbed non-trivial Noether symmetry generator take the form:

$$\begin{array}{cc}& {\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}={\partial }_t+ϵ\frac{s}{\alpha }{\partial }_s,{\mathsf{{\rm Y}}}_{\mathbf{2}}={\partial }_s,{\mathsf{{\rm Y}}}_{\mathbf{3}}={\partial }_{\varphi },\hfill \\ & {\mathsf{{\rm Y}}}_{\mathbf{4}}=(cos\varphi ){\partial }_{\theta }-(cot\theta sin\varphi ){\partial }_{\varphi },{\mathsf{{\rm Y}}}_{\mathbf{5}}=(sin\varphi ){\partial }_{\theta }+(cot\theta cos\varphi ){\partial }_{\varphi }.\hfill \end{array}$$

(23)

The symmetry generator ${\mathsf{{\rm Y}}}_{1a}$ re-scales the energy content of the quantum-corrected AdS–Schwarzschild spacetime as it is the only generator that contains a non-trivial approximate part. The corresponding conservation laws are given in

Table 2. First Integrals.

Gen	First Integrals
${\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}$	$E_a=2\mathsf{\Omega }\left(r\right)\dot{t}+\frac{ϵ}{\alpha }(2t\dot{t}\mathsf{\Omega }\left(r\right)-s{\pounds }_e)$
${\mathsf{{\rm Y}}}_{\mathbf{2}}$	$-\pounds =-(1+\frac{ϵt}{\alpha })\left(\mathsf{\Omega }\left(r\right){\dot{t}}^2+\frac{1}{\mathsf{\Omega }\left(r\right)}{\dot{r}}^2-r^2({\dot{\theta }}^2-{\sin }^2\theta {\dot{\varphi }}^2\right)$
${\mathsf{{\rm Y}}}_{\mathbf{3}}$	$-{Ł}_{za}=-2(1+\frac{ϵt}{\alpha })r^2{sin}^2\theta \dot{\varphi }$
${\mathsf{{\rm Y}}}_{\mathbf{4}}$	${\varphi }_{4a}=-2(1+\frac{ϵt}{\alpha })r^2(cos\varphi \dot{\theta }-cot\theta sin\varphi \dot{\varphi })$
${\mathsf{{\rm Y}}}_{\mathbf{5}}$	${\varphi }_{5a}=-2(1+\frac{ϵt}{\alpha })r^2(sin\varphi \dot{\theta }+cot\theta cos\varphi \dot{\varphi })$

:

4. Thermodynamics of the Black Hole

Consider the line element of time-conformal QC-AdS-SBH as

$$d{s}^2=\left(1+\frac{ϵt}{\alpha }\right)d{s}^2,$$

(24)

where $ϵ$ is a dimensionless parameter introduced in the line element that causes the perturbation in the spacetime. The parameter $\alpha$ has dimensions equal to time, which leads to the dimensionless term $\frac{t}{\alpha }$. The horizon of the time-conformal spacetime given Equation (24) is calculated as

$$\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}=0.$$

By asymptotic approximation for $r>>a$ and neglecting the higher order terms of the quantum-corrected parameter a, we obtain the following form:

$$1-\frac{a^2}{2r^2}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\approx 0,$$

which gives two event horizons, i.e., (inner $r_{*}$ and outer $r^{*}$) of time-conformal QC AdS-SBH:

$$\begin{array}{c}\hfill r_{*}\approx -\frac{1}{2}\sqrt{-\frac{2}{\mathsf{\Lambda }}+\frac{m_1}{3\sqrt[3]{2}}+\frac{\sqrt[3]{2}\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}{3m_1}}-\frac{1}{2}\sqrt{-\frac{4}{\mathsf{\Lambda }}-m_2-\frac{m_1}{3\sqrt[3]{2}}-\frac{\sqrt[3]{2}\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}{3m_1}},\end{array}$$

$$\begin{array}{c}\hfill r^{*}\approx -\frac{1}{2}\sqrt{-\frac{2}{\mathsf{\Lambda }}+\frac{m_1}{3\sqrt[3]{2}}+\frac{\sqrt[3]{2}\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}{3m_1}}+\frac{1}{2}\sqrt{-\frac{4}{\mathsf{\Lambda }}-m_2-\frac{m_1}{3\sqrt[3]{2}}-\frac{\sqrt[3]{2}\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}{3m_1}},\end{array}$$

where

$$m_1=\sqrt[3]{\frac{54}{{\mathsf{\Lambda }}^3}-\frac{324a^2}{{\mathsf{\Lambda }}^2}+\frac{972M^2}{{\mathsf{\Lambda }}^2}+m_3},$$

$$m_2=\frac{\frac{48M}{\mathsf{\Lambda }}}{\sqrt[4]{\frac{-2}{\mathsf{\Lambda }}+\frac{m_1}{\sqrt[3]{2}}+\frac{\sqrt[3]{2}\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}{3m_1}}},$$

$$m_3=\sqrt{{\left(\frac{54}{{\mathsf{\Lambda }}^3}-\frac{324a^2}{{\mathsf{\Lambda }}^2}+\frac{972M^2}{{\mathsf{\Lambda }}^2}\right)}^2-4{\left(\frac{9}{{\mathsf{\Lambda }}^2}-\frac{18a^2}{\mathsf{\Lambda }}\right)}^3}.$$

One can calculate the Hawking temperature for inner and outer horizon of time-conformal QC-AdS-SBH as

$$T_{*}=\left(1+\frac{ϵt}{\alpha }\right)\frac{{\mathsf{\Omega }}^{\prime }\left(r\right)}{4\pi }{\mid }_{r=r_{*}}\hspace{1em}\mathrm{and}\hspace{1em}{T}^{*}=\left(1+\frac{ϵt}{\alpha }\right)\frac{{\mathsf{\Omega }}^{\prime }\left(r\right)}{4\pi }{\mid }_{r=r^{*}},$$

(25)

and the Bekenstein–Hawking entropy [26,27] of black hole takes the form

$$S=\frac{A}{4}=\frac{4\pi r^2}{4}=\pi r^2.$$

(26)

From Equation (26), the local properties of a limited BH, which have infinite mass and area, give a clear picture of the entropy of the black bole, which is proportional to its surface area. The entropy for inner and outer horizons of time-conformal QC-AdS-SBH takes the form

$$S_{*}=\pi {r_{*}}^2\hspace{1em}\mathrm{and}\hspace{1em}{S}^{*}=\pi {r^{*}}^2.$$

(27)

5. Einstein’s Field Equations

The Einstein field equations link the geometry of spacetime to the matter distribution within it. For spacetime (1), the energy-momentum tensor is given as ($G=c=1$)

$$T^{\mu \nu }=(\rho +p)u^{\mu }{u}^{\nu }-p{g}^{\mu \nu }.$$

(28)

In the above equation, $T^{\mu \nu }$ is the stress-energy momentum tensor of perfect fluid. This type of fluid is an approximation to the early universe, which is fully characterized by pressure p and mass density $\rho$. In Equation (28), if $p\to 0$, the nature of the fluid will transform from perfect fluid into dust. The four-velocity for a co-moving observer is $\overrightarrow{u}=(\sqrt{g^{11}},0,0,0)$. The Einstein field equations of the time-conformal QC-AdS-SBH take the following form:

$$\frac{{\mathsf{\Psi }}_o\left(r\right){(r^2-a^2)}^{\frac{3}{2}}+{\mathsf{\Psi }}_1\left(r\right)}{12r^3{({\alpha }^2+ϵt)}^2{(r^2-a^2)}^{\frac{3}{2}}}=8\pi \rho ,$$

(29)

$$-\frac{3\left({\mathsf{\Psi }}_o\left(r\right){(r^2-a^2)}^{\frac{3}{2}}+{\mathsf{\Psi }}_1\left(r\right)\right)}{4r{(\alpha +ϵt)}^2{(r^2-a^2)}^{\frac{3}{2}}{\left(\mathsf{\Lambda }{r}^3-6M+3\sqrt{r^2-a^2}\right)}^2}=8\pi p.$$

(30)

where the functions ${\mathsf{\Psi }}_o\left(r\right)$ and ${\mathsf{\Psi }}_1\left(r\right)$ are given below:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathsf{\Psi }}_o\left(r\right)=24M{\alpha }^2+12{\alpha }^{2}r+8{\mathsf{\Lambda }}^2\alpha tϵr^5-8\mathsf{\Lambda }\alpha r^{3}tϵ-24\mathsf{\Lambda }M{\alpha }^2{r}^2\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+48M\alpha tϵ+24\alpha rtϵ+4{\mathsf{\Lambda }}^2{r}^5{\alpha }^2-4\mathsf{\Lambda }{\alpha }^2{r}^3-48\mathsf{\Lambda }M\alpha r^{2}tϵ,\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathsf{\Psi }}_1\left(r\right)=24a^2{r}^2{\alpha }^2-24M{r}^3{\alpha }^2+16\mathsf{\Lambda }{\alpha }^2{r}^6+24a^4{r}^2\alpha \mathsf{\Lambda }tϵ+48M{a}^2\alpha rtϵ+48a^2\alpha r^{2}tϵ-48M\alpha r^{3}tϵ\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-56a^2{r}^4\alpha \mathsf{\Lambda }tϵ+32\mathsf{\Lambda }\alpha r^{6}tϵ+24M{\alpha }^2{a}^{2}r-24\alpha r^{4}tϵ+12a^4\mathsf{\Lambda }{\alpha }^2{r}^2-28a^2\mathsf{\Lambda }{\alpha }^2{r}^4\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-12a^2{r}^4-24\alpha a^{4}tϵ-12a^4{\alpha }^2.\hfill \end{array}\end{array}$$

6. Dynamics of Neutral Particles

Consider the motion of neutral particle in the orbits of the time-conformal QC-AdS-SBH, in the absence of magnetic field. From Table 2, one can calculate the square of the total angular momentum $L^2$ and the total approximate energy $E_a$ as

$$L^2=(1+\frac{ϵt}{\alpha })(r^2{\upsilon }_e+\frac{{{Ł}_z}^2}{{sin}^2\theta }),$$

(31)

$$E_a=(1+\frac{ϵt}{\alpha })(E-\frac{ϵs}{\alpha }).$$

(32)

In Equation (31), the ${\upsilon }_e$ is the velocity of the test particle; it escapes from the orbits of the time-conformal QC-AdS-SBH. The physical quantities E and ${\upsilon }_e$ are defined as

$${\upsilon }_e=r^2{\dot{\theta }}^2,E=\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\dot{t},$$

(33)

the normalization condition of the time-conformal QC-AdS-SBH takes the form

$${\dot{y}}^{\mu }{\dot{y}}_{\mu }=1.$$

(34)

From the condition given in Equation (34), the approximate Euler Lagrange equation for neutral particle takes the form

$${\dot{r}}^2=E^2-\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\left((1-\frac{ϵt}{\alpha })+\frac{{Ł}_z^2(1-\frac{2ϵt}{\alpha })}{r^2{sin}^2\theta }\right).$$

(35)

For the motion of neutral particle on the equatorial plane ($\dot{r}=0$ and $\theta =\frac{\pi }{2}$), the effective potential is obtained as

$$E^2=\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\left((1-\frac{ϵt}{\alpha })+\frac{{Ł}_z^2(1-\frac{2ϵt}{\alpha })}{r^2}\right)=U_E.$$

(36)

For the effective force, one can proceed as

$$F_E=-\frac{1}{2}{U}_E^{\prime }\left(r\right),$$

(37)

explicitly,

$$\begin{array}{c}\hfill \begin{array}{c}{F}_E=(1-\frac{2ϵt}{\alpha })\left(\frac{{Ł}_z^2(3\sqrt{r^2-a^2}-6M+\mathsf{\Lambda }{r}^3)}{3r^4}\right)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left((1-\frac{ϵt}{\alpha })+(1-\frac{2ϵt}{\alpha })\frac{{Ł}_z^2}{r^2}\right)\left(\frac{3a^2+2\sqrt{r^2-a^2}(3M+\mathsf{\Lambda }{r}^3)}{6r^2\sqrt{r^2-a^2}}\right).\end{array}\end{array}$$

(38)

At the local minima $r_o$ of the effective potential given in Equation (36), the azimuthal angular momentum and energy of the neutral particle are

$${Ł}_{z_o}^2=\frac{(1-\frac{ϵt}{\alpha }){\mathsf{\Omega }}_1\left(r_o\right)}{2(1-\frac{2ϵt}{\alpha }){\mathsf{\Omega }}_2\left(r_o\right)-(1-\frac{ϵt}{\alpha }){\mathsf{\Omega }}_1\left(r_o\right)},$$

(39)

$${E_o}^2=\left(\frac{\sqrt{r_o^2-a^2}}{r_o}-\frac{2M}{r_o}+\frac{\mathsf{\Lambda }{r}_o^2}{3}\right)\left(\frac{2(1-\frac{3ϵt}{\alpha }){\mathsf{\Omega }}_2\left(r_o\right)-\left(\frac{ϵt}{\alpha }\right){\mathsf{\Omega }}_1\left(r_o\right)}{2(1-\frac{2ϵt}{\alpha }){\mathsf{\Omega }}_2\left(r_o\right)-(1-\frac{ϵt}{\alpha }){\mathsf{\Omega }}_1\left(r_o\right)}\right).$$

(40)

where ${\mathsf{\Omega }}_1\left(r_o\right)$ and ${\mathsf{\Omega }}_2\left(r_o\right)$ have the following values:

$${\mathsf{\Omega }}_1\left(r_o\right)=3a^2+2\sqrt{r_o^2-a^2}(3M+\mathsf{\Lambda }{r}_o^3),$$

$${\mathsf{\Omega }}_2\left(r_o\right)=3(r_o^2-a^2)+\sqrt{r_o^2-a^2}(\mathsf{\Lambda }{r}_o^3-6M).$$

When the neutral test particle is moving in ISCO and collides with other incoming particles, the energy and momentum of the test particle will change according to the following equations:

$$L_z\to L_z+r{\upsilon }_e,E^2=\mathsf{\Omega }\left(r\right)\left(1-\frac{ϵt}{\alpha }+\frac{{(L_z+r{\upsilon }_e)}^2(1-\frac{2ϵt}{\alpha })}{r^2}\right)=U_E.$$

(41)

This energy is higher than the energy of the test particle before collision because the colliding particle provides some its energy and momentum to the orbiting test particle. After the simplification of Equation (40), one can obtain the following expression for the escape velocity:

$${\upsilon }_e=-\frac{L_z}{r}\pm \sqrt{\frac{3r{E}^2(1+\frac{2ϵt}{\alpha })-(3\sqrt{r^2-a^2}-6M+r^3\mathsf{\Lambda })(1+\frac{ϵt}{\alpha })}{3\sqrt{r^2-a^2}-6M+r^3\mathsf{\Lambda }}}.$$

(42)

This velocity is orthogonal to the equatorial plane of the orbit. The effective force in the present case takes the following form:

$$\begin{array}{c}\hfill \begin{array}{c}{F}_E=(1-\frac{2ϵt}{\alpha })\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\left(\frac{{Ł}_z({Ł}_z+r{\upsilon }_e)}{r^3}\right)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left(1-\frac{ϵt}{\alpha }+\frac{{(L_z+r{\upsilon }_e)}^2(1-\frac{2ϵt}{\alpha })}{r^2}\right)\left(\frac{a^2}{r^2\sqrt{r^2-a^2}}+\frac{2M}{r^2}+\frac{2\mathsf{\Lambda }r}{3}\right).\end{array}\end{array}$$

(43)

7. Dynamics of Charged Particles

By introducing the magnetic field B around ISCO due to the presence of charge q of the test particle, the new constants of motion are defined as

$$\dot{t}=\frac{(1-\frac{ϵt}{\alpha })E}{\mathsf{\Omega }\left(r\right)},\dot{\varphi }=\frac{{(1-\frac{ϵt}{\alpha })}_z}{r^2{sin}^2\theta }-B,$$

(44)

where $B=\frac{qA}{2m}$, q is the charge and m is the mass of the test particle. A is the vector potential of the magnetic field. Using these values in the Lagrangian given in (12), and using the normalization condition given Equation (34), we obtain the following equation for energy:

$$E^2={\dot{r}}^2+r^2\mathsf{\Omega }\left(r\right){\dot{\theta }}^2+\mathsf{\Omega }\left(r\right)\left((1-\frac{ϵt}{\alpha })+{sin}^2\theta {\left(\frac{L_z(1-\frac{ϵt}{\alpha })}{r{sin}^2\theta }-Br\right)}^2\right),$$

(45)

at the equatorial plane the effective potential of the charged particle will take the following form:

$$U_E=\mathsf{\Omega }\left(r\right)\left((1-\frac{ϵt}{\alpha })+{\left(\frac{L_z(1-\frac{ϵt}{\alpha })}{r}-Br\right)}^2\right).$$

(46)

Equation (46) will lead to the new form of effective force:

$$\begin{array}{c}\hfill \begin{array}{c}{F}_E=\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\left(\frac{(1-\frac{ϵt}{\alpha })({Ł}_z+r{\upsilon }_{)}}{2})-Br\right)\left[(1-\frac{ϵt}{\alpha })\left(\frac{(1-\frac{ϵt}{\alpha }){Ł}_z}{r^2}+B\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left[(1-\frac{ϵt}{\alpha })+{\left(\frac{(1-\frac{ϵt}{\alpha }){Ł}_z}{r^2}-Br\right)}^2\right]\left(\frac{a^2}{r^2\sqrt{r^2-a^2}}+\frac{2M}{r^2}+\frac{2\mathsf{\Lambda }r}{3}\right).\hfill \end{array}\end{array}$$

(47)

Collision of Charged Particles

When the collision of the charged particle takes place in the orbit of the black hole, the colliding particles will shift some energy and momentum to the charged particle. In this case, the effective potential will take the form

$$\begin{array}{c}\hfill E^2=U_E=\mathsf{\Omega }\left(r\right)\left[(1-\frac{ϵt}{\alpha })+{\left(\frac{(L_z+r{\upsilon }_e)(1-\frac{ϵt}{\alpha })}{r}-Br\right)}^2\right].\end{array}$$

(48)

By using Equation (48), one can obtain the following form of effective force for the charged particle

$$\begin{array}{c}\hfill \begin{array}{c}{F}_E=\left(\frac{(1-\frac{ϵt}{\alpha }){Ł}_z}{r^2}+B\right)\left(\frac{(L_z+r{\upsilon }_e)(1-\frac{ϵt}{\alpha })}{r}-Br\right)\left(\frac{\sqrt{r^2-a^2}}{r}-\frac{2M}{r}+\frac{\mathsf{\Lambda }{r}^2}{3}\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left[(1-\frac{ϵt}{\alpha })+{\left(\frac{(1-\frac{ϵt}{\alpha })({Ł}_z+r{\upsilon }_e)}{r}-Br\right)}^2\right]\left(\frac{3a^2+2\sqrt{r^2-a^2}(3M+\mathsf{\Lambda }{r}^3)}{6r^2\sqrt{r^2-a^2}}\right).\hfill \end{array}\end{array}$$

(49)

Additionally, the expression for the escape velocity (orthogonal to the equatorial plane) is

$$\begin{array}{c}\hfill {\upsilon }_e=-\frac{L_z}{r}+(1+\frac{ϵt}{\alpha })\left(Br\pm \sqrt{\frac{3r{E}^2(1+\frac{2ϵt}{\alpha })-(3\sqrt{r^2-a^2}-6M+r^3\mathsf{\Lambda })(1+\frac{ϵt}{\alpha })}{3\sqrt{r^2-a^2}-6M+r^3\mathsf{\Lambda }}}\right).\end{array}$$

(50)

8. Orbit Stability

To check the stability of the orbits of time-conformal QC-AdS-SBH, we use the Lyapunov exponent

$$\begin{array}{c}\hfill \lambda ={\left(\frac{-U_E^{″}\left(r_o\right)}{2{\dot{t}}^2\left(r_o\right)}\right)}^{\frac{1}{2}},\end{array}$$

(51)

Using Equations (33) and (46) in Equation (51) we obtain

$$\begin{array}{c}\hfill \lambda ={\left(\frac{{\lambda }_1}{54r_o^5{E}^2{(r_o^2-a^2)}^{\frac{3}{2}}}+\frac{{\lambda }_2}{54r_o^3{E}^2\sqrt{r_o^2-a^2}}+\frac{{\lambda }_3}{27r_o^4{E}^2}\right)}^{\frac{1}{2}},\end{array}$$

(52)

where

$$\begin{array}{c}\hfill \begin{array}{cc}& {\lambda }_1=\left[(1-\frac{ϵt}{\alpha })+{\left(\frac{(1-\frac{ϵt}{\alpha }){Ł}_z}{r_o}-B{r}_o\right)}^2\right]\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(6a^4-9a^2{r}_o^2+2(\mathsf{\Lambda }{r}_o^3-6M){(r_o^2-a^2)}^{\frac{3}{2}}-\mathsf{\Lambda }{r}_o^3\right){(3\sqrt{r_o^2-a^2}-6M+\mathsf{\Lambda }{r}_o^3)}^2,\hfill \end{array}\end{array}$$

$$\begin{array}{c}{\lambda }_2=2\left(\frac{3(1-\frac{2ϵt}{\alpha })L_z^2}{r_o^4}+B^2\right){\left(6M-3\sqrt{r_o^2-a^2}-\mathsf{\Lambda }{r}_o^3\right)}^3,\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }_3=2\left(\frac{(1-\frac{ϵt}{\alpha })L_z^2}{r_o^3}-B{r}_o\right){\left(3\sqrt{r_o^2-a^2}-6M+\mathsf{\Lambda }{r}_o^3\right)}^2\left(3a^2+2(3M+\mathsf{\Lambda }{r}_o^3)\sqrt{r_o^2-a^2}\right).\hfill \end{array}$$

9. Results and Discussions

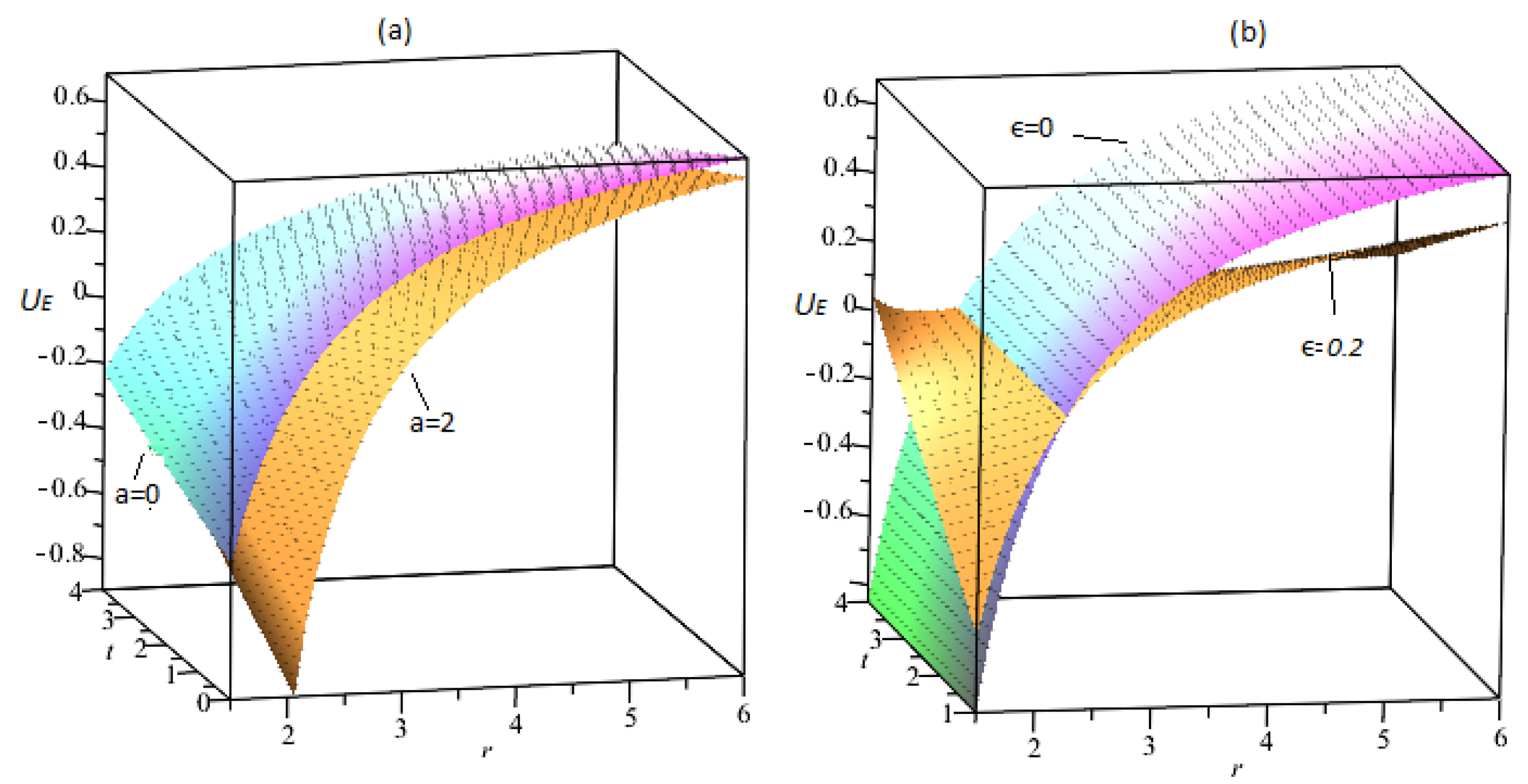
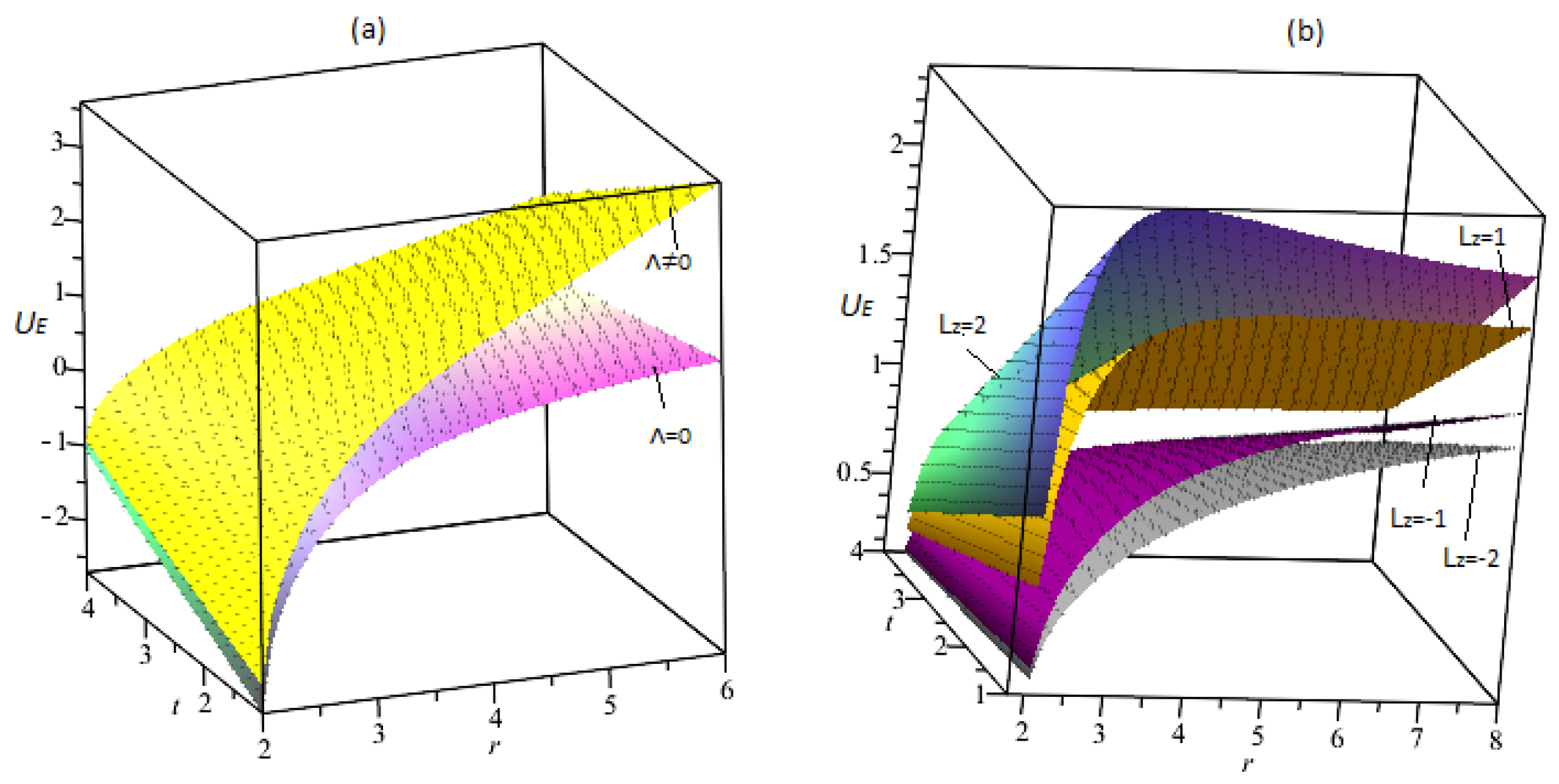
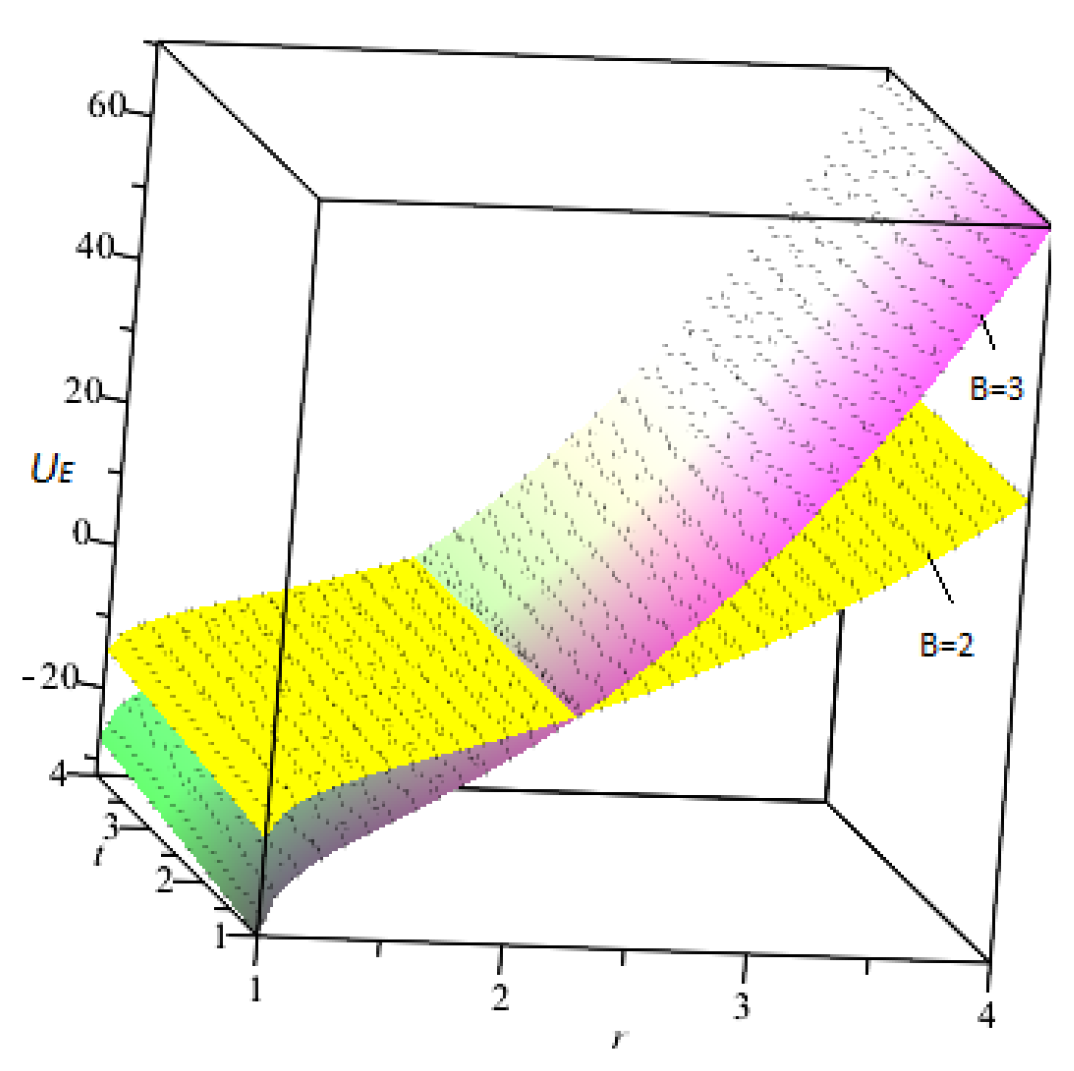
9.1. Effective Potential

In Figure 1, we captured the graphs for the effective potential of neutral particle. Figure 1a describes the effects of the quantum-corrected parameter a on the motion of the test particle. It is observed that increasing values of the quantum-corrected parameter decreases the effective potential on the neutral test particle. For time-conformal AdS-SBH, the effective potential $U_E$ is higher than the time-conformal QC-AdS-SBH. In Figure 1b, we observed the dual nature of time-conformal parameter $ϵ$. In a small range, it has a direct relation with the effective potential $U_E$, but for the large radial coordinate the time-conformal parameter reduces $U_E$. Figure 2 displays the profiles of effective potential of the neutral particle after collision. In Figure 2a, a significant effect of the cosmological constant $\mathsf{\Lambda }$ is observed, and it is noted that both $U_E$ and $\mathsf{\Lambda }$ are directly related to each other. In Figure 2b, considerable growth is observed in $U_E$ for growing values of angular momentum ${Ł}_z$. Figure 3 shows a twofold display of the profiles of effective potential for varying values of magnetic field parameter B. In a small range, $U_E$ and B behave inversely, but for large distances they are directly related.

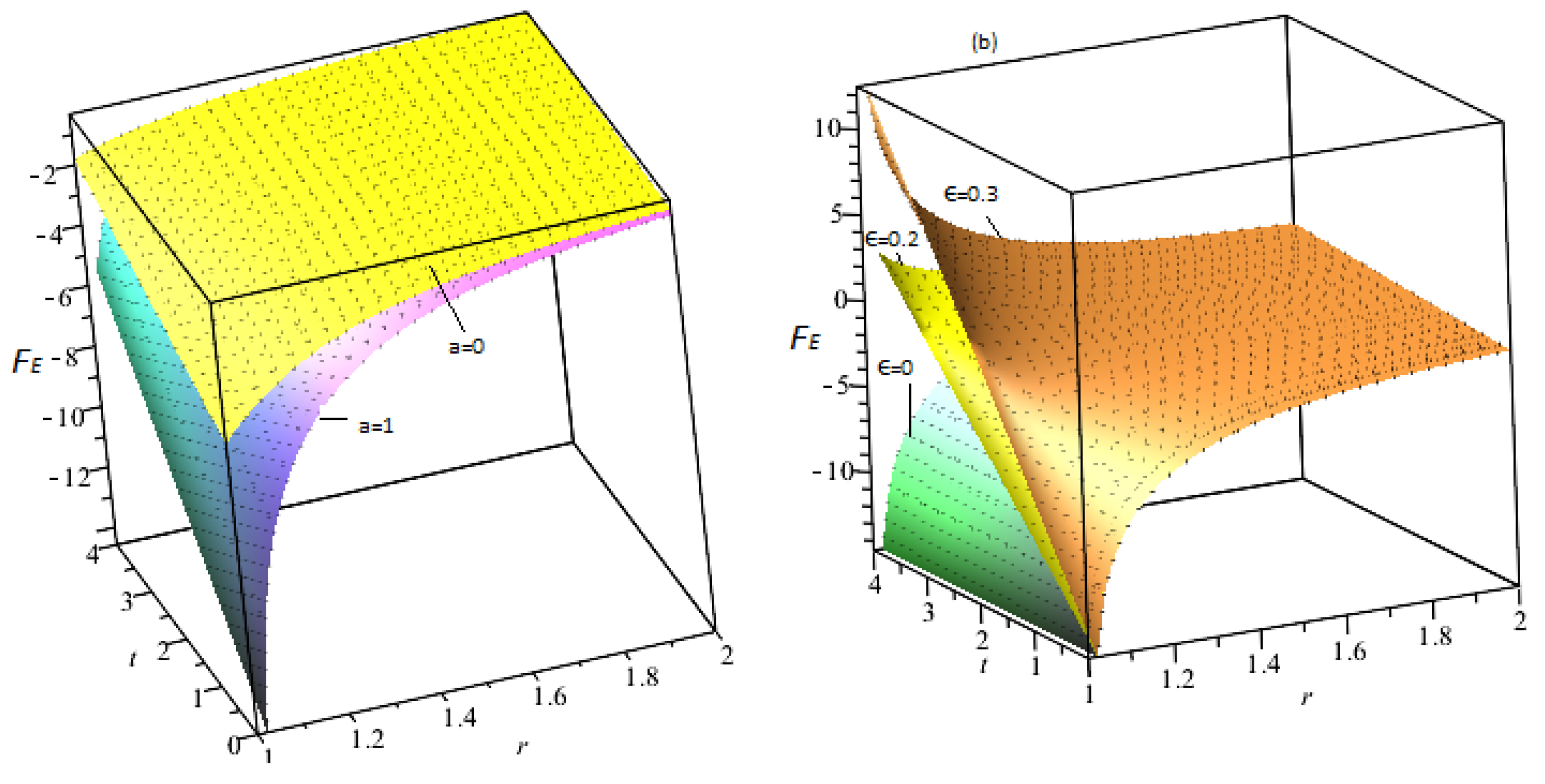
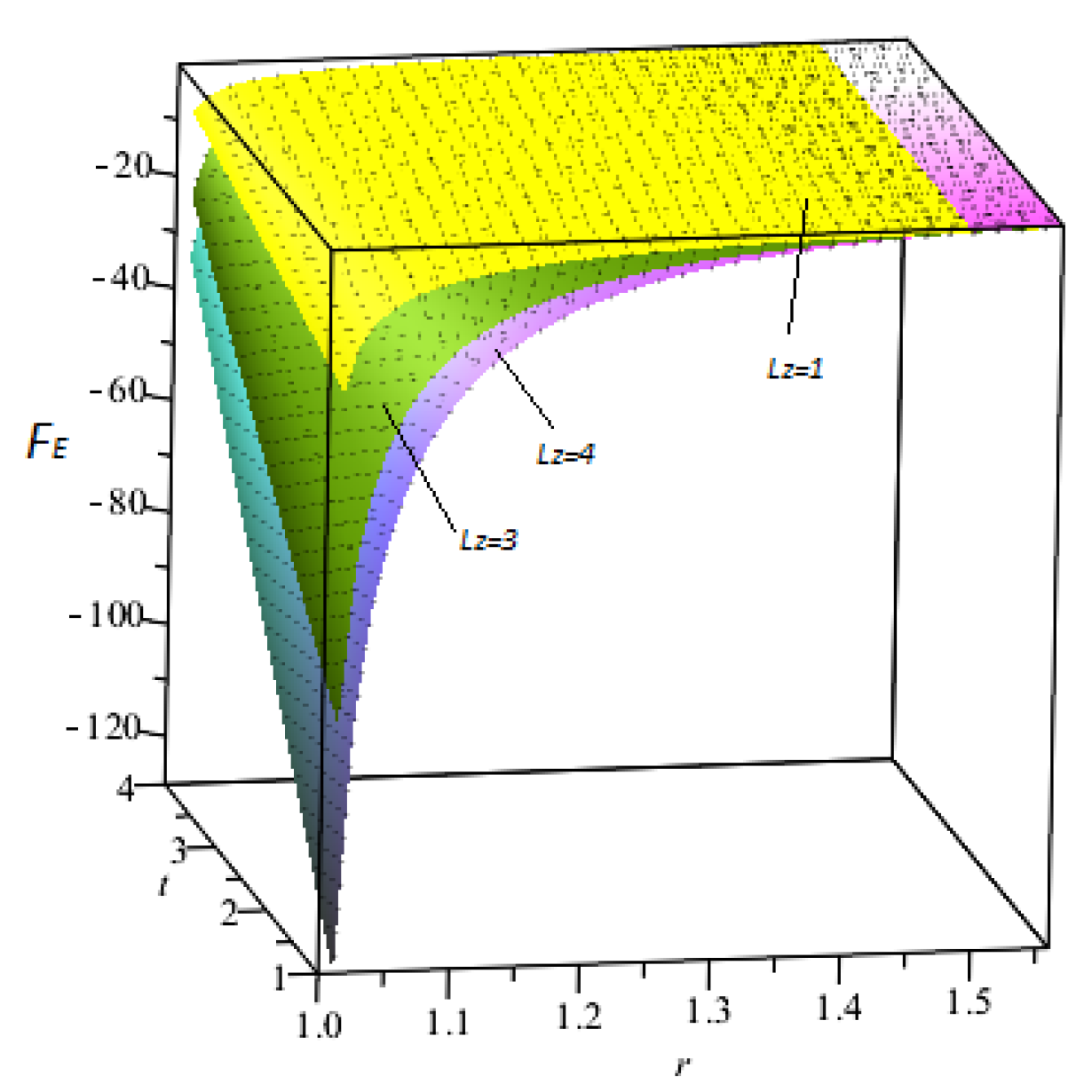
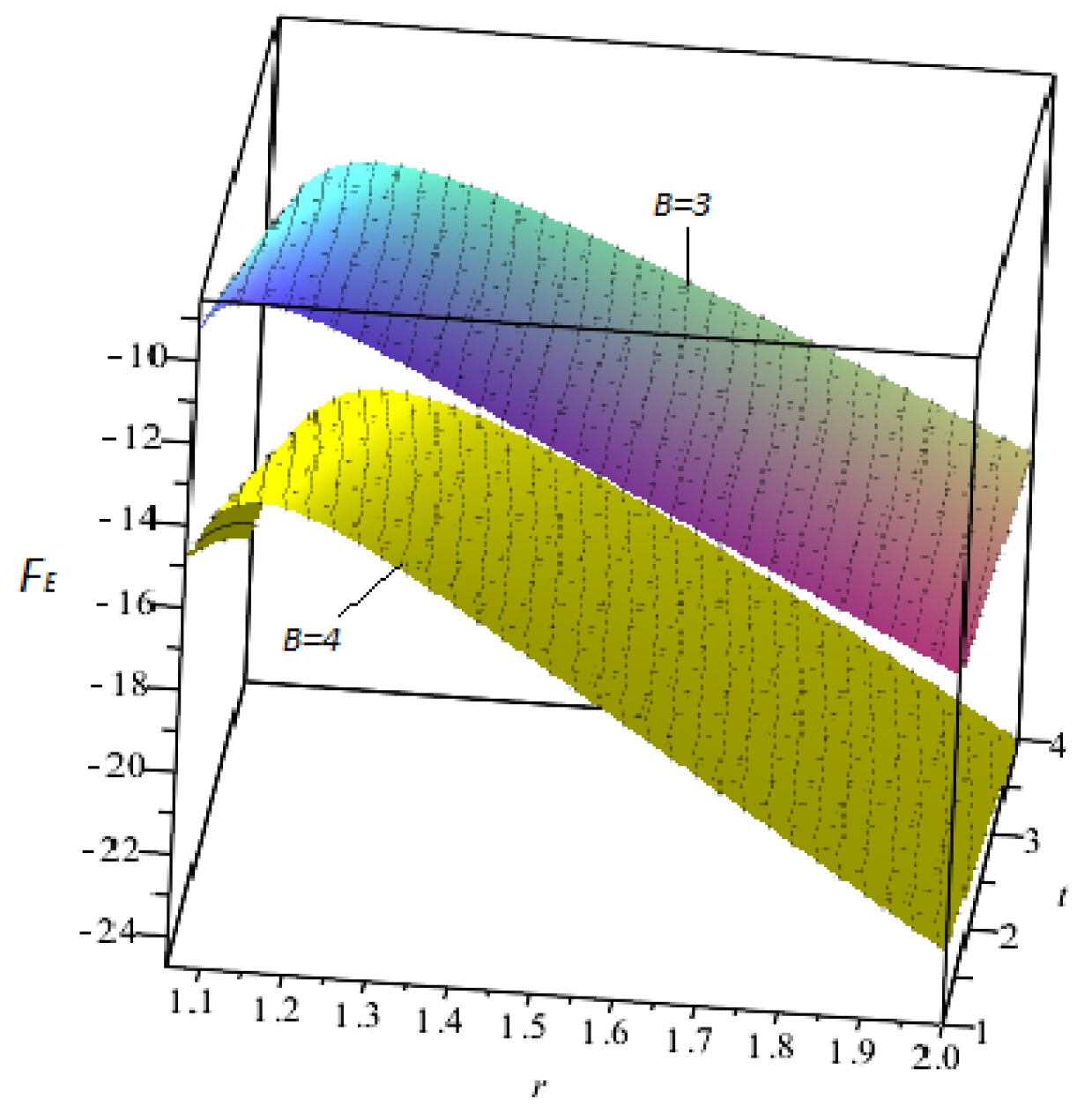
9.2. Effective Force

Figure 4 displays the influence of the quantum-corrected term a and time-conformal parameter $ϵ$ on effective force. In Figure 4a, it is noted that higher values of the quantum-corrected term decreases the repulsive effective force, where in Figure 4b it is noted that the repulsive effective force varies directly as the values of time-conformal parameter increase. Figure 5 shows the decreasing behavior of effective force for increasing values of angular momentum. In Figure 6, the attractive behavior of the effective force is observed, and it is also noticed that the higher influence of the magnetic field reduces the effect of the effective force.

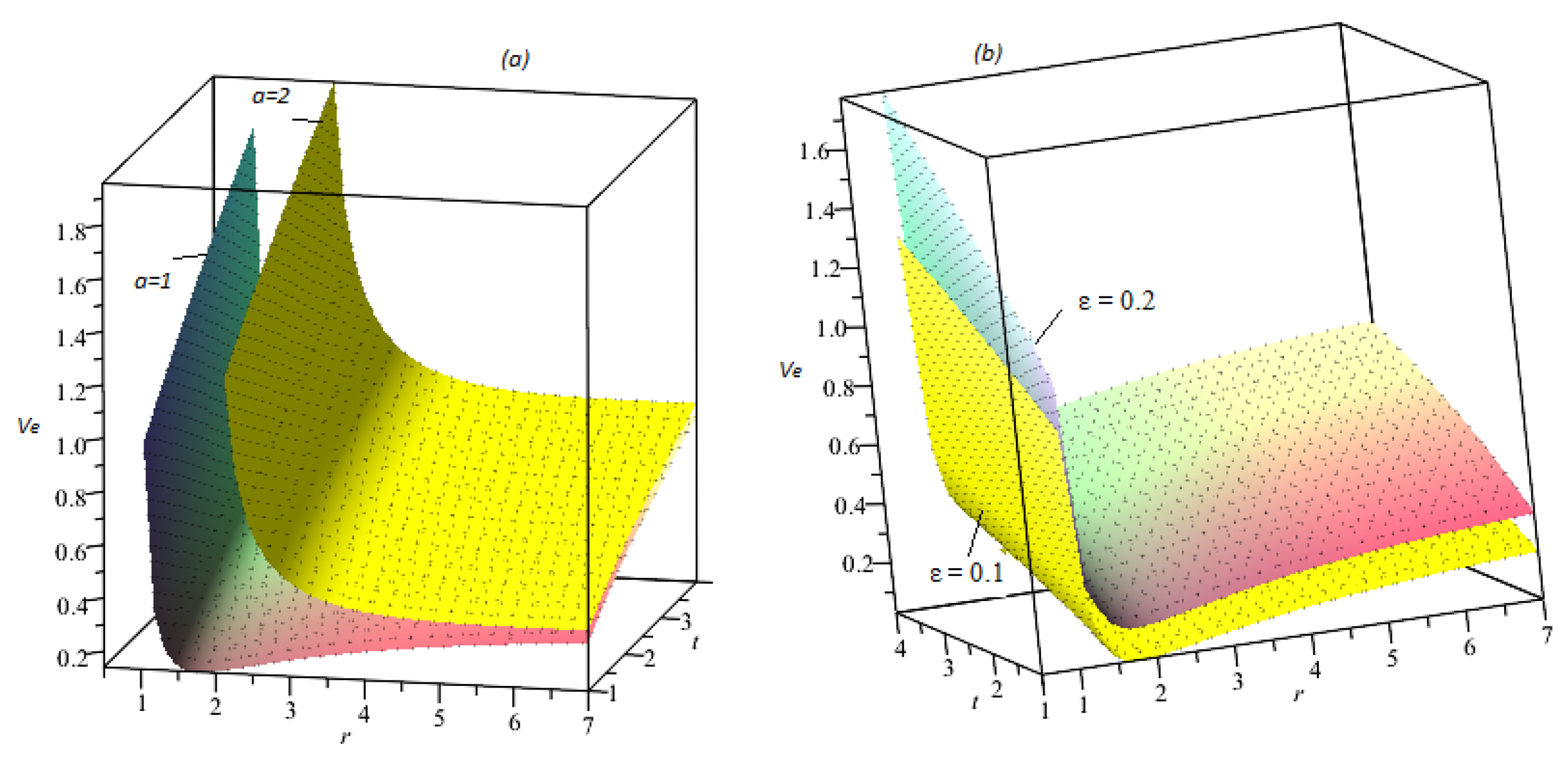
9.3. Escape Velocity

Figure 7 shows a significant hold of quantum-corrected term a and time-conformal parameter $ϵ$ on the escape velocity of the particle. From Figure 7a, it is clear that increasing the values of the quantum-corrected term a, increases the escape velocity of the particle from the orbits of the black hole. Similarly, the increasing behavior of the escape velocity is observed in Figure 7b, demonstrating the increasing influence of the time-conformal parameter $ϵ$. Figure 8 reports the profiles of escape velocity for the test particle for variation in magnetic effect and angular momentum. In Figure 8a, it is noticed that the escape velocity increases with the increase in magnetic field strength. Figure 8b shows that the angular momentum is directly related to the escape velocity of the particle.

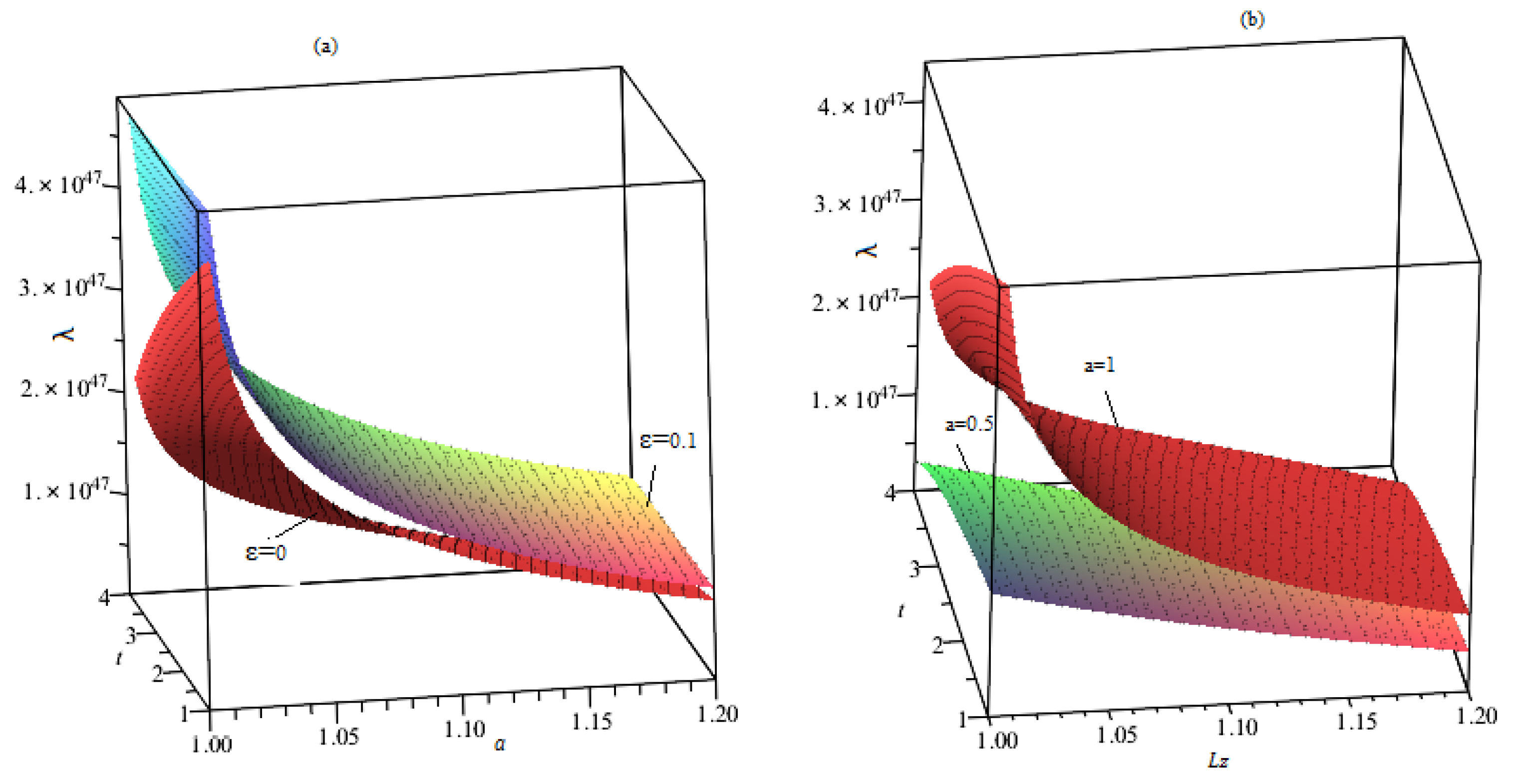
9.4. Orbit Stability

Figure 9 represents the profiles of the Lyapunov exponent for the quantum-corrected term a and the time-conformal parameter $ϵ$. From Figure 9a, it can be observed that the higher values of the time-conformal parameter increase the Lyaponov exponent and decreases the stability of the orbits of the time-conformal QC-AdS-SBH. Figure 9b reveals that the higher inclusion of the quantum-corrected term a increases the the Lyaponov exponent and decreasing the stability of the orbits of the black hole.

10. Conclusions

This manuscript reports the dynamics of test particles (neutral and charged) in the vicinity of time-conformal quantum-corrected AdS–Schwarzschild black hole (QC-AdS-SBH). The time-conformal perturbation is introduced to study the phenomenon of the formation of gravitational waves. As we know that the black hole radiates energy and momentum in the form of gravitational waves (there are other radiations such as the Hawking radiation, which also decreases the mass and energy of the black hole), the mass and energy (ultimately the curvature) of black hole spacetime is decreasing with the passage of time. This suggests that the metric tensor of the black hole should depend on time because its curvature (mass, gravity) is decreasing with time. This is the main motivation behind this type of perturbation (to re-scale the energy and momentum of the black hole). We perturbed the spacetime metric of the given black hole without violating the symmetry structure of the black hole and retained all of the killing vector fields. ${\mathsf{{\rm Y}}}_{\mathbf{1}}$ given in Equation (9) is the killing vector field of spacetime (1), and the energy corresponding to Equation (9) is given in Table 1. After perturbation, the spacetime (1) became the perturbed spacetime given in Equation (11). The Noether symmetries corresponding to the Lagrangian of spacetime given in Equation (11) are given in Equation (23), where ${\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}$ is the first-order perturbed Noether symmetry corresponding to the energy content in spacetime (11). The approximate energy corresponding to ${\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}$ is given in Table 2 as $\left(Ea\right)$. For $ϵ=0$ we have $Ea=E$ (compare Table 1 and Table 2). This means that the perturbation we considered in our work re-scales the energy content in the given spacetime. Thus, the spacetime (1) admits the time-conformal perturbation without losing its symmetry structure and becomes the perturbed spacetime given in Equation (11). After admitting the perturbation, the killing vector field corresponding to the energy content also admits perturbation (compare ${\mathsf{{\rm Y}}}_{\mathbf{1}}$ of Equation (9) and ${\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}$ of Equation (23)). Therefore, ${\mathsf{{\rm Y}}}_{\mathbf{1}}$ is the killing vector field corresponding to the energy content in spacetime (1) and ${\mathsf{{\rm Y}}}_{\mathbf{1}\mathbf{a}}$ is the killing vector field corresponding to the energy content in spacetime given in Equation (11). In other words, E given in Table 1 is the exact energy content in the exact spacetime (1) and $Ea$ given in Table 2 is the approximate energy content in the perturbed spacetime given in Equation (11). Expressions for Hawking temperature and Bekenstein–Hawking entropy are obtained for the inner and outer horizon for the time-conformal black hole QC-AdS-SBH. Expressions for effective potential, effective force, and escape velocity are calculated for neutral and charged particles. Einstein’s field equations are also calculated for time-conformal QC-AdS-SBH. To check the stability of the orbits of the said black hole, we used the Lyapunov exponent. Finally, the effects of the different parameters are discussed with the help of graphical representation. In a nutshell, we have the following concluding remarks:

• The increasing values of the quantum-corrected term a decrease the effective potential.
• The effective potential displays a dual response to the time-conformal parameter $ϵ$. For small ranges, they behave alike. Over large distances, they are inversely proportional to each other.
• The parameters of the cosmological constant $\mathsf{\Lambda }$ and the angular momentum $L_z$ are directly related to the effective potential of the field produced by the given BH.
• In small radial coordinates, the increasing effects of the magnetic field strength are directly related to the effective potential, but for large ranges they are inversely proportional.
• Effective force is directly proportional to the time-conformal parameter $ϵ$, which is inversely related to the quantum-corrected parameter a and the magnetic effects.
• For higher values of quantum-corrected parameter a and time-conformal parameter $ϵ$, the particle can escape more quickly from the orbits of the time-conformal QC-AdS-SBH.
• The angular momentum and the escape velocity are inversely related.
• The magnetic field strength increases the escape velocity of the test particle.
• The orbits of the time-conformal QC-AdS-SBH exhibit stable behavior for higher values of the time-conformal parameter $ϵ$.
• The orbits of the black hole show more stability for higher influences of the quantum-corrected term a.