Abstract
We discuss a method of analysis of symmetric electromagnetic components with magnetic media based on magnetic group theory. In this description, some of the irreducible corepresentations assume complex values with the real parameter . A possible physical interpretation of this parameter is given. We demonstrate the application of the symmetry-adapted linear combination method combined with the corepresentation theory to the problem of current modes in an array of magnetized graphene elements where Faraday and Kerr effects can exist. The elements are described by the magnetic symmetry or . The scattering matrix of the array and its eigensolutions are defined and analyzed and some numerical simulations are presented as well. An example of a waveguide described by symmetry with a specific type of degeneracy is also discussed.
1. Introduction
Symmetry and group theoretical methods play essential roles in quantum mechanics, solid-state physics, crystallography, and photonics (see, for example, [1,2,3,4]). These methods are helpful in obtaining a deeper understanding of physical problems, predicting new solutions, and speeding up numerical calculations [5].
In electrical engineering and electromagnetic problems, the range of applications of group-theoretical methods is very large, starting from symmetric electric circuits [6] and waveguides [7] to parity-time (PT) symmetric systems consisting of both optical loss and gain [8]. A review of the application of group theory to optics and photonics is presented in [9]. In the area of metamaterials [10], for example, the author used the concept of symmetry-adapted linear combination (SALC) of eigensolutions to find longitudinal current modes in metamaterials based on ring resonators. An extended version of this approach was suggested in [11] with an example of a symmetric graphene array, and for this structure, the authors considered both the longitudinal and vertical currents in the structure.
Magneto-optical effects are used in many photonic components. These components include isolators, circulators, routers, sensors, modulators, magnetometers, etc. A review of the magnetoplasmonic effects and devices is given in [12] and a review of magnetically controllable metasurfaces can be found in [13]. Graphene magnetic structures, particularly with the Faraday effect, have been investigated in several works both theoretically [14,15,16,17] and experimentally [18,19].
The symmetry description of magnetic structures requires the inclusion, along with unitary operators, of some nonunitary ones, which present a combination of unitary operators with the time reversal (see, for instance, [1,20,21,22,23,24]). Magnetic group theory and the theory of corepresentations have been used for PT symmetry-breaking systems [8,25,26] and topological magnetic materials [27].
The theory of nonmagnetic groups is a common tool used in classical electromagnetic theory. However, a few works have analyzed the theory of magnetic groups. In some cases, the symmetry description of a magnetic structure can be reduced to nonmagnetic groups, but the complete description in terms of magnetic groups can give valuable additional information, which is the main aim of this work.
As an illustrative example, we chose an array of graphene elements magnetized by a DC magnetic field. In the mathematical description, the magnetic field bias leads to algebra with antiunitary operators of the corresponding group. We apply the SALC approach to the 2D description of the structure where the magnetic group theory is used instead of the classical point group theory. As a result, corepresentations with a free real phase parameter appear. We discuss the physical meaning of this parameter. Another example, namely, a waveguide with a special type of degeneracy due to magnetic symmetry is also given. The 3D description of the Faraday effect by the scattering matrix and its eigensolutions calculated with the help of the magnetic group theory was developed. We discuss several special cases of the scattering matrix solutions. Some numerical results illustrating the theoretical analysis are presented as well.
2. The Problem Description
We shall consider a free-standing infinite array of graphene elements shown in Figure 1. A linearly polarized–normally incident wave with frequency is described by the electric field and by the wave vector (), i.e., . is a uniform DC magnetic field, and are the angles of the Faraday and Kerr rotations, respectively. Four ports (1, 2, 3, 4) are defined as shown in Figure 1 and used below in the circuit theory analysis. A square graphene element is placed symmetrically in a square unit cell. The unit cell of the periodic structure with the associated elements of symmetry is presented in Figure 2a. The center of Cartesian coordinates coincides with the center of the unit cell.
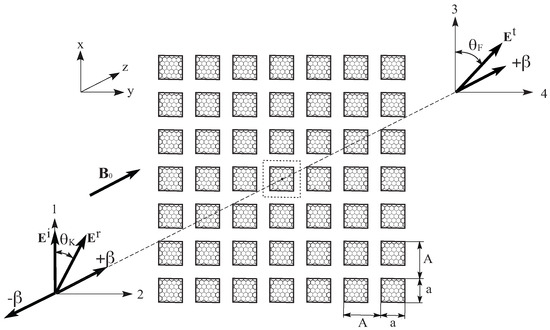
Figure 1.
Array of free-standing square graphene elements where x, y, z is the Cartesian coordinate system; , , and are the electric fields of the incident, transmitted, and reflected waves, respectively, and is the wave vector. is the DC magnetic field and and are the angles of Faraday and Kerr rotation, respectively. Ports 1, 2, 3, and 4 are used in the circuit theory description. A unit cell (dotted line square) is shown in the center of the array.
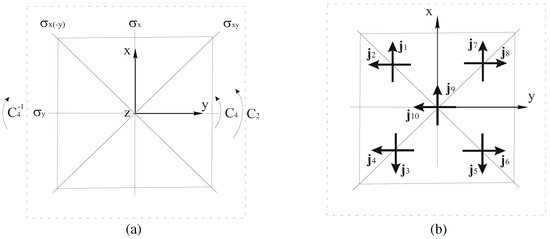
Figure 2.
Square graphene element (solid line square) in a unit cell (dotted line square) of the investigated metasurface: (a) elements of geometrical symmetry of group and (b) current basis .
In the group-theoretical analysis, we do not take into account the translational symmetry of the array, i.e., we work in the long-wave approximation. Such an approximation is fulfilled for sufficiently small dimensions of the unit cell compared to the wavelength of the incident wave, i.e., when the graphene squares and the period have sub-wavelength dimensions. In our case, the period of the array is several times smaller than the electromagnetic wavelength in free space.
Below, we present some numerical results obtained by the eigenfrequency and full-wave simulations using the finite-element method (FEM) implemented in the commercial electromagnetic solver COMSOL Multiphysics®. Floquet boundary conditions on four sides of the unit cells, namely along the x- and y-axis, are used to simulate the periodic structure in the -plane. In the vertical direction (z-axis), the computational domain is limited by two perfectly matched layers backed by scattering boundary conditions in the case of the eigenfrequency analysis. Full-wave simulations were performed by implementing four ports as defined in Figure 1, corresponding to the two linear polarizations of the normally-impinging plane wave at the excitation (ports 1 and 2) and transmission (ports 3 and 4).
The side of the unit cell, i.e., the period of the array, used in numerical calculus is µm and the side of the graphene square is µm. Since the dimensions of the unit cell are subwavelength, no diffraction occurs in the periodic array, hence there is no need to define additional ports. The physical parameters of graphene are given in Appendix A. Graphene’s Drude-type dispersion was naturally implemented in full-wave FEM simulations. In the eigenfrequency analysis, an iterative scheme taking into account graphene’s dispersion was employed for the calculation of the complex eigenfrequencies.
3. Definition of the Scattering Matrix
In optical and microwave problems, different types of matrix methods are used, for example, classical Jones and Mueller matrix techniques, or the matrix technique of Teitler and Henvis [28] and Berreman [29]. In our case, we shall use a more convenient tool that is suitable for our group-theoretical treatment. In the long-wave approximation, one can calculate the structure of the scattering matrix using point symmetry arguments. Notice that this description is valid for the far-field region. The reflected and incident waves are connected by the matrix :
i.e., the scattering matrix can be defined as follows:
where ports 1 and 3 are oriented in the x-direction and ports 2 and 4 in the y-direction (see Figure 1). Ports 1 and 2 and ports 3 and 4 are placed symmetrically with respect to the array plane, i.e., at equal distance from the array.
The scattering matrix of the 4-port must be invariant under any operation of the corresponding group of symmetry [23]. For the unitary operators, we use the commutation relations,
and for the antiunitary ones,
where is the 4D representation of a symmetry operator of the group [23], t in (4) means transposition. For our purposes, in (3) and (4), it is sufficient to use only generators of the corresponding group. Notice that in the scattering matrix description, its structure depends on all of the possible resonant and non-resonant modes, i.e., in our case, it includes left-handed (LH) and right-handed (RH) rotating modes of the graphene current, necessary for the Faraday effect.
4. Symmetry Analysis, Nonmagnetic Case, Symmetry
4.1. Description of Symmetry
In the following, we will use the Schoenflies system of notations of the group elements of symmetry operations, and the notations of the groups [4]. Notice that the notations of the group elements and the notations of the groups themselves may coincide. For example, symbol denotes the operation of the rotation about an axis by , but it also may denote the group , consisting of four elements (see below).
In a nonmagnetic case, the DC magnetic field equals zero. Firstly, we shall restrict our consideration by 2D point symmetry. The square unit cell with the square graphene resonator is described by the group , which consists of eight elements:
- e is the unit element;
- and are reflections in the planes , , respectively;
- and are reflections in the planes passing through the waveguide axis z and the axes and , respectively;
- are rotations by about the axis z;
- and are rotations about the axis z by and , respectively.
Strictly speaking, the whole group in the nonmagnetic case is , where is the time reversal (see Appendix A). However, the elements are usually omitted because they do not provide new information.
Now we shall consider the effects of the symmetry operators on the wave vector and DC magnetic field , which are parallel to the planes , , , and . The unit element e and the rotations , , and preserve the sign of and . The reflection operators , , , and also preserve the sign of (it is a polar vector) but change the sign of because is an axial one (see Table 1). The DC magnetic field is uniform with a fixed direction, which means that in the magnetic case, the elements , , , and cannot exist. These planes are transformed in the antiplanes , , , and (Appendix A). The antiplanes leave invariant (see a discussion in Section 6.1). For the same reason, the pure time reversal operator in the magnetic case cannot also be an element of the group because it changes the sign of .

Table 1.
Effects of the symmetry operators on the wave vector and on DC magnetic field .
4.2. SALCs
Group possesses five irreducible representations (IRs) presented in Table 2. Four of them, namely, , , , and , are one-dimensional (1D), and E is two-dimensional (2D) IR. The relatively high symmetry and the presence of 2D IRs will allow us to discuss the group-theoretical approach more profoundly. The discussion will be conducted in terms of the 2D current densities in the graphene resonator, which are shown in Figure 2b. The unit vectors and belong to orthogonal subspaces; therefore, they can be considered separately.

Table 2.
Irreducible representations of group and possible modes of the square unit cell.
By applying successively the projection operator (A9) of Appendix B to the unit vectors , one can obtain the desired SALCs. A simple example of such calculus is given in Appendix D. In the case of symmetry, eight projection operators exist because there are four 1D representations and one 2D. However, for the 2D IR, one can use only diagonal elements. Therefore, the number of operators is reduced to six. Moreover, due to the symmetry , one can use in calculus only four vectors , say, and , and and . Thus, using Table 2 and Table 3, the SALCs can be easily calculated. They are presented in Table 4.

Table 3.
The basis set change according to the group .

Table 4.
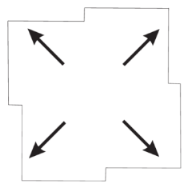
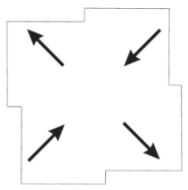
Eigenmodes of the graphene square with symmetry in terms of vectors (see Figure 2b) and the calculated structures of currents and the magnetic field .
Due to the 2D nature of the currents in the graphene and the framework of edge surface plasmon polaritons (SPPs) with exponential dependence of the eigenmode fields along the axis z, not all of the modes predicted by symmetry can be realized in the square graphene resonator, such as , , and . Numerical simulations presented in Table 4 demonstrate that the possible eigenmodes correspond to the IRs (radial mode), and (quadrupole modes), and E (dipole modes). We do not consider higher angular modes, such as hexapole and octopole ones, and higher modes defined by variations of the field along the radial coordinate. Notice that the circular mode , which was not found in the numerical analysis of the SPP eigenfrequencies, can describe, for example, a magnetic dipole resonance in a dielectric resonator [30]. The quadrupole modes and can also exist in dielectric structures [31].
The 1D radial and 1D quadrupole modes and are symmetry-protected dark modes, i.e., they cannot be excited by a plane wave with normal incidence without symmetry breaking [32,33]. In order to excite the dark modes, one needs to reduce symmetry in a special manner. Notice that the unique bright mode is the dipole one belonging to the IR E. Its excitation is polarization-independent because its IR is 2D (see Appendix D).
In contrast to the all-dielectric metasurfaces [34], the imaginary parts of the calculated numerically eigenfrequencies , , and (they are presented in the fourth column of Table 4), in this case, are not zero. However, this is not related to the coupling with external incident fields. The imaginary parts are conditioned by the intrinsic losses in graphene. Notice that the imaginary parts of the resonant frequencies of the dipole modes are higher than those for other modes because they include (along with resistive losses) the effect of coupling with the incident wave.
5. Symmetry Analysis, Magnetic Case, symmetry
5.1. SALCs
We start our discussion on magnetic structures with a lower symmetry . In order to reduce the symmetry , the square graphene patch is cut off at the corners. Possible geometry of the graphene patch possessing symmetry is shown in Figure 3. If the field , the group of symmetry of the unit cell with the patch is of the first category (it is called nonmagnetic group), i.e., it contains the time reversal operator. When the field , the group of symmetry of the unit cell is of the second category (magnetic group), and this group does not have the time reversal operator. The IRs of are given in Table 5. The symmetry degeneration of group in is presented in Appendix C, see Table A3.
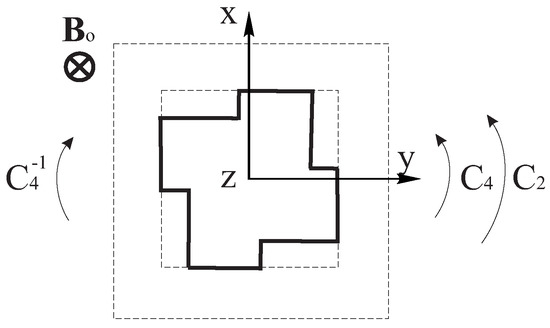
Figure 3.
Graphene element (solid line figure) with symmetry in a square unit cell, is the DC magnetic field.

Table 5.
Irreducible representations of the group.
In groups and , there are only 1D representations, but the IRs and are complex conjugates. Two of these representations define the complex conjugate pair of eigenvectors. Without the DC magnetic field, i.e., in the corresponding group of the first category when symmetry, with respect to the time reversal, exists, such a pair can be considered as one representation E with a dimensionality of two. Therefore, we have a specific two-fold degeneracy. If the system is under the DC magnetic field, the symmetry with respect to time reversal is removed, and the two complex conjugate representations correspond to different eigenvalues.
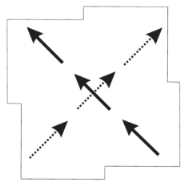
The sense of polarization rotation for the mode and also for the mode (see Table 6)) defined with respect to , does not depend on the direction of the wave propagation. The Faraday effect is defined by the sum of the RH rotating dipole mode of the ICR and the LH rotating dipole of the ICR .

Table 6.
Eigenmodes of the graphene element shown in Figure 3 with symmetry in terms of vectors and calculated structure of currents. The dotted arrow in a RH- or LH-rotated dipole mode means a vector multiplied by the imaginary unit i, i.e., it has the phase shift .
5.2. Scattering Matrix
In a nonmagnetic group , the time reversal operator is a member of the group, and it corresponds to the reciprocity of an object independently of other symmetry elements. In the circuit theory description, this is equivalent to the symmetry of the scattering matrix with respect to the main diagonal.
In both cases, the nonmagnetic group and magnetic group , one can choose as a generator the four-fold rotation . In the 3D symmetry of the diffraction problem, we add in calculus the symmetry plane , which is (see Figure 1). This plane exists in both nonmagnetic and magnetic cases. Using (3), one comes to the matrices for the nonmagnetic () and magnetic () cases, respectively:
The matrix has the simplest form with two complex parameters. The numerical values of depend on the parameters and dimensions of the graphene square and the chosen distance between the ports. Ports 1 and 2, as well as 3 and 4, are decoupled from each other.
Matrix for the magnetic case has four complex parameters. In contrast to the nonmagnetic case, ports 1 and 2, and also 3 and 4 are coupled in a nonreciprocal fashion. The same is true for coupling between ports 1 and 4, and also 2 and 3. Thus, the matrix describes a nonreciprocal structure, where nonreciprocity is related to the angular rotation of fields. However, the coupling between ports 1 and 3 and also between 2 and 4 is reciprocal. Analyzing the matrix for the magnetic case, one can see that in this symmetry Faraday and Kerr effects are possible. With the incident wave , the angle of Faraday rotation can be calculated from Figure 1 as follows: , and the angle of Kerr rotation is defined by . In the following, we will not discuss the details of polarization characteristics.
6. Symmetry Analysis, Magnetic Case, Symmetry
6.1. ICRs
The magnetic group of symmetry of the square graphene element magnetized normally to its plane by the field (see Figure 1 and Figure 2a) is . One can consider the transition from the nonmagnetic to magnetic states from the point of view of the reduction of the symmetry of the system by the DC magnetic field.
The group of the third category belongs to case a) described in Appendix C, i.e., due to the Herring criterion of reducibility of corepresentations [35] (see (A8) of Appendix B), no new degeneracy is introduced by this corepresentation (an example of such degeneracy is given in Appendix E). Comparing Table 2 and Table 7 below, we see that under applied DC magnetic field, four planes of symmetry convert into antiplanes and the unitary subgroup contains only rotations.

Table 7.
Irreducible corepresentations of the group.
The antireflection operators , , , and , where is the restricted time reversal operator [21] (see Appendix B), change the sign of , because is a polar odd in the time vector. However, is an axial odd in time vector and therefore the combined antireflection produces a double change of the sign preserving the sign of the field . Therefore, the antireflection operators transform the forward-traveling wave into the backward-traveling one and the backward wave propagates in the same environment as the forward wave ( is preserved), see Table 1.
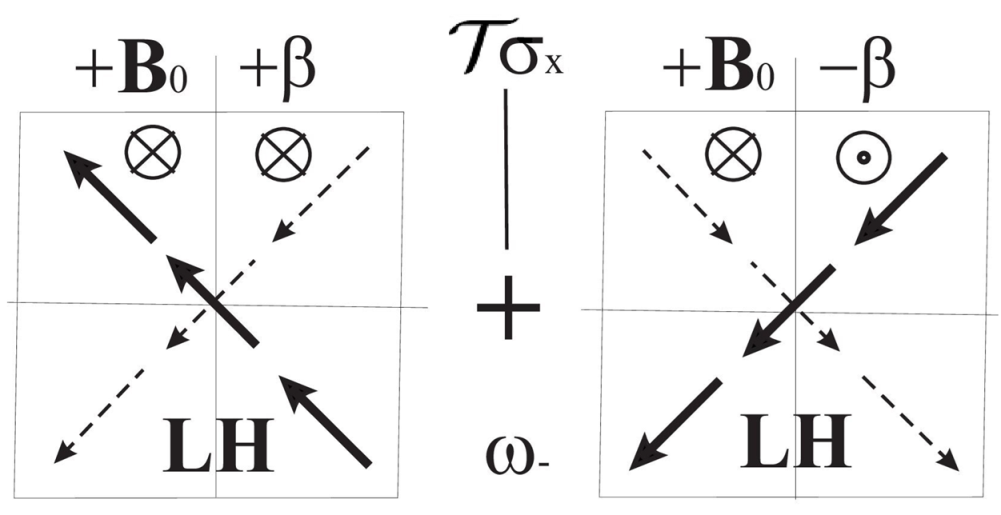
To calculate the ICRs of the given magnetic group, the method of Wigner (see Appendix C) can be used. For our problem, it is straightforward to calculate ICR from the representations of the unitary subgroup listed in Table 5. The calculated ICRs for the group are written in Table 7. In the complex number called phase-function , the parameter can assume any real value. The two signs in the ICRs or of Table 7 for the antiunitary elements correspond to two possible solutions, but these solutions are equivalent.
In our problem, a physical interpretation of parameter s can be as follows. There are several scenarios where a backward wave can exist. For example, (a) the array is situated between two sources, (b) the array is in a resonator with a standing wave, (c) the array is placed on a dielectric substrate, and reflections at the interface between the dielectric and air appear. The unitary part of in 2D space gives the symmetry relations for the currents produced, for example, by the forward wave, but the antiunitary elements define relations for the currents produced by the backward wave. If the 3D symmetry is not given, the waves traveling in the opposite directions arrive at the array with arbitrary phases and this explains the undefined parameter . In a 3D symmetry with the plane of symmetry , the forward and backward waves travel the same way from the sources to the array and arrive at the array with the same phases; therefore, one can set and . This gives constructive interference to the waves. However, in 3D geometry without , is not defined. This problem can be solved by Maxwell’s equations with the corresponding boundary conditions.
6.2. SALCs
The TEM plane wave with normal incidence excites all the currents (for example, ) in a graphene square with the same phase and this phase can be set to zero. The harmonic time dependence of the unit currents is preserved for the given and time-reversed quantities [21]. Therefore, the complex conjugation of the antiunitary elements in Table 8 can be omitted.

Table 8.
The basis set change according to the group.
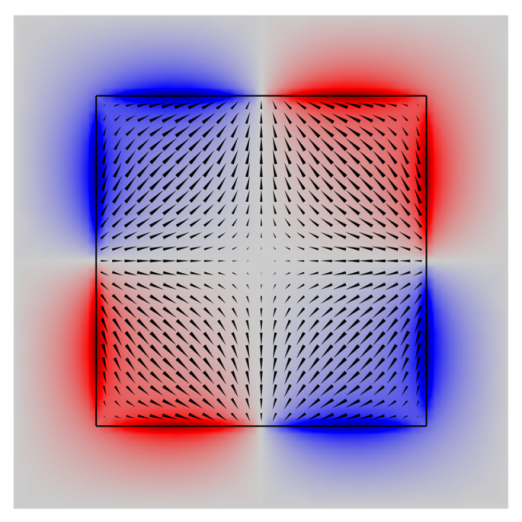
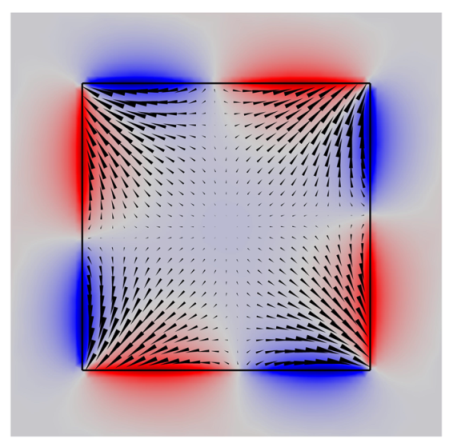
Using the projection operator of (A9) in Appendix B, Table 7 and Table 8, we calculate and present in Table 9 the eigenmodes of graphene square with symmetry in terms of vectors . We used in calculus the upper signs in the ICRs of the antiunitary elements presented in Table 7. The numerically calculated structure of the currents and the magnetic field are given in the last column of Table 9.

Table 9.
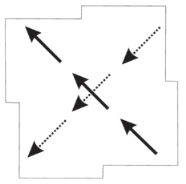
Eigenmodes of the graphene square with symmetry in terms of vectors (see Figure 2b), the calculated structures of the currents, and the magnetic field . is the antiplane of the symmetry. The dotted arrow in the LH or RH rotated dipole mode means a vector multiplied by the imaginary unit i, i.e., a phase shift of . The sense of polarization rotation for the modes and is defined with respect to . The resonance frequency for the LH mode is and for the RH mode is .
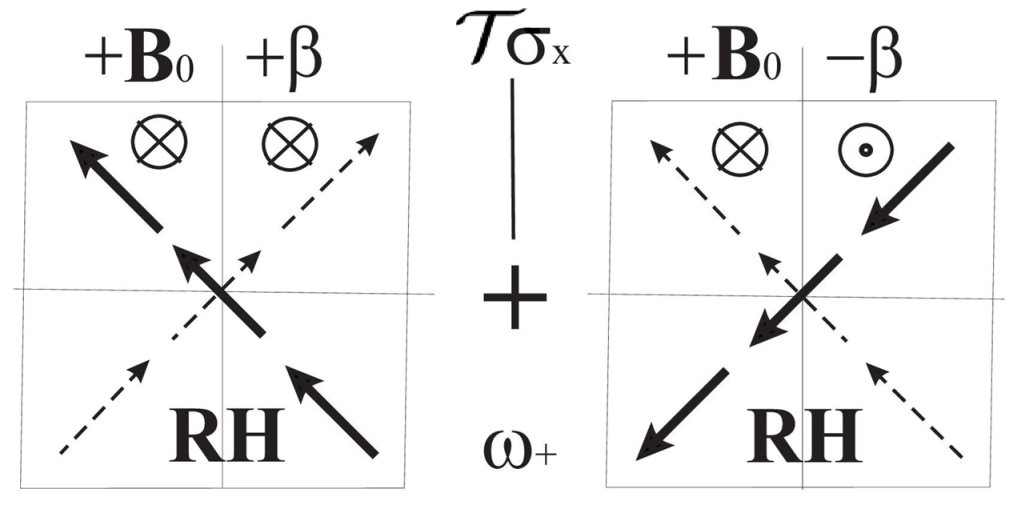
The obtained results can be interpreted as follows. Let us consider, for example, the ICR . It is known from the theory of magnetic groups that antiunitary elements can be obtained by multiplying any chosen antiunitary element by all the elements of the unitary subgroup. In our case, this can be written as ()=(, ). The antiunitary element changes the direction wave of propagation, i.e., and reflects the currents in the plane , changing their directions, preserving the LH or RH sense of rotation due to the combined effects of and . Therefore, the antiunitary elements add to the current structure of group discussed in Section 5.1, the currents with the same structure but for the wave propagating in the opposite direction. In the plane of the array, the sum of these currents related by the multiplier appears. With , the current structure of the ICRs corresponds to the constructive interference. For the ICR , the constructive interference is produced by the parameter .
In the third column of Table 9, we present a schematic illustration of the mathematical expression for the currents given in the second column. For example, for the ICR the RH rotating current mode is produced by the forward wave (the first square). By reflection in the antiplane (this element is a member of the group) one obtains the RH rotating current mode corresponding to the backward wave (the second square) with the same orientation of .
The Faraday effect is defined by a sum of the RH rotating dipole mode of ICR with the resonance frequency and the LH rotating dipole of IR with the resonance frequency . The central frequency of this effect is defined approximately as .
The splitting of the dipole resonance by the DC magnetic field obtained by numerical calculus in eigenfrequency analysis of COMSOL software is demonstrated in Figure 4. These results are confirmed by full-wave analysis assuming an x-polarized incident plane wave in Figure 5 where due to the application of , two dimples in the transmission curve stemming from the resonances of the LH and RH rotating modes appear.
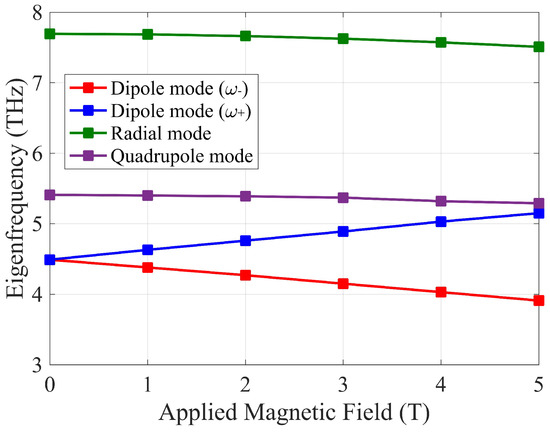
Figure 4.
Dependence of the resonant frequencies of the radial and quadrupole modes on the DC magnetic field and splitting of the dipole resonance by the magnetic field, calculated by eigenfrequency analysis.
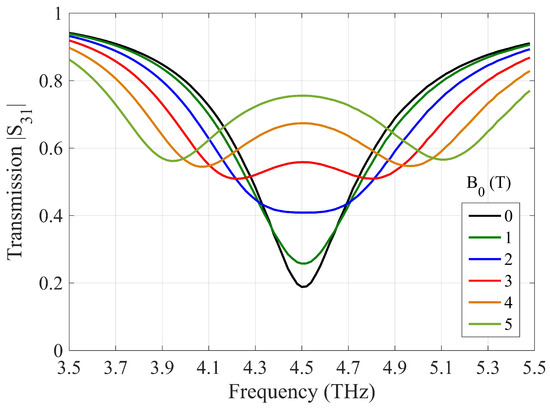
Figure 5.
Transmission spectra of the investigated graphene element array for different values of the DC magnetic field, calculated by full-wave simulations.
6.3. Scattering Matrix, Eigenvalues, and Eigenvectors
The calculated scattering matrices for the nonmagnetic and magnetic cases are, respectively:
Comparing (5) and (6), one can see that despite the different symmetries of the unit cells, the scattering matrices have the same structure.
Now we calculate the eigenvalues of the matrix by solving the equation
where is an eigenvector and is an eigenvalue of the matrix .
The calculated eigenvalues are
where and (and also and ) are complex conjugated. From (8), one can obtain the relations between the scattering matrix elements and the eigenvalues:
The calculated normalized eigenvectors corresponding to eigenvalues are as follows:
In every vector , the first two elements present the RH or LH circular polarized wave entering port 1 and port 2, i.e., from one side of the array, and the other two elements describe the wave entering from the other side of the array, i.e., from port 3 and port 4. These eigenvectors can be used in theoretical and experimental investigations of this and other structures with the same symmetry. Notice that the excitation of only port 1 is determined by the sum of eigenvectors (9), i.e.,
One can simplify further the obtained matrices (6). Using the unitary conditions [36]
where is the unit matrix, means transposition, denotes complex conjugation, one comes to the scattering matrices for the matched nonmagnetic structure without losses:
Let us apply this to the magnetic case. The unitary condition (11) for in (6) leads to the following system of equations:
In the following, we shall consider an ideally matched array with .
In a general case, , and , and
These three simultaneous equations cannot be solved in the used approximations of lossless and ideally matched four-port. In order to resolve this problem, one can put an additional restriction on the matrix elements, such as , , or . Considering, for example, , then , , and the scattering matrix acquires the following form:
where we have omitted the overall phase multiplier. This matrix is defined by one scalar parameter. It describes a nonreciprocal directional coupler with the Faraday effect. It should be noted that our results follow from general symmetry considerations and with the above approximations in the matrix calculus, one loses the effect of possible ellipticity in the transmitted wave. Moreover, in cases of lossless media and ideal matching of the four-port, the symmetry analysis does not permit the Kerr and the Faraday effects to co-exist. Removing these restrictions allows one to consider both the Kerr and the Faraday effects with possible ellipticity of polarization characteristics of the transmitted and reflected waves.
7. Conclusions
We demonstrated the application of group-theoretical methods to electromagnetic structures with magnetic media. The discussed methods are general and can be applied to electromagnetic structures with different geometries, physical parameters, and physical effects. Using the symmetry approach, we calculated and analyzed the scattering matrix of the discussed array of graphene elements. The eigenvalues and eigenvectors of this matrix are defined. The SALC method was extended here to structures described by magnetic groups with antiunitary elements. We clarified the physical meaning of the parameter in the irreducible corepresentations. Considering a square waveguide with ferrite media magnetized by a quadrupole DC magnetic field, we demonstrated the existence of a special degeneracy related to magnetic symmetry. This degeneracy is defined by the Herring test. Most of the discussion was related to the electric currents in graphene. However, it can also be fulfilled in terms of electromagnetic fields. We believe that the presented results and developed methods can be useful in the design and optimization of new electromagnetic components with magnetic media.
Author Contributions
Conceptualization, V.D. and L.P.V.M.; formal analysis, V.D., L.P.V.M. and D.C.Z., methodology, V.D. and L.P.V.M.; software, D.C.Z.; visualization, all authors; writing—original draft preparation, V.D. and L.P.V.M.; writing—review and editing, all authors; supervision, V.D.; funding acquisition, V.D. and D.C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the CNR-FAPESP biennial (2022–2023) bilateral project StReAM “Strongly Resonant All-dielectric Metasurfaces based on quasi-dark and toroidal modes”. V.D. thanks also the Brazilian Agency National Council of Technological and Scientific Development (CNPq) for financial support. D.C.Z. acknowledges the support of the project ECS00000024 “Ecosistemi dell’Innovazione”—Rome Technopole of the Italian Ministry of University and Research, public call n. 3277, PNRR-Mission 4, Component 2, Investment 1.5, financed by the European Union, Next GenerationEU.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Graphene Parameters
The optical properties of graphene can be determined by the surface conductivity , which describes the interaction between graphene with electromagnetic radiation and can be given by Drude’s semi-classical model [37]:
where is the Drude weight, is the minimum conductivity of graphene, eV is the Fermi energy of graphene, ℏ is the reduced Planck’s constant, e is the electron charge, ps is the relaxation time, 1/s and is frequency of the incident electromagnetic wave.
Application of the external magnetic field leads to the circulation of charge carriers in graphene in cyclotron orbits due to the Lorentz force. In this case, the 2D conductivity tensor of graphene with non-zero off-diagonal components can be described by [37]
where is the cyclotron frequency, m/s is the Fermi velocity, and and are the longitudinal (diagonal) and transverse (off-diagonal) parts, respectively. For the device operating the THz frequency range, we consider only the intraband contributions for the calculation of the components of the graphene conductivity tensor []. The influence of interband transitions can be neglected, since the condition is satisfied [38].
Appendix B. Elements of Magnetic Group Theory
Time reversal operator. The time reversal T, which changes the sign of the time, and its combination with geometrical symmetry elements are called the antiunitary operators [1]. The time reversal operator reverses the direction of currents, magnetic fields, and the Poynting vector. In the frequency domain, it also conjugates electromagnetic quantities and this property can be shown easily by the Fourier transform of the time-reversed quantities [21].
It should be stressed that due to causality, the time-reversal symmetries in physical processes do not exist. Moreover, the dissipative processes are not time-reversible. A modified version of this operator called the restricted time reversal operator was suggested in [21]. It is not applied to the dissipative terms of the electromagnetic quantities preserving thus the passive or active nature of the media.
Categories of magnetic groups. The magnetic groups can be divided into three categories. The group of the first category G presents a unitary subgroup H and products of the time reversal with the elements of H. The magnetic groups of the second category do not contain time reversal T. The notations of the groups of the first category and those of the second category coincide. In order to distinguish them, we use the bold-face type for the groups of the second category.
The groups of the third category , which are the most interesting for us, have the so-called antiunitary elements, which present the product of T and the geometrical symmetry elements. We call these elements antielements (for example, antiplane of symmetry). The group of the third category can be described as . These groups can be defined also in a different way, namely, , where B is any antiunitary element of group G. A description of these categories of magnetic groups is given in Table A1

Table A1.
Content of magnetic groups of symmetry.
Table A1.
Content of magnetic groups of symmetry.
| First Category | Second Category | Third Category |
|---|---|---|
| G | ||
| including T | without T | T only in combination |
| with rotation-reflections |
Co-representations. Wigner [1] introduced in the group theory the so-called corepresentations where the term “corepresentation” reminds one of the complex conjugate signs in the matrix multiplication scheme [see (A7) below]. The corepresentations are defined as follows:
where and a are antiunitary elements, u is a unitary one, is an irreducible representation of H.
Homomorphism scheme. The multiplication scheme for corepresentations in the group of the third category, for unitaries and anti-unitaries, is as follows:
Herring rule. This rule [35] defines three special cases:
where is the subgroup order, is the character of corepresentation , where a is an antiunitary element. This rule permits determining the reducibility of the corepresentation. For our purposes, this rule can be read as follows. In case (a), no new degeneracy is introduced; in case (b), the degeneracy of is doubled, i.e., a given representation appears twice and the eigenvectors are different and orthogonal but the eigenvalues are identical; in case (c), the representation is degenerate with the representation , i.e., a pair of different eigenvectors has the same eigenvalue. Hence, in case (a), we may discuss the problem of the degeneracy of group , investigating only the unitary subgroup H. In case (b), the degeneracy of one of the eigenvalues appears, though this degeneracy is absent in subgroup H. In case (c), the degeneracy of two different eigenvectors exists, though it is also not predicted by subgroup H (see Appendix E).
Projection operator. In order to obtain SALCs in the case of a magnetic group of the third category, we use the projection operator [39], which for 2D ICR is written as follows:
where the summation in the first sum is over the unitary elements u, and in the second sum is over the antiunitary ones a, are elements of the corepresentation.
Appendix C. Splitting of IR E of in
The field removes the degeneracy which exists in the square non-magnetized structure due to the representation E. In order to find the representations of the group, which are contained in the representation E of , we write out the characters (i.e., traces of the IR) of Table 2 for IR E corresponding to the operations of the group. It is presented in Table A2.

Table A2.
Characters of the irreducible representation E of group .
Table A2.
Characters of the irreducible representation E of group .
| e | ||||
| E | 2 | −2 | 0 | 0 |
The number of times a given IR appears in the reducible representation is defined by the following relation:
where is the character of the reducible representation, is the character of the irreducible representation. Using this formula, we find:
Therefore, the representation E of of the non-magnetized waveguide splits into the representations and of the unitary subgroup of the magnetized waveguide. The results are presented in Table A3. Many tables of this type are given in [32].

Table A3.
Symmetry degeneration of group in and .
Appendix D. The 2D Eigenvectors of Cases and
In the microwave circuit wave theory [36], one deals with voltage waves. In 2D vector space (see Figure 1), the two-component eigenvectors (wave vectors) and of the incident wave in port 1 and port 2 can be written as follows
In the symmetry , these two modes are degenerate because they belong to the 2D IR E. Under symmetry operators, they are transformed into each other or themselves. For example, the operator applied to and gives
i.e., the basis vector is transformed into and is transformed into . Hence, due to the square form of the unit cell, we deal with the 2D polarization degeneracy.
Any linear combination of the two degenerate eigenvectors and , for example,
is also an eigenvector. This combined vector is transformed also according to the 2D IR E of Table 2.
Now we shall find the symmetry-adapted 2D voltage wave vectors of our magnetized structure with magnetic symmetry . Using the projection operator (A9) of Appendix B for the 1D representation of group and choosing of (A15) as an arbitrary vector , we obtain:
In Equation (A18), , , , . This equation can be explained as follows. The operator e preserves the vector and , so that the first term of the sum is . The operator changes the sign of , i.e., . With , the second term becomes . The operator transforms the vector into and . As a result, we obtain the third term . The last term of the sum is .
Analogously, for the representation , we can write:
The vectors in (A20) describe two circularly polarized modes in the polar representation (rotating basis). They are also eigenvectors of the non-magnetized structure. However, unlike the non-magnetized array with symmetry , vectors and are not degenerate because they belong to different 1D representations of .
Appendix E. Example of Degeneracy Due to Case (C) of (A8), Group
Now we apply it to an object with another magnetic symmetry. In the microwave region, a square metal waveguide filled with ferrite and magnetized by a quadrupole DC magnetic field (Figure A1), as presented in [40]. Here, we discuss this structure from the point of view of the magnetic group theory and Herring rule.
In the nonmagnetic case with symmetry , the two-component eigenvectors and of the incident wave in port 1 and port 2 are given by (A15).
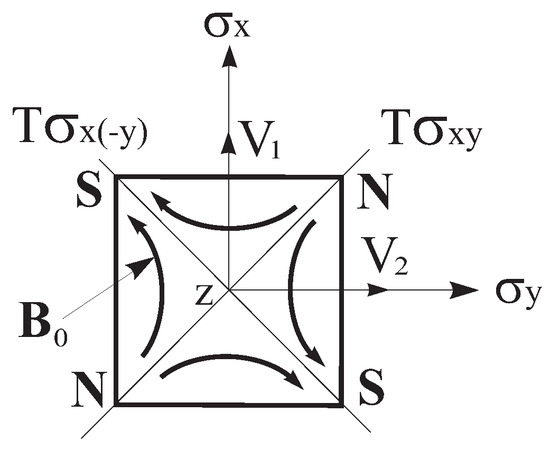
Figure A1.
Cross-section of square metal waveguide with ferrite. Magnetization by a quadrupole DC magnetic field , , and are the poles of the magnet system. and are planes of symmetry, and are antiplanes of symmetry.
In the magnetic case with the quadrupole field , the magnetic group of the third category is . The degeneracy of in is presented in Table A3. The ICRs and of this group are given in Table A4. It is case (c) of (A8). The ICRs and are equivalent because they can be transformed one into another by a unitary matrix.
Considering as an independent group of the first category, we see from Table A5 that no degeneracy is predicted by this group because all of its representations are 1D. The symmetry describes, for example, the rectangular waveguide. The polarization degeneracy in the rectangular waveguide is impossible. Summarizing, the square waveguide with isotropic medium with the symmetry has the polarization degeneracy described by vectors (A15), and the rectangular waveguide with the symmetry does not have such a degeneracy, but the magnetic square waveguide with the symmetry has a degeneracy again. However, the latter degeneracy differs from that of the isotropic square waveguide.

Table A4.
Irreducible corepresentations and of group , .
Table A4.
Irreducible corepresentations and of group , .
| e | ||||||||

Table A5.
Irreducible representations of group .
Table A5.
Irreducible representations of group .
| e | ||||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 |
It is easy to show that the vectors (A15) in the symmetry are not degenerate in the usual sense as it was in the case of the nonmagnetic square waveguide. The antiunitary operators of Table A4 change the sign of the wave vector (see Table 1). Under these operators, the vector is transformed into the vector and vice versa. It means that these two vectors are degenerate if we consider wave propagating in one direction in the waveguide and wave propagating in the opposite direction. A two-component vector is transformed in accordance with 2D IRCs and of Table A4. The overall parameter in the antiunitary operators defines a possible phase shift between the forward and backward waves, i.e., a nonreciprocal phase shift. In our 2D description, this parameter is not defined. If we include into consideration the third coordinate, and there exists the two-fold rotation symmetry with the axis , it gives , and vectors and are interchanged under this operator, i.e., it corresponds to degeneracy and the parameter can be equal to 1. Thus, one can see that this case with is quite different from the one discussed in the main part of the paper case with .
References
- Wigner, E.P. Group Theory; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Harris, D.; Bertolucci, M. Symmetry and Spectroscopy; Dover Publications: New York, NY, USA, 1989. [Google Scholar]
- Lax, M. Symmetry Principles in Solid State and Molecular Physics; Mineola, N.Y., Ed.; Dover Publications Inc.: New York, NY, USA, 2001. [Google Scholar]
- Bradley, C.; Cracknell, A. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups; OUP: Oxford, UK, 2009. [Google Scholar]
- Cohoon, D.K. Reduction of the cost of solving an integral equation arising in electromagnetic scattering through the use of group theory. IEEE Trans. Antennas Propag. 1980, 28, 104–107. [Google Scholar] [CrossRef]
- Riblet, G.P. Eigenvalue-S Matrix Element Relations for Some Common Devices with Two-Fold Symmetry Using Group Theory. IEEE Trans. Circuits Syst. 1980, 27, 1205–1210. [Google Scholar] [CrossRef]
- McIsaak, P.R. Mode Orthogonality in Reciprocal and Nonreciprocal Waveguides. IEEE Trans. Microw. Theory Tech. 1991, 39, 1808–1816. [Google Scholar] [CrossRef]
- Mock, A. Characterization of Parity-Time Symmetry in Photonic Lattices Using Heesh-Shubnikov Group Theory. Opt. Express 2016, 24, 22693–22707. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Lara, B.M.; El-Ganainy, R.; Guerrero, J. Symmetry in optics and photonics: A group theory approach. Sci. Bull. 2018, 63, 244–251. [Google Scholar] [CrossRef]
- Padilla, W.J. Group theoretical description of artificial electromagnetic metamaterials. Opt. Express 2007, 15, 1639–1646. [Google Scholar] [CrossRef]
- Dmitriev, V.; Nascimento, C.; Prosvirnin, S. Extended group-theoretical approach to metamaterials with application to THz graphene fish scale array. IEEE Trans. Antennas Propag. 2015, 63, 5893–5897. [Google Scholar] [CrossRef]
- Maccaferri, N.; Zubritskaya, I.; Razdolski, I.; Chioar, I.A.; Belotelov, V.; Kapaklis, V.; Oppeneer, P.M.; Dmitriev, A. Nanoscale magnetophotonics. J. Appl. Phys. 2020, 127, 080903. [Google Scholar] [CrossRef]
- Bi, Y.; Huang, L.; Li, X.; Wang, Y. Magnetically controllable metasurface and its application. Front. Optoelectron. 2021, 14, 154–169. [Google Scholar] [CrossRef]
- Sounas, D.L.; Caloz, C. Electromagnetic nonreciprocity and gyrotropy of graphene. Appl. Phys. Lett. 2011, 98, 021911. [Google Scholar] [CrossRef]
- Tamagnone, M.; Fallahi, A.; Mosig, J.R.; Perruisseau-Carrier, J. Fundamental limits and near-optimal design of graphene modulators and non-reciprocal devices. Nat. Photon. 2014, 8, 556–563. [Google Scholar] [CrossRef]
- Jiao, N.; Kang, S.; Han, K.; Shen, X.; Wang, W. Shape effects on graphene magnetoplasmons. Phys. Rev. B 2019, 99, 195447. [Google Scholar] [CrossRef]
- Ottomaniello, A.; Zanotto, S.; Baldacci, L.; Pitanti, A.; Bianco, F.; Tredicucci, A. Symmetry enhanced non-reciprocal polarization rotation in a terahertz metal-graphene metasurface. Opt. Express 2018, 26, 3328–3340. [Google Scholar] [CrossRef]
- Yan, H.; Li, Z.; Li, X.; Zhu, W.; Avouris, P.; Xia, F. Infrared Spectroscopy of Tunable Dirac Terahertz Magneto-Plasmons in Graphene. Nano Lett. 2012, 12, 3766–3771. [Google Scholar] [CrossRef]
- Poumirol, J.M.; Liu, P.Q.; Slipchenko, T.M.; Nikitin, A.Y.; Martin-Moreno, L.; Faist, J.; Kuzmenko, A.B. Electrically controlled terahertz magneto-optical phenomena in continuous and patterned graphene. Nat. Commun. 2017, 8, 14626. [Google Scholar] [CrossRef]
- Dimmock, J.O.; Wheeler, R.G. Symmetry properties of wave functions in magnetic crystals. Phys. Rev. 1962, 127, 391–404. [Google Scholar] [CrossRef]
- Altman, C.; Suchy, K. Reciprocity, Spacial Mapping and Time Reversal in Electromagnetics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Bradley, C.J.; Davies, B.L. Magnetic groups and their corepresentations. Rev. Mod. Phys. 1968, 40, 359. [Google Scholar] [CrossRef]
- Barybin, A.A.; Dmitriev, V.A. Modern Electrodynamics and Coupled-Mode Theory: Application to Guided-Wave Optics; Rinton Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Dmitriev, V.; Santos, S.; Evlyukhin, A.B.; Kupriianov, A.S.; Tuz, V.R. Toroidic and antitoroidic orders in hexagonal arrays of dielectric trimers: Magnetic group approach. Phys. Rev. B 2021, 103, 165402. [Google Scholar] [CrossRef]
- Zhao, H.; Feng, L. Parity–Time symmetric photonic. Natl. Sci. Rev. 2018, 5, 183–199. [Google Scholar] [CrossRef]
- Ge, L.; Stone, A. Parity-Time Symmetry Breaking beyond One Dimension: The Role of Degeneracy. Phys. Rev. X 2014, 4, 031011. [Google Scholar] [CrossRef]
- Zhang, R.X.; Liu, C.X. Topological magnetic crystalline insulators and corepresentation theory. Phys. Rev. B 2015, 91, 115317. [Google Scholar] [CrossRef]
- Teitler, S.; Henvis, B.W. Refraction in Stratified, Anisotropic Media. J. Opt. Soc. Am. 1970, 60, 830–834. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in stratified and anisotropic media: 4×4-matrix formulation. J. Opt. Soc. Am. 1972, 62, 502–510. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Algorri, J.F.; López-Higuera, J.M.; Hernandez-Figueroa, H.E.; Dmitriev, V. Quasi-dark resonances with antiferromagnetic order in silicon metasurfaces. Sci. Rep. 2022, 12, 12975. [Google Scholar] [CrossRef]
- Algorri, J.F.; Dell’Olio, F.; Roldán-Varona, P.; Rodríguez-Cobo, L.; López-Higuera, J.M.; Sánchez-Pena, J.M.; Dmitriev, V.; Zografopoulos, D.C. Analogue of electromagnetically induced transparency in square slotted silicon metasurfaces supporting bound states in the continuum. Opt. Express 2022, 30, 4615–4630. [Google Scholar] [CrossRef]
- Overvig, A.C.; Malek, S.C.; Carter, M.J.; Shrestha, S.; Yu, N. Selection rules for quasibound states in the continuum. Phys. Rev. B 2020, 102, 035434. [Google Scholar] [CrossRef]
- Chernyak, A.M.; Barsukova, M.G.; Shorokhov, A.S.; Musorin, A.I.; Fedyanin, A.A. Bound States in the Continuum in Magnetophotonic Metasurfaces. JETP Lett. 2020, 11, 46–49. [Google Scholar] [CrossRef]
- Dmitriev, V.; Zografopoulos, D.C.; Santos, S.D.S.; da Silva Barros, G.F. Flat metasurfaces with square supercells of 2×2 dielectric disk quadrumers: Tailoring the fine structure of toroidal mode local field. J. Phys. D Appl. Phys. 2022, 55, 205104. [Google Scholar] [CrossRef]
- Hering, C. Effect of Time-Reversal Symmetry on Energy Bands of Crystals. Phys. Rev. 1937, 52, 361. [Google Scholar] [CrossRef]
- Altman, J.L. Microwave Circuits; Van Nostrand: New York, NY, USA, 1964. [Google Scholar]
- Gonçalves, P.A.D.; Peres, N.M. An Introduction to Graphene Plasmonics; World Scientific Publishing: Singapore, 2016. [Google Scholar]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.; Vasilevskiy, M.I. A primer on surface plasmon-polaritons in graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef]
- Rudra, P. On irreducible corepresentations of finite magnetic groups. J. Math. Phys. 1974, 15, 2031–2035. [Google Scholar] [CrossRef]
- Helszajn, J.; Leeson, W.; Lynch, D.J.; O’Donnell, B.C. Normal Mode Nomenclature of Quadrupole Gyromagnetic Waveguides. IEEE Trans. Microw. Theory Tech. 1991, 39, 461–470. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).