A Study of Positivity Analysis for Difference Operators in the Liouville–Caputo Setting
Abstract
1. Introduction
2. Discussions and Results
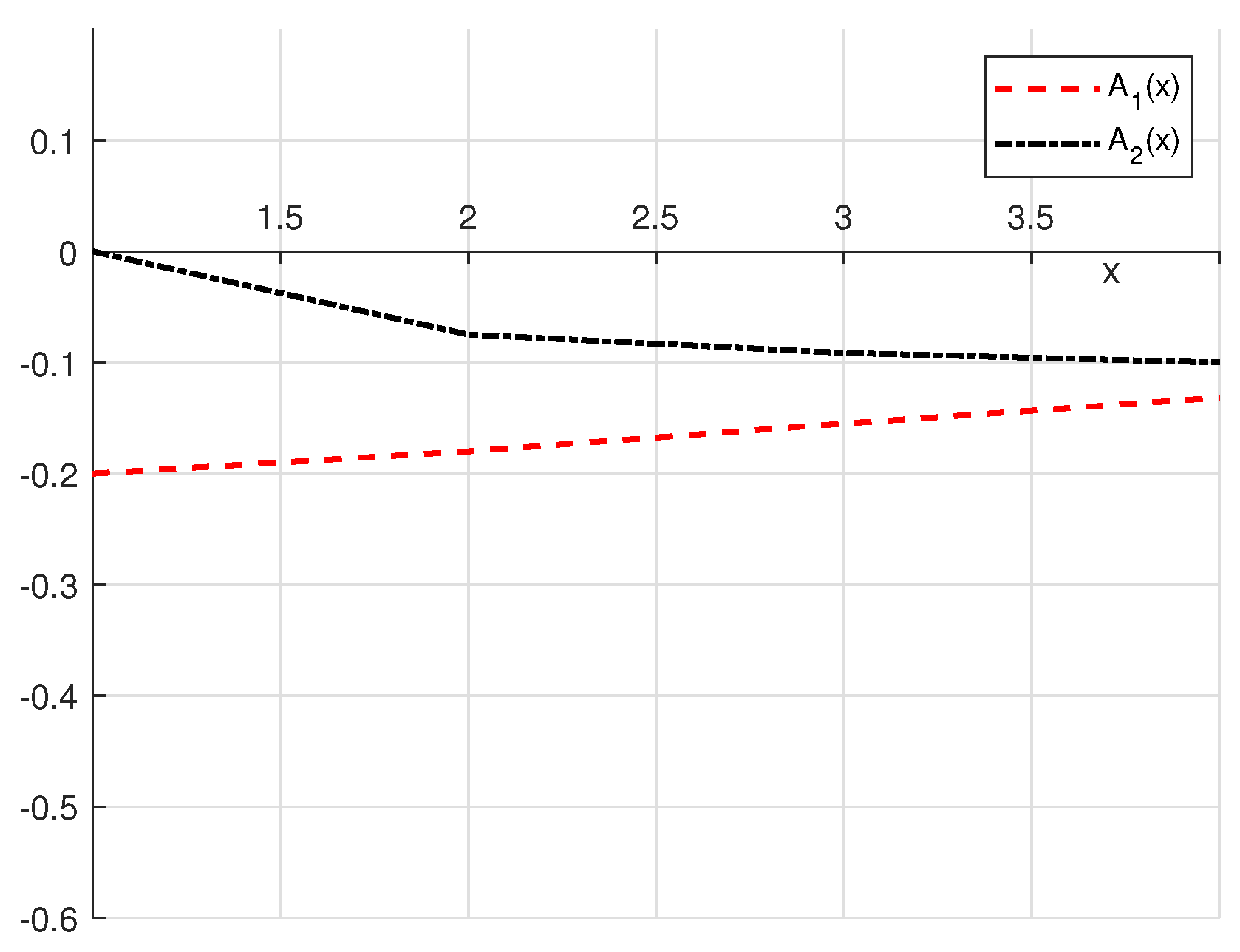
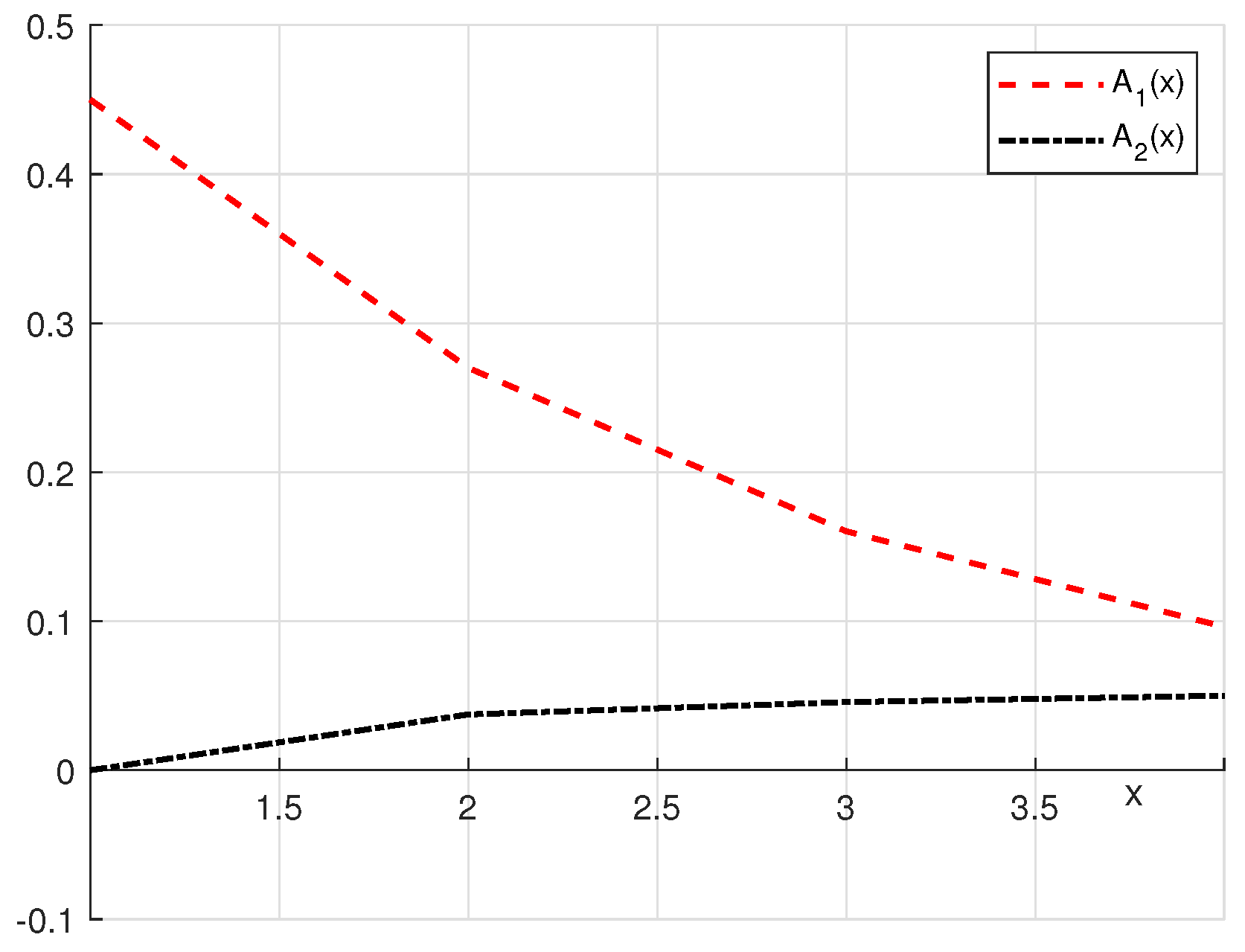
3. Test Examples
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atici, F.M.; Eloe, P.W. A transform method in discrete fractional calculus. Int. J. Differ. Equ. 2007, 2, 165–176. [Google Scholar]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, I, 1–2. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Al-Mdallal, Q.M.; Hajji, M.A. Arbitrary order fractional difference operators with discrete exponential kernels and applications. Discret. Dyn. Nat. Soc. 2017, 2017, 4149320. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Atici, F. On the definitions of nabla fractional operators. Abstr. Appl. Anal. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. Monotonicity analysis of a nabla discrete fractional operator with discrete Mittag-Leffler kernel. Chaos Solitons Fractals 2017, 116, 1–5. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Madjidi, F. Lyapunov-type inequalities for fractional difference operators with discrete Mittag-Leffler kernel of order 2<α<5/2. Eur. Phys. J. Spec. Top. 2017, 226, 3355–3368. [Google Scholar]
- Chen, C.R.; Bohner, M.; Jia, B.G. Ulam-hyers stability of Caputo fractional difference equations. Math. Methods Appl. Sci. 2019, 42, 7461–7470. [Google Scholar] [CrossRef]
- Ferreira, R.A.C.; Torres, D.F.M. Fractional h-difference equations arising from the calculus of variations. Appl. Anal. Discret. Math. 2011, 5, 110–121. [Google Scholar] [CrossRef]
- Lizama, C. The Poisson distribution, abstract fractional difference equations, and stability. Proc. Am. Math. Soc. 2017, 145, 3809–3827. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dyn. 2015, 80, 1697–1703. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Peterson, A.C. Discrete Fractional Calculus; Springer: Berlin, Germany, 2015. [Google Scholar]
- Dahal, R.; Goodrich, C.S. A monotonicity result for discrete fractional difference operators. Arch. Math. 2014, 102, 293–299. [Google Scholar] [CrossRef]
- Atici, F.; Uyanik, M. Analysis of discrete fractional operators. Appl. Anal. Discret. Math. 2015, 9, 139–149. [Google Scholar] [CrossRef]
- Baoguo, J.; Erbe, L.; Peterson, A. Some relations between the Caputo fractional difference operators and integer-order differences. Electron. J. Differ. Equ. 2015, 2015, 1–7. [Google Scholar]
- Bravo, J.; Lizama, C.; Rueda, S. Qualitative properties of nonlocal discrete operators. Math. Methods Appl. Sci. 2022, 45, 6346–6377. [Google Scholar] [CrossRef]
- Dahal, R.; Goodrich, C.S. Mixed order monotonicity results for sequential fractional nabla differences. J. Differ. Equ. Appl. 2019, 25, 837–854. [Google Scholar] [CrossRef]
- Du, F.; Jia, B.; Erbe, L.; Peterson, A. Monotonicity and convexity for nabla fractional (q, h)-differences. J. Differ. Equ. Appl. 2016, 22, 1224–1243. [Google Scholar] [CrossRef]
- Erbe, L.; Goodrich, C.S.; Jia, B.; Peterson, A. Monotonicity results for delta fractional differences revisited. Math. Slovaca 2017, 67, 895–906. [Google Scholar] [CrossRef]
- Goodrich, C.S. A note on convexity, concavity, and growth conditions in discrete fractional calculus with delta difference. Math. Inequal. Appl. 2016, 19, 769–779. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Jonnalagadda, J.M.; Lyons, B. Convexity, monotonicity, and positivity results for sequential fractional nabla difference operators with exponential kernels. Math. Methods Appl. Sci. 2021, 44, 7099–7120. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Lizama, C. A transference principle for nonlocal operators using a convolutional approach: Fractional monotonicity and convexity. Israel J. Math. 2020, 236, 533–589. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Lyons, B.; Velcsov, M.T. Analytical and numerical monotonicity results for discrete fractional differences with negative lower bound. Commun. Pure Appl. Anal. 2021, 20, 339–358. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Muellner, M. An analysis of the sharpness of monotonicity results via homotopy for sequential fractional operators. Appl. Math. Lett. 2019, 98, 446–452. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammed, P.O.; Srivastava, H.M.; Al-Sarairah, E.; Hamed, Y.S. On convexity analysis for discrete delta Riemann–Liouville fractional differences analytically and numerically. J. Inequal. Appl. 2023, 2023, 4. [Google Scholar] [CrossRef]
- Liu, X.; Du, F.; Anderson, D.; Jia, B. Monotonicity results for nabla fractional h-difference operators. Math. Methods Appl. Sci. 2020, 44, 1207–1218. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Almutairi, O.; Agarwal, R.P.; Hamed, Y.S. On convexity, monotonicity and positivity analysis for discrete fractional operators defined using exponential kernels. Fractal Fract. 2022, 6, 55. [Google Scholar] [CrossRef]
- Atici, F.M.; Atici, M.; Nguyen, N.; Zhoroev, T.; Koch, G. A study on discrete and discrete fractional pharmacokinetics-pharmacodynamics models for tumor growth and anti-cancer effects. Comput. Math. Biophys. 2019, 7, 10–24. [Google Scholar] [CrossRef]
- Atici, F.M.; Atici, M.; Belcher, M.; Marshall, D. A new approach for modeling with discrete fractional equations. Fund. Inform. 2017, 151, 313–324. [Google Scholar]
- Mohammed, P.O.; Baleanu, D.; Abdeljawad, A.; Al-Sarairah, E.; Hamed, Y.S. Monotonicity and extremality analysis of difference operators in Riemann-Liouville family. AIMS Math. 2023, 8, 5303–5317. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Abdeljawad, T.; Hamasalh, F.K. On Riemann-Liouville and Caputo fractional forward difference monotonicity analysis. Mathematics 2021, 9, 1303. [Google Scholar] [CrossRef]
- Mohammed, P.O.; O’Regan, D.; Brzo, A.B.; Abualnaja, K.M.; Baleanu, D. Analytical results for positivity of discrete fractional operators with approximation of the domain of solutions. AIMS Math. 2022, 7, 15812–15823. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Dahal, R.; Goodrich, C.S.; Hamed, Y.S.; Baleanu, D. Analytical and numerical negative boundedness of fractional differences with Mittag–Leffler kernel. AIMS Math. 2023, 8, 5540–5550. [Google Scholar] [CrossRef]
- Wu, F.; Liu, J. Discrete fractional creep model of salt rock. J. Comput. Complex. Appl. 2016, 2, 1–6. [Google Scholar]
- Atici, F.; Şengül, S. Modeling with discrete fractional equations. J. Math. Anal. Appl. 2010, 369, 1–9. [Google Scholar] [CrossRef]
| 0 |
| 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Mohammed, P.O.; Guirao, J.L.G.; Baleanu, D.; Al-Sarairah, E.; Jan, R. A Study of Positivity Analysis for Difference Operators in the Liouville–Caputo Setting. Symmetry 2023, 15, 391. https://doi.org/10.3390/sym15020391
Srivastava HM, Mohammed PO, Guirao JLG, Baleanu D, Al-Sarairah E, Jan R. A Study of Positivity Analysis for Difference Operators in the Liouville–Caputo Setting. Symmetry. 2023; 15(2):391. https://doi.org/10.3390/sym15020391
Chicago/Turabian StyleSrivastava, Hari Mohan, Pshtiwan Othman Mohammed, Juan Luis G. Guirao, Dumitru Baleanu, Eman Al-Sarairah, and Rashid Jan. 2023. "A Study of Positivity Analysis for Difference Operators in the Liouville–Caputo Setting" Symmetry 15, no. 2: 391. https://doi.org/10.3390/sym15020391
APA StyleSrivastava, H. M., Mohammed, P. O., Guirao, J. L. G., Baleanu, D., Al-Sarairah, E., & Jan, R. (2023). A Study of Positivity Analysis for Difference Operators in the Liouville–Caputo Setting. Symmetry, 15(2), 391. https://doi.org/10.3390/sym15020391












