Analytical Explicit Formulas of Average Run Length of Homogenously Weighted Moving Average Control Chart Based on a MAX Process

Abstract

Statistical process control (SPC) is used for monitoring and detecting anomalies in processes in the areas of manufacturing, environmental studies, economics, and healthcare, among others. Herein, we introduce an innovative SPC approach via mathematical modeling and report on its application via simulation studies to examine its suitability for monitoring processes involving correlated data running on advanced control charts. Specifically, an approach for detecting small to moderate shifts in the mean of a process running on a homogenously weighted moving average (HWMA) control chart, which is symmetric about the center line with upper and lower control limits, is of particular interest. A mathematical model for the average run length (ARL) of a moving average process with exogenous variables (MAX) focused only on the zero-state performance of the HWMA control chart is derived based on explicit formulas. The performance of our approach was investigated in terms of the ARL, the standard deviation of the run length (SDRL), and the median run length (MRL). Numerical examples are given to illustrate the efficacy of the proposed method. A detailed comparative analysis of our method for processes on HWMA and cumulative sum (CUSUM) control charts was conducted for process mean shifts in many situations. For several values of the design parameters, the performances of these two control charts are also compared in terms of the expected ARL (EARL), expected SDRL (ESDRL), and expected MRL (EMRL). It was found that the performance of the HWMA control chart was superior to that of the CUSUM control chart for several process mean shift sizes. Finally, the applicability of our method on a HWMA control chart is provided based on a real-world economic process.

1. Introduction

One aspect of statistical process control (SPC), the control chart, is a graphical tool used in quality control and process management to monitor quality, reduce variability, continually improve operability, etc. It is used for operations in many fields, such as the natural sciences, engineering, finance, and medicine. The main objective of a control chart is to detect the occurrence of an out-of-control situation as quickly as possible. There are several types of control charts, each of which can be used to monitor and analyze different parts of a process. In general, the selection of a control chart depends on the type of process and the purpose of the process monitoring. For instance, the Shewhart control chart can track and display large variations in a process parameter over time, whereas the exponentially weighted moving average (EWMA) control chart [1], in which more weight is placed on recent data points, is responsive to small to medium changes in a process parameter. Page [2] proposed the cumulative sum (CUSUM) control chart that can also detect small to moderate shifts in a process parameter by cumulatively summing deviations from the target value over time. Abbas [3] proposed the homogeneously weighted moving average (HWMA) control chart in which specific weights are applied to the current and previous samples. After studying the performance of the HWMA control chart for non-normal processes, they determined that the parameters of the chart could be modified to make it more robust to non-normality. Additionally, recent research by Abbas [3] examined that the relative efficacy of the HWMA control chart was superior to that of the CUSUM and EWMA control charts. Recently, Knoth et al. [4] focused attention on several concerns regarding the HWMA control chart by stating, “In steady-state, the HWMA chart loses performance relative to the EWMA chart”. In order to address these concerns, the performance of the HWMA control chart has been reinvestigated under steady and zero conditions at various shifts and smoothing parameters, Riaz et al. [5]. It has been found that the HWMA control chart is superior to the EWMA control chart for several shift sizes under zero state. Consequently, the authors aimed to provide an explicit formula for the average run length of the HWMA control chart in order to compare how well the control charts identified process changes. We have assumed that a change in the process occurs at the very beginning, the so-called zero-state.

Usually, control charts such as EWMA, CUSUM, and HWMA control charts are designed with symmetric two-sided upper and lower control limits. However, some real applications might require a one-sided approach involving either the upper or the lower limit. Usually, control charts have been conceptualized to monitor and analyze processes involving independent and identically distributed (i.i.d) data. However, in some cases, processes can exhibit autocorrelation in which previous data points can influence the current data point. Autocorrelation can lead to non-random patterns in the data that may affect the effectiveness of traditional control charts. In such situations, specialized control charts or adjustments to deal with autocorrelation are needed.

The most popular model for autocorrelated processes is the autoregressive (AR) moving average (MA) model comprising AR and MA components, which has been shown to provide relatively high forecasting accuracy. Autocorrelated processes can be influenced by internal and external factors that can influence the time series being modeled. Thus, the MA and ARMA models with exogenous variables (MAX(q,r) and ARMAX, respectively) have been developed. This combination allows for a more comprehensive approach to time series forecasting by considering both the inherent dynamics of the time series and the impact of external factors. An explanatory variable is used to support better the accuracy of the forecast. For example, the autoregressive integrated moving average model with exogenous variables has been found to be a valuable tool for energy traders and other market participants seeking to enhance their decision-making capabilities in the intraday market, Lucic and Xydis [6]. As a result, this study focuses on the MAX model due to its usefulness to real-world data.

The average run length (ARL) commonly used to measure the performance of a control chart comprises two components. ARL₀ is the expected number of observations when the process is in control before the control chart signals that it is out of control, and its value should be as large as possible. On the other hand, ARL₁ is the expected number of observations when the process is out of control before the control chart signals that it is out of control, and its value should be as small as possible.

Several approaches have been used to estimate the ARL, including the Markov Chain approach (MCA), Monte Carlo simulation, numerical integral equation (NIE), and explicit formulas. Each has its merits. MCA provides a structured framework to model the control chart’s behavior and state transitions [7], while Monte Carlo simulation can handle complex interactions and variability [8]. The NIE method provides a mathematical framework for analyzing the control chart properties [9] and obtaining analytical expressions for the ARL under certain conditions.

The explicit formula method provides direct analytical solutions for the ARL under specific assumptions. Several researchers have used this approach and checked the accuracy of their solutions. For instance, Chananet and Phanyaem [10] proposed a solution for the ARL using explicit formulas for detecting changes in the mean of a seasonal autoregressive model with exogenous variables running on a CUSUM control chart. Phanyaem [11] used explicit formulas to derive the ARL for detecting changes in the mean of an AR-integrated MA (ARIMA(p,d,q)) model running on an EWMA control chart. Supharakonsakun [12] used explicit formulas to derive the ARL for detecting changes in the mean of a seasonal MA of order q (SMA(q)) process running on a modified EWMA control chart. Recently, Petcharat [13] provided explicit formulas for the ARL for detecting changes in the mean of a stationary seasonal autocorrelated process with a trend running on a CUSUM control chart. Peerajit [14] solved explicit formulas for the ARL for monitoring changes in the mean of a long memory seasonal fractionally integrated MAX model running on a CUSUM control chart. Petcharat [15] studied the performance of a seasonal MA process with exogenous variables running on an EWMA control chart. Recently, Suriyakat and Petcharat [16] proposed explicit formulas and numerical integral equation (NIE) approaches for the ARL to detect changes in the mean of a stationary MA process with exogenous variables running on an EWMA control chart and compare their performances.

The aim of the present study is to derive explicit formulas for the ARL to detect changes in the mean of a MAX(q,r) model with exponential white noise running on an HWMA control chart, which, to the best of our knowledge, has not yet been reported. We also conducted a simulation study to compare the performance of our method to detect changes in the mean of a MAX(q,r) model with exponential white noise running on HWMA and CUSUM control charts.

2. Materials and Methods

The characteristics of the MAX(q,r) process and HWMA and CUSUM control charts are presented here.

2.1. Control Charts

2.1.1. Homogenously Weighted Moving Average (HWMA) Control Chart

The HWMA statistic is considered under the assumption $\{H_t;\hspace{0.17em} t=1,2,3,\dots \},$ as a sequence of i.i.d continuous random variables with a common probability density function. The HWMA statistic $(H_t)$ is an upper HWMA statistic based on the MAX(q,r) process $H_t.$ The recursive formula can express it as in (1)

$$H_t=\lambda Y_t+(1-\lambda ){\overline{Y}}_{t-1}, \mathrm{for} t=1,\hspace{0.17em}2,\dots \hspace{0.17em}\hspace{0.17em},\hspace{0.17em}$$

(1)

where $Y_t$ is a sequence of the MAX(q,r) process with exponential white noise, the starting value ${\overline{Y}}_0=u$ is an initial value, and $u\in [0,b]$ where $b$ is a control limit of the HWMA chart.

The control limits of the HWMA control chart consist of

$$\mathrm{Upper}\mathrm{control}\mathrm{limit}:UC{L}_t=\left\{\begin{array}{c}\mu +L\sqrt{\frac{{\sigma }^2{\lambda }^2}{n}},t=1\hfill \\ \mu +L\sqrt{\frac{{\sigma }^2}{n}[{\lambda }^2+\frac{{(1-\lambda )}^2}{(t-1)}]},t>1\hfill \end{array}\right.$$

$$\mathrm{Center}\mathrm{Line}: CL=\mu$$

$$\mathrm{Lower}\mathrm{control}\mathrm{limit}:LC{L}_t=\left\{\begin{array}{c}\mu -L\sqrt{\frac{{\sigma }^2{\lambda }^2}{n}},t=1\hfill \\ \mu -L\sqrt{\frac{{\sigma }^2}{n}[{\lambda }^2+\frac{{(1-\lambda )}^2}{(t-1)}]},t>1\hfill \end{array}\right.$$

where $L$ is the width of the control limits.

The HWMA stopping time (${\tau }_b$) with a predetermined threshold $b$ is defined as

$${\tau }_b=\inf \left\{t>0\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}{H}_t\ge b\right\}, \mathrm{for} b>u.$$

2.1.2. Cumulative Sum (CUSUM) Control Chart

Page [2] proposed the CUSUM control chart for quality control, which can be used to spot minor differences in process mean. The CUSUM statistics based on the MAX(q,r) process can be expressed using the algorithm in (2) as follows:

$$C_t=C_{t-1}+Y_t-a \mathrm{for} t=1,\hspace{0.17em}2,\dots \hspace{0.17em}\hspace{0.17em},\hspace{0.17em}$$

(2)

where $C_t$ is a sequence of the MAX(q,r) process with exponential white noise where $h$ is a control limit and $a$ usually called the CUSUM control chart’s reference value.

The CUSUM stopping time (${\tau }_h$) with a predetermined threshold $h$ is defined

$${\tau }_h=\inf \left\{t>0\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}{C}_t\ge h\right\}, \mathrm{for} h>u.$$

2.2. Characteristics of Average Run Length

Let, $\left\{{\epsilon }_t,\hspace{0.17em} t=1,2,3,\dots \right\}$ be a sequence of independent and identically distributed random variables with a probability density function $f(x)$ with the parameter $\alpha ={\alpha }_0,$ which is before a change-point time $\theta \le \infty ;$ the parameters ${\alpha }_1>{\alpha }_0$ are after the change-point time. Generally, the change-point times are considered. The expectation $E_{\theta }(.)$ for fixed $\theta$ under probability density function $f(x)$ with parameter ${\alpha }_1$ is that the change-point occurs at a point $\theta .$ In statistical process control (SPC), it is generally desirable to have an appropriate control chart that provides a large Average Run Length (ARL) at the change point time for $\theta =\infty .$ A large ARL means that, under normal operating conditions (when the process is in control), the control chart will typically require a long sequence of data points before signaling a false alarm or indicating a shift in the process. This is the behavior of the in-control state of ARL, denoted by ARL_0, or the state of no change $(\alpha ={\alpha }_0).$ The expectation of the run length ${\tau }_b$ for the in-control state can be defined as

$$AR{L}_0=E_{\theta }({\tau }_b).$$

Meanwhile, if $\theta =1,$ in the case of the change-point time from ${\alpha }_0$ to ${\alpha }_1$, then the ARL is evaluated as the out-of-control state of ARL, denoted by ARL_1, which can be defined as

$$AR{L}_1=E_{\theta }({\tau }_b|{\tau }_b\ge 1).$$

3. Average Run Length for MAX(q,r) Process

3.1. The Explicit Formula Method

Theorem 1.

The explicit formula of $G(u)$ the ARL of MAX(q,r) process with an exponential white noise

For the in-control process $\left(\alpha ={\alpha }_0\right),$ the ARL of the HWMA control chart can be expressed as follows:

$$AR{L}_0=1-\frac{[e^{\frac{-b}{{\alpha }_0\lambda }}-1]e^{\frac{(1-\lambda )u+\lambda (\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}})}{{\alpha }_0\lambda }}}{1+\frac{e^{\frac{\lambda (\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}})}{{\alpha }_0\lambda }}}{\lambda }(e^{\frac{-b}{{\alpha }_0}}-1)}.$$

(3)

Meanwhile, the out-of-control process ($\alpha ={\alpha }_1$), as well as ${\alpha }_1=(1+\delta ){\alpha }_0$, the ARL of the HWMA control chart, can be expressed as follows:

$$AR{L}_1=1-\frac{[e^{\frac{-b}{{\alpha }_1\lambda }}-1]e^{\frac{(1-\lambda )u+\lambda (\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}})}{{\alpha }_1\lambda }}}{1+\frac{e^{\frac{\lambda (\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}})}{{\alpha }_1\lambda }}}{\lambda }(e^{\frac{-b}{{\alpha }_1}}-1)}.$$

(4)

Proof of Theorem 1 is shown in Appendix A.

3.2. Numerical Integral Equation Method

After the explicit formula of the ARL is proved, we will use the NIE method to check the accuracy of the results. Numerical Integral Equations were first proposed by Crowder [17] to approximate ARL for Gaussian distributions. Afterward, Champ and Rigdon [18] thoroughly investigated them by comparing the run length distributions derived from the MCA and the Integral Equation approach for the case of a Gaussian distribution. Extensive investigations of the Integral Equation have been conducted by Srivastava and Wu [19] for continuous-time systems and by Srivastava and Wu [20] for discrete processes. The advantage of using the NIE method with quadrature rules is that it provides a computationally efficient and accurate way to estimate the ARL. The ARL estimated via the NIE method derived with quadrature rules denoted $\tilde{G}\left(u\right)$ is a well-known technique as given in Appendix B that can verify the ARL via the explicit formula. Different quadrature rules can be employed to obtain similar ARL estimates, and the results obtained from these rules are generally very close [21].

The approximation of the numerical integral for the function $G\left(u\right)$ is,

$$\tilde{G}\left(u\right)=1+\frac{1}{\lambda }{\displaystyle \sum _{k=1}^n{w}_{k}G(a_k)f(\frac{a_k-\left(1-\lambda \right)u-\mu +{\theta }_{1}e+{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}-{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\lambda })}.$$

(5)

3.3. Existence and Uniqueness of ARL

Banach’s Fixed-point Theorem provides theoretical support for the ARL equation’s validity, ensuring a unique solution to the integral equation for explicit formulas. Let $T$ be an operation on the class of all continuous functions defined by

$$\begin{array}{l}T(G(u))=1+\frac{1}{\lambda }{\displaystyle \underset{0}{\overset{b}{\int }}G(W)f(}\frac{W-\left(1-\lambda \right)u-\mu +{\theta }_{1}e+{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}-{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\lambda })dW\\ \end{array}$$

(6)

According to Banach’s Fixed-point Theorem, if an operator $T$ is a contraction, the fixed-point equation $T(G(u))=G(u)$ has a unique solution. The theorem can be used as follows below to show that the equation in (6) exists and has a unique solution.

Theorem 2.

Banach’s Fixed-point Theorem

Let $(X,d)$ be defined on a complete metric space and $T:X\to X$ satisfy the conditions of a contraction mapping with contraction constant $0\le r<1$ such that $‖T(G_1)-T(G_2)‖\le r‖G_1-G_2‖,$ $\forall G_1,G_2\in X.$ There exists a unique $G(\cdot )\in X$ such that $T(G(u))=G(u)$, i.e., a unique fixed-point in $X$ [22].

Proof of Theorem 2.

Let T, defined in (6), be a contraction mapping for $G_1,$ $G_2\in F[0,b],$ such that $‖T(G_1)-T(G_2)‖\le r‖G_1-G_2‖,$$\forall G_1,G_2$$\in F[0,b]$ with $0\le r<1$ under the norm ${‖G‖}_{\infty }=\underset{u\in [0,b]}{\sup }\left|G(u)\right|$, so

$$\begin{array}{l}{‖T(G_1)-T(G_2)‖}_{\infty }=\underset{u\in [0,b]}{\sup }\left|\frac{1}{\alpha \lambda }{e}^{\frac{\left(1-\lambda \right)u+\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\alpha \lambda }}{\displaystyle \underset{0}{\overset{b}{\int }}(G_1(W)-G_2(W))e^{-\frac{W}{\alpha \lambda }}dW}\right|\\ \le \underset{u\in [0,b]}{\sup }\left|‖G_1-G_2‖\frac{1}{\alpha \lambda }{e}^{\frac{\left(1-\lambda \right)u+\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\alpha \lambda }}(-\alpha \lambda )(e^{-\frac{b}{\alpha \lambda }}-1)\right|\\ ={‖G_1-G_2‖}_{\infty }\underset{u\in [0,b]}{\sup }\left|e^{\frac{\left(1-\lambda \right)u+\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\alpha \lambda }}\right|\left|1-e^{-\frac{b}{\alpha \lambda }}\right|\le r{‖G_1-G_2‖}_{\infty }\end{array}$$

where $r=\underset{u\in [0,b]}{\sup }\left|e^{\frac{\left(1-\lambda \right)u+\mu -{\theta }_{1}e-{\displaystyle \sum _{i=2}^q{\theta }_i{\epsilon }_{1-i}}+{\displaystyle \sum _{j=1}^r{\beta }_j{X}_{j1}}}{\alpha \lambda }}\right|\left|1-e^{-\frac{b}{\alpha \lambda }}\right|$; $0\le r<1$. □

4. Numerical Results

We conducted a simulation study to compare the efficacies of the explicit formulas ($G\left(u\right)$) and NIE $(\tilde{G}\left(u\right))$ methods for the ARL of an MAX(q,r) process running on an HWMA control chart via the following steps.

Step 1: Setting up the control limit for the MAX(q,r) process:

i

Determine the exponential white noise $({\alpha }_0)$ and smoothing parameters for the in-control process.

ii

Determine the initial values for the MAX(q,r) process and the HWMA statistic.

iii

Select acceptable values for ARL₀ and the shift sizes $(\delta ).$

iv

Compute the upper control limit (b) that yields the desired ARL for the control process using (3).

Step 2: For the in-control ARL:

i

Compute ARL₀ using (3) when given the upper control limit (b) from Step 1.

ii

Approximate the value of ARL₀ via the NIE method by using (5).

iii

If necessary, change the value of b according to the desired ARL₀ value.

Step 3: For the out-of-control ARL:

i

Compute ARL₁ for various shift sizes and ${\alpha }_1=(1+\delta ){\alpha }_0$ by using (4) and the value of b from Step 1.

ii

Approximate ARL₁ via the NIE method by using (5).

iii

Compare the ARL values obtained using the explicit formulas and NIE methods.

To compare these, the absolute relative change (ARC) is computed as follows:

$$ARC(\%)=\frac{\left|G(u)-\tilde{G}(u)\right|}{G(u)}\times 100$$

(7)

Next, the efficiency of the HWMA control chart is compared with that of the CUSUM control chart. Several performance measures are commonly used to assess a control chart’s ability to detect process variations. First, the relative mean index (RMI) [23] is a statistical metric used to assess which control chart more efficiently detects shifts or changes in the process mean. A lower RMI indicates a more efficient control chart. The RMI is calculated as follows:

$$RMI=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[\frac{AR{L}_i(r)-AR{L}_i(s)}{AR{L}_i(s)}\right]},$$

(8)

where $AR{L}_i(r)$ is the ARL value for each control chart for the determined shift size $i,$ $AR{L}_i(s)$ and is the lowest ARL for $i$ obtained by each of the control charts.

The standard deviation run length (SDRL) and median run length (MRL) are tools for assessing the performance of control charts in maintaining process stability and quickly detecting an out-of-control situation [24]. For the in-control process, th7e SDRL and MRL are calculated as follows:

$$AR{L}_0=\frac{1}{\varsigma }, SDR{L}_0=\sqrt{\frac{1-\varsigma }{{\varsigma }^2}}, MR{L}_0=\frac{\log (0.5)}{\log (1-\varsigma )},$$

(9)

where $\varsigma$ represents a type I error. In this study, ARL₀ was fixed at 370, and it can be calculated as SDRL₀ and MRL₀ by (9) at approximately 370 and 256, respectively. On the other hand, for out-of-control situations, SDRL₁ and MRL₁ are calculated by

$$AR{L}_1=\frac{1}{1-\psi }, SDR{L}_1=\sqrt{\frac{\psi }{{(1-\psi )}^2}}, MR{L}_1=\frac{\log (0.5)}{\log \psi },$$

(10)

where $\psi$ represents type II error.

The control chart’s effectiveness in detecting various types of process variations can be evaluated by considering the values of SDRL₁, MRL₁, and ARL₁, after which informed decisions about its performance can be made. Lower values of these measurements indicate better performance in terms of sensitivity and efficiency. Furthermore, the comparison of the performances of the HWMA and CUSUM control charts in terms of the expected ARL (EARL), expected SDRL (ESDRL), and expected MRL (EMRL) is calculated as follows:

$$EARL=\frac{1}{\Delta }{\displaystyle \sum _{\delta ={\delta }_{\min }}^{{\delta }_{\max }}ARL(\delta )}, ESDRL=\frac{1}{\Delta }{\displaystyle \sum _{\delta ={\delta }_{\min }}^{{\delta }_{\max }}SDRL(\delta )}, EMRL=\frac{1}{\Delta }{\displaystyle \sum _{\delta ={\delta }_{\min }}^{{\delta }_{\max }}MRL(\delta )}.$$

(11)

For the results, a simulation of the in-control process is given with ARL₀ = 370, and then the initial parameter value was studied ${\alpha }_0=1$. The out-of-control process ${\alpha }_1=(1+\delta ){\alpha }_0$ is computed by determining shift sizes $(\delta )$ to be 0.001, 0.003, 0.005, 0.01, 0.03, 0.05, 0.1, 0.3, and 0.5. The control limits for the HWMA control chart running a MAX(q,r) process when ARL₀ = 370 are provided in Table 1. For example, for a MAX(2,1) process with parameter values $\delta =1,$ ${\theta }_1=0.1, {\theta }_2=0.2, {\beta }_1=0.2$, the control limit is 0.00179. In Table 2 and Table 3, the ARL values obtained using the explicit formulas and NIE methods for the MAX(1,1) and MAX(2,3) models running on an HWMA control chart for λ = 0.1 or 0.2 are presented. It can be seen that the ARL values from both methods are similar. This was confirmed by the ARC values being very low.

Table 1. Control limits of HEWMA control chart with MAX processes.

Models	Coefficients
	$\mathit{\delta }$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\beta }}_3$	$\mathit{\lambda }$ = 0.1	$\mathit{\lambda }$ = 0.2	$\mathit{\lambda }$ = 0.3
MAX(1,1)	1	0.1			0.2			0.0014638	0.06065	0.10252
MAX(1,2)	1	0.1			0.2	0.3		0.0010800	0.04440	0.074865
MAX(1,3)	1	0.1			0.2	0.3	0.4	0.0007230	0.02944	0.049523
MAX(2,1)	1	0.1	0.2		0.2			0.0017900	0.07483	0.12679
MAX(2,2)	1	0.1	0.2		0.2	0.3		0.0013220	0.05464	0.09227
MAX(2,3)	1	0.1	0.2		0.2	0.3	0.4	0.0008850	0.03614	0.060845
MAX(3,1)	1	0.1	0.2	0.3	0.2			0.0024200	0.10300	0.17547
MAX(3,2)	1	0.1	0.2	0.3	0.2	0.3		0.0017900	0.07483	0.12679
MAX(3,3)	1	0.1	0.2	0.3	0.2	0.3	0.4	0.0011950	0.04925	0.08309

Table 2. The ARL of HWMA control chart for MAX(1,1) using explicit formula against NIE method is given ${\beta }_1=0.2,\hspace{0.17em} \delta =1$, and ${\alpha }_0=1$.

${\mathit{\theta }}_{\mathbf{1}}$	$\mathit{\delta }$	$\mathit{\lambda }=$ 0.1 b = 0.001195		ARC(%)	$\mathit{\lambda }\mathbf{=}$ 0.2 b = 0.04925		ARC(%)
		Explicit Formula	NIE		Explicit Formula	NIE
−0.1	0	370.3770885	370.377	2.390 × 10−5	370.5593435	370.559	9.270 × 10−5
	0.001	366.1943273	366.194	8.938 × 10−5	362.1715955	362.172	0.00011677
	0.003	357.9938367	357.994	4.560 × 10−5	346.3219822	346.322	5.133 × 10−6
	0.005	350.0079350	350.008	1.858 × 10−5	331.600544	331.60	1.641 × 10−5
	0.01	330.9408108	330.941	5.718 × 10−5	299.0211502	299.021	5.023 × 10−5
	0.03	265.9258522	265.926	5.558 × 10−5	209.3451951	209.345	9.320 × 10−5
	0.05	215.4434020	215.443	0.00018659	156.1001736	156.100	0.00011124
	0.1	131.5709136	131.571	6.564 × 10−5	87.70901617	87.7090	1.844 × 10−5
	0.3	26.90378287	26.9038	6.368 × 10−5	21.56693573	21.5669	0.00016565
	0.5	8.762648041	8.76265	2.236 × 10−5	9.417738995	9.41774	1.067 × 10−5
	1.0	2.039095587	2.03910	0.00021643	3.137729377	3.13773	1.984 × 10−5
	3.0	1.039333882	1.03933	0.00037350	1.245405834	1.24541	0.00033454
	5.0	1.011101932	1.01110	0.00019107	1.102469633	1.10247	3.333 × 10−5
${\mathit{\theta }}_{\mathbf{1}}$	$\mathit{\delta }$	$\mathit{\lambda }=$ 0.1 b = 0.001463		ARC(%)	$\mathit{\lambda }=$ 0.2 b = 0.06065		ARC(%)
		Explicit Formula	NIE		Explicit Formula	NIE
0.1	0.00	370.7863113	370.786	8.395 × 10−5	370.6764977	370.676	0.00013428
	0.001	366.6757192	366.676	7.658 × 10−5	362.7898379	362.790	4.467 × 10−5
	0.003	358.6141296	358.614	3.614 × 10−5	347.8319481	347.832	1.493 × 10−5
	0.005	350.7601349	350.760	3.845 × 10−5	333.8731750	333.873	5.240 × 10−5
	0.01	331.9940916	331.994	2.760 × 10−5	302.7570590	302.757	1.948 × 10−5
	0.03	267.8441508	267.844	5.630 × 10−5	215.4444901	215.444	0.0002275
	0.05	217.8316782	217.832	0.00014800	162.3849054	162.385	5.823 × 10−5
	0.10	134.2173814	134.217	0.00028400	92.75953887	92.7595	4.190 × 10−5
	0.30	28.19757214	28.1976	9.881 × 10−5	23.43661469	23.4366	6.269 × 10−5
	0.50	9.321311662	9.32131	1.783 × 10−5	10.33587079	10.3359	0.00028256
	1.0	2.151737413	2.15174	0.00012000	3.431153045	3.43115	8.875 × 10−5
	3.0	1.045822609	1.04582	0.00024900	1.290008218	1.29001	0.00013814
	5.0	1.013149215	1.01315	7.748 × 10−5	1.122724333	1.12272	0.00038594

Table 3. The ARL of HWMA control chart for MAX(2,3) using explicit formula against NIE method given ${\theta }_1=0.1,\hspace{0.17em} {\beta }_1=0.1,\hspace{0.17em} {\beta }_2=0.15,\hspace{0.17em} {\beta }_3=0.2,\hspace{0.17em} \mu =1$ and ${\alpha }_0=1$.

${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{\delta }$	$\mathit{\lambda }\mathbf{=}$ 0.1 b = 0.00093		ARC (%)	$\mathit{\lambda }\mathbf{=}$ 0.2 b = 0.03805		ARC (%)
		Explicit Formula	NIE		Explicit Formula	NIE
−0.2	0.00	370.5910199	370.591	5.373 × 10−6	370.8965713	370.897	0.00011557
	0.001	366.3099585	366.310	1.133 × 10−5	361.8637773	361.864	6.154 × 10−5
	0.003	357.9201174	357.920	3.281 × 10−5	344.8749336	344.875	1.924 × 10−5
	0.005	349.7541889	349.754	5.401 × 10−5	329.1876507	329.188	0.00010610
	0.01	330.2752321	330.275	7.026 × 10−5	294.7876499	294.788	0.00011877
	0.03	264.0649507	264.065	1.868 × 10−5	202.3095739	202.310	0.00021061
	0.05	212.9132635	212.913	0.000123736	148.9225782	148.923	0.00028323
	0.10	128.5909253	128.591	5.811 × 10−5	82.05570162	82.0557	1.969 × 10−6
	0.30	25.42355065	25.4236	0.000194101	19.53869351	19.5387	3.320 × 10−5
	0.5	8.132070895	8.13207	1.100 × 10−5	8.434958529	8.43496	1.744 × 10−5
	1.0	1.915696782	1.91570	0.000167977	2.829546229	2.82955	0.00013327
	3.0	1.032573160	1.03257	0.000306078	1.199966562	1.19997	0.00028652
	5.0	1.009005379	1.00901	0.000457928	1.082068426	1.08207	0.00014546
${\mathit{\theta }}_{\mathbf{2}}$	$\mathit{\delta }$	$\mathit{\lambda }\mathbf{=}$ 0.1 b = 0.00000003275		ARC(%)	$\mathit{\lambda }\mathit{=}$ 0.2 b = 0.05756		ARC(%)
		Explicit Formula	NIE		Explicit Formula	NIE
0.2	0.00	370.4632642	370.463	7.133 × 10−5	370.4063980	370.406	0.00010745
	0.001	366.3370877	366.337	2.395 × 10−5	362.4032052	362.403	5.661 × 10−5
	0.003	358.2455837	358.246	0.00011600	347.2378814	347.238	3.416 × 10−5
	0.005	350.3632872	350.363	8.197 × 10−5	333.1015864	333.102	0.00012416
	0.01	331.5330963	331.533	2.904 × 10−5	301.6456317	301.646	0.00012209
	0.03	267.2044272	267.204	0.000160	213.7943893	213.794	0.00018209
	0.05	217.1032216	217.103	0.000102	160.7119670	160.712	2.054 × 10−5
	0.10	133.4717712	133.472	0.000171	91.42614601	91.4261	5.032 × 10−5
	0.30	27.85211472	27.8521	5.287 × 10−5	22.94278370	22.9428	7.104 × 10−5
	0.50	9.173071617	9.17307	1.762 × 10−5	10.09279629	10.0928	3.672 × 10−5
	1.0	2.121802777	2.12180	0.000131	3.353117041	3.35312	8.826 × 10−5
	3.0	1.044079725	1.04408	2.634 × 10−5	1.278045727	1.27805	0.00033430
	5.0	1.012596861	1.01260	0.00031	1.117274099	1.11727	0.00036684

A comparison of the ARL₁ results for MAX(1,1) and MAX(2,3) processes running on HWMA and CUSUM control charts is provided in Table 4 and Table 5. In this case, the parameter values were set as ARL₀ = 370, λ = 0.1, 0.2, or 0.3, and the reference value (a) = 4. The ARL values derived by using the explicit formulas were lower for the HWMA control chart than for the CUSUM control chart for all shift sizes and all values of $\lambda .$ In addition, as $\lambda .$ was increased, the ARL₁ values decreased accordingly. Moreover, the SDRL and MRL values were the same as the ARL values. Subsequently, the ARL values obtained from each control chart using the explicit formulas method in Table 4, Table 5 and Table 6 were used to calculate the EARL, ESDRL, and EMRL values. It was found that the proposed method for the HWMA control chart provided the best performed the best because it obtained the lowest EARL, ESDRL, and EMRL values. Therefore, it can be concluded that the HWMA control chart performs better than the CUSUM control chart for this scenario, where the results of the performance comparison are consistent with Abbas [3].

Table 4. The ARL of HWMA control chart for MAX(1,1) using explicit formula against CUSUM control chart given ${\theta }_1=-0.1,\hspace{0.17em} {\beta }_1=0.2,\hspace{0.17em} \mu =1$ and ${\alpha }_0=1$.

$\mathit{\lambda }$		$\mathit{\lambda }=$ 0.1		$\mathit{\lambda }=$ 0.2		$\mathit{\lambda }=$ 0.3
$\mathit{\delta }$	Control Chart	HWMA	CUSUM	HWMA	CUSUM	HWMA	CUSUM
	UCL	0.001195	2.249	0.04925	2.249	0.08309	2.249
0.00	ARL0	370.3770885	370.531000	370.5593435	370.531000	370.0709468	370.531000
	SDRL0	369.8767506	370.030662	370.0590057	370.030662	369.5706086	370.030662
	MRL0	256.3791049	256.485788	256.5054345	256.485788	256.1669035	256.485788
0.001	ARL1	366.1943273	368.30800	362.1715955	368.308000	338.4953143	368.30800
	SDRL1	365.6939855	367.80766	361.6712499	367.807660	337.9949445	367.80766
	MRL1	253.479834	254.944921	250.6914870	254.944921	234.2803282	254.944921
0.003	ARL1	357.9938367	363.91300	346.3219822	363.913000	288.8651605	363.91300
	SDRL1	357.4934871	363.412656	345.8216208	363.412656	288.3647271	363.412656
	MRL1	247.7956834	251.898537	239.7053649	251.898537	199.8792977	251.898537
0.005	ARL1	350.007935	359.588000	331.6000544	359.588000	251.6370603	359.588000
	SDRL1	349.5075773	359.087652	331.0996769	359.087652	251.1365626	359.087652
	MRL1	242.2602744	248.900674	229.5008948	248.900674	174.0747153	248.900674
0.01	ARL1	330.9408108	349.070000	299.0211502	349.070000	189.5958457	349.070000
	SDRL1	330.4404325	348.569641	298.5207315	348.569641	189.0951846	348.569641
	MRL1	229.0439415	241.610147	206.9189001	241.610147	131.0709468	241.610147
0.03	ARL1	265.9258522	310.873000	209.3451951	310.873000	92.93583386	310.873000
	SDRL1	265.4253813	310.372597	208.8445966	310.372597	92.43448156	310.372597
	MRL1	183.9789635	215.133984	144.7601816	215.133984	64.07101272	215.133984
0.05	ARL1	215.443402	278.070000	156.1001736	278.070000	59.89936967	278.070000
	SDRL1	214.9428204	277.569550	155.5993703	277.569550	59.39726524	277.569550
	MRL1	148.9871443	192.396655	107.8534504	192.396655	41.17153316	192.396655
0.10	ARL1	131.5709136	214.156000	87.70901617	214.156000	29.91698008	214.156000
	SDRL1	131.0699599	213.655415	87.20758282	213.655415	29.41273053	213.655415
	MRL1	90.85099354	148.094784	60.44802133	148.094784	20.38833309	148.094784
0.30	ARL1	26.90378287	92.0224000	21.56693573	92.0224000	8.151352721	92.0224000
	SDRL1	26.39904827	91.5210342	21.06100142	91.5210342	7.634998262	91.5210342
	MRL1	18.29951979	63.4378624	14.59974484	63.4378624	5.295955662	63.4378624
0.50	ARL1	8.762648041	49.5367000	9.417738995	49.5367000	4.318200765	49.5367000
	SDRL1	8.247505844	49.0341508	8.903710956	49.0341508	3.785321265	49.0341508
	MRL1	5.720233585	33.9884724	6.174822970	33.9884724	2.63137715	33.9884724
RMI		0	0.918	0	1.173	0	3.836
EARL		228.194	265.06	202.584	265.06	140.424	265.06
ESDRL		227.69	264.559	202.08	264.559	139.92	264.559
EMRL		157.824	183.378	140.073	183.378	96.985	183.378

Table 5. The ARL of HWMA control chart for MAX(2,3) using explicit formula against CUSUM control chart given ${\theta }_1=0.1,\hspace{0.17em} {\theta }_2=0.2,\hspace{0.17em} {\beta }_1=0.1,\hspace{0.17em} {\beta }_2=0.15,\hspace{0.17em} {\beta }_3=0.2,\hspace{0.17em} \mu =1$ and ${\alpha }_0=1$.

$\mathit{\lambda }$		$\mathit{\lambda }=$ 0.1		$\mathit{\lambda }=$ 0.2		$\mathit{\lambda }=$ 0.3
$\mathit{\delta }$	Control Charts	HWMA	CUSUM	HWMA	CUSUM	HWMA	CUSUM
	UCL	0.00139	2.0899	0.05756	2.0899	0.09725	2.0899
0.00	ARL0	370.4632642	370.086000	370.4063980	370.086000	370.1734101	370.086000
	SDRL0	369.9629264	369.585662	369.9060601	369.585662	369.673072	369.585662
	MRL0	256.4388374	256.177338	256.3994207	256.177338	256.2379257	256.177338
0.001	ARL1	366.3370877	367.874000	362.4032052	367.874000	340.1548137	367.874000
	SDRL1	365.8367461	367.373660	361.9028598	367.373660	339.6544456	367.373660
	MRL1	253.578788	254.644095	250.8520267	254.644095	235.4306064	254.644095
0.003	ARL1	358.2455837	363.501000	347.2378814	363.501000	292.4145378	363.501000
	SDRL1	357.7452343	363.000656	346.7375209	363.000656	291.9141096	363.000656
	MRL1	247.9701813	251.612961	240.3402183	251.612961	202.3395410	251.612961
0.005	ARL1	350.3632872	359.198000	333.1015864	359.198000	256.1488957	359.198000
	SDRL1	349.8629299	358.697652	332.6012106	358.697652	255.6484068	358.697652
	MRL1	242.5065860	248.630346	230.5416782	248.630346	177.2020854	248.630346
0.01	ARL1	331.5330963	348.733000	301.6456317	348.733000	194.8249504	348.733000
	SDRL1	331.0327187	348.232641	301.1452166	348.232641	194.3243071	348.232641
	MRL1	229.4544829	241.376556	208.7380538	241.376556	134.6954942	241.376556
0.03	ARL1	267.2044272	310.716000	213.7943893	310.716000	97.00143645	310.716000
	SDRL1	266.7039585	310.215597	213.2938032	310.215597	96.50014113	310.215597
	MRL1	184.8652052	215.025160	147.8441338	215.025160	66.88910003	215.025160
0.05	ARL1	217.1032216	278.054000	160.7119670	278.054000	62.90341186	278.054000
	SDRL1	216.6026445	277.553550	160.2111868	277.553550	62.40140873	277.553550
	MRL1	150.1376457	192.385564	111.0501127	192.385564	43.25382335	192.385564
0.10	ARL1	133.4717712	214.370000	91.42614601	214.370000	31.63968451	214.370000
	SDRL1	132.9708311	213.869416	90.92477126	213.869416	31.13567008	213.869416
	MRL1	92.16857389	148.243117	63.02456647	148.243117	21.58252945	148.243117
0.30	ARL1	27.85211472	92.4299000	22.94278370	92.4299000	8.695418863	92.4299000
	SDRL1	27.34754431	91.9285403	22.43721329	91.9285403	8.180152220	91.9285403
	MRL1	18.95692921	63.7203227	15.55357815	63.7203227	5.673576353	63.7203227
0.50	ARL1	9.173071617	49.8698000	10.09279629	49.8698000	4.606655310	49.8698000
	SDRL1	8.658647196	49.3672680	9.579756821	49.3672680	4.076103266	49.3672680
	MRL1	6.005049270	34.2193677	6.643193915	34.2193677	2.832394987	34.2193677
RMI		0	0.878	0	1.088	0	3.597
EARL		229.031	264.972	204.817	264.972	143.154	264.972
ESDRL		228.53	264.471	204.31	264.471	142.65	264.471
EMRL		158.405	183.318	141.6201	183.318	98.8777	183.318

Table 6. Comparison of the ARL values for a MAX(3,1) process running on HWMA and CUSUM control charts when ARL₀ = 370, ${\theta }_1=-1.085, \hspace{0.17em}{\theta }_2=-0.765,\hspace{0.17em} {\theta }_3=-0.435, {\beta }_1=24.40$, and ${\alpha }_0=29.42908$.

$\mathit{\lambda }$		$\mathit{\lambda }=$ 0.1		$\mathit{\lambda }=$ 0.2		$\mathit{\lambda }=$ 0.3
$\mathit{\delta }$	Control Chart	HWMA	CUSUM	HWMA	CUSUM	HWMA	CUSUM
	UCL	1.28909	8.9	2.63636	8.9	4.04585	8.9
0.00	ARL0	370.1444170	370.020000	370.5206530	370.020000	370.0740739	370.020000
	SDRL0	369.6440789	369.519662	370.0203152	369.519662	369.5737357	369.519662
	MRL0	256.2178292	256.131590	256.4786163	256.131590	256.169071	256.131590
0.001	ARL1	362.8410891	369.946000	362.1731457	369.946000	361.5464713	369.946000
	SDRL1	362.3407441	369.445662	361.6728001	369.445662	361.0461250	369.445662
	MRL1	251.1555449	256.080297	250.6925615	256.080297	250.2581836	256.080297
0.003	ARL1	349.0679755	369.797000	346.5604091	369.797000	345.6210733	369.797000
	SDRL1	348.5676169	369.296662	346.0600479	369.296662	345.1207111	369.296662
	MRL1	241.6087437	255.977018	239.8706300	255.977018	239.2195315	255.977018
0.005	ARL1	336.3044216	369.648000	332.2412574	369.648000	331.0428014	369.648000
	SDRL1	335.8040493	369.147661	331.7408806	369.147661	330.5424232	369.147661
	MRL1	232.7617160	255.873739	229.9453431	255.873739	229.1146361	255.873739
0.01	ARL1	308.1450636	369.277000	301.1467802	369.277000	299.4763387	369.277000
	SDRL1	307.6446573	368.776661	300.6463644	368.776661	298.9759207	368.776661
	MRL1	213.2431207	255.616581	208.3922759	255.616581	207.2344131	255.616581
0.03	ARL1	230.8967203	367.798000	219.2027893	367.798000	216.8787189	367.798000
	SDRL1	230.3961777	367.297660	218.7022177	367.297660	216.3781412	367.297660
	MRL1	159.6985864	254.591416	151.5929576	254.591416	149.9820320	254.591416
0.05	ARL1	184.6809502	366.327000	172.3987162	366.327000	170.0814255	366.327000
	SDRL1	184.1802715	365.826658	171.8979890	365.826658	169.5806884	365.826658
	MRL1	127.6641927	253.571796	119.1507744	253.571796	117.5445464	253.571796
0.10	ARL1	123.2147895	362.683000	112.5553949	362.683000	110.6446094	362.683000
	SDRL1	122.7137709	362.182655	112.0542794	362.182655	110.1434746	362.182655
	MRL1	85.05893965	251.045966	77.67036555	251.045966	76.34590106	251.045966
0.30	ARL1	53.18429732	348.583000	47.51179380	348.583000	46.54370778	348.583000
	SDRL1	52.68192464	348.082641	47.00913482	348.082641	46.04099289	348.082641
	MRL1	36.51687573	241.272584	32.58486361	241.272584	31.91381168	241.272584
0.50	ARL1	34.12578910	335.208000	30.35834753	335.208000	29.72494727	335.208000
	SDRL1	33.62207151	334.707627	29.85416080	334.707627	29.22066979	334.707627
	MRL1	23.30590301	232.001734	20.69429472	232.001734	20.25521318	232.001734
RMI		0	3.396	0	3.858	0	3. 948
EARL		200.072	356.393	194.040	356.393	192.748	356.393
ESDRL		199.570	355.892	193.5379	355.892	192.246	355.892
EMRL		138.332	246.686	134.151	246.686	133.255	246.686

5. Practical Applications with Real Data

In this section, the ARL formula has been applied to real data with the following steps.

• To estimate parameters from interesting data such as stock price, which must include a MAX model.
• To estimate the parameter of exponentially distributed residuals.
• Using the parameter values from 1 and 2, determine the ARL value in Equations (3) and (4).
• To compare the performance using the ARL value calculated from 3 and other control charts.
• To detect changes in the process mean, determine the UCL value using the equation in (3) and use actual data to compute control chart statistics before plotting the control chart statistics on a graph.

In the application to a real problem, the S&P 500 index was gathered as the observations for the MAX(q,r) process, and the AAPL stock price was collected as the exogenous variable (X).

The explicit formulas for the ARL of a MAX(q,r) process on the HWMA control chart are applied and compared with the performance with the CUSUM control chart using 41 real-world data observations of the S&P 500. The exogenous variable is Apple Inc. (AAPL) stock price from April 2023 to May 2023.

Time series model MAX in the practical real data S&P 500 with exogenous AAPL stock price decomposes the actual series into fitted values and residuals. The parameters of the practical time series model MAX are estimated using the Kolmogorov–Smirnov test. Then, the exponential distribution of residuals behaving as white noise was subsequently determined.

The model has an improvement pattern with three MAX processes, i.e., MAX(1,1), MAX(2,1), and MAX(3,1), so these models should be included in the model estimation as shown in Table 7. Consequently, the MAX(3,1) has the lowest RMSE, MAPE, and MAE, implying that the MAX(3,1) is the best model, as shown in Table 8. Based on the final result of the coefficient parameter in Table 9, the MAX(3,1) coefficient parameters are obtained as follows: ${\widehat{\theta }}_1=$−1.085, ${\widehat{\theta }}_2=$−0.765, ${\widehat{\theta }}_3=$−0.435, $\widehat{\beta }=$ 24.40. The in-control parameter is equal to 29.42908, as shown in Table 9. The parameters of this prediction model can be assigned as follows:

$${\widehat{Y}}_t=1.085{\epsilon }_{t-1}+0.765{\epsilon }_{t-2}+0.435{\epsilon }_{t-3}+24.40X_t.$$

Table 7. MAX estimate for S&P 500 with Apple Inc. (AAPL) stock price as exogenous variable.

Process	Variable	Coefficient	Std. Error	t	Sig.
MAX(1,1)	MA(1) ($\widehat{\theta }$)	−0.846	0.103	−8.227	0.00
	Apple Inc. stock price ($\widehat{\beta }$)	24.429	0.098	250.237	0.00
MAX(2,1)	$\mathrm{MA}\left(1\right) \left({\widehat{\theta }}_1\right)$	−1.222	0.126	−9.695	0.00
	$\mathrm{MA}\left(2\right) \left({\widehat{\theta }}_2\right)$	−0.667	0.128	−5.204	0.00
	Apple Inc. stock price ($\widehat{\beta }$)	24.417	0.117	207.912	0.00
MAX(3,1)	$\mathrm{MA}\left(1\right) \left({\widehat{\theta }}_1\right)$	−1.085	0.158	−6.850	0.00
	$\mathrm{MA}\left(2\right) \left({\widehat{\theta }}_2\right)$	−0.765	0.211	−3.627	0.00
	$\mathrm{MA}\left(3\right) \left({\widehat{\theta }}_3\right)$	−0.435	0.165	−2.647	0.01
	Apple Inc. stock price ($\widehat{\beta }$)	24.400	0.131	186.435	0.00

Table 8. Model fit.

Process	RMSE	MAPE	MAE
MAX(1,1)	58.951	1.120	46.329
MAX(2,1)	46.407	0.856	35.411
MAX(3,1)	45.571	0.794	32.829

Table 9. Exponential white noise of residual using the Kolmogorov–Smirnov goodness of fit test.

Process	$\mathbf{Mean} \left({\mathit{\alpha }}_0\right)$	Kolmogorov–Smirnov	Sig.
MAX(3,1)	29.42908	0.679	0.745

The ARL values for MAX(3,1) on the HWMA and CUSUM control charts were compared using the explicit formula method, the results of which are summarized in Table 6; it can be seen that the results are obviously in agreement with those in Table 4 and Table 5. The table shows that the HWMA control chart has the lowest RMI, EARL, ESDRL, and EMRL of all $\lambda$ levels, as shown in Figure 1. To sum up, the explicit formula approach is a good alternative for practical applications in detecting mean process changes on the HWMA control chart. In addition, the HWMA (H_t) and CUSUM (C_t) statistics for the S&P 500 with Apple Inc. (AAPL) stock price as an exogenous variable fitted to the MAX(3,1) model are presented in Figure 2. These results indicate that the HWMA control chart can detect a shift at the first time at the fifth observation, while the CUSUM scheme is found the first time at the sixth observation. That is to say, the first hitting time for the HWMA control chart for the S&P 500 dataset fitted to the MAX(3,1) process with exogenous (AAPL) stock price takes a smaller hitting time than for the CUSUM control chart.

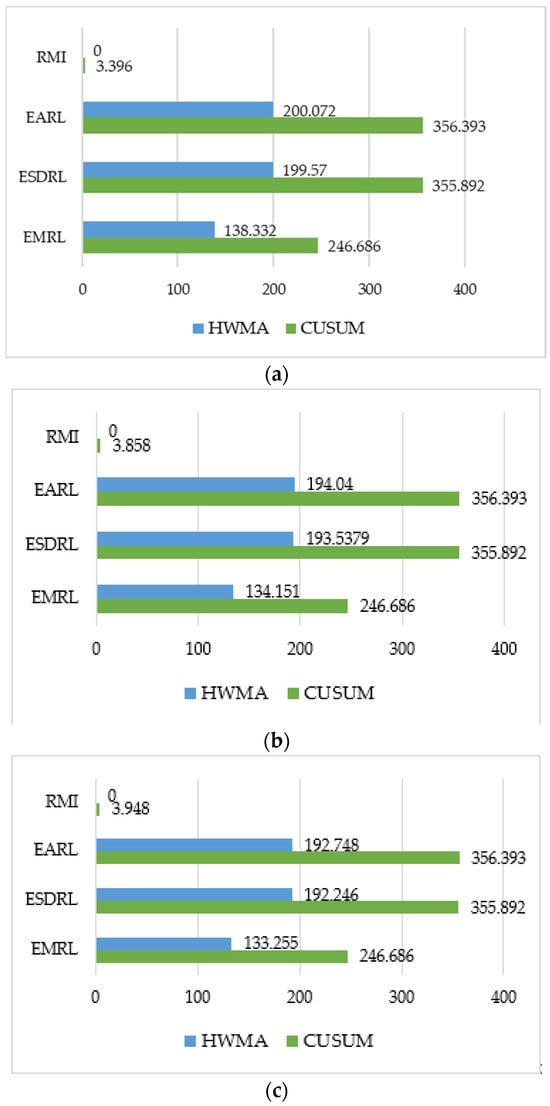
Figure 1. The RMI, EARL, ESDRL, and EMRL values on the control charts for MAX(3,1) when (a) $\lambda$ = 0.1, (b) $\lambda$ = 0.2, and (c) $\lambda$ = 0.3.

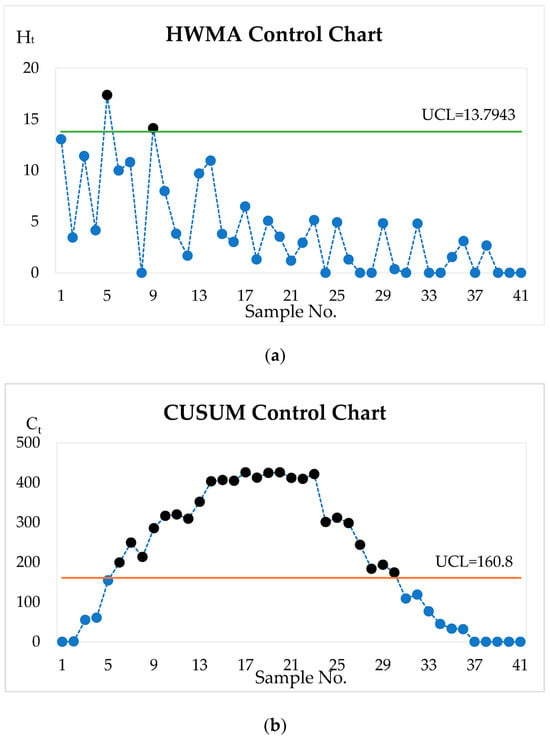
Figure 2. The S&P 500 dataset fitted to MAX(3,1) process running on (a) HWMA control chart and (b) CUSUM control chart.

Hence, the results show that the HWMA control chart for the S&P 500 dataset fitted to the MAX(3,1) process with exogenous (AAPL) stock price is more effective than the CUSUM control chart.

6. Discussion and Conclusions

The zero-stated ARL derivations based on the explicit formulas and NIE methods for an MAX process with exponential white noise running on an HWMA control chart with a symmetric one-sided control limit were derived and evaluated. The control charts, such as EWMA and DEWMA control charts, which have similar characteristics to the HWMA control chart, were reviewed in the literature. However, the HWMA control chart, a recent control chart between EWMA and DEWMA control charts, was selected to compare the results with the CUSUM control chart. The efficiencies of the proposed method for MAX processes running on HWMA and CUSUM control charts were compared considering the differences between their parameters (the smoothing parameter for the HWMA control chart and the reference value for the CUSUM control chart). Consequently, the fixed parameter values for the HWMA and CUSUM control charts were independently selected. We will consider optimal parameters for the HWMA and CUSUM control charts in future research. Although only exponential white noise was considered in the present research, it is representative of real data with events occurring randomly with nonlinear noise. Thus, this supports the applicability of our approach to real situations, such as the S&P 500 index with the AAPL stock price as an exogenous variable. The ARL values obtained by using the explicit formulas and NIE methods were similar. Furthermore, the existence and uniqueness of the ARL derivation based on the explicit formulas were proved. The ARL, SDRL, and MRL values obtained using the proposed method for MAX processes running on HWMA and CUSUM control charts were used to compare their performances. While varying the value of $\lambda$, the ARL, SDRL, and MRL values for the HWMA control chart were less than those for the CUSUM control chart. When applying the proposed method to real data from the S&P 500 index with the AAPL stock price as an exogenous variable, the ARL values for the HWMA control chart were less than those for the CUSUM control chart. Furthermore, the first out-of-control value detected by the HWMA control chart was sooner than that detected by the CUSUM control chart. The advantage of this research is that it brings these concepts and results for making strategies to detect the change in stock price level based on control limits of the proposed control charts. The detected change in the movement of stock price can generate the buying and selling signals for the investor.

In summary, the results indicate that the HWMA control chart performed better than the CUSUM control chart for all magnitudes of changes. In addition, the results obtained for a real-world scenario involving S&P 500 stock price datasets were consistent with those obtained in the simulation study. Although the proposed explicit formula derivation for the ARL can be applied to other scenarios, it is limited to cases involving exponential white noise and to the MAX model only. If the examined data contains further white noise patterns, determining the ARL value could require the use of alternative techniques, such as the NIE or Markov Chain approach, etc. For future research, explicit formulations for the ARL will be developed for other models relevant to real-world situations. (e.g., ARX, ARMAX, and ARIMAX) running on a HWMA control chart.