Statistical Fuzzy Reliability Analysis: An Explanation with Generalized Intuitionistic Fuzzy Lomax Distribution
Abstract
:1. Introduction
2. Definitions
2.1. Generalized Intuitionistic Fuzzy Set (GIFS)
2.2. Generalized Intuitionistic Fuzzy Number (GIFN)
2.3. Alpha–Beta Cut Sets of GIFN
2.4. Some Operations on GIFN
3. Model Description
3.1. Generalized Intuitionistic Fuzzy (GIF) Reliability Characteristics
- If and , then ,
- If , then .
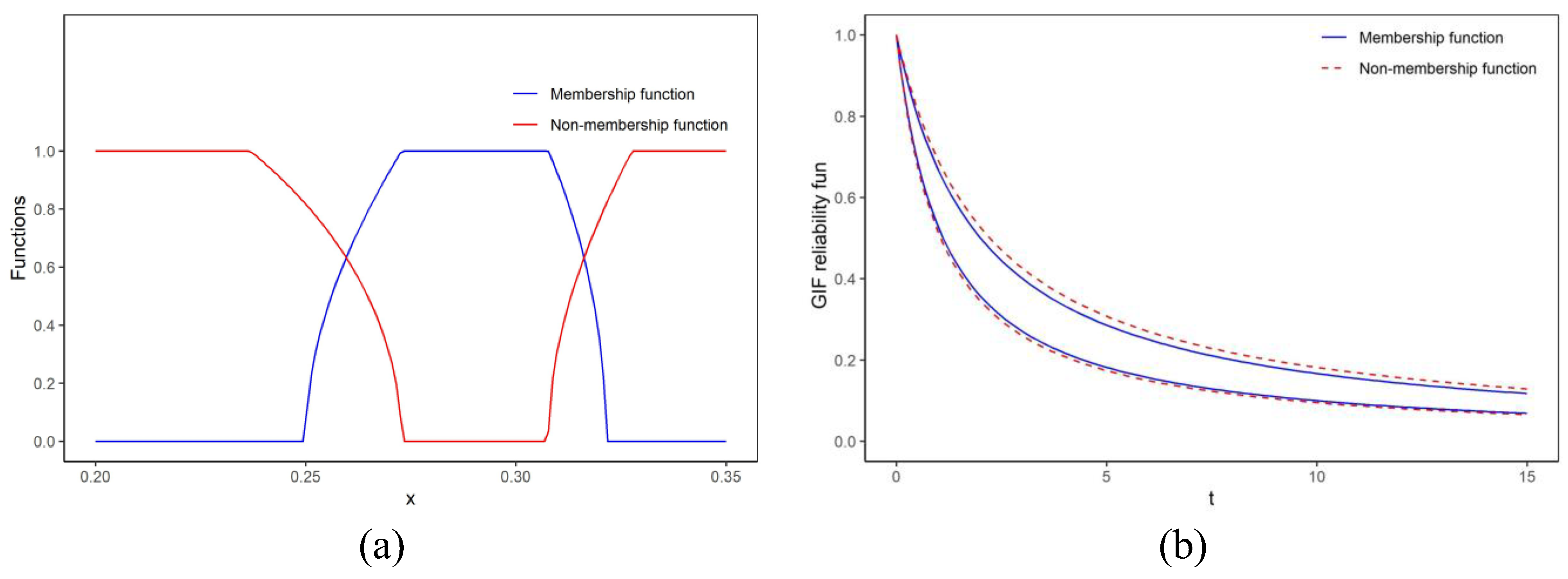
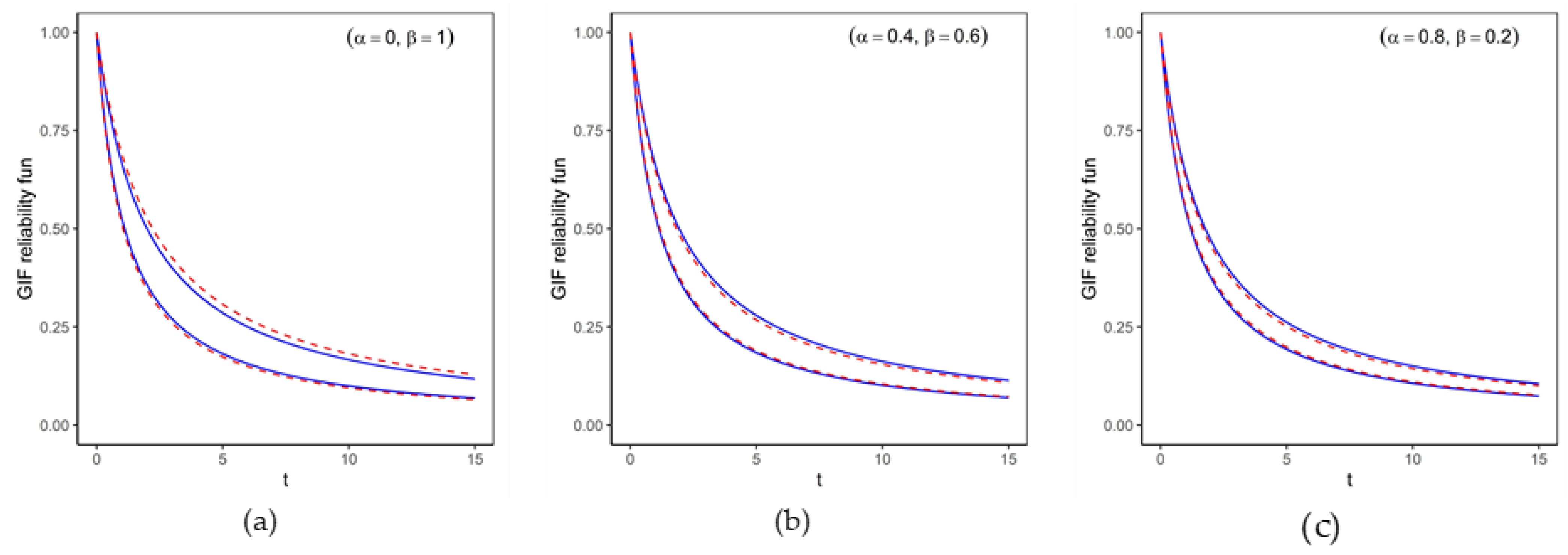
3.2. GIF Reliability Function
- ,
- ,
- .
3.3. GIF Conditional Reliability Function
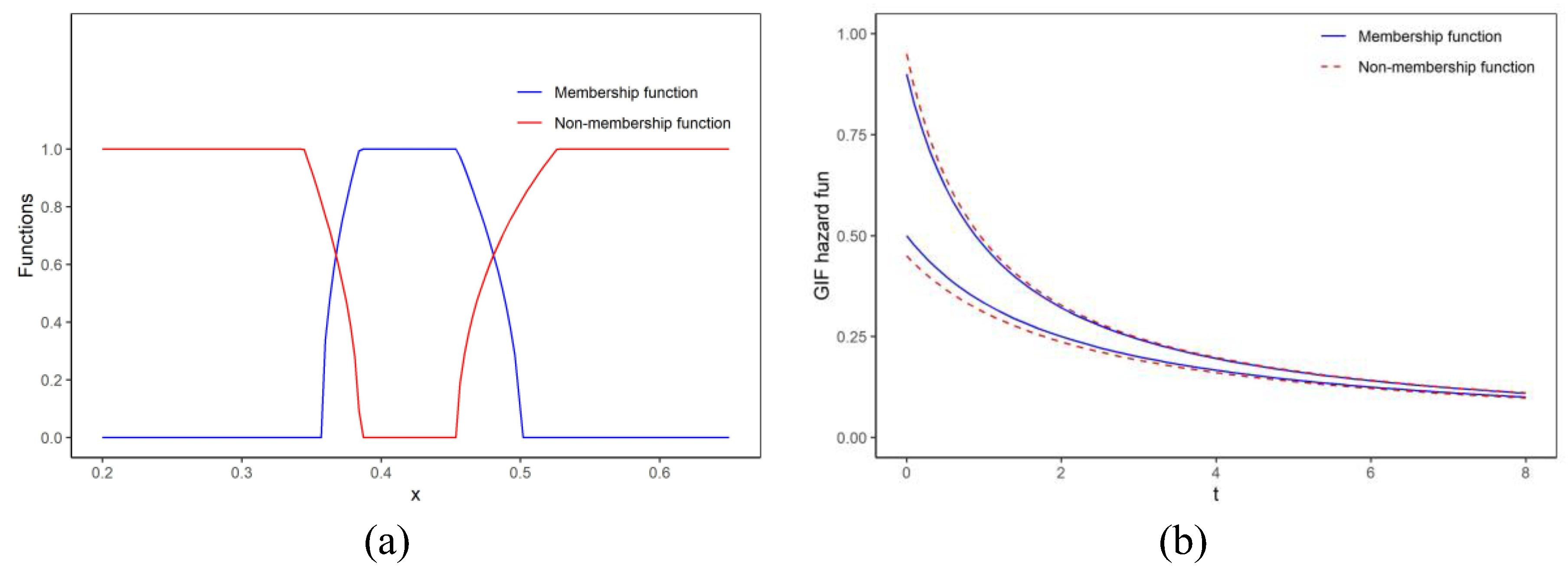
3.4. GIF Hazard Function
3.5. GIF Odds Function
4. Numerical Illustration
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Type-1 fuzzy sets and intuitionistic fuzzy sets. Algorithms 2017, 10, 106. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Alcantud, J.C.R. Complemental Fuzzy Sets: A Semantic Justification of $ q $-Rung Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2023, 1–9. [Google Scholar] [CrossRef]
- Varghese, P.J.; Rosario, G.M. A study on reliability using pendant, hexant, octant fuzzy numbers. J. Reliab. Stat. Stud. 2021, 491–526. [Google Scholar] [CrossRef]
- Mahapatra, G.; Roy, T. Reliability evaluation using triangular intuitionistic fuzzy numbers arithmetic operations. World Acad. Sci. Eng. Technol. 2009, 50, 574–581. [Google Scholar]
- Kumar, M.; Singh, S.; Kumar, D. System reliability analysis based on Pythagorean fuzzy set. Int. J. Math. Oper. Res. 2023, 24, 253–285. [Google Scholar] [CrossRef]
- Panchal, D. Reliability analysis of turbine unit using Intuitionistic Fuzzy Lambda-Tau approach. Rep. Mech. Eng. 2023, 4, 47–61. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence theory and intuitionistic fuzzy sets. Appl. Intell. 2018, 48, 3950–3962. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z. Priorities of intuitionistic fuzzy preference relation based on multiplicative consistency. IEEE Trans. Fuzzy Syst. 2014, 22, 1669–1681. [Google Scholar] [CrossRef]
- Liu, F.; Tan, X.; Yang, H.; Zhao, H. Decision making based on intuitionistic fuzzy preference relations with additive approximate consistency. J. Intell. Fuzzy Syst. 2020, 39, 4041–4058. [Google Scholar] [CrossRef]
- Yang, W.; Jhang, S.T.; Fu, Z.W.; Xu, Z.S.; Ma, Z.M. A novel method to derive the intuitionistic fuzzy priority vectors from intuitionistic fuzzy preference relations. Soft Comput. 2021, 25, 147–159. [Google Scholar] [CrossRef]
- Feng, F.; Zheng, Y.; Alcantud, J.C.R.; Wang, Q. Minkowski weighted score functions of intuitionistic fuzzy values. Mathematics 2020, 8, 1143. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.; Ram, M. Systems reliability assessment using hesitant fuzzy set. Int. J. Oper. Res. 2020, 38, 1–18. [Google Scholar] [CrossRef]
- Kumar, A.; Bisht, S.; Goyal, N.; Ram, M. Fuzzy reliability based on hesitant and dual hesitant fuzzy set evaluation. Int. J. Math. Eng. Manag. Sci. 2021, 6, 166. [Google Scholar] [CrossRef]
- Malik, S.; Rathee, R. Reliability modelling of a parallel system with maximum operation and repair times. Int. J. Oper. Res. 2016, 25, 131–142. [Google Scholar] [CrossRef]
- Garg, H. A novel approach for analyzing the reliability of series-parallel system using credibility theory and different types of intuitionistic fuzzy numbers. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1021–1035. [Google Scholar] [CrossRef]
- Hao, Z.; Xu, Z.; Zhao, H.; Su, Z. Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl.-Based Syst. 2017, 127, 16–28. [Google Scholar] [CrossRef]
- Akbari, M.G.; Hesamian, G. Time-dependent intuitionistic fuzzy system reliability analysis. Soft Comput. 2020, 24, 14441–14448. [Google Scholar] [CrossRef]
- Chachra, A.; Kumar, A.; Ram, M.; Triantafyllou, I.S. Statistical Fuzzy Reliability Assessment of a Blended System. Axioms 2023, 12, 419. [Google Scholar] [CrossRef]
- Bhandari, A.S.; Kumar, A.; Ram, M. Fuzzy reliability evaluation of complex systems using intuitionistic fuzzy sets, in Advancements in Fuzzy Reliability Theory. IGI Global 2021, 166–180. [Google Scholar]
- Faulin, J.; Juan, A.A.; Martorell, S.; Ramírez-Márquez, J.-E. (Eds.) Simulation Methods for Reliability and Availability of Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 315. [Google Scholar] [CrossRef]
- Glushkov, A. Methods of a Chaos Theory; Astroprint: Odessa, Ukraine, 2012. [Google Scholar]
- Shalizi, C.R. Methods and techniques of complex systems science: An overview. Complex Syst. Sci. Biomed. 2006, 33–114. [Google Scholar]
- Lomax, K.S. Business failures: Another example of the analysis of failure data. J. Am. Stat. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Bryson, M.C. Heavy-tailed distributions: Properties and tests. Technometrics 1974, 16, 61–68. [Google Scholar] [CrossRef]
- Pak, A.; Mahmoudi, M.R. Estimating the parameters of Lomax distribution from imprecise information. J. Stat. Theory Appl. 2018, 17, 122–135. [Google Scholar] [CrossRef]
- Al-Noor, N.H. On the Fuzzy Reliability Estimation for Lomax Distribution; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]
- Baloui, J.E. Analyzing system reliability using fuzzy Weibull lifetime distribution. 2014. Int. J. Appl. Oper. Res. 2014, 4, 93–102. [Google Scholar]
- Kumar, P.; Singh, S. Fuzzy system reliability using intuitionistic fuzzy Weibull lifetime distribution. Int. J. Reliab. Appl. 2015, 16, 15–26. [Google Scholar]
- Cramer, E. Ordered and censored lifetime data in reliability: An illustrative review. Wiley Interdiscip. Rev. Comput. Stat. 2023, 15, e1571. [Google Scholar] [CrossRef]
- Mondal, T.K.; Samanta, S. Generalized intuitionistic fuzzy sets. J. Fuzzy Math. 2002, 10, 839–862. [Google Scholar]
- Jamkhaneh, E.B.; Nadarajah, S. A new generalized intuitionistic fuzzy set. Hacet. J. Math. Stat. 2015, 44, 1537–1551. [Google Scholar] [CrossRef]
- Shabani, A.; Jamkhaneh, E.B. A new generalized intuitionistic fuzzy number. J. Fuzzy Set Valued Anal. 2014, 24, 1–10. [Google Scholar] [CrossRef]
- Roohanizadeh, Z.; Jamkhaneh, E.B.; Deiri, E. The reliability analysis based on the generalized intuitionistic fuzzy two-parameter Pareto distribution. Soft Comput. 2023, 27, 3095–3113. [Google Scholar] [CrossRef] [PubMed]
- Roohanizadeh, Z.; Jamkhaneh, E.B.; Deiri, E. A novel approach for analyzing system reliability using generalized intuitionistic fuzzy Pareto lifetime distribution. J. Math. Ext. 2021, 16. [Google Scholar]
- Atanassov, K.T.; Stoeva, S. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalam, A.; Cheng, W.; Du, Y.; Zhao, X. Statistical Fuzzy Reliability Analysis: An Explanation with Generalized Intuitionistic Fuzzy Lomax Distribution. Symmetry 2023, 15, 2054. https://doi.org/10.3390/sym15112054
Kalam A, Cheng W, Du Y, Zhao X. Statistical Fuzzy Reliability Analysis: An Explanation with Generalized Intuitionistic Fuzzy Lomax Distribution. Symmetry. 2023; 15(11):2054. https://doi.org/10.3390/sym15112054
Chicago/Turabian StyleKalam, Abdul, Weihu Cheng, Yang Du, and Xu Zhao. 2023. "Statistical Fuzzy Reliability Analysis: An Explanation with Generalized Intuitionistic Fuzzy Lomax Distribution" Symmetry 15, no. 11: 2054. https://doi.org/10.3390/sym15112054
APA StyleKalam, A., Cheng, W., Du, Y., & Zhao, X. (2023). Statistical Fuzzy Reliability Analysis: An Explanation with Generalized Intuitionistic Fuzzy Lomax Distribution. Symmetry, 15(11), 2054. https://doi.org/10.3390/sym15112054







