Origin of Giant Rashba Effect in Graphene on Pt/SiC
Abstract
1. Introduction
2. Materials and Methods
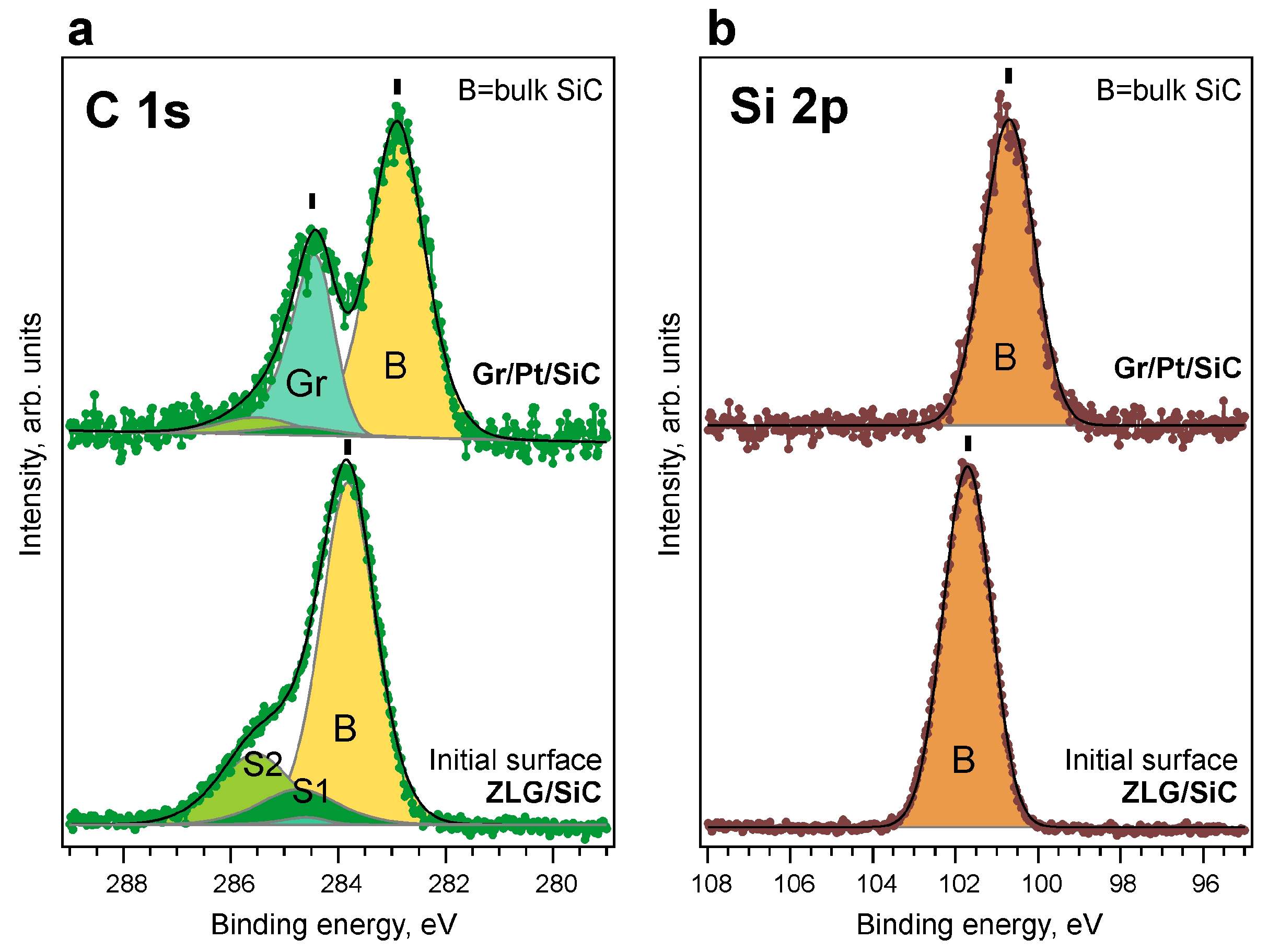
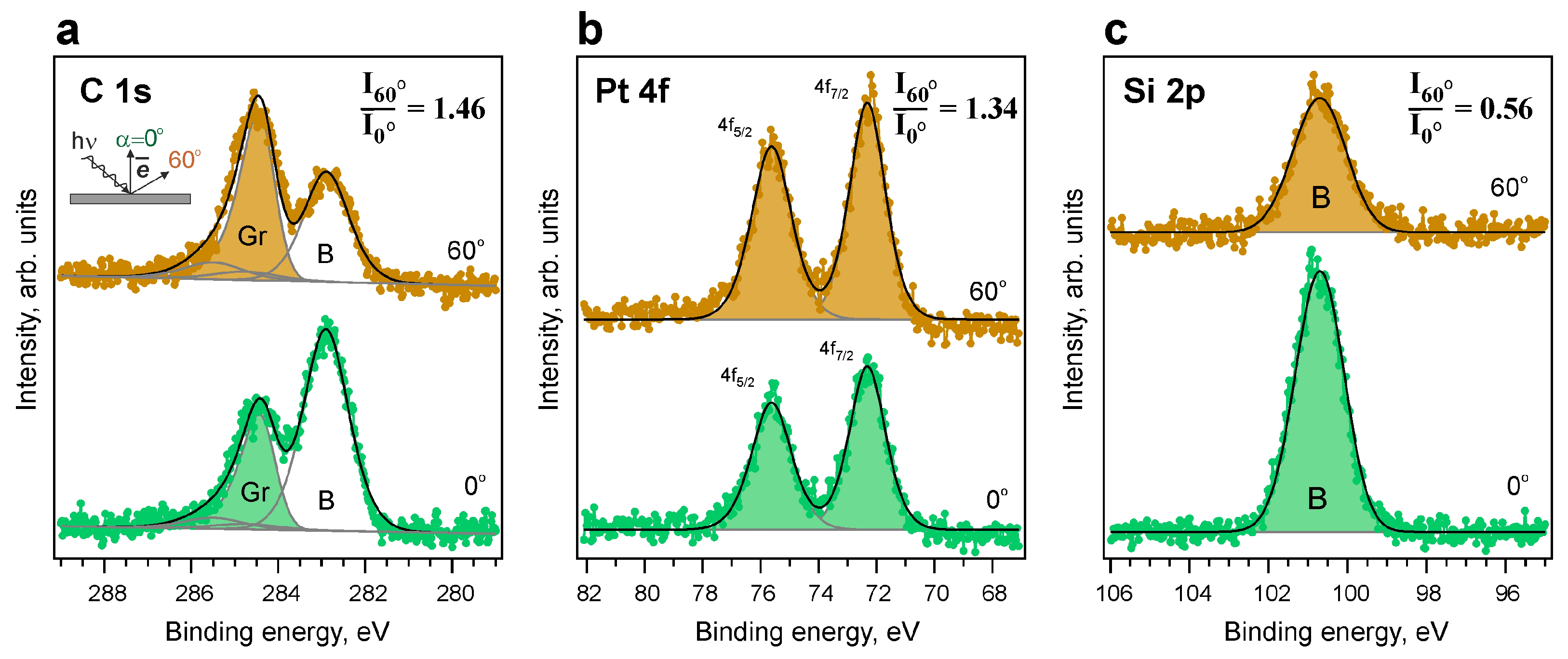
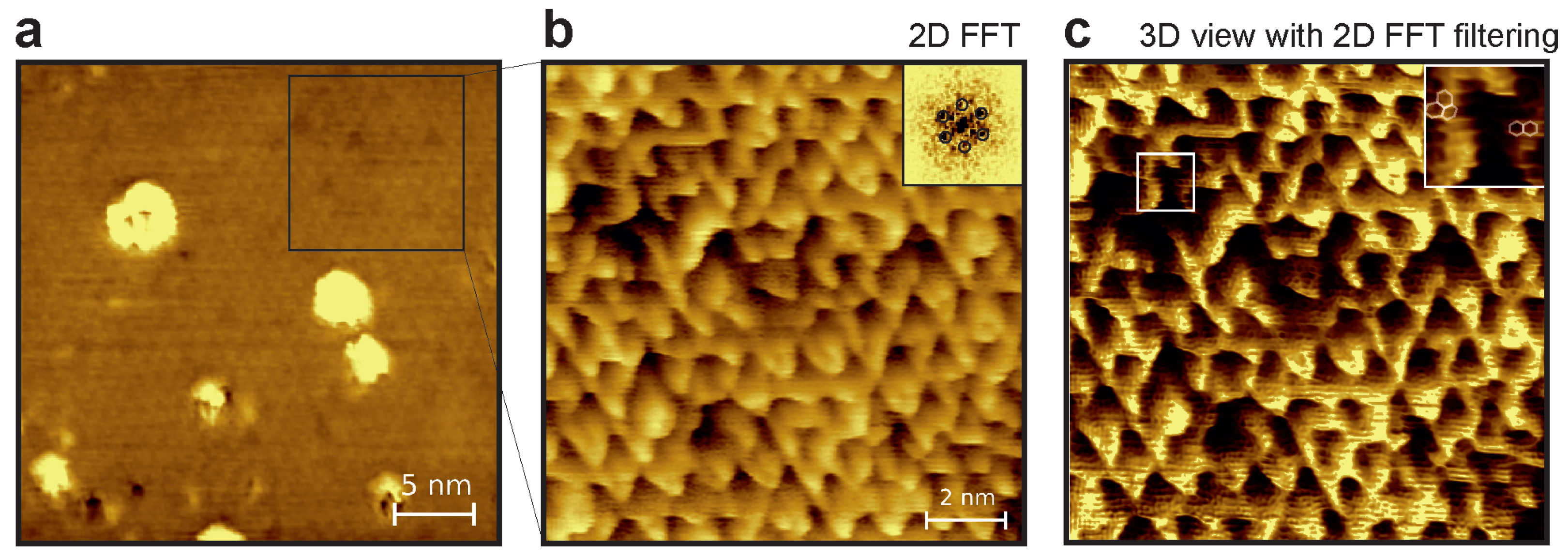
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kane, C.L.; Mele, E.J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef]
- Phong, V.T.; Walet, N.R.; Guinea, F. Effective interactions in a graphene layer induced by the proximity to a ferromagnet. 2D Mater. 2017, 5, 014004. [Google Scholar] [CrossRef]
- Eryzhenkov, A.V.; Tarasov, A.V.; Shikin, A.M.; Rybkin, A.G. Non-Trivial Band Topology Criteria for Magneto-Spin-Orbit Graphene. Symmetry 2023, 15, 516. [Google Scholar] [CrossRef]
- Chen, L.; Li, F.; Ding, X.M. Rashba spin–orbit coupling induced rectified currents in monolayer graphene with exchange field and sublattice potential. Chin. Phys. B 2023, 32, 087103. [Google Scholar] [CrossRef]
- Buša, J.; Pudlák, M.; Nazmitdinov, R. Rippled Graphene as an Ideal Spin Inverter. Symmetry 2023, 15, 1593. [Google Scholar] [CrossRef]
- Weeks, C.; Hu, J.; Alicea, J.; Franz, M.; Wu, R. Engineering a Robust Quantum Spin Hall State in Graphene via Adatom Deposition. Phys. Rev. X 2011, 1, 021001. [Google Scholar] [CrossRef]
- Shikin, A.M.; Rybkin, A.G.; Marchenko, D.; Rybkina, A.A.; Scholz, M.R.; Rader, O.; Varykhalov, A. Induced spin–orbit splitting in graphene: The role of atomic number of the intercalated metal and pi–d hybridization. New J. Phys. 2013, 15, 013016. [Google Scholar] [CrossRef]
- Avsar, A.; Tan, J.Y.; Taychatanapat, T.; Balakrishnan, J.; Koon, G.K.W.; Yeo, Y.; Lahiri, J.; Carvalho, A.; Rodin, A.S.; O’Farrell, E.C.T.; et al. Spin–orbit proximity effect in graphene. Nat. Commun. 2014, 5, 4875. [Google Scholar] [CrossRef]
- Brey, L. Spin-orbit coupling in graphene induced by adatoms with outer-shell p orbitals. Phys. Rev. B 2015, 92, 235444. [Google Scholar] [CrossRef]
- Ng, S.W.; Noor, N.; Zheng, Z. Graphene-based two-dimensional Janus materials. NPG Asia Mater. 2018, 10, 217–237. [Google Scholar] [CrossRef]
- Sino, P.A.L.; Feng, L.Y.; Villaos, R.A.B.; Cruzado, H.N.; Huang, Z.Q.; Hsu, C.H.; Chuang, F.C. Anisotropic Rashba splitting in Pt-based Janus monolayers PtXY (X,Y = S, Se, or Te). Nanoscale Adv. 2021, 3, 6608–6616. [Google Scholar] [CrossRef]
- Gong, Q.; Zhang, G. Rashba Splitting and Electronic Valley Characteristics of Janus Sb and Bi Topological Monolayers. Int. J. Mol. Sci. 2022, 23, 7629. [Google Scholar] [CrossRef]
- Klimovskikh, I.I.; Tsirkin, S.S.; Rybkin, A.G.; Rybkina, A.A.; Filianina, M.V.; Zhizhin, E.V.; Chulkov, E.V.; Shikin, A.M. Nontrivial spin structure of graphene on Pt(111) at the Fermi level due to spin-dependent hybridization. Phys. Rev. B 2014, 90, 1–10. [Google Scholar] [CrossRef]
- Marchenko, D.; Varykhalov, A.; Sánchez-Barriga, J.; Seyller, T.; Rader, O. Rashba splitting of 100 meV in Au-intercalated graphene on SiC. Appl. Phys. Lett. 2016, 108, 172405. [Google Scholar] [CrossRef]
- Krivenkov, M.; Golias, E.; Marchenko, D.; Sánchez-Barriga, J.; Bihlmayer, G.; Rader, O.; Varykhalov, A. Nanostructural origin of giant Rashba effect in intercalated graphene. 2D Mater. 2017, 4, 035010. [Google Scholar] [CrossRef]
- Rybkin, A.G.; Tarasov, A.V.; Rybkina, A.A.; Usachov, D.Y.; Petukhov, A.E.; Eryzhenkov, A.V.; Pudikov, D.A.; Gogina, A.A.; Klimovskikh, I.I.; Di Santo, G.; et al. Sublattice Ferrimagnetism in Quasifreestanding Graphene. Phys. Rev. Lett. 2022, 129, 226401. [Google Scholar] [CrossRef] [PubMed]
- López, A.; Colmenárez, L.; Peralta, M.; Mireles, F.; Medina, E. Proximity-induced spin-orbit effects in graphene on Au. Phys. Rev. B 2019, 99, 085411. [Google Scholar] [CrossRef]
- Cano, B.M.; Gudín, A.; Sánchez-Barriga, J.; Clark, O.J.; Anadón, A.; Díez, J.M.; Olleros-Rodríguez, P.; Ajejas, F.; Arnay, I.; Jugovac, M.; et al. Rashba-like spin textures in Graphene promoted by ferromagnet-mediated Electronic-Hybridization with heavy metal. arXiv 2023, arXiv:2206.04351. [Google Scholar]
- Guo, G.Y.; Murakami, S.; Chen, T.W.; Nagaosa, N. Intrinsic Spin Hall Effect in Platinum: First-Principles Calculations. Phys. Rev. Lett. 2008, 100, 096401. [Google Scholar] [CrossRef]
- Klimovskikh, I.I.; Vilkov, O.; Usachov, D.Y.; Rybkin, A.G.; Tsirkin, S.S.; Filianina, M.V.; Bokai, K.; Chulkov, E.V.; Shikin, A.M. Variation of the character of spin-orbit interaction by Pt intercalation underneath graphene on Ir(111). Phys. Rev. B 2015, 92, 165402. [Google Scholar] [CrossRef]
- Briggs, N.; Gebeyehu, Z.M.; Vera, A.; Zhao, T.; Wang, K.; De La Fuente Duran, A.; Bersch, B.; Bowen, T.; Knappenberger, K.L.; Robinson, J.A. Epitaxial graphene/silicon carbide intercalation: A minireview on graphene modulation and unique 2D materials. Nanoscale 2019, 11, 15440–15447. [Google Scholar] [CrossRef]
- Xia, C.; Johansson, L.I.; Niu, Y.; Zakharov, A.a.; Janzén, E.; Virojanadara, C. High thermal stability quasi-free-standing bilayer graphene formed on 4H-SiC(0001) via platinum intercalation. Carbon 2014, 79, 631–635. [Google Scholar] [CrossRef]
- Premlal, B.; Cranney, M.; Vonau, F.; Aubel, D.; Casterman, D.; De Souza, M.M.; Simon, L. Surface intercalation of gold underneath a graphene monolayer on SiC(0001) studied by scanning tunneling microscopy and spectroscopy. Appl. Phys. Lett. 2009, 94, 1–4. [Google Scholar] [CrossRef]
- Yagyu, K.; Tajiri, T.; Kohno, A.; Takahashi, K.; Tochihara, H.; Tomokage, H.; Suzuki, T. Fabrication of a single layer graphene by copper intercalation on a SiC(0001) surface. Appl. Phys. Lett. 2014, 104, 053115. [Google Scholar] [CrossRef]
- Sung, S.J.; Yang, J.W.; Lee, P.R.; Kim, J.G.; Ryu, M.T.; Park, H.M.; Lee, G.; Hwang, C.C.; Kim, K.S.; Kim, J.S.; et al. Spin-induced band modifications of graphene through intercalation of magnetic iron atoms. Nanoscale 2014, 6, 3824. [Google Scholar] [CrossRef]
- Yang, D.; Xia, Q.; Gao, H.; Dong, S.; Zhao, G.; Zeng, Y.; Ma, F.; Hu, T. Fabrication and mechanism of Pb-intercalated graphene on SiC. Appl. Surf. Sci. 2021, 569, 151012. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, Q.; Yang, H.; Ma, Y.; Zhang, T.; Liu, L.; Gao, H.J.; Wang, Y. Advances in two-dimensional heterostructures by mono-element intercalation underneath epitaxial graphene. Prog. Surf. Sci. 2021, 96, 100637. [Google Scholar] [CrossRef]
- Gierz, I.; Suzuki, T.; Weitz, R.T.; Lee, D.S.; Krauss, B.; Riedl, C.; Starke, U.; Höchst, H.; Smet, J.H.; Ast, C.R.; et al. Electronic decoupling of an epitaxial graphene monolayer by gold intercalation. Phys. Rev. B 2010, 81, 235408. [Google Scholar] [CrossRef]
- Shikin, A.M.; Rybkina, A.A.; Rybkin, A.G.; Klimovskikh, I.I.; Skirdkov, P.N.; Zvezdin, K.A.; Zvezdin, A.K. Spin current formation at the graphene/Pt interface for magnetization manipulation in magnetic nanodots. Appl. Phys. Lett. 2014, 105, 042407. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Starke, U. Structural and electronic properties of epitaxial graphene on SiC (0 0 0 1): A review of growth, characterization, transfer doping and hydrogen intercalation. J. Phys. D Appl. Phys. 2010, 43, 374009. [Google Scholar] [CrossRef]
- Riedl, C.; Coletti, C.; Iwasaki, T.; Zakharov, A.A.; Starke, U. Quasi-free-standing epitaxial graphene on SiC obtained by hydrogen intercalation. Phys. Rev. Lett. 2009, 103, 1–4. [Google Scholar] [CrossRef]
- Emtsev, K.V.; Speck, F.; Seyller, T.; Ley, L.; Riley, J.D. Interaction, growth, and ordering of epitaxial graphene on SiC{0001} surfaces: A comparative photoelectron spectroscopy study. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 1–10. [Google Scholar] [CrossRef]
- Yazdi, G.R.; Iakimov, T.; Yakimova, R. Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals 2016, 6, 53. [Google Scholar] [CrossRef]
- Sohn, Y.; Shin, W.; Ryu, S.; Huh, M.; Cha, S.; Kim, K. Graphene p-n junction formed on SiC(0001) by Au intercalation. J. Korean Phys. Soc. 2021, 78, 40. [Google Scholar] [CrossRef]
- Jain, V.; Biesinger, M.C.; Linford, M.R. The Gaussian-Lorentzian Sum, Product, and Convolution (Voigt) functions in the context of peak fitting X-ray photoelectron spectroscopy (XPS) narrow scans. Appl. Surf. Sci. 2018, 447, 548–553. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 Three-Dimens. Vis. Crystal, Vol. Morphol. Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Merino, P. Structural Characterization of Epitaxial Graphene. Doctoral Thesis, Universidad Autónoma de Madrid, Madrid, Spain, 2014. [Google Scholar]
- Emtsev, K. Electronic and Structural Characterizations of Unreconstructed SiC(0001) Surfaces and the Growth of Graphene Overlayers. Doctoral Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2009. [Google Scholar]
- Tedesco, J.L.; Rowe, J.E.; Nemanich, R.J. Conducting atomic force microscopy studies of nanoscale cobalt silicide Schottky barriers on Si(111) and Si(100). J. Appl. Phys. 2009, 105, 083721. [Google Scholar] [CrossRef]
- Rybkin, A.G.; Rybkina, A.A.; Tarasov, A.V.; Pudikov, D.A.; Klimovskikh, I.I.; Vilkov, O.Y.; Petukhov, A.E.; Usachov, D.Y.; Estyunin, D.A.; Voroshnin, V.Y.; et al. A new approach for synthesis of epitaxial nano-thin Pt5Gd alloy via intercalation underneath a graphene. Appl. Surf. Sci. 2020, 526, 146687. [Google Scholar] [CrossRef]
- Riedl, C.; Starke, U.; Bernhardt, J.; Franke, M.; Heinz, K. Structural properties of the graphene-SiC(0001) interface as a key for the preparation of homogeneous large-terrace graphene surfaces. Phys. Rev. B 2007, 76, 245406. [Google Scholar] [CrossRef]
- Merino, P.; Svec, M.; Pinardi, A.L.; Otero, G.; Martín-Gago, J.A. Strain-Driven Moiré Superstructures of Epitaxial Graphene on Transition Metal Surfaces. ACS Nano 2011, 5, 5627–5634. [Google Scholar] [CrossRef] [PubMed]
- Usachov, D.; Brzhezinskaya, M.; Shikin, A.M.; Adamchuk, V.K. Electronic Structure of Pentacene on Ni(110): Comparison with Graphene. Fuller. Nanotub. Carbon Nanostructures 2010, 18, 487–492. [Google Scholar] [CrossRef]
- Meier, F.; Dil, J.H.; Osterwalder, J. Measuring spin polarization vectors in angle-resolved photoemission spectroscopy. New J. Phys. 2009, 11, 125008. [Google Scholar] [CrossRef]
- Otero, G.; González, C.; Pinardi, A.L.; Merino, P.; Gardonio, S.; Lizzit, S.; Blanco-Rey, M.; Van de Ruit, K.; Flipse, C.F.J.; Méndez, J.; et al. Ordered Vacancy Network Induced by the Growth of Epitaxial Graphene on Pt(111). Phys. Rev. Lett. 2010, 105, 216102. [Google Scholar] [CrossRef]
- Wang, Q.; Pang, R.; Shi, X. Molecular Precursor Induced Surface Reconstruction at Graphene/Pt(111) Interfaces. J. Phys. Chem. C 2015, 119, 22534–22541. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rybkina, A.A.; Gogina, A.A.; Tarasov, A.V.; Xin, Y.; Voroshnin, V.Y.; Pudikov, D.A.; Klimovskikh, I.I.; Petukhov, A.E.; Bokai, K.A.; Yuan, C.; et al. Origin of Giant Rashba Effect in Graphene on Pt/SiC. Symmetry 2023, 15, 2052. https://doi.org/10.3390/sym15112052
Rybkina AA, Gogina AA, Tarasov AV, Xin Y, Voroshnin VY, Pudikov DA, Klimovskikh II, Petukhov AE, Bokai KA, Yuan C, et al. Origin of Giant Rashba Effect in Graphene on Pt/SiC. Symmetry. 2023; 15(11):2052. https://doi.org/10.3390/sym15112052
Chicago/Turabian StyleRybkina, Anna A., Alevtina A. Gogina, Artem V. Tarasov, Ye Xin, Vladimir Yu. Voroshnin, Dmitrii A. Pudikov, Ilya I. Klimovskikh, Anatoly E. Petukhov, Kirill A. Bokai, Chengxun Yuan, and et al. 2023. "Origin of Giant Rashba Effect in Graphene on Pt/SiC" Symmetry 15, no. 11: 2052. https://doi.org/10.3390/sym15112052
APA StyleRybkina, A. A., Gogina, A. A., Tarasov, A. V., Xin, Y., Voroshnin, V. Y., Pudikov, D. A., Klimovskikh, I. I., Petukhov, A. E., Bokai, K. A., Yuan, C., Zhou, Z., Shikin, A. M., & Rybkin, A. G. (2023). Origin of Giant Rashba Effect in Graphene on Pt/SiC. Symmetry, 15(11), 2052. https://doi.org/10.3390/sym15112052




