Abstract
This paper presents a controller design technique for cascade control systems based on the grey wolf optimization (GWO) algorithm. In the proposed control scheme, the proportional-integral-proportional-derivative (PI-PD) controller structure is used to control both the open-loop unstable process in the primary loop and the stable process in the secondary loop. To determine the optimal controller parameters, a new optimization algorithm is used in which the Euclidean distance function is used as a multi-objective function. A symmetry property of the Euclidean distance function is that its distance does not depend on the starting point and destination. The multi-objective function is designed according to system time response specifications such as settling time, overshoot, and steady-state error. Thus, the optimization algorithm allows the simultaneous determination of all controller parameters according to the desired output response. Three simulation studies are presented in the paper and the results are compared with studies using various methods based on internal model control, a modified Smith predictor, and a genetic algorithm. The simulation results reveal that the proposed method improves the performances of the systems in the control of cascade processes.
1. Introduction
Cascade control is a frequently preferred structure to control parameters such as pressure, temperature, and flow in the process control industry [1]. Single-loop control structures to be designed with controllers such as classical PID controllers are insufficient in these systems. In particular, the existence of disturbance effects in the control system causes the expected control performance from the system to not be achieved. The cascade control scheme comprises two loops. In this way, the dynamic performance of the system is increased by suppressing any disturbance in the inner loop. Besides, it is well known that unstable systems with a time delay are more difficult to control than stable processes. Cascade control offers very successful results in the control of these systems.
Cascade control was first used by Franks and Worley [2] in chemical reactors and many studies were presented in the literature in the following years. Cascade control of heating, ventilation, and air conditioning systems [3] and cascade control of time-delayed unstable and integrating systems [4,5,6] are studies reported in the literature. Apart from these, cascade control is used in work areas such as load frequency control [7], some studies in power electronics [8], and electrical machines [9,10].
For example, Uma et al. presented a modified Smith predictor-based simple control method for time-delay integrating cascade processes [11]. Their proposed control scheme consists of three controllers, one in the inner loop and two controllers in the outer loop. The authors stated that the presented method provides noteworthy disturbance rejection in both primary and secondary loops. In another paper, a method was presented based on the Smith predictor for time-delayed unstable cascade systems [1]. They stated that their study aimed to present a control structure that would be particularly effective in disturbances rejection. The proposed control scheme has three controllers, and the first controller improves the transient response of the system, while the other two controllers are used to eliminate disturbances in the inner and outer loops. As a result, they emphasized that the method they proposed is simple and advanced the outputs. A study on the design of cascade control systems for time-delayed unstable processes has contributed to the literature [12]. Two controllers designed using internal model control (IMC) principles are used in the cascade control structure presented in the paper. The fact that the number of controllers and their parameters is low can be considered as the advantage of the study. The authors emphasized that the study is superior to existing studies by making comparisons according to integral absolute error (IAE) and total variation (TV) performance criteria and obtaining small values. For open loop unstable processes, Santosh and Chidambaram [13] proposed a basic approach for designing parallel cascade controllers. In their work, they used a proportional controller for the secondary loop and a proportional integral controller for the primary loop. Another piece of research proposed a parallel cascade control structure for unstable and integrating systems with time delays [5]. There are three controllers in Smith predictor-based parallel cascade control: a set-point tracking controller, stabilizing controller, and disturbance rejection controller. The nominal and perturbed system responses of the controlled systems were examined, and it was stated that there was a remarkable improvement in the performances of the systems. In another analysis, the authors realized optimal controller designs based on genetic algorithms for open-loop stable, unstable, and integrating cascade systems [14]. They stated that they obtained better system output responses, particularly for set-point tracking, with the classical cascade control structure in which they used the PI controller in the inner loop and the PID controller in the outer loop. Fan et al. [15] proposed a new series structure based on cascaded control for unstable processes with large delay times. Their method consists of a controller designed based on IMC principles in the inner loop. The set-point tracking controller in the outer loop is designed according to H2 optimum performance. For time-delayed unstable cascade processes, Chandran et al. [16] presented a simple controller design method based on fractional order calculations. They designed fractional-order PI and fractional-order PD designs in the primary loop and controller designs based on the IMC principle in the secondary loop according to the synthesis method. An unstable cascade process with a time delay was controlled by a generalized predictive control scheme in another study [17]. In their study, they proposed a control scheme in which they used an IMC-based controller in the inner loop and a set-point achievement controller in the outer loop. The technique proposed by Kalim and Ali [18] improves the servo response of the system in the outer loop while performing disturbance rejection in the inner loop in serial cascade systems. An enhanced series cascaded control approach with Smith predictor was designed in this work [19] by combining some techniques. Based on the direct synthesis approach and the pole placement method, the study designs controllers in cascade controller structure for some processes with dead time [20]. One of the recent studies on the cascade control of time-delayed unstable processes is presented by Mukherjee et al. [4]. Two of the three controllers used in the proposed method are fractional order controllers designed using the IMC approach. The other controller used as a stabilizer is in the PD structure. The controller parameters are determined by an artificial bee colony algorithm using a multi-objective objective function. The authors emphasized that the presented technique provides good improvement in closed-loop system responses according to some studies.
The focus of this study is the cascade control of unstable systems with a time delay, which we often encounter in industrial processes. In the control of time-delayed unstable systems, the classical PID controller cannot provide the desired output response. The PI-PD controller offers better control than the classical PID controller in the control of unstable and integrating systems with a time delay [21]. Since the PI-PD controller is known to provide good performance, the PI-PD controller is used in the inner and outer loop of the cascade control scheme in the proposed method. In the proposed design procedure, controller parameters are determined simultaneously with a grey wolf optimization (GWO) algorithm-based method. A multi-objective function based on the Euclidean distance function with a symmetrical property is proposed in the optimization algorithm and the controller parameters are determined according to the desired output responses.
The main contribution of this article to the literature can be summarized as follows.
- The article improves both the set-point tracking and disturbance rejection performances in the control of unstable cascade systems by presenting a novel control scheme given in Section 2.
- The Grey wolf optimizer algorithm, which uses the Euclidean distance function as the objective function, is introduced to the literature as an effective method for determining the controller parameters in the proposed control scheme.
The paper is planned as follows. In the second section, the proposed cascade control scheme, and mathematical background are presented. The third section is about the GWO algorithm used to determine the controller parameters. In this section, the GWO algorithm is briefly introduced, the multi-objective function is defined, and its use in the cascade control structure is explained. Section 4 includes the simulation study. In this section, the proposed method is presented in comparison with the studies reported in the literature on three time-delayed unstable processes. The last section is the Conclusions.
2. Fundamentals of Cascade Control and Proposed Cascade Control Scheme
The block diagram of the basic cascade control consisting of two nested loops is given in Figure 1 [22]. One of the advantages of cascade control is that it can eliminate disturbance without losing the ability to follow the set point value well [23]. Gp1 and Gp2 are system transfer functions of processes belonging to primary (outer) and secondary (inner) systems, respectively. Gc1 and Gc2 indicate controllers of primary and secondary systems. In addition, d1 and d2 represent disturbance inputs affecting the outer and inner loops. In the cascade control block diagram, the controller of the secondary system is used to provide the stability in the inner loop, while the controller of the primary system is used to provide the stability in the outer loop.
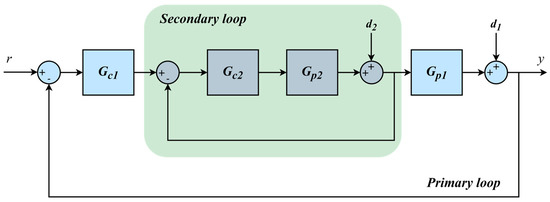
Figure 1.
Classical cascade control block diagram.
This basic cascade control structure has been developed over the years and many different cascade control structures are reported in the literature. In this study, a novel control scheme based on the PI-PD controller structure is proposed and is shown in Figure 2. The proposed control scheme is carried out in order to carry the success of the PI-PD controller structure in the control of unstable systems with a time delay to the cascade control structure. While the PD controller structure is used in primary and secondary loop feedback, the PI controller structure is used in the forward path of both loops. Among the reasons why this cascade control structure is preferred is to increase the dynamic performance of the system by suppressing the disturbances affecting the system very quickly. In addition, increasing the speed of the system and eliminating the negative effects of time delay are other reasons.
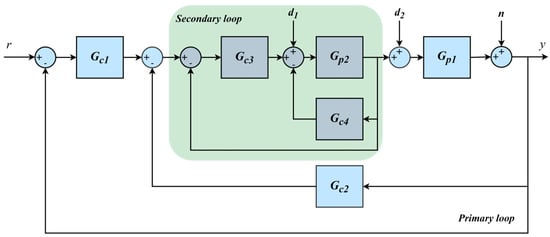
Figure 2.
Proposed cascade control scheme.
The equations of the controllers in the control scheme are given in Equations (1), (2), (3). and (4), respectively [21].
Outer loop controller equations:
Inner loop controller equations:
In this paper, the outer loop process is considered as an open loop unstable process with a time delay as shown Equation (5). The inner loop process is planned as an open loop stable process with a time delay as given in Equation (6).
In addition, d1 and d2 illustrate disturbance inputs for the inner and outer loop, respectively.
3. Tuning of Controller Parameters Based on the GWO Algorithm
Optimal controller parameter determination is one of the key topic of control theory. It ensures that the control system will be stable and provide the desired output. Considering that there are four controllers and two parameters for each controller in the proposed control scheme for the control of cascade systems, it can be easily understood that it is not an easy controller design procedure. In order to overcome this difficult design process, it is inevitable to create an effective control algorithm.
In the last few decades, interest in the tuning of controller parameters has increased and hundreds of studies have appeared in the literature. The popularity of tuning methods based on optimization algorithms, which offer much more effective and faster solutions than conventional tuning methods, is increasing day by day. The classification of some popular meta-heuristic algorithms is given in Figure 3.
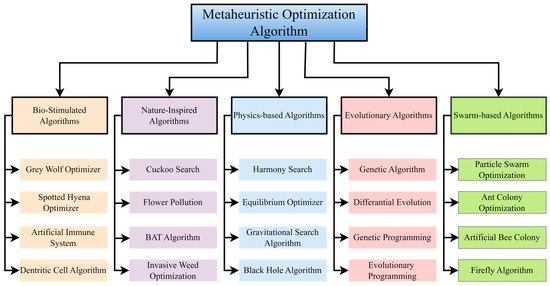
Figure 3.
Summary of some meta-heuristic algorithm [24].
In the proposed method, there is an aim to determine the optimal control parameters simultaneously. In the study, controller parameters are obtained with the heuristic algorithm-based GWO algorithm. The GWO algorithm is a population-based heuristic algorithm developed by Mirjalili et al. which models the leadership hierarchy and hunting mechanism of grey wolves [25]. The hunting strategy in grey wolves can be described as locating the prey and encircling the prey under the leadership of the alpha-wolf. Alpha, beta, and delta wolves are assumed to provide better prey location information in mathematical models. For this reason, the three best solutions are used to update the positions of the wolves in the GWO algorithm. Alpha is at the top of the swarm’s overall hierarchy. Alpha wolves are followed by beta, delta, and omega wolves, respectively. Omega wolves help meet the needs of these three groups of wolves. The following hunting strategies of grey wolves are referenced for mathematical modelling [25].
- Tracking, chasing, and approaching the prey
- Pursuing, encircling, and harassing the prey until it stops moving
- Attack toward the hunt
Mirjalili et al. mathematically modelled this hunting method and the social hierarchy of grey wolves to perform optimization. The most suitable individuals in the mathematical model are considered to be alphas. Generally, the second and third best solutions are considered beta and delta individuals, and all other solutions are omega individuals. Grey wolves encircle their prey during a hunt. Equations (7) and (8) are used to model the behavior of wolves encircling the prey [26].
In the above equations, is the distance between the prey and p is the position vector of the prey. t is the number of iterations and is the position vector of the grey wolf. In addition, and represent coefficient vectors for grey wolves. , and are calculated by Equations (9) and (10), respectively [26].
In the above equations, is the vector where the vector decreases linearly between [2, 0] during optimization. , and vectors are vector with random values in the range [0–1].
To mathematically model the hunting behavior of grey wolves, the following equations are proposed by Mirjalili et al., assuming that alpha, beta, and delta have better information about the potential position of the prey [26].
The graph in Figure 4 shows how the positions have changed within the GWO.
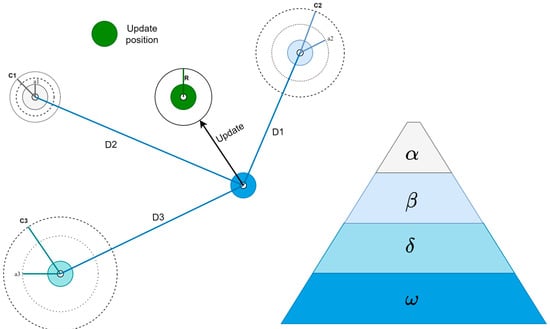
Figure 4.
Position updating in the GWO algorithm [27].
The flowchart of the GWO algorithm is given in Figure 5. In addition, [25] can be examined for more detailed information about GWO.
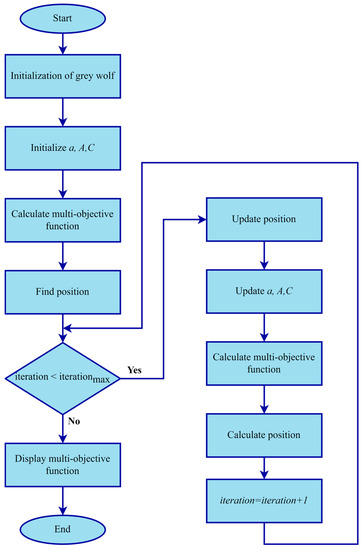
Figure 5.
GWO algorithm flowchart [25].
In the optimization algorithm, the multi-objective function is needed to tune the controller parameters using GWO. Assuming that the Euclidean distance function will perform well, the Euclidean distance function is proposed as a multi-objective function in the optimization algorithm. In mathematics, the Euclidean distance between two points in the Euclidean space is the length of a line segment between the two points. This implies that the Euclidean distance function is symmetrical regardless of which of the two points the starting point is and which is the destination. In the Euclidean plane, the distance between x and y is given by Equation (14) [28,29]. In the study, a multi-objective function is defined to minimize the distance between the target value and the actual value and it is given by Equation (15).
In Equation (15), xt1, xt2 and xt3 represent target settling time, steady-state error, and maximum percent overshoot, respectively. Similarly, ya1, ya2, and ya3 show the actual settling time, steady-state error, and maximum percent overshoot.
The block diagram of the proposed optimization technique is presented in Figure 6.
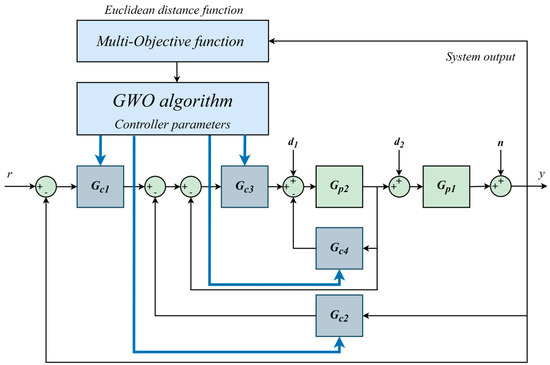
Figure 6.
Block diagram of the proposed optimization technique.
First of all, the desired settling time, percent overshoot, and steady-state error of the cascade process to be controlled are decided and the multi-objective function is determined. Information such as the iteration number, population size, and controller parameter value range is entered into the optimization algorithm. Optimization runs by generating random values for the controller parameters. The output information of the cascade system is taken and evaluated in the optimization algorithm. When the optimization reaches the maximum number of iterations, the algorithm stops and the optimal controller parameters are determined. In this study, each controller parameter range is selected as (0–15). In addition, the population size is determined as 30 and the maximum number of iterations is determined as 100.
4. Simulation Study
For the simulation studies, three process models reported in the literature are selected which are in an unstable cascade process with a time delay. In all cases, the nominal responses of the systems and controller signal responses are presented comparatively. Furthermore, the perturbed responses of the systems are given for the robustness analysis of the processes. In addition, the performance measures such as IAE and TV given in Equations (16) and (17), respectively, are presented in the table for comparison purposes [30].
Example 1.
The primary and secondary loop process models are as follows:
For this process reported in the literature, Dasari et al. [12] and Yin et al. [31] realized various controller designs. In Dasari’s method, the transfer function of the set-point filter is FR(s) = 1/(6.821s + 1). In addition, the primary and secondary process controllers are Gc1(s) = 0.4780 [1 + (1/0.99s) + 0.2130s] [(6.8210s + 1)/(0.5670s + 1)] and Gc2(s) = (2.07s + 1)/(0.3s + 1). In Yin’s method, the designed controllers (GCS, and GCD) are as GCS(s) = 4.6456[1 + (1/4.2549s) + 0.2798s][(0.4695s + 1)/(0.23s + 1)]. In addition, the secondary process controller and set-point filter are Gc2(s) = (2.07s + 1)/(0.3s + 1) and F(s) = 1/(1.1904s2 + 4.2549s + 1), respectively.
Firstly, the desired values of settling time, percent overshoot value, and steady-state error are determined for Example 1. While determining the multi-objective function, the settling time is targeted as 5 s and the percent overshoot value and steady-state error are considered as zero. These values are determined by taking the studies in the literature as a reference and aiming for the better values. By rearranging the multi-objective function according to the desired values, the optimization algorithm is run and the controller parameters are determined as in Table 1. The table also shows the controller parameters obtained for Examples 2 and 3. For all cases, the optimization algorithms are run 20 times with 100 iterations. For Example 1, it can be seen from the convergence curve in Figure 7 that the objective function reaches its value at approximately the 70th iteration. Since other examples have similar convergence curves, they are not presented in the study.

Table 1.
Controller parameters for examples.
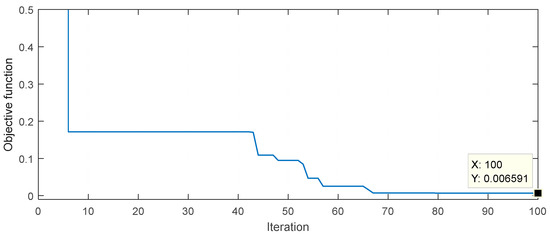
Figure 7.
Convergence curve for Example 1.
To evaluate the performance of the proposed method, a comparison is achieved with some of the studies of Dasari et al. and Yin et al. The performance of the closed-loop system is assessed by giving a negative disturbance of magnitude 2 at t = 30 s and a negative unit step change in the disturbance at t = 70 s. For a fair comparison, disturbances in all of the examples are applied just up to the front of both the primary and secondary processes. System output responses and control signals are given in Figure 8. In Figure 8, it is conspicuous that the presented technique provides a faster response than the others and it gives very good results in both the first and second disturbance rejection. It is noteworthy that there are deteriorations in the control signals, especially in Yin’s method.
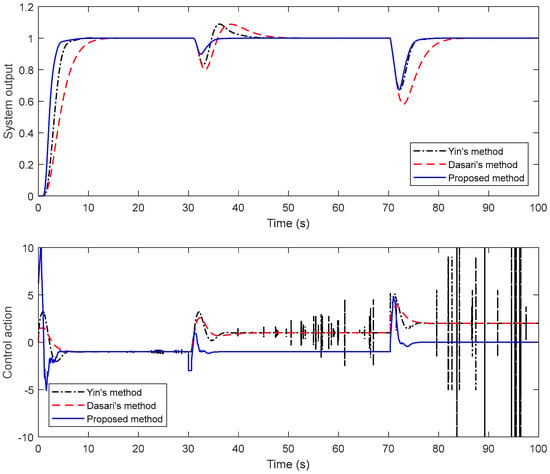
Figure 8.
Closed-loop responses (top) and control actions (bottom) for Example 1.
For the robustness analysis of the system, the parameters of both the primary and the secondary process are perturbed by 15%, and the closed-loop responses obtained are shown in Figure 9. It is assumed that there are −15% perturbations in the time constants of the primary and secondary systems and +15 perturbations in the time delays. As in regulatory responses, disturbance inputs with −2 magnitude at t = 30 s and −1 magnitude at t = 70 s are applied to the perturbed system. It is seen from Figure 9 that the proposed method provides a faster response despite a smaller oscillation than the other methods and it is quite good at disturbance rejection. For all of the methods, a band-limited white noise block is added to the system outputs to analyze the measurement noise effect. The parameters of the filter block are set as noise power = 0.0001, sampling time = 0.5, and seed = 0. The measurement noise for Example 1 is shown in Figure 10. In addition, IAE and TV performance measures for both nominal systems and perturbed systems are given in Table 2 for all of the examples.
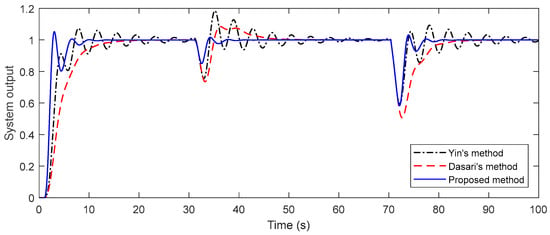
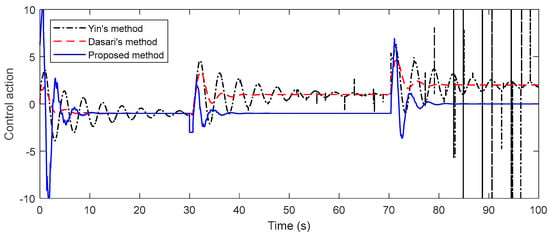
Figure 9.
Closed-loop responses (top) and control action (bottom) of the perturbed system for Example 1.
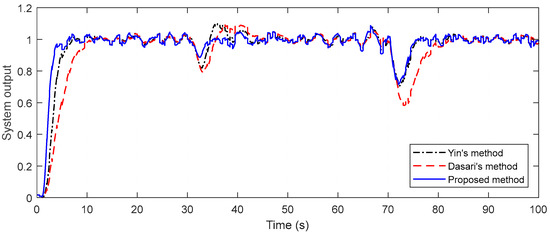
Figure 10.
Measurement noise for Example 1.

Table 2.
Performance measures of the systems.
Example 2.
In this example, the unstable process with time delay, whose transfer functions are given below, is discussed.
In this case, the methods are compared by considering two studies from the literature, Dasari et al.’s method [12] and Yin et al.’s method [31]. In Dasari’s method, the primary-secondary process controllers and set-point filter are Gc1(s) = 0.438 × [1 + (1/6.71s) + 0.85s] × [(39.76s + 1)/(4.21s + 1)], Gc2(s) = (20s + 1)/(2s + 2) and FR(s) = 1/(39.76s + 1), respectively.
In another piece of work, Yin’s method, GCS and GCD controllers are the same values, and GCS(s) = 4.6456 × [1 + (1/4.2549s) + 0.2798s] × [(0.4695s + 1)/(0.23s + 1)]. The secondary process controller and set-point filter are Gc2(s) = (2.07s + 1)/(0.3s + 1) and F(s) = 1/(33.51s2 + 34.31s + 1), respectively.
Before the controller design, the desired values are set as follows: settling time = 40 s, maximum overshoot = 0%, and steady-state error = 0. The controller parameters obtained by applying the proposed technique to the process models are seen in Table 1. For the controller performances, disturbance inputs with a magnitude of −1 are applied to the processes at t = 150 s and t = 300 s and the results are presented in Figure 11. In Figure 11, both closed-loop step responses and control signals are given comparatively. When the figure is examined, it is apparent that the proposed technique both improves the transient response and responds well to both disturbance inputs. It is noticeable from the figure that the proposed method is also acceptable in the control signal. In order to examine the robustness performance of the designed controllers, the time delays of the primary and secondary systems are perturbed as +10% and the time constants of the primary and secondary systems are perturbed as −10%. Figure 12 illustrates the closed-loop unit step responses of the perturbed system. It is noticeable from the figure that the proposed method exhibits good performance in the perturbed system compared to the others. The proposed method is also evaluated in point of measurement noise effect using the settings given in Example 1, and it can be seen from Figure 13 that it is superior to the other methods.
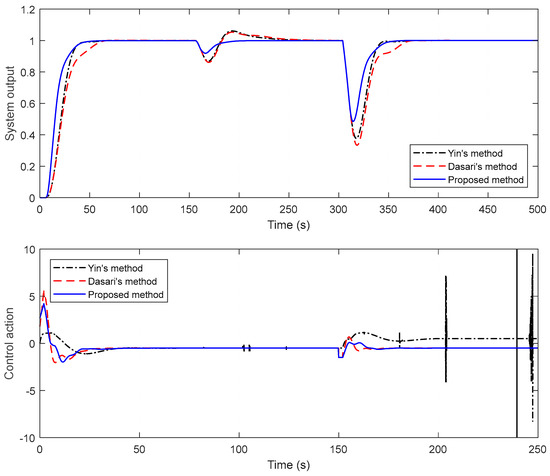
Figure 11.
Closed-loop responses (top) and control actions (bottom) for Example 2.
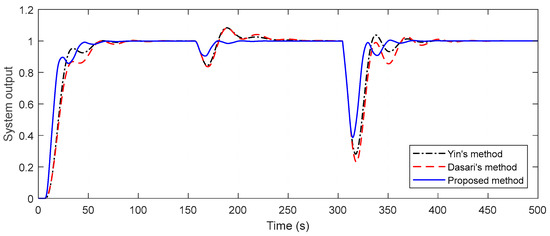
Figure 12.
Closed-loop responses of the perturbed system for Example 2.
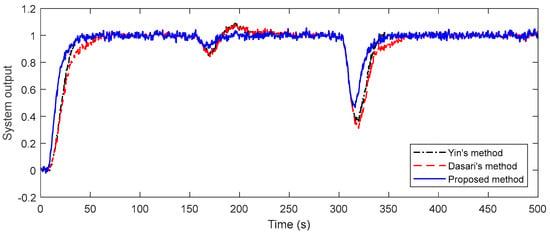
Figure 13.
Measurement noise effect for Example 2.
Example 3.
For this case, the following transfer functions studied by Kaya and Nalbantoglu [14] and Dasari et al. [12] are selected.
In Kaya’s method, the inner loop controller is considered as PI, the outer loop controller is the PID controller, and the controller parameters are given as follows; Kc = 0.6495 and Ti = 2.2043 (for PI), Kc = 2.5245, Ti = 23.5919 and Td = 1.6901 (for PID).
In Dasari’s method, the primary and secondary process controllers are Gc1(s) = 0.1223 × [1 + (1/5.50s) + 1.7280s] × [(72.25s + 1)/(0.8856s + 1)] and Gc2(s) = (s + 1)/(6s + 2). The set-point filter is as FR(s) = 1/(72.25s + 1).
Considering this example, it can be accepted as a good response if the system’s settling time is 30 s or less than 30 s. The maximum overshoot and steady-state error are desired to be approximately zero. The multi-objective function created in this direction plays an important role in obtaining optimal controller parameters. The controller parameters in Table 1 are obtained after the optimization algorithm is run 20 times, each with 100 iterations. By using these controller parameters, simulation examples are realized by applying disturbances with a magnitude of −0.5 change at t = 150 s and t = 300 s. By putting the determined controller parameters in the control system, the system output response and control signal are obtained as in Figure 14. The figure also includes responses obtained from two different methods in the literature. When the methods are compared in terms of set-point tracking, it is noteworthy that Kaya’s method has an overshoot of about 270%, while Dasari’s method has a long settling time. While the proposed method provides a shorter settling time than the other two methods, the percent overshoot value is also zero. In terms of disturbance rejection, the proposed method outperforms Dasari’s method in both disturbances. Compared to Kaya’s method, similar responses are provided in the first disturbance. The settling time is the same, although there is a slight difference in the amplitudes of the second disturbance. Furthermore, appropriate control signals are obtained by all three methods. Robustness analysis is performed to see the performance of the control designs. The time delays in the primary and secondary processes are increased by 10%. The time constants are also reduced by 10% on both plants. For all of the methods, the closed-loop unit step responses of perturbed systems are presented in Figure 15. It is discernible from the figure that the proposed method provides a good response in both set-point tracking, and disturbance rejection. Moreover, the methods are compared in point of measurement noise as in the other examples, and the superiority of the proposed method is readily apparent from Figure 16.
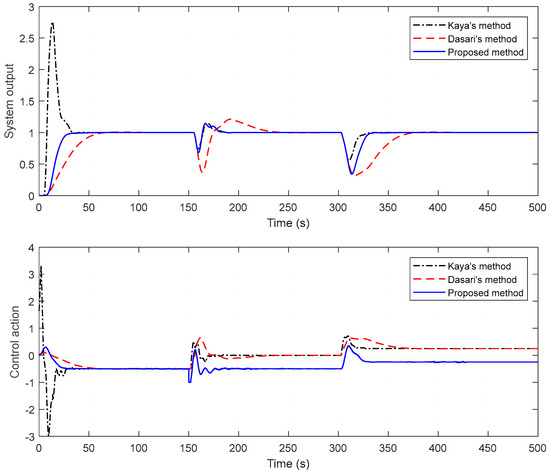
Figure 14.
Closed-loop responses (top) and control actions (bottom) for Example 3.
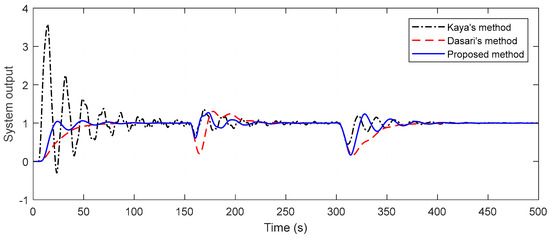
Figure 15.
Closed-loop responses of the perturbed system for Example 3.
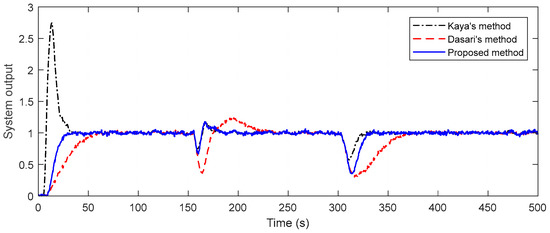
Figure 16.
Measurement noise effect for Example 3.
5. Conclusions
In this paper, a control technique based on PI-PD controller principles and a new optimization algorithm is proposed for cascade control systems. The method is applied to time-delayed unstable systems in the primary process and to time-delayed stable processes in the secondary process. The PI-PD controller structure, which provides very successful results in the control of time-delayed, and unstable systems, is located in both the primary loop and the secondary loop in the proposed control scheme. Furthermore, the use of the Euclidean distance function as a multi-objective function and the optimal determination of the controller parameters according to the desired settling time and overshoot represent the original aspect of this study. The performance of the proposed method is compared with some of the studies reported in the literature, based on measures such as set-point tracking, disturbance rejection, and robustness analysis. With the proposed method, it is observed that fast responses without overshoot are provided in the set-point tracking in all cases. It is noticeable in the comparisons that the proposed control technique also provides very good results in disturbance rejection. It has also been observed that the designed controllers are effective against parameter changes. As a result, the control of cascade systems is improved by proposing a novel control scheme and algorithm.
In future studies, the use of the proposed control algorithm in the control of real-time systems will contribute to the literature.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Padhan, D.G.; Majhi, S. Enhanced cascade control for a class of integrating processes with time delay. ISA Trans. 2013, 52, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Franks, R.G.; Worley, C.W. Quantitative Analysis of Cascade Control. Ind. Eng. Chem. 1956, 48, 1074–1079. [Google Scholar] [CrossRef]
- Ivanova, D.; Valov, N.; Deyanov, M. Application of the genetic algorithm for cascade control of a HVAC system. MATEC Web Conf. 2019, 292, 01064. [Google Scholar] [CrossRef]
- Mukherjee, D.; Raja, G.; Kundu, P. Optimal fractional order IMC-based series cascade control strategy with dead-time compensator for unstable processes. J. Control Autom. Electr. Syst. 2021, 32, 30–41. [Google Scholar] [CrossRef]
- Raja, G.L.; Ali, A. Smith predictor based parallel cascade control strategy for unstable and integrating processes with large time delay. J. Process Control 2017, 52, 57–65. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Anwar, M.; Laskar, S. Enhanced control of unstable cascade systems using direct synthesis approach. Chem. Eng. Sci. 2021, 232, 116322. [Google Scholar] [CrossRef]
- El-Ela, A.; Adel, A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.-G. Enhanced coyote optimizer-based cascaded load frequency controllers in multi-area power systems with renewable. Neural Comput. Appl. 2021, 33, 8459–8477. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, W.; Hu, J.; Ye, X. Closed-loop analysis and cascade control of a nonminimum phase boost converter. IEEE Trans. Power Electron. 2010, 26, 1237–1252. [Google Scholar] [CrossRef]
- Pisano, A.; Davila, A.; Fridman, L.; Usai, E. Cascade control of PM DC drives via second-order sliding-mode technique. IEEE Trans. Ind. Electron. 2008, 55, 3846–3854. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, X.; Song, B.; Tao, J.; Li, H.; Ye, B. Data-based cascade control of permanent magnet synchronous motor with industrial robot application. J. Eng. 2018, 2018, 1930–1934. [Google Scholar] [CrossRef]
- Uma, S.; Chidambaram, M.; Seshagiri Rao, A.; Yoo, C.K. Enhanced control of integrating cascade processes with time delays using modified Smith predictor. Chem. Eng. Sci. 2010, 65, 1065–1075. [Google Scholar] [CrossRef]
- Dasari, P.R.; Alladi, L.; Rao, A.S.; Yoo, C. Enhanced design of cascade control systems for unstable processes with time delay. J. Process Control 2016, 45, 43–54. [Google Scholar] [CrossRef]
- Santosh, S.; Chidambaram, M. A simple method of tuning parallel cascade controllers for unstable FOPTD systems. ISA Trans. 2016, 65, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Kaya, İ.; Nalbantoğlu, M. Simultaneous tuning of cascaded controller design using genetic algorithm. Electr. Eng. 2016, 98, 299–305. [Google Scholar] [CrossRef]
- Fan, Z.; Ren, Z.; Chen, A. A Modified Cascade Control Strategy for Tobacco Re-Drying Moisture Control Process With Large Delay-Time. IEEE Access 2020, 8, 2145–2152. [Google Scholar] [CrossRef]
- Chandran, K.; Murugesan, R.; Gurusamy, S.; Mohideen, K.A.; Pandiyan, S.; Nayyar, A.; Abouhawwash, M.; Nam, Y. Modified cascade controller design for unstable processes with large dead time. IEEE Access 2020, 8, 157022–157036. [Google Scholar] [CrossRef]
- Bhaskaran, A.; Rao, A.S. Predictive control of unstable time delay series cascade processes with measurement noise. ISA Trans. 2020, 99, 403–416. [Google Scholar] [CrossRef]
- Kalim, M.I.; Ali, A. New tuning strategy for series cascade control structure. IFAC-Pap. 2020, 53, 195–200. [Google Scholar] [CrossRef]
- Raja, G.L.; Ali, A. Enhanced tuning of Smith predictor based series cascaded control structure for integrating processes. ISA Trans. 2021, 114, 191–205. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Anwar, M.; Laskar, S.; Mahboob, M. A unified approach to design controller in cascade control structure for unstable, integrating and stable processes. ISA Trans. 2021, 114, 331–346. [Google Scholar] [CrossRef]
- Kaya, I. A PI-PD controller design for control of unstable and integrating processes. ISA Trans. 2003, 42, 111–121. [Google Scholar] [CrossRef] [PubMed]
- Kaya, I. Improving performance using cascade control and a Smith predictor. ISA Trans. 2001, 40, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Kaya, İ.; Tan, N.; Atherton, D.P. Improved cascade control structure for enhanced performance. J. Process Control 2007, 17, 3–16. [Google Scholar] [CrossRef]
- Kumar, A.; Bawa, S. A comparative review of meta-heuristic approaches to optimize the SLA violation costs for dynamic execution of cloud services. Soft Comput. 2020, 24, 3909–3922. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Dai, S.; Niu, D.; Li, Y. Daily peak load forecasting based on complete ensemble empirical mode decomposition with adaptive noise and support vector machine optimized by modified grey wolf optimization algorithm. Energies 2018, 11, 163. [Google Scholar] [CrossRef]
- Alagoz, B.B.; Deniz, F.N.; Koseoglu, M. An efficient PID-based optimizer loop and its application in De Jong’s functions minimization and quadratic regression problems. Syst. Control Lett. 2022, 159, 105090. [Google Scholar] [CrossRef]
- Patel, S.P.; Upadhyay, S.H. Euclidean distance based feature ranking and subset selection for bearing fault diagnosis. Expert Syst. Appl. 2020, 154, 113400. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Yin, C.-q.; Wang, H.-t.; Sun, Q.; Zhao, L. Improved cascade control system for a class of unstable processes with time delay. Int. J. Control Autom. Syst. 2019, 17, 126–135. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).