Abstract
Motivated by recent studies of circuit complexity in weakly interacting scalar field theory, we explore the computation of circuit complexity in Even Effective Field Theories ( EEFTs). We consider a massive free field theory with higher-order Wilsonian operators such as , , and To facilitate our computation, we regularize the theory by putting it on a lattice. First, we consider a simple case of two oscillators and later generalize the results to N oscillators. This study was carried out for nearly Gaussian states. In our computation, the reference state is an approximately Gaussian unentangled state, and the corresponding target state, calculated from our theory, is an approximately Gaussian entangled state. We compute the complexity using the geometric approach developed by Nielsen, parameterizing the path-ordered unitary transformation and minimizing the geodesic in the space of unitaries. The contribution of higher-order operators to the circuit complexity in our theory is discussed. We also explore the dependency of complexity on other parameters in our theory for various cases.
1. Prologue
In recent years, tools and techniques from quantum information have played a vital role in developing new perspectives in areas such as quantum field theory and holography, particularly for AdS/CFT duality. A particular line of study in the context of AdS/CFT correspondence is deciphering the emergence of bulk physics using information from the boundary CFT [1]. It was shown in [2,3,4] that the codimension-2 extremal surfaces in the AdS are associated with the entanglement entropy (EE) of the boundary CFT. However, in recent years, studies in black hole physics have suggested that EE is not sufficient to capture the complete information, which led Susskind et al. to introduce a new measure known as Quantum Computational Complexity (QCC) [5,6,7,8,9,10,11,12,13]. In the context of AdS/CFT, the QCC of the dual CFT is proposed to be associated with the properties of the codimension-0 and codimension-1 extremal surfaces. This aroused the study of QCC in QFTs.
The complexity of quantum states has aroused a significant amount of interest not only in the context of holography but across different subfields of physics (from quantum computing and information to many-body physics), as it appears to be a better measure of information. In [14,15], the notion of circuit complexity was defined and studied for free bosonic field theory, and in [16,17], it was defined and studied for free fermionic field theory. For a weakly interacting field theory, the authors of [18] extended the study to the theory, where in addition to the study of QCC, its relationship with renormalization group flows was also explored. The growth of complexity in the quantum circuit model was studied in [19]. Circuit complexity was also discussed in the context of chaos, quantum mechanics, and quantum computing in [20,21,22,23]. It has been probed in relation to conformal and topological field theories and the Chern–Simmons theory [24,25,26,27]. Active study in the context of many-body quantum systems has been also gaining interest in recent years [28]. QCC has been studied in many other contexts. It has been explored extensively in holography [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. The thermodynamic properties of QCC were studied in [58,59,60]. In addition, various applications and properties of QCC were investigated in [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84].
In this paper, we extend the work in [18] by including even higher-order Wilsonian operators, which we denote with EEFT (Even Effective Field Theory). Our theory contains the interaction terms , , and . These are weakly coupled to the free scalar field theory via the coupling constants , , and respectively. The primary motivation for studying QCC in this context is to compute and understand QCC by including higher-order terms. The organization of the paper is as follows. In Section 2, we summarize Nielsen’s method for computing circuit complexity. In Section 3, we briefly discuss the pertinent details of EFT related to our work. In Section 4, we illustrate the computation of QCC for our theory by first giving an example of two coupled oscillators. In Section 5, we generalize the calculation to the N oscillator case. Since we could not observe any analytical expression for the relevant eigenvalues for N oscillators, in Section 6, we resort to numerical computation of the QCC. We plot the corresponding graphs of QCC with the relevant parameters in our theory. We finish up by summarizing and providing possible future prospects for our work.
2. Circuit Complexity and Its Purposes
Computationally, circuit complexity is defined as a measure of the minimum number of elementary operations required by a computer to solve a certain computational problem [85,86,87,88,89,90]. In quantum computation, a quantum operation is described by a unitary transformation. Therefore, quantum circuit complexity is the length of the optimized circuit that performs this unitary operation. As the size of the input increases, if the complexity grows polynomially, then the problem is called “easy”, but if it grows exponentially, then the problem is called “hard”.
Quantum information-theoretic concepts, such as entanglement, have proven to be helpful in areas other than quantum computing [91,92,93,94]. Quantum circuit complexity (QCC) is emerging as one such quantum information-theoretic concept that has the potential to explain phenomena in several areas of quantum physics. However, the lower bounding quantum circuit complexity is an extremely challenging open problem.
For our purpose, we will consider the geometric approach to computing quantum circuit complexity developed by Nielsen et al. [85,87]. The prime reason to consider a geometric approach is that it is much easier to minimize a smooth function in a smooth space than to minimize an arbitrary function in a discrete space. Since the unitaries are continuous, this method of optimization suits our needs well. Interestingly, this approach allows us to formulate the optimal circuit-finding problem in the language of the Hamiltonian control problem, for which a mathematical method called the calculus of variations can be employed to find the minima. Another reason is that this method is similar to the general Lagrangian formalism, where the motion of the test particle is obtained from minimizing a global functional. For example, in general relativity, test particles move along geodesics of spacetime described by the following geodesic equation:
where represents the coordinates for the position on the manifold and represents the Christoffel symbols given by the geometry of the spacetime. Thus, the problem of finding an optimal quantum circuit is related to “freely falling” along the minimal geodesic curve connecting the identity to the desired operation, and the path is given by the “local shape” of the manifold. If we have information about the local velocity and the geometry, then it is possible to predict the rest of the path. In this regard, geometric analysis of quantum computation is quite powerful, as it allows one to design the rest of the shortest quantum circuit with information about only part of it.
2.1. Main Mathematical Ideas
Our goal is to understand how difficult it is to implement an arbitrary unitary operation generated by a time-dependent Hamiltonian :
where is the path-ordering operator and the space of the circuits is parameterized by s. The path-ordering operator is the same as the time-ordering operator, which indicates that the circuit runs from right to left. We can expand the Hamiltonian as follows:
where represents the generalized Pauli matrices and the coefficient represents the control functions that tell us the gate to be applied at particular values of s.
The Schrödinger equation describes the evolution of the unitary operation:
where at the final time , .
We can impose a cost function on the Hamiltonian control which will tell us how difficult it is to apply a specific unitary operation . One can then define a Riemannian geometry in the space of the unitary operations with this cost function. Then, the problem of finding an optimal control function is translated to the problem of finding the minimal geodesic in this geometry, and we can define a notion of distance in . For this, we have to define a curve between the identity operation I and the desired unitary , which is a smooth function such that and . The length of this curve is defined as
This length gives the total cost of synthesizing the Hamiltonian that describes the motion along the curve. In particular, the distance is also a lower bound on the number of one- and two-qubit quantum gates necessary to exactly simulate U. The proof is available in the original papers of Nielsen [85]. Therefore, one can also consider the distance as an alternative description of the complexity.
The cost function F has to satisfy certain properties, such as continuity, positivity, positive homogeneity, and triangle inequality [77]. If we also demand F to be smooth (i.e., ), then the manifold is referred to as the Finsler manifold. Since the field of differential geometry is relatively mature, we hope that borrowing tools from differential geometry can provide a unique perspective on quantum complexity.
In the literature, there are several alternative definitions of the cost function . Some of them are
where , the linear cost functional measure, is the concept closest to the classical concept of counting gates, while , the quadratic cost functional, can be understood as the proper distance in the manifold. is similar to but with penalty parameters used to favor certain directions over others.
In Figure 1 the left figure represents a unitary transformation from a reference state to a target state using quantum gates, and the right figure represents geometrizing the problem of calculating the minimum number of gates representing the transformation.
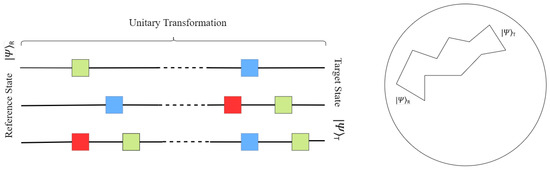
Figure 1.
The left figure represents a unitary transformation from a reference state to a target state using quantum gates (square blocks), and the right figure represents geometrizing the problem of calculating the minimum number of gates representing the transformation.
2.2. Geometric Algorithm to Compute Circuit Complexity
We will now describe the algorithm for computing the circuit complexity. These algorithms are not rigorously proven, but from an operational point, these general steps are implemented to calculate the circuit complexity:
- Give the Hamiltonian corresponding to a particular physical system;
- Specify the reference state , the target state , and the unitary operation that takes the former to the latter, where ;
- Now, we need to choose some set of elementary gates , where represents the generators of the group corresponding to the choice of gates and is a controllable parameter. For simplicity, we often choose generators satisfying .
- With the basis of generators , we parametrize the unitary operation as ;
- The velocity component can be explicitly computed usingFor generators obeying , reduces toThe right invariant metric in the space is given bywhere gives the penalty parameters. If (i.e., assigning an equal cost to every choice of gate), and having an extra condition , we obtain a metric of the reduced simple form
- The general form of the circuit complexity would beThe circuit complexity for the metric (i.e., ) is then
- From the boundary conditions of the evolution of unitary operations, we can compute the geodesic path and geodesic length. This length then gives a measure of circuit complexity.
In the literature, circuit complexity, using this geometric approach, is computed mostly for Gaussian wave functions because of its simpler structure compared with non-Gaussian wave functions. A Gaussian wave function can be represented as follows:
where and are the bases of vector v. If we can simultaneously diagonalize the reference and target states, then a common pattern observed in the complexity is that it will be given by some function of the ratio of the eigenvalues of and . Here, represents the reference state, and represents the target state.
We would like to mention that our approach to computing complexity is based on Nielsen’s geometric approach, which suffers from ambiguity in choosing the elementary quantum gates and states. However, these choices of our gates significantly simplify the calculation. Furthermore, the previous works on complexity in QFT and interacting QFT [14,18], using similar quantum gates to ours, have been connected to a holographic proposal, which is the original motivation to study quantum circuit complexity in QFT. Recently, Krylov complexity has been proposed as a tool for studying operator growth and associated quantum chaos [95,96,97,98,99,100,101,102,103]. Contrary to Nielsen’s geometric approach, the Krylov complexity is independent of such arbitrary choices, making it a good candidate for complexity in QFT and holography. However, Krylov complexity does not have a good operational meaning, such as in Nielsen’s geometric measure. Nielsen’s measure not only gives the state complexity but also gives us a method of constructing an optimal quantum circuit. This feature makes it more appealing than the Krylov complexity. In the future, we would like to study the Krylov complexity for our case too.
3. Effective Field Theory in a Nutshell
An effective field theory (EFT) is a theory corresponding to the dynamics of a physical system at energies that are smaller than the cutoff energy. EFTs have made a significant impact on several areas of theoretical physics, including condensed matter physics [104], cosmology [105,106,107,108,109,110,111], particle physics [112,113], gravity [114,115], and hydrodynamics [116,117]. The idea behind an EFT is that we can compute results without knowing the full theory. In the context of quantum field theory, this implies that using the method of EFTs, one can study the low energy aspect of the theory without having a full theory in the high energy limit. If the high-energy theory is known, then one can obtain an EFT using the “top-down” approach [118], where one has to eliminate high-energy effects. Using the “bottom-up” approach, one can obtain an EFT if the theory for high energy is not available. Here, one has to impose constraints given by symmetry and “naturalness” on suitable Lagrangians.
The Hamiltonian of our theory is
where the coefficients are called the “Wilson coefficients” for the EEFTs in arbitrary dimensions. These coefficients depend on the scaling of the theory. These coefficients are expected to be functions of the s, the cutoffs of our theory, and this functional dependence can be found by solving the renormalization group equations or Callan–Symanzik equations. s are called the “Wilson operators” in EEFTs. and are called “relevant operators of EEFTs”, and this theory is renormalizable up to . Beyond that, all the higher-order even terms, which are and in our case, are called “non-renormalizable irrelevant operators of EEFTs”. However, it should be noted that even though this theory goes up in the “Wilson operator” order, the contributions from those terms decrease gradually. Therefore, it is an infinite convergent series. Building upon this, we go on to compute the circuit complexity in the EEFT.
4. Circuit Complexity with Interaction for the Case of Two Harmonic Oscillators
We work with massive scalar field theory and with the even interaction terms , , and , which are weakly coupled to the free field theory via the coupling constants , , and , respectively. The inequality between the coupling constants is . The Hamiltonian for this scalar field in d spacetime dimensions is
where the mass of the scalar field is m. We work in the weak coupling regime () so that perturbative methods can be used to investigate the theory. The system can be reduced to a chain of harmonic oscillators if we regulate the theory by placing it on a () dimensional square lattice with lattice spacing . We are taking the infinite system in Equation (14) and discretizing it to a finite N oscillator system because if we have an infinite convergent theory and an infinite number of terms in the Hamiltonian, then we do not have the finite symmetries that we are interested in. Therefore, the discretized Hamiltonian becomes
where denotes the spatial position vectors of the points on the lattice in d dimensions and represents the unit vectors along the lattice. We make the following substitutions to simplify the form of the Hamiltonian:
After the substitutions, we obtain
We observe that the Hamiltonian obtained is identical to that of an infinite family of coupled anharmonic oscillators. The nearest term interaction comes from the kinetic part, and the self-interactions come from the remaining portion of the Hamiltonian. We start with the simple case of two coupled oscillators and generalize it to the case of N oscillators later in this paper. By setting , the Hamiltonian takes the form
Now, let us consider the normal mode basis:
In the normal mode basis, the unperturbed Hamiltonian becomes decoupled. Then, the eigenfunctions and eigenvalues for the unperturbed Hamiltonian can be easily solved, which is just a product of the ground-state eigenfunctions of the oscillators in the normal basis:
Here, s denote Hermite polynomials of an order n. The ground state wavefunction with first-order perturbative correction in , , and has the following expression:
Here, , , and are the terms representing the first-order perturbative corrections to the ground state wavefunction due to the , , and interactions, respectively, which are as follows:
We can approximate the total ground state wave function in Equation (20) in exponential form as the values of , , :
We shall take as the general target state wavefunction for calculating complexity in the following sections. The coefficients involved in the approximate wavefunction Equation (21) are given in the Table 1.

Table 1.
Expression for coefficients , present in the wavefunction.
4.1. Circuit Complexity
We will describe complexity in terms of a quantum circuit model. To calculate the circuit complexity for the two-oscillator system with even interactions up to , we need to fix our reference state, target state, and a set of elementary gates. We will construct the unitary transformation using these gates. This unitary transformation will take the system from the reference state () to the target state () (i.e., ). The minimum number of gates needed to construct such a unitary transformation is the complexity of the target state. Since our wave functions are nearly Gaussian, we can consider our space of states as the space of positive quadratic forms. This space can be parameterized as a function of a smooth parameter s as follows:
Here, is the normalization constant, and the parameter s runs from 0 to 1. If , then the circuit represents the target state in Equation (21) with , and at , the circuit is in the reference state. The continuous unitary transformation, specified by the s parameter, gives us the target state from the reference state. Writing the states in the form of Equation (22) helps us formulate the matrix version of our problem. Now, we want to represent the exponent of the wavefunction, which is a polynomial in the matrix form :
Here , , and are the initial coupling constants for , , and respectively. By transforming them into the normal coordinates, we obtain
We represent the exponent of the reference state shown above in a block diagonal matrix form as follows:
The basis chosen for this representation is
We need to ensure that the determinants of the and matrices are positive so that the wavefunction remains square-integrable everywhere. It should be noted that the matrix elements of A (i.e., ) are matrices themselves as shown below:
We have introduced a few parameters (b, p, k, c, d, and e) to ensure that the determinant of each block diagonal matrix is positive definite. Because we are considering higher even interactions, it is necessary to consider various quadratic and other higher-order terms. To find the positive determinant of the block, the value of b must be in the range . To eliminate the off-diagonal components, we set , as it would give the minimum line element. In the block, we fix , and the determinant becomes
We set p as in the range to satisfy the condition . Similarly, to ensure that the determinant of the block is positive and the line element is at its minimum, we set and .
Using the same basis as that mentioned in Equation (26), the target state matrix can be written as another matrix:
where we have the following block diagonal entries:
Here as well, we fix , , and to be one to make the off-diagonal terms zero and keep , , and for the positivity of all the block matrices.
As we are considering a closed quantum system, the reference state evolves into the target state via a certain unitary operator. Now, we represent this as
We represent the unitary matrix in the following form:
We have to enact the operators in a particular order. The s depend on the specific order in which the s are acting on the reference state. To find the minimum complexity, we try to have a geometric understanding of this unitary evolution process. Then, we can write the expression in Equation (29) as follows:
where represents the generators satisfying
Here, runs from 1 to 196. As mentioned above, is the reference state which undergoes a unitary transformation to find the target state . It enables us to calculate the boundary conditions that lead us to calculate the complexity functional. Thus, we have
This leads to the expression
Hence, we obtain
Now, the line element can be defined in terms of ’s as follows:
Here, we should mention that does not denote the total differential for . When observing the structure of the matrix A, we find that can be considered an element of with a positive determinant. Now, we will express the matrix with a similar structure to that in the target state matrix, and the unitary matrix contains four block diagonal matrices:
where
We have decomposed in terms of four block diagonal matrices. First, we note that the quadratic part of the first block is always diagonal, which induces a flat space, and thus we have . In the unitary operator , we do not allow the off-diagonal terms as in the final state, and only the block diagonal form remains. Thus, if we allow off-diagonal terms, we will have an increased line element, which we do not want. Now, can be expressed as , and so we observe that our has an group structure. We will parameterize each block matrix in as performed in [18] (i.e., we will parameterize it as an space):
Using these parameters for , we can then calculate the infinitesimal line element in Equation (35), which now becomes
We need to find the shortest path between the reference and the target state in this geometry, described by metric expressed in Equation (38). This shortest path will be the circuit complexity for our problem. For this purpose, we also need to calculate the proper boundary conditions denoting the reference and target states.
4.2. Boundary Conditions for the Geodesic
As we mentioned before, the minimal geodesic will be equivalent to finding the geodesic in the group manifold. The geodesic can be found by minimizing the following equation on the distance functional:
The boundary conditions from Equation (32) are
where and .
For solving the geodesic equations, we have to find conserved charges using the results of [14], as our metric is . Using Equations (40) and (42), we obtain
where, and :
With the same arguments in [14], we set
where and are constants which do not depend on s. Therefore, we have the freedom to choose any constant value of here which indicates that it will leave the origin in any direction. (Note: When we are calculating , any arbitrary constant value will not provide us an analytical expression, so we choose to be zero to find the simple analytical expression in Equation (42)) By taking into account all of these terms and conditions, we find the complexity functional as follows:
which is a straight line, as there is no off-diagonal term for when we set to be 0 and to be independent of s, according to Equation (41).
For the particular choice of a cost function that we used (i.e., ), the complexity functional is
As was shown in Equation (44), the complexity functional can be written in terms of some boundary values only. It can also be proven that this functional can just involve the eigenvalues of the reference and target matrix:
The proof of this expression is explicitly constructed in Appendix B. This result is very crucial, and we exploit this relation to generalize the complexity to N oscillators.
5. Analysis for Oscillators
To this point, our discussion in this paper has been concerned with two coupled harmonic oscillators involving higher-order interactions. To extend our analysis to effective field theories, we first need to generalize our results to N coupled harmonic oscillators with interaction terms. Then, we will gradually move toward the continuum limit for this problem. With that in mind, we consider the following Hamiltonian:
Now, we will assume that the periodic boundary condition is valid on this lattice of N oscillators such that (as it allows us to impose translational symmetry and use a Fourier transform for expression in terms of the normal mode coordinates). Then, we perform discrete a Fourier transform for this lattice using
Using the above Equations (48) and (49), we can transform the spatial coordinates into normal mode coordinates. The resultant Hamiltonian is then
where ,, and are the contributions from the , , and interaction terms, respectively. Now, we have
The proof of transformation of the interaction Hamiltonian in a Fourier space is given in Appendix A.
The target state wavefunction is given by
where the total perturbation wavefunction is
where , and are first-order perturbation corrections for the self-interaction terms , and , respectively.
The expression of along with the B terms was taken from [18].
The expression for is
The expression for is
where the terms , , …, are given according to the Table 2.

Table 2.
Expression for the terms , ….
The expression for is
The terms are given in the Table 3.

Table 3.
Expression for the terms .
Now, for finding the complexity, we represent the N oscillator wavefunction in the following way:
Once again, we have to choose a particular basis. Now, there are many choices for bases, but we consider the choice of bases in the following way:
Here, a, b, c, d, e, f, g, and h are indices that can have any value in the range from 0 to and must not be equal to each other. In the last term in , we mention a term that can be used to kill off-diagonal entries just as we did for the two-oscillator case. There will be many more terms like this on this basis. Expressing them explicitly is not necessary for our current work, and so we have not mentioned them.
Now, we will represent the matrix for N oscillators in a block diagonal fashion. In this format, the matrix will look like this:
where and are the so-called unambiguous and ambiguous blocks. Once we fix the target or reference stats, the coefficients in the unambiguous blocks are fixed. However, this is not the case for the ambiguous block, as it contains numerous parameters which are not fixed beforehand.
In the unambiguous block , we have all of the coefficients of terms such as and in Equation (54) multiplied by . On the other hand, the coefficients (multiplied by ) for terms such as
are there on the block.
To compute the complexity, we choose a particular non-entangled reference state for arbitrary N oscillators:
which can be represented as follows: S
where the matrix can be written as in the normal mode basis:
Here, is the N dimensional unit matrix. We are assuming that all the natural frequencies are (i.e., for all it is true that ). However, cannot be represented as easily as the first block because there are many undetermined parameters. Nevertheless, we can choose these parameters in such a way that the block becomes diagonal, just as we did for the two-oscillator case.
The complexity functional depends on the particular cost function that we choose. For the different cost functions mentioned in Equation (5), we find a different expression for the complexity functional. However, we will work with the following cost function for the rest of the paper:
With respect to this particular choice for the cost function, the complexity functional becomes
Here, we set all the variables to be one to put all directions in the circuit space on equal footing. Now, if we choose the parameters of such that is diagonal, then obviously, and will commute. If this is the case, then all can be written in a single equation as mentioned in [18]:
Here, represents the eigenvalues of the unambiguous block of the matrix and and denote the contributions to the complexity functional for the unambiguous and ambiguous blocks, respectively. From here on, we will use the complexity functional.
Commenting on and the Ambiguous Block
Here, we comment on the difficulties and issues with defining the ambiguous block , as has also been discussed in [18] for the interaction theory. One of the reasons for calling the matrix ambiguous is that there is a lot of arbitrariness in defining this block of the matrix; that is, there are many possible choices for defining the coefficients of the block, such as some terms which can be defined in the diagonal entries as well as in the off-diagonal entries and several higher-order cross terms, including , which can be defined in several forms. One possible solution to this is to try to define the matrix with the most general entries in which the coefficients are placed among all possible places in the block so that the determinant of the matrix should be positive definite. For the ambiguous block, the complexity can be defined with eigenvalues , and the total complexity will be given by Equation (68). However, due to the great arbitrariness or ambiguities in defining the block, we cannot easily define the complexity . One could think of using the renormalization approach to find the general form of , as was performed in [18] for the interaction, but the theory in our case is non-renormalizable beyond the term, so it is also not possible to use the standard renormalization procedure for our case.
Here, we calculate the complexity of the unambiguous block, which is easy to analyze. We use this expression to evaluate the complexity functional in the next section.
6. Numerical Evaluation of the Complexity Functional
Up to this point, we have always set the value of in the two-oscillator Hamiltonian and N oscillator Hamiltonian. However, for a generic analysis and also for the continuum limit, we need to put the M factor back in H. If we reinstate the factor of M in the Hamiltonian, we obtain the following expression for the Hamiltonian:
The overall factor in front of the Hamiltonian does not have any effect on the structure of the eigenfunctions of this Hamiltonian. However, some of the factors need to be rescaled in presence of the M factor, which are given below:
Here, we would like to mention again that . Using these rescaled parameters, we assume that the general form of the eigenvalues of represent the N oscillator Hamiltonian with first-order perturbative correction:
where N denotes the number of lattice points in each spatial dimension and the indices run from 0 to for each dimension. Then, the dimensional spatial volume becomes .
Here, is the contribution from the interaction, and f, g, , and denote the additional contributions to the eigenvalues in the presence of and interaction. The form of , as mentioned in [18], is
These additional terms f, g, , and cannot be calculated analytically. Therefore, we resort to numerical methods to calculate these.
The work carried out in [18] had a proper analytical expression for the eigenvalues, which made it easier to study the RG flows. However, when we consider higher-order interactions such as and , such analytic expressions for the RG flows and complexity cannot be found. This makes it difficult for us to study the RG flows and MERA and is beyond the scope of our model. Instead, we will focus only on complexity. The eigenvalues we obtained were small corrections to the one obtained in [18], so the connection they made will not be affected by the addition of higher interacting terms. Now, we will resort to numerical methods in the next section.
Numerical Analysis of the Complexity Functional
We will calculate the complexity for the unambiguous block first for an increasing number of oscillators. We have found the wavefunction for the Hamiltonian in Equation (47). As we reinserted the M term, we will just update the complexity using the rescaled parameters mentioned in the previous subsection. We set the following relevant parameter values:
where L is the length of the periodic chain. We chose N and so that was always satisfied. We will use the functional for the unambiguous block.
Case I: Increasing the Interactions
In Figure 2, we have plotted numerically the behavior of the complexity of the unambiguous block as a function of N, which is the number of oscillators in dimensions. In Figure 2a, we have two complexities, where the points in blue represent the complexity of the theory, which has no interaction term, and this complexity is due to the self-interaction between pairs of oscillators. We also see the points in orange and light orange, which represent the complexity of the theory with interaction. We notice that there is a bump initially in the graph for small N values, but in Figure 2a–c, we can observe that the values of the complexity with the free theory and the complexity with interactions became the same as we increased the value of N. We see that grew linearly with increasing N values, and the contributions to due to even interaction terms became negligible, while the behavior of the complexity for the unambiguous block would be same as if we were dealing only with the free theory. In Figure 2d, we have plotted for N being an odd number of oscillators for even interactions of , and we see that the initial values of the complexity increased as we included higher-order terms in the theory, but when we increased N, the contribution from these perturbative terms died out, and the graph followed a linear pattern of .
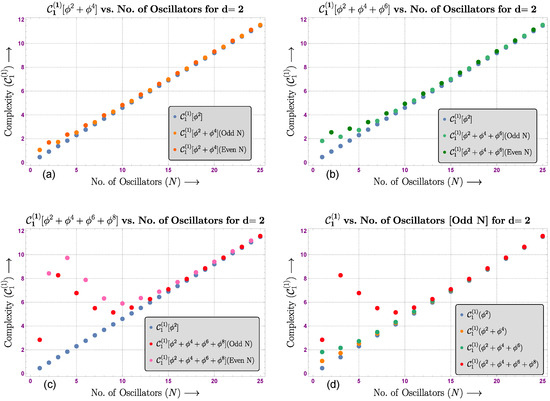
Figure 2.
Plot: (a–c) represents the complexity (from the unambiguous block) vs. the number of oscillators (N) for dimensions with different interactions. In plot (d), complexity vs. an odd number of oscillators (even resembling the same pattern) from all the interactions are placed together in the same plot, showing the contribution from each interaction.
Case II: Increasing the Dimension
In Figure 3, we show six different plots. In the first two plots, the complexity for the unambiguous block (up to interaction) is plotted with respect to the number of oscillators in dimensions and 4. Here, we notice that as we increased the dimensions, the contribution to due to the interaction term increased, and we saw a similar pattern as we included other higher-order even terms (i.e, the third and fourth graphs have interactions, and the fifth and sixth graphs contain interactions). However, in higher dimensions, the contributions of these interactions to the complexity also became negligible when we increased the value of N, and the behavior of this complexity became similar to the case where we had only the term and it grew linearly.
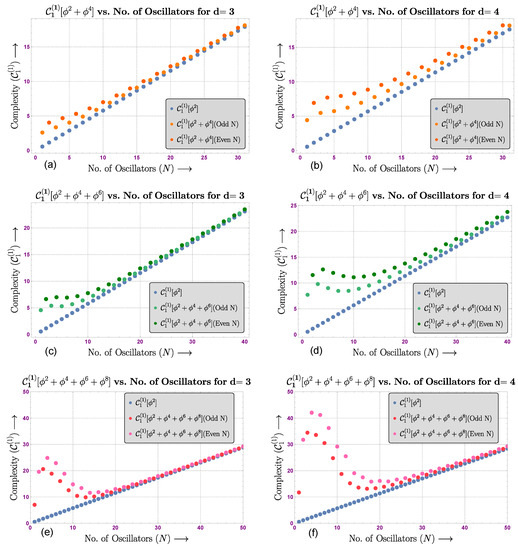
Figure 3.
Plot of complexity vs. number of oscillators in and , respectively, is shown in (a–f) for ().
Case III: vs.
In Figure 4, we have plotted the variation in the complexity versus for a particular value of oscillators , and we also show the variation in the same plot for different dimensions . As we increased the number of dimensions, the complexity of the unambiguous block increased, and in a particular dimension, the complexity value increased as we increased the number of interactions, which was noticeable for low values of . However, as we increased the value of , the behavior became similar to the free scalar theory.
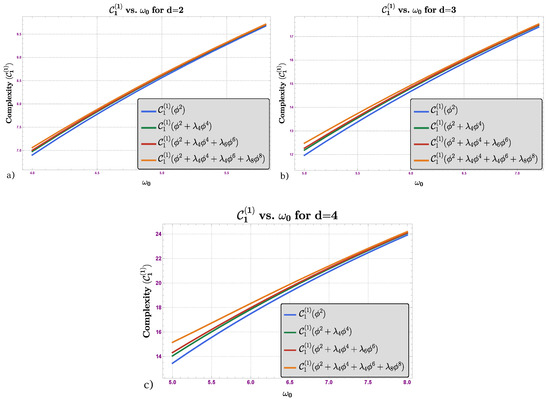
Figure 4.
Plot of complexity vs. (a) for , (b) for , and (c) for .
Case IV: Fractional Change in
We define the fractional change in complexity for a particular N value as
Here, we have an increment of two in the definition because odd and even branches of N can possibly show different behavior, as was the case for the complexity.
For small values of N, the even and odd complexities were different from each other. This is directly related to the fact that one can distinguish the system with an even or odd number of oscillators, but as we went for a large number of oscillators or in the continuum limit, the distinction between the even and odd numbers of oscillators faded away. In Figure 5, we have plotted the complexity of the unambiguous block, and we find that, initially, the fractional change in complexity was large for small N values, but it decreased continuously as we moved toward a large number of oscillators.
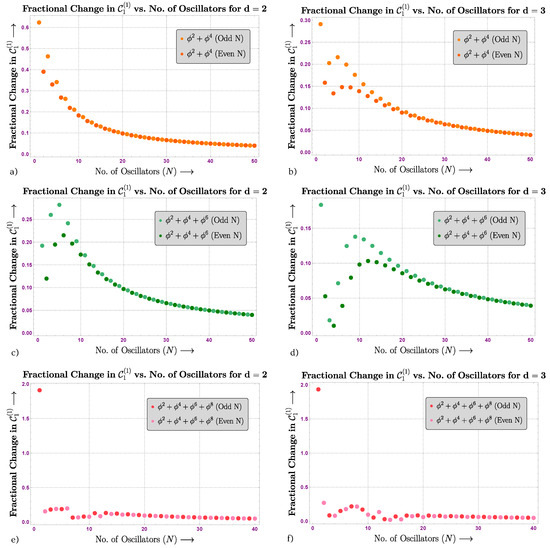
Figure 5.
The Plot of fractional change in complexity vs. number of oscillators.
7. Conclusions and Future Prospects
This work studied the circuit complexity for weakly interacting scalar field theory with , , and Wilsonian operators coupled via , , and to a free scalar field theory, respectively. The values of the coupling constants were chosen in the framework of an EEFT such that the perturbation analysis was valid. The reference state was an unentangled, nearly Gaussian state, and the target state was an entangled, nearly Gaussian state which was calculated using a first-order perturbation theory. First, we worked with the case of two oscillators, where the unitary evolution , which took us from the reference state to the target state, was parameterized using the AdS parameters. With this, we calculated the line element and found the complexity functional by imposing the appropriate boundary conditions. Then, we proceeded to the N oscillator case. Here, the circuit complexity depended on the ratio of the eigenvalues of the target to the reference states of the N oscillators. Since we could not observe any analytical expression of the eigenvalues of the target state of the N oscillators, we resorted to numerical analysis. The target matrix for N oscillators had a part where the bases could be uniquely determined (unambiguous part) and another part where the bases could not be determined (ambiguous part). The contribution to the total complexity came from the ambiguous as well as the unambiguous parts. In our work, we focused mainly on the computation of the complexity for the unambiguous part, denoted by the matrix. The following are the results that we observed:
- From our numerical analysis, the QCC with for the free field theory increased linearly with the number of oscillators. As we included the higher even Wilsonian terms, the growth of the complexity (contribution from the unambiguous part) was no longer linear for a small number of oscillators. For the large N limit, the contribution to the complexity from the interacting part vanished, and the linearity was restored.
- From the graph of complexity vs. , we see that upon fixing the dimensions and the number of oscillators, the complexity from the unambiguous part increased with an increasing value for .
- Another pattern inferred from our analysis is that as the dimension increases, the contribution to due to the interaction term increases for a fixed number of oscillators. We observed this pattern using degenerate frequencies for higher dimensions. One would expect a similar pattern, even if the frequencies were non-degenerate.
In [18], the eigenvalues had a proper analytical expression, which makes it easier to study RG flows. On the other hand, after adding higher-order corrections, there is no analytical expression of the eigenvalues. This makes it very challenging to study the RG and MERA connection. The eigenvalues we obtained were small corrections to the one obtained in [18], so the connection they made would not be affected by the addition of higher interacting terms. In upcoming works, we will address this issue.
In our analysis, we used in our complexity functional , but there are other different and useful kinds of measures that one can explore to gain new insights into circuit complexity.
Our approach to computing complexity is based on Nielsen’s geometric approach, which suffers from ambiguity in choosing the elementary quantum gates and states. Recent works have attempted to develop a new notion of complexity that is independent of these choices. As for our future goals, we have in mind the following:
- We can calculate the circuit complexity for odd Wilsonian terms in the effective theory, such as , , and . We can further generalize the study by adding both even and odd interaction terms together.
- We can study the behavior of circuit complexity in a similar theory when there is a quantum quench in the interaction and mass. We have already performed this for a interacting theory [119].
- We can further analyze circuit complexity in fermionic field theories and gauge theories.
- We can explore this problem in the context of the Krylov complexity [95,103,120], which is currently a melting pot in this research area.
- We can compare the Krylov complexity and circuit complexity for such theories to know which is a better measure of information for such cases.
Author Contributions
Conceptualization, S.C.; Methodology, S.C., S.M., N.P., A.R., S.S. and S.S.S.; Software, K.A., S.K., S.M., N.P., A.R., S.S., P.S. and S.S.S.; Validation, S.C.; Formal analysis, K.A., S.C., S.K., S.M., N.P., A.R., S.S., P.S. and S.S.S.; Investigation, S.C.; Writing—original draft, K.A., S.C., S.K., S.M., N.P. and A.R.; Writing—review & editing, S.C.; Supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
S.C. would like to thank the work friendly environment and all the members of CCSP, SGT University. The research fellowship of S.C. was supported by the J. C. Bose National Fellowship of Sudhakar Panda. S.C. also would like to thank the School of Physical Sciences at the National Institute for Science Education and Research (NISER) in Bhubaneswar for providing a work-friendly environment. S.C. also thanks all the members of our newly formed virtual international non-profit consortium “Quantum Structures of the Space-Time & Matter” (QASTM) for their elaborative discussions. S.C. would also like to thank all the speakers of the QASTM zoominar series from different parts of the world (For the uploaded YouTube link, see https://www.youtube.com/playlist?list=PLzW8AJcryManrTsG-4U4z9ip1J1dWoNgd) for supporting the research forum by giving outstanding lectures and their valuable time during the COVID pandemic time. Kiran Adhikari would like to thank TTK, RWTH, JARA, and the Institute of Quantum Information for the fellowships. Saptarshi Mandal, Nilesh Pandey, Abhishek Roy, Soumya Sarker, Partha Sarker, and Sadaat Salman Shariff would like to express their heartiest thanks to Jadavpur University, the University of Dhaka, NIT Karnataka, IIT Jodhpur, the University of Madras, and Delhi Technological University, respectively, for imparting knowledge and their enthusiasm for this research. Abhishek Roy would like to thank Sujit Damase for the discussions related to group generators. Partha Sarker would like to thank Syed Hasibul Hasan Chowdhury for the relevant discussions. K.A. would also like to thank David Di Vincenzo for his help in understanding quantum information theoretic concepts such as entanglement entropy and complexity. Finally, we would like to acknowledge our debt to the people belonging to various parts of the world for their generous and steady support for research in the natural sciences.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Interacting Part of the Hamiltonian in a Fourier Basis
The interacting part in the N oscillator Hamiltonian is
Now, we apply the discrete Fourier transform as in Equation (48) to find the interaction:
We apply the sum over index a and use the relation
to obtain
Now, the Kronecker delta will reduce one of the indices, such as to . Now, only runs from , whereas has possible values in the range . To obtain a valid index value for , we use the relation and write . This will return a valid index value for . Then, we have
Using similar arguments, we can find and .
Appendix B. in Terms of the Ratio of the Target and Reference Matrix Eigenvalues
We claimed in Equation (46) that can be expressed in terms of the ratio of eigenvalues of the target and reference matrix (i.e., and , respectively). This was due to the nature of the unitary operator U and the diagonal block structure of and .
To prove this, let us look at the complexity functional in Equation (44). The parameters in the blocks on the U matrix have AdS parametrization, and they appear in in , where . We can find these values for and from the boundary conditions we obtained in Equation (42). These values can be represented by the eigenvalues of and in the following way:
Here, and are the eigenvalues of the block in the matrix corresponding to the block in U, whereas and are diagonal elements of the similar block in . We can use the relation
to find the following for :
Then, our desired part in will be
Now, , and we have a different scenario. These are the lone diagonal parameters in the U matrix and have boundary conditions such as
References
- Harlow, D. TASI Lectures on the Emergence of Bulk Physics in AdS/CFT. arXiv 2018, arXiv:1802.01040. [Google Scholar]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Hubeny, V.E.; Rangamani, M.; Takayanagi, T. A Covariant holographic entanglement entropy proposal. JHEP 2007, 7, 062. [Google Scholar] [CrossRef]
- Rangamani, M.; Takayanagi, T. Holographic Entanglement Entropy; Springer: Berlin/Heidelberg, Germany, 2017; Volume 931. [Google Scholar] [CrossRef]
- Susskind, L. Computational Complexity and Black Hole Horizons. Fortsch. Phys. 2016, 64, 24–43, Addendum: Fortsch. Phys. 2016, 64, 44–48. [Google Scholar] [CrossRef]
- Stanford, D.; Susskind, L. Complexity and Shock Wave Geometries. Phys. Rev. D 2014, 90, 126007. [Google Scholar] [CrossRef]
- Susskind, L.; Zhao, Y. Switchbacks and the Bridge to Nowhere. arXiv 2014, arXiv:1408.2823. [Google Scholar]
- Susskind, L. Entanglement is not enough. Fortsch. Phys. 2016, 64, 49–71. [Google Scholar] [CrossRef]
- Brown, A.R.; Roberts, D.A.; Susskind, L.; Swingle, B.; Zhao, Y. Complexity, action, and black holes. Phys. Rev. D 2016, 93, 086006. [Google Scholar] [CrossRef]
- Brown, A.R.; Roberts, D.A.; Susskind, L.; Swingle, B.; Zhao, Y. Holographic Complexity Equals Bulk Action? Phys. Rev. Lett. 2016, 116, 191301. [Google Scholar] [CrossRef]
- Brown, A.R.; Susskind, L.; Zhao, Y. Quantum Complexity and Negative Curvature. Phys. Rev. D 2017, 95, 045010. [Google Scholar] [CrossRef]
- Couch, J.; Fischler, W.; Nguyen, P.H. Noether charge, black hole volume, and complexity. JHEP 2017, 3, 119. [Google Scholar] [CrossRef]
- Susskind, L. Three Lectures on Complexity and Black Holes; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Jefferson, R.; Myers, R.C. Circuit complexity in quantum field theory. JHEP 2017, 10, 107. [Google Scholar] [CrossRef]
- Chapman, S.; Heller, M.P.; Marrochio, H.; Pastawski, F. Toward a Definition of Complexity for Quantum Field Theory States. Phys. Rev. Lett. 2018, 120, 121602. [Google Scholar] [CrossRef] [PubMed]
- Khan, R.; Krishnan, C.; Sharma, S. Circuit Complexity in Fermionic Field Theory. Phys. Rev. D 2018, 98, 126001. [Google Scholar] [CrossRef]
- Hackl, L.; Myers, R.C. Circuit complexity for free fermions. JHEP 2018, 7, 139. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Shekar, A.; Sinha, A. Circuit complexity in interacting QFTs and RG flows. JHEP 2018, 10, 140. [Google Scholar] [CrossRef]
- Haferkamp, J.; Faist, P.; Kothakonda, N.B.T.; Eisert, J.; Halpern, N.Y. Linear growth of quantum circuit complexity. Nat. Phys. 2022, 18, 528–532. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Chemissany, W.; Haque, S.S.; Murugan, J.; Yan, B. The Multi-faceted Inverted Harmonic Oscillator: Chaos and Complexity. SciPost Phys. Core 2021, 4, 002. [Google Scholar] [CrossRef]
- Ali, T.; Bhattacharyya, A.; Haque, S.S.; Kim, E.H.; Moynihan, N.; Murugan, J. Chaos and Complexity in Quantum Mechanics. Phys. Rev. D 2020, 101, 026021. [Google Scholar] [CrossRef]
- Eisert, J. Entangling Power and Quantum Circuit Complexity. Phys. Rev. Lett. 2021, 127, 020501. [Google Scholar] [CrossRef]
- Roberts, D.A.; Yoshida, B. Chaos and complexity by design. JHEP 2017, 4, 121. [Google Scholar] [CrossRef]
- Camilo, G.; Melnikov, D.; Novaes, F.; Prudenziati, A. Circuit Complexity of Knot States in Chern-Simons theory. JHEP 2019, 7, 163. [Google Scholar] [CrossRef]
- Couch, J.; Fan, Y.; Shashi, S. Circuit Complexity in Topological Quantum Field Theory. Fortsch. Phys. 2022, 70, 9–10. [Google Scholar] [CrossRef]
- Chagnet, N.; Chapman, S.; de Boer, J.; Zukowski, C. Complexity for Conformal Field Theories in General Dimensions. Phys. Rev. Lett. 2022, 128, 051601. [Google Scholar] [CrossRef]
- Flory, M.; Heller, M.P. Conformal field theory complexity from Euler-Arnold equations. JHEP 2020, 12, 091. [Google Scholar] [CrossRef]
- Jaiswal, N.; Gautam, M.; Sarkar, T. Complexity and information geometry in the transverse XY model. Phys. Rev. E 2021, 104, 024127. [Google Scholar] [CrossRef]
- Barbon, J.L.F.; Rabinovici, E. Holographic complexity and spacetime singularities. JHEP 2016, 1, 084. [Google Scholar] [CrossRef]
- Alishahiha, M. Holographic Complexity. Phys. Rev. D 2015, 92, 126009. [Google Scholar] [CrossRef]
- Yang, R.Q. Strong energy condition and complexity growth bound in holography. Phys. Rev. D 2017, 95, 086017. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Complexity of Formation in Holography. JHEP 2017, 1, 062. [Google Scholar] [CrossRef]
- Carmi, D.; Myers, R.C.; Rath, P. Comments on Holographic Complexity. JHEP 2017, 3, 118. [Google Scholar] [CrossRef]
- Reynolds, A.; Ross, S.F. Divergences in Holographic Complexity. Class. Quant. Grav. 2017, 34, 105004. [Google Scholar] [CrossRef]
- Zhao, Y. Complexity and Boost Symmetry. Phys. Rev. D 2018, 98, 086011. [Google Scholar] [CrossRef]
- Flory, M. A complexity/fidelity susceptibility g-theorem for AdS3/BCFT2. JHEP 2017, 6, 131. [Google Scholar] [CrossRef][Green Version]
- Reynolds, A.; Ross, S.F. Complexity in de Sitter Space. Class. Quant. Grav. 2017, 34, 175013. [Google Scholar] [CrossRef]
- Carmi, D.; Chapman, S.; Marrochio, H.; Myers, R.C.; Sugishita, S. On the Time Dependence of Holographic Complexity. JHEP 2017, 11, 188. [Google Scholar] [CrossRef]
- Couch, J.; Eccles, S.; Fischler, W.; Xiao, M.L. Holographic complexity and noncommutative gauge theory. JHEP 2018, 3, 108. [Google Scholar] [CrossRef]
- Yang, R.Q.; Niu, C.; Zhang, C.Y.; Kim, K.Y. Comparison of holographic and field theoretic complexities for time dependent thermofield double states. JHEP 2018, 2, 082. [Google Scholar] [CrossRef]
- Abt, R.; Erdmenger, J.; Hinrichsen, H.; Melby-Thompson, C.M.; Meyer, R.; Northe, C.; Reyes, I.A. Topological Complexity in AdS3/CFT2. Fortsch. Phys. 2018, 66, 1800034. [Google Scholar] [CrossRef]
- Swingle, B.; Wang, Y. Holographic Complexity of Einstein-Maxwell-Dilaton Gravity. JHEP 2018, 09, 106. [Google Scholar] [CrossRef]
- Reynolds, A.P.; Ross, S.F. Complexity of the AdS Soliton. Class. Quant. Grav. 2018, 35, 095006. [Google Scholar] [CrossRef]
- Fu, Z.; Maloney, A.; Marolf, D.; Maxfield, H.; Wang, Z. Holographic complexity is nonlocal. JHEP 2018, 2, 072. [Google Scholar] [CrossRef]
- An, Y.S.; Peng, R.H. Effect of the dilaton on holographic complexity growth. Phys. Rev. D 2018, 97, 066022. [Google Scholar] [CrossRef]
- Bolognesi, S.; Rabinovici, E.; Roy, S.R. On Some Universal Features of the Holographic Quantum Complexity of Bulk Singularities. JHEP 2018, 6, 016. [Google Scholar] [CrossRef]
- Chen, B.; Li, W.M.; Yang, R.Q.; Zhang, C.Y.; Zhang, S.J. Holographic subregion complexity under a thermal quench. JHEP 2018, 7, 034. [Google Scholar] [CrossRef]
- Abt, R.; Erdmenger, J.; Gerbershagen, M.; Melby-Thompson, C.M.; Northe, C. Holographic Subregion Complexity from Kinematic Space. JHEP 2019, 1, 012. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N.; Sugishita, S. Thoughts on Holographic Complexity and its Basis-dependence. Phys. Rev. D 2018, 98, 046002. [Google Scholar] [CrossRef]
- Flory, M.; Miekley, N. Complexity change under conformal transformations in AdS3/CFT2. JHEP 2019, 5, 003. [Google Scholar] [CrossRef]
- Couch, J.; Eccles, S.; Jacobson, T.; Nguyen, P. Holographic Complexity and Volume. JHEP 2018, 11, 044. [Google Scholar] [CrossRef]
- Hosseini Mansoori, S.A.; Jahnke, V.; Qaemmaqami, M.M.; Olivas, Y.D. Holographic Complexity of Anisotropic Black Branes. Phys. Rev. D 2019, 100, 046014. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Holographic complexity in Vaidya spacetimes. Part I. JHEP 2018, 6, 046. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Holographic complexity in Vaidya spacetimes. Part II. JHEP 2018, 6, 114. [Google Scholar] [CrossRef]
- Caceres, E.; Chapman, S.; Couch, J.D.; Hernandez, J.P.; Myers, R.C.; Ruan, S.M. Complexity of Mixed States in QFT and Holography. JHEP 2020, 3, 012. [Google Scholar] [CrossRef]
- Ben-Ami, O.; Carmi, D. On Volumes of Subregions in Holography and Complexity. JHEP 2016, 11, 129. [Google Scholar] [CrossRef]
- Abad, F.J.G.; Kulaxizi, M.; Parnachev, A. On Complexity of Holographic Flavors. JHEP 2018, 1, 127. [Google Scholar] [CrossRef]
- Brown, A.R.; Susskind, L. Second law of quantum complexity. Phys. Rev. D 2018, 97, 086015. [Google Scholar] [CrossRef]
- Bernamonti, A.; Galli, F.; Hernandez, J.; Myers, R.C.; Ruan, S.M.; Simón, J. First Law of Holographic Complexity. Phys. Rev. Lett. 2019, 123, 081601. [Google Scholar] [CrossRef]
- Bernamonti, A.; Galli, F.; Hernandez, J.; Myers, R.C.; Ruan, S.M.; Simón, J. Aspects of The First Law of Complexity. J. Phys. A Math. Theor. 2020, 53, 294002. [Google Scholar] [CrossRef]
- Cai, R.G.; Ruan, S.M.; Wang, S.J.; Yang, R.Q.; Peng, R.H. Action growth for AdS black holes. JHEP 2016, 9, 161. [Google Scholar] [CrossRef]
- Lehner, L.; Myers, R.C.; Poisson, E.; Sorkin, R.D. Gravitational action with null boundaries. Phys. Rev. D 2016, 94, 084046. [Google Scholar] [CrossRef]
- Moosa, M. Evolution of Complexity Following a Global Quench. JHEP 2018, 3, 031. [Google Scholar] [CrossRef]
- Moosa, M. Divergences in the rate of complexification. Phys. Rev. D 2018, 97, 106016. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N.; Sugishita, S. Time evolution of complexity in Abelian gauge theories. Phys. Rev. D 2017, 96, 126001. [Google Scholar] [CrossRef]
- Chapman, S.; Eisert, J.; Hackl, L.; Heller, M.P.; Jefferson, R.; Marrochio, H.; Myers, R.C. Complexity and entanglement for thermofield double states. SciPost Phys. 2019, 6, 034. [Google Scholar] [CrossRef]
- Guo, M.; Hernandez, J.; Myers, R.C.; Ruan, S.M. Circuit Complexity for Coherent States. JHEP 2018, 10, 011. [Google Scholar] [CrossRef]
- Camargo, H.A.; Caputa, P.; Das, D.; Heller, M.P.; Jefferson, R. Complexity as a novel probe of quantum quenches: Universal scalings and purifications. Phys. Rev. Lett. 2019, 122, 081601. [Google Scholar] [CrossRef]
- Doroudiani, M.; Naseh, A.; Pirmoradian, R. Complexity for Charged Thermofield Double States. JHEP 2020, 1, 120. [Google Scholar] [CrossRef]
- Chapman, S.; Chen, H.Z. Charged Complexity and the Thermofield Double State. JHEP 2021, 2, 187. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Nandy, P.; Sinha, A. Renormalized Circuit Complexity. Phys. Rev. Lett. 2020, 124, 101602. [Google Scholar] [CrossRef]
- Bhargava, P.; Choudhury, S.; Chowdhury, S.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D. Quantum aspects of chaos and complexity from bouncing cosmology: A study with two-mode single field squeezed state formalism. SciPost Phys. Core 2021, 4, 026. [Google Scholar] [CrossRef]
- Lehners, J.L.; Quintin, J. Quantum Circuit Complexity of Primordial Perturbations. Phys. Rev. D 2021, 103, 063527. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Haque, S.S.; Underwood, B. Rise of cosmological complexity: Saturation of growth and chaos. Phys. Rev. Res. 2020, 2, 033273. [Google Scholar] [CrossRef]
- Choudhury, S.; Dutta, A.; Ray, D. Chaos and Complexity from Quantum Neural Network: A study with Diffusion Metric in Machine Learning. JHEP 2021, 4, 138. [Google Scholar] [CrossRef]
- Choudhury, S.; Chowdhury, S.; Gupta, N.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D.; Singha, C.; Swain, A. Circuit Complexity From Cosmological Islands. Symmetry 2021, 13, 1301. [Google Scholar] [CrossRef]
- Adhikari, K.; Choudhury, S.; Chowdhury, S.; Shirish, K.; Swain, A. Circuit complexity as a novel probe of quantum entanglement: A study with black hole gas in arbitrary dimensions. Phys. Rev. D 2021, 104, 065002. [Google Scholar] [CrossRef]
- Adhikari, K.; Choudhury, S.; Pandya, H.N.; Srivastava, R. PGW Circuit Complexity. arXiv 2021, arXiv:2108.10334. [Google Scholar]
- Choudhury, S.; Selvam, S.P.; Shirish, K. Circuit Complexity from Supersymmetric Quantum Field Theory with Morse Function. Symmetry 2022, 14, 1656. [Google Scholar] [CrossRef]
- Bai, C.; Li, W.H.; Ge, X.H. Towards the non-equilibrium thermodynamics of the complexity and the Jarzynski identity. arXiv 2021, arXiv:2107.08608. [Google Scholar]
- Caputa, P.; Kundu, N.; Miyaji, M.; Takayanagi, T.; Watanabe, K. Liouville Action as Path-Integral Complexity: From Continuous Tensor Networks to AdS/CFT. JHEP 2017, 11, 097. [Google Scholar] [CrossRef]
- Caputa, P.; Magan, J.M. Quantum Computation as Gravity. Phys. Rev. Lett. 2019, 122, 231302. [Google Scholar] [CrossRef]
- Boruch, J.; Caputa, P.; Takayanagi, T. Path-Integral Optimization from Hartle-Hawking Wave Function. Phys. Rev. D 2021, 103, 046017. [Google Scholar] [CrossRef]
- Boruch, J.; Caputa, P.; Ge, D.; Takayanagi, T. Holographic path-integral optimization. JHEP 2021, 7, 016. [Google Scholar] [CrossRef]
- Nielsen, M.A. A Geometric Approach to Quantum Circuit Lower Bounds. arXiv 2005, arXiv:quant-ph/0502070. [Google Scholar] [CrossRef]
- Nielsen, M.A. Quantum Computation as Geometry. Science 2006, 311, 1133–1135. [Google Scholar] [CrossRef]
- Dowling, M.R.; Nielsen, M.A. The Geometry of Quantum Computation. Quantum Inf. Comput. 2008, 8, 861–899. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Dowling, M.R.; Gu, M.; Doherty, A.C. Optimal control, geometry, and quantum computing. Phys. Rev. A 2006, 73, 062323. [Google Scholar] [CrossRef]
- Watrous, J. Quantum Computational Complexity. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 7174–7201. [Google Scholar]
- Aaronson, S. The Complexity of Quantum States and Transformations: From Quantum Money to Black Holes. arXiv 2016, arXiv:1607.05256. [Google Scholar]
- Orús, R. Tensor networks for complex quantum systems. APS Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Nishioka, T.; Ryu, S.; Takayanagi, T. Holographic Entanglement Entropy: An Overview. J. Phys. A 2009, 42, 504008. [Google Scholar] [CrossRef]
- Almheiri, A.; Dong, X.; Harlow, D. Bulk Locality and Quantum Error Correction in AdS/CFT. JHEP 2015, 4, 163. [Google Scholar] [CrossRef]
- Swingle, B. Entanglement Renormalization and Holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- Caputa, P.; Magan, J.M.; Patramanis, D. Geometry of Krylov complexity. Phys. Rev. Res. 2022, 4, 013041. [Google Scholar] [CrossRef]
- Parker, D.E.; Cao, X.; Avdoshkin, A.; Scaffidi, T.; Altman, E. A Universal Operator Growth Hypothesis. Phys. Rev. X 2019, 9, 041017. [Google Scholar] [CrossRef]
- Roberts, D.A.; Stanford, D.; Streicher, A. Operator growth in the SYK model. JHEP 2018, 6, 122. [Google Scholar] [CrossRef]
- Rabinovici, E.; Sánchez-Garrido, A.; Shir, R.; Sonner, J. Operator complexity: A journey to the edge of Krylov space. JHEP 2021, 6, 062. [Google Scholar] [CrossRef]
- Barbón, J.L.F.; Rabinovici, E.; Shir, R.; Sinha, R. On The Evolution of Operator Complexity Beyond Scrambling. JHEP 2019, 10, 264. [Google Scholar] [CrossRef]
- Jian, S.K.; Swingle, B.; Xian, Z.Y. Complexity growth of operators in the SYK model and in JT gravity. JHEP 2021, 3, 014. [Google Scholar] [CrossRef]
- Dymarsky, A.; Gorsky, A. Quantum chaos as delocalization in Krylov space. Phys. Rev. B 2020, 102, 085137. [Google Scholar] [CrossRef]
- Dymarsky, A.; Smolkin, M. Krylov complexity in conformal field theory. Phys. Rev. D 2021, 104, L081702. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Caputa, P.; Magan, J.; Wu, Q. A new measure of quantum state complexity. arXiv 2022, arXiv:2202.06957. [Google Scholar]
- Shankar, R. Effective Field Theory in Condensed Matter Physics; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Cheung, C.; Creminelli, P.; Fitzpatrick, A.L.; Kaplan, J.; Senatore, L. The Effective Field Theory of Inflation. JHEP 2008, 3, 014. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Field Theory for Inflation. Phys. Rev. D 2008, 77, 123541. [Google Scholar] [CrossRef]
- Agarwal, N.; Holman, R.; Tolley, A.J.; Lin, J. Effective field theory and non-Gaussianity from general inflationary states. JHEP 2013, 5, 085. [Google Scholar] [CrossRef]
- Burgess, C.P. Intro to Effective Field Theories and Inflation. arXiv 2017, arXiv:1711.10592. [Google Scholar]
- Choudhury, S. Field Theoretic Approaches to Early Universe. Ph.D. Thesis, Indian Statistical Institute, Calcutta, India, 2016. [Google Scholar]
- Choudhury, S. Can Effective Field Theory of inflation generate large tensor-to-scalar ratio within Randall–Sundrum single braneworld? Nucl. Phys. B 2015, 894, 29–55. [Google Scholar] [CrossRef]
- Naskar, A.; Choudhury, S.; Banerjee, A.; Pal, S. EFT of Inflation: Reflections on CMB and Forecasts on LSS Surveys. arXiv 2017, arXiv:1706.08051. [Google Scholar]
- Pich, A. Effective field theory: Course. Les Houches Summer School in Theoretical Physics, Session 68: Probing the Standard Model of Particle Interactions. arXiv 1998, arXiv:hep-ph/9806303. [Google Scholar]
- Burgess, C.P. Introduction to Effective Field Theory. Ann. Rev. Nucl. Part. Sci. 2007, 57, 329–362. [Google Scholar] [CrossRef]
- Donoghue, J.F. Introduction to the effective field theory description of gravity. arXiv 1995, arXiv:gr-qc/9512024. [Google Scholar]
- Donoghue, J.F. The effective field theory treatment of quantum gravity. AIP Conf. Proc. 2012, 1483, 73–94. [Google Scholar] [CrossRef]
- Dubovsky, S.; Hui, L.; Nicolis, A.; Son, D.T. Effective field theory for hydrodynamics: Thermodynamics, and the derivative expansion. Phys. Rev. D 2012, 85, 085029. [Google Scholar] [CrossRef]
- Crossley, M.; Glorioso, P.; Liu, H. Effective field theory of dissipative fluids. JHEP 2017, 9, 095. [Google Scholar] [CrossRef]
- Choudury, S. Cosmic Microwave Background from Effective Field Theory. Universe 2019, 5, 155. [Google Scholar] [CrossRef]
- Choudhury, S.; Gharat, R.M.; Mandal, S.; Pandey, N. Circuit Complexity in an interacting quenched Quantum Field Theory. arXiv 2022, arXiv:2209.03372. [Google Scholar]
- Adhikari, K.; Choudhury, S.; Roy, A. Krylov Complexity in Quantum Field Theory. arXiv 2022, arXiv:2204.02250. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).