A New Program to Estimate the Parameters of Preston’s Equation, a General Formula for Describing the Egg Shape of Birds
Abstract
1. Introduction
2. Materials and Methods
2.1. Egg Samples and Image Processing
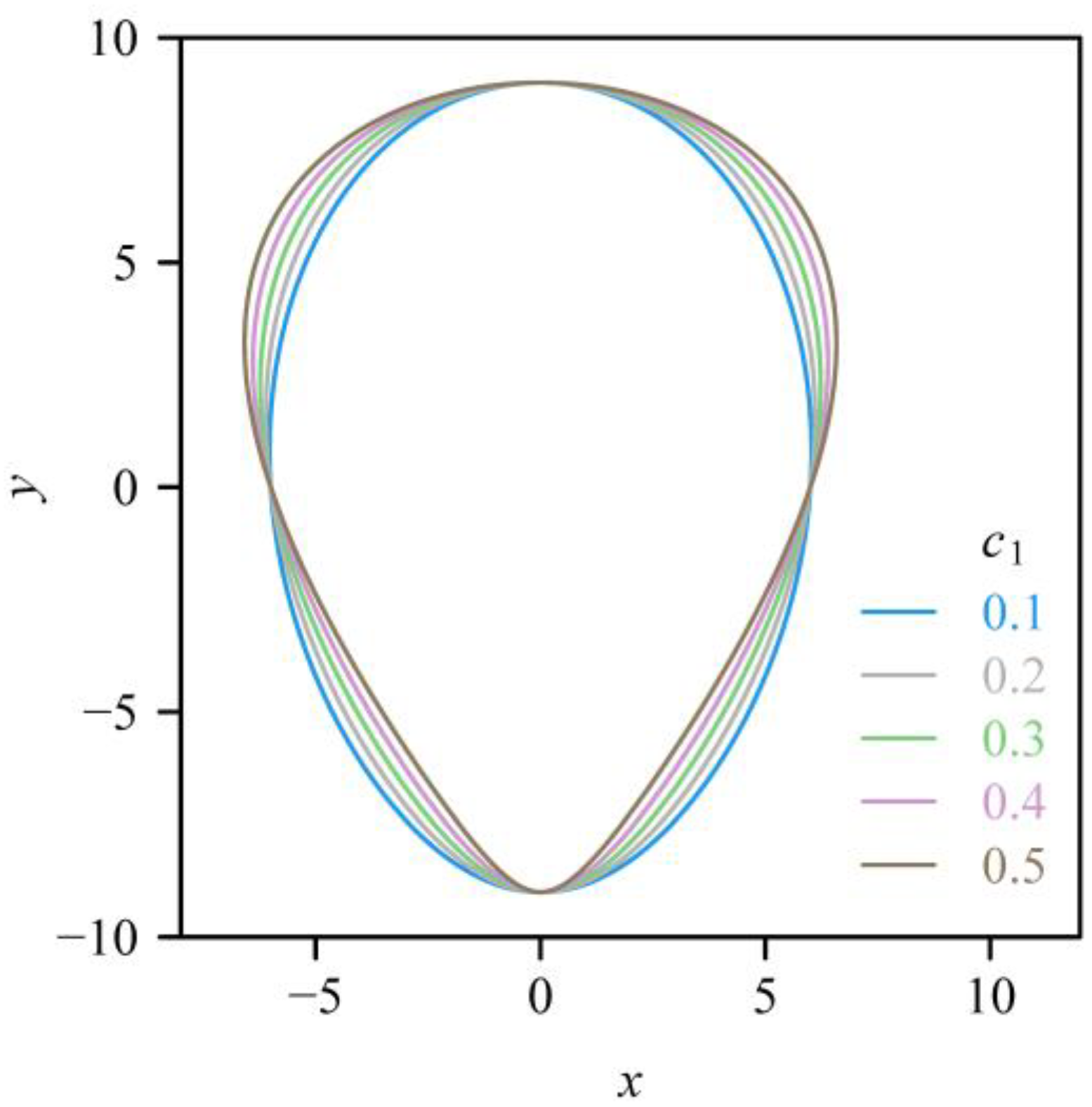
2.2. Models and Data-Fitting Approaches
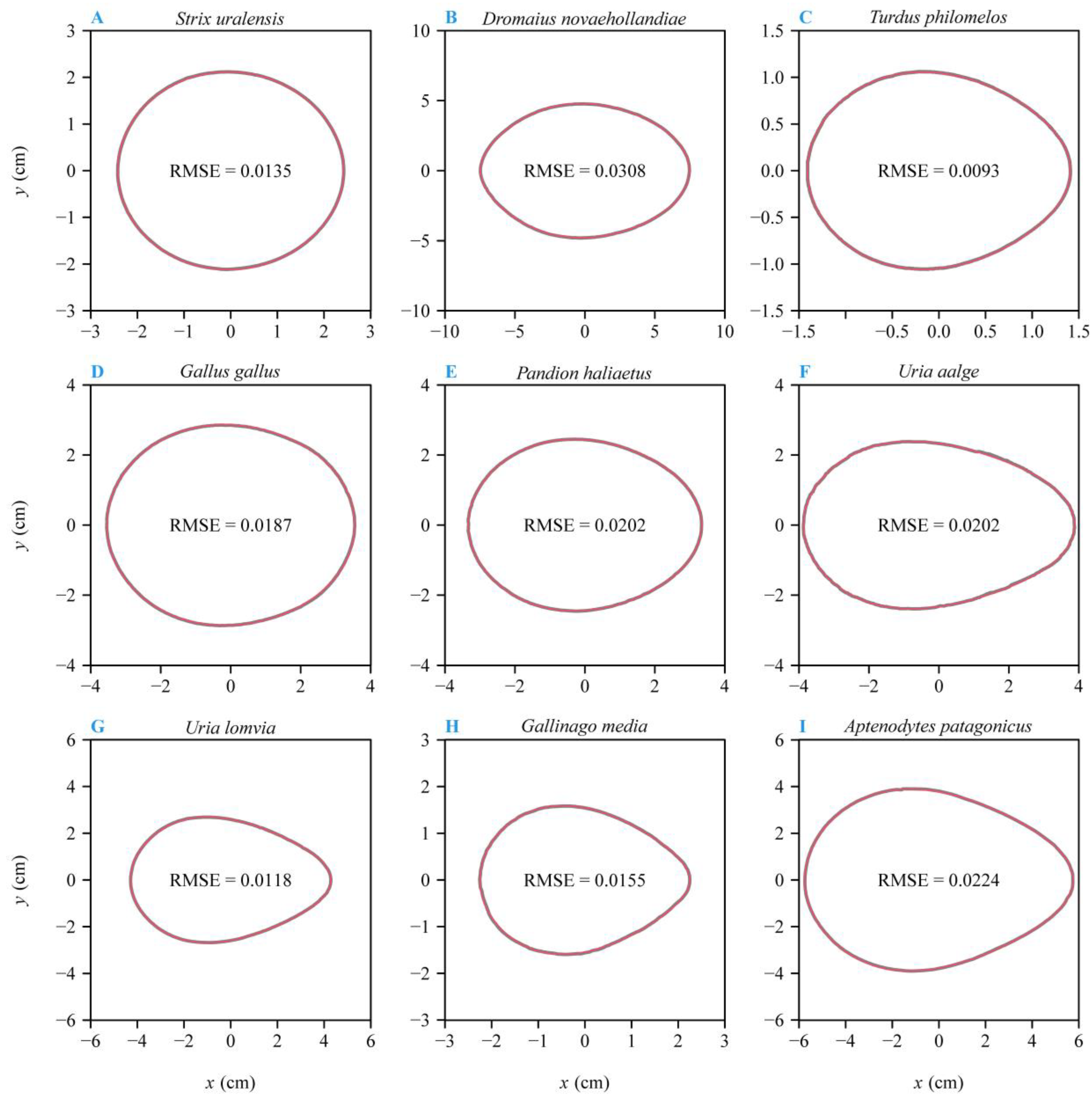
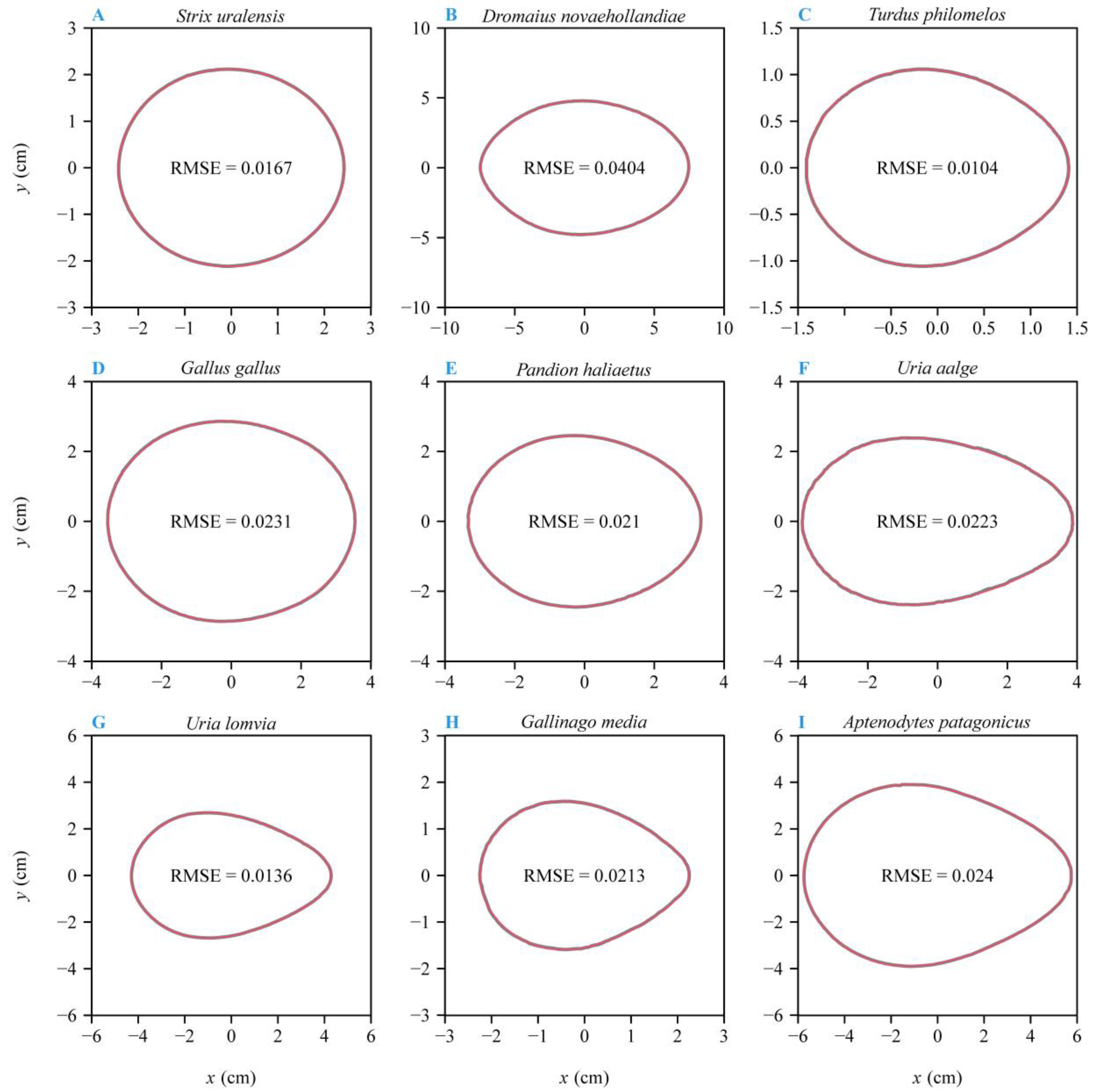
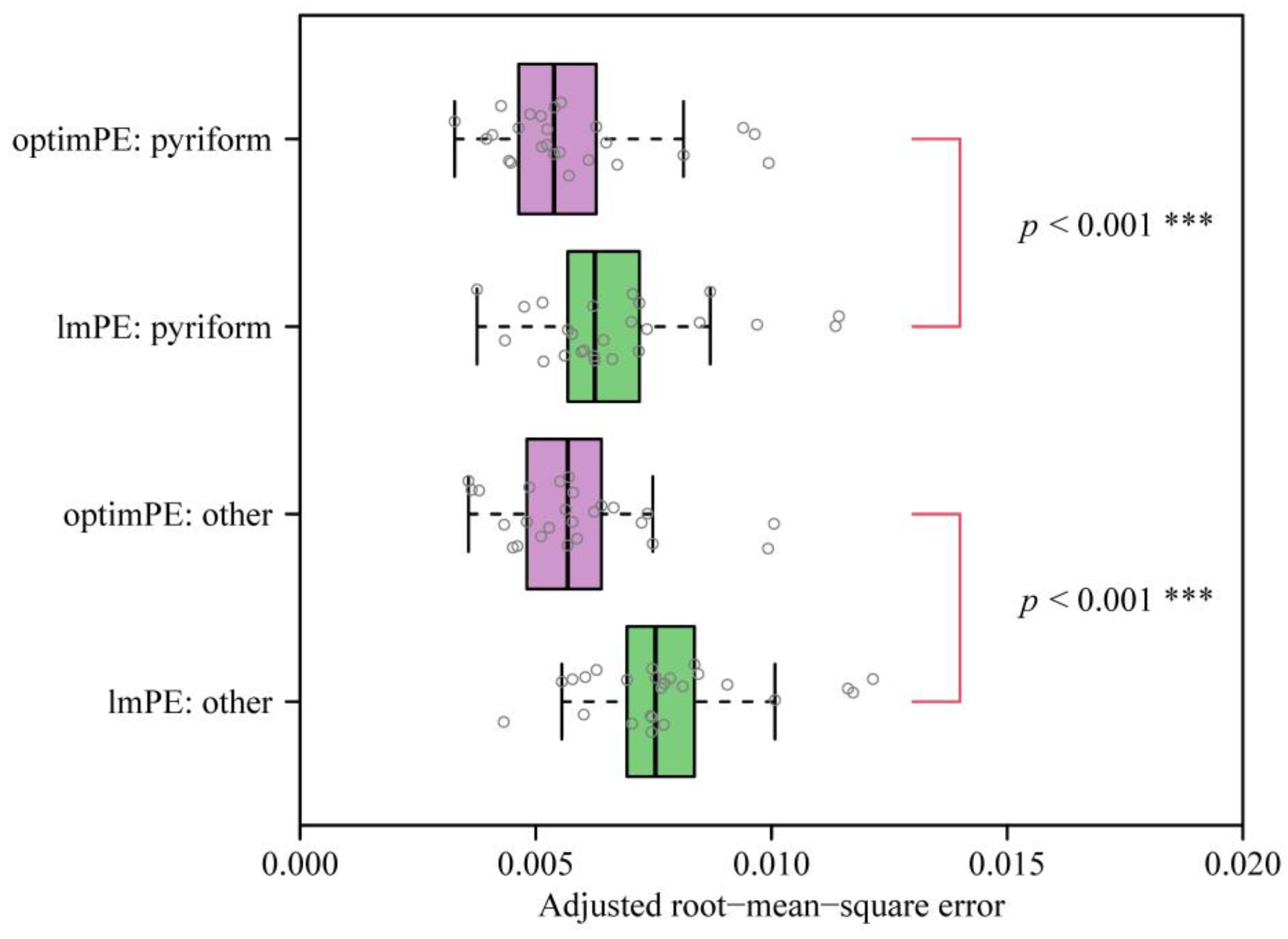
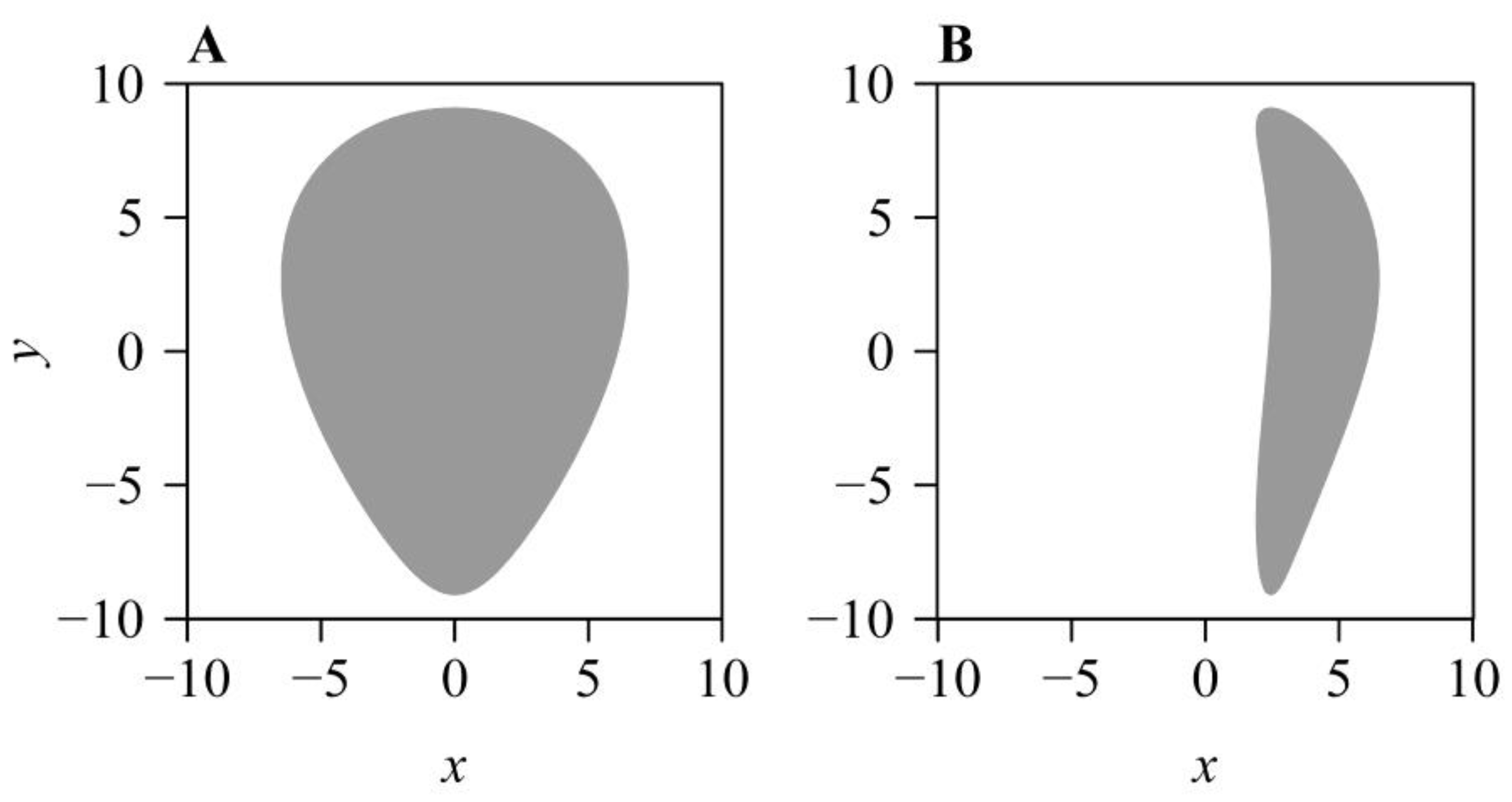
3. Results
4. Discussion
4.1. The Optimization Versus Multiple Linear Regression Method for Estimating Parameters of Preston’s Equation
4.2. The Potential Extension of Preston’s Equation to Other Egg Shapes
4.3. Recommendations for Field Biologists
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Preston, F.W. The shapes of birds’ eggs. Auk 1953, 70, 160–182. [Google Scholar] [CrossRef]
- Narushin, V.G.; Romanov, M.N.; Griffin, D.K. Egg and math: Introducing a universal formula for egg shape. Ann. N. Y. Acad. Sci. 2021, 1505, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Gielis, J.; Niklas, K.J. Comparison of a universal (but complex) model for avian egg shape with a simpler model. Ann. N. Y. Acad. Sci. 2022, 1514, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Gielis, J. A general geometric transformation that unifies a wide range of natural and abstract shapes. Amer. J. Bot. 2003, 90, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Biggins, J.D.; Montgomerie, R.; Thompson, J.E.; Birkhead, T.R. Preston’s universal formula for avian egg shape. Ornithology, 2022; 139, in press. [Google Scholar] [CrossRef]
- Biggins, J.D.; Thompson, J.E.; Birkhead, T.R. Accurately quantifying the shape of birds’ eggs. Ecol. Evol. 2018, 8, 9728–9738. [Google Scholar] [CrossRef] [PubMed]
- Todd, P.H.; Smart, I.H.M. The shape of birds’ eggs. J. Theor. Biol. 1984, 106, 239–243. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Xu, Q.; Sandhu, H.S.; Gielis, J.; Ding, Y.; Li, H.; Dong, X. Comparison of dwarf bamboos (Indocalamus sp.) leaf parameters to determine relationship between spatial density of plants and total leaf area per plant. Ecol. Evol. 2015, 5, 4578–4589. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Gielis, J.; Quinn, B.K.; Niklas, K.J.; Ratkowsky, D.A.; Schrader, J.; Ruan, H.; Wang, L.; Niinemets, Ü. ‘biogeom’: An R package for simulating and fitting natural shapes. Ann. N. Y. Acad. Sci. 2022, 1516, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Biggins, J.D.; Montgomerie, R.; Thompson, J.E.; Birkhead, T.R. Data from: Preston’s Universal Formula for Avian Egg Shape; Dryad. 2022. Available online: https://doi.org/dryad.547d7wmbz (accessed on 1 October 2022).
- Shi, P.; Ratkowsky, D.A.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. A general leaf area geometric formula exists for plants – Evidence from the simplified Gielis equation. Forests 2018, 9, 714. [Google Scholar] [CrossRef]
- Su, J.; Niklas, K.J.; Huang, W.; Yu, X.; Yang, Y.; Shi, P. Lamina shape does not correlate with lamina surface area: An analysis based on the simplified Gielis equation. Glob. Ecol. Conser. 2019, 19, e00666. [Google Scholar] [CrossRef]
- Shi, P.; Chen, L.; Quinn, B.K.; Yu, K.; Miao, Q.; Guo, X.; Lian, M.; Gielis, J.; Niklas, K.J. A simple way to calculate the volume and surface area of avian eggs. Ann. N. Y. Acad. Sci. 2022; under review. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 1 June 2022).
- Maritz, M.F.; Douglas, R.M. Shape quantization and the estimation of volume and surface area of reptile eggs. J. Herpetol. 1994, 28, 281–291. [Google Scholar]
- D’Alba, L.; Goldenberg, J.; Nallapaneni, A.; Parkinson, D.Y.; Zhu, C.; Vanthournout, B.; Shawkey, M.D. Evolution of eggshell structure in relation to nesting ecology in non-avian reptiles. J. Morphol. 2021, 282, 1066–1079. [Google Scholar] [CrossRef] [PubMed]
- Church, S.H.; Donoughe, S.; de Medeiros, B.A.S.; Extavour, C.G. Insect egg size and shape evolve with ecology but not developmental rate. Nature 2019, 571, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Li, Y.; Niklas, K.J.; Gielis, J.; Ding, Y.; Cao, L.; Shi, P. A superellipse with deformation and its application in describing the cross-sectional shapes of a square bamboo. Symmetry 2020, 12, 2073. [Google Scholar] [CrossRef]
- Bridge, E.S.; Boughton, R.K.; Aldredge, R.A.; Harrison, T.J.E.; Bowman, R.; Schoech, S.J. Measuring egg size using digital photography: Testing Hoyt’s method using Florida Scrub-Jay eggs. J. Field Ornithol. 2007, 78, 109–116. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Wang, L.; Quinn, B.K.; Gielis, J. A New Program to Estimate the Parameters of Preston’s Equation, a General Formula for Describing the Egg Shape of Birds. Symmetry 2023, 15, 231. https://doi.org/10.3390/sym15010231
Shi P, Wang L, Quinn BK, Gielis J. A New Program to Estimate the Parameters of Preston’s Equation, a General Formula for Describing the Egg Shape of Birds. Symmetry. 2023; 15(1):231. https://doi.org/10.3390/sym15010231
Chicago/Turabian StyleShi, Peijian, Lin Wang, Brady K. Quinn, and Johan Gielis. 2023. "A New Program to Estimate the Parameters of Preston’s Equation, a General Formula for Describing the Egg Shape of Birds" Symmetry 15, no. 1: 231. https://doi.org/10.3390/sym15010231
APA StyleShi, P., Wang, L., Quinn, B. K., & Gielis, J. (2023). A New Program to Estimate the Parameters of Preston’s Equation, a General Formula for Describing the Egg Shape of Birds. Symmetry, 15(1), 231. https://doi.org/10.3390/sym15010231








